扩展功能
文章信息
- 邱欣, 洪皓珏, 杨青, 肖上霖
- QIU Xin, HONG Hao-jue, YANG Qing, XIAO Shang-lin
- 基于APRIORI-GBDT算法的沥青路面路表温度预测
- Prediction of Temperature of Asphalt Pavement Surface Based on APRIORI-GBDT Algorithm
- 公路交通科技, 2019, 36(5): 1-10, 19
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 1-10, 19
- 10.3969/j.issn.1002-0268.2019.05.001
-
文章历史
- 收稿日期: 2018-09-29
冰冻灾害性天气是影响道路交通安全的主要因素之一,道路表面温度和状态的变化会直接影响道路的交通安全水平和通行效率,而气象条件是影响道路表面温度变化的重要因素。因此,如何识别影响道路表面温度变化的关键气象因素,准确预测道路表面温度变化规律对道路交通安全有重要的理论和现实意义。
目前,国内外研究者针对道路表面温度的变化规律进行了广泛研究,研究内容主要集中于道路表面温度的预测。1975年,Barder[1]对道路表面温度进行了统计分析,并通过热传导方程建立了道路表面最高温度预估模型。随后,美国的SHRP研究计划开始推行,大量道路表面温度实测数据和气象数据得到积累,许多研究人员开始采用回归分析方法建立道路表面温度预估模型。如Huber[2]为克服热平衡方程需要反复试算的不足之处,对当地气温和道路表面温度进行了回归分析,最终建立了相对简单的道路表面最高温度回归预测模型。随着道路表面温度预估模型的逐步完善,各国研究者开始注重对模型输入参数的选择,如Hermansson[3]与Grimbacher[4]等人选择相关性较强的气象因素建立道路表面温度预估模型;又如Krsmanc[5]提出了一种基于分步线性回归分析的纯统计方法对道路表面温度进行预测,并给出了输入参数的选择依据。综上所述,当前道路表面温度研究方法仍处于统计分析和线性回归分析阶段,该类方法的模型简单,在多数研究中均能进行准确的预测,但随着数据量的增加,模型的建立过程变得复杂,加之人为选择构建模型所需输入参数等不确定性因素的存在,使预测模型的精确度难以保证。因此,如何准确地识别相关因素,并建立高精确度的沥青路面路表温度(以下简称路表温度)预测模型是本研究重点。
机器学习的出现打破了传统方法的局限性,机器学习算法在关联规则挖掘及模型的集成预测方面都表现出了优秀的性能。关联规则(Association Rules)挖掘属于机器学习中的无监督学习算法,Apriori算法是其代表。该算法最早由Agrawal[6]提出,属于一种布尔关联规则频繁项集挖掘算法,Apriori算法通过循环迭代的方式扫描数据库中的频繁项集,并提取关联规则,挖掘因素间的相关关系。该算法起初用于分析顾客购买商品之间的关联性,随后许多学者如Borgelt[7]等开始将其应用于数据间的关联规则分析,并发现Apriori算法在封闭数据集关联规则挖掘上准确率高,相比于Eclat算法有较大优势。又如Guo[8]通过研究发现,Apriori算法可以有效地挖掘风速和其他气象因素之间的关联规则,且挖掘结果在风速预测值校正方面表现出强大的能力。但是,随着数据量的增加,Apriori算法运算效率低的问题变得突出,于是该算法的改进形式得到了快速发展,如Park[9]提出了一种基于Hash的Apriori算法改进形式,通过过滤候选项集中的非频繁项集来提高关联规则挖掘效率;又如Han[10]通过改进Apriori算法的运算过程,提出了FP-growth方法,通过搜索数据集中的频繁项和包含该频繁项的子数据集中的其他频繁项,确定频繁项集,提高了关联规则挖掘的效率。可以看出,Apriori算法在数据关联规则挖掘方面应用广泛,且在关联性分析领域表现出了良好的应用效果,由于Apriori算法相比于FP-growth得到的关联规则结果更为全面,本研究采用基于Hash改进形式的Apriori算法挖掘气象因素与路表温度之间的关联性。
梯度提升树(GBDT)最早由Firedman[11]教授提出,属于机器学习中的决策树集成算法,在梯度提升树模型的建立过程中,串联的决策树均学习前一棵树的预测结果和残差,并往预测结果残差减少的方向迭代,以逐步提高模型的预测精度[12-13]。近年来,越来越多的学者开始选择以迭代的算法框架提升预测模型的准确率,这使得梯度提升树逐渐成为预测领域的新方向[14]。例如,Ding[15]选择梯度提升树对地铁客流量进行预测,预测结果表明:GBDT模型在改善短期地铁客流量预测方面具有相当大的优势。同样,Yang[16]也提出了一种基于梯度提升树的短期交通预测方法,并得出了GBDT模型的预测误差要小于SVM和BPNN,且预测效果优异的结论。鉴于GBDT算法在预测领域内的广泛应用,本研究利用GBDT建立路表温度预测模型,并与随机森林(RF)和线性回归(LR)所建温度预测模型进行对比分析,以确定GBDT模型在路表温度预测领域的适用性和使用性能。
基于此,本研究选取浙中金华地区2015年12月至2018年1月冬季小时气象观测数据,在Apriori算法挖掘气象观测数据中气象数据与路表温度数据之间关联规则的基础上,识别出了影响路表温度变化的关键气象因素,并通过建立基于梯度提升树的路表温度预测模型验证了GBDT模型的优势。研究成果为冬季路表温度准确预测提供了技术支撑。
1 数据预处理 1.1 数据清洗气象观测数据库内数据量庞大,在采集和存储的过程中难免会存在缺失和错误的情况,数据清洗旨在处理数据集中的异常数据,规范数据集形式,为数据挖掘研究提供数值准确、形式标准的数据集。本研究以Python平台为基础,利用pandas函数读取气象数据,并用dropna函数删除缺失数据所在的数据组,得到了3 261组有效数据。
1.2 数据离散化研究用于关联分析的气象观测数据主要包括:气温(T),露点温度(D),气压(P),相对湿度(H),风速(W),降水量(R),能见度(V)和路表温度(APT)。Apriori进行数据的关联性分析前,需要对各数据进行离散化处理[8]。气象观测数据的离散化通常以各气象观测数据的国家分级标准为基础,并通过扩大等级划分区间,减少各因素的分级数量,以提升Apriori算法的运算效率。
本研究将《短期天气预报》(GB/T 21984—2008)[17]作为气象观测数据的等级划分标准,结合温度、风力、降水量和水平能见度等国家分级标准对各气象因素进行等级划分。限于露点温度、气压、相对湿度和路表温度等因素的等级划分没有直观的参考标准,为得到较好的关联规则,通过分析4个因素的取值范围确定其等级划分,并利用关联规则挖掘部分中的关联规则挖掘结果对等级划分进行修正,最后得到的气象观测数据等级划分标准如表 1所示。
| 气象观测数据 | 等级1 | 等级2 | 等级3 | 等级4 |
| T/℃ | T≤0 | 0 < T≤13.9 | 13.9 < T≤21.9 | 21.9 < T |
| D/℃ | D≤-9.9 | -9.9 < D≤0 | 0 < D≤9.9 | 9.9 < D |
| P/MPa | P≤101 | 1 010 < P≤102 | 1 020 < P≤103 | 103 < P |
| H/% | H≤25 | 25 < H≤50 | 50 < H≤75 | 75 < H |
| W/(m·s-1) | W≤3.4 | 3.4 < W≤10.7 | 10.7 < W≤20.7 | 20.7 < W |
| R/(mm·h-1) | R≤2.6 | 2.6 < R≤8.1 | 8.1 < R≤16 | 16 < R |
| V/m | V≤50 | 50 < V≤500 | 500 < V≤2 000 | 2 000 < V |
| APT/℃ | APT≤0 | 0 < APT≤10 | 10 < APT≤20 | 20 < APT |
将数据库内的数据按表 1中的等级划分标准进行赋值转换,得到用于关联规则挖掘的事务集。以1 h内8个气象因素的等级作为一个事务项I,可表示为I={Ti,Di,Pi,Hi,Wi,Ri,Vi,APTi},i为各因素的等级。例如,2015年12月5日8:00的数据项为{6.4,1.9,1 020.9,73,2,0.2,94,8.1},每个数据分别对应{气温,露点温度,气压,相对湿度,风速,降水量,能见度,路表温度},参照表 1可将数据项转换为事务项I={T2,D3,P3,H3,W1,R1,V2,APT2}。依据该转换规则,将数据库内所有数据项转换成事务项后即可得到用于关联规则挖掘的事务集。
2 关联规则挖掘 2.1 关联规则挖掘过程Apriori属于两阶段递推算法,第1阶段是扫描事务集找出所有满足最小支持度的频繁项集,第2阶段是从频繁项集中提取满足最小置信度的关联规则。所以,在关联规则挖掘前,需要人为预设最小支持度和最小置信度[6]。预设的最小支持度越小,保留的频繁项集越多,可提取的关联规则越多,关联规则置信度的取值范围越广,因此需要设定合理的最小置信度约束关联规则的置信度取值,支持度(support)与置信度(confident)的计算公式如下:
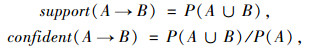
|
式中,支持度表示事件A和事件B同时出现的概率,置信度表示在事件A出现的前提下事件B同时出现的概率。
利用Apriori算法扫描频繁项集的过程中有两个主要步骤:连接和剪枝。在连接过程中,Apriori算法通过逐层迭代的搜索方式穷尽事务集中的所有项集,即利用K项集搜索K+1项集。剪枝过程与连接过程交叉进行,其目的是将不满足最小支持度的项集舍弃,保留频繁项集。该过程的核心思想是:所有频繁项集的非空子集都是频繁的,非频繁项集的超集一定是非频繁的[18]。
利用Apriori算法找到所有频繁项集后,基于各频繁项集可提取不同关联规则,将所有不满足最小置信度的关联规则舍弃,保留的关联规则即为Apriori算法的挖掘结果。在此过程中,高维关联规则的生成以低维关联规则为基础,相当于是对低维关联规则准确性的条件补充,且同时满足最小支持度和最小置信度的关联规则称为强关联规则。
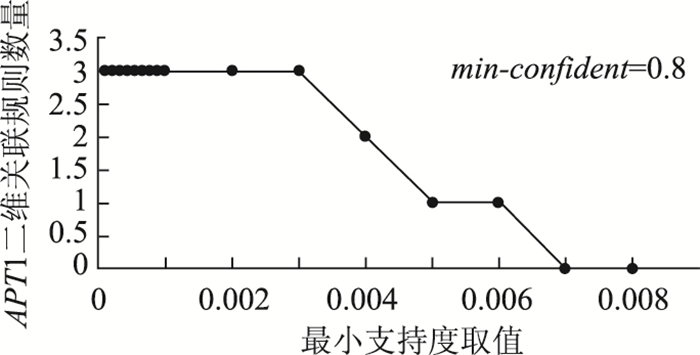
2.2 关联规则挖掘结果关联规则分析中将置信度大于0.75的规则称为有用规则[19],且为使提取的关联规则拥有较高的准确性,最小置信度(min_confident)的取值一般要大于0.75,因此本研究将最小置信度设定为0.8。鉴于浙中金华地区冬季路表温度处于0 ℃以下的天气极少,为保证关联规则挖掘结果的全面性和可靠性,尤其需要关注路表温度低于零度的关联规则。因此,需用Apriori算法对事务集进行大量试算,以确定最小支持度(min_support)的取值,其试算结果如图 1所示。当支持度不大于0.003时,路表温度为零下的二维关联规则一直稳定为3条,因此本研究将最小支持度设定为0.003。
|
| 图 1 Apriori算法试算结果 Fig. 1 Apriori algorithm trial result |
| |
对于Apriori算法挖掘得到的全部关联规则,后项为路表温度(APT)的关联规则是本研究分析的重点。研究中用于关联规则挖掘的因素有8个,挖掘结果可生成7个维度的关联规则,通过分析各维关联规则间的关系发现:四维关联规则已能涵盖所有气象因素,且从五维关联规则开始出现了大量无效关联规则。因此,研究中重点进行了一、二、三、四维关联规则的分析。值得一提的是,无效关联规则的存在会直接影响分析结果的准确性,分析过程中应对其进行剔除。例如,在三维关联规则的分析中,如果二维关联规则{H3, P4}→APT1的置信度为0.833 3,且三维关联规则{H3, W1, P4}→APT1的置信度也为0.833 3,则该三维关联规则被判定为无效关联规则,需要将其剔除。
Apriori算法挖掘一共得到了58条关联规则,包括7条后项为APT1关联规则,28条后项为APT2关联规则,22条后项为APT3关联规则和1条后项为APT4关联规则。其中,APT1代表路表温度小于等于0 ℃的等级,APT2代表路表温度在0~13.9 ℃之间的等级,APT3代表路表温度在13.9~21.9 ℃之间的等级,APT4代表路表温度高于21.9 ℃的等级。
表 2为后项为APT1的关联规则,一共7条。其中,二维关联规则3条,三维关联规则4条,无一维关联规则,四维关联规则全为无效关联规则。
| 编号 | 前项 | 后项 | 置信度 |
| 1 | H3, D1 | APT1 | 1.0 |
| 2 | H4, T1 | APT1 | 0.923 0 |
| 3 | H3, P4 | APT1 | 0.833 3 |
| 4 | P3, H3, T1 | APT1 | 0.916 6 |
| 5 | D1, W1, T1 | APT1 | 0.894 7 |
| 6 | P4, W1, D1 | APT1 | 0.85 |
| 7 | P4, W1, T1 | APT1 | 0.823 5 |
表 3为后项为APT2的关联规则,一共28条。其中,二维关联规则2条,三维关联规则12条,四维关联规则14条,无一维关联规则。
| 编号 | 前项 | 后项 | 置信度 |
| 1 | P3, R1 | APT2 | 0.822 5 |
| 2 | D3, R2 | APT2 | 0.818 1 |
| 3 | P3, V4, R1 | APT2 | 1.0 |
| 4 | P1, V3, D3 | APT2 | 1.0 |
| 5 | W1, R2, D3 | APT2 | 1.0 |
| 6 | P3, R1, D3 | APT2 | 0.903 8 |
| 7 | V4, R1, D3 | APT2 | 0.838 7 |
| 8 | H3, T2, D2 | APT2 | 0.837 2 |
| 9 | P3, V3, D3 | APT2 | 0.833 3 |
| 10 | P3, D3, H4 | APT2 | 0.819 9 |
| 11 | P3, R1, W1 | APT2 | 0.819 6 |
| 12 | P3, R1, H4 | APT2 | 0.816 6 |
| 13 | P3, T2, H4 | APT2 | 0.809 3 |
| 14 | P3, D2, H3 | APT2 | 0.802 1 |
| 15 | V4, T2, D2, H4 | APT2 | 1.0 |
| 16 | P3, R1, W1, D3 | APT2 | 0.901 9 |
| 17 | P3, R1, H4, D3 | APT2 | 0.9 |
| 18 | V4, R1, H4, D3 | APT2 | 0.844 4 |
| 19 | V4, R1, W1, D3 | APT2 | 0.831 4 |
| 20 | P3, T2, D2, H3 | APT2 | 0.829 2 |
| 21 | H3, T2, D2, W1 | APT2 | 0.829 2 |
| 22 | P3, V4, T2, H4 | APT2 | 0.822 4 |
| 23 | P3, V3, D3, H4 | APT2 | 0.82 |
| 24 | P3, W1, H4, D3 | APT2 | 0.818 5 |
| 25 | V4, W2, H4, D3 | APT2 | 0.818 1 |
| 26 | P3, V4, D3, H4 | APT2 | 0.817 3 |
| 27 | P3, W1, R1, H4 | APT2 | 0.813 5 |
| 28 | P3, T2, W1, H4 | APT2 | 0.807 9 |
表 4为后项为APT3的关联规则,一共22条。其中,一维关联规则1条,二维关联规则11条,三维关联规则7条,四维关联规则3条。
| 编号 | 前项 | 后项 | 置信度 |
| 1 | D4 | APT3 | 0.873 5 |
| 2 | D4, P1 | APT3 | 1.0 |
| 3 | D4, R1 | APT3 | 1.0 |
| 4 | D4, T2 | APT3 | 1.0 |
| 5 | D4, V3 | APT3 | 1.0 |
| 6 | D4, V2 | APT3 | 1.0 |
| 7 | D4, H4 | APT3 | 0.986 5 |
| 8 | V2, R1 | APT3 | 0.958 3 |
| 9 | T3, H4 | APT3 | 0.909 0 |
| 10 | D4, W1 | APT3 | 0.869 8 |
| 11 | P2, D4 | APT3 | 0.866 6 |
| 12 | P2, V2 | APT3 | 0.846 1 |
| 13 | D4, H4, W1 | APT3 | 0.986 1 |
| 14 | P2, D4, H4 | APT3 | 0.985 7 |
| 15 | D4, V4, H4 | APT3 | 0.971 0 |
| 16 | P2, V2, R1 | APT3 | 0.954 5 |
| 17 | V2, R1, D3 | APT3 | 0.909 0 |
| 18 | V4, T3, H4 | APT3 | 0.888 8 |
| 19 | P2, D4, W1 | APT3 | 0.862 5 |
| 20 | P2, D4, W1, H4 | APT3 | 0.985 1 |
| 21 | P2, D4, V4, H4 | APT3 | 0.970 5 |
| 22 | D4, V4, W1, H4 | APT3 | 0.969 2 |
表 5为后项为APT4的关联规则,由于冬季路表温度处于APT4等级的天气极少,挖掘结果只得到了1条二维关联规则,更高维的关联规则均为无效关联规则。
2.3 关联规则分析
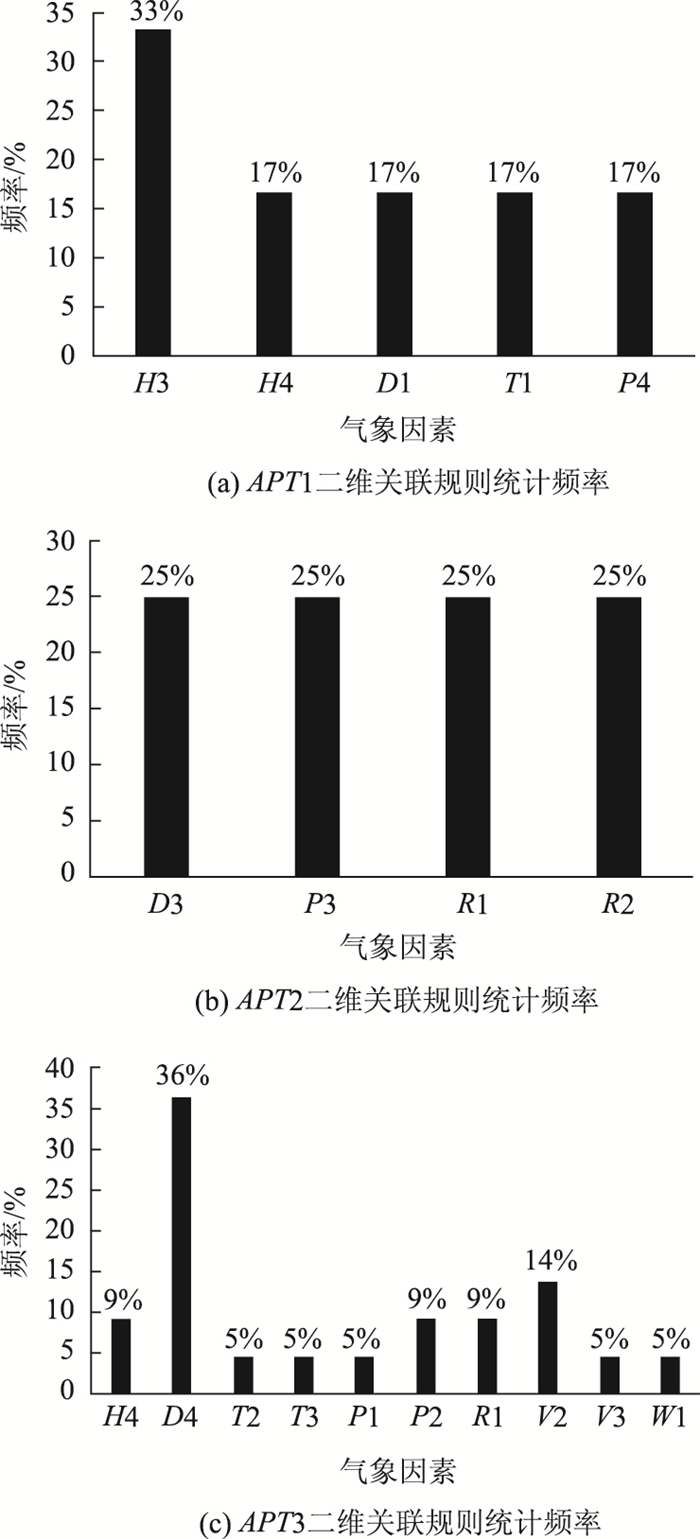
二维关联规则统计分析结果如图 2所示,分析结果发现:不同路表温度等级的二维关联规则中,前项均出现了露点温度D和气压P两个气象因素,且两者的等级都随着路表温度等级APT的变化而变化,可知露点温度与气压是影响路表温度变化的2个关键因素。
|
| 图 2 二维关联规则统计分析结果 Fig. 2 Statistical analysis result of 2D association rules |
| |
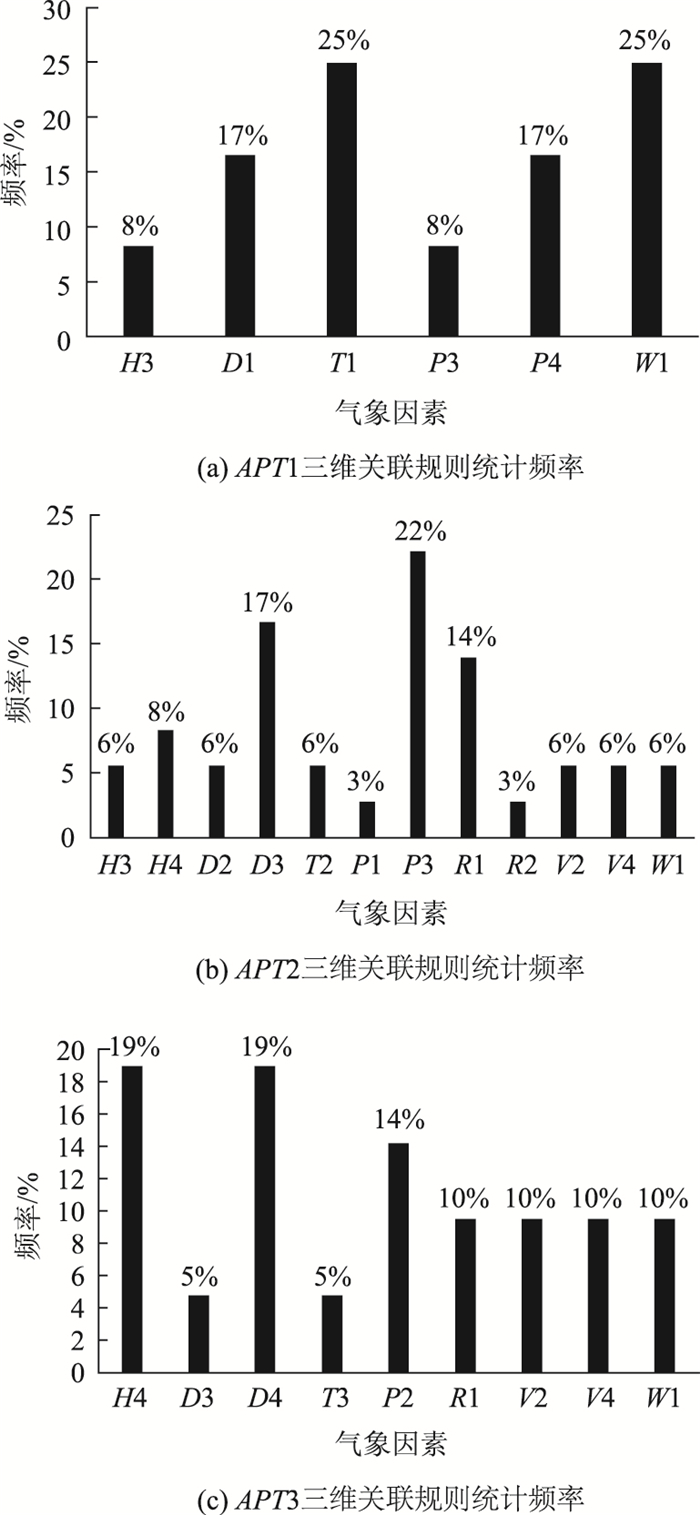
三维关联规则统计分析结果如图 3所示,分析结果发现:相对湿度H和气温T两个因素在不同路表温度等级关联规则中均有出现,且都随着路面路表温度等级的变化而变化,统计结果表明相对湿度和气温同样也是影响路表温度变化的2个关键气象因素。然而风速W、能见度V和降水量R未出现类似规律,则仍无法判定是否为相关因素。
|
| 图 3 三维关联规则统计分析结果 Fig. 3 Statistical analysis results of 3D association rules |
| |
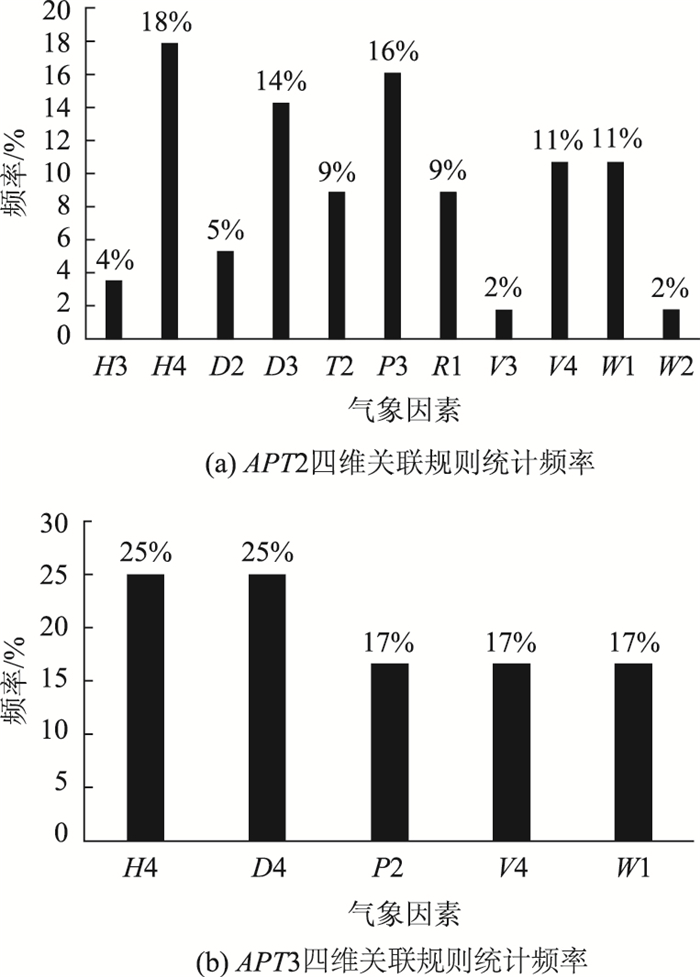
四维关联规则统计分析结果如图 4所示,结合三维关联规则统计分析结果,深入分析风速W、能见度V和降水量R与路表温度的关联性,分析结果发现:风速、能见度和降水量的等级不随路表温度等级的变化而变化,且能见度V与降水量R两个因素均未在后项为APT1的关联规则中出现,则可以判定风速、能见度和降水量不是影响路表温度变化的关键气象因素。
|
| 图 4 四维关联规则统计分析结果 Fig. 4 Statistical analysis result of 4D association rules |
| |
分析结果中的一维关联规则和后项为APT4的关联规则均只有一条,不再单独作图分析。同理,由{D4}→APT3和{H3, D4}→APT4两条关联规则也可得出已知结论:露点温度D和相对湿度H与路表温度具有强相关关系。由上述关联规则分析结果可知,影响路表温度变化的关键气象因素主要有4个,分别是:露点温度、气压、相对湿度和气温。
2.4 关联规则挖掘结果验证为验证Apriori关联规则挖掘结果的准确性,对气象数据与路表温度数据之间的关系进行线性拟合,并计算皮尔逊(Pearson)相关系数。其中,Pearson相关系数主要用于度量两个变量之间的线性相关程度,其值介于-1和1之间,相关系数绝对值大小表示的相关程度规则如下:区间[0,0.2]内表示极弱相关或不相关;区间(0.2,0.4]内表示弱相关;区间(0.4,0.6]内表示中等程度相关;区间(0.6,0.8]内表示强相关;区间(0.8,1]内表示极强相关,其计算公式如式(1)所示。
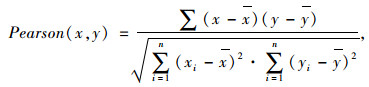
|
(1) |
式中,x和y为两个独立变量;x和y为两独立变量的均值;n为变量个数;i为变量序号。
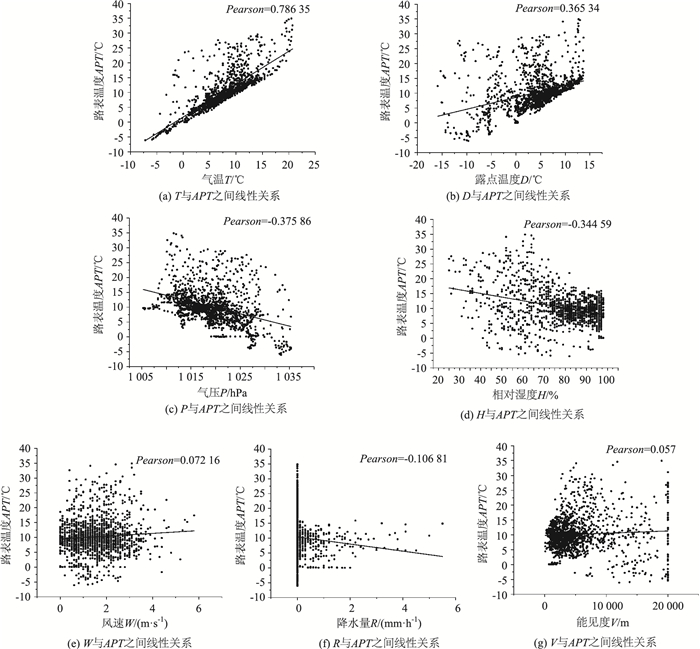
各气象数据与路表温度数据的线性拟合图如图 5所示,各图右上角为对应气象数据与路表温度数据的Pearson相关系数。
|
| 图 5 各气象因素与路表温度之间线性关系 Fig. 5 Linear relationship between meteorological factors and road surface temperature |
| |
结合直线拟合图和Pearson相关系数可知:露点温度、气压、相对湿度和气温对路表温度的变化有较大影响,该结果与Apriori算法得到的结论一致。由此可见,Apriori算法在关联规则挖掘方面具有较高的准确性,且与线性拟合方法相比,具有无需作图或计算相关系数即可得到不同因素间相关关系的优势,极大提高了关联性分析的效率。
3 路表温度预测本部分研究以Apriori算法的关联分析结果为基础,将露点温度、气压、相对湿度和气温作为输入变量,路表温度作为输出变量,建立基于梯度提升树(GBDT)的路表温度预测模型,并引入随机森林(RF)和线性回归(LR)2个算法进行对比分析。3个模型建立及预测过程均依托Python平台的sklearn库实现。
3.1 预测模型建立过程以浙中金华地区冬季气象观测数据作为模型的数据样本,利用Python平台中的train_test_split函数从3 261组气象数据中随机选取3 221组数据作为训练样本建立路表温度预测模型,并将剩余的40组数据作为测试样本验证所建模型的预测效果。
(1) 梯度提升树
GBDT属于机器学习,是一种基于决策树的集成算法,由分类回归树(CART),梯度迭代(Gradient Boosting)以及缩减(Shrinkage)组成。GBDT中所有分类回归树呈“串联”状态,且各分类回归树不能无限生长;Boosting是Valiant [20]提出的一种分类学习方法,梯度迭代则是基于Boosting的一种算法集成框架;缩减用于控制模型的学习速率,缩减的思想认为走一小步比走一大步所产生的偏差要小,本质上是为了放慢模型的学习过程,防止过拟合。GBDT的核心思想是:级联的回归树都学习前一棵树的预测结果和残差,控制学习速率,往残差减小的方向进行梯度迭代,其运算思路如图 6所示,图中Tn表示第n棵分类回归树的预测结果。

|
| 图 6 GBDT运算过程图 Fig. 6 GBDT operation process |
| |
假设GBDT模型的训练集为(X,Y),其中输入变量X包括露点温度、气压、相对湿度和气温4个因素,输出变量Y是路表温度。在建模过程中,预测误差的控制通常由损失函数完成,对于连续数据,误差平方和是Boosting迭代框架中的经典损失函数[16],其方程如式(2)所示。
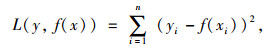
|
(2) |
式中,x为输入变量; y为输出变量; f(x)为预测值; i为迭代次数。
在Boosting迭代框架下,经M次迭代后的GBDT模型预测结果如式(3)所示,其中f0(x)为初始预测值,fi(x)(i=1, 2, …, M)为第i次迭代的函数增量,预测值f(x)为初始预测值和各函数增量的和。
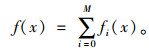
|
(3) |
在GBDT预测模型的建立过程中,为提高其精确度,将预测结果往残差减少的梯度方向上迭代是建模的终极目标。因此,在梯度迭代过程中,需选择损失函数下降最快的方向作为梯度方向,第m次迭代的最优梯度方向计算公式如式(4)所示。同时,每次迭代最优步长βm的计算公式如式(5)所示,其中hm(x)为第m次迭代所创建的分类回归树,则经m次迭代后的预测结果可表示为式(6)。
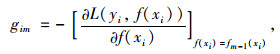
|
(4) |
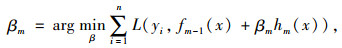
|
(5) |
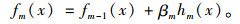
|
(6) |
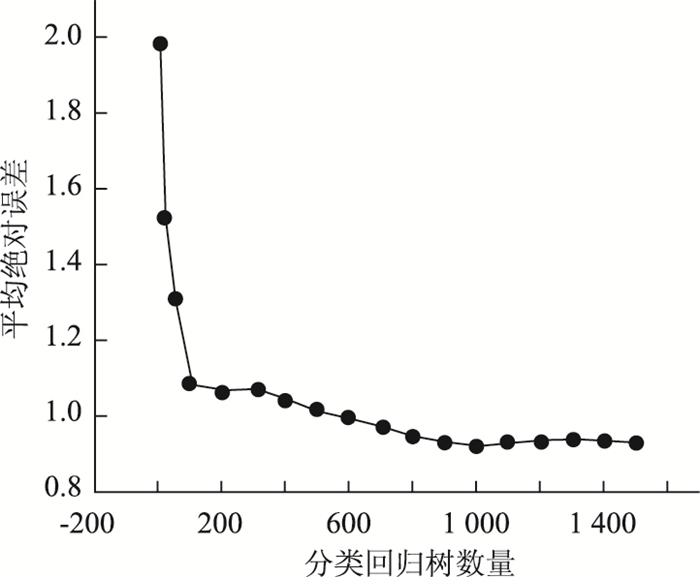
在利用Python平台建立模型的过程中,GBDT模型除了需要设置梯度迭代框架的学习步长(learning)、损失函数(loss)以及最大迭代次数(n-estimators)3个主要参数外,还需设置分类回归树的深度(max-depth)以及最大特征数(max-features)2个重要参数。模型学习步长的默认参数为0.1,本研究为了减慢模型的学习速率,提高模型精确度,将learning设置为0.01。损失函数用于计算预测结果的残差,本研究选用的是均方损失函数,如式(2)所示。由于训练样本中只有4个特征,且均为相关因素,因此将max-features设置为None,表示全部特征都会用于模型的建立。在此基础上,先将分类回归树的深度设为默认值,通过多次试算来确定最大迭代次数的取值。由图 7可知,当分类回归树的数量达到1 000后,GBDT预测结果的平均绝对误差趋于稳定,因此将模型的最大迭代次数设定为1 000。同理,对分类回归树的深度进行试算,由图 8可知,当树深度为4时,预测结果的平均误差最小,因此将max-depth设定为4。
|
| 图 7 平均绝对误差随分类回归树数量的变化趋势 Fig. 7 Trend of mean absolute error varying with number of CART |
| |
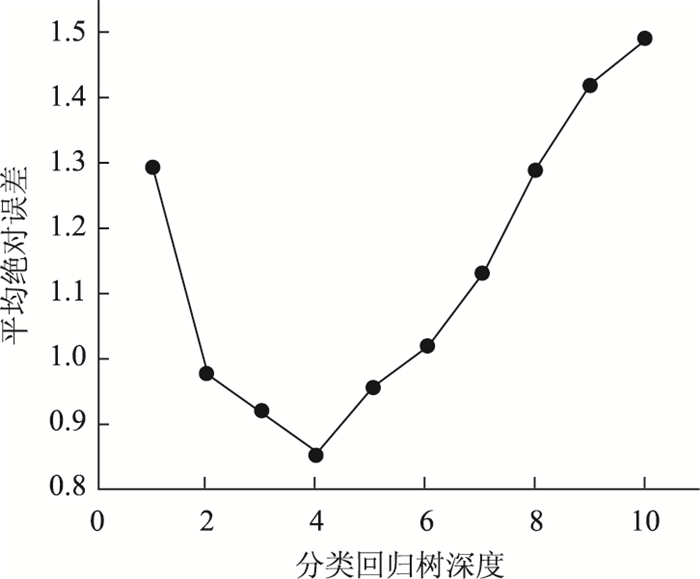
|
| 图 8 平均绝对误差随分类回归树深度的变化趋势 Fig. 8 Trend of mean absolute error varying with depth of CART |
| |
(2) 随机森林
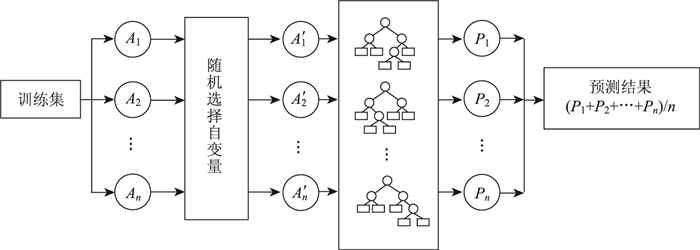
随机森林也属于机器学习,是决策树与bagging框架[21]的集成算法,且每一棵决策树都相互独立[22]。在构建随机森林的过程中,bagging的思想是:对于给定的训练样本,随机有放回地选择N个样本构成训练样本子集来训练不同决策树,每一棵决策树在训练之前会随机选择自变量个数进行建模[23-24]。当随机森林用于预测时,构成随机森林的决策树是CART,而CART的预测结果是各叶子节点的均值,因此其预测结果是所有分类回归树结果的均值,其运算思路如图 9所示。其中,An为训练样本子集;A′n为随机选择自变量后的训练样本子集;Pn为各回归树的预测值。
|
| 图 9 随机森林运算过程图 Fig. 9 Random forest operation process |
| |
随机森林在建立模型进行预测的过程中采用的是最小均方差原则,在训练集(X,Y)中,对于任意划分特征X′和任意划分点d划分出的两个不同数据集G1和G2,通过计算G1和G2均方差之和的最小值确定对应的特征值划分点,以得到模型训练的最优特征,其计算公式如式(7)所示。
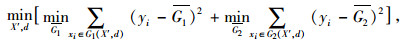
|
(7) |
式中,
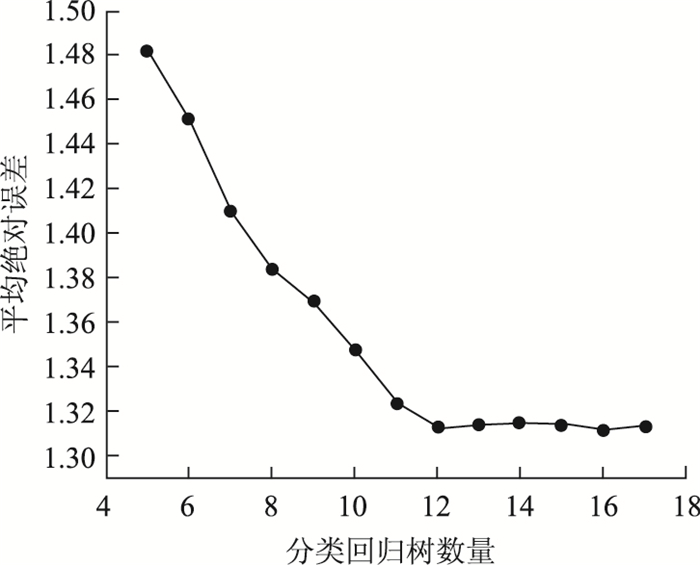
在利用Python平台建立随机森林模型的过程中,需要设置分类回归树深度(max-depth)、最大特征数(max-features)以及分类回归树数量(n-estimators)3个主要参数。由于随机森林中每棵树都相互独立,且预测结果互不影响,则可将max-depth设置为None,表示不限制分类回归树的深度。max-features的默认设定参数为auto,但是鉴于训练样本中只有4个特征,且均为相关因素,因此将max-features设置为None,表示全部特征都会用于模型的建立。在此基础上,n-estimators的取值通过多次试算来确定。由图 10可知,当分类回归树的数量达到12后,随机森林预测的平均绝对误差趋于稳定,因此将n-estimators设定为12。
|
| 图 10 平均绝对误差随分类回归树数量的变化趋势 Fig. 10 Trend of mean absolute error varying with number of CART |
| |
(3) 线性回归
线性回归是利用线性模型建立因变量与多个自变量之间关系的方法,线性回归模型根据输入参数求出相应回归系数,并将回归系数与对应自变量乘积后累加得到因变量。其方程可表示为公式(8),其中,y为因变量,x为自变量,a为回归系数,b为常数。
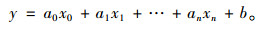
|
(8) |
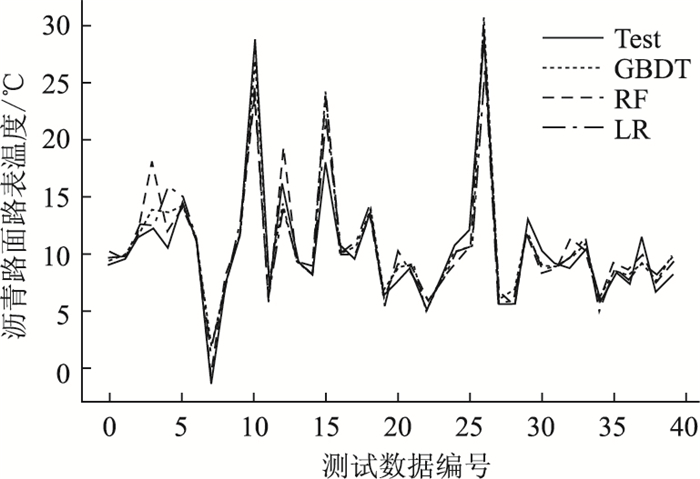
梯度提升树、随机森林和线性回归的预测结果如图 11所示,图中Test为测试数据,GBDT为梯度提升树预测结果,RF为随机森林预测结果,LR为线性回归预测结果。
|
| 图 11 各温度预测模型的路表温度预测结果 Fig. 11 Prediction result of road surface temperature by each temperature prediction model |
| |
为进一步表征各路表温度预测模型的准确性,分别计算GBDT、随机森林和线性回归3个模型预测结果的均方误差,计算公式如式(9)所示,经多次运算后得到的各模型均方误差变化趋势图如图 12所示。
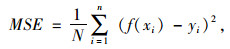
|
(9) |
|
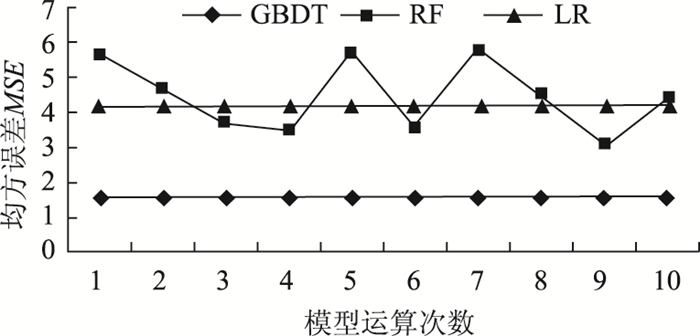
| 图 12 各温度预测模型的均方误差变化趋势 Fig. 12 MSE variation trend of each temperature prediction model |
| |
式中,N为预测数总个数;x为输入自变量;y为对应因变量;f(x)为预测值;i为测试数据编号。
由均方误差变化趋势图可知:GBDT预测结果的均方误差最小,鲁棒性高,在路表温度预测上有很大优势;随机森林预测结果的均方误差一直处于波动状态,经分析后初步认定原因是:由于随机森林中每棵决策树都相互独立,在训练样本数量的约束下,以bagging方式划分的训练样本子集无法涵盖所有情况的样本,反而会影响随机森林预测的准确度;线性回归所建预测模型与GBDT模型一样都非常稳定,但在预测精度上的优势较小。综上所述,GBDT所建模型的预测效果好,且具有良好的泛化能力和鲁棒性,在路表温度的预测上具有很好的适用性。
4 结论(1) Apriori算法在关联分析上表现优异,无需作图或计算相关系数即能准确找到相关因素,与线性拟合等方法相比,在处理大量数据时有极大优势,能有效提高关联分析的效率。
(2) Apriori算法挖掘得到影响浙中金华地区路表冬季温度变化的关键气象因素主要有4个,分别是:露点温度、相对湿度、气压和气温。鉴于本研究使用的气象数据有限,后续研究还可继续增加其他气象因素,以挖掘得到更全面的结果。
(3) GBDT与随机森林都属于决策树的集成算法,在训练样本数量有限的情况下,梯度提升树相比于随机森林拥有更高的预测精度,更适合建立预测模型。
(4) GBDT建立的路表温度预测模型拥有较好的泛化能力和鲁棒性,能够较为准确地预测路表温度的变化,对路表温度的预估具有一定可行性,为机器学习算法在预测方面的应用提供了理论与实践依据。
| [1] |
BARBER E S. Calculation of Maximum Pavement Temperatures from Weather Reports[J]. Highway Research Board Bulletin, 1957, 168: 1-8. |
| [2] |
HUBER G A. Weather Database for the Superpave Mix Design System[EB/OL]. Washington, D. C.: Transportation Research Board of the National Academy of Sciences(1999-03-19)[2018-08-06]. http://onlinepubs.trb.org/onlinepubs/shrp/SHRP-A-648A.pdf
|
| [3] |
HERMANSSON A. Mathematical Model for Calculation of Pavement Temperatures:Comparison of Calculated and Measured Temperatures[J]. Transportation Research Record, 2001, 1764: 180-188. |
| [4] |
GRIMBACHER T, SCHMID W. Nowcasting Precipitation, Clouds, and Surface State in Winter[J]. Atmospheric Research, 2005, 77(1): 378-387. |
| [5] |
KRSMANC R, SLAK A S, DEMSAR J. Statistical Approach for Forecasting Road Surface Temperature[J]. Meteorological Applications, 2013, 20(4): 439-446. |
| [6] |
AGRAWAL R, SRIKANT R. Fast Algorithms for Mining Association Rules[C]//Proceedengs of 20th International Conference on Very Large Data Bases.Santiago, Chile: Very Large Data Base Endowment(VLDB), 1994: 487-499.
|
| [7] |
BORGELT C. Efficient Implementations of Apriori and Eclat[C]//Proceedings of IEEE ICDM Workshop on Frequent Item Set Mining Implementations. Melbourne: IEEE, 2003.
|
| [8] |
GUO Z, CHI D, WU J, et al. A New Wind Speed Forecasting Strategy Based on the Chaotic Time Series Modelling Technique and the Apriori Algorithm[J]. Energy Conversion & Management, 2014, 84: 140-151. |
| [9] |
PARK J S, CHEN M S, YU P S. An Effective Hash-based Algorithm for Mining Association Rules[J]. ACM SIGMOD Record, 1997, 24(2): 175-186. |
| [10] |
HAN J, PEI J, YIN Y. Mining Frequent Patterns without Candidate Generation[J]. ACM SIGMOD Record, 2000, 29(2): 1-12. |
| [11] |
FRIEDMAN J H. Greedy Function Approximation:A Gradient Boosting Machine[J]. Annals of Statistics, 2001, 29(5): 1189-1232. |
| [12] |
FRIEDMAN J H. Stochastic Gradient Boosting[J]. Computational Statistics & Data Analysis, 2002, 38(4): 367-378. |
| [13] |
LIU L, JI M, BUCHROITHNER M. Combining Partial Least Squares and the Gradient-boosting Method for Soil Property Retrieval Using Visible Near-Infrared Shortwave Infrared Spectra[J]. Remote Sensing, 2017, 9(12): 1299. |
| [14] |
HONG T, PINSON P, FAN S, et al. Probabilistic Energy Forecasting:Global Energy Forecasting Competition 2014 and Beyond[J]. International Journal of Forecasting, 2016, 32(3): 896-913. |
| [15] |
DING C, WANG D, MA X, et al. Predicting Short-term Subway Ridership and Prioritizing Its Influential Factors Using Gradient Boosting Decision Trees[J]. Sustainability, 2016, 8(11): 1-16. |
| [16] |
YANG S, WU J, DU Y, et al. Ensemble Learning for Short-term Traffic Prediction Based on Gradient Boosting Decision Trees[J]. Journal of Sensors, 2017, 2024: 1-15. |
| [17] |
G/T 21984-2008, 短期天气预报[S]. G/T 21984-2008.Short-term Weather Forecast[S]. |
| [18] |
WU X, KUMAR V, QUINLAN J R, et al. Top 10 Algorithms in Data Mining[J]. Knowledge & Information Systems, 2007, 14(1): 1-37. |
| [19] |
KIM J C, CHUNG K. Emerging Risk Forecast System Using Associative Index Mining Analysis[J]. Cluster Computing, 2016, 20(1): 547-558. |
| [20] |
VALIANT L G. A Theory of the Learnable[J]. Communications of ACM, 1984, 27(11): 1134-1142. |
| [21] |
BREIMAN L. Bagging Predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
| [22] |
LIAW A, WIENER M. Classification and Regression by Random Forest[J]. R News, 2002, 23(2/3): 18-22. |
| [23] |
CUTLER A, CUTLER D R, STEVENS J R. Random Forests[J]. Machine Learning, 2004, 45(1): 157-176. |
| [24] |
SVETNIK V, LIAW A, TONG C, et al. Random Forest:A Classification and Regression Tool for Compound Classification and QSAR Modeling[J]. Journal of Chemical Information & Computer Sciences, 2003, 43(6): 1947-1958. |
 2019, Vol. 36
2019, Vol. 36
