扩展功能
文章信息
- 邓社军, 钟煜一, 叶晓飞, 陈峻, 于世军
- DENG She-jun, ZHONG Yu-yi, YE Xiao-fei, CHEN Jun, YU Shi-jun
- 多因素耦合作用下的停放车辆行驶时间模型
- A Travel Time Model of Parking Vehicles under Multi-factor Coupling
- 公路交通科技, 2019, 36(4): 125-134
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(4): 125-134
- 10.3969/j.issn.1002-0268.2019.04.018
-
文章历史
- 收稿日期: 2017-09-25
2. 宁波大学 海运学院, 浙江 宁波 315211;
3. 东南大学 交通学院, 江苏 南京 210000
2. School of Maritime and Transportation, Ningbo University, Ningbo Zhejiang 315211, China;
3. School of Transportation, Southeast University, Nanjing Jiangsu 210000, China
路外停车对动态交通影响的表现形式主要体现为车辆的进出过程对主路机非车流的影响,而相对于车辆驶出,驶入对主路车流的影响更大。停放车辆在穿越非机动车道驶入停车场的过程中,一方面将对非机动车的正常行驶造成影响,如导致整体车流的车速降低等;另一方面非机动车流与停车场设施等,也将会对停放车辆造成影响,如当非机动车流量过大、停车场周转率较低时,将会导致停放车辆在入口道处排队时间过长,进而增大主路社会车辆的行车延误、形成交通阻塞和诱发交通冲突等。因此,结合停车驶入穿越非机动车道的阶段,分析穿越时间及其影响因素,对于深入剖析路外停车对路段车流的影响特性具有重要的理论价值与现实意义。
目前针对路外停车场的停车穿越时间的研究成果并不多,相似的研究主要体现在机非交通冲突和出入口管理等方面。美国科罗拉多州公路委员会将AM(Access Management)策略应用于公路,并且提出根据道路等级和功能的不同,道路出入口控制标准和方法相应有所差异,而出入口管理指南[1]、出入口管理手册[2]和密歇根州的出入口管理指南[3]也在长度、转弯半径等方面对道路出入口的设置提出了一些原则性的要求。曹晓奎、裴玉龙[4]在分析停车场出入口几何设计影响因素的基础上,给出了出入口布置方法,伊轩轩[5]等从优化出入口交通设计的角度,遵循出入口管理策略的基本原则, 对城市公建群的机动车出入口细部进行优化设计。熊娟、陈峻[6]等通过调查南京市商业中心区路外停车设施出入口与主路接驳处的交通情况, 分析出入口和主路的交通特性以及驶入驶出车辆对主路车辆造成的延误。王学明运用交通冲突技术和模糊评价方法,对道路自行车的安全进行了评价,并提出了一些具体的改进措施[7]。以上研究成果未能对停车驶入所受到的影响因素进行系统的分析,对停车穿越时间受到非机动车流影响的动态变化特征等,也未作相关研究。本研究旨在分析停放车辆及其非机动车流的特性,研究受到非机动车流等因素影响下的穿越行驶时间,并进行理论建模与验证分析。
1 穿越时间的影响因素分析 1.1 基本定义定义停放车辆在穿越非机动车道驶入停车场入口的过程中,在机动车道的等待与在非机动车道的行驶时间之和为穿越时间t穿越,其中停放车辆在机动车道的等待时间为穿越等待时间t穿等,停放车辆从驶入非机动车道开始,到其进入停车场入口道结束这段时间为穿越行驶时间t穿行,即:
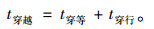
|
(1) |
对停放车辆的行进过程分析可知:当非机动车辆没有可接受的临界间隙出现,停放车辆将会在机动车道停留;当停放车辆已经开始穿越行驶,若部分非机动车辆仍然继续行驶,此时会导致停放车辆减速或等待;若受到停车场入口道的影响,也会导致车辆在非机动车道的穿越行驶时间过长。因此综合分析穿越时间的主要影响因素有以下几方面:
(1) 非机动车道宽度
驶入过程就是停放车辆穿越非机动车道,进入路外停车场入口道的过程。当非机动车道宽度不同时,在相同的行驶速度下,行驶的时间也会不一样。因此当车道宽度不同时,车辆在穿越过程中受到的影响也会存在一定的差异性。
(2) 机非隔离带宽度
当机非隔离带越宽时,停放车辆在穿越时可以占用的空间就越大,此时对非机动车流的影响也会越小,同时在隔离带区域行驶时,若隔离带越宽,则受非机动车辆的影响越小。相关研究者[8]提出不同功能的机非隔离带最小宽度值:当隔离带为绿化时,建议宽度为2.5 m;当隔离带为自行车停车时,建议宽度为2~2.5 m;当隔离带为机动车停车时,建议宽度为3~5 m;当隔离带为公交站台时,建议宽度为2.5 m或5.5 m。
(3) 非机动车流量
停放车辆在驶入的过程中,受到非机动车流量的干扰,当流量大时则会造成停放车辆的减速或者停车等待。
(4) 停车到达率
停放车辆在驶入进入道的过程中若驶入率较高,此时可能会造成停放车辆在入口道排队等待,使得停车穿越行驶时间增加,对主路机动车流造成影响。
(5) 可穿越临界间隙
停放车辆在进出过程中,非机动车流出现的可供穿越的临界时间长度t临。
2 穿越时间的分析与建模 2.1 穿越等待时间相关研究[9]表明,q非=0.51辆/(s·m),非机动车群的间隙的临界点,当q非≥0.51辆/(s·m)时,群间隙为0,此时停放车辆将完全无法穿越;当q非<0.51辆/(s·m)时,群间隙大于0,此时停放车辆可以根据群间隙的大小选择性的实施穿越。因此,有必要对两种情形下的穿越等待时间分别进行讨论。
(1) 当q非≥0.51辆/(s·m)
此时非机动车流量很大,即群间隙为0,停放车辆将无法穿越必须完全停车等待,等待时间为:
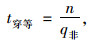
|
(2) |
式中,n为每1 m宽的非机动车道在1 s内通过的非机动车辆数;q非为非机动车流量。
(2) 当0<q非<0.51辆/(s·m)
此时非机动车群的空隙大于0,群到达的空隙服从对数正态分布,当非机动车群的空隙大于安全间隙时,此时停放车辆可直接穿越,则可以被接受的概率为:
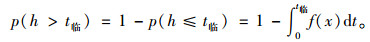
|
(3) |
被拒绝的概率为:
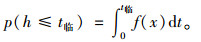
|
(4) |
假设任意一个被拒绝的空隙分布为G(t),
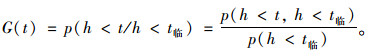
|
(5) |
由分布函数与条件概率定义得出:
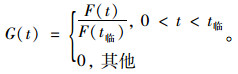
|
(6) |
故被拒绝空隙时间的平均长度为:
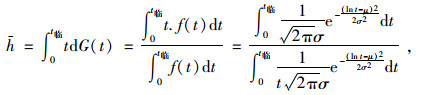
|
(7) |
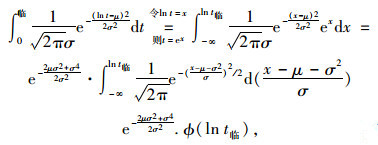
|
(8) |
式中,μ为均值;σ2为方差。
由式(8)可得出:
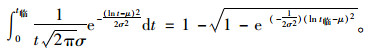
|
(9) |
将式(8)、式(9)代入式(7),则:
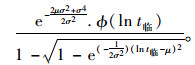
|
(10) |
假设停放车辆在n+1个空隙穿越非机动车群,则其需要等待n个空隙且都小于t临,则拒绝n个不可穿越的空隙概率为:
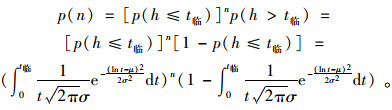
|
(11) |
所以,停放车辆等待即拒绝的平均间隙数为:
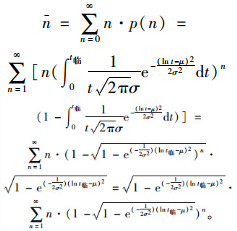
|
(12) |
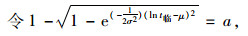
|
(13) |
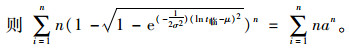
|
(14) |
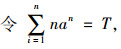
|
(15) |
则有:
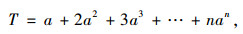
|
(16) |
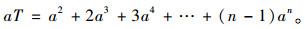
|
(17) |
整理式(16)与式(17)得出:
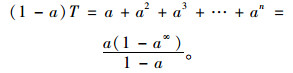
|
又由式(13)可知a∈(0,1),所以:
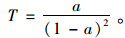
|
(18) |
故式(12)转化为:
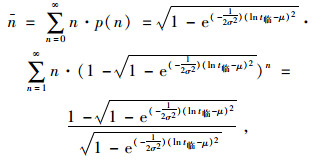
|
(19) |
则停放车辆的平均等待时间为被拒绝的平均间隙数n与平均长度h的乘积,即:
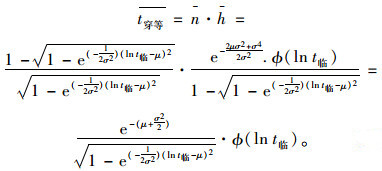
|
(20) |
文献[10-13]研究表明,非机动车流具有多变性的特征,主要表现为速度和流向很容易发生改变。主要是因为当非机动车的流量从较低到较高的上升变化过程中,部分骑行者会寻找前方空挡进行穿行超车,此时速度和方向的变化都会增加。因此,在道路条件已知的情形下,停放车辆在穿越行驶过程中将会受到部分强行超车的非机动车的影响,导致穿越行驶时间的增加。另外当停放车辆到达率很高时,此时可能会造成在进口处的排队等待,这也会增加穿越行驶的时间。因此,穿越行驶时间主要由穿越非动车道行驶时间与入口道排队等待时间两部分组成。
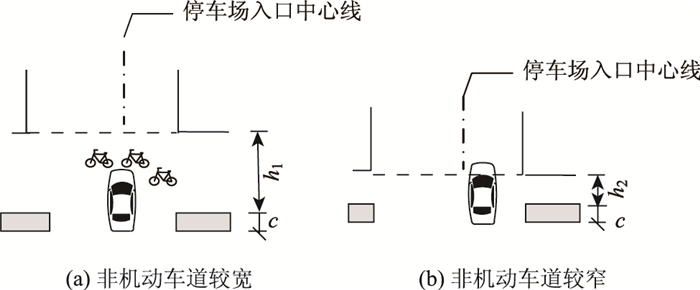
2.2.1 道路条件对穿越行驶时间的影响分析假设停放穿越车辆的长度为L,停放车辆穿越非机动车道的最短距离为h, 机非隔离带宽度为c。
(1) 当L≤c+h时
当机非隔离带宽度与非机动车道的宽度之和大于停放车辆的长度时,停放车辆在驶离机动车道后,车头与入口道的距离大于0,此时在穿越行驶过程中主要受非机动车影响。图 1(a)所示为当停放车辆为1辆时的情形。当停放车辆的平均到达率较低时,入口道处系统的排队车辆仅为1辆时,行驶时间为穿越非机动车道行驶时间;但是如果停放车辆的到达率较高时,即当入口道处排队等待车辆超过1辆时,此时可能会因为入口道长度不够而对机动车道车辆有影响,此时行驶时间为穿越非机动车道行驶时间与入口道的影响时间之和。
|
| 图 1 驶入车辆在不同的非机动车道宽度下受到的影响 Fig. 1 Entry vehicles affect by different non-motorized vehicle lane widths |
| |
(2) 当L>c+h时
当机非隔离带宽度与非机动车道的宽度之和小于等于停放车辆的长度时,停放车辆在驶离机动车道穿越行驶过程中主要不仅受到非机动车影响,而且与入口道处的交通强度有关,行驶时间为穿越时间与入口道的影响时间之和,如图 1(b)所示为停放车辆为1辆时的情形。
目前城市路外停车场的停放车辆以中小型汽车为主,表 1为国内城市道路常见的中小型汽车的几何尺寸,可以看出车身长度范围为3.57~5.02 m,车宽的范围为1.60~1.87 m。本研究结合实际观测数据,选取车身平均长度为4.53 m进行相关分析。
| 车型 | 长/mm | 宽/mm |
| 奥迪A6 | 5 015 | 1 874 |
| 大众迈腾 | 4 865 | 1 820 |
| 别克君威 | 4 830 | 1 865 |
| 现代索纳塔 | 4 820 | 1 835 |
| 雪铁龙C5 | 4 805 | 1 860 |
| 大众朗逸 | 4 605 | 1 765 |
| 荣威350 | 4 521 | 1 788 |
| 标致207 | 4 260 | 1 680 |
| 大众POLO | 3 970 | 1 682 |
| 铃木奥拓 | 3 570 | 1 600 |
本研究通过现场调查发现,绿化带宽度最小值为1.25 m,因此分别取值1,2.5,3.5 m进行讨论。
2.2.2 交通条件对穿越非机动车道行驶时间的影响分析(1) 穿越行驶效率
在道路条件确定的情形下,停放车辆在驶入过程中,首先是受到非机动车辆的影响。因此,定义停放车辆的理论穿越非机动车道行驶时间与实际穿越非机动车道时间的比值为穿越行驶效率E驶,则:
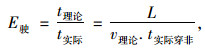
|
(21) |
式中, L为穿越的车长,意义同上;v理论为停放车辆在无干扰时的理论行驶车速;t实际穿非为停放车辆的实际穿越非机动车道行驶时间。
(2) 相关性分析与模型构建
本研究以南京市中山北路停车场为例,以单个停放车辆为研究对象,观测在不同的非机动车流量下,不同的实际穿越非机动车道行驶时间。由式(21)得出驶入效率与非机动车流量之间的关系。表 2为根据观测数据计算出的停放车辆穿越效率与非机动车流量的相关性分析,从表中可以看出两者的相关系数为0.615,说明相关性较强。
| 穿越效率 | 非机动车流量 | ||
| 穿越效率 | Pearson相关性 | 1 | -0.758 |
| 显著性(双侧) | — | 0.000 | |
| N | 1 052 | 102 | |
| 非机动车流量 | Pearson相关性 | -0.758 | 1 |
| 显著性(双侧) | 0.000 | — | |
| N | 102 | 102 |
因此,通过回归进一步分析穿越效率与非机动车流量的关系曲线,如图 2所示。
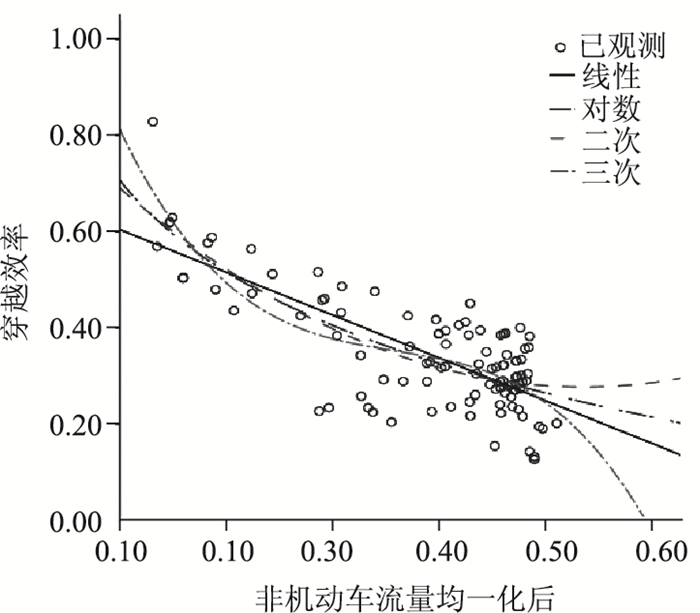
|
| 图 2 穿越效率与非机动车流量的拟合曲线 Fig. 2 Regression curve of crossing efficiency and non-motorized vehicle volume |
| |
综合运用直线关系模型、对数关系模型、二次函数模型、三次函数模型进行拟合度分析,具体如表 3所示,可以看出三次函数模型的R2值最大,为0.628,但是通过发现曲线的变化趋势发现三次函数模型在非机动车流量为0.59辆/(s·m)时,穿越效率变成了0,这与实际变化规律不太符合;二次函数模型当非机动车流量大于0.51辆/(s·m)时,呈现出随流量增大效率也增大的趋势,这与实际也不相符合;对数模型的曲线随流量增大呈现下降的变化趋势,R2值为0.606,相关性较好。因此,选用对数函数作为非机动车流量与穿越效率的关系模型。
| 方程 | 模型描述 | 参数估计 | ||||||||
| R Square | F | df1 | df2 | Sig. | 常数 | b1 | b2 | b3 | ||
| 线性 | 0.575 | 135.188 | 1 | 100 | .000 | .694 | -0.894 | |||
| 对数 | 0.609 | 155.891 | 1 | 100 | .000 | .072 | -0.276 | |||
| 二次 | 0.606 | 76.077 | 2 | 99 | .000 | .903 | -2.348 | 2.199 | ||
| 三次 | 0.628 | 55.236 | 3 | 98 | .000 | 1.463 | -8.591 | 22.954 | -21.324 | |
因此,最终确定二者的函数形式为:
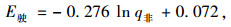
|
(22) |
式中q非为非机动车流量。
(3) 模型验证分析
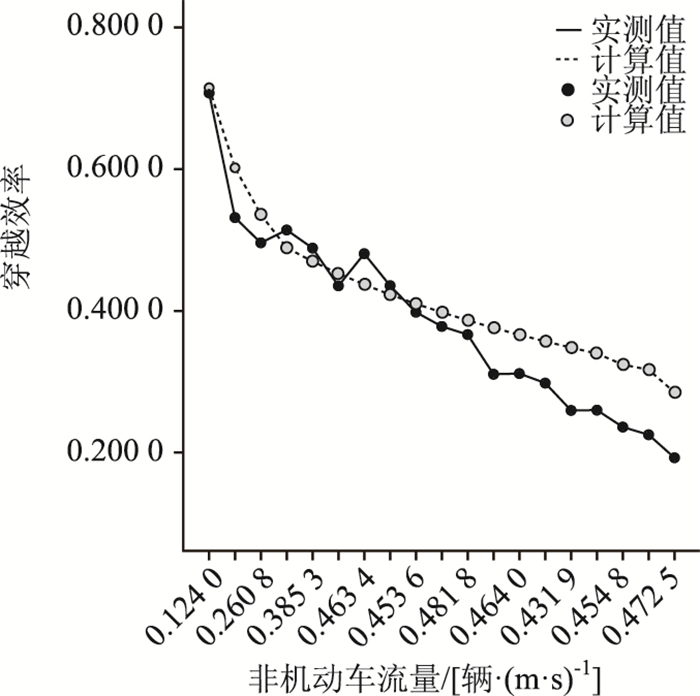
本研究以南京市中山南路商贸大厦停车场的实测数据进行了对比分析。根据实测驶入时间计算出实际的驶入效率,与模型的效率进行比较分析,见表 4。
| 序号 | 非机动车流量/ [辆·(m·s)-1] | 实际驶入时间/s | 理论驶入时间/s | 穿越效率 | |
| 实测值 | 计算值 | ||||
| 1 | 0.124 035 | 4.607 | 3.26 | 0.707 618 841 | 0.715 017 01 |
| 2 | 0.186 376 | 6.132 | 3.26 | 0.531 637 312 | 0.489 051 029 |
| 3 | 0.260 847 | 6.572 | 3.26 | 0.496 043 822 | 0.452 678 63 |
| 4 | 0.360 523 | 6.34 | 3.26 | 0.514 195 584 | 0.422 960 216 |
| 5 | 0.385 348 | 6.673 | 3.26 | 0.488 535 891 | 0.422 960 216 |
| 6 | 0.381 512 | 7.489 | 3.26 | 0.435 305 114 | 0.409 913 255 |
| 7 | 0.463 412 | 6.782 | 3.26 | 0.480 684 164 | 0.409 913 255 |
| 8 | 0.458 059 | 7.485 | 3.26 | 0.435 537 742 | 0.409 913 255 |
| 9 | 0.453 57 | 7.189 | 3.26 | 0.453 470 58 | 0.397 833 655 |
| 10 | 0.463 822 | 7.624 | 3.26 | 0.427 597 062 | 0.386 587 817 |
| 11 | 0.481 812 | 7.295 | 3.26 | 0.446 881 426 | 0.376 068 038 |
| 12 | 0.435 374 | 7.5 | 3.26 | 0.434 666 667 | 0.366 186 225 |
| 13 | 0.463 999 | 8.94 | 3.26 | 0.364 653 244 | 0.356 869 403 |
| 14 | 0.470 097 | 8.468 | 3.26 | 0.384 978 744 | 0.324 160 08 |
| 15 | 0.431 936 | 8.568 | 3.26 | 0.380 485 528 | 0.316 914 443 |
| 16 | 0.455 394 | 8.548 | 3.26 | 0.381 375 76 | 0.303 323 241 |
| 17 | 0.454 827 | 9.82 | 3.26 | 0.331 975 56 | 0.296 930 264 |
| 18 | 0.453 577 | 9.488 | 3.26 | 0.343 591 906 | 0.290 778 591 |
| 19 | 0.472 534 | 8.93 | 3.26 | 0.365 061 59 | 0.284 850 665 |
图 3为二者对比分析,可以看出该模型具有一定的精度。
|
| 图 3 实测值与计算值对比分析 Fig. 3 Comparative analysis of measured values and calculated values |
| |
(4) 实际穿越非机动车道行驶时间t实际穿非的计算
综上研究可知,单个车辆穿越非机动车道行驶时间为:
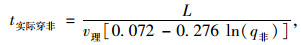
|
(23) |
式中v理为停放车辆的理想安全行驶速度,取值范围为0~5 km/h;
2.2.3 停车到达率与入口道平均等待时间关系分析停放车辆在穿越非机动车道后驶进入口道的过程,可以看出是停车需求与提供服务的过程。由于停放场入口道数正常为1条,则可以看成是单通道排队服务系统。如果停车平均到达率较高时,则可能会导致车辆在入口道排队等待,此时将会延长穿越行驶时间,因此有必要对停车平均到达率的大小进行分析。
相关研究[14-18]表明停放车辆的平均到达率λ服从泊松分布,因此当车辆到达停车场出入口时,可以将车辆驶入路外停车场看成是停车需求与提高服务的过程。由于停车场入口道数正常为1条,则可以看成是单通道排队服务系统。假设停车场对停放车辆的平均服务率为μ,由随机服务理论可知,若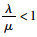
(1) λ < 400辆/h
由排队论知识可知,入口道车辆的平均等待时间:
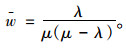
|
(24) |
排队系统中的平均车辆数:
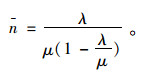
|
(25) |
根据实际观测的平均到达率,计算出平均等待时间、平均车辆数与平均到达率的关系,见表 5。
| 序号 | 平均到达率/(辆·h-1) | 平均等待时间/s | 平均车辆数/辆 |
| 1 | 327 | 40.5 | 5 |
| 2 | 300 | 27.0 | 3 |
| 3 | 280 | 20.3 | 2 |
| 4 | 257 | 16.2 | 2 |
| 5 | 230 | 12.0 | 1 |
| 6 | 225 | 11.6 | 1 |
| 7 | 200 | 9.0 | 1 |
| 8 | 180 | 7.4 | 1 |
| 9 | 129 | 4.3 | 1 |
| 10 | 103 | 3.1 | 0 |
| 11 | 30 | 0.7 | 0 |
平均等待时间、平均车辆数与平均到达率的关系曲线分别见图 4与图 5。
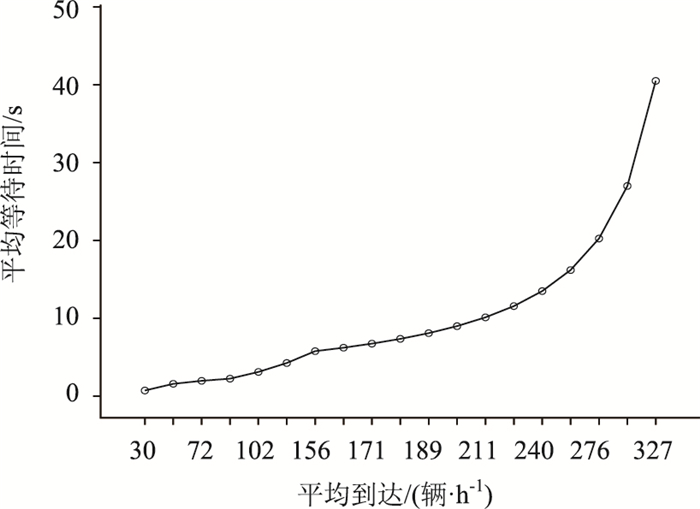
|
| 图 4 平均等待时间与停车到达率的关系 Fig. 4 Relationship between average wait time and average arrival rate |
| |
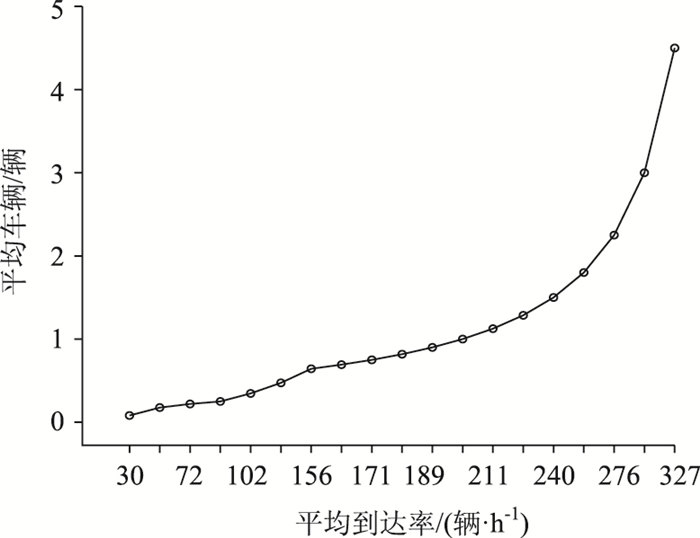
|
| 图 5 系统中平均车辆数与停车到达率的关系 Fig. 5 Relationship of average vehicle number and parking arrival rate in system |
| |
停车到达率与系统中平均车辆数的关系曲线见图 5。
当平均到达率λ≤230辆/h,系统中的平均等待车辆数n≤1,平均等待时间0≤w≤12 s,此时可以认为车辆的到达没有排队现象;
当平均到达率230辆/h < λ≤280辆/h,系统中的平均等待车辆数n≤2,平均等待时间12 s < w≤20 s,可以认为此时已经开始排队;
当平均到达率280辆/h < λ≤400辆/h,系统中的平均等待车辆数n>2,平均等待时间w>20 s。无论是平均等待时间还是系统中的平均车辆数都会随到达率变化幅度较大,可以认为此时的排队长度将随平均到达率呈现快速增长的趋势。
(2) λ≥400辆/h
此时系统不稳定,因此不能用排队论的知识求解。此时排队的车辆以一定的平均服务时间接受服务,并以一定的规律到达,此时第1辆车的等待时间为0,第2辆车辆到达时需要等待第1辆车服务结束,此时等待时间为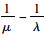
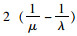
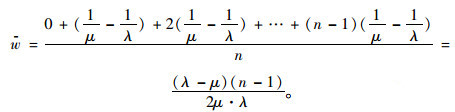
|
(26) |
(3) 平均等待时间w的取值分析
平均等待时间是排队系统中车辆的平均等待时间,如果排队车辆都在入口道与机非隔离带开口区域范围内,此时的等待将不会对主路车辆造成影响,反之将会对主路车辆造成干扰,因此在分析停车驶入时间时必须对w的取值进行具体分析,即:
当单个车辆在入口道等待,且0 < L≤h+c时,对主路机动车流没有影响,此时w为0。
当入口道到达的停放车辆为n辆,且n>1,nL>h+c,此时有排队现象,车辆在入口道等待对主路机动车流有影响,此时n与w的值根据λ大小由式(23)、式(24)与式(25)确定。
2.2.4 停放车辆的穿越时间计算模型综合以上研究内容,可以得出停放车辆以不同到达率驶入时,穿越时间的计算公式为:
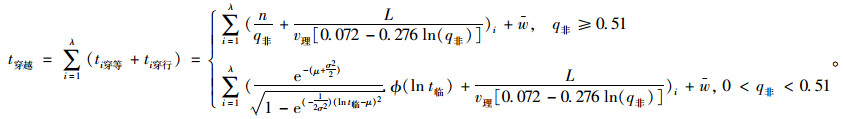
|
(27) |
对停放车辆驶入率的实测数据进行了统计,分析见表 6。
| 序号 | 驶入率分布范围/(辆·min-1) | 平均驶入率/(辆·min-1) | 比例/% |
| 1 | 0 ≤λ≤2 | 1.0 | 86.5 |
| 2 | 2 < λ≤6 | 4.0 | 5.7 |
| 3 | 6 < λ≤8 | 7.0 | 3.8 |
| 4 | λ>8 | — | 4.0 |
从表中可以发现,当平均停车驶入率大于8辆/分钟时,虽然可以反映峰值的大小,但由于其所占比例仅为4%,在进行规划设计时经济性较差;当2 < λ < 8辆/min,即120 < λ < 480辆/h,所占比例也仅为9.5%;而当0 < λ < 2辆/min,即平均停车驶入率选用1辆/分钟时,则具有一定的代表性,因此本研究选择停车驶入率λ=1辆/min(即60辆/h),并结合不同的非机动车道宽度、非机动车流量等参数值进行分析。由式(23)、式(24)可知当取λ=60辆/h,n=1因此只需要考虑单个车辆的情形,平均等待时间w=1.6 s。因此综合运用式(27)进行分析,结果见表 7。
| 非机动车流量/[辆·(m·s)-1] | 停车穿越时间/s | |||||
| (0, 0.05) | (0.05,0.1) | (0.1,0.15) | (0.15,0.20) | (0.20,0.25) | ||
| 非机动车道宽度/m | 3.5 | <10.3 | (10.3, 11.3) | (11.3, 12.1) | (12.1, 13.0) | (13.0, 13.8) |
| 4.0 | <8.7 | (8.7, 9.7) | (9.7, 10.6) | (10.6, 11.4 | (11.4, 12.3) | |
| 4.5 | <7.7 | (7.7, 8.7) | (8.7, 9.6) | (9.6, 10.46) | (10.46, 11.3) | |
| 5.0 | <7.1 | (7.1, 8.1) | (8.1, 8.9) | (8.9, 9.8) | (9.8, 10.6) | |
| 5.5 | <6.6 | (6.6, 7.6) | (7.6, 8.5) | (8. 5, 9.3) | (9.3, 10.2) | |
| 6.0 | <6.3 | (6.3, 7.2) | (7.2, 8.1) | (8.1, 8.9) | (8.9, 9.8) | |
| 6.5 | <6.0 | (6.0, 7.0) | (7.0, 7.8) | (7.8, 8.7) | (8.7, 9.5) | |
| 7.0 | <5.8 | (5.8, 6.7) | (6.7, 7.6) | (7.6, 8.5) | (8.5, 9.3) | |
| 非机动车流量/[辆·(m·s)-1] | (0.25, 0.3) | (0.30,0.35) | (0.35,0.40) | (0.40,0.50) | >0.50 | |
| 非机动车道宽度/m | 3.5 | (13.8, 14.7) | (14.7, 15.7) | (15.7, 16.7) | (16.7, 19.0) | >19.0 |
| 4.0 | (12.3, 13.2) | (13.2, 14.1) | (14.1, 15.1) | (15.1, 17.5) | >17.5 | |
| 4.5 | (11.3, 12.2) | (12.2, 13.1) | (13.1, 14.2) | (14.2, 16.5) | >16.5 | |
| 5.0 | (10.6, 11.5) | (11.5, 12.5) | (12.5, 13.5) | (13.5, 15.8) | >15.8 | |
| 5.5 | (10.2, 11.1) | (11.1, 12.0) | (12.0, 13.0) | (13.0, 15.4) | >15.4 | |
| 6.0 | (9.8, 11.0) | (11.0, 11.6) | (11.6, 12.7) | (12.7, 15.0) | >15.0 | |
| 6.5 | (9.5, 10.4) | (10.4, 11.4) | (11.4, 12.4) | (12.4, 14.7) | >14.7 | |
| 7.0 | (9.3, 10.2) | (10.2, 11.1) | (11.1, 12.2) | (12.2, 14.5) | >14.5 | |
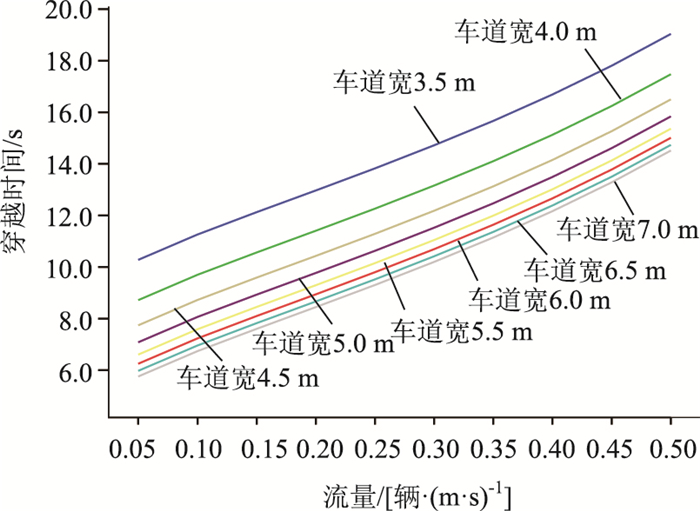
图 6为各种在不同非机动车道宽度下,基于不同非机动车流量时的穿越时间。
|
| 图 6 不同非机动车道宽度的穿越时间 Fig. 6 Crossing time under different non-motorized vehicle widths |
| |
从图中分析可以看出,
当非机动车流量增加时,穿越时间都呈现上升的趋势,说明受到非机动车流量的干扰较大。
在相同流量的条件下,穿越时间与车道宽度成反比关系。
相同流量的条件下,当车道宽度小于5 m时穿越时间的变化幅度显著;当车道宽度大于6 m时,穿越时间的变化幅度较小。
这主要是因为在相同的非机动车流量下,当车道越宽时,非机动车的行驶空间越大,行驶路径选择的自由度越高,此时对停放车辆的干扰越小;而当车道越窄时则自由度降低,对停放车辆的干扰增大所造成。
4 结论本研究基于理论分析并结合现场数据调查,建立了基于非机动车流等因素影响的路外停放车辆穿越行驶时间模型。结合案例具体参数的标定,对模型进行了敏感性分析,得出以下主要结论:相对于非机动车道宽度而言,穿越时间受非机动车流量大小的影响更为明显;在相同流量的条件下,穿越时间的变化与非机动车道宽度成反比;当非机动车道宽度小于5 m时,穿越时间受其影响变化显著;当非机动车道宽度大于6 m时,穿越时间受其影响变化较小。
| [1] |
BUTORAC M A, WEN J C. Access Management on Crossroads in the Vicinity of Interchanges[M]. Washington, D.C.: Transportation Research Board, 2004.
|
| [2] |
GLUCK J, LEVINSON H S, STOVER V. Impacts of Access Management Techniques[M]. Washington, D.C.: Transportation Research Board, 1999.
|
| [3] |
American Association of State Highway and Transportation Officials. A Policy on Geometric Design of Highways and Streets[M]. Washington D.C.: Transportation Research Board, 2001.
|
| [4] |
曹晓奎, 裴玉龙. 停车场出入口布置相关问题研究[J]. 城市交通, 2010, 8(2): 61-65, 74. CAO Xiao-kui, PEI Yu-long. A Study on Parking Entrance/Exit Layout Design[J]. Urban Transport of China, 2010, 8(2): 61-65, 74. |
| [5] |
伊轩轩, 潘晓冬, 杨轸. 基于AM的城市公建群出入口规划及优化设计[J]. 华东交通大学报, 2009, 26(2): 22-28. YI Xuan-xuan, PAN Xiao-dong, YANG Zhen. Research on Access Planning and Optimum Design of the Public Buildings Based on Access Management[J]. Journal of East China Jiaotong University, 2009, 26(2): 22-28. |
| [6] |
熊娟, 陈峻, 张辉. 城市路外停车场出入口接驳处交通调查分析[J]. 交通科技与经济, 2007, 9(6): 75-77. XIONG Juan, CHEN Jun, ZHANG Hui. Analysis on the Junction of Main Road and Driveway[J]. Technology and Economy in Areas of Communications, 2007, 9(6): 75-77. |
| [7] |
王学明.基于交通冲突技术的自行车交通安全评价研究[D].北京: 北京交通大学, 2005. WANG Xue-ming. Research on Bicycle Traffic Safety Evaluation Based on Traffic Conflict Technology[D].Beijing: Beijing Jiaotong University, 2005. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y741756 |
| [8] |
黄斌, 褚浩然. 城市道路机非隔离带宽度研究[J]. 北京规划建设, 2010(2): 127-128. HUANG Bin, CHU Hao-ran. Research on the Width of Non-isolation Belt of Urban Road[J]. Beijing Planning Review, 2010(2): 127-128. |
| [9] |
梁春岩.自行车交通流特性及其应用研究[D].长春: 吉林大学, 2008. LIANG Chun-yan. Research on Bicycle Traffic Flow Characteristics and Its Application[D].Changchun: Jilin University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10183-2007095654.htm |
| [10] |
马国忠, 明士军, 吴海涛. 电动自行车安全特性分析[J]. 中国安全科学学报, 2006, 16(4): 48-52. MA Guo-zhong, MING Shi-jun, WU Hai-tao. On Safety Character of Electric Bicycle[J]. China Safety Science Journal, 2006, 16(4): 48-52. |
| [11] |
王紫.非机动车道上的机动车辆停放对动态交通影响分析[D].南京: 东南大学, 2012. WANG Zi. Analysis on Impact of Motor Vehicles Parking Non-motorized Lanes on Dynamic Traffic[D].Nanjing: Southeast University, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2187790 |
| [12] |
叶晓飞, 陈峻, 冯树民, 等. 路内停车影响下非机动车流速度模型[J]. 哈尔滨工业大学学报, 2016, 48(3): 115-119. YE Xiao-fei, CHEN Jun, FENG Shu-min, et al. Model of Non-motorized Vehicle Flow Speed Influenced by Curbside Parking[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 115-119. |
| [13] |
邓社军, 叶晓飞, 陈峻. 路外停车驶入对出入口交通流影响模型研究[J]. 哈尔滨工业大学学报, 2016, 48(3): 101-107. DENG She-jun, YE Xiao-fei, CHEN Jun. A Model to Describe the Influence of the Traffic Flow on the Main Road due to Off-street Parking at the Section of Access[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 101-107. |
| [14] |
熊娟.城市路外停车设施出入口设置研究[D].南京: 东南大学, 2008. XIONG Juan. Research on Entrance and Exit Settings of Urban Off-road Parking Facilities[D].Nanjing: Southeast University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1244555 |
| [15] |
闫星辰.路外停车场车辆出入对城市三幅路交通影响研究[D].南京: 东南大学, 2012. YAN Xing-chen. Study on Impact of Vehicle Entry and Exit in Outside Parking Lots on Urban Three-way Traffic[D].Nanjing: Southeast University, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2187914 |
| [16] |
邓社军.路外停车驶入对停车场出入口路段影响特性分析与模型研究[D].南京: 东南大学, 2014. DENG She-jun. Characteristic Analysis and Model Study on Impact of Off-road Parking on Parking Entrance and Exit Section[D].Nanjing: Southeast University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2708126 |
| [17] |
邓社军, 叶晓飞, 陈峻. 路外停车右转驶入对主路上游车流影响的动态长度模型[J]. 公路交通科技, 2014, 31(3): 125-132. DENG She-jun, YE Xiao-fei, CHEN Jun. A Model for Describing Dynamic Influence Length of Upstream Following Vehicles on Main Road when Front Vehicles Turning Right and Entering into Off-street Parking Lot[J]. Journal of Highway and Transportation Research and Development, 2014, 31(3): 125-132. |
| [18] |
蔡蕾.基于路段机动车速度影响的城市道路不同类型出入口接入条件研究[D].南京: 东南大学, 2015. CAI Lei. Study on Access Conditions of Different Types of Entrances and Exits of Urban Road Based on Effect of Vehicle Speed in Section[D].Nanjing: Southeast University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016755815.htm |
 2019, Vol. 36
2019, Vol. 36
