扩展功能
文章信息
- 谭仪忠, 刘元雪, 蔡守军, 王培勇, 陈俞龙
- TAN Yi-zhong, LIU Yuan-xue, CAI Shou-jun, WANG Pei-yong, CHEN Yu-long
- 浅埋隧道单侧扩建施工方案优化
- Optimization of Extension Scheme of Single-sided Shallow Tunnel
- 公路交通科技, 2019, 36(4): 108-116
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(4): 108-116
- 10.3969/j.issn.1002-0268.2019.04.016
-
文章历史
- 收稿日期: 2017-05-19
2. 中国人民解放军陆军工程大学 训练基地, 江苏 徐州 221004;
3. 中国人民解放军陆军勤务学院, 重庆 401311
2. Training Base, Army Engineering University of PLA, Xuzhou Jiangsu 221004, China;
3. Army Logistics University of PLA, Chongqing 401311, China
21世纪以来,我国城市地下空间的开发数量明显增加,利用体系也得到不断地完善,特大级城市地下空间开发利用的总体规模和发展速度已步入世界同类城市的先进行列。“19世纪是桥梁的世纪,20世纪是高层建筑的世纪,21世纪则是人类开发利用地下空间的世纪”,中国目前已经成为世界上城市地下空间开发利用的大国[1]。但由于城市规划的不合理以及对交通量增长的预测不足,原有的隧道的截面已经不能满足现在的需求,这就需要我们对已有隧道进行扩建来满足当前的使用要求或新增要求。由于浅层地下空间大都已接近饱和,为达到道路扩容要求,只能对已有隧道进行改扩建,增建一至两个车道。国内外对地下空间扩建也有一些研究,如国内的羊石隧道[2]、关村坝隧道[3]、重庆渝中区鹅岭隧道扩建工程[4-6]、日本名神高速公路的天王山隧道、意大利Nazzano隧道[7]、美国的White Haven和Rockport隧道[8]等。但浅埋隧道的扩建开挖对施工工序的要求很高,且不同的改扩建形式和方法对围岩稳定性的影响也很大,目前大多数隧道的扩建方式及施工方法仍然采用新建隧道的施工方法,与新建隧道相比仅仅是相对减少了土方量,却并没有专门采取针对隧道扩建时能够充分利用原隧道稳定性条件选取适合扩建的施工方法, 因此, 开展对浅埋隧道的扩建优化施工方案的研究是十分必要和迫切的。
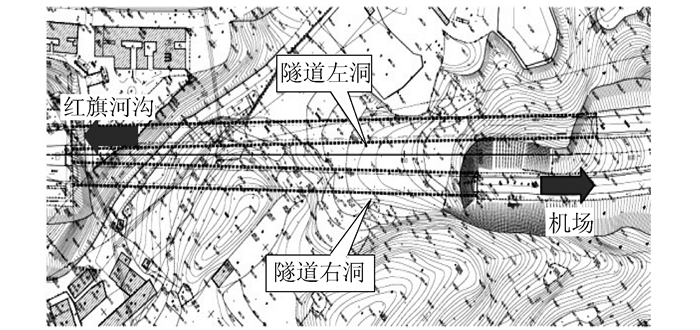
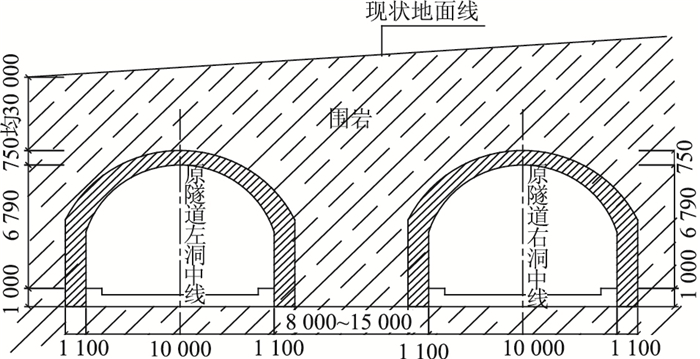
1 工程概况现状渝州隧道为平面成喇叭型布置的圆拱直墙式双洞隧道,位于构造剥蚀丘陵地貌,地面标高为435~488 m,下伏基岩主要为侏罗系中统沙溪庙组的砂岩、泥岩,岩层倾角为20°~25°。根据调查工程勘察,原隧道现状稳定,洞壁无地下水渗出,地下水不发育,根据相邻场地工程地质条件及重庆地区经验,隧道所经过地段为第四纪人工填筑及洪坡积层,基层为砂岩、泥岩地层,岩体较完整,节理一般不发育,隧道全长范围内围岩级别为Ⅳ级,隧道平均埋深约30 m,其平面布置及剖面布置图见图 1和图 2所示。
|
| 图 1 渝州隧道平面布置图 Fig. 1 Plane layout of Yuzhou tunnel |
| |
|
| 图 2 渝州隧道剖面布置图(单位:mm) Fig. 2 Sectional layout of Yuzhou tunnel(unit: mm) |
| |
根据现场施工条件,隧道扩建采取钻爆法全断面开挖,初期支护具体流程及要求如下:
(1) 喷射作业紧跟开挖面,混凝土终凝到下一循环放炮时间,不应小于3 h;喷射混凝土宜用湿喷工艺;喷射混凝土应采用普通硅酸盐水泥或硅酸盐水泥,强度等级不低于42.5 MPa。
(2) 先喷后锚,首次喷射砼厚度不小于50 mm,喷射作业中随时观察围岩变化情况;锚杆施工宜在喷射混凝土终凝3 h后进行;锚杆的抗拔力不低于规范标准,每300根锚杆抽样一组,进行抗拔力试验,每组不少于3根,并应符合《岩土锚杆与喷射混凝土支护工程技术规范》(GB 50086—2015)的规定;钢筋网应随受喷面的起伏铺设,钢筋网混凝土保护层厚20 mm,且与锚杆联结牢固。
(3) 钢架安装允许偏差,横向和高程均为±50 mm,垂直度为±2°;钢架立柱埋入底板深度应满足设计要求,并置于基岩上,钢架与岩壁之间必须楔紧,相邻钢架连接牢固,钢架与围岩之间的混凝土保护层厚40 mm,临空一侧的混凝土保护层厚为20 mm。
2 现场监控量测 2.1 监控量测方法(1) 观测工程地质和支护状况。每次爆破及初期支护喷射混凝土后均需通过肉眼、锤击和地质罗盘检查隧道的掌子面,详细记录和描述围岩地质情况:地下水情况、岩层产状、岩性、裂隙、围岩完整性与稳定性。判断围岩类别是否与设计相符并观察支护效果。
(2) 确定量测频率。根据量测断面距离掌子面距离、位移发展速率和量测断面开挖时间取最高频率。根据渝州隧道围岩的情况确定量测频率见表 1。
| 项目名称 | 方法及工具 | 量测间隔时间 | |||
| 1~15 d | 16 d~1月 | 1~3月 | 3个月以后 | ||
| 拱顶下沉 | 钢卷尺、精密水准仪、塔尺 | 1~2次/ d | 1次/ 2d | 1~2次/周 | 1~3次/月 |
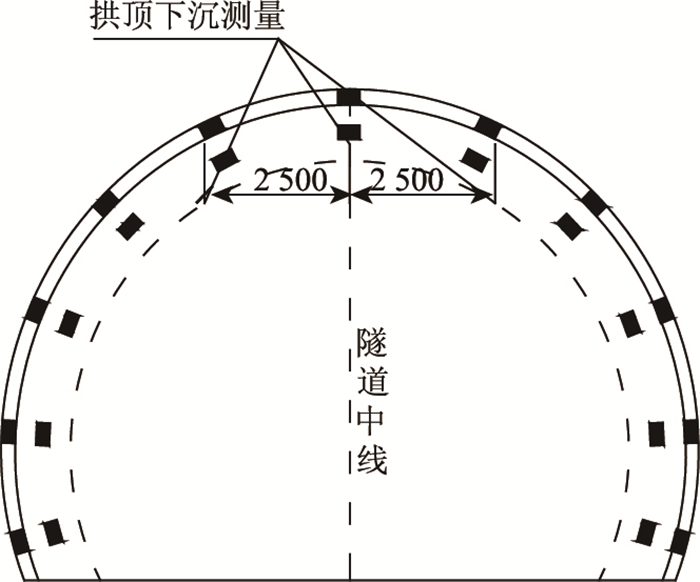
(3) 拱顶下沉量测。进行拱顶下沉的量测方法是在隧道开挖毛洞的拱顶及轴线左右各2~3 m处设3个带挂钩的锚桩,测深为30 cm,钻孔直径ϕ42,用快凝水泥固定,测桩头需设保护罩。用精密水准仪、钢卷尺量测拱顶下沉,测点布置见图 3所示。
|
| 图 3 隧道单洞断面拱顶下沉测点布置(单位:cm) Fig. 3 Layout of measuring points of vault subsidence of cross section of single tunnel(unit:cm) |
| |
2.2 拱顶下沉监测结果
根据本研究的内容和要求,选取右洞YK0+530~ YK0+570的区段为研究对象,此区段最大埋置深度为21.16 m,根据现行规范的条文规定计算属浅埋隧道。YK0+570断面在隧道开挖的监测中为必测项目,对拱顶下沉共监测了38 d,直至所选区段开挖贯通,各测点在不同开挖进尺下的位移变化情况列于表 2,可看出左侧测点下沉累计8.25 mm,右侧测点下沉累计9.07 mm。从位移变化情况看,围岩变形整体已趋于稳定。
| 开挖进尺/ m | 左测点/ mm | 右测点/ mm |
| 0 | 0 | 0 |
| 2 | 1.32 | 1.3 |
| 4 | 2.029 | 2.41 |
| 6 | 2.8 | 3.17 |
| 8 | 3.1 | 3.45 |
| 10 | 2.89 | 3.38 |
| 12 | 2.28 | 3.15 |
| 14 | 3.58 | 3.94 |
| 16 | 4.89 | 4.79 |
| 18 | 5.69 | 5.43 |
| 20 | 5.94 | 5.61 |
| 22 | 5.8 | 5.84 |
| 24 | 5.77 | 5.64 |
| 26 | 6.14 | 6.07 |
| 28 | 6.8 | 6.73 |
| 30 | 7.2 | 6.58 |
| 32 | 7.97 | 6.83 |
| 34 | 8.12 | 7.01 |
| 36 | 8.33 | 7.28 |
| 38 | 8.59 | 7.35 |
| 40 | 9.07 | 7.6 |
根据现场监测中得出的量测结果可知,拱顶下沉在开挖早期的变形速率较大,开挖后12 d内的变形占整个观测周期内变形的85%,在27 d后围岩的变形趋于稳定,从此桩号的拱顶位移的监测情况来看,两侧拱顶的变化趋势是一致的。从位移变化来看,施工中选择在开挖20~26 m左右开始施做二衬是比较合理的,此时的左右侧拱顶位移值基本达到最终值的70%,施做二衬后预留部分变形后可进一步减小围岩对二衬的压力。
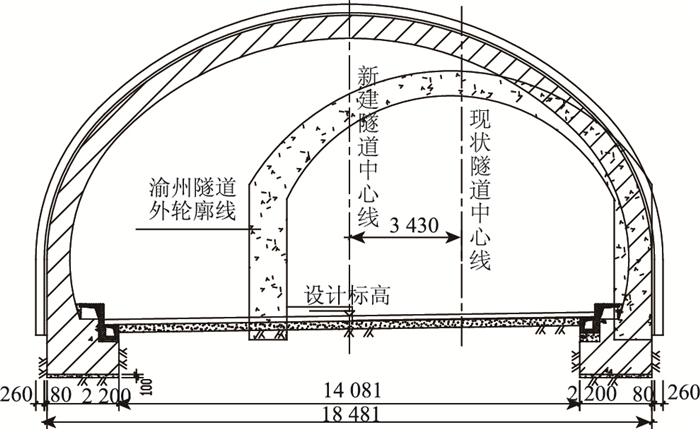
3 浅埋隧道单侧扩建三维数值分析 3.1 原施工方案数值计算还原现场施工方案拟采用全断面开挖, 见下图 4所示,由于在计算时传统的摩尔-库伦屈服准则的计算结果有较大误差,所以采用摩尔-库伦等面积圆D-P屈服准则来代替传统摩尔-库伦准则,实践也是证明了与现实情况比较接近,该准则要求偏平面上的摩尔-库伦不等角六角形与D-P圆的面积相等,故本计算采用Drucker-Prager弹塑性模型进行模拟计算采用摩尔-库伦不等角六边形外接圆D-P屈服准则[9-10],计算单元的选取时,围岩采用Solid45三维实体单元,喷射混凝土及钢拱架简化为壳单元[11-14]。桩号为YK0+530的覆盖层厚度为21.16 m,YK0+570的覆盖层厚度为20.31 m,由于此段上覆岩体的覆盖层厚度相差不大,故在三维计算时采用平均埋深20.735 m。选取从桩号YK0+570到YK0+530区段所在区域进行计算,为减少边界效应的影响,选取计算范围大于3倍洞跨,具体尺寸为160 m×40 m×50 m,数值计算模型见图 5,计算参数的选取采用地勘资料及规范的综合评定值,钢拱架的作用可采用等效方法予以考虑,将钢拱架的弹模按公式[15]进行换算给混凝土(具体参数见下表 3),隧道的开挖进尺的选取实际工程一样采用循环进尺为2.0 m。
|
| 图 4 隧道单侧扩建示意图(单位:mm) Fig. 4 Schematic diagram of single sided tunnel extension (unit:mm) |
| |
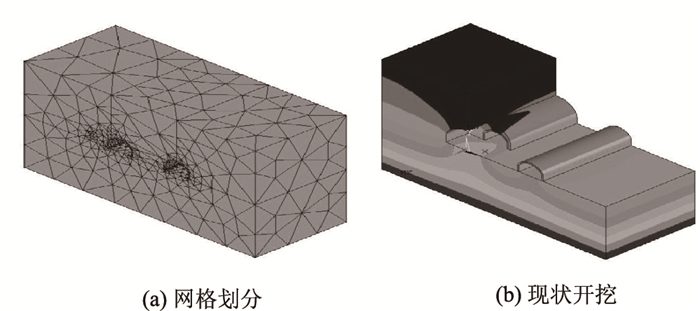
|
| 图 5 现状开挖数值计算模型图 Fig. 5 Numerical calculation model for current excavation |
| |
| 岩性 | 天然重度γ/ (kN·m-3) | 变形模量E/MPa | 泊松比μ | 内摩擦角φ/(°) | 内聚力C/kPa |
| 砂质泥岩 | 22 | 2 500 | 0.34 | 32.8 | 681 |
| C15混凝土 | 25.0 | 2 600 | 0.13 | 50.7 | 1 780 |
| 规范Ⅳ围岩 | 20~23 | 1 300~ 1 600 | 0.3~ 0.35 | 27~39 | 200~700 |
具体分析计算具体实施步骤按照:(1)按图 4和表 3确定开挖隧道的几何参数及围岩支护的力学参数;(2)确定计算区域及建立围岩支护分析模型;(3)由于隧道扩建是在原既有隧道的稳定状态下进行的,所以进行初始位移场计算时认为围岩是稳定的,直接进行计算;(4)按施工进尺进行计算,每步开挖完成立即进行初衬的施做,并进行计算;(5)直到所选区段隧道扩挖全部贯通,得到每步开挖及最终贯通后的应力场和位移场。
根据数值计算结果监测目标研究断面YK0+570拱圈处围岩拱顶处不同开挖进尺的位移,见表 4。
| 开挖进尺/m | 拱顶位移/m | |
| 左侧沉降 | 右侧沉降 | |
| 0 | 0.00 | 0.00 |
| 2 | 1.30 | 1.20 |
| 4 | 2.43 | 2.26 |
| 6 | 3.31 | 3.12 |
| 8 | 4.06 | 3.83 |
| 10 | 4.67 | 4.43 |
| 12 | 5.18 | 4.93 |
| 14 | 5.61 | 5.36 |
| 16 | 5.98 | 5.73 |
| 18 | 6.30 | 6.05 |
| 20 | 6.58 | 6.33 |
| 22 | 6.82 | 6.57 |
| 24 | 7.04 | 6.79 |
| 26 | 7.23 | 6.98 |
| 28 | 7.40 | 7.14 |
| 30 | 7.55 | 7.30 |
| 32 | 7.69 | 7.43 |
| 34 | 7.81 | 7.56 |
| 36 | 7.93 | 7.68 |
| 38 | 8.06 | 7.81 |
| 40 | 8.24 | 7.99 |
由此可以看出在距开挖面8~20 m时的沉降速率最大,20 m时达到总位移的79.9%,20 m以后速率放缓,直到选定区段开挖完成,左侧拱顶最终沉降为8.24 mm,右侧拱顶最终沉降为7.99 mm。从数据统计表中左右拱顶位移可以看出,数值计算的最终沉降结果略小于现场监测值,但两者的拱顶位移的变化趋势基本相同,证明数值计算在模拟现场施工上得出的结果是可信的。
根据计算监测隧道开挖后围岩的大主应力和小主应力的变化列于表 5。
| 进尺/ m | σ1/MPa | σ3/MPa | |||
| σ1max | σ1min | σ3max | σ3min | ||
| 0 | 0.119 | -1.08 | 0.029 | -4.81 | |
| 2 | 0.162 | -1.08 | 0.029 | -4.93 | |
| 4 | 0.165 | -1.09 | 0.029 | -5.18 | |
| 6 | 0.160 | -1.11 | 0.029 | -5.42 | |
| 8 | 0.246 | -1.12 | 0.029 | -5.56 | |
| 10 | 0.169 | -1.15 | 0.037 | -5.77 | |
| 12 | 0.203 | -1.18 | 0.040 | -5.68 | |
| 14 | 0.186 | -1.24 | 0.040 | -5.68 | |
| 16 | 0.202 | -1.32 | 0.038 | -5.60 | |
| 18 | 0.213 | -1.06 | 0.036 | -5.56 | |
| 20 | 0.220 | -1.08 | 0.034 | -5.59 | |
| 22 | 0.225 | -1.11 | 0.032 | -5.74 | |
| 24 | 0.230 | -1.13 | 0.030 | -5.81 | |
| 26 | 0.234 | -1.17 | 0.028 | -5.59 | |
| 28 | 0.237 | -1.22 | 0.029 | -5.91 | |
| 30 | 0.240 | -1.09 | 0.028 | -6.09 | |
| 32 | 0.257 | -1.10 | 0.028 | -5.70 | |
| 34 | 0.283 | -1.13 | 0.028 | -5.85 | |
| 36 | 0.316 | -1.12 | 0.028 | -5.89 | |
| 38 | 0.349 | -1.12 | 0.027 | -5.81 | |
| 40 | 0.304 | -1.14 | 0.057 | -4.05 | |
从结果中可以看出,原衬砌进行拆除后,应力会逐渐释放,随着不同的开挖进尺的进行,主应力中σ2max随开挖掌子面的推进逐渐增大为0.119~0.304 MPa,表现为洞周局部受拉;σ1min主要在1.0a~1.2 MPa左右波动,表现为受压σ3在未开挖时为4.81 MPa,当对衬砌进行拆除后压应力逐渐增大,最大压应力为开挖30 m时为6.09 MPa,此时所受的最大压应力主要表现未拆除衬砌上,当衬砌完全拆除后压应力为4.05 MPa,此时围岩释放的压应力大部分由初期支护承担,根据初期支护的抗压强度来说还是可以承担的,只需在拆除原衬砌后注意对未拆除部分进行保护,若是采用钻爆发施工时应当适当控制爆破的强度,以免对初期支护和未拆除部分原隧道衬砌造成大范围的扰动。
监测目标断面YK0+570处初衬左右拱脚、左右拱腰及拱顶处的大小主应力值列于表 6。
| 进尺/m | 左拱腰 | 右拱腰 | 拱顶 | 左拱脚 | 右拱脚 | |||||||||
| σ1/MPa | σ3/MPa | σ1/MPa | σ3/MPa | σ1/MPa | σ3/MPa | σ1/MPa | σ3/MPa | σ1/MPa | σ3/MPa | |||||
| 2 | -0.028 | -0.308 | -0.043 | -0.397 | -0.032 0 | -0.147 | -0.191 | -0.608 | -0.241 | -0.836 | ||||
| 4 | -0.022 | -0.346 | -0.039 | -0.423 | -0.016 2 | -0.090 | -0.202 | -0.715 | -0.253 | -0.935 | ||||
| 6 | -0.023 | -0.384 | -0.041 | -0.455 | -0.010 4 | -0.087 | -0.220 | -0.798 | -0.266 | -0.997 | ||||
| 8 | -0.024 | -0.415 | -0.042 | -0.480 | -0.006 6 | -0.088 | -0.234 | -0.857 | -0.278 | -1.04 | ||||
| 10 | -0.026 | -0.439 | -0.044 | -0.501 | -0.004 4 | -0.089 | -0.246 | -0.900 | -0.287 | -1.07 | ||||
| 12 | -0.027 | -0.458 | -0.045 | -0.518 | -0.003 0 | -0.091 | -0.255 | -0.932 | -0.294 | -1.10 | ||||
| 14 | -0.028 | -0.473 | -0.046 | -0.532 | -0.002 0 | -0.092 | -0.262 | -0.956 | -0.300 | -1.12 | ||||
| 16 | -0.028 | -0.486 | -0.047 | -0.544 | -0.001 3 | -0.092 | -0.268 | -0.975 | -0.305 | -1.14 | ||||
| 18 | -0.029 | -0.496 | -0.048 | -0.554 | -0.000 8 | -0.092 | -0.273 | -0.991 | -0.309 | -1.16 | ||||
| 20 | -0.030 | -0.504 | -0.049 | -0.563 | -0.000 4 | -0.092 | -0.276 | -1.000 | -0.312 | -1.17 | ||||
| 22 | -0.030 | -0.511 | -0.049 | -0.570 | -0.000 1 | -0.092 | -0.279 | -1.010 | -0.315 | -1.18 | ||||
| 24 | -0.030 | -0.517 | -0.050 | -0.576 | 0.000 2 | -0.092 | -0.282 | -1.020 | -0.318 | -1.18 | ||||
| 26 | -0.031 | -0.522 | -0.050 | -0.581 | 0.000 4 | -0.092 | -0.284 | -1.030 | -0.320 | -1.19 | ||||
| 28 | -0.031 | -0.526 | -0.051 | -0.585 | 0.000 6 | -0.092 | -0.285 | -1.030 | -0.322 | -1.19 | ||||
| 30 | -0.031 | -0.530 | -0.051 | -0.589 | 0.000 7 | -0.092 | -0.287 | -1.040 | -0.323 | -1.20 | ||||
| 32 | -0.031 | -0.533 | -0.051 | -0.592 | 0.000 9 | -0.092 | -0.288 | -1.040 | -0.324 | -1.20 | ||||
| 34 | -0.032 | -0.535 | -0.052 | -0.595 | 0.000 1 | -0.092 | -0.289 | -1.050 | -0.325 | -1.21 | ||||
| 36 | -0.032 | -0.538 | -0.052 | -0.598 | 0.001 1 | -0.092 | -0.290 | -1.050 | -0.326 | -1.21 | ||||
| 38 | -0.032 | -0.540 | -0.052 | -0.601 | 0.001 2 | -0.092 | -0.291 | -1.050 | -0.327 | -1.21 | ||||
| 40 | -0.032 | -0.544 | -0.053 | -0.604 | 0.001 4 | -0.092 | -0.293 | -1.060 | -0.328 | -1.22 | ||||
从表 6中的数据来看当开挖进尺为第一步开挖时最大为0.147 MPa,14~40 m区段压应力保持在0.092 MPa,在开挖24 m时拱顶出现拉应力,但对初衬混凝土构件来说值比较小,可以忽略,即施工过程中初期支护是安全的。
3.2 优化施工方案数值计算文献[16]和文献[17]分别进行了横向施工方案及纵向施工方案的力学行为的优化研究,这里根据前期所研究的计算方法得出的结论进行组合,确定优化施工方案。由于渝州隧道的开挖方法为单侧扩建,且为全断面开挖,故在采用横向施工方案上作比较时,也应采用全段面开挖,即根据文献[16]沿合理拱轴线进行一次开挖;纵向采用跳槽开挖,根据文献[17]的组合拱效应的计算得到合理槽宽及预留间隔均为5 m,具体开挖步序及数值计算模型见图 6和图 7。
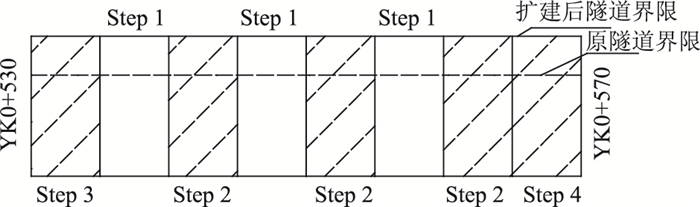
|
| 图 6 隧道扩建纵向跳槽施工界限断面示意图 Fig. 6 limiting excavation cross-section of longitudinal jump-drilling in tunnel extension |
| |
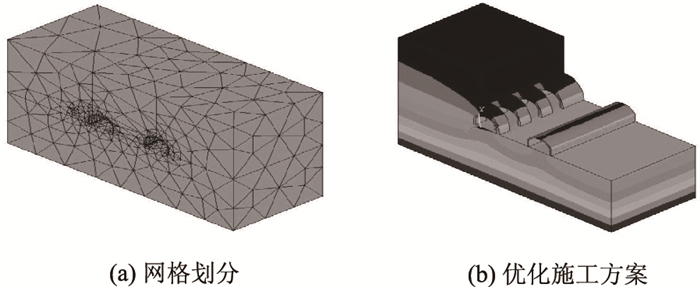
|
| 图 7 优化施工方案数值计算模型图 Fig. 7 Numerical calculation model for optimized construction scheme |
| |
Step 1:选定第1个开挖目标断面,然后每隔5 m确定其他几个同时施工的目标段,从确定的几个目标面开始同时进行开挖,横向断面仍按照合理拱轴线进行开挖,开挖完成后可立即施做初衬。
Step 2:由于Step 1完成后施做了初期支护,可以确保开挖后隧道围岩的稳定性,所以除首尾两端外,其他作为预留各段的开挖可同时进行,当开挖完成后进行初期支护。
Step 3~ Step 4:对首尾两段分别进行开挖和支护,此时完成YK0+530~YK0+570区段的开挖和初期支护,之后便可统一施作二衬。
监测优化施工方案扩建开挖的拱顶位移,列于表 7。
| 拱顶位移/ mm | 开挖进尺 | ||||
| 0 m | 15 m | 30 m | 35 m | 40 m | |
| 左侧点 | 0 | 0.95 | 2.31 | 7.02 | 7.33 |
| 右侧点 | 0 | 1.00 | 2.43 | 6.45 | 6.85 |
可以看出采用优化施工方案开挖完成后左右拱顶测点最终位移分别为7.33 mm和6.85 mm,且每步开挖的位移变化比较均匀,在step 3的开挖时虽然只向前掘进了5 m,但是对选定区段内的围岩来说,失去原隧道衬砌柱的作用后位移量变化较大,直到选定区段开挖贯通后位移区域稳定。
将优化后施工方案每步开挖计算后监测的大小主应力的最大最小值列于表 8。
| 开挖步序 | σ1max | σ1min | σ1max | σ1min |
| Step 0 | 0.089 | -0.806 | 0 | -5.46 |
| Step 1 | 0.297 | -1.05 | 0 | -6.27 |
| Step 2 | 0.314 | -1.24 | 0.020 | -7.02 |
| Step 3 | 0.310 | -0.832 | 0.020 | -5.85 |
| Step 4 | 0.237 | -0.827 | 0.030 | -4.09 |
可以看出, 在对原衬砌进行跳格拆除后,应力会逐渐释放转移到未拆除的原衬砌上,随着不同的开挖步,主应力中σ2max随跳槽开挖的进行会有相应的变化(先增大后减小),从0.089 MPa增大到0.314 MPa,表现为原隧道洞周出现局部受拉,隧道贯通后为0.237 MPa,此时的拉应力为隧道地面底鼓产生的力。σ2min先增大后减小,开挖前和开挖后的应力基本表现为受压。σ3max随着不同开挖步的进行而逐渐增大,但在受力上表现也不太明显;σ3min的变化趋势较为明显,从各步的小主应力变化来看,也主要表现在原衬砌的受压且先大后小,这是由于跳槽开挖使上覆岩土体的拱效应发挥出来,理由同文献[17]中所述,两边跳槽后产生的拱效应的拱脚力全部作用在原衬砌上,所以在实际开挖过程中可适当在计算槽宽的基础上多预留原衬砌的长度,以此保证跳槽开挖时的围岩稳定性,当开挖完成后, 围岩应力进行释放调整产生的压应力大部分由施做的初期支护承担。
从计算得出的初衬大主应力值可以看出,在开挖过程中,最大压应力出现在开挖贯通后为1.36 MPa,基本没有出现拉应力,而现状渝州隧道的施工方法的初衬贯通后初衬最大压应力为1.22 MPa,拱顶会出现局部拉应力为0.349 MPa,从受力角度可以得出改进方法比现状渝州隧道的施工方法有着较显著的优势,将优化施工方案不同开挖进尺时的初衬左右拱腰、左右拱脚及拱顶处的主应力列于表 9。
| 进尺/m | 左拱腰 | 右拱腰 | 拱顶 | 左拱脚 | 右拱脚 | |||||||||
| σ1/MPa | σ3/MPa | σ1/MPa | σ3/MPa | σ1/MPa | σ3/MPa | σ1/MPa | σ3/MPa | σ1/MPa | σ3/MPa | |||||
| 15 | -0.212 | -0.678 | -0.156 | -0.506 | -0.143 | -0.434 | -0.341 | -0.833 | -0.457 | -1.100 | ||||
| 30 | -0.244 | -0.775 | -0.163 | -0.564 | -0.176 | -0.495 | -0.395 | -0.914 | -0.498 | -1.190 | ||||
| 35 | -0.030 | -0.374 | -0.034 | -0.277 | -0.0113 | -0.128 | -0.288 | -0.950 | -0.326 | -1.350 | ||||
| 40 | -0.030 | -0.379 | -0.034 | -0.280 | -0.013 | -0.129 | -0.291 | -0.958 | -0.328 | -1.360 | ||||
4 结果比较分析 4.1 原方案计算与现场监测位移比较
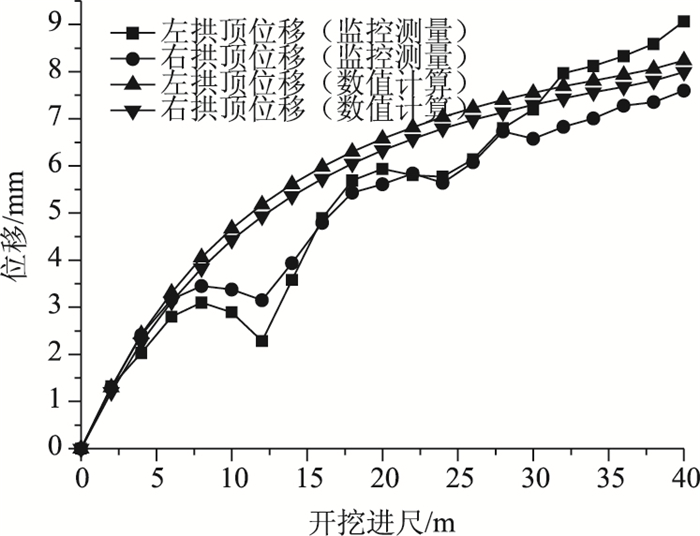
从现场监控测量和数值模拟计算结果曲线绘于图 8。
|
| 图 8 监控测量和数值计算的拱顶位移曲线 Fig. 8 Vault displacement curves of monitoring measurement and numerical calculation |
| |
从图 8可以看出,现场监控测量与数值模拟计算所得左右拱顶位移相差不大,开挖进尺为32 m之前数值计算的位移略大于现场实测值,开挖完成后的最终沉降值略小于现场实测值为0.84 mm。但两者的变化趋势是一致的,两者的区别究其原因是数值模拟采用的是理想弹塑性条件下有限元计算模型,而实际工程中的岩石介质是非完全弹塑性介质,需考虑天然裂隙及孔隙水的影响,同时在钻爆法施工条件下,岩体的性质又会发生变化,所以导致结果的不一致性。
此外,根据两者的数据对比发现,单侧扩建时左侧拱顶产生的位移大于右侧拱顶,即在单侧扩建时远离原隧道一侧受力条件比靠近原隧道一侧要差,在具体的施工过程中需要重点监测远离原隧道一侧的位移变化情况,以便及时做出相应措施进行支护。
4.2 优化方案与原方案比较(1)位移比较
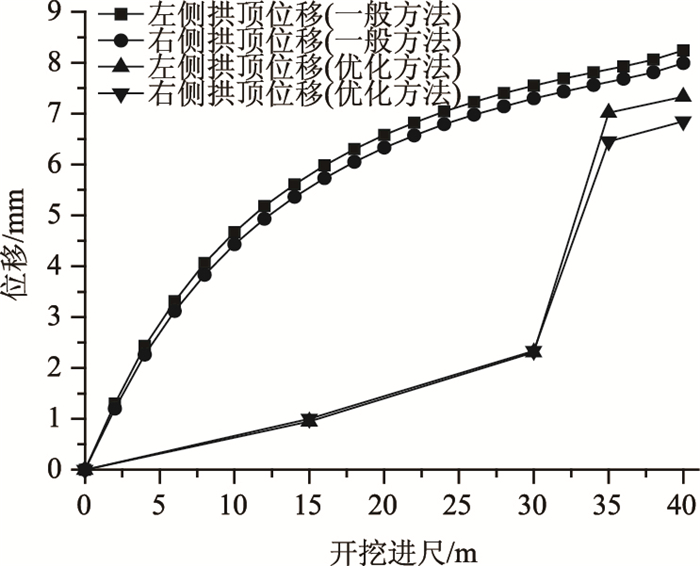
将前面计算出的两种方案的拱顶位移绘于图 9。
|
| 图 9 优化方案与原方案计算的拱顶位移曲线 Fig. 9 Calculated vault displacements of optimized construction scheme and original scheme |
| |
根据优化方案与原方案计算的拱顶位移曲线可以看出,整个开挖过程中优化方案的开挖方法的拱顶位移均比原方案小,在整体开挖进尺为30 m时,优化方案产生的拱顶位移约为原方案的28%,所选定的区段全部贯通后,所选桩号断面的拱顶最终沉降位移比渝州现状开挖方法小14%左右,但是从曲线上看在开挖30 m时位移发生突变(左侧拱顶从2.31~7.02 mm,右侧拱顶从2.34~6.45 mm),此时是因为选定区域内中间部分移除后, 在开挖首尾部分时消去原衬砌的支撑作用使得因掏槽后产生的岩石拱失去了拱脚,因而发生位移的突变[18]。所以单从拱顶位移角度来看,优化的施工方案明显发挥了其优势,此法能够有效地利用原隧道衬砌的支撑作用抵制围岩自动调整产生的位移进一步发展。
所以在施工过程中(首尾预留段位开挖前),先对中间部分进行跳槽开挖,直到初期支护和二次衬砌全部施做完成后再将首尾预留段挖除,这样既避免了在进洞和出洞时对围岩的大范围破坏,也可相应地减少常规的高密度支护来保持洞口的围岩稳定性。若围岩稳定性本身比较差,可以在中间部分围岩全部挖除并完成二衬的施做后,通过管棚施工及预加固手段来降低口部因既有衬砌拆除后产生的位移突变。
(2)应力比较
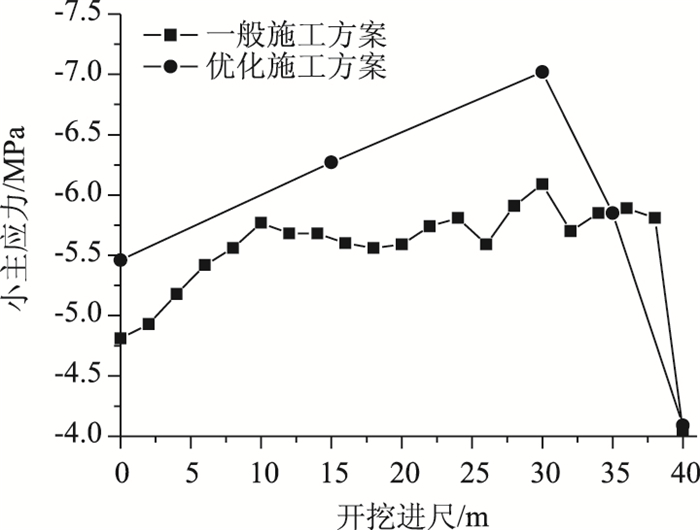
从图 10曲线可知,现状开挖方案的小主应力随开挖进尺的增加先增大至6.09 MPa,开挖完成后逐渐降低至4.05 MPa,此时的最小小主应力表现在初期支护上;优化施工方案的小主应力随开挖进尺的增加也是先增大至7.02 MPa,开挖完成后逐渐降低至4.09 MPa。在开挖完成后优化施工方案的初期支护最大压应力大于现状施工方案,在开挖过程中,由于优化施工方案纵向采用跳槽开挖,使得间隔开挖后的围岩形成岩石拱将部分压力传递到未开挖的原隧道衬砌上,增加了原隧道衬砌的压应力。
|
| 图 10 初衬砌小主应力随开挖进尺的变化 Fig. 10 Minimum primary stress of original lining in different footages |
| |
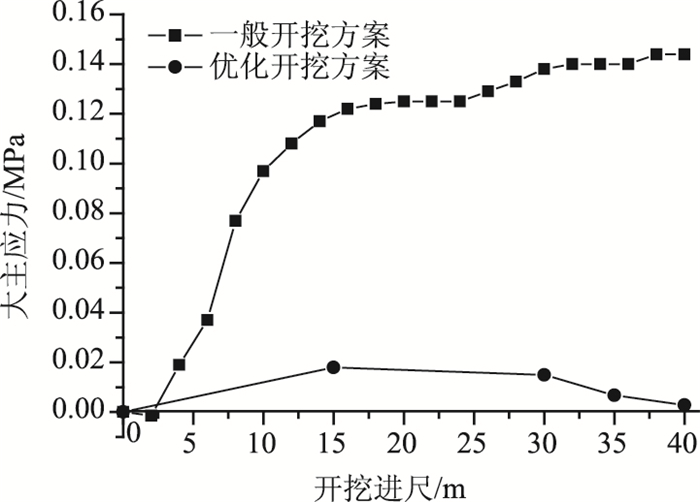
其次,比较在开挖过程中直到所选区段全部贯通后各开挖断面中最大拉应力,将结果绘于图 11。
|
| 图 11 初衬大主应力随开挖进尺的变化 Fig. 11 Maximum primary stress of original lining in different footages |
| |
由曲线图可以看出采用优化的施工方案能够有效减小衬砌的拉应力,在隧道开挖贯通后,优化的施工方案的拉应力基本为零,而原开挖方案在开挖完成后最大拉应力为0.144 MPa,实践证明采用横向合理拱轴线布置,纵向采用跳槽开挖的优化方案不但能够减小拱顶沉降,还降低了衬砌的拉应力。
5 结论依托渝州隧道扩建实例,对本研究所提出的浅埋隧道单侧扩建优化施工方案进行了计算验证,得到如下结论:
(1) 通过ANSYS三维有限元进行了施工的过程模拟与现场监控量测对比,左右侧拱顶位移变化计算值与监控量测值总体吻合较好,证明采用数值计算模拟隧道施工是可行的。
(2) 采用优化施工方案时,随着开挖掌子面的推进,原衬砌受压应力变大,证明纵向跳槽开挖时未拆除的原隧道衬砌能够发挥柱的作用,承担因跳槽开挖而产生的围岩压力,提高了施工的安全稳定性。
(3) 数值模拟结果表明,优化方案在一定程度上改变了原围岩的应力路径,能够充分调动围岩的自稳能力,计算后,拱顶的最大位移约为7.33mm,平均比渝州隧道现状开挖方式的计算小约16%~20%,拱顶基本不出现受拉区域。
(4) 由于采用了纵向跳槽开挖,在确保围岩受力稳定的同时,间隔区段内同时平行开挖,可有效缩短施工工期,说明采用优化施工方案优势明显,可为类似工程的施工提供借鉴。
| [1] |
钱七虎. 迎接我国城市地下空间开发高潮[J]. 岩土工程学报, 1998, 20(1): 112-113. QIAN Qi-hu. Greeting Development Climax of Urban Underground Space in China[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(1): 112-113. |
| [2] |
刘冬, 高文学, 孙宝平, 等. 既有隧道扩建爆破振动数值模拟研究[J]. 岩土力学, 2016, 37(10): 3011-3017. LIU Dong, GAO Wen-xue, SUN Bao-ping, et al. Numerical Simulation of Blasting Vibration on Existing Tunnel Extension[J]. Rock and Soil Mechanics, 2016, 37(10): 3011-3017. |
| [3] |
李元福. 关村坝隧道改扩建施工技术[J]. 铁道建筑技术, 1996(4): 22-26. LI Yuan-fu. Construction Technology of Tunnel Extension for Guancunba Tunnel[J]. Railway Construction Technology, 1996(4): 22-26. |
| [4] |
彭念.原位扩建隧道围岩力学响应机理研究[D].重庆: 重庆大学, 2010. PENG Nian. Study on Surrounding Rock Mechanical Response Mechanism of In-situ Expanded Tunnel[D]. Chongqing: Chongqing University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10611-1011265506.htm |
| [5] |
高干, 刘元雪, 徐光伟, 等. 隧道扩建爆破震动控制研究[J]. 地下空间与工程学报, 2010, 6(6): 1285-1294. GAO Gan, LIU Yuan-xue, XU Guang-wei, et al. Study on the Blasting Vibration in Tunnel Extension[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(6): 1285-1294. |
| [6] |
高干, 刘元雪, 周结中, 等. 地下空间扩建型式研究[J]. 现代隧道技术, 2010, 6(6): 1-9. GAO Gan, LIU Yuan-xue, ZHOU Jie-zhong, et al. Study on Underground Space Enlargement Options[J]. Modern Tunnelling Technology, 2010, 6(6): 1-9. |
| [7] |
LUNARDI P. Widening the Load at Nazzano[J]. Tunnels & Tunneling International, 2003(7): 16-19. |
| [8] |
OZSANA A, KARPUZB C. Preliminary Support Design for Ankara Subway Extension Tunnel[J]. Engineering Geology, 2001, 59: 161-172. |
| [9] |
郑颖人, 赵尚毅, 李安洪. 有限元极限分析法及其在边坡中的应用[M]. 北京: 人民交通出版社, 2011. ZHENG Yin-ren, ZHAO Shang-yi, LI An-hong, et al. FEM Limit Analysis and Its Application in Slope Engineering[M]. Beijing: China Communications Press, 2011. |
| [10] |
安永林, 黄戡, 彭立敏, 等. 强度折减法分析隧道整体稳定性[J]. 公路交通科技, 2001, 28(4): 91-96. AN Yong-lin, HUANG Kan, PENG Li-min, et al. Analysis of Tunnel Stability Based on Strength Reduction Method[J]. Journal of Highway and Transportation Research and Development, 2001, 28(4): 91-96. |
| [11] |
李煜川.既有隧道扩建工程的施工力学行为研究[D].成都: 西南交通大学, 2008. LI Yu-chuan. Study on Mechanical Behavior of Extension of Existing Tunnel Project[D]. Chendu: Southwest Jiaotong University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10613-2008177519.htm |
| [12] |
BHASIN R, GRIMSTAD E. The Use of Stress-strength Relationships in the Assessment of Tunnel Stability[J]. Tunnelling and Underground Space Technology, 1996, 11(1): 93-98. |
| [13] |
吴祖松.公路隧道围岩压力计算方法与监测研究[D].重庆: 重庆交通大学, 2008. WU Zu-song. Research on Calculation Method and Monitoring of Surrounding Rock Pressure for Highway Tunnel[D]. Chongqing: Chongqing Jiaotong University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10618-2008071368.htm |
| [14] |
王永甫.有限元强度折减法在隧洞稳定性分析中的应用[D].重庆: 重庆交通大学, 2010. WANG Yong-fu. Application of Strength Reduction Finite Element Method in Tunnel Stability Analysis[D]. Chongqing: Chongqing Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10618-2010160576.htm |
| [15] |
王显春, 庄纪栋, 张宏博. 软岩浅埋隧道施工对地表及围岩变形的影响分析[J]. 隧道建设, 2006, 26(1): 21-24. WANG Xian-chun, ZHUANG Ji-dong, ZHANG Hong-bo. Analysis on Impact of Construction of Shallow-buried Soft Ground Tunnels on Deformations of Ground Surface and Surrounding Rock Mass[J]. Tunnel Construction, 2006, 26(1): 21-24. |
| [16] |
谭仪忠, 刘元雪, 周结中. 隧道扩建合理开挖步序的研究[J]. 后勤工程学院学报, 2011, 27(5): 8-12. TAN Yi-zhong, LIU Yuan-xue, ZHOU Jie-zhong. Research on Proper Excavation Steps in Tunnel Extension[J]. Journal of Logistical Engineering University, 2011, 27(5): 8-12. |
| [17] |
谭仪忠, 刘元雪, 周家伍. 隧道单侧扩建跳槽式开挖方法合理槽宽的确定[J]. 地下空间与工程学报, 2013, 9(1): 147-154. TAN Yi-zhong, LIU Yuan-xue, ZHOU Jia-wu. The Proper Driving Footage in the Jump-driving Method for Single-sided Tunnel Extension[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(1): 147-154. |
| [18] |
杨明辉, 汪罗成, 赵明华. 考虑土拱效应的双排抗滑桩桩侧土压力计算[J]. 公路交通科技, 2011, 28(10): 12-18. YANG Ming-hui, WANG Luo-cheng, ZHAO Ming-hua. Calculation of Soil Pressure against Double-row Anti-slide Piles Considering Soil Arching Effect[J]. Journal of Highway and Transportation Research and Development, 2011, 28(10): 12-18. |
 2019, Vol. 36
2019, Vol. 36
