扩展功能
文章信息
- 胡鸿运, 周晓军, 陈韬
- HU Hong-yun, ZHOU Xiao-jun, CHEN Tao
- 顺层岩体隧道地震行波效应的不对称性
- Asymmetry of Traveling Wave Effect of Seismic on Tunnel in Bedding Rock Mass
- 公路交通科技, 2019, 36(4): 102-107
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(4): 102-107
- 10.3969/j.issn.1002-0268.2019.04.015
-
文章历史
- 收稿日期: 2017-06-20
2. 四川建筑职业技术学院, 四川 成都 610399;
3. 西南交通大学 交通运输与物流学院, 四川 成都 610031
2. Sichuan College of Architectural Technology, Chengdu 610399, China;
3. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu Sichuan 610031, China
一方面,多项研究表明[1-7],对于隧道这样纵向尺度远大于横向尺度的细长结构,因地震波斜入射而产生的行波效应会显著增加隧道结构的内力和位移响应,从而对隧道抗震产生不利影响。另一方面,因大量震害表明隧道所处岩层结构对衬砌的地震响应影响极大[8-9],且隧道穿越软硬互层岩体时其衬砌的震害更是不容忽视[10]。可见,有必要开展研究层状岩体隧道在斜入射地震波作用下的行波效应特征。而顺层岩体隧道[11]作为层状岩体隧道的典型,更有必要研究其行波效应的特征。
目前,对于行波效应下隧道的抗震研究主要集中于盾构隧道、沉管隧道或均质岩体隧道[1-7],尚未检索到顺层岩体隧道地震行波效应的相关文献。
此外,隧道抗减震研究多将岩体简化为各向同性介质[12-13],但对于顺层岩体而言,将其简化为横观各向同性介质才能更为合理、真实地反映地震波对顺层岩体隧道的作用[11]。
为此,本研究将基于顺层岩体的横观各向同性的弹性本构关系,应用黏弹性边界的时域波动理论及输入方法[11],针对地震qP波入射方向与隧道纵断面平行但与隧道纵轴线不平行的情形,以某顺层岩体高铁隧道为工程背景,采用ANSYS软件进行数值分析,研究岩层倾角、岩层各向异性强度对隧道地震行波效应的影响。
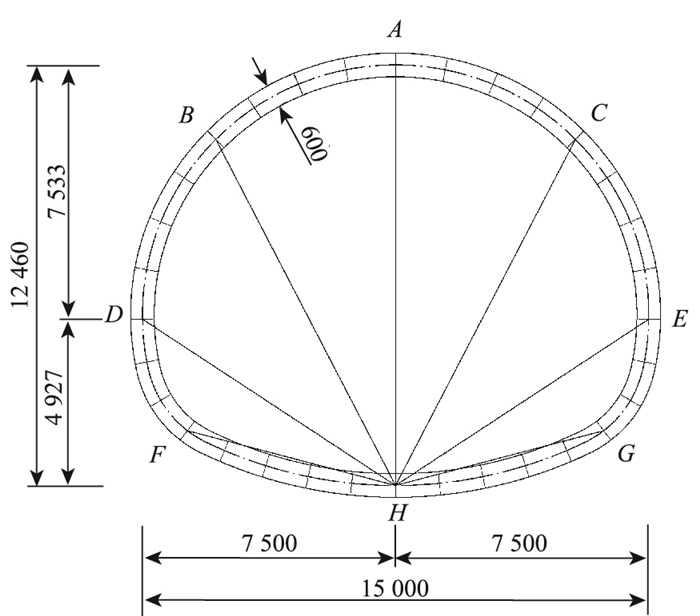
1 参数及计算模型 1.1 衬砌参数本研究选取衬砌断面如图 1所示:最大开挖宽度为15 m;二次衬砌厚度为600 mm,采用C35钢筋混凝土浇注,重度为25 kN/m3,泊松比0.2,弹性模量为31.5 GPa;研究中略去加固层和初期支护,以更为清晰地观察顺层岩体隧道地震纵向行波效应的规律。
|
| 图 1 衬砌断面尺寸及单元划分示意图(单位:mm) Fig. 1 Schematic diagram of section size and elements of lining(unit:mm) |
| |
1.2 岩体参数
为展开对比分析,从而得出鲜明可靠的结论,本研究设定5组顺层岩体,5组顺层岩体的重度均为27.0 kN/m3,平行于层面的弹性模量均为22.0 GPa,平行于层面的泊松比均为0.24,垂直于层面的弹性常数详见表 1,岩体组编号D1~D5,依顺序其各向异性强度依次增强且增幅均匀[14-16]。
| 岩体组编号 | D1 | D2 | D3 | D4 | D5 | |
| 垂直层面 | 弹性模量/GPa | 17.0 | 15.0 | 13.0 | 11.0 | 9.0 |
| 剪切模量/GPa | 7.2 | 6.2 | 5.2 | 4.2 | 3.2 | |
| 泊松比 | 0.26 | 0.26 | 0.26 | 0.26 | 0.26 | |
1.3 计算模型
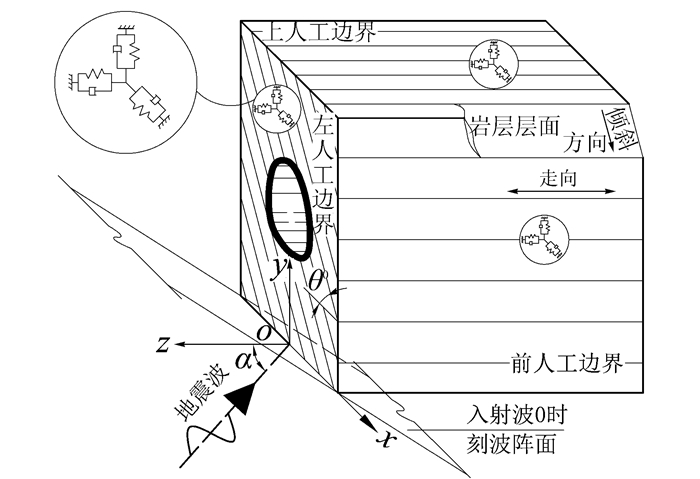
计算模型如图 2所示。其中,地震波场仅考虑入射波场和隧道反射波场,以更好地揭示顺层岩体隧道一般性的行波效应特征[11, 14];在有限计算区域(1 km的立方体,在ANSYS中采用单元solid45和shell63分别模拟围岩和二次衬砌)6个边界面上设置近似黏弹性边界(采用单元combin14模拟,弹簧刚度和阻尼系数计算详见文献[11])模拟无限域,积分步长0.01 s。
|
| 图 2 计算模型示意图 Fig. 2 Schematic diagram of calculation model |
| |
所建立的有限元模型中,隧道衬砌位移检测点A~H的布置如图 1所示。
图 2中,oxyz为观察坐标系(总体坐标系),ox′y′z′为传播坐标系。α为地震波入射角,即z轴与-z′′轴的夹角; θ0为岩层倾角[11]。
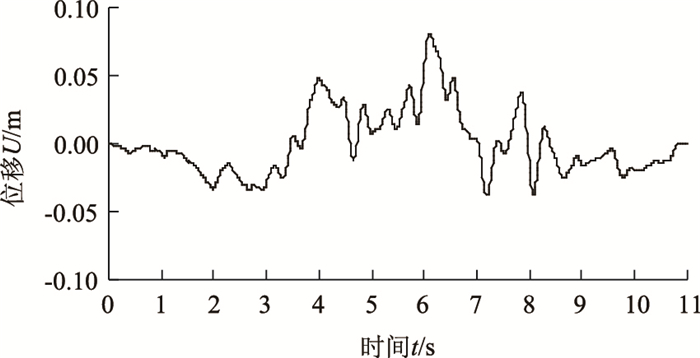
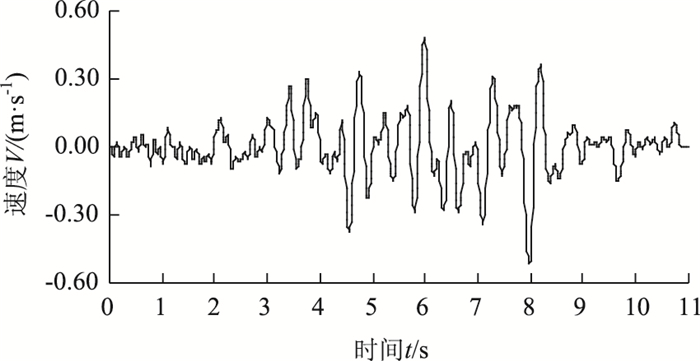
2 地震波参数工程所处地区设定抗震设防烈度为8度,设计基本地震加速度值为0.20g,设计地震分组为第1组(Ⅰ类场地,特征周期0.25 s),因此,提取汶川地震卧龙波中10~21 s波段,详见图 3和图 4。
|
| 图 3 入射波的位移时程 Fig. 3 Displacement time history of incident wave |
| |
|
| 图 4 入射波的速度时程 Fig. 4 Velocity time history of incident wave |
| |
3 顺层岩体中地震波的输入方法 3.1 波动输入公式
将地震动换算为边界节点的等效荷载,其计算公式为[17-18]:
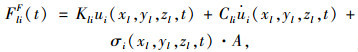
|
(1) |
式中, l为边界节点;i为方向;FliF (t)为节点等效荷载;xl,yl和zl为节点坐标;Kli为弹性系数;Cli为黏性系数;A为点l所代表的面积;已知入射的自由波场为u0 (x, y, z, t),其在边界上产生位移为:ui (xl, yl, zl, t), 速度为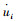
各边界上的位移分别为[11]:
(1) 入射波在z′轴向的位移分量
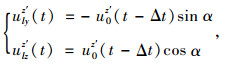
|
(2) |
式中,u0z′ (t-Δt)为入射波在z′上的位移分量,其在y轴上的投影为ulyz′ (t),在z轴上的投影为ulzz′ (t)。
(2) 入射波在y′轴向的位移分量
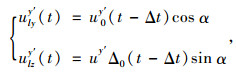
|
(3) |
式中,u0y′ (t-Δt)为入射波在y′上的位移分量,其在y轴上的投影为ulyy′(t),在z轴上的投影为ulzy′ (t)。
(3) 入射波在x′轴向的位移分量
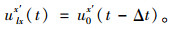
|
(4) |
式中,u0x′ (t-Δt)为入射波在x′上的位移分量,其在x轴上的投影为ulxx′ (t)。
对位移分量求导,即可得出速度分量[11]。
(4) 入射波的延迟时间
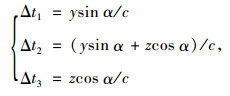
|
(5) |
式(2)~(3)中,Δt为入射波从零时刻波阵面传播到人工边界节点l所需时间,具体Δt1,Δt2,Δt3为相对于零时刻波阵面的延迟时间,分别对应入射qP波到达左边界、前后边界和底边界的情况;c为入射波波速;y和z分别为边界面点l到底边界和左边界的距离。
3.3 输入的等效节点力通过应力变换公式,将ox′y′z′坐标系下的一点应力状态变换至总体坐标系oxyz下,并具体化到黏弹性边界上,即得出人工边界上的等效节点力[11]。
4 岩层倾角对行波效应不对称的影响 4.1 工况设计本节分别选取表 1中岩层组D1和D3,并设定qP波10种工况,详见表 2。其中,岩层倾角分别设置为0°,25°,45°,70°和90°。工况编号说明:以D1-25°为例,D1为地层编号,25°为岩层倾角,余类推。
| 工况 | 偏振向量的纵波分量pz′ | 相速度/(m·s-1) |
| D1-0° | 0.998 | 2 936.9 |
| D1-25° | 0.997 | 2 981.2 |
| D1-45° | 0.997 | 3 065.0 |
| D1-70° | 0.999 | 3 169.0 |
| D1-90° | 1.000 | 3 201.4 |
| D3-0° | 0.993 | 2 753.0 |
| D3-25° | 0.988 | 2 841.0 |
| D3-45° | 0.986 | 3 018.1 |
| D3-70° | 0.997 | 3 241.3 |
| D3-90° | 1.000 | 3 309.8 |
表 2中,地震波偏振向量的纵波分量pz′均大于0.986,这表明D1组或D3组岩层中各工况所略去的横波分量均比较小。
4.2 相对位移的结果与分析隧道衬砌在斜入射qP波的作用下,横断面会产生扭曲变形,即横断面不再是一个平面,而是一个不规则的曲面;该曲面不规则的程度,可以采用在隧道纵轴线向上横断面衬砌各检测点相对衬砌某点的位移来表征。其中,dAH为A点和H点之间的相对位移,dBH~dGH类推。提取拱顶/仰拱弯矩峰值时刻的相对位移,详见表 3。
| 工况 | 时间/s | 检测点间相对位移/mm | ||||||
| dAH | dBH | dCH | dDH | dEH | dFH | dGH | ||
| D1-0° | 8.70 | 12.32 | 10.42 | 10.42 | 5.72 | 5.72 | 2.26 | 2.26 |
| D1-25° | 8.69 | 11.28 | 9.83 | 9.29 | 5.62 | 4.91 | 2.32 | 1.83 |
| D1-45° | 8.69 | 11.56 | 10.11 | 9.47 | 5.83 | 4.98 | 2.43 | 1.86 |
| D1-70° | 8.69 | 12.19 | 10.45 | 10.16 | 5.87 | 5.48 | 2.39 | 2.12 |
| D1-90° | 8.69 | 12.48 | 10.55 | 10.55 | 5.80 | 5.80 | 2.31 | 2.31 |
| D3-0° | 8.71 | 13.85 | 11.67 | 11.67 | 6.30 | 6.30 | 2.46 | 2.46 |
| D3-25° | 8.70 | 13.48 | 12.18 | 10.52 | 7.18 | 5.07 | 3.10 | 1.67 |
| D3-45° | 8.70 | 13.79 | 12.69 | 10.6 | 7.67 | 5.04 | 3.40 | 1.63 |
| D3-70° | 8.69 | 13.66 | 12.34 | 10.75 | 7.39 | 5.34 | 3.26 | 1.85 |
| D3-90° | 8.69 | 13.92 | 11.77 | 11.77 | 6.50 | 6.50 | 2.62 | 2.62 |
由表 3中数据可知:当岩层倾角为0°(即岩层水平)或90°(即岩层竖直)时,横断面左右对称位置上的相对位移相等,即横断面仍为平面;而当岩层倾角不为0°或90°(即岩层倾斜)时,左右对称位置上的相对位移却不等,即隧道衬砌横断面被扭为曲面,即由qP波斜入射引起的行波效应不对称。因该不对称性与岩层倾角相关,为分析二者之间的规律,定义参数位移差δU,其计算公式为:
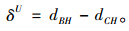
|
(6) |
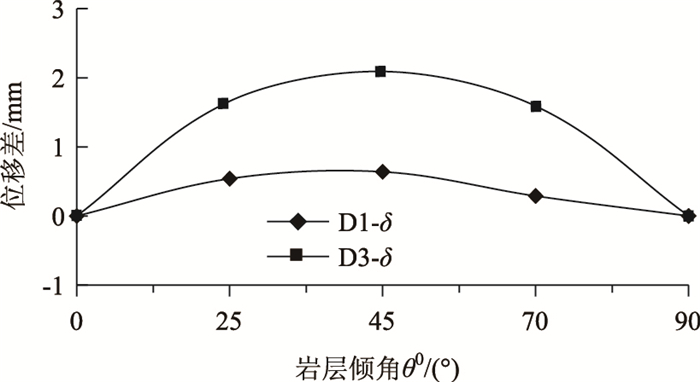
取表 3中数据,采用式(6)计算位移差,绘制图 5。由图 5可知:行波效应的不对称性随着岩层倾角的增大而先增强后减弱(约45°时不对称性最强),为非线性关系;也可见岩层倾角对行波效应不对称性的影响较为明显。
|
| 图 5 纵向对角线位移差曲线 Fig. 5 Curves of longitudinal diagonal displacement difference |
| |
5 岩层各向异性对行波效应不对称性的影响 5.1 工况设计
为进一步研究岩层倾斜时,岩层各向异性对行波效应不对称性的影响,选取D1~D5组岩层,30°和60°倾角进行计算。限于篇幅,本节设定qP波10种工况,见表 4。
| 工况 | 偏振向量的纵波分量pz′ | 相速度/(m·s-1) |
| D1-30° | 0.996 | 2 999.4 |
| D2-30° | 0.992 | 2 931.9 |
| D3-30° | 0.986 | 2 878.7 |
| D4-30° | 0.978 | 2 852.5 |
| D5-30° | 0.967 | 2 883.0 |
| D1-60° | 0.998 | 3 132.5 |
| D2-60° | 0.996 | 3 137.9 |
| D3-60° | 0.993 | 3 163.4 |
| D4-60° | 0.989 | 3 222.7 |
| D5-60° | 0.984 | 3 349.8 |
表 4中,偏振向量的纵波分量pz′在岩层倾角为30°或60°时均大于0.966,可知各工况所略去的横波分量均比较小。
5.2 相对位移的结果与分析提取拱顶/仰拱弯矩峰值时刻隧道衬砌横断面沿隧道轴线方向上的相对位移,见表 5。
| 工况 | 时间/s | 检测点间相对位移/mm | ||||||
| dAH | dBH | dCH | dDH | dEH | dFH | dGH | ||
| D1-30° | 8.69 | 11.34 | 9.91 | 9.31 | 5.69 | 4.90 | 2.37 | 1.82 |
| D2-30° | 8.70 | 13.12 | 11.56 | 10.63 | 6.69 | 5.48 | 2.82 | 1.99 |
| D3-30° | 8.70 | 13.70 | 12.50 | 10.59 | 7.47 | 5.04 | 3.27 | 1.63 |
| D4-30° | 8.70 | 13.26 | 12.77 | 9.43 | 8.02 | 3.77 | 3.73 | 0.82 |
| D5-30° | 8.70 | 13.00 | 12.87 | 8.83 | 8.32 | 3.03 | 4.00 | 0.30 |
| D1-60° | 8.69 | 11.92 | 10.32 | 9.85 | 5.87 | 5.25 | 2.42 | 2.00 |
| D2-60° | 8.69 | 12.42 | 11.03 | 10.00 | 6.48 | 5.14 | 2.78 | 1.86 |
| D3-60° | 8.69 | 13.32 | 12.36 | 10.19 | 7.61 | 4.82 | 3.44 | 1.53 |
| D4-60° | 8.69 | 14.40 | 13.63 | 10.75 | 8.63 | 4.83 | 4.07 | 1.36 |
| D5-60° | 8.69 | 16.87 | 15.83 | 12.83 | 9.98 | 5.99 | 4.67 | 1.86 |
由表 5可知:各工况下,隧道横断面左右对称位置的纵向相对位移不等,即行波效应不对称;且不对称的幅度也因地层而异。但众所周知,随着岩层组强度的降低,衬砌地震响应会增强,为消除其对行波效应不对称性的影响,从而分析岩层各向异性与行波效应不对称性二者间的关系,定义位移比κU:
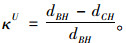
|
(7) |
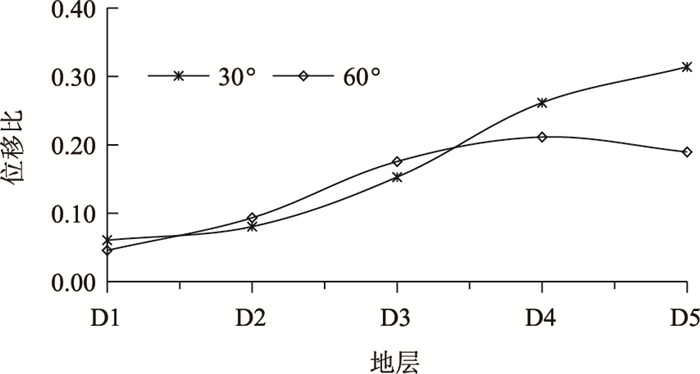
采用式(7)计算位移比,绘制如图 6所示。
|
| 图 6 纵向位移比曲线 Fig. 6 Curves of longitudinal displacement ratio |
| |
根据图 6可知,随着岩层各向异性强度的增强,位移比增强,且呈近似线性关系。其中,仅在岩层倾角为60°时,D5组与D4组数值相近。该结果充分表明:同等强度的地震波斜入射时,剔除不同岩层强度所产生的影响后,顺层岩体中隧道衬砌横断面被扭曲的幅度随着岩层各向异性的增强而增强,也即行波效应随岩层各向异性的增强而增强,且呈近似线性关系。
6 结论地震qP波沿隧道纵断面斜入射时:
(1) 横断面在岩层水平或竖直时却仍为平面,而岩层倾斜时却被扭为曲面,即地震行波效应是不对称的。且在本研究所有算例中,不对称性随岩层倾角的增大而先增强后减弱。
(2) 随岩层各向异性强度的增强,行波效应的不对称性也增强,并呈近似线性关系,也即衬砌横断面被扭转为不规则曲面后,其不对称程度随岩层各向异性的增强而线性增强。
| [1] |
JOHN ST C M, ZAHRAH T F. Aseismic Design of Underground Structures[J]. Tunnelling and Underground Space Technology, 1987, 2(2): 165-197. |
| [2] |
HASHASH Y M A, HOOK J J, SCHMIDT B, et al. Seismic Design and Analysis of Underground Structures[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2001, 16(4): 247-293. |
| [3] |
梁庆国, 边磊, 张钦鹏, 等. 大断面黄土隧道洞口段地震动力特性研究[J]. 公路交通科技, 2018, 35(7): 65-76. LIANG Qing-guo, BIAN Lei, ZHANG Qin-peng, et al. Study on Seismic Dynamic Characteristics of Large Section Loess Tunnel Portal[J]. Journal of Highway and Transportation Research and Development, 2018, 35(7): 65-76. |
| [4] |
张晋东, 梁庆国, 蒲建军, 等. 不同进洞高程黄土隧道洞口段振动台模型试验研究[J]. 公路交通科技, 2018, 35(7): 77-85. ZHANG Jin-dong, LIANG Qing-guo, PU Jian-jun, et al. Experimental Study on Shaking Table Model of Portal Section of Loess Tunnel with Different Tunneling Elevations[J]. Journal of Highway and Transportation Research and Development, 2018, 35(7): 77-85. |
| [5] |
YU H T, YAN X, BOBET A, et al. Multi-point Shaking Table Test of a Long Tunnel Subjected to Non-Uniform Seismic Loadings[J]. Bulletin of Earthquake Engineering, 2017(9): 1-19. |
| [6] |
晏启祥, 刘记, 何川. 公路盾构隧道地震响应的反应位移法分析[J]. 公路交通科技, 2011, 28(4): 96-99. YAN Qi-xiang, LIU Ji, HE Chuan. Analysis on Seismic Response of Highway Shield Tunnel Using Response Displacement Method[J]. Journal of Highway and Transportation Research and Development, 2011, 28(4): 96-99. |
| [7] |
袁勇, 禹海涛, 燕晓, 等. 超长沉管隧道多点振动台试验模拟与分析[J]. 中国公路学报, 2016, 29(12): 157-165. YUAN Yong, YU Hai-tao, YAN Xiao, et al. Multi-point Shaking Table Test Simulation and Analysis of a Super-long Immersed Tunnel[J]. China Journal of Highway and Transport, 2016, 29(12): 157-165. |
| [8] |
OKAMOTO S. Introduction to Earthquake Engineering[M]. 2nd ed. Tokyo: University of Tokyo Press.
|
| [9] |
SHARMA S, JUDD W R. Underground Opening Damage From Earthquakes[J]. Engineering Geology, 1991, 30(3/4): 263-276. |
| [10] |
吉随旺, 唐永建, 胡德贵, 等. 四川省汶川地震灾区干线公路典型震害特征分析[J]. 岩石力学与工程学报, 2009, 28(6): 1250-1260. JI Sui-wang, TANG Yong-jian, HU De-gui, et al. Analysis of Typical Seismic Damages of Highways in Wenchuan Earthquake-induced Hazard Areas in Sichuan Province[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(6): 1250-1260. |
| [11] |
张斌伟, 严松宏, 杨永东. 山岭隧道横截面抗震分析的近似方法[J]. 公路交通科技, 2012, 29(3): 118-123. ZHANG Bin-wei, YAN Song-hong, YANG Yong-dong. Approximate Seismic Analysis Method of Cross-section of Mountain Tunnel[J]. Journal of Highway & Transportation Research & Development, 2012, 29(3): 118-123. |
| [12] |
周佳媚, 袁松, 高波. 小净距隧道地震动力响应下的围岩应力场[J]. 公路交通科技, 2012, 29(2): 92-97. ZHOU Jia-mei, YUAN Song, GAO Bo. Surrounding Rock Stress Field under Earthquake-induced Dynamic Response of Tunnels with Small Spacing[J]. Journal of Highway & Transportation Research & Development, 2012, 29(2): 92-97. |
| [13] |
胡鸿运, 周晓军, 汪精河. 顺层岩体隧道地震响应的波动方法研究[J]. 岩石力学与工程学报, 2017, 36(6): 1373-1383. HU Hong-yun, ZHOU Xiao-jun, WANG Jing-he. A Wave Numerical Method for Seismic Response of Tunnels in Bedding Strata[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1373-1383. |
| [14] |
THOMSEN L. Weak Elastic Anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. |
| [15] |
WINTERSTEIN D F. Velocity Anisotropy Terminology for Geophysicists[J]. Geophysics, 1990, 55(8): 1070-1088. |
| [16] |
胡鸿运, 周晓军, 汪精河. 顺层岩体各向异性对隧道地震响应的影响[J]. 中国铁道科学, 2018, 39(1): 49-58. HU Hong-yun, ZHOU Xiao-jun, WANG Jing-he. Influence of Bedding Rock Mass Anisotropy on Tunnel Seismic Response[J]. China Railway Science, 2018, 39(1): 49-58. |
| [17] |
何建涛, 马怀发, 张伯艳, 等. 黏弹性人工边界地震动输入方法及实现[J]. 水利学报, 2010, 41(8): 960-969. HE Jian-tao, MA Huai-fa, ZHANG Bo-yan, et al. Method and Realization of Seismic Motion Input of Viscous-spring Boundary[J]. Journal of Hydraulic Engineering, 2010, 41(8): 960-969. |
| [18] |
杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49-56. DU Xiu-li, ZHAO Mi, WANG Jin-ting. A Stress Artificial Boundary in Fea for Near-field Wave Problem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 49-56. |
 2019, Vol. 36
2019, Vol. 36
