扩展功能
文章信息
- 韩普各, 赵伟, 陆森强
- HAN Pu-ge, ZHAO Wei, LU Sen-qiang
- 装配式混合连接钢-混凝土组合梁抗弯性能试验研究
- Experimental Study on Flexural Behavior of Assembled Hybrid Connected Steel-concrete Composite Beam
- 公路交通科技, 2019, 36(4): 58-65
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(4): 58-65
- 10.3969/j.issn.1002-0268.2019.04.009
-
文章历史
- 收稿日期: 2018-02-01
2. 浙江交通职业技术学院 桥隧工程研究所, 浙江 杭州 311112
2. Bridge and Tunnel Engineering Research Institute, Zhejiang Institute of Communications, Hangzhou Zhejiang 311112, China
装配式混合连接钢-混凝土组合梁采用黏结材料(如环氧树脂砂浆)和栓钉抗剪键将钢梁与预制混凝土板紧密连接在一起。与传统组合梁相比,具有黏结面积大,应力集中小,混凝土板与钢梁上的传力连续和受力更加合理等优点,同时可以避免现有中小跨径混凝土梁桥长期存在的病害问题[1],能有效降低桥梁生命周期成本。
国内外学者对栓钉连接件已进行了大量的研究,并得出了可以指导工程设计和施工的方法,但对黏结材料连接件,尤其是黏结材料与栓钉混合连接的抗剪键研究较少。Kim J-H[2]研究了黏结层厚度对连接性能的影响,并指出连接件的极限强度随黏结层厚度的增大而减小,还提出了连接件极限强度修正公式。Pankaj Kumar[3]等人对钢混组合梁中使用建筑结构胶及其影响因素进行了文献综述,考虑了建筑结构胶、被黏结物体的形状、胶结层厚度、黏结面几何形状、相对湿度及其固化温度和使用过程中的环境温度等因素对界面黏结强度的影响。L. Bouazaoui[4]认为环氧砂浆可作为最优的黏结剂,并研究了钢-高强混凝土组合梁静载下的受力性能[5]。Wolfgang Kurzl[6]研究了钢梁和混凝土界面不同表面预处理方法对组合梁黏结界面承载力的影响,结果表明,钢梁表面抛丸和混凝土板表面光滑的处理方式黏结力最大。Binhua Wang[7-8]认为可通过表面预处理或采用CNT/短纤维加固的方法提高环氧砂浆的黏结性能。Li A[9]利用推出试件证明了胶结连接件具有很好的力学性能,完全可以满足钢-混凝土组合梁连接件所需要的功能。苏庆田[10]基于不同的群钉布置进行了高强度砂浆包裹栓钉的推出试验,结果表明,高强度砂浆包裹栓钉连接件可以有效地将钢梁受力传递到混凝土中。高燕梅[11]考虑施工阶段提出了装配式钢-混凝土组合梁非线性全过程分析方法。B Jurkiewiez[12]基于多层梁模型和有限元模型分析了钢-混环氧砂浆胶结组合梁的非线性行为,得到胶结剪力键在预制板中的作用与栓钉行为相似。马增[13]利用试验法与有限元法分析了剪力槽孔间距、剪力连接度等对预制钢-混凝土组合梁受力性能的影响,研究发现,相同剪力连接度的簇钉群剪力连接组合梁与均布剪力连接件组合梁承载力基本一致,即栓钉的连接形式对组合梁承载能力的影响不大。
本研究提出的装配式混合连接钢-混凝土组合梁主要由主梁及横梁、预制桥面板、钢梁与桥面板间的黏结层和栓钉组成。通过两个运输单元试件的静力荷载试验,测试了混合连接组合梁的抗弯性能和混合连接件的可靠性,分析了混合连接组合梁的平截面假定,并提出了该组合梁极限承载力计算公式。
1 试件设计为了较为真实地反映工程实际,选择一个运输单元作为预制装配式钢-混凝土组合梁桥的试件,并为避免单个试件带来的偶然性,设计了两个相同的试件。试件跨度为10 m,宽2.4 m,试件编号分别为A和B。试件由3根主梁和3块预制混凝土板(3+4+3)m组成,其中钢梁为焊接钢板梁,混凝土板为带预留孔的预制板,钢梁与混凝土板通过栓钉和黏结材料组合成整体。
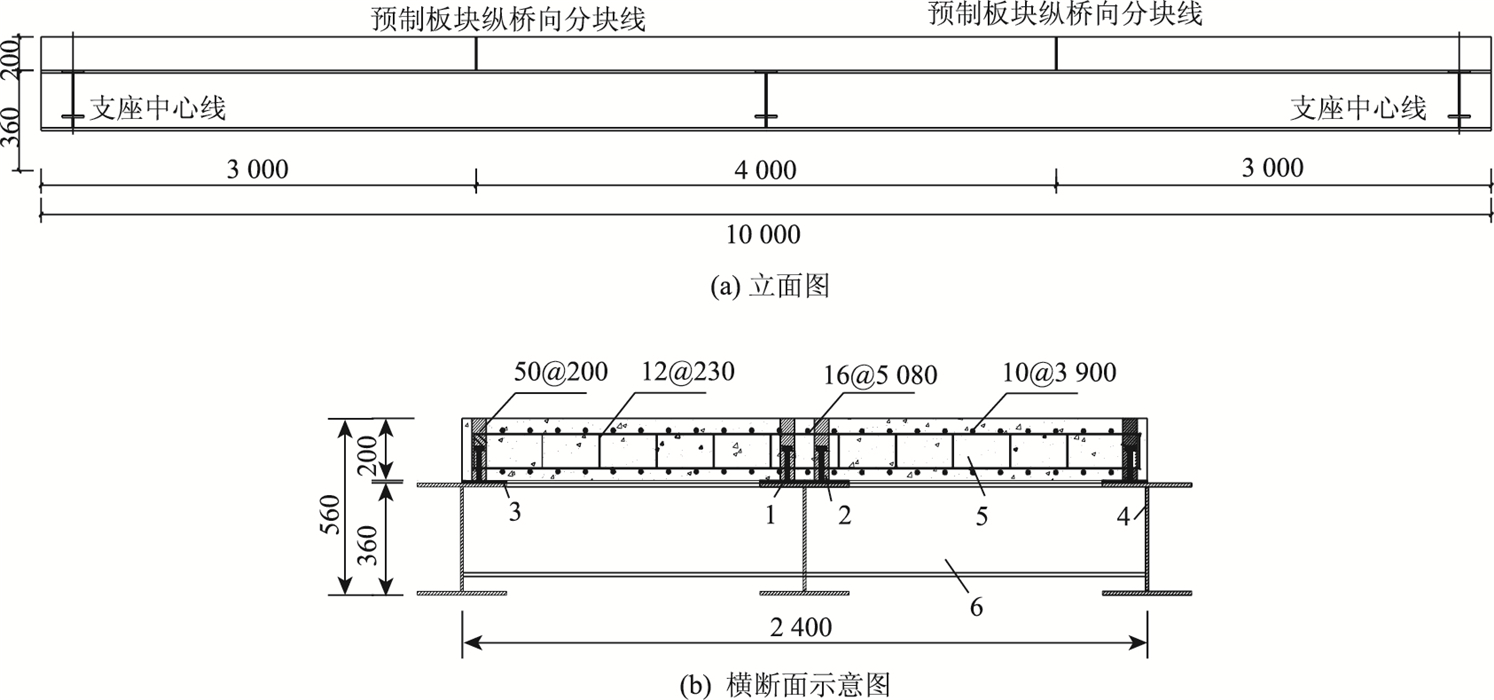
钢梁采用Q345qC钢,3根主梁通过3根横梁(边、中、边)连接成空间整体结构,钢梁上翼缘均匀布置了间距200 mm的栓钉,栓钉规格为ϕ16×120,材料为ML15。混凝土强度等级为C45,钢筋均为HRB500级,纵向钢筋直径10 mm,间距97 mm,横向钢筋直径16 mm,间距100 mm,箍筋直径12 mm,间距200 mm,试验梁构造及尺寸如图 1所示。
|
| 图 1 试验梁尺寸(单位:mm) Fig. 1 Dimensions of test girder(unit:mm) 注:1-栓钉;2-混凝土板预留孔;3-胶结层;4-钢主梁;5-预制混凝土板;6-横梁。 |
| |
试验采用的黏结材料和灌浆材料均为环氧砂浆,其中界面黏结材料为“金蛟龙A型”环氧砂浆,用于涂抹和封闭,兼做找平层;灌浆材料为“金蛟龙B型”环氧砂浆,呈流状,能够灌浆密实免振捣。混凝土实测抗压强度为49.2 MPa,其他各材料的力学性能如表 1~表 2所示。
| 材料 | Q345qC钢板 | HRB500钢筋 | ||||
| 厚度(直径) | t10 | t12 | t16 | d10 | d12 | d16 |
| 屈服强度/MPa | 472 | 475 | 451 | 575 | 567 | 573 |
| 拉压强度/MPa | 575 | 560 | 549 | 781.5 | 734 | 732 |
| 伸长率/% | 25 | 27 | 29.5 | 22.5 | 21 | 19 |
| 型号 | 抗拉强度/MPa | 抗压强度/MPa | 抗拉弹性模量/MPa | 抗压弹性模量/MPa | 凝固时间 |
| 金蛟龙A型 | 25.51 | 109.73 | 25 489.03 | 2 729.37 | 1 h10 min(21 ℃) |
| 金蛟龙B型 | 21.05 | 86.37 | 18 904.5 | 805.8 | 1 h30 min(15 ℃) |
2 测量和加载方案
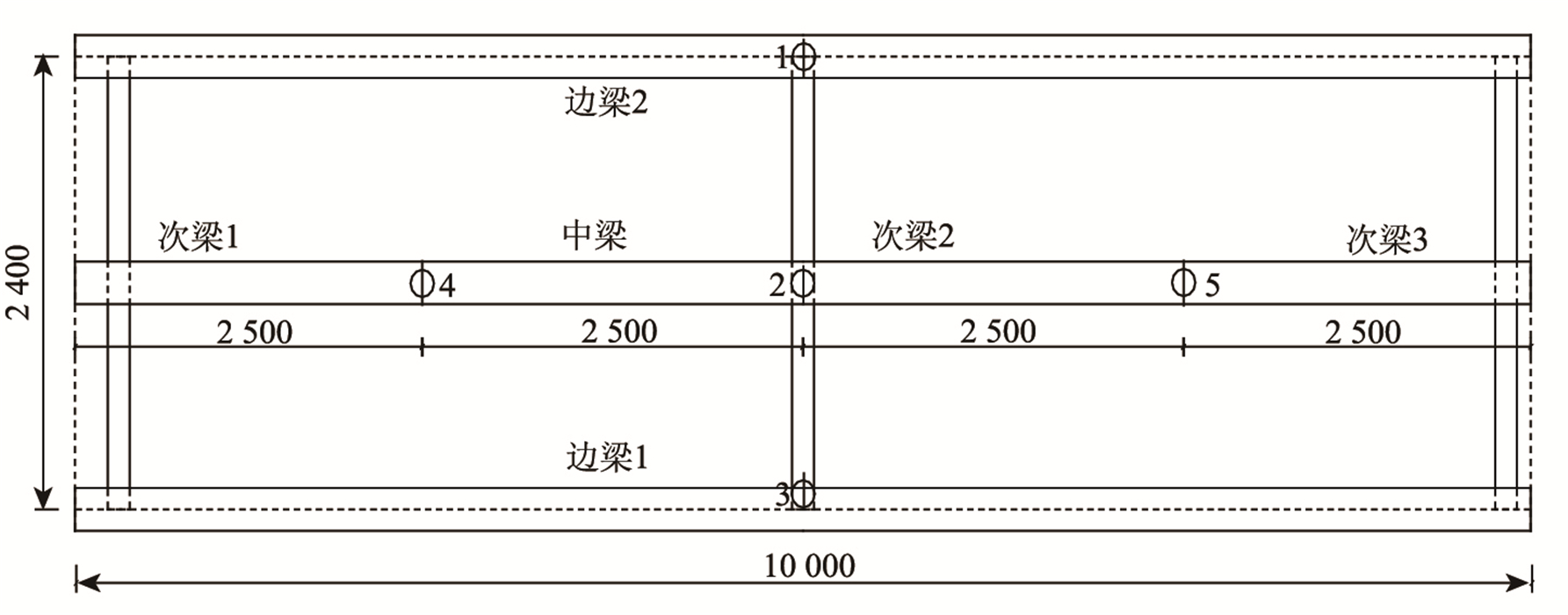
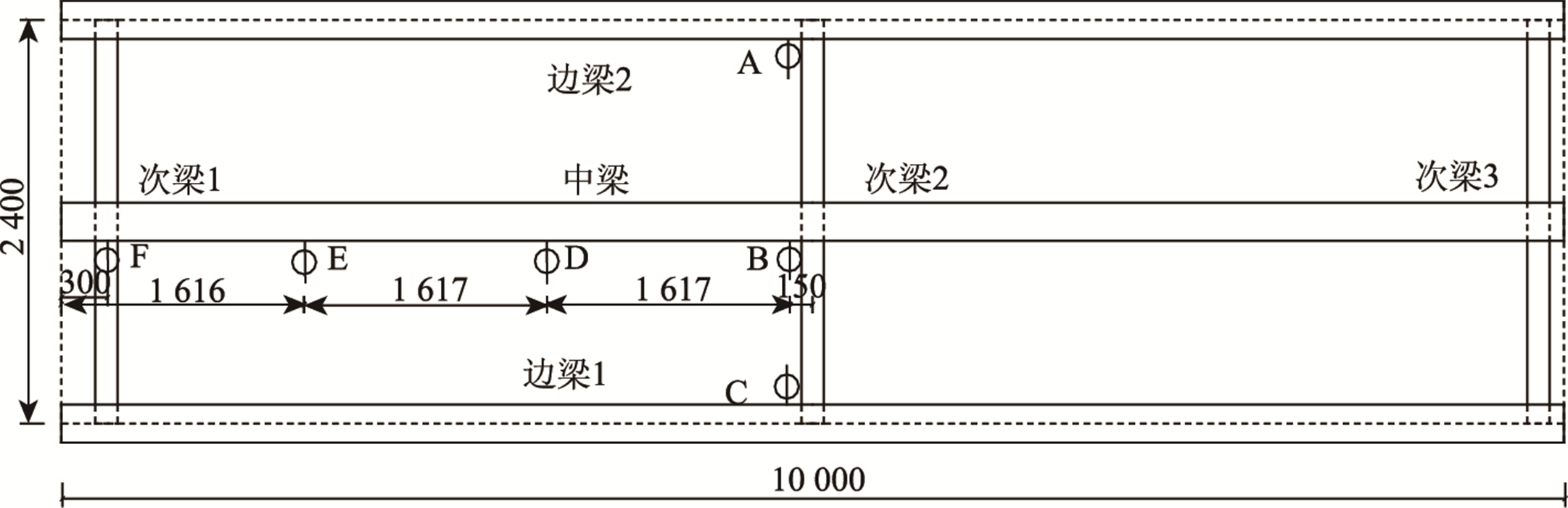
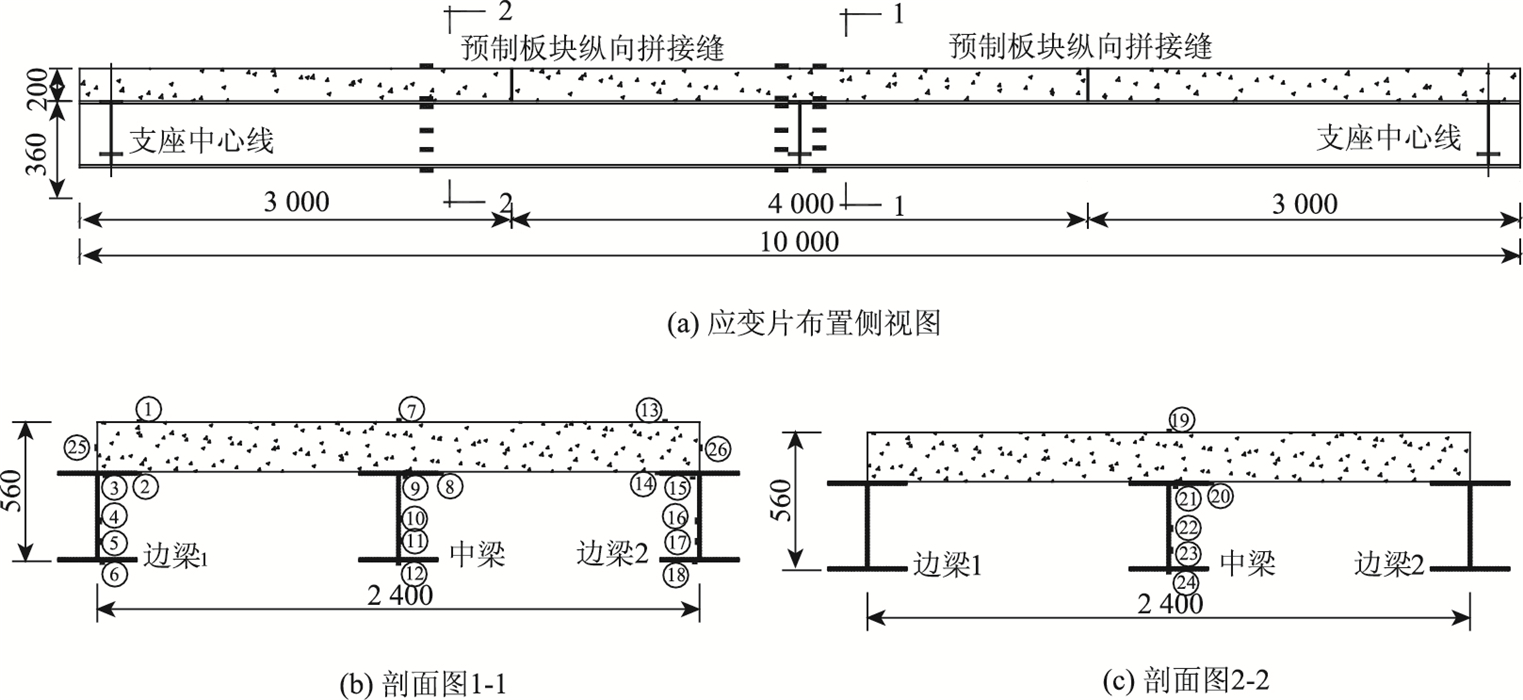
为测量试件的挠度和钢梁与桥面板之间的相对滑移,分别在支座、四分点和跨中设置了电阻式位移计。为获得截面应变沿梁高的变化规律,在同一截面沿梁高设置了单向应变片。各测点布置如图 2~图 4所示。
|
| 图 2 挠度测点布置(单位:mm) Fig. 2 Layout of deflection measuring points(unit:mm) |
| |
|
| 图 3 滑移测点布置(单位:mm) Fig. 3 Layout of slippage measuring points(unit:mm) |
| |
|
| 图 4 应变片布置(单位:mm) Fig. 4 Layout of strain gauges (unit:mm) |
| |
利用200T液压伺服加载器在梁跨中施加集中力,采用力-位移组合加载模式。先施加50 kN的预加荷载,确保各仪器正常工作后,每级加载30 kN;直到出现较强非线性(裂缝较多)时,改为位移加载,缓慢加载直至极限承载力。
3 试验结果和分析 3.1 主要试验结果试验的主要结果如表 3所示,P0为实际工作荷载; P1为出现第一条裂缝时的荷载; P2为界面出现水平裂缝时的荷载; P3为达到极限能力时的荷载;δ为极限荷载所对应的跨中竖向位移。
| 试件编号 | P0/ kN |
P1/ kN |
P1/ P0 |
P2/ kN |
P2/ P0 |
P3/ kN |
P3/ P0 |
δ/ mm |
| A | 330 | 960 | 2.91 | 1 507 | 4.57 | 1 695.3 | 5.14 | 130 |
| B | 330 | 910 | 2.76 | 1 425 | 4.32 | 1 676.4 | 5.08 | 140 |
| 差值/% | — | 5.2 | — | 5.4 | — | 1.1 | — | — |
3.2 混凝土板裂缝开展情况 3.2.1 试件A的裂缝发展
加载初期无任何异常现象;加载至约2.9倍工作荷载时,距离支座2.5 m处右侧桥面板两侧同时观察到第一条裂缝,从混凝土板板底开始,以45°向跨中延伸;裂缝随荷载的增大而不断增多,裂缝整体分布呈“八”字型,加载至4.57倍工作荷载时,试验梁发出间断的栓钉断裂声,随后有连续的脱胶声,观察到界面跨中位置出现水平裂缝;继续位移加载,直到部分斜裂缝几乎贯穿桥面板厚度,试件达极限承载力。达到极限承载力时,试件A的裂缝分布如图 5(a)所示。

|
| 图 5 混凝土板侧面裂缝分布 Fig. 5 Distribution of cracks on sides of concrete slabs |
| |
3.2.2 试件B的裂缝发展
试件B和A的裂缝发展情况大体相同,第1条裂缝出现在离支座2 m的位置处,开裂荷载及出现水平裂缝时的荷载均与试件A基本相同,但在相同荷载下B的裂缝数量比A的多,这些是由钢梁和混凝土板的制作质量引起的,达到极限承载力时,试件B的裂缝分布如图 5(b)所示。
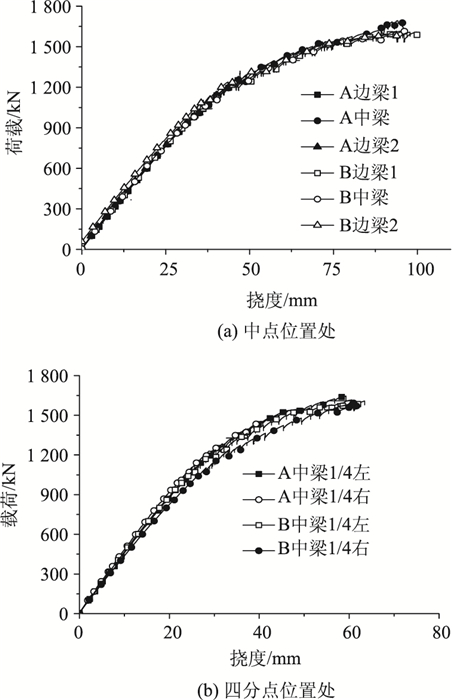
3.3 荷载-挠度曲线图 6为各测点受力过程中的挠度随荷载的变化曲线。其中,在试件A中,由于边梁1和边梁2的位移计量程仅有50 mm,没有测到塑性阶段的曲线变化。
|
| 图 6 荷载-位移曲线 Fig. 6 Load-displacement curves |
| |
由图 6可知,两个试件的荷载-挠度曲线均经历了弹性、弹塑性和塑性3个阶段。加载初期,荷载-挠度关系成线性增长,钢梁和混凝土板的组合作用良好;从外加荷载约为3倍工作荷载起,组合梁进入弹塑性阶段,组合梁刚度随荷载的增加而有所降低,挠度增长速度大于荷载的增加速度;当加载至4.5倍工作荷载时,挠度变形大幅度增长,当组合梁进入塑性工作阶段,荷载-变形曲线呈水平趋势发展。
3根主梁在中点位置处的挠度曲线基本完全重合,这表明在传力结构(混凝土桥面板、横梁、胶结连接件)的作用下,3根主梁可以共同承重,且基本上达到均匀受力。中梁四分点处的荷载-挠度曲线吻合较好,曲线走势与跨中的关系曲线变化一致,这表明预制板在拼接缝处没有发生变形突变,板间可以连续且均匀地传力,组合梁表现出良好的组合效果。
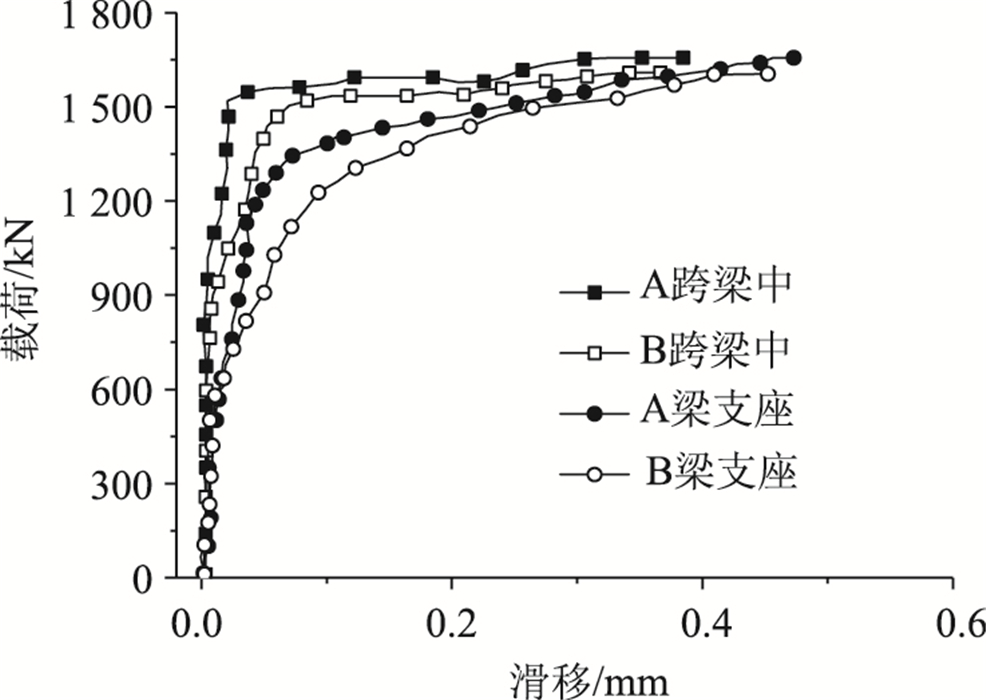
3.4 荷载-滑移曲线图 7为试验梁跨中及距离支座130 mm处的钢-混凝土板连接界面的荷载-滑移曲线图。由图 7可知,跨中滑移曲线近似双折线,分为斜线段和水平线段,而靠近支座的滑移曲线近似典型三折线现浇滑移曲线[14-15],连接界面在接近极限荷载时才发生黏结破坏,接着出现相对滑移。支座附近先发生滑移,且增加速度大于跨中。当达到极限承载力时,各测点的滑移量均较小,不超过0.6 mm,这表明增加环氧砂浆黏结层后,界面黏结力显著增强,可不考虑组合梁界面的滑移,钢梁与混凝土板之间可以实现完全组合作用。
|
| 图 7 荷载-滑移曲线 Fig. 7 Load-slip curves |
| |
3.5 应变变化曲线
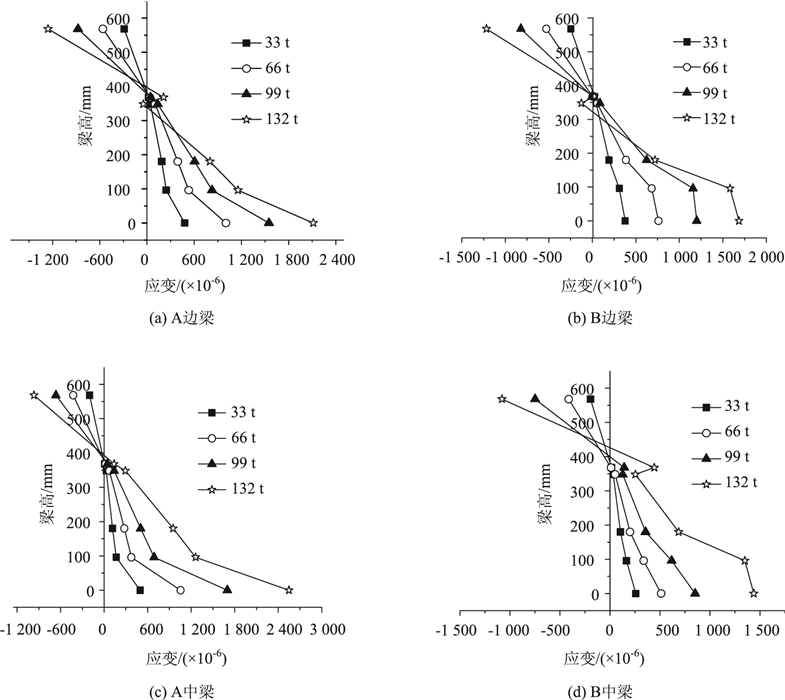
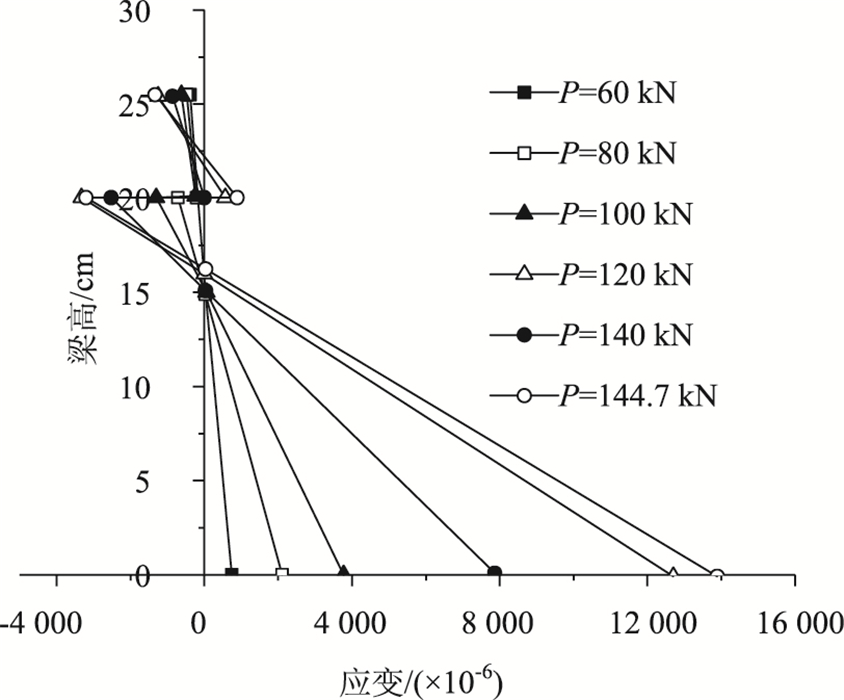
图 4给出了各应变测点沿试件高度方向的布置位置。由图 4可知,测点布置在混凝土板上、下表面,钢梁上、下翼缘的下表面,腹板1/2和1/4高处。图 8给出了两个试件跨中截面应变沿梁高的分布情况,图 9为文献[16]现浇钢混凝土组合梁试件截面应变沿梁高的分布情况。
|
| 图 8 梁高-应变曲线 Fig. 8 Height-strain curves |
| |
|
| 图 9 现浇试件梁高-应变曲线 Fig. 9 Height-strain curves of in-situ casted girder specimens |
| |
由图 8可知,在3倍工作荷载(990 kN)内,试件边梁和中梁的各测点应变沿梁高方向基本成线性分布。这表明在3倍工作荷载内组合梁截面符合平截面假定。在3倍工作荷载内,桥面板全截面受压,中和轴位置距离混凝土顶面约170 mm;钢梁与混凝土板之间无相对滑移;且边梁与中梁的最大压应变和拉应变的数值基本相等,这说明3根主梁与混凝土板在胶结连接件和横梁的作用下,可以很好地协同工作。由图 9可知,现浇组合梁在很小的荷载下,钢-混凝土连接界面就出现了滑移,截面不符合平截面假定。在4倍工作荷载时,本研究试件的应变在钢-混凝土连接界面附近发生突变,这表明混凝土板和钢梁界面处出现了滑移应变,中和轴向上发生一定的移动,且钢梁部分进入塑性,可用塑性简化理论[17-18]计算组合梁的承载力。
4 理论计算与对比 4.1 理论计算由上文分析可知,主梁在混凝土板和横梁等传力构件作用下整体受力,3根主梁要同等参与受力,并可按《钢-混凝土组合桥梁设计规范》GB 50917—2013[19]的塑性理论进行承载力计算,简要计算过程见表 4。表 4中Astd为栓钉的栓杆截面积;fc为混凝土板所用混凝土的抗压强度;facA为A型黏结材料的抗压强度;facB为B型黏结材料的抗压强度;fy为钢梁所用钢材的抗拉强度;fsd为栓钉的抗拉强度;fatA为A型黏结材料的抗拉强度;fatB为B型黏结材料的抗拉强度;fstd为栓钉的抗拉强度;Es为钢梁所用钢材的弹性模量;Ec为混凝土板所用混凝土的弹性模量;Esd为纵向钢筋的弹性模量;EaA为A型黏结材料的弹性模量;EaB为B型黏结材料的弹性模量;Fsd为Asd×fsd,即纵向钢筋的承载力;Fa为Aa×facA,即A型黏结材料的承载力。
| 构件名称 | 截面面积/mm2 | 抗压强度/MPa | 抗拉强度/MPa | 弹性模量/MPa | 换算系数 | 承载力/kN | |
| 钢梁360×250×10×12 | As=28 080 | — | fy=509.1 | Es=2.06×105 | — | Fs=14 295.27 | |
| 混凝土板2 400×200 | Ac=480 000 | fc=32.9 | — | Ec=34 420.04 | nc=5.98 | Fc=15 794.38 | |
| 纵向钢筋:d=10 | Asd=1 806.4 | — | fsd=479.2 | Esd=2.0×105 | nsd=1.03 | Fsd=1 038.68 | |
| 黏结材料 | A型 | Aa=4 000 | facA=109.73 | fatA=25.51 | EaA=25 489.03 | na=8.08 | Fa=102.04 |
| B型 | facB=86.37 | fatB=21.05 | EaB=18 904.5 | — | — | ||
| 栓钉杆:d=16 | Astd=201.1 | — | fstd=400 | Es=2.06×105 | — | — | |
由表 4可知,Fc>Fs,这表明塑性中和轴处于混凝土板内。
组合梁的换算截面:
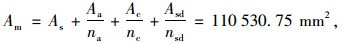
|
(1) |
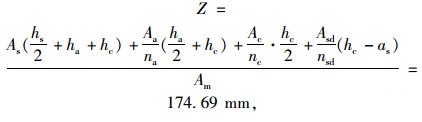
|
(2) |
式中,Fc为Ac×fc,即混凝土板的承载力;Fs为As×fy,即钢梁的承载力;Am为组合梁换算截面积;As为钢梁截面积;Ac为混凝土板截面积;Aa为黏结层界面面积;Asd为纵向钢筋截面面积;na为EaA/Es,即A型黏结材料换算成钢材的换算系数;nc为Ec/Es,即混凝土换算成钢材的换算系数;nsd为Esd/Es,即纵向钢筋换算成钢材的换算系数;hs为钢梁高度,ha为A型黏结材料的厚度,hc为混凝土板厚度。
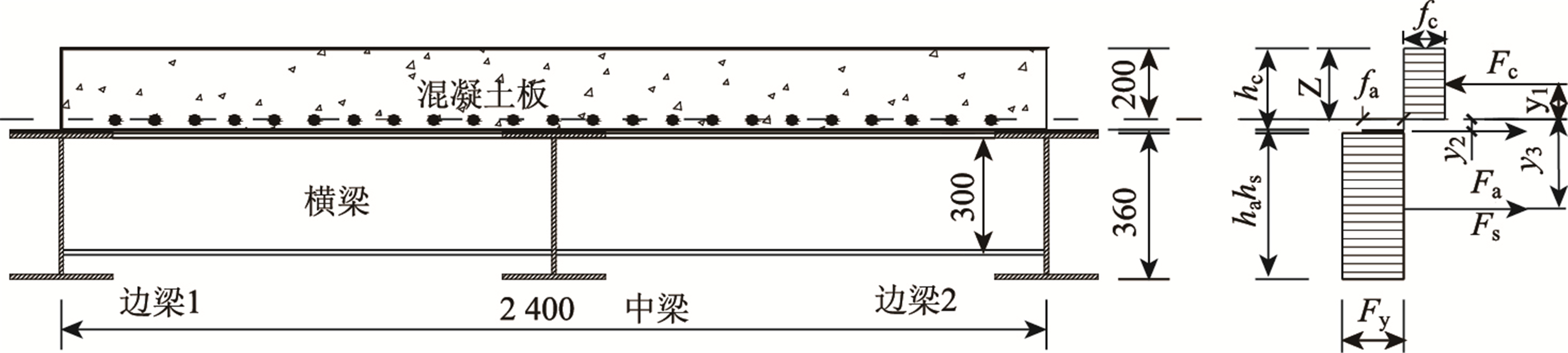
中和轴位于混凝土板内,与试验得到的中和轴高度(170 mm)基本一致,误差不超过2.7%,这表明理论计算方法适用,中和轴的位置如图 10所示。
|
| 图 10 塑性中和轴位置(单位:mm) Fig. 10 Position of plastic natural axis(unit:mm) |
| |
忽略纵向钢筋作用,塑性弯矩为:
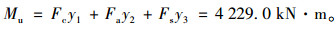
|
(3) |
极限承载力为:
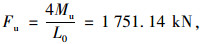
|
(4) |
式中,Mu为忽略纵向钢筋时组合梁的塑性弯矩;y1为混凝土板形心到中和轴的距离;y2为A型黏结材料形心到中和轴的距离;y3为钢梁形心到中和轴的距离;Fu为由塑性弯矩计算得到的极限承载力。
考虑滑移效应时,鉴于栓钉被“B型”环氧砂浆包裹,忽略环氧砂浆破坏对混凝土孔壁的影响,环氧砂浆与混凝土材性类似,故将文献[19]中的混凝土改为包裹栓钉的环氧砂浆参与计算分析,并代入文献[19]的公式得到考虑滑移效应时的拟合系数k=0.966,重要性系数r0为1.0,计算跨径L0为9.66 m,则塑性极限弯矩为:
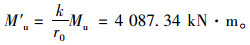
|
(5) |
故考虑滑移的极限承载力为:
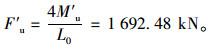
|
(6) |
理论计算结果与实测结果的比较如表 5所示,其中理论值1为不考虑滑移影响的极限承载力,理论值2为考虑滑移影响的极限承载力。
| 试件编号 | 试验值 | 理论值1 | 理论值1 误差/% |
理论值2 | 理论值2 误差/% |
| A | 1 695.3 | 1 751.14 | 3.29 | 1 692.48 | 0.17 |
| B | 1 676.4 | 1 751.14 | 4.82 | 1 692.48 | 0.96 |
由表 5可知,当不考虑滑移影响时,理论值与试验值的误差不超过5%;考虑滑移影响时,理论值与试验值的误差不超过1%。这表明,组合梁在混合连接作用下的抗弯性能可以采用我国钢-混凝土组合桥梁设计规范[19]的方法进行计算。
5 结论通过2根10 m足尺试件对装配式混合连接钢-混凝土组合梁体系的受力性能进行了试验研究,得出主要结论如下:
(1) 该装配式组合梁具有良好的塑性变形能力,其极限承载力约为工作荷载的5倍;
(2) 在3倍工作荷载内,组合梁的截面应变沿梁高呈线性分布,截面符合平截面假定;
(3) 给出了该装配式组合梁抗弯承载力计算公式。
| [1] |
陈娟娟, 刘杰. 装配式混凝土空心板铰缝病害分析[J]. 现代交通科技, 2012, 9(6): 52-55. CHEN Juan-juan, LIU Jie. Analysis on Disease of Hinge Joint in Precast Concrete Hollow Slab[J]. Modern Transportation Technology, 2012, 9(6): 52-55. |
| [2] |
KIM J H, SHIM C S, MATSUI S, et al. The Effect of Bedding Layer on the Strength of Shear Connection in Full-depth Precast Deck[J]. Engineering Journal, 2002, 39(3): 127-135. |
| [3] |
KUMAR P, PATNAIK A, CHAUDHARY S. A Review on Application of Structural Adhesives in Concrete and Steel-concrete Composite and Factors Influencing the Performance of Composite Connections[J]. International Journal of Adhesion and Adhesives, 2017, 77: 1-14. |
| [4] |
BOUAZAOUI L, PERRENOT G, DELMAS Y, et al. Experimental Study of Bonded Steel Concrete Composite Structures[J]. Journal of Constructional Steel Research, 2007, 63(9): 1268-1278. |
| [5] |
BOUAZAOUI L, JURKIEWIEZ B, DELMAS Y, et al. Static Behaviour of a Full-scale Steel-concrete Beam with Epoxy-bonding Connection[J]. Engineering Structures, 2008, 30: 1981-1990. |
| [6] |
WOLFGANG K, CHRISTOPHER K. Evaluation of Adhesive Bonded Steel Concrete Composite Structures[C]//American Society of Civil Engineers Structures Congress2010. Orlando, US: American Society of Civil Engineers, 2010.
|
| [7] |
WANG B H, BAI Y X, HU X Z, et al. Enhanced Epoxy Adhesion between Steel Plates by Surface Treatment and CNT/Short-fibre Reinforcement[J]. Composites Science and Technology, 2016, 127: 149-157. |
| [8] |
WANG Bin-hua, HU Xiao-zhi, LU Peng-min. Improvement of Adhesive Bonding of Grit-blasted Steel Substrates by Using Diluted Resin as a Primer[J]. International Journal of Adhesion and Adhesives, 2017, 73: 92-99. |
| [9] |
LUO Y J, LI A, KANG Z. Parametric Study of Bonded Steel-concrete Composite Beams by Using Finite Element Analysis[J]. Engineering Structures, 2012, 34: 40-51. |
| [10] |
苏庆田, 李雨. 高强度砂浆群钉连接件抗剪承载力试验[J]. 同济大学学报:自然科学版, 2015, 43(5): 699-705. SU Qing-tian, LI Yu. Shear Capacity of Grouped Stud Connector Embedded by High Strength Mortar[J]. Journal of Tongji University:Natural Science Edition, 2015, 43(5): 699-705. |
| [11] |
高燕梅, 刘东, 周志祥, 等. 考虑施工阶段的装配式钢-混凝土组合梁非线性全过程分析方法[J]. 公路交通科技, 2017, 34(9): 52-59. GAO Yan-mei, LIU Dong, ZHOU Zhi-xiang, et al. A Nonlinear Whole Process Analysis Method of Prefabricated Steel-concrete Composite Beam Considering Construction Stages[J]. Journal of Highway and Transportation Research and Development, 2017, 34(9): 52-59. |
| [12] |
JURKIEWIEZ B, MEAUD C, FERRIER E. Non-linear Models for Steel-concrete Epoxy-bonded Beams[J]. Journal of Constructional Steel Research, 2014, 100: 108-121. |
| [13] |
马增.新型装配式钢-混凝土组合箱梁桥结构设计与试验研究[D].南京: 东南大学, 2015. MA Zeng. Structural Design and Experimental Study of a New-type Fabricated Steel Box-concrete Composite Bridge[D].Nanjing: Southeast University, 2015. |
| [14] |
SHIM C S, LEE P G, YOON T Y. Static Behavior of Large Stud Shear Connectors[J]. Engineering Structures, 2004, 26(12): 1853-1860. |
| [15] |
廖崇庆, 吴冲.桥梁圆柱头焊钉连接件的荷载-滑移曲线[C]//中国钢协钢-混凝土组合结构分会第十一次年会论文集.哈尔滨: 《哈尔滨工业大学学报》编辑部, 2007: 420-423. LIAO Chong-qing, WU Chong. Load-slip Curve of Cheese Headed Stud Connectors in Bridge[C]//Proceedings of the 11th Annual Meeting of Steel-concrete Composite Structure Branch of China Steel Association. Harbin: Editorial Department of Journal of Harbin Institute of Technology, 2007: 420-423. |
| [16] |
SOUICI A, BERTHET J F, LI A, et al. Behaviour of Both Mechanically Connected and Bonded Steel-concrete Composite Beams[J]. Engineering Structures, 2013, 49: 11-23. |
| [17] |
聂建国. 钢-混凝土组合梁结构:试验、理论与应用[M]. 北京: 科学出版社, 2005. NIE Jian-guo. Steel-concrete Composite Beam Structure:Experiment, Theory and Application[M]. Beijing: Science Press, 2005. |
| [18] |
聂建国, 沈聚敏. 滑移效应对钢-混凝土组合梁抗弯强度的影响及其计算[J]. 土木工程学报, 1997, 30(1): 31-36. NIE Jian-guo, SHEN Ju-min. Slip Effect on Strength Composite Steel-concrete Beams[J]. Journal of Civil Engineering, 1997, 30(1): 31-36. |
| [19] |
GB 50917-2013, 钢-混凝土组合桥梁设计规范[S]. GB 50917-2013, Code for Design of Steel and Concrete Composite Bridges[S]. |
 2019, Vol. 36
2019, Vol. 36
