扩展功能
文章信息
- 张航, 张肖磊, 吕能超
- ZHANG Hang, ZHANG Xiao-lei, LÜ Neng-chao
- 高速公路停车视距可靠性设计
- Reliability Design for Stopping Sight Distance of Expressway
- 公路交通科技, 2019, 36(4): 44-49, 87
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(4): 44-49, 87
- 10.3969/j.issn.1002-0268.2019.04.007
-
文章历史
- 收稿日期: 2017-12-21
2. 武汉理工大学 智能交通系统研究中心, 湖北 武汉 430067
2. ITS Center, Wuhan University of Technology, Wuhan Hubei 430067, China
近年来,我国道路建设取得了巨大成就,但道路交通安全问题仍然十分严峻。其中,大多交通事故的发生与视距有密切关系,尤其是汽车高速行驶时,若视距不足将导致驾驶员遇见紧急情况时不能及时采取措施,事故发生不可避免。
很多学者就视距导致的安全问题做了相关研究[1-4]。赵永平等[5]通过分析在中央分隔带外侧超车道上驾驶员的视点位置以及横净距,计算该段道路提供的停车视距值不满足规范的要求,提出了相应的解决方案。袁浩等[6]从运动学的角度,用制动减速度来综合描述整个制动过程,得到新的停车视距计算模型。这些研究从多方面考虑行车安全中视距不足的问题。
停车视距在道路线形设计中越来越得到重视,在研究视距特点、取值满足规范及保证设计安全的同时,究竟其安全水平有多高,规范中没有说明。特别是当因受条件限制而取规范最小值时,设计指标的预期安全效果将会更加不明确。鉴于此,1990年,Navin等[7-11]最先将可靠性理论引入到道路工程中去,并采用相关案例进行说明。游克思等[12]将车速、路面摩擦系数作为随机变量,以汽车发生侧滑为失效条件构建可靠函数,分析汽车在曲线段的安全性。朱兴琳[13]以概率论为基础建立各个设计指标的可靠度模型,并分析各个指标数值的变化对相应可靠度模型的失效概率的影响。
基于此,本研究从汽车的实际制动过程出发,建立较符合实际的停车视距模型;由停车视距模型构建可靠度功能函数;在一级安全等级下,计算出不同设计速度下满足可靠度要求的停车视距值,探究基于可靠度理论的视距选用标准,给出相应指标的推荐值。
1 建立视距模型高速公路与一级公路以停车视距作为视距要求,二、三、四级公路以会车视距作为视距要求,其长度一般为停车视距的两倍。本研究主要讨论停车视距值的安全可靠性并计算其推荐值,供道路路线设计参考。
现行规范《公路工程技术标准》(JTG B01—2014)的停车视距由两部分组成:①驾驶者在反应时间内行驶的距离S1(m);②开始制动到刹车停止所行驶的距离,即制动距离S2(m)。停车视距计算公式为:
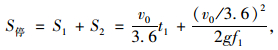
|
(1) |
式中,v0为汽车运行速度;f1为纵向摩阻系数,依车速及路面状况而定;g为重力加速度(9.8 m/s2);t1为驾驶者反应时间,取2.5 s(判断时间1.5 s,运行时间1.0 s)。
上述停车视距只将整个阶段分为两部分,这与汽车紧急制动时的实际情况存在偏差。当驾驶员接收到需要紧急停车的信号,大脑做出制动指令,驾驶员将脚移到制动踏板,踩下制动踏板。由于制动踏板存在自由行程,以及制动器存在间隙,即制动蹄片与制动鼓(盘)之间的间隙,所以制动器需要一段时间才能发挥作用。并且随着使用时间的增长,制动摩擦片会被不断磨损,其间隙增大,也会延长制动器的反应时间。现行规范的停车视距在制动阶段是假定汽车在制动开始时便得到最大制动力,忽略了制动力逐渐上升至最大值的这个阶段。
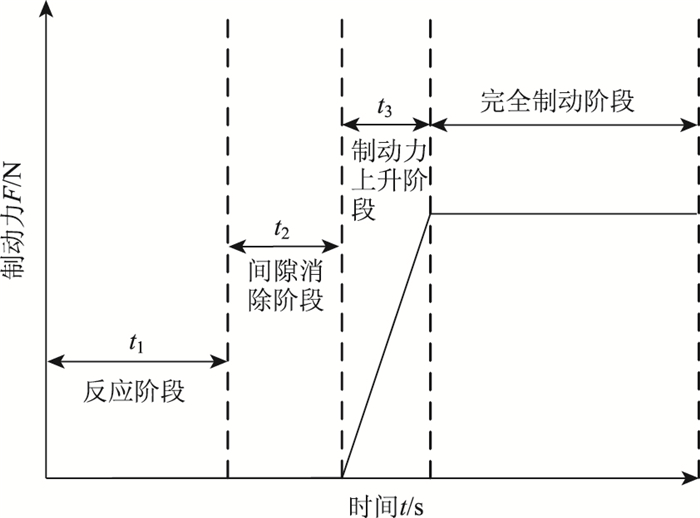
停车视距模型包含4个阶段,反应阶段、间隙消除阶段、制动力上升阶段和完全制动阶段,如图 1所示。
|
| 图 1 停车视距四阶段模型 Fig. 1 Four-stage stopping sight distance model |
| |
图中t1为反应阶段是驾驶员发现前方障碍物至其将脚移至制动踏板这个过程,即感应阶段和操作反应阶段,该阶段与规范相同行驶距离为S1。t2为间隙消除阶段,是从驾驶员的脚触碰到制动踏板至制动器间隙完全消除并开始起作用的这个过程,该阶段汽车行驶距离为S2。t3为制动力上升阶段,即制动力从零上升至最大值的过程,制动力与时间的关系近似为线性增长,该阶段汽车制动减速度与时间的关系相应简化为线性增长。该阶段汽车行驶距离为:
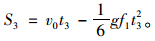
|
(2) |
汽车制动力达到最大值后,以最大减速度持续制动直至汽车停止行驶,即完全制动阶段:
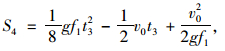
|
(3) |
则停车视距:
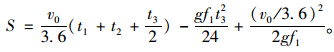
|
(4) |
根据《公路路线设计规范》(JTG D20—2006),反应时间t1取值2.5 s, 间隙消除时间t2取值0.05 s。不同类型的制动器所需时间各有差异,《机动车运行安全技术条件》(GB7258—2012)中规定:对液压制动的汽车不应大于0.35 s,对气压制动的汽车不应大于0.60 s;汽车列车和铰接客车、铰接式无轨电车的制动协调时间不应大于0.80 s。在考虑安全性和经济性的情况下,该停车视距模型的制动力上升的时间t3取0.60 s,使绝大多数的汽车能够满足其制动的需求。假定在纵坡坡度为零的潮湿路面条件下,停车视距式(4)计算值与现行规范的停车视距如表 1。
| 设计速度/ (km·h-1) |
运行速度/ (km·h-1) |
式(1)计算值/m | 规范值/ m |
式(4)计算值/m |
| 120 | 102 | 212.0 | 210 | 221.8 |
| 100 | 85 | 153.70 | 160 | 161.96 |
| 80 | 68 | 105.90 | 110 | 112.45 |
比较结果表明,在同样条件下,式(4)的计算值普遍大于现行规范的停车视距计算值,在安全性程度上比现行规范的停车视距要高。
2 基于可靠度理论的视距分析 2.1 停车视距可靠度功能函数建立停车视距的作用在于让驾驶员能够安全及时平稳地完成停车、会车、超车等行车行为。用于停车视距可靠性分析的功能函数应为两部分:一是由道路为驾驶员提供的行车视距,即公路技术规范标准值;二是驾驶员驾驶汽车行驶在道路上,为保证行车安全实际需要的行车视距。根据可靠度相关理论,可用式(5)描述分析行车视距可靠性的功能函数D:
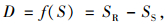
|
(5) |
式中,SR为公路技术规范行车视距规定值;SS为保证安全行车所需的行车视距。
2.2 可靠度功能函数参数分析功能函数D具体涉及的变量较多,现将驾驶员反应时间、汽车运行速度、路面摩擦系数等基本变量作为随机变量。由于不同的汽车采用不同的制动器,即使是同种制动器也会由于结构、材料差异导致性能差异,难以用同样的标准去衡量,故将制动器间隙消除时间、制动力上升时间这两个变量作为确定性变量。
目前,大多数研究认为驾驶员的反应时间近似服从正态分布或对数正态分布。李霖等[14]通过采集上海地区6种典型的危险交通工况中的驾驶员反应时间,发现反应时间能够很好地被对数正态分布拟合,并给出了其样本统计的均值与标准差。故本研究采用更符合国内情况的,其中反应时间最长的工况的参数,即均值为1.387 s,标准差为0.34 s,且服从对数正态分布。
汪双杰、方靖[15]等以处于自由流状态的行驶车辆为研究对象,验证运行速度服从正态分布的假设。王丽金[16]研究河南、广东、重庆、陕西等地的高速公路汽车运行速度分布情况,均较好地验证了其服从正态分布。本研究采用对高速公路汽车运行速度统计样本经SPSS软件K-S检验得到的正态参数,见表 2。
| 设计速度/(km·h-1) | 均值 | 标准差 |
| 120 | 105.096 6 | 14.699 52 |
| 100 | 86.802 6 | 8.570 46 |
| 80 | 75.416 3 | 12.467 62 |
汽车与路面的摩擦系数与路面材料、天气气候、车速、轮胎性能等因素有关。现有研究大多表明正态分布能够较好地描述路面摩擦系数。文献[17]给出了潮湿路面和干燥路面的摩擦系数服从正态分布的情况,见表 3。
| 路面状况 | 速度/(km·h-1) | 摩擦系数均值 | 摩擦系数标准差 |
| 潮湿 | 80.4 | 0.419 2 | 0.091 3 |
| 潮湿 | 85 | 0.401 3 | 0.091 3 |
| 潮湿 | 90 | 0.382 6 | 0.091 3 |
| 潮湿 | 95 | 0.357 1 | 0.091 3 |
| 潮湿 | 99.8 | 0.349 8 | 0.091 3 |
| 干燥 | 任意速度 | 0.885 2 | 0.094 9 |
2.3 停车视距可靠度求解
根据以上各参数的概率分布情况,采用式(4)构建可靠度函数来检验我国现有规范的停车视距的可靠性。因现有规范中没有对停车视距可靠度作出明确规定,一般来讲,由于视距不足而引发的事故程度与由路面结构引发的事故程度较接近,故以《公路工程结构可靠度设计统一标准》(GB/T 50283—1999)中对路面结构目标可靠度的规定为依据进行求解,见表 4。
| 安全等级 | 一级 | 二级 | 三级 |
| 公路等级 | 高速 | 一级 | 二级 |
| 目标可靠度PS/% | 95 | 90 | 85 |
| 目标可靠指标β | 1.645 | 1.282 | 1.036 |
现以求解设计速度为120 km/h时停车视距可靠度为例。
研究[18]表明路面摩擦系数随速度增加呈指数分布,随着速度增加,路面摩擦系数逐渐趋近于某一值,故设计速度为120 km/h时,其参数路面摩擦系数可以参照表 3中速度为99.8 km/h时的路面摩擦系数值。停车视距可靠性功能函数中采用的参数变量见表 5。
| 参数变量 | 分布类型 | 平均值 | 标准差 |
| 反应时间t1/s | 对数正态分布 | 1.387 | 0.34 |
| 运行速度v0/(km·h-1) | 正态分布 | 105.096 6 | 14.699 52 |
| 纵向摩阻系数f1 | 正态分布 | 0.349 8 | 0.091 3 |
根据视距可靠度功能函数式(5),SR为210 m,SS为本研究的停车视距计算式,通过JC法进行多次迭代计算得:
| 迭代次数 | t1* | v0* | f1* | β | Pf/% | PS/% |
| 1 | 1.387 | 105.096 6 | 0.349 8 | 0.606 1 | 27.22 | 72.78 |
| 2 | 1.383 462 | 112.020 6 | 0.316 458 | 0.603 1 | 27.32 | 72.68 |
| 3 | 1.378 119 | 111.484 5 | 0.312 598 | 0.603 2 | 27.32 | 72.68 |
| 4 | 1.377 564 | 111.461 4 | 0.312 397 | 0.603 3 | 27.32 | 72.68 |
| 5 | 1.377 534 | 111.461 | 0.312 379 | 0.603 3 | 27.32 | 72.68 |
结果表明,现行规范在设计速度为120 km/h对应的视距210 m的可靠指标仅为0.603 3,其失效概率为27.32%,可靠概率仅为72.68%,参照表 4,其在一定程度上没有符合安全等级为一级的可靠度要求。
若取SR为221.80 m,即表 1中停车视距式(4)的计算值,参数不变,经求解迭代结果显示:视距取SR=221.80 m时,可靠指标为0.772 3,其失效概率为22.01%,可靠概率为77.99%,可靠程度依然较低,不满足安全等级为一级的可靠度要求。较SR=210 m时的计算结果而言,可靠概率较大,该视距值更加可靠,同时证实了优化的停车视距计算模型较为可靠。
相应地,可求解出设计时速分别为100, 80 km/h时停车视距可靠度,结果汇总于表 7。
| 设计速度/(km·h-1) | t1* | v0* | f1* | SR | β | Pf/% | PS/% | 备注 |
| 120 | 1.387 | 105.096 6 | 0.349 8 | 210 | 0.603 3 | 27.32 | 72.68 | SR=210, 160, 110为规范视距值;SR=221.80, 161.96, 112, 45为停车视距式(4)的计算值 |
| 221.80 | 0.772 3 | 22 | 78 | |||||
| 100 | 1.387 | 86.802 6 | 0.349 8 | 160 | 0.907 8 | 18.2 | 81.8 | |
| 161.96 | 0.95 | 17.11 | 82.89 | |||||
| 80 | 1.387 | 75.416 3 | 0.419 2 | 110 | 0.709 4 | 23.9 | 76.1 | |
| 112.45 | 0.783 6 | 21.66 | 78.34 |
根据上述计算结果,现行规范在设计速度为120,100,80 km/h时停车视距可靠概率分别为72.68%,81.8%,76.1%,且均小于表 4中对应的可靠度要求。可知规范中规定的停车视距在建立的视距可靠度功能函数D的检验下,其失效概率较大。另外,求解时SR取表 1中停车视距式(4)计算值进行计算,得到的可靠概率虽仍不满足安全等级为一级可靠指标的要求,但均高于利用规范求得的值,优化后的停车视距计算模型更加安全可靠。
3 基于可靠度理论的停车视距选用标准根据表 4中高速公路对应的安全等级为一级可靠指标的要求,以及已知的参数变量,通过停车视距可靠度功能函数D反算出相应指标下道路所需提供的视距值SR,见表 8。
| 设计速度/(km·h-1) | 120 | 100 | 80 |
| 安全等级 | 一级 | 一级 | 一级 |
| 可靠概率/% | 95 | 95 | 95 |
| 停车视距计算值/m | 294.795 8 | 198.094 3 | 144.910 3 |
| 停车视距推荐选用值/m | 295 | 200 | 145 |
上表计算时采用可靠概率95%进行反算,即将失效概率降低至5%,120,100,80 km/h速度下停车视距失效概率较规范值而言分别降低22.32%,13.2%,18.9%。
4 实例分析现以某全封闭的六车道高速公路为例,选取桩号K156+000~K200+000区间段,长44 km,设计速度为120 km/h。根据该公路当年事故统计资料,全年共发生交通事故1 689起。根据不同的事故原因分类来说,追尾一般由视距不足引起,驾驶不当也与行车视距有一定的联系,由图 2可知,追尾和驾驶不当引发的交通事故占总的48.61%,而这也意味着有相当一部分的事故可能是由视距不足引发的。
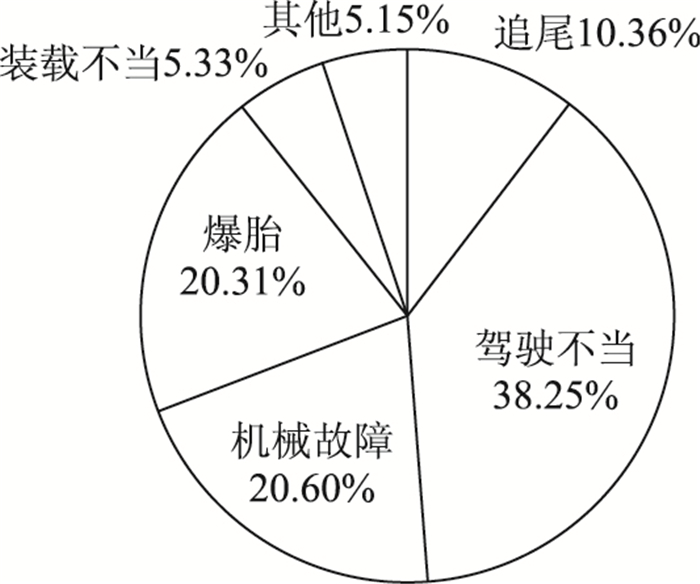
|
| 图 2 各类事故原因分布图 Fig. 2 Distribution of various accident causes |
| |
为了进一步研究视距与事故的联系,现将该公路的事故多发路段即单向每公里事故次数大于10的路段,列于表 9。
| 序号 | 桩号范围 | 方向 | 事故率/(次·km-1) |
| 1 | K157+100~K157+800 | 北行 | 22.86 |
| 2 | K160+080~K160+700 | 北行 | 18.57 |
| 3 | K173+100~K173+900 | 南行 | 21.25 |
| 4 | K184+350~K185+500 | 南行 | 11.30 |
| 5 | K189+000~K190+200 | 南行 | 27.50 |
| 6 | K194+900~K195+930 | 北行 | 22.33 |
4.1 行车视距失效概率
根据汽车在各个事故多发路段的运行速度最大值vmax与最小值vmin,采用停车视距可靠度功能函数D,通过蒙特卡罗法计算其停车视距的失效概率。安全等级一级要求的失效概率需小于0.05,根据相关研究,为保证计算精度,单次可靠度计算的抽样次数必须大于2 000次,工作量较大,故通过MATLAB编程进行计算。
将同一事故多发路段按照不同的纵坡划分,根据上述参数变量抽样类型,以及事故多发路段的纵坡大小,采用蒙特卡罗法,单个路段进行10 000次抽样计算现行规范的小客车停车视距失效概率以及满足95%可靠概率所需的视距,如表 10所示。
| 序号 | 桩号范围 | 运行速度/ (km·h-1) |
纵坡/ % |
失效概率Pf/% | 95%可靠视距/m | |
| 最大值 | 最小值 | |||||
| 1 | K157+100~K157+800 | 114.85 | 111.59 | 0.408 | 37.52 | 302.5 |
| 2 | K160+080~K160+700 | 118.00 | 116.10 | -0.900 | 55.45 | 337.2 |
| 3 | K173+100~K173+500 | 117.65 | 116.35 | -1.100 | 55.34 | 339.5 |
| K173+500~K173+900 | 116.35 | 107.00 | 0.450 | 34.09 | 295.1 | |
| 4 | K184+350~K184+550 | 111.77 | 108.71 | 0.400 | 30.49 | 287.9 |
| K184+550~K185+300 | 110.27 | 107.85 | -0.408 | 30.60 | 292.9 | |
| K185+300~K185+500 | 110.15 | 108.79 | 0.600 | 27.49 | 281.6 | |
| 5 | K189+000~K189+400 | 117.96 | 114.89 | -1.100 | 53.30 | 336.7 |
| K189+400~K190+200 | 117.73 | 110.86 | 1.000 | 39.02 | 301.5 | |
| 6 | K194+900~K195+100 | 113.20 | 109.19 | -0.350 | 36.10 | 302.8 |
| K195+100~K195+930 | 121.89 | 113.20 | -0.900 | 56.40 | 339.6 | |
4.2 结果分析
(1) 在设计速度为120 km/h的事故多发路段的视距失效概率均大于25%,小客车视距失效概率大于50%的事故多发路段占其总的41.67%,失效概率大于30%的事故多发路段占其总的93.33%。视距失效概率较大,表明视距设计不足,易引发交通事故,与前文所述这些路段均是单向每公里事故次数大于10的路段相符。
(2) 根据表中计算的事故多发路段所需满足一级安全等级、95%可靠概率的视距,可以看出其较好地符合表 8中基于可靠度理论的视距推荐值。
5 结论从汽车实际的制动原理出发,将制动过程分为4个阶段:驾驶员的感觉反应阶段、制动系统的间隙消除阶段、制动力上升阶段以及完全制动阶段。由此考虑了全过程的停车视距模型,在同样的限制条件下,其计算的停车视距大于现行规范值。
根据构建的停车视距,建立视距的可靠度功能函数,对现行规范的停车视距标准进行可靠度分析,发现其未达到相应安全等级的要求。并根据安全等级一级的可靠性要求计算出相应的停车视距值,给出了不同设计速度下基于可靠度理论的行车视距选用标准值,推行基于可靠度理论计算得到的停车视距值进行高速公路设计可提高道路安全性。
本研究中反应时间、运行速度、路面的摩擦系数等参数的分析是基于现有研究成果,因此,对设计变量的统计分析将是今后研究的主要内容,以提高可靠性分析准确性。现有规范中没有对停车视距可靠度作出明确规定,本研究以规范对路面结构目标可靠度的规定为依托求解可靠度函数,所以,停车视距可靠度如何规定也是今后需要研究的问题。
| [1] |
张驰, 杨少伟, 潘兵宏, 等. 基于空间有效视野的高速公路线形安全性评价[J]. 公路交通科技, 2010, 27(9): 132-137. ZHANG Chi, YANG Shao-wei, PAN Bing-hong, et al. Safety Evaluation of Expressway Alignment Based on Spatial Valid Vision[J]. Journal of Highway and Transportation Research and Development, 2010, 27(9): 132-137. |
| [2] |
秦勤, 唐琤琤, 彭道月. 山区双车道公路事故预测模型研究及在安全性评价中的应用[J]. 公路交通科技, 2009, 26(10): 139-143. QIN Qin, TANG Cheng-cheng, PENG Dao-yue. Study on Prediction Model of Traffic Accident on Two-lane Highways in Mountainous Area and Its Application in Safety Assessment[J]. Journal of Highway and Transportation Research and Development, 2009, 26(10): 139-143. |
| [3] |
王江锋, 邵春福, 闫学东, 等. 基于虚拟现实的车辆换道最小安全距离研究[J]. 公路交通科技, 2010, 27(8): 109-113. WANG Jiang-feng, SHAO Chun-fu, YAN Xue-dong, et al. Research on Minimum Safety Distance of Lane Changing Based on Virtual Reality[J]. Journal of Highway and Transportation Research and Development, 2010, 27(8): 109-113. |
| [4] |
李长城, 阚伟生. 高速公路平面线形与安全关系的探讨[J]. 公路交通科技, 2007, 24(1): 126-129, 146. LI Chang-cheng, KAN Wei-sheng. Discussion on Relationship between Expressway Crash and Horizontal Alignment[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1): 126-129, 146. |
| [5] |
赵永平, 杨少伟, 赵一飞. 具有中央分隔带公路弯道外侧超车车道的视距[J]. 长安大学学报:自然科学版, 2004, 24(5): 31-34. ZHAO Yong-ping, YANG Shao-wei, ZHAO Yi-fei. Passing Lane Stopping Sight Distance Outside of Median Divider in Freeway[J]. Journal of Chang'an University:Natural Science Edition, 2004, 24(5): 31-34. |
| [6] |
袁浩, 史桂芳, 黄晓明, 等. 停车视距制动模型[J]. 东南大学学报:自然科学版, 2009, 39(4): 859-862. YUAN Hao, SHI Gui-fang, HUANG Xiao-ming, et al. Braking Model of Stopping Sight Distance[J]. Journal of Southeast University:Natural Science Edition, 2009, 39(4): 859-862. |
| [7] |
NAVIN F P D. Safety Factors for Road Design:Can They Be Estimated?[J]. Transportation Research Record, 1990, 1280: 181-189. |
| [8] |
RICHL L, SAYED T. Evaluating the Safety Risk of Narrow Medians Using Reliability Analysis[J]. Journal of Transportation Engineering, 2006, 132(5): 366-375. |
| [9] |
ISMAIL K, SAYED T. Probabilistic Framework for Calibrating of Highway Geometric Design Models[C]//4th International Gulf Conference on Roads: Efficient Transportation and Pavement Systems: Characterization, Mechanisms, Simulation, and Modeling. London: Taylor & Francis Group, 2009: 349-369.
|
| [10] |
SARHAN M, HASSAN Y. Three-dimensional, Probabilistic Highway Design:Sight Distance Application[J]. Transportation Research Record, 2008, 2060: 10-18. |
| [11] |
朱兴琳, 方守恩. 公路路线设计可靠性分析[J]. 公路交通科技, 2009, 26(10): 135-138, 143. ZHU Xing-lin, FANG Shou-en. Analysis on Reliability of Highway Alignment Design[J]. Journal of Highway and Transportation Research and Development, 2009, 26(10): 135-138, 143. |
| [12] |
游克思, 孙璐, 顾文钧. 公路平曲线半径可靠性设计理论与方法[J]. 交通运输工程学报, 2012, 12(6): 1-6. YOU Ke-si, SUN Lu, GU Wen-jun. Reliability Design Theory and Method of Highway Horizontal Curve Radius[J]. Journal of Traffic and Transportation Engineering, 2012, 12(6): 1-6. |
| [13] |
朱兴琳. 基于可靠度理论的公路路线设计[J]. 长安大学学报:自然科学版, 2010, 30(4): 46-50. ZHU Xing-lin. Highway Geometric Design Based on Reliability Theory[J]. Journal of Chang'an University:Natural Science Edition, 2010, 30(4): 46-50. |
| [14] |
李霖, 朱西产, 马志雄. 驾驶员在真实交通危险工况中的制动反应时间[J]. 汽车工程, 2014, 36(10): 1225-1229, 1253. LI Lin, ZHU Xi-chan, MA Zhi-xiong. Driver Brake Reaction Time under Real Traffic Risk Scenarios[J]. Automotive Engineering, 2014, 36(10): 1225-1229, 1253. |
| [15] |
汪双杰, 方靖, 周荣贵, 等. 公路运行速度特征研究[J]. 中国公路学报, 2010, 23(增1): 24-27, 46. WANG Shuang-jie, FANG Jing, ZHOU Rong-gui, et al. Research on Operating Speed Characteristics of Highway[J]. China Journal of Highway and Transport, 2010, 23(S1): 24-27, 46. |
| [16] |
王丽金.高速公路限速与运行速度的关系研究[D].北京: 北京工业大学, 2011. WANG Li-jin. Research on Relationship between Speed Limit and Operating Speed for Freeway[D]. Beijing: Beijing University of Technology, 2011. |
| [17] |
游克思.基于车辆动力学和可靠性理论的道路安全分析及优化设计研究[D].南京: 东南大学, 2012. YOU Ke-si. Vehicle Dynamics and Reliability Based Highway Safety Analysis and Design Optimization[D]. Nanjing: Southeast University, 2012. |
| [18] |
ECHAVEGUREN T, BUSTOS M, DE SOLMINIHAC H. Assessment of Horizontal Curves of an Existing Road Using Reliability Analysis Concepts[J]. Canadian Journal of Civil Engineering, 2005, 32(6): 1030-1038. |
 2019, Vol. 36
2019, Vol. 36
