扩展功能
文章信息
- 孙月峰, 许明昊, 张表志, 张小永, 蒋民阳
- SUN Yue-feng, XU Ming-hao, ZHANG Biao-zhi, ZHANG Xiao-yong, JIANG Min-yang
- 基于改进关键链法的高速公路建设项目进度管理
- Schedule Management of Expressway Project Based on Improved Critical Chain Method
- 公路交通科技, 2019, 36(4): 36-43
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(4): 36-43
- 10.3969/j.issn.1002-0268.2019.04.006
-
文章历史
- 收稿日期: 2018-02-05
2. 交通运输部公路科学研究院, 北京 100088;
3. 北京市密云区发展和改革委员会, 北京 101500;
4. 湖北交投襄随高速公路建设指挥部, 湖北 宜城 441400
2. Reseach Institute of Highway, Ministry of Transport, Beijing 100088, China;
3. Beijing Miyun District Development and Reform Commission, Beijing 101500, China;
4. Xiangyang-Suizhou Expressway Construction Headquarters of Hubei Transport Investment Group, Yicheng Hubei 441400, China
随着我国的经济高速发展,高速公路的建设事业也得到了蓬勃的发展。截至2016年底,我国高速公路里程已经突破13万km,稳居全球首位,基本覆盖了全国城镇人口20万以上的城市[1]。我国提出了自2013年至2030年长达27 a的国家公路网规划,投资额约为4.7万亿元。然而高速公路建设项目是一个复杂的系统工程,其具有线路长、涉及面广、施工工艺复杂、工程量大、专业性强、人员分散等特点。因此高速公路建设项目的进度管理与其他工程项目的进度管理相比,其长期性、复杂性、多方协调性的需求更为突出,这也是其进度管理的难点。对于即将到来的大规模建设的高速公路项目,如何有效地进行进度管理已成为一个重要问题。
在项目进度管理方面,以色列物理学家高德拉特(Goldratt)将约束理论(TOC)应用到项目管理中,提出了一种新的进度管理方法——关键链法。其内涵是强调对项目中不确定因素进行系统分析,将约束理论、聚集原理等运用到进度计划的制订中,通过设置项目缓冲、控制关键链、避免资源并行分配等措施,降低不确定因素对项目的影响。该方法将工序的工期时间分为活动时间d和安全时间Δt,认为传统关键线路法中的安全时间因为学生综合征、帕金森定律等因素隐藏在工序中被浪费掉,通过将安全时间统一管理的方法,以应对可能的进度风险。因此,设置缓冲区是关键链技术的核心,缓冲区设置的大小直接决定着项目计划工期及项目进度风险[2]。
关键链缓冲区的设置有3类,分别是在关键链末端附加整块的安全时间的项目缓冲(PB)、在关键链汇入口处添加缓冲时间的输入缓冲(FB)和防止关键链上工序因资源没有及时到位的资源缓冲(RB)。目前,缓冲区大小的确定还没有统一的方法,主要有剪切-粘贴法[3](Cut and Paste method,C & PM)和根方差法[4](Root and Square Error Method,RESM)。很多学者都在这两种方法的基础上对缓冲区设置进行了改进。周阳、丰景春[5]指出了传统缓冲区设置的缺点,提出应利用排队论来确定在单资源约束下缓冲区的大小,以满足资源的充分利用。蔡晨、万伟[6]提出了采用两点估计方法进行项目工期估计,并利用两点法计算缓冲区大小,利用工期弹性系数吸收不确定因素。王雪青[7]研究在多资源约下,利用专家打分法来确定缓冲区大小。张善从[8]提出一种考虑了在项目执行全生命周期中遇到的项目风险,通过测算风险概率与进度延误程度来计算缓冲区的新的缓冲区fuzzy-CCPM模型。褚春超[9]综合考虑了项目资源紧张度、网络图结构复杂度和管理者风险偏好等因素的影响,使链路上无论工序数的多少都能确保缓冲适当。刘书庆等[10]综合考虑了EPC项目缓冲区设置影响因素中团队素质、施工组织等因素,提出基于影响因素权重及其对不同工序影响程度的工序综合权重计算模型,建立项目缓冲区及输入缓冲区定量确定模型。
综合上述研究发现,诸多学者对缓冲区大小计算方法进行了改进,但仍存在一定的局限性。大多考虑单一资源的约束程度,较少考虑多资源多工序情况下的资源受限度;在考虑项目工序的约束度时,仅分析工序的紧前工序数,未从位置系数和紧前工序两方面分析;缓冲区影响因素的设置中,过分依赖项目管理者的经验,多采用层次分析法和专家打分法定性分析;缓冲区设置的影响因素虽考虑团队素质等因素,但多为单一因素,未综合团队胜任力对缓冲区的影响。
目前在团队胜任力方面的研究较少,Thomas[11]考虑了团队素质满足性的影响,分析了设计成员掌握的核心技术与项目设计技术需求的匹配程度,但未分析施工水平与团队素质的关系。吴振东等[12]、王思琦等[13]对项目团队胜任力模型进行了研究,但其均采用反映性测量模型进行分析,未能充分考虑团队胜任力中各潜变量与观察指标间的因果关系是否与反映性测量模型相匹配。
针对以上研究的局限性,结合高速公路建设项目进度管理中存在的资源受限度高、工序约束度大、施工团队不确定因素多等特点,对关键链技术进行改进,提出一种基于多资源受限度、工序约束度和团队胜任力的关键链缓冲区大小计算方法。基于项目中各工序的位置系数和紧前工序数确定工序约束度;以形成性和反映性混合的观察指标作为测量模型,通过结构方程模型定量分析项目团队中各项指标,构建团队胜任力模型,进而确定团队胜任力系数;最后将本研究提出的改进关键链技术运用到某高速公路工程建设项目进度管理中。
1 缓冲区大小计算的改进方法高速公路建设项目要求土建、交通安全设施、机电工程和附属设施等在批准工期内同步完成,众多施工工序交叉导致资源受限度增强;各分项目施工工艺复杂、工程量巨大,工序前后衔接受到制约;参与单位繁多,同一单位工程量大,施工团队的组织水平与团队素质参差不齐,团队不确定性因素多。因此,结合进度管理的资源受限度高、工序约束度大、施工团队不确定性因素多等特点,提出了基于多资源受限度、工序约束度和团队胜任力的关键链缓冲区大小计算方法。其中通过结构方程模型分析得到各潜变量之间的回归方程,构建并验证团队胜任力模型,确定团队胜任力系数。进而计算确定项目缓冲(PB)和输入缓冲(FB)。关键链缓冲区大小的计算流程如图 1所示。
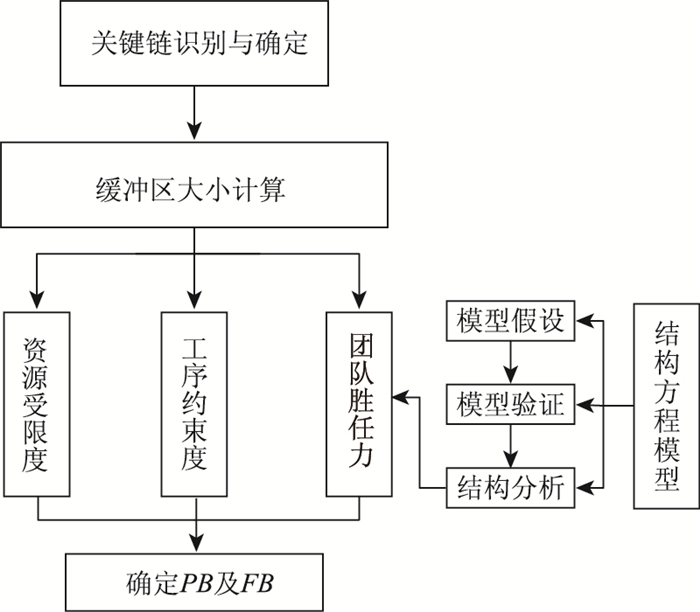
|
| 图 1 关键链缓冲区大小计算流程图 Fig. 1 Flowchart of critical chain buffer size calculation method |
| |
1.1 多资源受限度
αi表示项目中每道工序的在不同资源约束下的受限程度[14]:
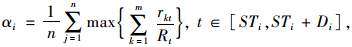
|
(1) |
式中,n表示工序i在t时段运行中使用到的不同资源种类数量;Rt是指在t时间段中资源的可用限量;rkt是指在t时间段运行工序k所需要的资源量;m是指在t时间段内运行工序的总数;STi为工序运行的开始时间;Di为工序运行的持续时间。
1.2 工序约束度采用βi来表示工序受约束度,其中Np是指该工序i所在链路的位置系数,首工序的Np=1;Nq表示该工序i的紧前工序数;N表示为工序i所在链路的工序总数。
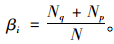
|
(2) |
项目团队的素质对于项目进度管理起着巨大作用,不同团队的胜任能力对工程的控制不尽相同,在不同组织中的胜任特征也不尽相同。在胜任力结构模型的评价与测量的研究中,对于形成性测量模型与反映性测量模型的界定存在着一些偏颇。因此,正确的使用形成性测量模型来描述团队胜任力是非常必要的。
因此,本研究以形成性和反映性混合的观察指标作为测量模型,通过结构方程模型来分析高速公路建设项目团队胜任力影响因素。
1.3.1 结构方程模型结构方程模型可分为测量模型和结构模型两部分。测量方程描述潜变量与观察变量之间的关系,结构模型则反映潜变量之间的相互影响。根据观察变量性质的不同,可以区分为反映性指标和形成性指标两种,在反映性测量模型中,潜变量是“因”,观测变量是“果”,在形成性测量模型中,观测变量是“因”,潜变量是“果”。
反映性指标测量模型通常表示成:
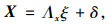
|
(3) |
式中,X为测量指标组成的向量; ξ为潜变量; Λx为测量指标和潜变量的影响系数; δ为外生测量指标的残差。
形成性测量模型通常表示成:
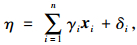
|
(4) |
式中,xi为i个测量指标组成的向量; η为潜变量; γi为测量指标和外生潜变量的影响系数; δi为测量指标的残差。
结构模型通常表示成:
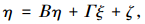
|
(5) |
式中, Β为内生潜变量之间的影响系数; Γ为外生潜变量和内生潜变量之间的影响系数; ζ为结构方程模型的残差。
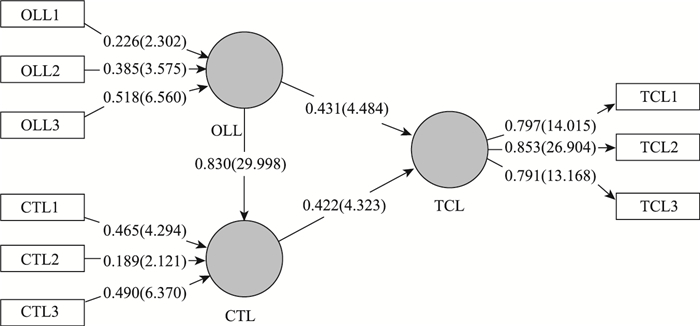
1.3.2 指标设定在现有胜任力模型相关研究的基础上[10-13, 15-17],综合考虑组织领导水平和施工团队水平两个方面,结合专家讨论确定最终题项,形成调查问卷。团队胜任力模型中所有潜变量测量均采用李克特10分量表,并以Jarvis等[18]的决策规则为准则来设定测量模型,如表 1所示。
| 潜变量 | 显变量 | 主要出处 | 模型设定 |
| 组织领导水平(OOL) | 大学入学率(OOL1)、以往合同履约率(OOL2)、以往工期准时交付率(OOL3) | 刘书庆、Thomas、吴振东 | FM |
| 施工团队水平(CTL) | 技术人员比例(CTL1)、3 a以上工作经验比例(CTL2)、30岁以上比例(CTL3) | 王思琦、徐慧玲 | FM |
| 团队胜任力(TCL) | 成本控制度(TCL1)、质量控制度(TCL2)、进度控制度(TCL3) | 郭丽芳、张春松 | PM |
综合考虑通过对13家高速公路工程项目的调研,收集相应的数据和材料,由于研究内容是团队胜任力模型,不同部门的了解程度不能一致的反应出真实情况。所以,在样本选择时,主要采取工程领导部门和施工团队的人员进行调研,调查问卷共发放400份,收回372份,其中有效问卷的数量为368份,调查样本的情况如表 2所示。
| 项目 | 人数 | 百分比 | 项目 | 人数 | 百分比 |
| 性别 | 学历 | ||||
| 男 | 200 | 0.54 | 专科 | 44 | 0.12 |
| 女 | 168 | 0.46 | 本科 | 250 | 0.68 |
| 年龄 | 硕士 | 74 | 0.2 | ||
| 30岁以下 | 100 | 0.27 | 博士 | 26 | 0.07 |
| 31~40岁 | 128 | 0.35 | 其他 | 11 | 0.03 |
| 41~50岁 | 64 | 0.17 | |||
| 51以上 | 76 | 0.21 |
1.3.3 模型分析
使用Smartpls2.0软件来分析团队胜任力模型。首先通过PLS算法和自助法(Bootstrap-ping)来分析形成性测量模型和反映性测量模型的观察指标的因子载荷和权重,以及结构模型的路径系数和显著性水平T值,以验证结构模型与测量模型的有效性。
(1) 交叉载荷效度检验
本研究的测量模型属于形成性与反映性混合模型,虽然在形成性测量模型中,各个观察指标不需要有较强的相关性,但是反映性测量模型可以通过分析交叉载荷,来进行区别效度的分析,因子载荷分析结果如表 3所示。
| CTL | OLL | TCL | |
| CTL1 | 0.911 | 0.770 | 0.696 |
| CTL2 | 0.803 | 0.664 | 0.630 |
| CTL3 | 0.867 | 0.709 | 0.689 |
| OLL1 | 0.747 | 0.881 | 0.671 |
| OLL2 | 0.780 | 0.882 | 0.638 |
| OLL3 | 0.698 | 0.891 | 0.741 |
| TCL1 | 0.655 | 0.566 | 0.797 |
| TCL2 | 0.670 | 0.701 | 0.853 |
| TCL3 | 0.579 | 0.636 | 0.791 |
从表 3可以看出,组织领导水平、施工团队水平和团队胜任力的各项观测指标的载荷系数,都高于和其他潜变量的载荷系数,且均大于0.7,表现出了较好的区别效度。
(2) 形成性测量模型检验
为检验形成性测量模型,需要进行权重系数的显著性检验以及多重共线性检验,分析结果如表 4所示。
| 载荷系数 | 载荷T值 | 权重 | 权重T值 | VIF | |
| CTL1→CTL | 0.911 | 30.043 | 0.465 | 4.294 | 3.100 |
| CTL2→CTL | 0.803 | 17.703 | 0.189 | 2.121 | 2.638 |
| CTL3→CTL | 0.867 | 18.754 | 0.490 | 6.370 | 1.586 |
| OOL1→OOL | 0.881 | 22.010 | 0.226 | 2.302 | 3.783 |
| OOL2→OOL | 0.882 | 24.661 | 0.385 | 3.575 | 3.445 |
| OOL3→OOL | 0.891 | 23.555 | 0.518 | 6.560 | 1.726 |
| 注: T值=1.65(P值=0.1),1.96(P值=0.05),2.58(P值=0.01) | |||||
以Henseler等[19]建议为标准,即权重值应大于0.1,且达到95%的显著性水平,方差膨胀因子(VIF)应小于5,从表 4的统计结果可以看出,所有显变量的权重均大于0.1,载荷系数均大于0.7,并且T值大于2,显著性满足要求,VIF都小于5,这说明不存在多重共线性。
(3) 反映性测量模型检验
为检验反映性测量模型,需要对其信度与效度进行评价。在PLS分析模型中,分别通过α值和组合信度(CR)进行信度检验,通过分析内敛效度和判别效度进行效度检验,分析结果如表 5所示。
| 载荷系数 | 载荷T值 | α值 | 组合信度(CR) | 平均抽取变异量(AVE) | |
| TCL1→TCL | 0.797 | 14.015 | 0.746 | 0.855 | 0.663 |
| TCL2→TCL | 0.853 | 26.904 | |||
| TCL3→TCL | 0.791 | 13.168 | |||
| 注: T值=1.65(P值=0.1),1.96(P值=0.05),2.58(P值=0.01) | |||||
信度系数α值一般认为大于0.7[20],组合信度(CR)应不低于0.6,平均方差萃取量(AVE)应不低于0.5[21]。通过表 5可以看出,α值为0.746,组合信度(CR)为0.63,均满足要求,说明内部一致性很好。所有潜变量因子载荷均大于0.7,且T值均大于2.58,显著性较好,说明潜变量的内敛效度满足要求。AVE为0.663,远高于0.5,这表明有较好的内敛效度。
(4) 结构模型检验
结构模型的检验包括方差膨胀因子(VIF)、路径系数、拟合优度R2和预测效度Q2。通过运行结果得到所有外生潜变量的VIF均低于5,这说明不存在多重共线性;施工团队水平和团队胜任力的拟合优度R2分别为0.690,0.666,超过标准值0.5[22],这说明结构模型的解释力较好。运行Blindfolding程序,计算出代表PLS路径模型的预测相关性的Q2值,得到Q2分别为0.469和0.409,均大于临界值0,这表明预测相关性较好,其中路径系数分析结果如表 6所示。
| 路径系数 | 样本均值(M) | 标准差(STDE) | T统计量(O/STDE) | |
| CTL→TCL | 0.422 | 0.408 | 0.098 | 4.323 |
| OOL→CTL | 0.83 | 0.838 | 0.028 | 29.998 |
| OOL→TCL | 0.431 | 0.452 | 0.096 | 4.484 |
| 注: T值=1.65(P值=0.1),1.96(P值=0.05),2.58(P值=0.01) | ||||
从表 6可知,两个潜变量的路径系数均大于0.4,并且T值大于4,满足显著性要求,表明组织领导水平对团队胜任力有较好的正向影响。具体效果图如图 2所示,可以看出,团队胜任力的各因素影响程度由大到小分别为组织领导水平和施工团队水平,其影响效用分别为0.641、0.431。
|
| 图 2 团队胜任力效果 Fig. 2 Effect of team competency |
| |
变量间结构分析的回归方程如下
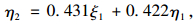
|
(6) |
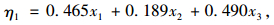
|
(7) |
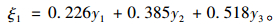
|
(8) |
工序在运行过程中占用资源量越大,越接近其可供量水平,则所在链路更容易出现延期,应考虑的缓冲区需更大一些;项目所涉及的工序以及相应之间逻辑顺序较多,关系较为复杂,缓冲区需考虑大一些;团队胜任力越低,延期的可能性越高,则缓冲区需要大一些。
综合考虑资源受限度、工序约束度、团队胜任力、以及每道工序所消减的安全时间等因素,得出项目缓冲区大小B计算方法如下:
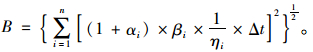
|
(9) |
以某高速公路的路况项目为研究对象进行实例分析。经WBS分解后,共有14道工序,所需资源为X(人力)、Y(机器),最大供应量为15、30个单位,其中1单位X为40人,1单位Y为20台机器,具体相关数据如表 7所示。
| 工序 | 工期 | 紧前工作 | 资源单位数 | ||
| X | Y | ||||
| A | 施工准备 | 66 | — | 1 | 0 |
| B | 路基土石方工程1 | 90 | A | 8 | 20 |
| C | 路基土石方工程2 | 360 | B | 8 | 20 |
| D | 路基土石方工程3 | 75 | C | 8 | 20 |
| E | 路基交工验收整改 | 45 | D,F | 1 | 1 |
| F | 路基防护及排水工程 | 420 | B | 3 | 2 |
| G | 路面面层施工准备 | 180 | A | 1 | 0 |
| H | 路面基层施工准备 | 120 | A | 1 | 0 |
| I | 路面基层施工1 | 120 | I,E | 4 | 4 |
| J | 路面基层施工2 | 60 | G,H | 4 | 4 |
| K | 路面基层施工3 | 75 | J | 4 | 4 |
| L | 路面面层施工1 | 120 | G,H | 3 | 2 |
| M | 路面面层施工2 | 90 | K,L | 3 | 2 |
| N | 路面面层施工3 | 75 | M | 3 | 2 |
2.1 关键链识别
根据各工序之间的逻辑关系和资源受限程度,识别出关键链为A-B-C-D-E-I-J-K-M-N,其余活动为非关键链的工序,同时在项目末尾引入项目缓冲,在非关键链工作汇入处引入输入缓冲。设置缓冲区后的关键链网络图如图 3所示。
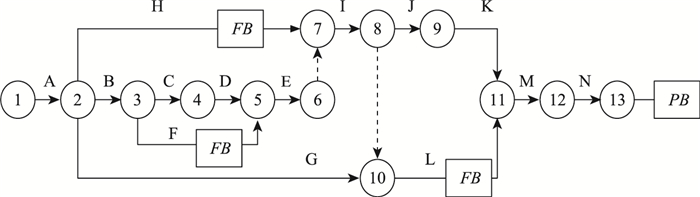
|
| 图 3 设置缓冲区后的关键链网络图 Fig. 3 Network diagram of key chain after setting buffer |
| |
2.2 缓冲区大小计算
如表 7所示,X、Y最大资源供应量为15、30个单位,且各工序最多只有两种资源,根据公式(1)即可求各工序资源受限度。如图 3所示,已知各工序顺序位置和紧前工序数,根据公式(2)可计算出工序约束度。通过统计该项目施工团队人员的技术人员比例、3年以上工作经验比例、30岁以上比例,组织领导团队的大学入学率、以往合同履约率、以往工期准时交付率,根据公式(6)计算出团队胜任力系数。鉴于篇幅原因,不列出具体计算过程,计算结果如下表 8所示。
| 工序 | 资源受限度 | 工序约束度 | 团队胜任力系数 |
| A | 1/15 | 1/10 | 0.95 |
| B | 2/3 | 3/10 | 0.93 |
| C | 4/5 | 2/5 | 0.95 |
| D | 4/5 | 1/2 | 0.94 |
| E | 1/10 | 7/10 | 0.96 |
| F | 4/5 | 4/9 | 0.97 |
| G | 4/5 | 3/5 | 0.94 |
| H | 4/5 | 3/7 | 0.96 |
| I | 1/5 | 4/5 | 0.95 |
| J | 2/3 | 9/10 | 0.95 |
| K | 2/3 | 9/10 | 0.97 |
| L | 2/3 | 1 | 0.96 |
| M | 4/15 | 11/10 | 0.93 |
| N | 4/15 | 11/10 | 0.94 |
通过改进后的缓冲区大小计算方法,得到此高速公路路况项目的关键链工期为528 d,项目缓冲(PB)大小为178 d,在考虑项目缓冲的情况下,总工期为706 d,比原计划工期1 056 d少了350 d。为验证本方法合理度,分别与剪切-粘贴法、根差法以及褚春超提出的方法[9]相对比,结果如表 9所示。
由表 9可以看出,剪切-粘贴法所得缓冲最大,褚春超法[9]所得缓冲最小,本研究所提方法适中,工期均较传统根差法和剪切法短。虽然褚春超法[9]所得缓冲最小,但项目工期并非是越小越好,过短的工期可能会引发更高的工期偏差和更多的资源占用,导致项目在实际执行中出现问题。因此本文所提方法计算的工期更加贴合实际。
3 结论结合高速公路建设项目进度管理中存在的资源受限度高、工序约束度大、施工团队不确定性因素多等特点,本研究对关键链技术进行了改进,提出了一种基于多资源受限度、工序约束度和团队胜任力的缓冲区大小计算方法。与其他研究相比,主要创新之处如下:(1)基于项目中各工序的位置系数和紧前工序数确定了工序约束度,更加充分考虑工序在运行过程中的约束程度。(2)引入结构方程模型定量分析了团队胜任力的影响因素,充分考虑团队胜任力中各潜变量与观测指标间的因果关系,采用形成性和反映性混合的观察指标作为测量模型,确定了团队胜任力系数。(3)通过用改进的关键链技术对某高速公路工程建设项目进行实例分析,工期比原计划的1 056 d减少了350 d,有效地缩短了计划工期,并将本研究方法与3种常规的缓冲区计算方法进行了对比分析,发现所提方法计划工期大小适中,更加贴合实际,有较强的合理性。
本研究提出的改进关键链技术有效地解决了高速公路建设项目中出现的资源冲突、进度管理困难等问题,对高速公路建设项目的进度管理具有重要的借鉴意义。但高速公路项目的施工过程面临的不确定性因素很多,在将来的研究中还需进一步考虑缓冲区的其他影响因素和影响程度。
| [1] |
交通运输部科学研究院. 2016年中国高速公路运行分析报告[EB/OL]. (2017-9-14)[2017-11-28]. http://www.chinahighway.com/zt/zt_new.php?id=669. China Academy of Transportation Science. Analysis Report of China Expressway Operation in 2016[EB/OL]. (2017-9-14)[2017-11-28]. http://www.chinahighway.com/zt/zt_new.php?id=669. |
| [2] |
胡晨, 徐哲, 于静. 基于工期分布和多资源约束的关键链缓冲区大小计算方法[J]. 系统管理学报, 2015, 24(2): 237-242. HU Chen, XU Zhe, YU Jing. Calculation Method of Buffer Size on Critical Chain with Duration Distribution and Multi-resource Constraints[J]. Journal of Systems & Management, 2015, 24(2): 237-242. |
| [3] |
GOLDRATT E M. Critical Chain[M]. New York: The North River Press, 1997.
|
| [4] |
HERROELEN W, LEUS R. On the Merits and Pitfalls of Critical Chain Scheduling[J]. Journal of Operations Management, 2000, 19(5): 559-577. |
| [5] |
周阳, 丰景春. 基于排队论的关键链缓冲区研究[J]. 科技进步与对策, 2008, 25(2): 174-176. ZHOU Yang, FENG Jing-chun. Research on Critical Chain Method Buffer Based on Queuing Theory[J]. Science & Technology Progress and Policy, 2008, 25(2): 174-176. |
| [6] |
蔡晨, 万伟. 基于PERT/CPM的关键链管理[J]. 中国管理科学, 2003, 11(6): 36-40. CAI Chen, WAN Wei. Critical Chain Project Management Based on PERT/CPM[J]. Chinese Journal of Management Science, 2003, 11(6): 36-40. |
| [7] |
王雪青, 郭留洋, 符桃. 基于关键链技术的工程项目进度规划问题研究[J]. 河北工业大学学报, 2005, 34(6): 20-23. WANG Xue-qing, GUO Liu-yang, FU Tao. Construction Project Scheduling Problem Research Based on Critical Chain Technique[J]. Journal of Hebei University of Technology, 2005, 34(6): 20-23. |
| [8] |
张善从, 马丽丛. 高新技术项目的关键链风险缓冲区讨论:基于熵权模糊评价法[J]. 现代管理科学, 2016(10): 9-11. ZHANG Shan-cong, MA Li-cong. Discussion of Critical Chain Risk Buffer for Hi-tech Project:Based on Fuzzy Entropy Evaluation Method[J]. Modern Management Science, 2016(10): 9-11. |
| [9] |
褚春超. 缓冲估计与关键链项目管理[J]. 计算机集成制造系统, 2008, 14(5): 1029-1035. CHU Chun-chao. Buffer Sizing and Critical Chain Project Management[J]. Computer Integrated Manufacturing Systems, 2008, 14(5): 1029-1035. |
| [10] |
刘书庆, 罗丹, 刘佳, 等. EPC项目关键链缓冲区设置模型研究[J]. 运筹与管理, 2015, 24(5): 270-280. LIU Shu-qing, LUO Dan, LIU Jia, et al. Research on The Critical Chain Buffer Setting Model of EPC Project[J]. Operations Research & Management Science, 2015, 24(5): 270-280. |
| [11] |
THOMAS S R, LEE S H, PARK H S. Design-information Technology and Performances in Building and Industry[J]. Canadian Journal of Civil Engineering, 2008, 35(10): 1102-1113. |
| [12] |
吴振东. 项目管理团队胜任力模型及案例研究[J]. 武汉理工大学学报, 2010, 32(3): 511-514. WU Zhen-dong. Competency Model of Project Management Teams and Case Study[J]. Journal of WUHAN University of Technology, 2010, 32(3): 511-514. |
| [13] |
王思琦, 张惠波, 吕文学. 海外EPC项目管理团队胜任力评价研究[J]. 工程管理学报, 2015, 29(6): 85-90. WANG Si-qi, ZHANG Hui-bo, LÜ Wen-xue. Team Competence Evaluation Research of Oversea EPC Project[J]. Journal of Engineering Management, 2015, 29(6): 85-90. |
| [14] |
曹吉鸣. 项目进度规划与控制原理[M]. 北京: 科学出版社, 2013. CAO Ji-ming. Project Schedule Planning and Control Principles[M]. Beijing: Science Press, 2013. |
| [15] |
郭丽芳.矿建工程项目团队胜任力与绩效关系研究[D].北京: 中国矿业大学, 2013: 15-21. GUO Li-fang. Relationship between Competency of Mine Construction Project Team and Performance[D]. Beijing: China University of Mining and Technology, 2013: 15-21. |
| [16] |
徐慧玲.国际工程总承包项目经理胜任力研究[D].北京: 中国矿业大学, 2010: 14-16. XU Hui-ling. Research on Competence of International General Contract Project Managers[D]. Beijing: China University of Mining and Technology, 2010: 14-16. |
| [17] |
张春松.国际工程项目管理人才胜任力评价模型研究[D].天津: 河北工业大学, 2012: 47-56. ZHANG Chun-song. Research of International Engineering Project Management Personnel Competency Evaluation Model[D]. Tianjin: Hebei University of Technology, 2012: 47-56. |
| [18] |
JARVIS C B, MACKENZIE S B, PODSAKOFF P M. A Critical Review of Construct Indicators and Measurement Model Misspecification in Marketing and Consumer Research[J]. Journal of Consumer Research, 2003, 30(2): 199-218. |
| [19] |
HENSELER J, RINGLE C M, SINKOVICS R R. The Use of Partial Least Squares Path Modeling in International Marketing[J]. Social Science Electronic Publishing, 2009, 20(4): 277-319. |
| [20] |
KLINE R B. Principles and Practice of Structural Equation Modeling[J]. Journal of the American Statistical Association, 2010, 101(12): 77-111. |
| [21] |
WETZELS M, ODEKERKEN-SCHRÖDER G, OPPEN C V. Using PLS Path Modeling for Assessing Hierarchical Construct Models:Guidelines and Empirical Illustration[J]. MIS Quarterly, 2009, 33(1): 177-195. |
| [22] |
PAUWELS P, PATTERSON P G, RUYTER K D, et al. The Propensity to Continue Internationalization:a Study of Entrepreneurial Decision-making in Australian Service Firms[J]. Advances in International Marketing, 2009, 20(20): 11-36. |
 2019, Vol. 36
2019, Vol. 36
