扩展功能
文章信息
- 马亚锋, 刘澜, 骆晨
- MA Ya-feng, LIU Lan, LUO Chen
- 基于累积流量比里程分布的区域交通状态评价
- Evaluation of Regional Traffic Status Based on VKT Distribution of Accumulative Volume Ratio
- 公路交通科技, 2019, 36(3): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 152-158
- 10.3969/j.issn.1002-0268.2019.03.022
-
文章历史
- 收稿日期: 2017-08-21
2. 华东交通大学 交通运输与物流学院, 江西 南昌 330013;
3. 综合交通运输智能化国家地方联合工程实验室, 四川 成都 610031
2. School of Transportation & Logistics, East China Jiaotong University, Nanchang Jiangxi 330013, China;
3. National United Engineering Laboratory of Integrated Intelligent Transport, Chengdu Sichuan 610031, China
随着中国城市化进程的逐步加快,城市规模不断扩大,机动车保有量逐年上升,一方面极大地改善了人们的出行条件,提高了国民的生活质量;另一方面,也导致了机动车出行需求激增,使得交通供给与需求的矛盾日益突出,交通系统面临越来越大的压力,随之产生了交通拥挤。近年来,交通拥挤在我国各大、中型城市愈演愈烈,并逐渐演变为阻碍城市可持续发展的重要因素。
准确的交通状态判别和评估是制定合理的交通拥挤管理和控制策略的前提。为此,国内外专家学者提出了很多评价指标并建立了相应的评价模型,涵盖了单个交叉口、路段、交通干线,交通网络等多种范围的研究对象。对于单个交叉口和路段,其评价指标参数多可以通过铺设在道路上及路侧的交通检测器直接获取或简单运算即可获得,如流密速参数、占有率、排队长度、饱和度等,直接通过状态阈值匹配进行交通状态评价。这方面的研究主要见于各国的交通技术规范,且已形成一套完备的体系。如美国明尼苏达州将高速公路运行速度在45 km/h以下定为交通拥挤[1];韩国公路管理局规定车流速度低于30 km/h为拥挤车流,一个月内发生10次以上持续时间超过2 h的拥挤即为常发性交通拥挤[2];日本规定车流速度小于40 km/h,或排队长度大于1 000 m,或拥挤持续时间超过10 min即为交通拥挤[3]等。而对于交通干线,由于干线上交通流之间的相关性,多通过集成多个指标,构造可以反映交通状态变化的指数或方法来进行交通状态评价,如美国德州交通协会基于理想行程时间与实际行程时间构造的行程时间指数[4],关伟等[5]基于各车道交通流同态程度构造的同态度量指数,岳园园等[6]基于速度里程分布构造的快速路宏观交通状态指数,郑建湖等[7]基于交通量和占有率建立的交通状态模糊识别方法等。在区域路网交通状态评价方面,Herman等[8]提出的二流理论将路网中的车辆分为运动车辆和静止车辆,从而有效地描述了城市交通网络中的集中流特征。在此基础上,王殿海等[9]基于二流理论,对路网宏观交通状态参数之间的关系进行了推导,从而建立了一种新的网络交通状态评价模型;田亮等[10]也基于二流理论建立了网络交通状态评估模型并证明了其可行性。但是,二流理论单纯地将网络上的车辆划分为运动车辆和静止车辆,与实际交通运行状况不符,对实际交通管理与控制意义有限。Geroliminis和Daganzo[11]在前人的基础上,通过研究日本横滨的交通检测器数据,发现单个检测器检测的流量和占有率的函数关系的离散度较大,而全网的流量和占有率之间却具有稳定的函数关系,且这种函数关系只与路网本身有关,与网络的交通需求无关,由此提出了路网的宏观基本图(MFD, Macroscopic Fundamental Diagram)模型,并对其特性[12]及在交通网络中的应用[13-14]进行了研究。随后,GAO[15], Boyac等[16]的研究也证明了城市路网中MFD的存在性,王福建等[17]以路网平均速度和密度为评价指标,建立了宏观基本图的城市路网交通状态判别模型,将网络交通流划分为自由流、稳定流、不稳定流、限制流、强制流5种状态。由北京交通发展研究中心提出并应用于实际的道路交通运行指数(TPI)以车公里数为权重对各等级道路的拥挤里程进行加权,计算得到全市路网拥挤里程比例,结合交通参与者的拥挤感知调研,进行转换计算而得[18],虽然能够实时反映交通状态及其变化,但是只考虑了严重拥挤里程的比例,以局部反映整体,对实际交通状态描述的准确程度有待进一步验证。
在以上研究的基础上,本研究以成都市金牛区二环路、人民北路二段、一环路、沙湾路围合成的局域路网为例,将宏观基本图理论引入区域交通状态评价中,建立基于路段累积流量比(Accumu-lating Volume Ratio, AVR)里程分布的区域交通状态指数(RTSI)评价模型,并通过实例分析验证模型的适用性。
1 模型的建立 1.1 城市道路交通状态多级划分在交通流运行中,各项参数如交通量、车流密度、速度、占有率等的变化是一个连续的过程,但是,研究表明:当交通流参数处于不同的区间时,交通流的外部运行特征完全不同,同时,交通参与者也会有不同的服务感受。在此基础上,B.S. Kerner[19]对德国高速公路上的交通流运行状况进行了分析,根据交通流外部运行特征将其划分为3种状态:自由流、同步流和宽移动阻塞流。这种划分对于中低速交通流比较粗糙,不利于稳定流及拥挤交通流的准确描述。故本研究在三相交通流理论基础上,细分同步流以及宽移动阻塞流,从而将交通状态划分5级,即畅通、基本畅通、轻微拥挤、中度拥挤和严重拥挤及堵塞。各级状态的特性文献[6]和[13]均已有对应描述,本研究不再赘述。
城市交通网络是由路段和交叉口组成的有机整体,其交通特性与路段和交叉口紧密相关,但不是路段和交叉口的交通特性的简单叠加。宏观基本图(MFD)模型从路网的整体结构出发,通过对路网中的多个路段的流量、密度、速度、占有率等参数进行加权处理,以定量地反映宏观交通流参数之间的关系,以流量为例,路网的加权流量q为:
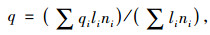
|
(1) |
式中,qi,li,ni分别为第i条路段的单车道流量、长度及车道数。为了反映路段交通流量的短时变化特性,文中的各路段单车道流量由5 min车辆数等效转换而得。同理,定义加权累积流量比CD为:
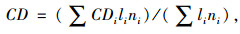
|
(2) |
式中,CDi为第i条路段的累积流量比,CDi=Ni/Nimax;Ni为第i条路段的累积流量,是分布于第i条路段具有匹配关系的驶入断面和驶出断面间的车辆数量,是在一定时段内由驶入流量和驶出流量综合作用的结果;Nimax为第i条路段的最大累积流量,是第i条路段完全处于停车排队状态下的累积流量。由上述定义可知,任一时刻Ni≤Nimax,即CDi≤1。
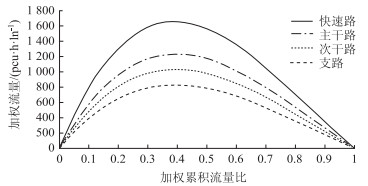
利用成都市金牛区二环路、人民北路二段、一环路、沙湾路围合成的局域路网中的交通卡口监测数据,应用Van Aerde模型,以路段长度和车道数为权重,分别计算路网中各等级道路基本图的加权流量与加权累积流量比并对其关系进行标定,得出各等级道路在不同交通状态下流量和累积流量比的特征阈值如图 1所示。
|
| 图 1 各等级道路宏观交通流状态等级划分 Fig. 1 Division of macroscopic traffic statuses of different levels of roads |
| |
由图 1中可以看出,在不同交通状态下,虽然不同等级的道路的加权流量差异很大,但是其交通状态与加权累积流量比之间具有很好的对应关系,并且不同等级城市道路在相同交通状态下的AVR区间是比较接近和相对固定的。所以,本研究最终确定各级交通状态对应的AVR区间如表 1所示。
| 交通状态划分 | 畅通 | 基本畅通 | 轻微拥挤 | 中度拥挤 | 严重拥挤 |
| AVR区间 | [0, 0.072] | (0.072, 0.176] | (0.176, 0.464] | (0.464, 0.670] | (0.670, 1] |
1.2 区域路网累积流量比里程分布模型
以实地交通调查数据为VISSIM仿真输入,采集区域路网中各路段上驶入、驶出断面交通流数据,然后计算各路段的累积流量比及其动态变化,建立局域路网的累积流量比里程分布模型。
任意选定一个时刻,若路段i上某一车流运行方向的累积流量为Ni,(对应对向累积流量为Ni′),设此路段此方向的最大累积流量为Nimax,则其累积流量比为:
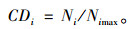
|
(3) |
相应地,对向的累积流量比为:
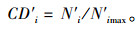
|
(4) |
设任一时间间隔内,累积流量比为CDi的路段有m条,则累积流量比为CDi的路段里程占比为:
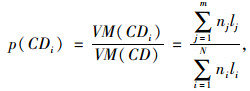
|
(5) |
式中,ni为路段i的车道数;li为路段i的长度,N为居于路网总的路段数(分方向)。
对CDi进行集计分析即可得局域路网累积流量比的里程分布,将集计分析结果转化为其概率密度函数f(CD),则局域路网累积流量比的里程分布的概率分布函数为:
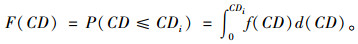
|
(6) |
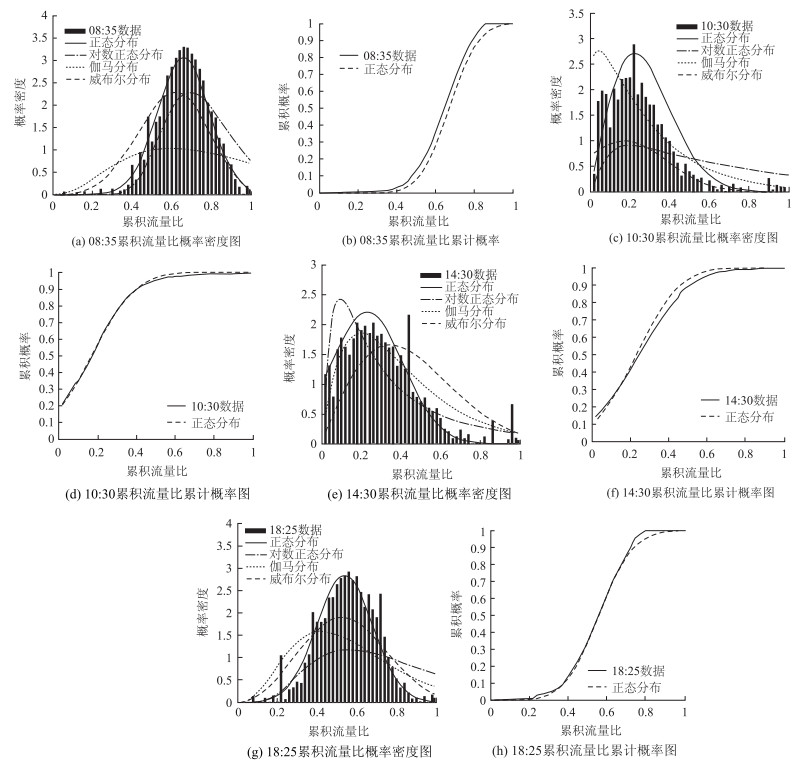
对上述局域路网的交通运行状况进行仿真,采集每5 min各路段上的驶入、驶出流量,然后选定2个高峰(早高峰8:35,晚高峰18:25)及2个平峰(10:30,14:30)共4个时刻,计算各路段的累积流量,再结合各路段的特征属性,分别按式(5)、式(6)统计并绘制累积流量比的概率密度图和概率分布图。同时采用4种常用分布函数(正态分布、对数正态分布、伽马分布及威布尔分布)对其进行拟合(如图 2所示)。对比4种拟合结果即可发现,局域路网上路段累积流量比里程分布服从正态分布,如式(7)所示。
|
| 图 2 累积流量比概率密度及累积概率分布图 Fig. 2 Distributions of AVR probability densities and accumulative probabilities |
| |
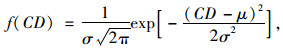
|
(7) |
式中, CD为仿真时段局域路网中路段的累积流量比;μ和σ分别为累积流量比里程分布概率模型的均值和标准差,由0≤CD≤1可知,0≤μ≤1,σ > 0。
对于某一时刻,统计局域路网中所有路段的累积流量比并进行参数估计,即可得出对应的均值μ和标准差σ,计算公式为:
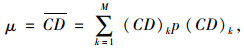
|
(8) |
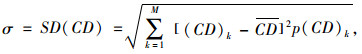
|
(9) |
式中,M为AVR的取值区间数;CD和SD(CD)分别为AVR里程分布的均值和标准差。
将式(8)、式(9)计算得出的μ和σ代入式(7)即可得出AVR里程分布的概率密度函数,则其累积概率分布函数为:
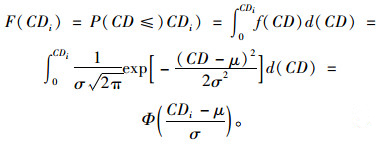
|
(10) |
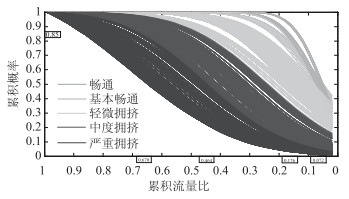
运用区域路网早高峰至晚高峰(6:30—20:30)的路段驶入、驶出断面的流量数据,依据式(6)计算时间间隔为5 min的AVR里程分布累积概率分布曲线,共得到168条累积概率分布曲线,如图 3所示,其中横坐标为数字次序反转的累积流量比,纵坐标即其累积里程分布概率。图 3中不同的线条落在不同的区域,表明交通状态不同时,相应地,区域路网累积流量比里程分布的概率分布也会不同。
|
| 图 3 基于累积流量比里程分布的宏观交通状态累积流量比阈值划分 Fig. 3 Division of macroscopic traffic status AVR thresholds based on VKT distribution of AVR |
| |
1.3 基于AVR里程分布的网络交通状态测度模型
设图 3中任一概率分布曲线上任意一点的纵坐标值为F(CDi),表示局域路网中累积流量比低于CDi的里程占总里程的比例。参考中国公路限速的规定,以85%分位里程对应的累积流量比,即F(CDi)=85%,为临界点,并以其为自变量对路网交通状态进行测度,建立局域路网交通状态指数如式(11)所示,其中CD85%表示路网中85%分位里程所对应的累积流量比值。因为累积流量比的取值上限为1,所以,当F(CDi)=85%所对应的累积流量比为1时,即85%里程的路段发生严重拥挤时,本研究直接将区域路网交通状态定为严重拥挤,RTSI=10。
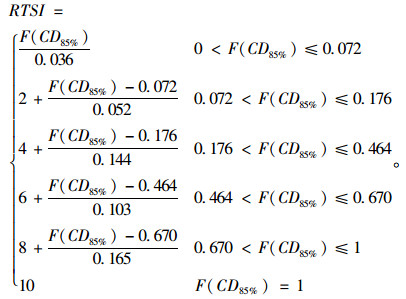
|
(11) |
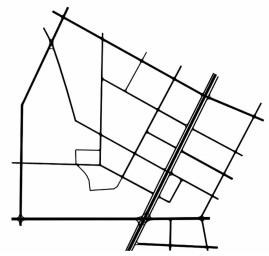
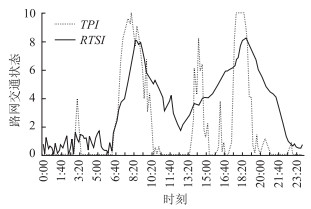
以成都市某局域路网(如图 4所示)为例,利用2015年某日的交通调查数据,采集每10 min的交通流参数,分别采用北京交通发展研究中心提出的TPI指数和本研究提出的RTSI指数对路网交通状态进行评价,结果如图 5所示。
|
| 图 4 成都市某局域路网图 Fig. 4 A regional road network of Chengdu |
| |
|
| 图 5 成都市某局域路网宏观交通状态评价对比 Fig. 5 Comparison of evaluation results of macroscopic traffic status of a regional network in Chengdu |
| |
由图 5可以看出,在局域路网宏观交通状态评价过程中, 本研究提出的基于累积流量比里程分布的RTSI指数与TPI指数的契合程度达到85%以上,有力地证明了本研究模型的有效性。与此同时,因为累积流量比是渐变参数,且本研究的TRSI指数是集成了网络中所有路段的累积流量比而提出的,其变化过程是连续的,没有骤增和骤减的情况,因此其变化趋势对交通拥挤发生、发展、蔓延及消散过程的描述更贴近于实际。而TPI指数通过严重拥堵路段里程占比反映整个路网的运行情况,导致其在路网交通状态测度过程中极易出现剧烈震荡,具体表现在如下方面:在低谷(夜间)或平峰时段,路网中基本没有严重拥堵路段,此时TPI指数会骤降为0;若此时发生局部交通拥挤,TPI指数会急剧上升,事实是低谷(夜间)和平峰时段的局部交通拥挤通过局域路网本身的自我调节即可避免其进一步恶化,基本不会引发大规模的网络交通拥挤。在运用TPI指数描述交通拥挤消散过程中,也会出现剧烈震荡的情况。综上分析,在网络交通状态评价过程中,本研究提出的RTSI指数相较于TPI指数具有更好的适用性。
3 结论本研究以“建立区域交通状态评价模型”为目标,构建了基于累积流量累积流量比里程分布的RTSI评价方法。在模型建立过程中:(1)基于宏观基本图理论,将路网的交通状态划分为畅通、基本畅通、轻微拥挤、中度拥挤、严重拥挤5个等级,并标定了不同状态下累积流量比的区间;(2)基于实际交通流调查数据,通过VISSIM仿真软件,建立了累积流量比累积里程分布模型,并得出局部路网上累积流量比的里程分布服从正态分布;(3)分别采用TPI和RTSI同时对成都市某区域路网的交通运行态势进行识别和评价,结果表明:综合考虑了大部分路段交通状态的RTSI对交通状态的评价更贴近于实际,具有更好的适用性。
本研究建立的基于累积流量累积流量比里程分布的区域交通状态评价模型,可以实现局部路网的交通状态识别和评价,这一方面丰富了网络交通状态评估理论,另一方面也对出行者的交通出行和交管部门的交通管理和控制具有一定的指导意义。此外,虽然研究中引入了宏观基本图模型,但是文中路网规模较小,模型结构简单,在更大规模和不同结构的路网上的适用性也有待验证。后续将进一步改进模型并扩大路网研究范围,以进一步论证模型的合理性并提高模型的适用性。
| [1] |
BERTINI R L, RUFOLO A M. Technology Considerations for the Implementation of a Statewide Road User Fee System[J]. Research in Transportation Economics, 2004, 8(1): 337-361. |
| [2] |
CHOI D I, KIM T S, LEE S. Analysis of a Queueing System with a General Service Scheduling Function, with Applications to Telecommunication Network Traffic Control[J]. European Journal of Operational Research, 2007, 178(2): 463-471. |
| [3] |
刘澜, 马亚锋. 基于出入流率的交通拥挤量化研究[J]. 公路交通科技, 2013, 30(3): 111-117, 124. LIU Lan, MA Ya-feng. Traffic Congestion Measurement Based on Inflow and Outflow Rates[J]. Journal of Highway and Transportation Research and Development, 2013, 30(3): 111-117, 124. |
| [4] |
SCHRANK D L, LOMAX T J. 2009 Urban Mobility Report, DTRT06-G-0044[R]. Austin: Texas A&M Transportation Institute, 2009.
|
| [5] |
关伟, 何蜀燕, 马继辉. HMI:城市快速路发生交通拥堵的一个预警指标[J]. 交通运输系统工程与信息, 2008(5): 26-31. GUAN Wei, HE Shu-yan, MA Ji-hui. HMI:Prewarning Index of Traffic Jam Formation on Urban Freeway[J]. Journal of Transportation Systems Engineering and Information Technology, 2008(5): 26-31. |
| [6] |
岳园圆, 于雷, 朱琳, 等. 基于速度里程分布的快速路宏观交通状态评价模型[J]. 交通运输系统工程与信息, 2014(4): 85-92. YUE Yuan-yuan, YU Lei, ZHU Lin, et al. Macroscopic Model for Evaluating Traffic Conditions on the Expressway Based on Speed-Specific VKT Distributions[J]. Journal of Transportation Systems Engineering and Information Technology, 2014(4): 85-92. |
| [7] |
郑建湖, 文子娟, 黄明芳, 等. 交通拥挤状态模糊识别方法的设计与应用[J]. 华东交通大学学报, 2009(1): 29-33. ZHENG Jian-hu, WEN Zi-juan, HUANG Ming-fang, et al. Application and Design of Traffic Congestion Identification Method Using Fuzzy Logic[J]. Journal of East China Jiaotong University, 2009(1): 29-33. |
| [8] |
HERMAN R, PRIGOGINE I. A Two-fluid Approach to Town Traffic[J]. Science, 1979, 204(4389): 148-151. |
| [9] |
王殿海, 陈松, 魏强, 等. 基于二流理论的路网宏观交通状态判断模型[J]. 东南大学学报:自然科学版, 2011(5): 1098-1103. WANG Dian-hai, CHEN Song, WEI Qiang, et al. Discrimination Model for Macroscopic Traffic Conditions of Urban Networks Using Two-fluid Theory[J]. Journal of Southeast University:Natural Science Edition, 2011(5): 1098-1103. |
| [10] |
田亮, 刘其鑫. 基于二流理论的宏观交通评价模型的建立[J]. 交通科技与经济, 2008(1): 83-84. TIAN Liang, LIU Qi-xin. Macroscopic Traffic Evaluation Model Based on the Second Level Theory[J]. Technology & Economy in Areas of Communications, 2008(1): 83-84. |
| [11] |
GEROLIMINIS N, DAGANZO C F. Existence of Urban-scale Macroscopic Fundamental Diagrams:Some Experimental Findings[J]. Transportation Research Part B:Methodological, 2008, 42(9): 759-770. |
| [12] |
DAGANZO C F, GEROLIMINIS N. An Analytical Approximation for the Macroscopic Fundamental Diagram of Urban Traffic[J]. Transportation Research Part B:Methodological, 2008, 42(9): 771-781. |
| [13] |
DAGANZO C F, GAYAH V V, GONZALES E J. Macroscopic Relations of Urban Traffic Variables:Bifurcations, Multi-valuedness and Instability[J]. Transportation Research Part B:Methodological, 2011, 45(1): 278-288. |
| [14] |
DAGANZO C F. On the Macroscopic Stability of Freeway Traffic[J]. Transportation Research Part B:Methodological, 2011, 45(5): 782-788. |
| [15] |
GAO F. Macroscopic Fundamental Diagrams for Stockholm Using FCD Data[D]. Stockholm: Royal Institute of Technology, 2011.
|
| [16] |
BOYAC B, GEROLIMINIS N. Estimation of the Network Capacity for Multimodal Urban Systems[J]. Procedia-Social and Behavioral Sciences, 2011, 16: 803-813. |
| [17] |
王福建, 韦薇, 王殿海, 等.基于宏观基本图的城市路网交通状态判别与监控[C]//第七届中国智能交通年会优秀论文集.北京: 电子工业出版社, 2012: 35-40. WANG Fu-jian, WEI Wei, WANG Dian-hai, et al. Urban Road Network Traffic State Identification and Monitoring Based on Macroscopic Fundamental Diagram[C]//Proceedings of the Seventh China Intelligent Transportation Conference. Beijing: Publishing House of Electronics Industry, 2012: 35-40. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZJTX201209001008.htm |
| [18] |
郑淑鉴, 杨敬锋. 国内外交通拥堵评价指标计算方法研究[J]. 公路与汽运, 2014(1): 57-61. ZHENG Shu-jian, YANG Jing-feng. Research on Computational Methods of Traffic Congestion Evaluation Indexes at Home and Abroad[J]. Highways & Automotive Applications, 2014(1): 57-61. |
| [19] |
KERNER B S. Three-phase Traffic Theory and Highway Capacity[J]. Physica A:Statistical Mechanics and Its Applications, 2004, 333(1): 379-440. |
 2019, Vol. 36
2019, Vol. 36
