扩展功能
文章信息
- 周记国, 张敏江, 薛晓锋
- ZHOU Ji-guo, ZHANG Min-jiang, XUE Xiao-feng
- 基于流固耦合的行车临界风速研究
- Analysis on Critical Wind Speed for Driving Based on Fluid-solid Coupling
- 公路交通科技, 2019, 36(3): 144-151
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 144-151
- 10.3969/j.issn.1002-0268.2019.03.021
-
文章历史
- 收稿日期: 2017-07-22
2. 白城师范学院 土木工程学院, 吉林 白城 137000;
3. 长安大学 公路学院, 陕西 西安 710064
2. School of Civil Engineering, Baicheng Normal University, Baicheng Jilin 137000, China;
3. School of Highway, Chang'an University, Xi'an Shaanxi 710064, China
车辆行驶过程中发生交通事件的一个主要客观因素为恶劣天气,我国恶劣天气引起交通事件占比约为50%[1],在恶劣天气下有71%是重大事故,65%是直接经济损失。风荷载作用下车辆在桥上行驶时,汽车及桥梁受到风荷载的作用,同时汽车及桥梁系统的振动对风荷载特性产生影响,车桥周围风荷载特性的改变使车桥系统的气动力特性发生变化,因此由自然风环境与车桥系统的耦合作用形成了风-汽车-桥梁耦合系统。
目前对风-车-桥系统的研究主要有数值模拟[2-5]和风洞试验[6]两种方法。韩艳等[7]以常见的大客车为对象,通过数值模拟得到车、桥各个单体与车-桥耦合时两种不同情况下车辆的气动力系数存在较大差异。李永乐等[8]以轨道交通列车为研究对象,分别对两辆列车交会及车辆在桥上行驶经过桥塔过程进行了车辆气动力系数的试验测试,得到了行驶过程中突变风荷载作用下车辆气动力的变化规律及相关影响因素。郭薇薇、夏禾等[9]以列车、简支梁桥为研究对象,通过风洞试验测得车辆及桥梁的三分力系数,通过数值模拟对风-列车-桥梁耦合振动进行了研究,得到了桥上有、无风障时列车在桥上行驶的安全临界风速。
一些专家、学者进行了风-车-桥系统数值分析的相关程序或数值计算软件的研发。韩万水、陈艾荣[10]进行了程序编制并进行了数值模拟软件的研发,研究风荷载作用下车辆在桥上行驶过程中车-桥系统的振动特性。周立、葛耀君[11]以钢箱梁桥为研究对象,对风-车-桥系统的振动特性进行了模拟研究,开发了数值分析程序,并对系统的振动特性及疲劳特性进行了研究。
对风-车-桥系统的振动分析已经有了较多有价值的研究成果[12-15],现有对风-车-桥系统的研究大多是基于车辆静止在桥上所得的车辆及桥梁的气动力系数再进行系统的振动研究,没有充分考虑车辆的行驶及车-桥耦合系统的振动与车桥周围风场间的耦合影响。考虑风环境、汽车及桥梁三者间的耦合影响,对车辆的行车安全还有研究的必要。本研究通过应用双向流固耦合数值分析,考虑车辆在桥上行驶过程中车桥耦合系统的振动与车桥周围风环境的耦合作用,建立三维空间分析模型,分析车辆的行车安全。
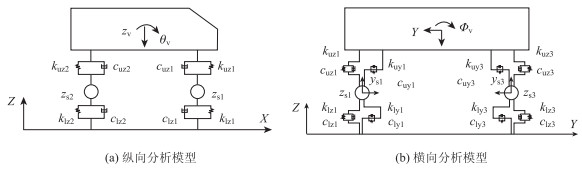
1 风-车-桥系统数值建模 1.1 固体域数值模拟以常见的大客车为研究对象,车辆宽度、高度、长度分别为2.5,3.6,10.49 m。将所研究车辆在数值建模的动力分析过程中简化为车体与车轮刚体构件,用弹性及阻尼元件连接车体与车轮[10]。车体有3个自由度,车轮有1个自由度。车辆动力分析模型如图 1所示。
|
| 图 1 车辆动力模型 Fig. 1 Vehicle dynamic model |
| |
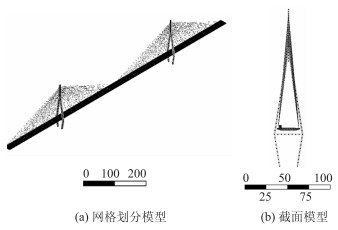
以半飘浮斜拉桥为分析对象,斜拉桥各跨径为(295+612+295)m。斜拉索的垂度效应采用等效弹性模量进行考虑,建立风-车-桥系统中汽车-桥梁系统数值模型考虑应力刚化效应,分别应用实体单元、梁单元、索单元模拟梁、桥塔及斜拉索,分别应用COMBIN14,CONTA174及TARGE170模拟汽车弹簧、车辆与桥梁的接触,分析模型如图 2所示。
|
| 图 2 车-桥分析模型(单位:m) Fig. 2 Vehicle-bridge analysis model(unit:m) |
| |
1.2 流体域数值模拟
对风-车-桥耦合系统的流场分析采用动网格技术进行数值模拟研究。首先与文献[6]的桥梁气动力系数对比验证,文献中试验测得的桥上无车及车辆静止在桥上时桥梁的气动力对比研究如表 1所示。
| 气动力 系数 |
桥梁上无车 | 误差/% | 桥梁上有车 | 误差/% | ||
| 风洞测试 | 数值模拟 | 风洞测试 | 数值模拟 | |||
| CS | 0.148 | 0.150 | 0.94 | 0.260 | 0.224 | 13.8 |
| CD | 0.058 | 0.054 | 6.17 | 0.066 | 0.056 | 15.1 |
| CR | -0.017 | -0.018 | 5.14 | -0.014 | -0.013 | 7.1 |
由于两种研究对车辆及车轮模型的建立存在差异,所以导致当桥上有车辆状况下桥梁的气动力系数的误差较大,表中误差说明本研究数值模拟数据与文献中的风洞测试数据对比误差较小,由此说明流场模型数值分析结果可靠。
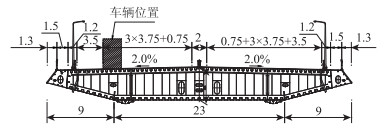
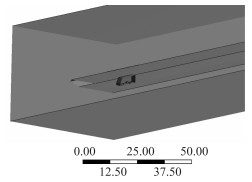
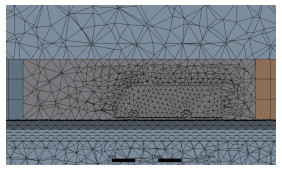
流场数值分析模型中速度入口边界为迎风侧边界,压力出口为背风侧边界,其余为对称边界。考虑堵塞效应确定流体计算的数值模型尺寸,使模型的迎风面积相比数值风洞的截面面积小于5%。流场数值模型中的车辆及桥梁的壁面网格划分加密,壁面函数y+在30~300之间[16]。速度入口的风荷载统一为湍流强度5%、湍动黏度比5的脉动空间风场。桥梁断面形式及车辆在桥上的位置如图 3所示,车辆位于桥梁断面的迎风侧,横截面的左侧为来流方向。流场数值风洞模型如图 4、图 5所示。
|
| 图 3 桥梁横断面(单位:m) Fig. 3 Bridge cross-section (unit: m) |
| |
|
| 图 4 数值风洞模型截面(单位:m) Fig. 4 Numerical wind tunnel model cross-section(unit:m) |
| |
|
| 图 5 数值风洞网格截面 Fig. 5 Numerical wind tunnel mesh cross-section |
| |
1.3 流固耦合数值模拟
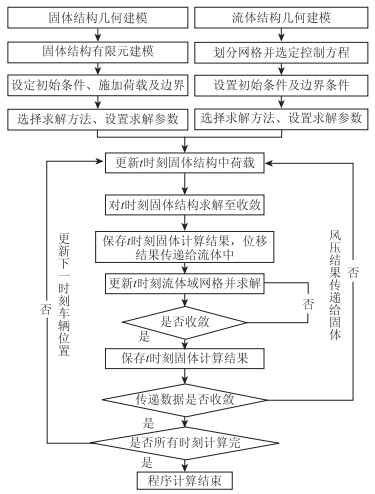
根据车-桥系统的振动与车-桥周围风场的相互影响、车-桥系统固体域与流体域的边界相互作用,本研究提出对风-车-桥系统应用流固耦合分析方法进行数值分析。对风-车-桥系统流体域、固体域数值分析过程中采用的主要假设有:(1)流体域中不考虑斜拉索、桥梁栏杆等细部构件对流场的影响;(2)主要研究车辆远离桥塔位置行驶时风-车-桥系统的振动特性;(3)车辆匀速行驶,并且车轮与桥面始终接触;(4)车辆的阻尼系统为黏性阻尼,弹簧悬挂系统均为线性。车辆、桥梁外表面为耦合边界以实现流体分析与固体分析的数值传递,每一荷载步中分别进行流体与固体数值计算。对风-汽车-桥梁系统数值分析流程如图 6所示。
|
| 图 6 流固耦合分析流程 Fig. 6 Flowchart of fluid-solid coupling analysis |
| |
2 基于耦合振动的车辆气动及振动特性分析 2.1 车辆气动特性
车辆行驶过程中受到联合风荷载作用,共受到3个分量的气动力有作用,分别为气动侧向力FS、气动升力FL、气动阻力FD,同时共受到3个分量的气动力矩作用,分别为俯仰力矩MP、偏转力矩MY、倾覆力矩MR作用。气动力较大时会使车辆产生倾覆及侧滑等危险,桥面高程及流场的结构绕流等因素影响使风荷载作用下桥上车辆的行车安全分析问题更加突出[13],在行驶过种程,常见的行车安全为车辆倾覆与侧滑,其中车辆三分力系数定义为:
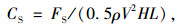
|
(1) |

|
(2) |
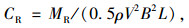
|
(3) |
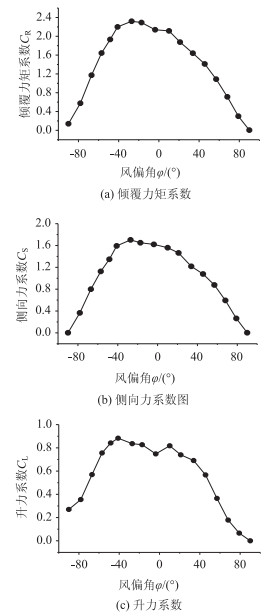
式中,CS,CL,CR分别为侧向力系数、升力系数和倾覆力矩系数;ρ为空气密度;V为车辆行驶所产生的纵向风与不同角度风荷载的合成风速;H,B,L分别为汽车的高度、宽度和长度。采用体轴表示车辆的气动力,其中风荷载侧向作用时为0°,正面作用时为+90°。以90 km/h行驶,基于风-车-桥耦合振动系统的车辆气动三分力系数变化律如图 7所示。
|
| 图 7 车辆气动力系数 Fig. 7 Aerodynamic force coefficients of vehicle |
| |
由计算可得,-90°~0°时气动侧向力系数及倾覆力矩系数随风偏角同步增大,-90°~90°范围内CR,CS大致呈正弦曲线变化。同时可以看出车辆的CR,CS最大值并不一定在0°位置。风荷载以0°风偏角作用时,车辆外表面所产生的风压相对较均匀,所以侧向力及倾覆力矩不一定为极大值。由于车辆表面的风压在车辆的表面分布不均匀,使风偏角不为0°时气动侧向力及倾覆力矩系数最大。
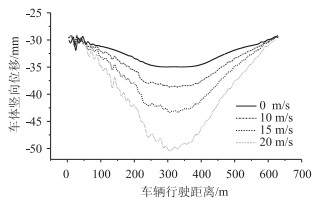
2.2 车辆振动特性当车辆以90 km/h行驶在光滑路面上,无风荷载及分别受到不同风速的侧向风荷载作用时,车辆车体与桥梁中跨跨中截面的竖向振动及车轮竖向接触力的变规律如图 8~图 10所示。
|
| 图 8 车体竖向振动位移 Fig. 8 Vertical vibration displacement of vehicle |
| |
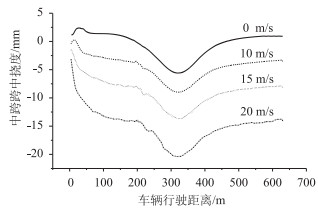
|
| 图 9 桥梁主跨跨中截面竖向振动位移 Fig. 9 Vertical vibration displacement of mid-span cross-section of bridge main span |
| |
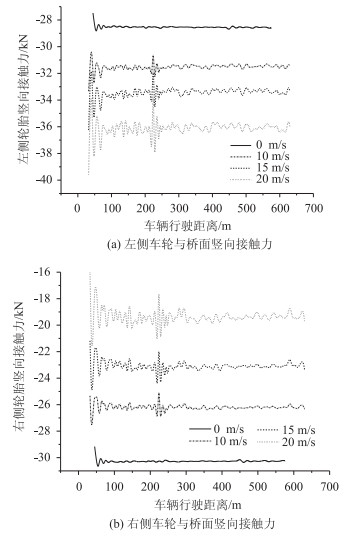
|
| 图 10 车辆车轮竖向接触力 Fig. 10 Vertical contact forces of vehicle wheel |
| |
图 8、图 9中横坐标为车辆在桥梁上的行驶距离,车辆在桥梁的中跨端点开始行驶时为坐标零点;纵坐标分别为车辆及桥梁的绝对竖向振动位移。对比分析车-桥系统的竖向振动可以看出,车辆在桥上行驶过程中,车-桥系统的振动大小与风速呈正比,不同风速下的车-桥系统的振动在行驶过程中变化基本一致。
从车轮与桥面的接触力变化可以得出,车轮的接触力随着车辆行驶逐渐趋于平稳。通过对比可以得到,风荷载作用下左侧竖向接触力比右侧略大,这是由于有侧向滚动的自由度。内侧车轮与桥面的接触力与风速成正比,外侧车轮与桥面的接触力与风速成反比,这是与实际相同的,证明本程序模型的正确。车辆在桥上行驶无风荷载作用及受不同风速的风荷载作用时,对比分析车辆及桥梁的竖向振动特性、车轮竖向接触力的变化可以看出,车辆的振动特性由车-桥系统的特性决定,数值大小受风荷载影响。
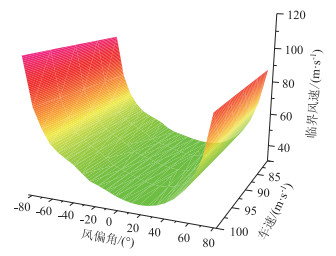
3 基于耦合振动的车辆安全性分析 3.1 车辆倾覆临界风速车辆行驶过程中,车轮与桥面的竖向接触力大小随时间的变化假定成正态分布[17],采用95%保证率的不脱空轮压对车辆的行驶安全进行评价。车辆分别在干、湿、雪、冰的路面上行驶时与车辆的倾覆临界风速计算采用一致的分析模型,基于随风偏角变化的车辆气动力系数及车辆行驶时车轮与桥面接触力变化规律对车辆的临界风速进行研究。倾覆临界风速变化规律如图 11、表 2所示,其中侧向临界风速表示车辆在桥上行驶产生倾覆时受到侧向风荷载的大小,最小临界风速表示±90°范围内的风荷载作用下发生倾覆时的最小风速。
|
| 图 11 倾覆临界风速 Fig. 11 Critical overturning wind speed |
| |
| 临界风速 | 行车速度 | ||
| 80 km/h | 90 km/h | 100 km/h | |
| 侧向临界风速/(m·s-1) | 39.09 | 38.32 | 37.63 |
| 最小临界风速/(m·s-1) | 37.05 | 36.13 | 35.07 |
由图 11对比倾覆临界风速可得,当20°偏角的风荷载作用下车辆最容易发生倾覆,而当风荷载侧向作用在行驶的车辆上时不是发生倾覆的最危险状况,即当风荷载以20°风偏角作用时车辆更容易发生倾覆。
对比表 2中车辆发生倾覆时的临界风速可以看出,分别以80,90,100 km/h在桥上行车,侧向临界风速及最小临界风速随行车速度增大而减小;同时可得出,倾覆时的最小临界风速均小于侧向临界风速,由此可以说明当对车辆进行倾覆安全分析,取侧向风作用不一定是最不利状况。
3.2 车辆侧滑临界风速取车辆的侧向附着系数μS干路面为0.7,湿路面为0.5,雪路面为0.15及冰路面时为0.07[18]。不同路面状况下侧滑临界风速变化规律如图 12、表 3所示,其中侧向临界风速表示侧向风荷载作用下车辆在桥上行驶发生侧滑时的风速,最小临界风速表示±90°偏角内的风荷载作用下车辆在桥上行驶发生侧滑时对应的最小风速。

|
| 图 12 不同路面状况时的侧滑临界风速 Fig. 12 Critical sideslip wind speeds under different pavement conditions |
| |
| 路面状况 | 临界风速/ (m·s-1) |
行车速度/(km·h-1) | ||
| 80 | 90 | 100 | ||
| 干 | 侧向临界风速 | 39.43 | 38.84 | 38.11 |
| 最小临界风速 | 37.30 | 36.23 | 35.26 | |
| 湿 | 侧向临界风速 | 33.99 | 33.23 | 32.20 |
| 最小临界风速 | 31.56 | 30.54 | 29.67 | |
| 雪 | 侧向临界风速 | 16.98 | 15.97 | 15.10 |
| 最小临界风速 | 15.95 | 15.30 | 14.47 | |
| 冰 | 侧向临界风速 | 10.56 | 10.02 | 9.54 |
| 最小临界风速 | 10.19 | 9.59 | 9.03 | |
由图 12临界风速变化规律可以看出,当受侧向风荷载作用,侧滑的临界风速并不是最小值。通过对比不同偏角风荷载作用可以得到,干、湿路面状况下自然风荷载以20°偏角作用时于车辆最容易发生侧滑,冰路面状况下风荷载以10°偏角作用时车辆最容易侧滑。
对比表 3中看出,不同路面状况下车辆分别以不同速度在桥上行驶,侧滑时的侧向临界风速及侧滑时的最小临界风速均随行车速度增大而减小;同时可得出,侧滑时的最小临界风速均小于侧滑时的侧向临界风速,说明进行车辆的侧滑分析时取侧向风荷载作用不一定为最不利状况。
对比分析不同路面状况下表 2与表 3的临界风速数值大小可以得到,车辆在干路面的桥上行驶受风荷载作用时车辆更容易发生倾覆,在湿、雪、冰路面的桥上行驶受风荷载时更容易发生侧滑。
4 结论考虑车辆运动、车-桥系统的振动与车-桥周围风荷载的相互影响,建立了空间数值分析模型,对桥上行驶车辆的气动特性、振动特性及行车安全进行分析,基于研究得出以下结论:
(1) 基于双向的流固耦合分析方法所建立的风-车-桥三维分析模型能够较精确的模拟风-车-桥系统。
(2) 车辆在桥上行驶过程中车辆的振动特性主要由汽车-桥梁系统决定,其中车-桥系统的竖向振动幅度及车辆轮压大小受风荷载影响。
(3) 侧向风荷载作用下车辆在大跨径桥上行驶时,车辆的倾覆力矩系数及侧向力系数并不一定为最大值,所以取用侧向荷载作用进行车辆的行车安全分析不一定为最不利状况。
| [1] |
肖卓.恶劣天气影响下的高速公路车速管理策略研究[D].长沙: 湖南大学, 2013. XIAO Zhuo. Research on Strategy of Freeway Speed Management under Adverse Weather[D]. Changsha: Hunan University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10532-1014121149.htm |
| [2] |
周记国, 胡兆同, 薛晓锋, 等. 侧向风作用下车辆荷载突变效应的CFD模拟研究[J]. 公路交通科技, 2015, 32(1): 145-152. ZHOU Ji-guo, HU Zhao-tong, XUE Xiao-feng, et al. Simulation of Effect of Sudden Change of Vehicle Loads under Cross Wind by CFD Method[J]. Journal of Highway and Transportation Research and Development, 2015, 32(1): 145-152. |
| [3] |
刘多特, 李永乐, 向活跃. 错列双钝体断面气动绕流干扰效应的数值模拟[J]. 公路交通科技, 2014, 31(7): 97-102. LIU Duo-te, LI Yong-le, XIANG Huo-yue. Numerical Simulation of Aerodynamic Ambient Flow Interference Effect on Dual Bluff Body Section in Staggered Arrangement[J]. Journal of Highway and Transportation Research and Development, 2014, 31(7): 97-102. |
| [4] |
艾辉林, 陈艾荣. 跨海大桥桥塔区风环境数值风沿模拟[J]. 工程力学, 2010, 27(增1): 196-199. AI Hui-lin, CHEN Ai-rong. Study on the Crosswind Environment around the Tower and Deck of Sea-crossing Bridge by CFD[J]. Engineering Mechanics, 2010, 27(S1): 196-199. |
| [5] |
王润建, 李海光. 基于CFD方法的大跨高墩刚构桥梁风荷载数值识别[J]. 公路交通科技, 2010, 27(10): 72-76. WANG Run-jian, LI Hai-guang. Numerical Identification of Wind Load Based on CFD Method for Rigid-frame Bridge with Long-spans and High-piers[J]. Journal of Highway and Transportation Research and Development, 2010, 27(10): 72-76. |
| [6] |
韩艳, 胡揭玄, 蔡春声, 等. 横风下车桥系统气动特性的风洞试验研究[J]. 振动工程学报, 2014, 27(1): 67-74. HAN Yan, HU Jie-xuan, CAI Chun-sheng, et al. Wind Tunnel Measurement on Aerodynamic Characteristics of Vehicles and Bridges under Cross Winds[J]. Journal of Vibration Engineering, 2014, 27(1): 67-74. |
| [7] |
韩艳, 蔡春声. 风-车-桥耦合系统的车桥气动特性[J]. 长沙理工大学学报:自然科学版, 2009, 6(4): 21-26. HAN Yan, CAI Chun-sheng. The Aerodynamic Characteristics of the Vehicle and Bridge for the Coupled Wind-vehicle-bridge System[J]. Journal of Changsha University of Science and Technology:Natural Science Edition, 2009, 6(4): 21-26. |
| [8] |
李永乐, 胡朋, 张明金, 等. 风-车-桥系统车辆风荷载突变效应风洞试验研究[J]. 空气动力学学报, 2011, 29(5): 548-554. LI Yong-le, HU Peng, ZHANG Ming-jin, et al. Effect of Sudden Change of Vehicle Wind Loads in Wind-vehicle-bridge System by Wind Tunnel Test[J]. Acta Aerodynamica Sinica, 2011, 29(5): 548-554. |
| [9] |
郭薇薇, 夏禾, 张田. 桥梁风屏障的气动效应及其对高速列车运行安全的影响分析[J]. 工程力学, 2015, 32(8): 112-119. GUO Wei-wei, XIA He, ZHANG Tian. Analysis on Aerodynamic Effects of Bridge Wind Barrier and Its Influence on Running Safety of a High-speed Train[J]. Engineering Mechanics, 2015, 32(8): 112-119. |
| [10] |
韩万水, 陈艾荣. 风-汽车-桥梁系统空间耦合振动研究[J]. 土木工程学报, 2007, 40(9): 53-58. HAN Wan-shui, CHEN Ai-rong. Three-dimensional Coupling Vibration of Wind-vehicle-bridge Systems[J]. China Civil Engineering Journal, 2007, 40(9): 53-58. |
| [11] |
周立.大跨度桥梁风振和车辆振动响应及其疲劳性能研究[D].上海: 同济大学, 2008. ZHOU Li. Research on Response of Wind Vibration and Vehicle Vibration and Fatigue Performance of Long-span Bridge[D]. Shanghai: Tongji University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1416661 |
| [12] |
李永乐, 赵凯, 陈宁, 等. 风-汽车-桥梁-系统耦合振动及行车安全性分析[J]. 工程力学, 2012, 29(5): 206-212. LI Yong-le, ZHAO Kai, CHEN Ning, et al. Wind-vehicle-bridge System Coupling Vibration and Traffic Safety Analysis[J]. Engineering Mechanics, 2012, 29(5): 206-212. |
| [13] |
KIM S J, YOO C H, KIM H K. Vulnerability Assessment for the Hazards of Crosswinds when Vehicles Cross a Bridge Deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 156: 62-71. |
| [14] |
LIU Yang, YIN Xin-feng, DENG Lu, et al. Ride Comfort of the Bridge-traffic-wind Coupled System Considering Bridge Surface Deterioration[J]. Wind and Structures:An International Journal, 2016, 23(1): 19-43. |
| [15] |
丁泉顺, 朱乐东. 桥梁主梁断面气动耦合颤振分析与颤振机理研究[J]. 土木工程学报, 2007, 40(3): 69-73, 91. DING Quan-shun, ZHU Le-dong. Aerodynamically Coupling Flutter Analysis and Flutter Mechanism for Bridge Deck Sections[J]. China Civil Engineering Journal, 2007, 40(3): 69-73, 91. |
| [16] |
王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2016. WANG Fu-jun. Computational Fluid Dynamics Analysis:Principle and Application of CFD Software[M]. Beijing: Tsinghua University Press, 2016. |
| [17] |
郭向荣, 何玮, 朱志辉, 等. 横风作用下货物列车通过大跨度铁路斜拉桥的走行安全性研究[J]. 中国铁道科学, 2016, 37(2): 41-47. GUO Xiang-rong, HE Wei, ZHU Zhi-hui, et al. Running Safety of Freight Train Passing Long-span Cable-stayed Railway Bridge under Cross Wind[J]. China Railway Science, 2016, 37(2): 41-47. |
| [18] |
陈晓冬.大跨桥梁侧风行车安全分析[D].上海: 同济大学, 2007. CHEN Xiao-dong. Analysis of Vehicle Safety under Cross Wind on Long Span Bridges[D].Shanghai: Tongji University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10247-2008066540.htm |
 2019, Vol. 36
2019, Vol. 36
