扩展功能
文章信息
- 杨少伟, 杨荟, 潘兵宏, 欧阳江湖
- YANG Shao-wei, YANG Hui, PAN Bing-hong, OUYANG Jiang-hu
- 高速公路连续长大下坡终点与主线收费站间的净距研究
- Study on Net Distance between End of Continuous Long Downhill Section of Expressway and Main Line Toll Station
- 公路交通科技, 2019, 36(3): 117-123
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 117-123
- 10.3969/j.issn.1002-0268.2019.03.017
-
文章历史
- 收稿日期: 2017-09-13
2. 长安大学特殊地区公路工程教育部重点试验室, 陕西 西安 710064
2. Key Laboratory for Special Area Highway Engineering of Ministry of Education, Xi'an Shaanxi 710064, China
目前我国高速公路建设重心逐渐向山区转移,由于地形的特殊性,会出现连续长大下坡后接主线收费站的设计方案,若这种设计方案和设计参数取值不合理,将极易导致汽车制动器因发热失效或者超速冲撞收费站及收费站内的车辆的交通事故。我国高速公路收费里程约占高速公路总里程的90%,截止2015年全国主线收费站约1 588个,在一定程度上主线收费站设计的合理与否决定了我国高速公路的运行效率及服务水平。由于我国以省为单位对高速公路进行投资和运营管理,所以主线收费站主要设置在省际高速公路上。然而,由于我国目前缺少主线收费站的相关规范,设计人员无法对连续长大下坡路段终点后主线收费站合理位置的设置进行准确把握。
Yang H[1]等人提出了智能交通系统能促进高速公路开放式收费的发展这一理念,这种全新的收费方式能够实实在在地解决高速公路障碍(收费站);Jr M D,Jr RES[2]指出现行收费站的设计规范不完备,在文中提出了收费站的平面和纵面设计指标。纪仕光[3]通过对主线收费站的高峰流量的分析预测,提出在拥堵情况发生之前采取措施,防止主线收费站前拥堵情况的发生;罗宜美[4]等人通过分析主线收费站车辆的到达时间和服务水平分布特点,用M/G/K排队模型对通行能力和服务水平进行评估,提出增加主线收费站前广场的占地面积和划分出后广场的一部分区域用以增设收费口;安文娟[5]等人从行车安全的角度出发,以苏埃隧道为例,提出苏埃隧道出口与其主线收费站的最小间距计算值;钟纪楷[6]从收费管理和节省占地的角度出发,提出将主线收费站和喇叭式立交合建;《高速公路交通工程及沿线设施设计通用规范》[7]提出主线收费站位置选择的相关原则,并分析了各个原则之间的相互关系;《公路路线设计规范》(JTG D20—2006)[8]规定服务区、停车区和公共汽车停靠站等区段内的主线的技术指标参照互通式立体交叉的有关规定,但是并没有给出收费站的具体线型设计要求。
综上可以看出,国内外对主线收费站的研究大多都集中于拥堵问题、主线收费站的建设模式、净距和选址规划等方面,对主线收费站的线形设计以及设置位置方面的研究很少,而对于山区高速公路连续长大下坡后设置主线收费站的相关研究较少。本研究通过分析载重汽车在不同平均坡度的连续长大下坡路段行驶时的制动情况和影响主线收费站设置的各种因素,考虑制动器在连续制动情况下发热而导致制动性能衰减对其产生的减速度的影响,在保证载重汽车可以安全制动的前提下,计算连续长大下坡终点与主线收费站间的净距建议值。
1 连续长大下坡路段后设置主线收费站的影响因素分析不同的车型在连续长大下坡上行驶时,其速度、制动性能等都不同。我国载重汽车载重较大,国内大多载重汽车多采用鼓式制动器,抗热衰退能力较差,在经历长大下坡后出现制动器失效的概率较大。相对载重汽车而言,小汽车的质量较轻,且采用的多为与空气直接接触的盘式制动器,散热速度快,不易发生制动器失灵的现象,所以研究车型采用载重汽车。
连续长大下坡的坡度和坡长问题一直是我国山区高速公路设计的重难点。坡度越大,坡长越长,汽车所进行制动的次数越多,制动时间越长,制动器升温就越快,制动器的制动性能会越差。当制动器温度超过某个临界温度时,制动器失效,刹车失灵,容易造成车祸。要在连续长大下坡后设置主线收费站的首要条件是载重汽车经过连续长大下坡之后其制动性能仍然良好,这样才能保证载重汽车可以继续减速至安全速度驶入主线收费站,所以连续长大下坡技术指标的取值极大地影响了主线收费站的设置。
2 连续长大下坡路段终点与主线收费站间的净距模型 2.1 车型选择根据《公路工程技术标准》 (JTG B01—2014),我国公路设计所采用设计车辆有:小客车、大型客车、铰接客车、载重汽车、铰接列车。随着我国公路网的逐步完善,高速公路的快速发展使得公路运输条件得到极大的改善,而在高速公路运输车辆中,长距离的大型载重汽车占绝大比例,中小型载重汽车多用于短距离运输。所以本研究采用东风EQ5208XXY2型载重货物运输车为主导车型,车体尺寸为11 960 mm×2 470 mm×3 895 mm,额定载重10~12 t,满载总质量为20.9 t,功率重量比为7.42 W/kg。本研究计算模型中假设车辆均为满载情况。
2.2 制动减速度衰减与坡长、平均坡度的关系载重汽车在连续长大下坡行驶后,制动器仍然可以产生足够的制动力是设置主线收费站位置需要考虑的关键因素。载重汽车驾驶员出于对车辆的最小磨损和最短运行时间的考虑,除了刹车失灵的情况之外,大部分司机都采用较大档位,多次、长时间的制动加快了制动器温度的上升速度,加剧了制动器的磨损。而连续长大下坡的坡长和平均坡度是影响制动时间与制动次数的重要因素,制动时间的长短和制动次数的多少则影响制动器温度上升的速度,最终影响制动性能衰减的快慢。本研究根据制动器的衰减性能,提出一个减速度衰减系数K1,计算公式为:
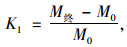
|
(1) |
式中,K1为制动器的衰减系数;M0为制动器的最大制动力矩;M终为制动器在连续长大下坡终点所能产生的制动力矩。
驾驶员利用制动器制动时,主要是踩制动踏板将踏板力通过传动机构传到制动器上,制动器上的制动蹄和制动鼓接触产生摩擦力,这种摩擦力就是行车制动的制动力,所产生的制动力矩与摩擦力成正比例函数关系,制动器上的摩擦力会造成制动器温度的增加,通过数据拟合,得出制动力矩与制动器温度的关系如式(2)[9]:
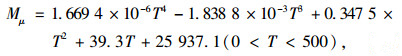
|
(2) |
式中,Mμ为制动器中摩擦力所产生的制动力矩;T为制动器温度。
根据式(2)可得出制动力矩与制动器温度的关系,如图 1所示。
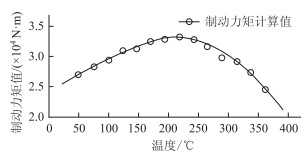
|
| 图 1 制动力矩与制动器温度的关系 Fig. 1 Relationship between braking moment and brake temperature |
| |
汽车在正常情况下行驶时,制动器温度在200 ℃以下,在连续制动的情况下制动器温度可以达到300 ℃以上,如果强度较高,甚至会高达400 ℃以上[10]。而由图 1可以看出,制动力矩在220 ℃之后急剧降低,制动器的制动性能发生明显衰退。根据上述情况分析,对温度进行取值,T0为220 ℃,T终为400 ℃,结合式(1)和(2)计算可得衰减系数K1为0.375 6。
在连续下坡过程中,制动器温度持续上升的变化基本符合二次方程,采用最小二乘法对主制动器温度进行拟合,然后将重力势能与坡度、坡长联系,可以得到在无辅助制动情况下主制动器温度与坡度、坡长之间的关系[11],如式(3)所示。
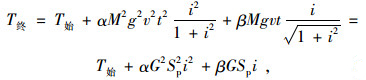
|
(3) |
式中,T终为制动器的最终温度;T始为制动器的初始温度;α,β为回归系数,取1.663×10-13,3.33×10-6;M为汽车总质量;g为重力加速度,一般取9.8 m/s2;v为汽车在连续长大下坡路段的平均行驶速度;t为汽车在连续长大下坡路段的运行时间;i为连续长大下坡的平均纵坡;G为车辆的总重力;Sp为连续长大下坡的纵坡坡长。
在保证载重汽车行驶完连续长大下坡后仍然可以制动减速前提下,确定制动器温度与连续长大下坡的平均坡度与坡长的关系(见图 2)。在计算坡长时,以本研究确定的主导车型进行计算,总质量为20.9×103 kg,考虑满载情况,以最不利情况取值,环境温度取35 ℃,计算结果见表 1。
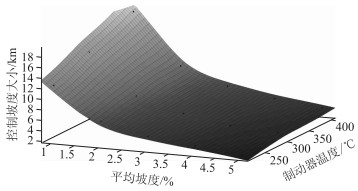
|
| 图 2 无辅助制动情况下温度与平均坡度、坡长的关系图 Fig. 2 Relationship of temperature with average slope gradient and length without auxiliary braking |
| |
| 制度器 温度/℃ |
不同平均纵坡/%纵坡坡长/km | ||||
| 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | |
| 220 | 12.5 | 6.5 | 4.5 | 3.5 | 2.5 |
| 300 | 15.5 | 8.0 | 5.5 | 4.0 | 3.5 |
| 400 | 19.0 | 9.5 | 6.5 | 5.0 | 4.0 |
考虑最不利情况下制动器的温度为400 ℃,在满足表 1的平均坡度与长度情况下,载重汽车经历长大下坡后制动器仍有效,此时,制动器减速度的衰减系数为0.375 6。
2.3 建立计算模型当车辆行驶过连续长大下坡路段终点,进入主线收费站之前,驾驶员首先需要对主线收费站的预告标志进行识别并判断,然后再采取减速措施,并准确判断收费站信息后驶入收费车道,这段过渡段称为连续长大下坡路段终点到主线收费站的最小净距,连续长大下坡路段到主线收费站之间的最小净距组成如图 3所示。
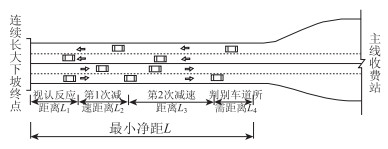
|
| 图 3 连续长大下坡与主线收费站最小净距 Fig. 3 Minimum net distance between continuous long downhill and main line toll station |
| |
由图 3可知,连续长大下坡路段终点到主线收费站之间的最小净距由4部分组成,计算公式为:
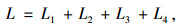
|
(4) |
式中,L为最小净距长度;L1为驾驶员辨认主线收费站标志并反应所需距离;L2为第1次减速所需长度;L3为第2次减速所需长度;L4为判别收费站信息所需长度。
在连续长大下坡路段终点后设置主线收费站时,为了更好地减速,一般将连续长大下坡与主线收费站的这段过渡段设置为平坡或者是上坡,坡度可根据高速公路的设计速度进行取值,收费站广场的纵坡坡度不大于2%。
3 连续长大下坡路段终点与主线收费站间的净距计算 3.1 驾驶员视认主线收费站标志并反应所需距离当车辆驶过连续长大下坡路段之后进入主线收费站之前,驾驶员首先会看到主线收费站的预告标志,然后经过认读、反应之后才会采取措施,从驾驶员看到主线收费站预告标志到采取措施之前载重汽车所经过的距离为L1,计算公式为[12]:
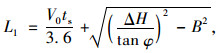
|
(5) |
式中,L1为驾驶员视认信息并反应所需距离;V0为初始速度;ts为驾驶员从视认到采取措施之前所用时间;ΔH为悬臂式标志牌高度与驾驶员视线的高差;φ为驾驶员观察单悬臂标志的视线与驾驶员眼睛所处水平线的夹角;B为载重汽车所处位置到悬臂式标志牌的侧距。
从安全角度出发,根据《公路项目安全性评价规范》[13],初始速度V0取载重汽车在纵坡行驶时的期望速度,当高速公路的设计速度为120,100 km/h和80 km/h时,载重汽车的期望速度是80 km/h;当设计速度为60 km/h时,载重汽车的期望速度是75 km/h。根据《交通工程手册》[14],驾驶员的视认并反应的整个过程需要3.0~4.5 s,本研究中ts取3.5 s。考虑载重汽车的装载高度以及驾驶员的视线高差,ΔH取值为5.2 m。《交通工程手册》中提出眼球运动时视力的有效范围约为18 °,夹角φ取18 °。一般情况下载重汽车在最外侧车道上行驶,单悬臂标志牌内缘距路肩边缘不得小于0.25 m[15],山区高速公路一般为双向四车道,侧距B为5.875 m。
上述取值均以最不利条件为基础,视认标志并进行反应所需距离见表 2。
| 设计速度/(km·h-1) | 120 | 100 | 80 | 60 |
| 距离L1/m | 95 | 95 | 95 | 90 |
3.2 视认标志后第1次减速所需距离
在驾驶员对标志进行视认、反应并进行决策之后,会决定是否需要立即减速,若载重汽车的速度不高且驾驶员认为载重汽车可以以安全速度到达收费站时,驾驶员不会采取制动措施。若载重汽车的速度较高时,驾驶员则会采取一系列制动措施来降低车速。在刚开始减速时,驾驶员还没有摆脱高速驾驶的惯性,一般会采取松开油门并利用发动机和道路阻力的方式进行第1次减速,使速度从V0降到V1,然后接着通过踩制动踏板的方式进行第2次减速,此时减速度由制动器产生的摩阻力提供。第1次减速距离一般为3 s行程[16],可以认为这段为均匀减速,第1次减速所需距离计算为L2,公式如下:
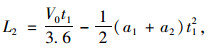
|
(6) |
式中,L2为驾驶员进行第1次减速所需距离;t1为第1次减速所需时间,取3 s;a1为发动机和道路阻力提供的减速度,根据我国汽车驾驶员手册,可取1.0~1.5 m/s2,本研究取1.0 m/s2;a2为在上坡路段,汽车自重在陡坡上提供的平行于陡坡向下的减速度,计算公式为:a2=g×sini,在平坡路段,减速度为0 m/s2。
采用式(6)进行长度计算,根据计算结果显示,过渡段纵坡坡度的大小对第1次减速所需距离几乎无影响,这是由于第1次减速时间太短的缘故,所以在计算第1次减速距离时可不考虑过渡段坡度的影响,计算结果见表 3。
| 设计速度/(km·h-1) | 120 | 100 | 80 | 60 |
| 距离L2/m | 65 | 65 | 65 | 60 |
3.3 视距视认后的第2次减速所需距离
第2次减速是驾驶员利用制动器进行制动减速,使载重汽车以收费站入口的期望速度V2驶入收费站,第2次减速所需最短距离为L3,计算公式如下:
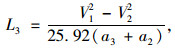
|
(7) |
式中,L3为第2次减速所需距离;V1为载重汽车在第1次减速后的速度;V2为载重汽车在驶入收费站入口时的期望速度;a3为在第2次减速中利用主制动器制动所提供的减速度。
(1) 第1次减速后的速度V1
载重汽车第1次利用发动力和道路阻力进行减速的时候由于时间较短,可认为是均匀减速运动,所以汽车在第1次减速后的速度可用式(8)计算:
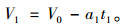
|
(8) |
将式(8)代入式(7),综合可得:
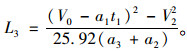
|
(9) |
(2) 驶入收费站广场时的期望速度V2
《日本高速公路设计要领》[17]中规定收费站广场的渐变率应小于1/3,以最不利情况进行计算,取渐变率为1/4,本研究根据车辆在收费广场渐变段的行车轨迹可以得出渐变率K2与车辆速度的关系为:
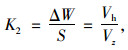
|
(10) |
式中,K2为收费广场渐变段的渐变率,取1/4;ΔW为车辆的横向位移距离;S为车辆的纵向位移距离;Vh为车辆的横移速度,一般取值为1 m/s;Vz为车辆的纵向速度,与V1一致。
所以渐变率与速度的关系可以简化为:
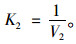
|
(11) |
根据在渐变段入口速度与渐变率的关系,可得出收费站入口的期望速度V2为14.4 km/h。
(3) 制动器提供的减速度a3
我国汽车驾驶员手册提出主制动器提供的减速度一般取值范围是1.5~2.0 m/s2,以最不利条件情况进行取值,为1.5 m/s2。载重汽车在经历连续长大下坡后制动性能的衰减会造成减速度的降低,根据2.2中的衰减系数进行计算,文中载重汽车在本段净距中主制动器所提供的减速度a3=1.5(1-K)=0.94 m/s2。
根据上述取值,计算结果见表 4。
| 不同设计速度/(km·h-1)所需距离/m | |||||
| 120 | 100 | 80 | 60 | ||
| 过渡段纵坡 坡度/% |
0 | 190 | 190 | 190 | 165 |
| 1 | 165 | 165 | 165 | 145 | |
| 2 | 150 | 150 | 150 | 125 | |
| 3 | 130 | 130 | 130 | 110 | |
| 4 | — | 120 | 120 | 100 | |
| 5 | — | — | 105 | 90 | |
| 6 | — | — | — | 80 | |
3.4 驾驶员判别收费站信息所需距离
驾驶员在进入收费站广场之前,收费站广场的信息首先会进入驾驶员视野,驾驶员需要分析所有信息,对进入哪条收费车道进行判断。然后根据自己的需求选择进入收费站广场中的车道,在这个过程中,驾驶员保持车速使车流为自由流状态,这段驾驶员判别收费站信息所需距离L4称为安全距离,通常取100 m[18]。
4 连续长大下坡与主线收费站之间净距分析根据第3节对驾驶员对标志牌的判别反应距离、减速距离和判别收费站信息所需距离的分析,可以得出在不同设计速度和平均坡度条件下连续长大下坡与主线收费站净距L的参考值,见表 5。
| 不同设计速度/(km·h-1)所需距离/m | |||||
| 120 | 100 | 80 | 60 | ||
| 过渡段纵坡 坡度/% |
0 | 450 | 450 | 450 | 415 |
| 1 | 425 | 425 | 425 | 395 | |
| 2 | 410 | 410 | 410 | 375 | |
| 3 | 390 | 390 | 390 | 360 | |
| 4 | — | 380 | 380 | 350 | |
| 5 | — | — | 365 | 340 | |
| 6 | — | — | — | 330 | |
5 结论
(1) 本研究通过分析载重汽车在连续长大下坡路段上行驶时的制动器温度情况,连续长大下坡终点与主线收费站间净距的影响因素,以及在车辆行驶过程中驾驶员的操作行为,选择了合适的车型,建立了连续长大下坡终点与主线收费站间的净距模型,从安全角度出发对各参数进行取值,提出在不同设计速度和不同过渡段纵坡条件下连续长大下坡终点与主线收费站间净距的建议值。
(2) 在连续长大下坡终点后设置主线收费站的关键在于驶过连续长大下坡之后载重汽车的制动器是否仍能产生足够的制动力,使载重汽车能够安全地到达收费站。在连续长大下坡上行驶时,载重汽车的连续制动会造成制动器性能衰减,所以本研究提出了制动器的衰减系数K1,确定制动器能提供的实际减速度。
(3) 本研究提出了制动器的衰减系数,并且只考虑了常温条件下的净距问题,所以气候因素对净距的影响程度,以及制动器制动力矩的衰减系数与减速度衰减系数的一致性都需要进一步研究。
(4) 本研究模型中未考虑驾驶员刹车的方式和次数、驾驶员脚踩制动踏板的力度以及持续时间对制动器温度的影响,对影响模型的因素进行了简化,只在宏观方面构建了净距模型,更为精确的模型需要进一步完善。
| [1] |
YANG H, OZBAY K, BARTIN B. Effects of Open Road Tolling on Safety Performance of Freeway Mainline Toll Plazas[J]. Transportation Research Record, 2012, 2324: 101-109. |
| [2] |
MCDONALD D R, STAMMER R E. Contribution to the Development of Guidelines for Toll Plaza Design[J]. Journal of Transportation Engineering, 2001, 127(3): 215-222. |
| [3] |
纪仕光. 高速公路主线收费站高峰流量预测分析及对策[J]. 电脑知识与技术, 2011, 7(23): 5661-5663. JI Shi-guang. Prediction Analysis and Countermeasures of Peak Volume at Expressway Main Line Toll Station[J]. Computer Knowledge and Technology, 2011, 7(23): 5661-5663. |
| [4] |
罗宜美, 宋毅, 纪宝泉. 高速公路主线收费站通行能力改善研究[J]. 物流技术, 2013, 32(3): 285-287, 330. LUO Yi-mei, SONG Yi, JI Bao-quan. Study on Improvement of Passthrough Capacity of Mainline Toll-stations on Expressways[J]. Logistics Technology, 2013, 32(3): 285-287, 330. |
| [5] |
安文娟, 李志锋, 李远哲. 公路隧道出口与主线收费站最小安全间距研究[J]. 公路交通技术, 2016, 32(3): 128-131. AN Wen-juan, LI Zhi-feng, LI Yuan-zhe. Research on Minimal Safe Clearance between Highway Tunnel Exit and Mainline Toll Gate[J]. Technology of Highway and Transport, 2016, 32(3): 128-131. |
| [6] |
钟纪楷, 刘浩, 司徒立华. 高速公路省界主线收费站建设模式研究[J]. 公路交通科技, 1999, 16(增1): 40-41, 35. ZHONG Ji-kai, LIU Hao, SITU Li-hua. Study on Freeway Mainline Toll Plaza at Provincial Border[J]. Journal of Highway and Transportation Research and Development, 1999, 16(S1): 40-41, 35. |
| [7] |
JTG D80-2006, 高速公路交通工程及沿线设施设计通用规范[S]. JTG D80-2006, General Specification of Freeway Traffic Engineering and Roadside Facilities[S]. |
| [8] |
JTG D20-2006, 公路路线设计规范[S]. JTG D20-2006, Design Specification for Highway Alignment[S]. |
| [9] |
国俭.载货汽车制动器温度监测及预警系统研究[D].长春: 吉林大学, 2014. GUO Jian. Research on Monitoring and Early-warning System of Truck Brake System Temperature[D].Changchun: Jilin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014270572.htm |
| [10] |
王博.山区高速公路平均纵坡的研究[D].西安: 长安大学, 2010. WANG Bo. Study on Average Longitudinal Slope of Mountainous Expressway[D].Xi'an: Chang'an University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010220354.htm |
| [11] |
潘兵宏.山区高速公路平均纵坡研究[D].西安: 长安大学, 2008. PAN Bing-hong. Study on Average Longitudinal Slope of Mountainous Expressway[D]. Xi'an: Chang'an University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1529061 |
| [12] |
王少飞, 李伟聪, 林志, 等. 三车道高速公路隧道出口与互通式立交最小间距研究[J]. 公路交通技术, 2013(6): 103-107. WANG Shao-fei, LI Wei-cong, LIN Zhi, et al. Research on Minimum Space between Tunnel Outlets of Three-lane Expressway and Interchange[J]. Technology of Highway and Transport, 2013(6): 103-107. |
| [13] |
JTG B05-2015, 公路项目安全性评价规范[S]. JTG B05-2015, Specifications for Highway Safety Audit[S]. |
| [14] |
中国公路学会《交通工程手册》编委会. 交通工程手册[M]. 北京: 人民交通出版社, 2001. China Road Association Editorial Committee of Traffic Engineering Handbook. Traffic Engineering Handbook[M]. Beijing: China Communications Press, 2001. |
| [15] |
李文权, 王炜. 高速公路路侧标志设置问题[J]. 东南大学学报:自然科学版, 2007, 37(1): 164-169. LI Wen-quan, WANG Wei. Setting Problem of Freeway Side Traffic Signs[J]. Journal of Southeast University:Natural Science Edition, 2007, 37(1): 164-169. |
| [16] |
王海君, 杨少伟. 高速公路互通式立交单车道减速车道长度研究[J]. 公路交通科技, 2015, 32(3): 124-128. WANG Hai-jun, YANG Shao-wei. Research of Length of Deceleration Lane at Expressway Interchange[J]. Journal of Highway and Transportation Research and Development, 2015, 32(3): 124-128. |
| [17] |
日本道路公团. 日本高速公路设计要领[M]. 西安: 陕西旅游出版社, 1991. Japan Highway Public Corporation. Main Points of Japanese Highway Design[M]. Xi'an: Shaanxi Tourism Press, 1991. |
| [18] |
赵一飞, 陈敏, 潘兵宏. 隧道与互通式立交出口最小间距需求分析[J]. 长安大学学报:自然科学版, 2011, 31(3): 68-71. ZHAO Yi-fei, CHEN Min, PAN Bing-hong. Minimum Spacing Demand Analysis between Tunnel and Exit of Interchange[J]. Journal of Chang'an University:Natural Science Edition, 2011, 31(3): 68-71. |
 2019, Vol. 36
2019, Vol. 36
