扩展功能
文章信息
- 谢全敏, 殷建强, 杨文东
- XIE Quan-min, YIN Jian-qiang, YANG Wen-dong
- 基于AHP和GC-TOPSIS的山区桥型方案比选
- Comparison and Selection of Bridge Type Schemes Based on AHP and GC-TOPSIS
- 公路交通科技, 2019, 36(3): 102-108
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 102-108
- 10.3969/j.issn.1002-0268.2019.03.015
-
文章历史
- 收稿日期: 2017-06-05
2. 中国市政工程西北设计研究院有限公司, 甘肃 兰州 730000
2. CSCEC AECOM Consultants Co., Ltd., Lanzhou Gansu 730000, China
山区公路桥梁建设投资规模大、结构复杂、施工困难多,建设周期长,受到多个因素的影响,确定科学合理的桥型方案,对于整个桥梁工程的实施是至关重要的[1-2]。目前山区桥型方案的确定主要采用调查分析、估算造价等方法来评价设计方案的各项指标,受到设计人员主观因素的限制,评价过程繁琐复杂,比选结果客观程度低,公认度差。虽然国内一些学者对桥梁选型决策做了许多研究,构建了基于突变优选理论[3-4]、层次分析理论[5]、模糊层次理论[6-7]、灰色关联分析理论[8-9]、模糊综合评价理论[10-11]、多属性评价决策理论[12]等桥型方案优选模型,但是这些模型都有一定局限性,应用范围相对有限,并不能完全适用于山区桥型方案的选择。
为此,本研究基于层次分析法、灰色关联分析和逼近理想解法的基本理论,建立山区桥型方案综合评价模型。该模型可以测度不同备选方案靠近理想解和远离负理想解的距离,引入各方案对正负理想解的相对贴近度作为评判标准,对各备选方案的可行性进行排序以确定最佳方案。该评价模型将加权TOPSIS方法与灰色关联分析相耦合,既能考虑曲线趋势,又能够综合分析桥型评选过程中各种隐蔽、复杂的因素,使得评判结果更为科学合理。将本研究所建立的评价模型应用于贵州普安县山区某公路桥型方案评价比选,获得其最优桥型方案,为该工程的决策提供科学依据。
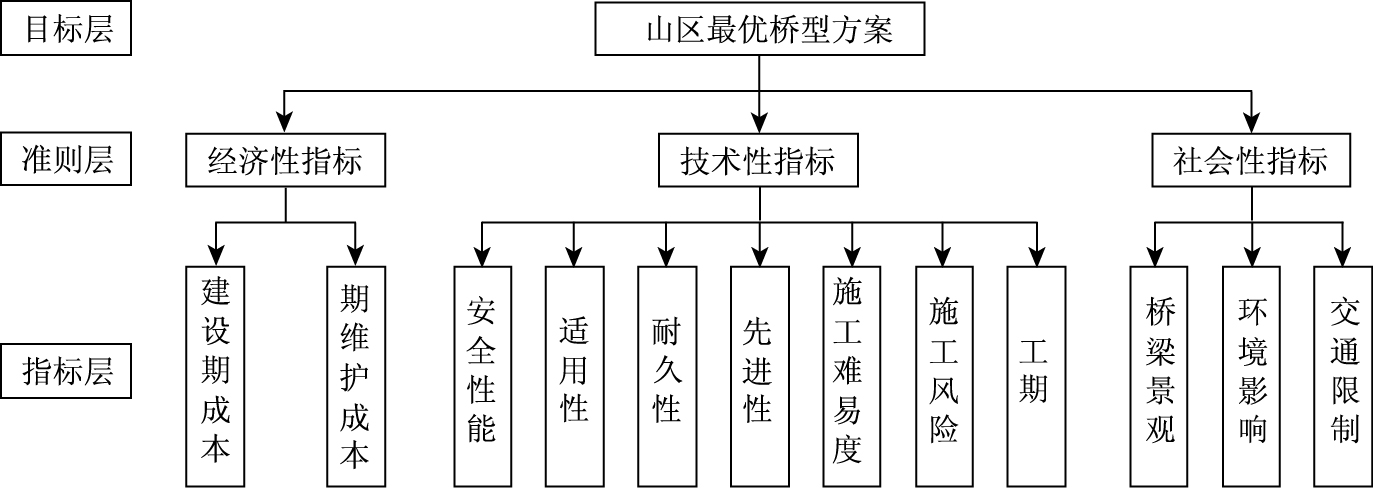
1 层次分析法 1.1 评价体系的建立桥型方案综合评价体系的建立是方案评价与决策的基础,选取科学、合理的评价指标是决定评判结果的关键。本研究从经济、技术、社会3个方面分析,建立桥型评价指标集U=U1(建设期成本)、U2(后期维护成本)、U3(安全性能)、U4(适用性)、U5(耐久性)、U6(先进性)、U7(施工难易程度)、U8(施工风险)、U9(工期)、U10(桥梁景观)、U11(环境影响)、U12(交通限制)。根据指标的属性,将指标值越小越好的划分为成本型指标,将指标值越大越好的划分为效益型指标。根据AHP法的基本原理,建立山区桥型方案综合评价指标体系以及递进层次结构框架,如表 1和图 1所示。
| 指标体系 | 内涵 | 指标类型 | |
| 经济性指标 | 建设期成本U1 | 桥梁造价以及临时工程费 | 成本型指标 |
| 后期维护成本U2 | 桥梁运营期间日常养护、检测加固的费用 | 成本型指标 | |
| 技术性指标 | 安全性能U3 | 结构的受力安全性、承载潜力、抵抗风险能力(抗震、抗风、抗碰撞以及抗爆炸)。 | 效益型指标 |
| 适用性U4 | 桥位自然环境适用性(地形、地质、水文、气候的适应性),使用功能适用性(桥面通行能力、桥下通航能力、行车舒适性) | 效益型指标 | |
| 耐久性U5 | 桥梁在全寿命周期内抵抗环境各种因素作用保持健康状态的能力,即材料、构件、结构体系的耐久性以及构件可维修更换能力 | 效益型指标 | |
| 先进性U6 | 桥梁设计理念和方法、施工管理和施工工艺的创新性 | 效益型指标 | |
| 施工难易程度U7 | 桥梁施工的组织管理和工艺的复杂程度 | 成本型指标 | |
| 施工风险U8 | 桥梁在施工期间的整体风险 | 成本型指标 | |
| 工期U9 | 施工周期 | 成本型指标 | |
| 社会性指标 | 桥梁景观U10 | 桥梁美学和景观设计的科学性,外观造型、线形比例与周围自然、人文环境的协调性 | 效益型指标 |
| 环境影响U11 | 桥梁材料的环保性能,施工期和运营期对周围环境的扰动和破坏 | 成本型指标 | |
| 交通限制U12 | 施工对周围交通的影响即影响车辆、船舶、行人通行的严重程度 | 成本型指标 | |
|
| 图 1 山区桥型方案综合评价体系 Fig. 1 Comprehensive evaluation system of mountainous bridge type scheme |
| |
1.2 指标权重的确定 1.2.1 建立判断矩阵
山区桥型方案综合评价体系建立完毕后,邀请有经验的桥梁专家采用Saaty提出的九标度法,对评价体系中的各上层元素所对应的下层元素进行两两比较和判断,构造判断矩阵B。通过MATLAB计算程序直接求得每一个判断矩阵的最大特征值和其对应的权重向量(特征单位向量)。
1.2.2 一致性检验由于建立判断矩阵过程中,专家评判具有主观片面性,为评价判断矩阵B的客观程度是否合理,需对判断矩阵进行一致性检验。一致性检验公式为:
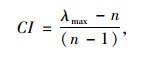
|
(1) |
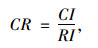
|
(2) |
式中,CI为一致性指标,其表征评判矩阵B非一致性的严重程度;CR为随机一致性比率,其作为度量判断矩阵的非一致性是否接受的标准;RI为平均随机一致性指标,其取值依据判断矩阵的阶数,通过查表获得[13],具体取值见表 2;λmax为判断矩阵B的最大特征根;n为矩阵阶数。
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
当CR < 0.10时认为判断矩阵一致性检验通过,若CR≥0.10则应重新调整判断矩阵B中的元素使其具有可接受的一致性。满足一致性检验的要求后,可得到层次总排序, 即山区桥型方案比选评价指标的权重向量为:
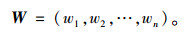
|
(3) |
山区桥型方案的选取是一个典型的多目标决策,在决策过程中利用模糊数学理论中的隶属度函数确定方法对各备选方案进行定量分析得到隶属度矩阵[14]。对隶属度矩阵做灰色关联分析以形成关联度矩阵,该矩阵表示待评价方案与相对最优方案之间的距离。该关联度矩阵即为决策矩阵,应用TOPSIS法得出各备选方案的优劣排序。
2.1 隶属度矩阵的建立定义以下方案集和其指标集:
桥型方案集:A= (A1, A2, …, Am);方案评判指标集:U= (U1, U2, …, Un)。指标集中的部分指标可以用确定的值进行描述,即定量指标;定量评判指标按其属性可细分为成本型指标和效益型指标。将数据作适当变换进行无量纲化处理,则可确定定量指标的隶属度,计算见式(4)和式(5)。
成本型指标计算公式为:
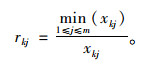
|
(4) |
效益型指标计算公式为:
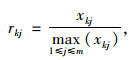
|
(5) |
式中,xkj为第j种方案在第k个评价指标下的特征值;rkj为第j种方案在第k个评价指标下的隶属度。
指标集中的另一部分指标难以有效地用明确的数值进行衡量,只能给出好或者坏的评价,即定性指标。对于不同桥型方案在同一定性指标下的优越性比较,可采用二元定量比较法[15-16]。将m个方案两两比较,若Ak比Al优越,则令ekl=1,elk=0;若Ak与Al同等优越,则令ekl=0.5,elk=0.5;若Al比Ak优越,则ekl=0,elk=1(k,l=1,2,…,m)定义ekl,elk为两个方案通过比较获得的比较值。由此即可得二元比较矩阵E为:
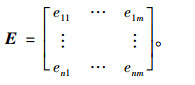
|
(6) |
当0≤eij≤1,eij+eji=1,eij=eji(i=j)时,E为优越性二元对比矩阵,eij为定性排序标度。将矩阵E按行求和后排序,将排序最高的方案依次与其他备选方案进行优越性比较,运用“同样”、“较为”、“十分”等语气副词,来体现优越程度的差异。语气算子可以将模糊的语气比较转变为明确的数值比较,即将语气副词定量化,每个语气副词对应的确定数值即为定量标度。通过查询语气算子与定量标度关系表[17](见表 3),将定性的优越程度比较转变为定量的评价值以及相对隶属度。
| 语气算子 | 定量标度 | 相对隶属度 |
| 同样 | 0.500 0.525 | 1.000 0.905 |
| 稍稍 | 0.550 0.575 | 0.818 0.739 |
| 略微 | 0.600 0.625 | 0.667 0.600 |
| 较为 | 0.650 0.675 | 0.538 0.481 |
| 明显 | 0.700 0.725 | 0.429 0.379 |
| 显著 | 0.750 0.775 | 0.333 0.290 |
| 十分 | 0.800 0.825 | 0.250 0.212 |
| 非常 | 0.850 0.875 | 0.176 0.143 |
| 极其 | 0.900 0.925 | 0.111 0.081 |
| 极端 | 0.950 0.975 | 0.053 0.026 |
| 无可比拟 | 1.000 | 0 |
| 注:语气位于相邻两个算子之间时,定量标度取二者均值。 | ||
本研究通过上述两种方法,消除不同量纲的影响,实现数据规范化,即可得到隶属度一致矩阵:
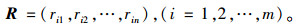
|
(7) |
定义rj+为理想最优桥型方案评价向量,按式(8)计算:
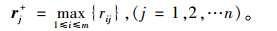
|
(8) |
隶属度矩阵中挑选出的最优指标向量组M = (r1+, r2+, …, rn+)为理想最优方案评价向量。各备选方案Ai的评价指标rij与相对理想最优方案评价向量中的r j+的灰色关联系数为[18]:
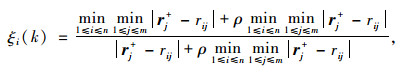
|
(9) |
式中,ρ∈[0, 1]为比较环境调节因子,通常取0.5。
灰色关联系数矩阵为:

|
(10) |
由于在桥型方案评选中各指标的重要性程度不同,需构造加权灰色关联系数决策矩阵H。
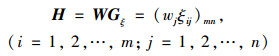
|
(11) |
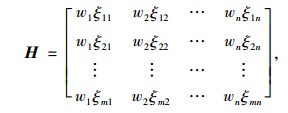
|
(12) |
式中, wj为评价指标的评价向量中第j个评价指标所对应的权重值;ξij为灰色关联矩阵中第i行第j列所对应的值。
2.3 灰色关联逼近理想解求解(1) 计算加权灰色关联系数矩阵H = (wjξij)的正负理想解V+和V-,可得:
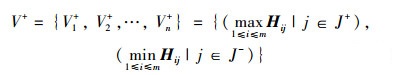
|
(13) |
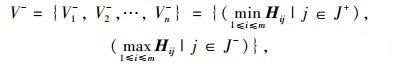
|
(14) |
式中,Hij为加权灰色关联决策矩阵中第i行第j列所对应的值;J+为极大值指标; J-为极小值指标。
(2) 各待评备选方案到正负理想解的欧式范数,即第i个桥型方案距正理想解和负理想解的距离,计算公式如下:
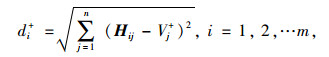
|
(15) |
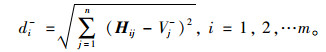
|
(16) |
(3) 计算各备选方案指标特征值与灰色关联理想解的相对贴近度:
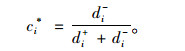
|
(17) |
相对贴近度ci*反映各备选桥型方案靠近正理想解远离负理想解的程度,ci*∈ [0, 1]。
(4) 按照相对贴近度ci*的大小,完成对备选方案排序,相对贴近度大者为优,表明可行性好,相对贴近度小者为劣,表明可行性差。ci*中的最大值所对应的备选方案为最优方案。
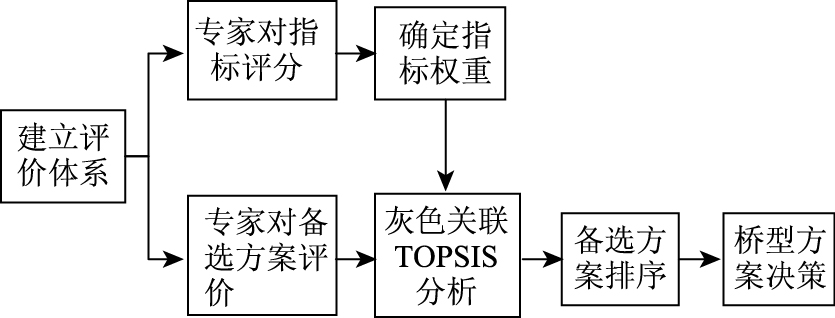
2.4 山区桥型方案评选决策流程将上述评价决策过程通过MATLAB实现程序化,计算流程图如图 2所示。
|
| 图 2 桥型方案决策流程图 Fig. 2 Flowchart of bridge type decision-making |
| |
3 工程实例应用
某桥为贵州普安县城至沪昆高铁普安站城市主干道上重要桥梁,地处乌蒙山脉南部,属低中山、中山侵蚀地貌。该桥上跨虎跳河,桥址下游为在建的沪昆高铁普安站,桥区位于河谷、冲沟地带,距沟底最大深度为23 m。虎跳河为北盘江中游流域北东岸支流系,属典型山区雨源型河流,常水位较低,在强烈的暴雨时期,易产生陡峻洪峰,该河流无通航要求。根据现场勘查,桥区地层从新到老依次为:第四系、二叠系上统峨眉山组第二段。第四系覆盖层主要为耕植土,二叠系上统峨眉山组第二段岩性主要为中厚-厚层状玄武岩。
3.1 桥型方案根据桥位处自然地理情况,初步拟定3种桥型方案。方案1(A1):采用桥跨组合为(3×30+3×40+3×30)m的装配式预应力混凝土先简支后连续T梁桥。该桥型结构形式简单,施工工艺成熟,在山区公路应用广泛。方案2(A2):采用(80+140+80)m的三跨预应力混凝土连续刚构桥,截面为单箱单室,支点到跨中截面高度以二次抛物线渐变。该桥型跨越能力强,在中西南部山区高速公路桥梁中得到大量应用。方案3(A3):采用(80+140+80)m预应力混凝土矮塔斜拉桥,受力模式以梁为主斜拉索为辅的索梁配合承载体系,兼有连续梁桥和斜拉桥的优点,桥型美观与周围环境适应性好,在国内外山区公路桥梁建造中得到成功实践。
3.2 桥型方案综合评价根据1.1节中建立的山区桥型方案综合评价体系,对建设期成本U1、施工风险U7、工期U8这3项进行定量评判,其中施工风险评判采用《公路桥梁和隧道工程施工安全风险评估指南》中的桥梁施工安全总体风险计算方法[19]确定3种方案的风险值。其余指标则依据5位专家给出的综合评价意见进行定性评判,3种方案综合评判见表 4。
| 评价指标 | 方案 | |||
| A1预应力 混凝土连续 T梁桥 |
A2预应力 混凝土连续刚 构桥 |
A3预应力 混凝土矮塔 斜拉桥 |
||
| 经济性指标 | 建设期成本U1 | 2 921万元 | 3 985万元 | 5 425万元 |
| 后期维护成本U2 | 一般 | 一般 | 较高 | |
| 技术性指标 | 安全性能U3 | 一般 | 较好 | 好 |
| 适用性U4 | 一般 | 较好 | 好 | |
| 耐久性U5 | 一般 | 较好 | 好 | |
| 先进性U6 | 较差 | 一般 | 较高 | |
| 施工难易程度U7 | 容易 | 较难 | 难 | |
| 施工风险U8 | 10 | 13 | 17 | |
| 工期U9 | 15 | 18 | 20 | |
| 社会性指标 | 桥梁景观U10 | 差 | 较好 | 好 |
| 环境影响U11 | 较小 | 较小 | 较大 | |
| 交通限制U12 | 小 | 小 | 小 | |
3.3 指标权重计算
运用层次分析法计算各判断矩阵,并满足一致性检验,得各指标层次总排序权重:

|
(18) |
依据表 4数据,对于定量指标运用式(2)、(3)计算其隶属度,对于定性指标采用二元比较查询语气算子确定其隶属度。定性指标计算以后期维护成本为例,根据专家给出的评判结果,将3个方案两两相比,得出二元比较矩阵E:

|
(19) |
A1方案比A3方案较为优越,A1方案与A2方案同样优越,根据“较为”和“同样”语气副词,查询表 3,可得出隶属度矩阵R2T=[1 1 0.538]。同理计算出其他定性指标下的隶属度矩阵,最终计算出一致矩阵隶属度R。

|
(20) |
将R输入MATLAB中编写好的GC-TOPSIS计算程序可得:加权灰色关联系数决策矩阵H;

|
(21) |
灰色关联正理想解V+;
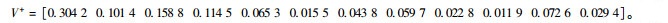
|
(22) |
灰色关联负理想解V-;
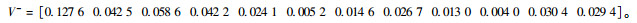
|
(23) |
备选桥型方案到灰色关联正理想解的距离:
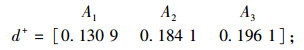
|
(24) |
备选桥型方案到灰色关联负理想解的距离:
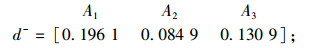
|
(25) |
备选桥型方案与灰色关联正理想解的相对贴近度:
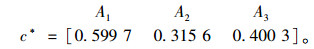
|
(26) |
综合上述计算结果,A1,A2,A3方案的灰色关联理想解的贴近度分别为:0.599 7,0.315 6,0.400 3,对3个方案进行排序,结果为:A1>A3>A2。由此得出普安县城至沪昆高铁普安站上跨虎跳河的最优桥型方案为A1方案,即桥跨布置为(3×30+3×40+3×30)m的装配式预应力混凝土连续T梁桥。
4 结论本研究通过山区桥型方案评价模型建立及其应用研究,获得了如下结论:
(1) 针对山区公路桥梁初步设阶段桥梁最优方案选择的特点,运用层次分析法从经济、技术、社会3个方面确定了12个评价指标,建立了山区桥型方案综合评价体系,并计算得出各指标权重。
(2) 运用模糊理论中的隶属函数法和二元对比优先关系法得出各备选方案在不同指标下的评价定量特征值,形成隶属度矩阵。通过对隶属度矩阵进行灰色关联分析,结合加权TOPSIS求解方法,得出各备选方案与正负理想解的相对贴近度,以此体现备选方案可行性好坏的程度,完成对方案的优劣排序,以普安县山区桥型比选实例对灰色关联TOPSIS的山区桥型方案评价模型进行了验证,证明GC-TOPSIS方法在桥梁工程实践中是有效可行的。
(3) 利用MATLAB实现层次分析法确定指标权重和灰色关联理想解求解程序化,提高了山区桥型方案决策过程中的计算精度和自动化程度。
| [1] |
周剑萍. 高原山区高速公路跨越沟谷地形时的桥型比选[J]. 公路, 2013(5): 81-84. ZHOU Jian-ping. Comparison and Selection of Bridge Types on Plateau Mountainous Expressway Crossing Valley Terrain[J]. Highway, 2013(5): 81-84. |
| [2] |
姚昌荣, 李亚东, 梁东, 等. 山区大跨度桥梁结构选型[J]. 桥梁建设, 2012, 42(6): 81-86. YAO Chang-rong, LI Ya-dong, LIANG Dong, et al. Structural Type Selection for Long Span Bridges in Mountainous Region[J]. Bridge Construction, 2012, 42(6): 81-86. |
| [3] |
马士宾, 王选仓, 魏连雨, 等. 突变优选理论在选择桥型方案中的应用[J]. 公路交通科技, 2007, 24(10): 68-71. MA Shi-bin, WANG Xuan-cang, WEI Lian-yu, et al. Bridge Scheme Selection Based on Mutation Theory[J]. Journal of Highway and Transportation Research and Development, 2007, 24(10): 68-71. |
| [4] |
旷志龙. 基于突变级数法的桥型方案适应性评价[J]. 公路工程, 2014, 39(3): 169-172. KUANG Zhi-long. Assessment of Bridge Types Adaptability Based on Catastrophe Progression Method[J]. Highway Engineering, 2014, 39(3): 169-172. |
| [5] |
姜忻良, 王丙兴, 窦远明, 等. 综合评价指标体系在桥梁选型中的应用研究[J]. 土木工程学报, 2009(7): 65-68. JIANG Xin-liang, WANG Bing-xing, DOU Yuan-ming, et al. Application of Comprehensive Indicator System for Optimization of Bridge Schemes[J]. China Civil Engineering Journal, 2009(7): 65-68. |
| [6] |
赵松旭, 钱才, 田元福. 多层次分析法和模糊评价在桥梁多方案评价中的应用[J]. 交通标准化, 2007(11): 75-78. ZHAO Song-xu, QIAN Cai, TIAN Yuan-fu. Application of AHP and Fuzzy Evaluation in the Multi-scheme Evaluation of Bridge[J]. Communications Standardization, 2007(11): 75-78. |
| [7] |
张哲, 王会利, 石磊, 等. 桥梁方案多层多目标模糊优选模型及其应用[J]. 哈尔滨工业大学学报, 2006, 38(9): 1567-1571. ZHANG Zhe, WANG Hui-li, SHI Lei, et al. Application of Multi-levels and Multi-objectives Fuzzy Optimization Model of Bridge Type Selection[J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1567-1571. |
| [8] |
孙吉书, 陈朝霞, 于龙, 等. 基于灰色关联分析法的桥梁型式多方案选择[J]. 河北工业大学学报, 2011, 40(6): 88-92. SUN Ji-shu, CHEN Zhao-xia, YU Long, et al. Multi-scheme Selection of Bridge Types Based on Grey Correlation Analysis[J]. Journal of Hebei University of Technology, 2011, 40(6): 88-92. |
| [9] |
王明慧. 用灰色关联分析法选择桥型设计方案[J]. 铁道建筑, 2012(9): 23-25. WANG Ming-hui. Selection of Bridge Type Design Scheme by Grey Correlation Analysis[J]. Railway Engineering, 2012(9): 23-25. |
| [10] |
万峰, 陈常松, 张晨, 等. 模糊综合评价法在桥型比选中的应用[J]. 中外公路, 2015, 35(2): 97-101. WAN Feng, CHEN Chang-song, ZHANG Chen, et al. Application of Fuzzy Comprehensive Evaluation in Bridge Type Comparison[J]. Journal of China & Foreign Highway, 2015, 35(2): 97-101. |
| [11] |
孙昊, 刘永健, 孙明钰, 等. 大跨装配式应急公路钢桥方案设计与模糊层次比选[J]. 长安大学学报:自然科学版, 2017, 37(2): 55-63. SUN Hao, LIU Yong-jian, SUN Ming-yu, et al. Comparison and Selection of Scheme Design and Fuzzy Hierarchy for Large-span Fabricated Emergency Highway Steel Bridge[J]. Journal of Chang'an University:Natural Science Edition, 2017, 37(2): 55-63. |
| [12] |
齐秀廷, 姚永春. 基于变异系数法和集对分析的桥梁设计多属性评价模型[J]. 科技通报, 2016, 32(2): 189-192. QI Xiu-ting, YAO Yong-chun. Multiple Attribute Evaluation Model for Bridge Design Based on Variation Coefficient Method and Set Pair Analysis[J]. Bulletin of Science and Technology, 2016, 32(2): 189-192. |
| [13] |
许树柏. 层次分析法原理[M]. 天津: 天津大学出版社, 1988. XU Shu-bai. Analytic Hierarchy Process[M]. Tianjin: Tianjin University Press, 1988. |
| [14] |
王涛. 模糊数学及其应用[M]. 沈阳: 东北大学出版社, 2005. WANG Tao. Fuzzy Mathematics and Its Application[M]. Shenyang: Northeastern University Press, 2005. |
| [15] |
LEE H, TOM M R. Adaptive Control Using a Universal Approximation for SISO Nonlinear Systems[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(1): 88-93. |
| [16] |
CHAN P T, RAD A B, WANG J. Indirect Adaptive Fuzzy Sliding Mode Control[J]. Fuzzy Sets and Systems, 2001, 119(1): 159-161. |
| [17] |
XIN Li-li, GENG Hui, WANG Yong-min, et al. General Limited Information Diffusion Method of Small-sample Information Analysis in Insurance[J]. Journal of Shanghai University:English Edition, 2007, 11(3): 259-262. |
| [18] |
刘思峰, 郭天榜, 党耀国. 灰色系统理论及其应用[M]. 北京: 科学出版社, 1999. LIU Si-feng, GUO Tian-bang, DANG Yao-guo. Gray System Theory and Its Application[M]. Beijing: Science Press, 1999. |
| [19] |
交通运输部工程质量监督局. 公路桥梁和隧道工程施工安全风险评估制度及指南解析[M]. 北京: 人民交通出版社, 2011. Engineering Quality Supervision Bureau of Department of Transport. Analysis on Risk Assessment System and Guide of Construction Safety in Bridge and Tunnel Engineering[M]. Beijing: China Communications Press, 2011. |
 2019, Vol. 36
2019, Vol. 36
