扩展功能
文章信息
- 陈淮, 冯冠杰, 王艳, 李杰
- CHEN Huai, FENG Guan-jie, WANG Yan, LI Jie
- 波形钢腹板矮塔斜拉桥施工阶段稳定性分析
- Analysis on Stability of Extradosed Cable-stayed Bridge with Corrugated Steel Webs under Construction
- 公路交通科技, 2019, 36(3): 95-101
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 95-101
- 10.3969/j.issn.1002-0268.2019.03.014
-
文章历史
- 收稿日期: 2018-01-17
朝阳沟波形钢腹板矮塔斜拉桥跨径布置为(58+118+88+108) m,主梁横断面为单箱4室斜腹板,波形钢腹板波形采用1600型,钢腹板厚度在不同节段取值有12,14,16,18,20,22 mm这6种;桥塔为双塔柱,采用组合式钢筋混凝土结构,主塔桥面以上高33 m;下部结构主墩(下塔柱)均为变宽度矩形双肢实心薄壁墩,墩高30 m;斜拉索为双索面单排索,最大悬臂状态共26对索,塔根附近主梁无索区长度40.0 m,梁上索距4.8 m,塔上索距1.0 m。采用悬臂浇注法施工,施工过程中结构体系转换频繁,变形和受力复杂[1-4],且施工过程中结构为静定的悬臂T构,在施工过程中的不利因素,如不平衡荷载、材性偏差、初始缺陷等影响下,结构稳定性问题突出[5-7],同时波形钢腹板的剪切屈曲与桥梁结构极限承载能力密切相关[8-10],因此需要对该桥型施工过程中波形钢腹板的剪切屈曲和稳定性进行研究。
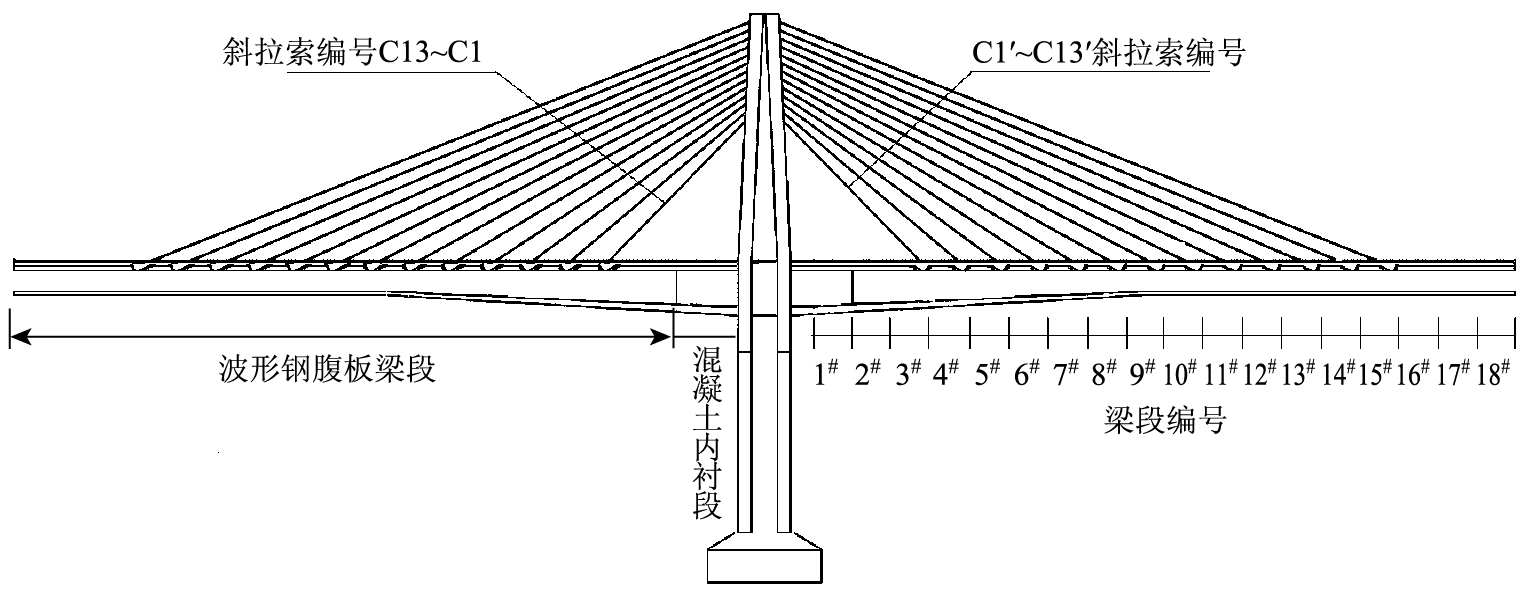
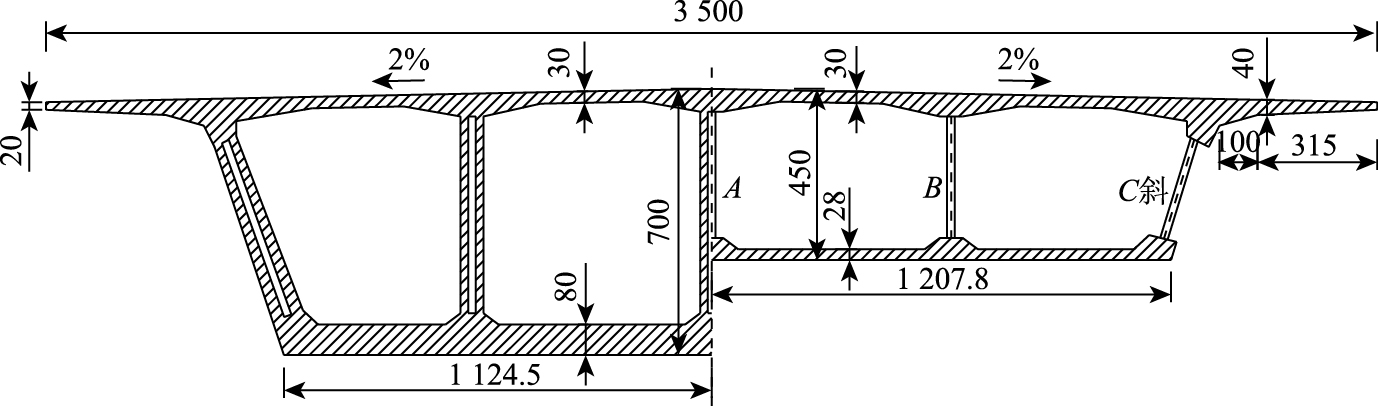
1 计算模型 1.1 施工阶段划分首先施工主墩等下部结构,再在主墩搭设支架现浇施工0#块;待0#块施工完毕,悬臂浇注1#~5#箱梁节段,并张拉悬臂顶板束;悬臂浇注6#节段,施工完毕后,安装第1排斜拉索并张拉,以后每悬浇1个节段就安装1排斜拉索,至18#节段施工完毕后安装张拉完所有斜拉索;最大悬臂状态立面图如图 1所示,箱梁截面如图 2所示。完成左右侧现浇段施工后,先主跨后边跨合龙。选取关键施工阶段进行稳定性分析,施工阶段见表 1。
|
| 图 1 最大悬臂状态立面图 Fig. 1 Elevation view of maximum cantilever state |
| |
|
| 图 2 箱梁横截面(单位:m) Fig. 2 Cross-section of box beam(unit:m) |
| |
| 工况 | 结构概况 |
| STAGE 0 | 主墩、0#块、主塔施工完成 |
| STAGE 1-5 | 挂篮悬臂浇注箱梁1#~5#段,张拉悬臂预应力顶板钢束 |
| STAGE 6 | 6#块张拉纵向钢束与1#斜拉索 |
| STAGE 7-18 | 同STAGE 6,循环施工7#~18#梁段 |
1.2 有限元建模
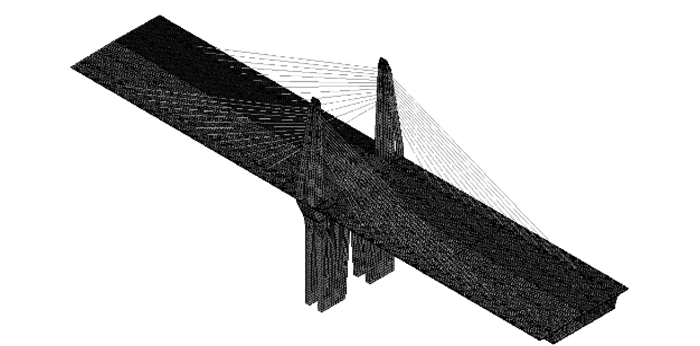
采用ANSYS有限元软件建立块体板壳组合元模型,用Solid65单元模拟混凝土结构,考虑混凝土材料的开裂、压碎以及非线性本构关系;用Shell181单元模拟波形钢腹板结构;用Link10单元模拟悬臂顶板预应力钢束,预应力效应通过单元的初应变施加, 预应力钢束通过自由度耦合建立与混凝土主梁最近节点的约束方程;斜拉索采用Link10单元模拟;普通钢筋采用beam188单元模拟,可以避免混凝土开裂后普通钢筋失去混凝土约束成为机动结构造成的奇异;桥墩底部按刚性固结处理,约束所有节点的全部自由度。结构有限元模型如图 3所示。
|
| 图 3 有限元模型 Fig. 3 Finite element model |
| |
1.3 材料参数取值及本构关系
弹性稳定性分析采用材料弹性参数,依据桥梁设计规范取值,主梁C55混凝土材料弹性模量、泊松比质量密度一侧取:3.55E+10 Pa,0.2,2.60E- 03 g/mm3;波形钢腹板Q345钢材依次取:2.06E+11 Pa,0.3,7.85E-03 g/mm3;预应力钢束Strand1860依次取1.95E+11Pa,0.3,7.85E-03 g/mm3;普通钢筋依次取2.0e11Pa,0.3,7.85E-03 g/mm3。
进行非线性分析需要定义材料非线性本构关系,C55混凝土非线性本构关系采用Hognestad [11]公式:
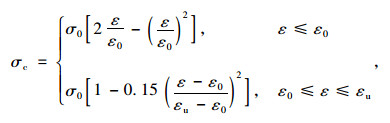
|
(1) |
式中,σ0为应力峰值,取为σ0=0.85f′c,f′c为圆柱体抗压强度,C55的f′c=55 MPa×0.8=44 MPa;ε0为应变峰值,取为0.002;εu为极限应变,取为0.003 8。
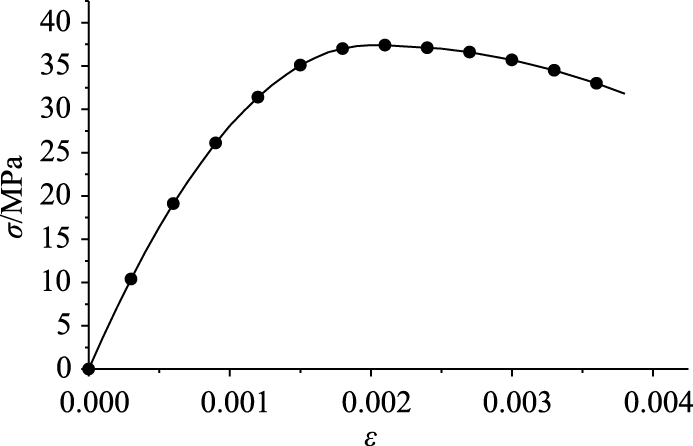
ANSYS有限元软件中考虑混凝土压碎和开裂行为时可选择Solid65单元,此时需打开混凝土开裂和压碎选项,其中张开裂缝剪力传递系数βt和闭合裂缝剪力传递系数βc取值见参考文献[12],C55混凝土非线性本构关系曲线如图 4所示。
|
| 图 4 C55混凝土本构关系 Fig. 4 Constitutive relation of C55 concrete |
| |
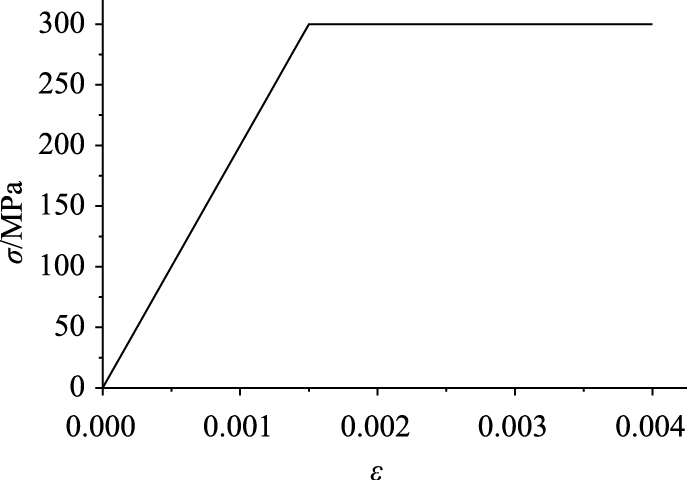
普通钢筋采用理想弹塑性本构关系,材料屈服强度300 MPa,材料的本构关系见图 5。
|
| 图 5 钢筋本构关系 Fig. 5 Constitutive relation of steel bar |
| |
2 计算结果分析 2.1 施工阶段波形钢腹板的稳定问题
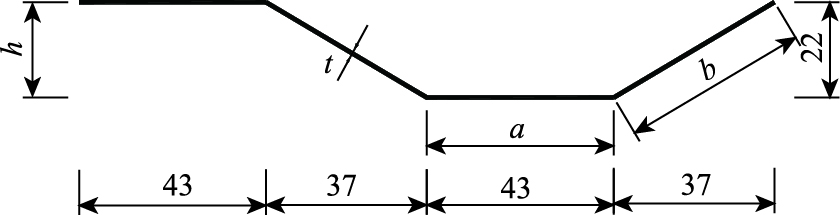
朝阳沟大桥采用1600型波形钢腹板(见图 6),箱梁节段波形钢腹板设计参数见表 2,选取稳定性最差的3个节段进行波形钢腹板稳定性分析。
|
| 图 6 1600型波形钢腹板形状(单位:cm) Fig. 6 Configurations of 1600-type corrugated web (unit: cm) |
| |
| 腹板几何参数 | 3.32-12 | 3.661-18 | 4.919-20 |
| τcr, L/MPa | 593.0 | 1 329.1 | 1 627.6 |
| τcr, G/MPa | 1 105.2 | 821.3 | 443.1 |
| 合成屈曲/MPa | 385.9 | 507.6 | 348.3 |
| 数值结果/MPa | 517.9 | 760.7 | 766.0 |
波形钢腹板箱梁受力时,剪力全部由波形钢腹板承担,弯矩全部由上下顶底板混凝土承担,较薄的钢腹板代替混凝土腹板,在剪力作用下的屈曲问题较为突出,现有研究指出波形钢腹板的剪切屈曲模态有3种形式:局部剪切屈曲、整体剪切屈曲和合成剪切屈曲,其中计算局部剪切屈曲强度和整体剪切屈曲强度的解析理论较为完善,计算公式为[8]:

|
(2) |
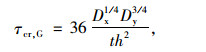
|
(3) |
对于4边简支板:
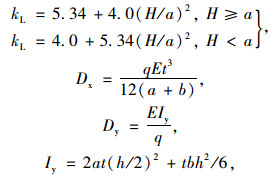
|
(4) |
式中,kL为局部剪切系数;E为波形钢腹板材料的弹性模量;v为材料的泊松比;Dx,Dy分别为单位宽度板在桥梁纵向和桥梁高度方向的面外抗弯刚度;g为单个波形的长度;Iy为单个波形对中性轴的抗弯惯性矩;w为a和b中的较大值,其中a为图 6中的钢腹板水平节段长度; b为钢腹板倾斜节段长度; t为波形钢腹板的厚度; h为波高; H为波形钢腹板板高; τcr, L为局部剪切屈曲强度; τcr, G为整体剪切屈曲强度。
波形钢腹板的合成剪切屈曲强度较为复杂,现有研究多采用式(5)描述弹性状态下的合成剪切屈曲强度与局部剪切强度和整体剪切强度的关系[13-14]:

|
(5) |
式中,τcr, I为合成剪切屈曲强度,当n取1值时,τcr, I可求得偏为保守的包络解。
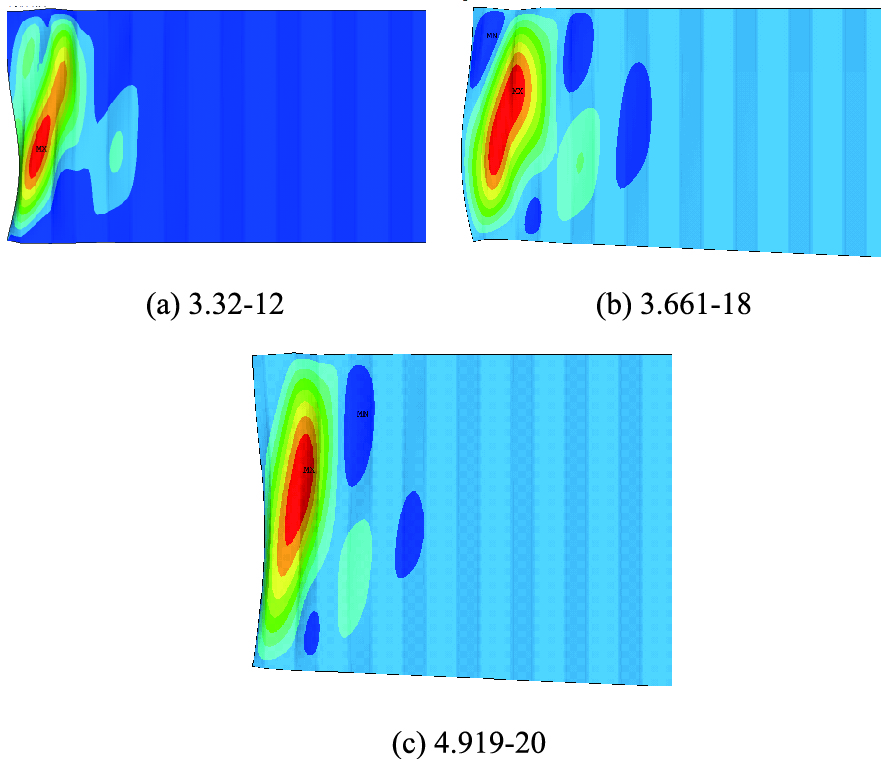
选取3种节段波形钢腹板,利用以上公式计算,并建立这些节段的有限元模型,分析4边简支纯剪切状态下的剪切屈曲,计算结果见表 3和图 7。
| 箱梁节段 | 节段波形钢腹板厚度/mm | 节段波形钢腹板最大高度/m |
| 0# | 混凝土段 | — |
| 1# | 22(内衬混凝土) | — |
| 2#~9# | 20 | 4.916~3.32 |
| 10#~11# | 18 | 3.32 |
| 12#~16# | 16 | 3.32 |
| 17#~18# | 12 | 3.32 |
|
| 图 7 波形钢腹板屈曲模态 Fig. 7 Buckling modes of corrugated steel webs |
| |
波形钢腹板设计以材料剪切屈服强度控制,需保证波形钢腹板的局部剪切屈曲、整体剪切屈曲和合成剪切屈曲强度大于材料的剪切屈服强度,图 7显示,波形钢腹板的第1阶屈曲模态为合成屈曲,由表 3可知,朝阳沟大桥的波形钢腹板设计以剪切屈服强度控制,屈曲强度大于材料的剪切屈服强度199 MPa,理论公式计算结果较有限元计算结果更为保守。
STAGE18最大悬臂状态施工完毕,建立2种模型进行弹性屈曲分析,分析在不同斜拉索初张力作用下,朝阳沟大桥的波形钢腹板屈曲特点。
模型1:STAGE18阶段,张拉悬臂顶板束,按设计初张力张拉斜拉索索力,施加重力加速度G。
模型2:STAGE18阶段,张拉悬臂顶板束,按1/2设计初张力张拉斜拉索索力,施加重力加速度G。
对2种模型进行弹性屈曲分析,考虑前100阶屈曲模态,对比第1次出现波形钢腹板屈曲时的失稳系数和模态阶数,以及前100阶屈曲模态中波形钢腹板屈曲模态出现的次数和钢腹板最大失稳系数,计算结果见表 4。
| 模型 | 模型1 | 模型2 |
| 波形钢腹板失稳模态 | 无 | 整体剪切屈曲 |
| 波形钢腹板失稳位置 | 无 | 2#块A,B腹板 |
| 第1次屈曲失稳系数 | 无 | 130.61(86阶) |
| 钢腹板屈曲模态次数 | 0 | 8 |
| 波形钢腹板失稳系数最大值 | 不存在 | 134.22 |
由表 4可知,模型2斜拉索初张力为设计初张力的1/2时,前100阶屈曲模态出现波形钢腹板局部屈曲的次数为8次,失稳系数在130.61~134.22范围之内,失稳位置在2#梁段的A,B腹板位置,C斜腹板没有屈曲失稳出现;斜拉索索力按设计文件初张力施加的模型1,前100阶屈曲模态中没有出现波形钢腹板的局部屈曲失稳,该模型第100阶屈曲模态的失稳系数为92.47。
由以上分析可知,波形钢腹板矮塔斜拉桥由于斜拉索对主梁的弹性支撑作用,可以减小主梁钢腹板的剪力内力值,提高波形钢腹板的剪切屈曲稳定性;朝阳沟大桥2#梁段A处钢腹板屈曲稳定性最差,但在悬臂施工最大状态的STAGE18前100阶屈曲模态中不会丧失稳定,失稳系数也大于92.47。
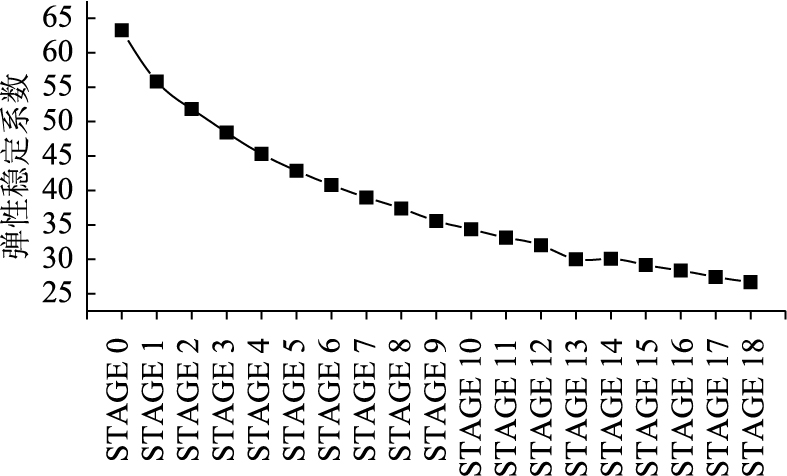
2.2 施工阶段稳定性分析在理想施工状态下,仅考虑施工阶段结构自重,计算关键施工阶段的弹性稳定系数和非线性稳定系数。非线性稳定分析时需要考虑结构初始缺陷,根据公路工程质量检验评定标准(JTGF80/1—2012)[15]对桥墩竖直度或斜度的质量验收要求,桥墩竖直度允许偏差为0.3%H且不大于20 mm,按最不利工况考虑结构初始缺陷墩顶纵桥向最大偏斜20 mm,悬臂施工阶段第1阶弹性稳定系数计算结果见图 8,施工阶段第1阶失稳模态都是面内主墩侧倾失稳,随着施工阶段的进行,结构的弹性稳定系数和非线性稳定系数都逐渐变小,最大悬臂状态STAGE 18为稳定性最差的施工阶段。
|
| 图 8 弹性稳定系数 Fig. 8 Elastic stability coefficients |
| |
弹性稳定分析前10阶屈曲稳定分析结果见表 5。施工阶段前10阶屈曲模态,结构整体失稳模态以主墩的面内侧倾、主墩轴向扭转、主墩面内2阶失稳为主,其中主墩面内侧倾为STAGE0-STAGE18施工阶段的1阶失稳模态,失稳系数由63.3减小到26.7;主墩的主墩轴向扭转和主墩面内2阶失稳两个模态在STAGE0-STAGE5施工阶段第2和第3阶模态出现,且失稳系数在165~222.6内变化;STAGE6-STAGE18的第4阶到第10阶失稳模态都为1#节段箱梁翼板局部压屈失稳,失稳系数在140.5~38.2内变化;施工过程的弹性稳定分析表明,施工阶段波形钢腹板的稳定性能较强,在前10阶失稳模态中无波形钢腹板剪切屈曲模态出现;矮塔斜桥的悬臂施工波形钢腹板箱梁的抗扭较大,施工阶段前10阶失稳模态中没有主梁扭转模态出现。
| 屈曲阶段 | 失稳模态 | 施工阶段 | 稳定系数 |
| 第1阶 | 主墩面内侧倾 | STAGE0-18 | 63.3~26.7 |
| 第2阶 | 主墩轴向扭转 | STAGE0-2 | 222.6~193.6 |
| 第2阶 | 主墩面内2阶失稳 | STAGE3-5 | 186.1~165.0 |
| 第2阶 | 1#节段箱梁翼板局部压屈 | STAGE6-18 | 186.1~33.4 |
| 第3阶 | 主墩面内2阶失稳 | STAGE0-2 | 243.2~199.2 |
| 第3阶 | 主墩轴向扭转 | STAGE3-5 | 187.1~187.1 |
| 第3阶 | 1#节段箱梁翼板局部压屈 | STAGE6-18 | 140.5~33.5 |
| 第4~10阶 | 1#节段箱梁翼板局部压屈 | STAGE6-18 | 145.1~38.2 |
对比弹性稳定系数和非线性稳定系数如表 6所示,非线性稳定系数远小于结构的弹性稳定系数,仅为弹性稳定系数的41%~34%,悬臂越长,非线性稳定系数比弹性稳定系数越小,非线性对稳定性的影响越显著。
| 施工阶段 | STAGE 5 | STAGE 6 | STAGE 9 | STAGE 12 | STAGE 15 | STAGE 18 |
| 特征值稳定系数 | 42.85 | 40.78 | 35.57 | 32.04 | 29.17 | 26.69 |
| 非线性稳定系数 | 17.54 | 16.55 | 13.87 | 12.16 | 10.88 | 9.15 |
| 比例/% | 40.94 | 40.59 | 38.99 | 37.96 | 37.30 | 34.29 |
| 失稳模态 | 主墩面内侧倾 | 主墩面内侧倾 | 主墩面内侧倾 | 主墩面内侧倾 | 主墩面内侧倾 | 主墩面内侧倾 |
2.3 施工阶段最不利工况稳定性分析
由2.1节分析可知,在波形钢腹板矮塔斜拉桥施工阶段稳定分析中,波形钢腹板的稳定问题不突出,其稳定性高于同规模的波形钢腹板连续梁桥的波形钢腹板稳定性,朝阳沟大桥施工阶段的稳定性主要为主墩失稳的稳定性问题,但是非线性对稳定性的影响不能忽略。另外桥梁施工过程中不可避免会偏离理想的设计状态,如主墩的偏斜、不对称的施工荷载、过大的施工误差等,都会对施工期间桥梁的稳定性产生不利影响,针对施工期间主墩偏斜、施工荷载最不利工况进行分析,确定朝阳沟大桥施工稳定性。
施工期间最大悬臂状态可能出现的荷载形式有[16-17]:(1)结构自重;(2)悬臂浇注施工的不平衡质量偏差,一侧偏大5%,另一侧偏小5%;(3)一侧挂篮掉落(挂篮自重2 000 kN),冲击系数取2;(4)横向风荷载根据JTG T D60-01—2004《公路桥梁抗风设计规范》[18]进行计算,横向风荷载FH=3.84 kN/m。
对以上荷载进行工况组合:
工况1:a;
工况2:a+b+c;
工况3:a+b+c+d。
在主墩偏斜率为20 mm,最大悬臂STAGE18阶段承受以上3种荷载组合,进行非线性稳定性分析,计算结果见表 7。
| 混凝土等级 | 工况1 | 工况2 | 工况3 |
| 稳定系数 | 8.54 | 5.16 | 5.13 |
| 失稳模态 | 主墩面内侧倾 | 主墩面内侧倾 | 主墩面内侧倾 |
由表 7可知,最大悬臂阶段施工荷载影响下稳定系数变化较大,工况3作用比工况1作用稳定系数降低39.95%;工况2作用比工况1作用稳定系数降低39.58%;考虑横向风荷载的作用,工况3比工况2的稳定系数降低0.62%,横向风荷载作用对结构的稳定性影响较小。悬臂施工阶段的施工荷载对结构稳定性影响较大,考虑最不利荷载工况下的稳定系数计算值为5.13,朝阳沟大桥施工阶段稳定性系数较高,能够满足施工阶段稳定性的要求。
3 结论(1) 朝阳沟大桥的波形钢腹板构造按弹性屈曲强度公式计算最小值为348.3 MPa (合成剪切屈曲),有限元方法计算的剪切屈曲最小值为517.9 MPa,大于材料剪切屈服强度199 MPa,结构承载力按剪切屈服强度控制。
(2) 波形钢腹板矮塔斜拉桥拉索的弹性支撑作用,减小了钢腹板的剪切内力,使得朝阳沟大桥STAGE18阶段,弹性屈曲前100阶失稳模态中不出现波形钢腹板的失稳模态,波形钢腹板稳定性较强。
(3) 朝阳沟大桥施工阶段的稳定性主要是主墩的平面内侧倾,钢腹板的稳定性较高,在施工阶段中不会出现失稳问题。
(4) 施工阶段考虑材料非线性和几何非线性,求得的非线性稳定系数仅为弹性稳定系数的38%~31%。
(5) 施工荷载对悬臂施工稳定性影响很大,最不利工况下非线性稳定系数仅为4.84,比仅考虑结构自重时的计算结果减小39.95%,但结构稳定性仍能满足规范要求。
| [1] |
聂建国, 陶慕轩, 吴丽丽, 等. 钢-混凝土组合结构桥梁研究新进展[J]. 土木工程学报, 2012, 45(6): 110-122. NIE Jian-guo, TAO Mu-xuan, WU Li-li, et al. Advances of Research on Steel-concrete Composite Bridges[J]. China Civil Engineering Journal, 2012, 45(6): 110-122. |
| [2] |
卜一之, 赵雷, 李乔. 苏通长江大桥结构非线性稳定性研究[J]. 土木工程学报, 2013, 46(1): 84-91. BU Yi-zhi, ZHAO Lei, LI Qiao. Structural Nonlinear Stability Analysis of Sutong Yangtze River Bridge[J]. China Civil Engineering Journal, 2013, 46(1): 84-91. |
| [3] |
赵雷, 孙才志, 杨兴旺. 鄂东长江大桥施工过程非线性稳定性分析[J]. 西南交通大学学报, 2012, 47(5): 741-747. ZHAO Lei, SUN Cai-zhi, YANG Xing-wang. Stability Analysis of Edong Yangtze River Bridge during Construction[J]. Journal of Southwest Jiaotong University, 2012, 47(5): 741-747. |
| [4] |
王艳, 魏春明, 陈淮. 部分斜拉桥施工力学性能分析[J]. 桥梁建设, 2012, 42(2): 46-52. WANG Yan, WEI Chun-ming, CHEN Huai. Analysis of Mechanical Properties of Extradosed Bridge in Construction Process[J]. Bridge Construction, 2012, 42(2): 46-52. |
| [5] |
辛延甫, 王雪霁, 侯炜, 等. 考虑桩土作用的高墩大跨连续结构几何非线性效应分析[J]. 公路交通科技, 2017, 34(11): 84-90. XIN Yan-fu, WANG Xue-ji, HOU Wei, et al. Analysis on Geometric Nonlinear Effect of High-pier and Long-span Continuous Structure Considering Pile-soil Interaction[J]. Journal of Highway and Transportation Research and Development, 2017, 34(11): 84-90. |
| [6] |
李国豪. 桥梁结构稳定与振动[M]. 北京: 中国铁道出版社, 2003. LI Guo-hao. Stability and Vibration of Bridge Structure[M]. Beijing: China Railway Publishing House, 2003. |
| [7] |
郭兰英. 单肢箱形薄壁高墩与双肢矩形薄壁高墩稳定性比较研究[J]. 公路交通科技, 2013, 30(9): 87-93. GUO Lan-ying. Comparative Study on Stability of Single-limb Box and Double-limb Rectangle Thin-wall High-rise Piers[J]. Journal of Highway and Transportation Research and Development, 2013, 30(9): 87-93. |
| [8] |
聂建国, 朱力, 唐亮. 波形钢腹板的抗剪强度[J]. 土木工程学报, 2013, 46(6): 97-109. NIE Jian-guo, ZHU Li, TANG Liang. Shear Strength of Trapezoidal Corrugated Steel Webs[J]. China Civil Engineering Journal, 2013, 46(6): 97-109. |
| [9] |
陈华婷, 迟啸起, 黄艳. 正弦波形波纹腹板工字型钢板梁的抗剪强度[J]. 公路交通科技, 2013, 30(5): 38-46. CHEN Hua-ting, CHI Xiao-qi, HUANG Yan. Shear Strength of I-shaped Steel Plate Girder with Sinusoidally Corrugated Webs[J]. Journal of Highway and Transportation Research and Development, 2013, 30(5): 38-46. |
| [10] |
胡华万, 李俊, 强士中. 波形钢腹板PC组合箱梁剪切屈曲性能研究[J]. 铁道工程学报, 2011, 28(2): 80-83, 102. HU Hua-wan, LI Jun, QIANG Shi-zhong. Study on Shear Buckling Property of Corrugated Steel Web PC Combined Box Girder[J]. Journal of Railway Engineering Society, 2011, 28(2): 80-83, 102. |
| [11] |
过镇海, 时旭东. 钢筋混凝土原理和分析[M]. 北京: 清华大学出版社, 2003. GUO Zhen-hai, SHI Xu-dong. Reinforced Concrete Theory and Analysis[M]. Beijing: Tsinghua University Press, 2003. |
| [12] |
江见鲸, 陆新征, 叶列平. 混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005. JIANG Jian-jing, LU Xin-zheng, YE Lie-ping. Finite Element Analysis of Concrete Structure[M]. Beijing: Tsinghua University Press, 2005. |
| [13] |
刘保东, 李祖硕, 陈海波, 等. 变截面波形钢腹板连续组合箱梁破坏试验研究[J]. 铁道工程学报, 2018, 35(3): 38-44. LIU Bao-dong, LI Zu-shuo, CHEN Hai-bo, et al. Research on the Failure Experiment on the Continuous Composite Box Girder with Variable Cross-section Corrugated Steel Webs[J]. Journal of Railway Engineering Society, 2018, 35(3): 38-44. |
| [14] |
YI J, GIL H, YOUM K, et al. Interactive Shear Buckling Behavior of Trapezoidally Corrugated Steel Webs[J]. Engineering Structures, 2008, 30(6): 1659-1666. |
| [15] |
JTG F80-1-2012, 公路工程质量检验评定标准[S]. JTG F80-1-2012, Quality Inspection and Evaluation Standards for Highway Engineering[S]. |
| [16] |
马如进, 李忠鹏. 连续梁倒拆施工倾覆稳定性的体系可靠度方法[J]. 同济大学学报:自然科学版, 2015, 43(8): 1167-1173. MA Ru-jin, LI Zhong-peng. System Reliability Method to Analyze Overturning Stability of Demolition Construction of Continuous Beam Bridges[J]. Journal of Tongji University:Natural Science Edition, 2015, 43(8): 1167-1173. |
| [17] |
张武洪, 黄元元. 基于可靠度反分析理论的连续梁桥悬臂施工整体倾覆稳定安全系数评估[J]. 施工技术, 2016, 45(增2): 319-322. ZHANG Wu-hong, HUANG Yuan-yuan. Overturning Stability Safety Factors Assessment of Continuous Girder Bridges in Cantilever Construction Based on Reliability Theory[J]. Construction Technology, 2016, 45(S2): 319-322. |
| [18] |
JTG T D60-01-2004, 公路桥梁抗风设计规范[S]. JTG T D60-01-2004, Wind-resistant Design Specifica-tion for Highway Bridges[S]. |
 2019, Vol. 36
2019, Vol. 36
