扩展功能
文章信息
- 李宁, 马骉, 李瑞, 司伟
- LI Ning, MA Biao, LI Rui, SI Wei
- 基于PUMA的单级和多级加载模式下碎石粒料性能研究
- Study on Performance of Unbound Granular Materials under Single-stage and Multi-stage Loading Modes Based on PUMA
- 公路交通科技, 2019, 36(3): 62-72
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 62-72
- 10.3969/j.issn.1002-0268.2019.03.010
-
文章历史
- 收稿日期: 2017-07-06
“一带一路”倡议稳步推进,建立了多层次、多级联网与合作的交通运输体系,各级用户对道路服务水平的期望也大幅提升,柔性路面服务质量成为关注焦点之一。粒料材料(Unbound Granular Materials, UGM)是柔性路面的一种典型基层材料,国内外已经有许多关于UGM力学性能、本构关系、材料组成和测试技术等方面的研究成果[1-4]。其中,力学性能是UGM最有吸引力的研究领域之一,弹性模量、永久变形、应力和应变是路面结构层在车辆荷载作用下最常用的力学性能指标[5]。
高启聚、Lekarp和Erlingsson等人[1, 3, 6-7]研究表明UGM的永久变形随着荷载作用次数增加呈现非线性变化,这是由UGM的非线性特性所决定。结构层在初始的几百次加载循环内,永久变形显著增加;之后,永久变形缓慢增长。同时,由于UGM具有应力依赖的特点,荷载作用水平对永久变形有明显影响。为了探究荷载作用水平和荷载作用次数对UGM性能的影响,研究人员通过三轴试验对UGM的性能进行试验研究。Erlingsson和Rahman[3-4]应用多级加载模式(Multi-stage Loading Mode, MSLM)和单级加载模式(Single-stage Loading Mode, SSLM)对UGM的永久应变展开分析,采用5种模型对永久应变进行理论预测,并提出了永久应变模型的修正方案。Cerni和Hornych等人[8-9]也采用MSLM对UGM的永久变形进行研究。然而,这些研究通常要经历数百万次加载周期才获取最终结果[4],但是UGM性能的变化阶段主要集中在初始阶段。因此,重点开展研究UGM初始阶段的性能,可以大幅减少数百万次重复加载循环的昂贵费用和长时工作。金刚等[10]通过大型三轴试验研究了UGM在不同加载水平下初始200次加载循环的性能,分析了不同因素对永久变形和弹性模量的影响。
弹性模量和CBR是评价碎石材料性能的常用指标[7, 11],Molenaar等人[12]提出了重复加载CBR试验,并建立了重复加载CBR和三轴试验之间的等效关系,通过重复CBR试验有效地估计UGM的弹性模量;Mohajerani等人[13]通过重复三轴试验建立了弹性模量和Clegg冲击锤值之间的相关性;考虑到围压变化对碎石材料性能的影响,Xiao、刘星等人[14-15]等人采用常围压模式(Constant Confining Pressure, CCP)和变围压模式(Variable Confining Pressure, VCP)计算弹性模量,获取了不同的试验结果。最近,通过精密非黏结材料分析仪(Precision Unbound Granular Analyser, PUMA)对碎石材料的性能进行研究,为快速开展重复荷载试验带来了极大的便利,可以准确测量粒料材料的永久变形、应力和应变等力学响应指标。但目前关于应用PUMA进行UGM动态重复荷载试验的研究成果尚不多见,Thom等人[16]借助于PUMA初步探索了冷拌沥青碎石的劲度模量和变形特性,为开展UGM研究提供重要参考。根据前述研究基础,可知粒料材料(UGM)的试验结果离散性较大,不利于对影响因素进行分析,为降低变异性对试验结果的影响,本研究从单粒径碎石粒料出发,并同两档料填充和三档料填充碎石粒料,采用PUMA进行SSLM和MSLM两种加载模式进行重复荷载试验,重点分析前400次加载循环的永久变形和弹性模量,探讨重复加载初期阶段对碎石粒料性能的影响,通过碎石粒料的研究成果对探讨UGM性能及其施工技术研究具有指导意义。
1 试验材料与方法 1.1 试验材料试验所用材料为的石灰岩碎石,产自陕西咸阳的碎石厂。试验采用3种单粒径碎石,分别为9.5 ~13.2 mm, 13.2~16 mm, 16~19 mm;两档料填充碎石,分别是4.75~9.5 mm与13.2~16 mm、9.5~13.2 mm与16~19 mm;三档料填充碎石,4.75~9.5 mm与9.5~13.2 mm与19~26.5 mm,其中两档料和三档料填充的最佳填充比, 采用振实填充试验的结果所确定的第一波谷[17-18]。根据《公路工程集料试验规程》(JTG E42-2005)所述方法[19],3类碎石的基本性能如表 1所示。以振实密度为依据,碎石粒料采用100%压实度;为简化分析,本研究暂不考虑含水量的影响,试验用材料均采用干燥碎石材料。
| 性能项目 | 3类碎石材料 | |||||||
| 单粒径碎石/mm | 两档料填充碎石/mm | 三档料填充碎石/mm | ||||||
| 9.5 | 13.2 | 16 | 4.75与13.2 | 9.5与16 | 4.75与9.5与19 | |||
| 填充质量比例/% | 100 | 100 | 100 | 30:70 | 26:74 | 7:20:73 | ||
| 毛体积密度/(g·cm-3) | 2.734 | 2.707 | 2.718 | — | — | — | ||
| 振实密度/(g·cm-3) | 1.557 | 1.562 | 1.535 | 1.564 | 1.617 | 1.705 | ||
| 针片状颗粒含量/% | 6.1 | 11.3 | 8.5 | — | — | — | ||
| 压碎值/% | — | 14.36 | — | — | — | — | ||
1.2 试验设备
PUMA也称“约束压缩试验”,如图 1所示。组装试模(图 2)是PUMA的特殊部件,特征之一是围压由“约束带”的限制作用提供,“约束带”是橡胶带和钢带两部分组成,橡胶带的弹性变形为试样提供径向变形空间,钢带用于测量橡胶带发生变形时的应变。另一个特征是模具由“H”形卡槽与弧形壁板组装而成,可以满足试件在径向一定范围内的变形要求。通过环箍将壁板和卡槽组成的模具固定,在试样成型时,将环箍锁紧,试件成型完成后小心地松开环箍,能够减少在成型、移动和安置时对试件造成二次扰动和破损,可以避免常规成型试件时乳胶膜对试件的影响。PUMA围压与传统三轴的围压模式存在不同,PUMA的围压是可变和被动围压,属于应变控制和刚性加载模式;而传统三轴围压是主动施加的,属于应力控制和柔性加载模式。

|
| 图 1 PUMA试验设备 Fig. 1 PUMA test equipment |
| |

|
| 图 2 组装试模 Fig. 2 Assembled mould |
| |
1.3 试验流程
PUMA试验依据EN 13286-7(BS 2004)[20]进行试件成型和试验设置,试件尺寸为高150 mm、直径150 mm。采用SSLM和MSLM两种加载模式对3类材料进行加载:在SSLM中,轴向荷载强度分别为80,160,240,320,400, 480 kPa,单级加载周期为4 000次,加载频率为1 Hz;在MSLM中,轴向荷载依次从80 kPa增加至560 kPa,每个级位的增量为40 kPa、加载次数为400次,加载频率为1 Hz。采用正弦波形加载,每组试验有4次平行试验。
2 结果与讨论 2.1 多级加载模式(MSLM)(1) 单粒径碎石粒料
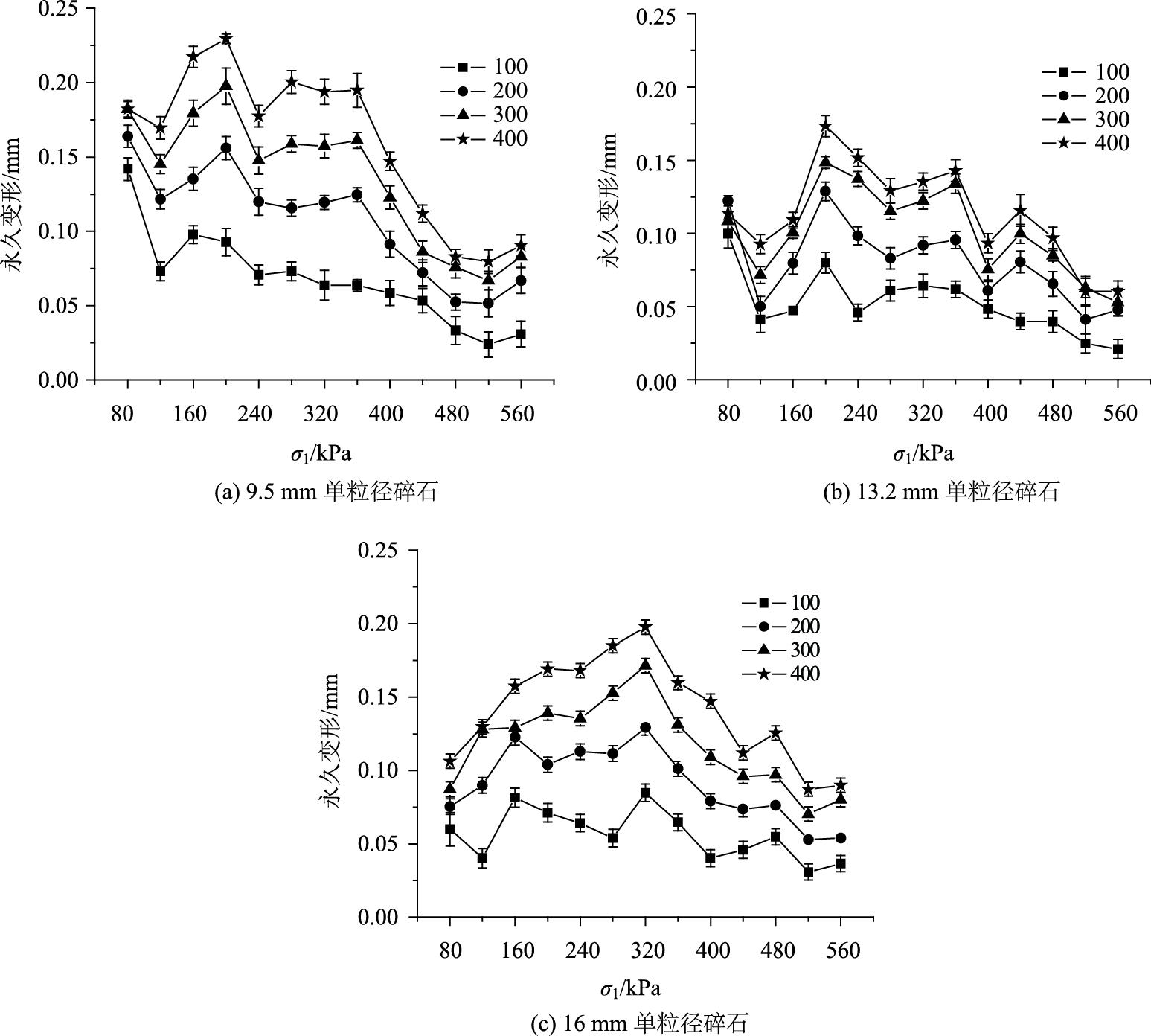
各级位加载的第100,200,300,400次加载循环的永久变形如图 3所示,3种单粒径碎石粒料的永久变形随加载强度增加具有相似的变化趋势,随着载荷强度增加而呈现出两个峰,第一个峰出现在约200 kPa,第二个峰在约340 kPa,但16 mm碎石更倾向于单峰曲线变化。当载荷强度小于340 kPa时,各阶段的永久变形较大,在荷载强度大于480 kPa后,永久变形显著降低,表明载荷强度对永久变形影响降低,这可能与碎石粒料的变形累积效应有关,在荷载作用(荷载等级和荷载次数)下,变形累计达到一定水平后,碎石粒料的结构和稳定性得到改善,其承载能力提高,相同的荷载增量不会引起相同的永久变形增量,永久变形增长速度减慢。由此推知,当累计永久变形达到一定量后,碎石粒料结构在路面中的永久变形不会受到在极限载荷条件下载荷强度等级的影响,即永久变形便不会再增加。
|
| 图 3 MSLM下3种单粒径碎石各级加载的永久变形 Fig. 3 Permanent deformations of each loading stage in MSLM for 3 single-size unbound granular materials |
| |
9.5,13.2,16 mm碎石结构的最大永久变形分别为0.23,0.17,0.2 mm,表明13.2 mm的碎石相比其他两种粒径碎石具有更强的抗变形能力。可能是因为13.2 mm碎石颗粒分布范围相对较小,颗粒相似程度更大,且颗粒粒径较大,它们之间不易发生相对移动变形;9.5 mm碎石的颗粒较小,等同空间内颗粒数量较多,且颗粒分布范围相对较宽,颗粒迁移和变形的概率更高,故而会产生更大的变形;对于16 mm碎石,粒径较大的颗粒倾向于形成大量的空隙,并且其骨架结构不如13.2 mm碎石稳定和致密,因此永久变形也相对较大。
(2) 填充碎石粒料
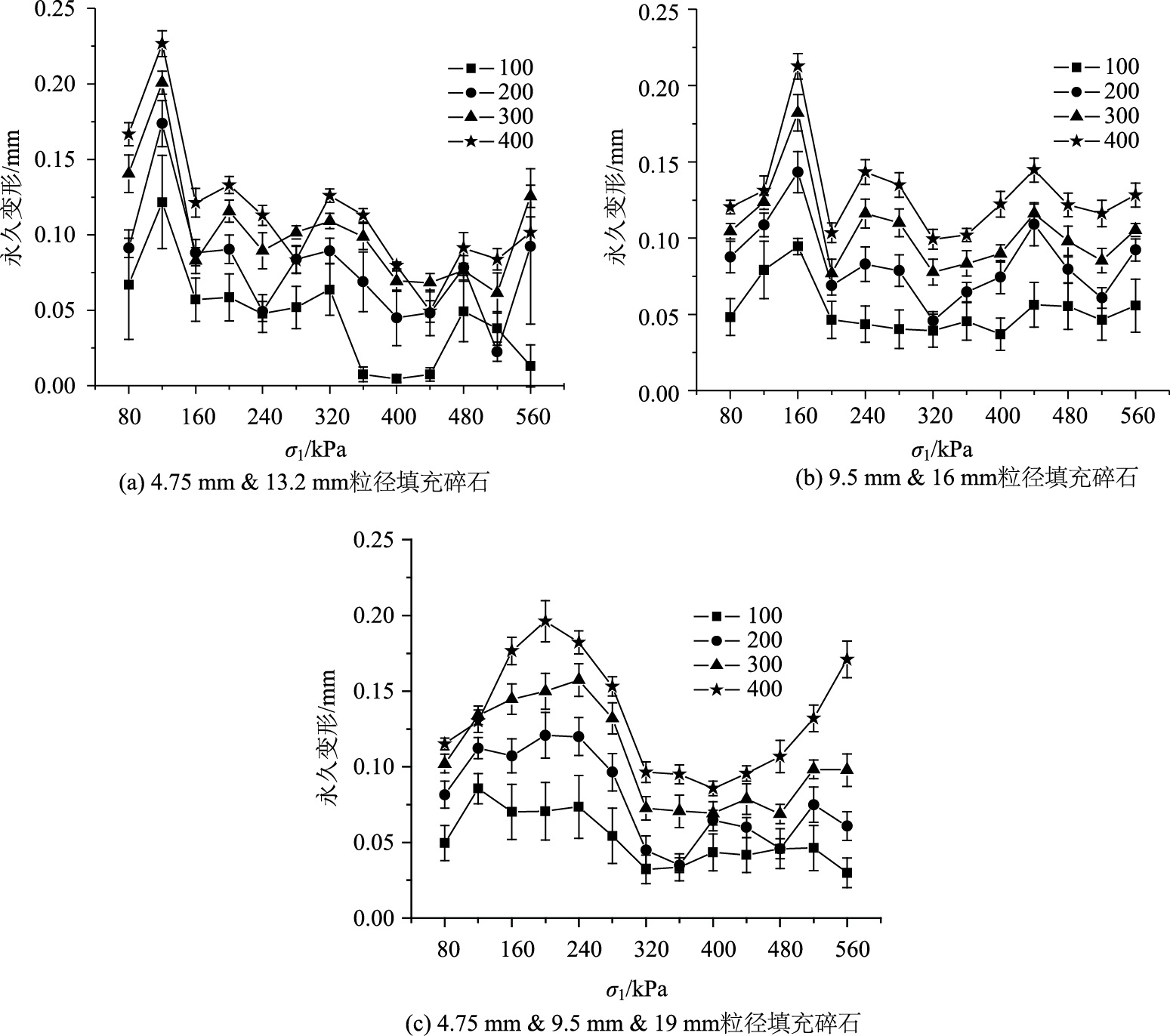
填充碎石材料在MSLM下的各级加载的永久变形如图 4所示,4.75 mm与13.2 mm与9.5 mm与16 mm两种填充碎石粒料的永久变形变化趋势相同,在荷载强度分别为120 kPa和160 kPa时,永久变形达到整个加载阶段的最大值,分别0.227 mm和0.213 mm;随着荷载强度增加,永久变形出现不同幅度的变化,整体保持在0.05 mm至0.12 mm范围之间。与两档料填充碎石不同,4.75 mm与9.5 mm与19 mm填充碎石粒料的永久变形呈现出正弦波形变化,在200 kPa左右出现波峰(峰值为0.196 mm),在360 kPa左右出现波谷,荷载次数为400次时波形变化趋势越加明显。
|
| 图 4 MSLM下3种填充碎石各级加载的永久变形 Fig. 4 Permanent deformations of each loading stage in MSLM for 3 mixed unbound granular materials |
| |
对比单粒径碎石粒料与填充碎石粒料在MSLM下的永久变形变化可知,单粒径碎石的永久变形存在多个峰值点,且峰值点的荷载强度相对较高。单粒径碎石达到永久变形的最大值需要更高的荷载强度,随着荷载强度升高,永久变形增量下降,表明在荷载强度达到一定程度后,单粒径碎石结构才能达到相对稳定状态,间接对单粒径碎石粒料的压实成型提高了要求。填充碎石粒料的永久变形在荷载强度较低时便出现了峰值,其后永久变形增量均保持在一个相对较低的水平,表明填充碎石粒料在相同荷载强度下更容易达到密实稳定状态。
另外,可以发现16 mm单粒径碎石和三档料填充碎石粒料的永久变形更趋向单峰形式,说明碎石类材料的最大粒径组成对材料性能有重要影响,碎石材料的粒径越大,破坏和发生变形时需要的能量越大。单粒径碎石中全部是16~19 mm的碎石,达到最大永久变形增量的荷载强度高达340 kPa;4.75 mm与9.5 mm与19 mm填充碎石粒料中4.75 mm和9.5 mm粒径碎石作为填充材料,降低了19 mm碎石发生迁移或变形所需的阻抗能量,故而其永久变形最大增量的荷载强度仅为200 kPa,表明填充碎石粒料更易于在荷载强度较低时达到稳定状态。同时,对比图 3和图 4中单粒径碎石材料和填充碎石粒料的误差值,可知单粒径碎石粒料永久变形的误差值相对较小,而填充碎石粒料永久变形的误差值较大,表明随着碎石粒料的粒径范围扩大,试验的误差范围同时也在增加,这也是采用单粒径碎石作为分析基础的原因之一。
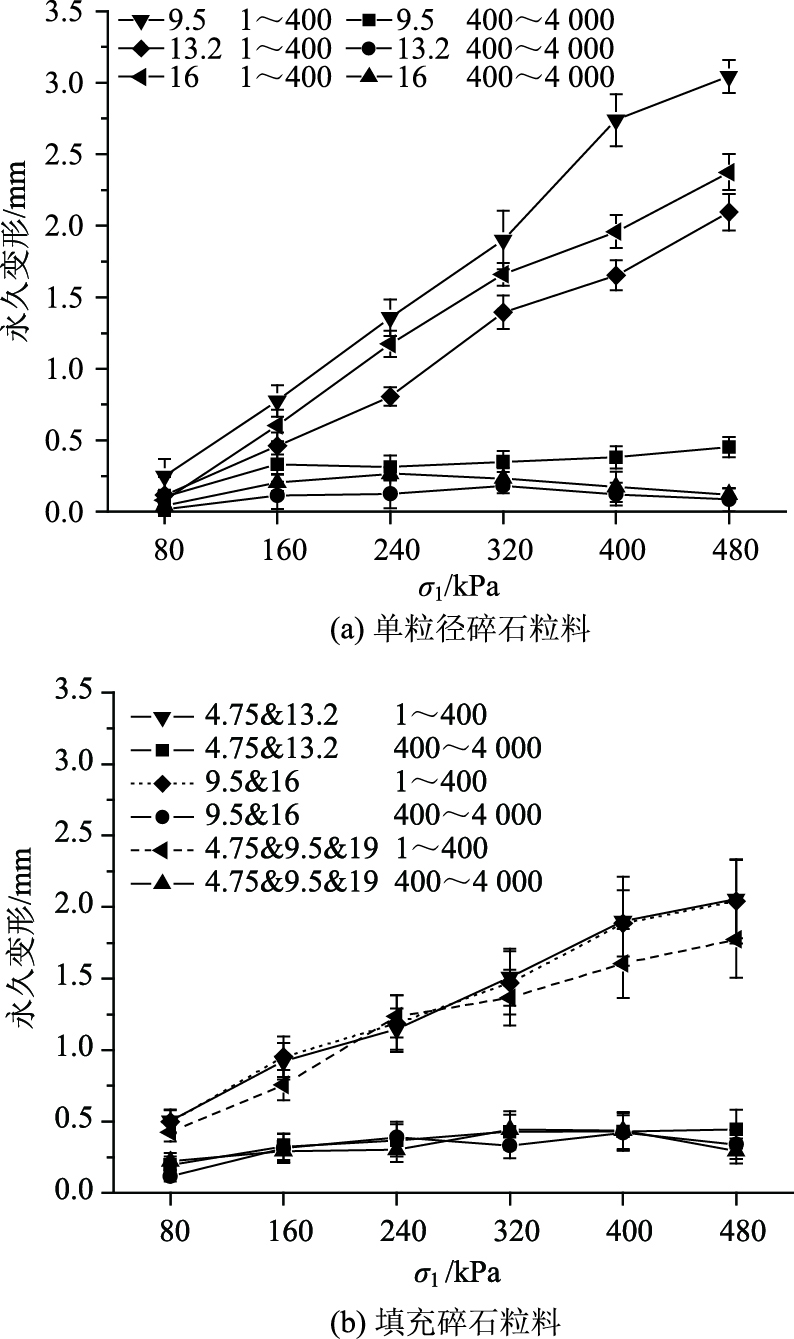
2.2 单级加载模式(SSLM)SSLM是研究UGM性能的常用方法,在4 000次荷载作用下,单粒径碎石粒料和填充碎石粒料的永久变形如图 5所示,图中有两组线,一组是1~400次加载,另一组是400~4 000次加载。当荷载强度升高时,永久变形在1~400次加载循环内迅速增加,但在400~4 000次加载循环内增长非常小,与已有研究结果一致。这种现象已由Werkmeister和El-Basyouny等人[21-22]解释:永久变形可分为两个阶段,后压实效应是初始阶段永久变形迅速增加的主要原因,颗粒破碎和迁移是第2阶段变形的主要原因,而初始阶段变形占整个变形的绝大部分,第2阶段则非常小。
|
| 图 5 SSLM下1~400和400~4 000次加载的永久变形 Fig. 5 Permanent deformations in SSLM with 1-400 and 400-4 000 loading cycles |
| |
对比图 5中单粒径和填充碎石粒料的永久变形可知,在400~4 000次加载区间内,两类碎石材料的永久变形几乎相同;1~400次加载区间内,填充碎石粒料的永久变形与单粒径碎石粒料的永久变形存在差异:当荷载强度小于240 kPa时,单粒径和填充碎石粒料的永久变形相差不大,填充碎石粒料的永久变形略大于单粒径碎石粒料;当荷载强度高于240 kPa后,单粒径碎石粒料的永久变形快速增长,而填充碎石粒料的永久变形增长速率较慢,最终填充碎石的永久变形小于单粒径碎石约1 mm,表明填充碎石粒料的荷载强度较高时具有显著的抗变形能力,在荷载强度较低时两类材料的抗变形能力相差不大。
由图 5可知,两个阶段的永久变形随着荷载强度近似呈线性变化,这与永久变形非线性特征略有不同。根据线性回归,两个阶段的回归相关系数(Adjust-R2)在见表 2,初始阶段的相关系数均大于0.94,而第2阶段相关系数不如初始阶段,这可能是与两个阶段的分界点相关。对于单粒径碎石粒料,选择第400次加载作为分界点,不是非常适合,相关系数甚至出现了负值,而填充碎石粒料的两阶段线性回归系数相对较好。为了进一步说明分界点对两阶段线性回归的影响,不同分界点的两阶段线性回归相关系数见表 2,由结果可知,即使分界点从第600次增至第1 600次加载,第2阶段的线性回归仍不佳,说明第2阶段不适宜采用线性回归描述永久变形。根据第2阶段的特点,再将其分为线性和非线性两部分,整个变形过程将具有3个阶段,即线性阶段(初始阶段)、非线性阶段(第2阶段)和线性阶段(第3阶段)。第2分界点可从第3阶段终点向第2阶段终点回归确定。然而,在4 000次加载时,UGM的永久变形尚未达到近似最终状态。因此,第2分界点的分析将在后续研究中进一步讨论。
| 分界点/次 | 加载阶段 | 碎石粒径/mm | |||||
| 9.5 | 13.2 | 16 | 4.75与13.2 | 9.5与16 | 4.75与9.5与19 | ||
| 400 | 初始阶段 | 0.990 | 0.991 | 0.987 | 0.989 | 0.977 | 0.961 |
| 第2阶段 | 0.710 | -0.019 | -0.213 | 0.843 | 0.361 | 0.315 | |
| 600 | 初始阶段 | 0.983 | 0.986 | 0.985 | 0.978 | 0.968 | 0.958 |
| 第2阶段 | 0.740 | 0.135 | -0.151 | 0.675 | 0.227 | 0.155 | |
| 800 | 初始阶段 | 0.986 | 0.985 | 0.979 | 0.982 | 0.956 | 0.962 |
| 第2阶段 | 0.753 | 0.230 | 0.096 | 0.383 | 0.285 | 0.018 | |
| 1 000 | 初始阶段 | 0.987 | 0.986 | 0.976 | 0.980 | 0.949 | 0.956 |
| 第2阶段 | 0.721 | 0.333 | 0.218 | 0.374 | 0.256 | 0.003 | |
| 1 200 | 初始阶段 | 0.989 | 0.986 | 0.981 | 0.979 | 0.942 | 0.953 |
| 第2阶段 | 0.647 | 0.168 | 0.128 | 0.487 | 0.235 | 0.002 | |
| 1 400 | 初始阶段 | 0.990 | 0.987 | 0.980 | 0.979 | 0.937 | 0.956 |
| 第2阶段 | 0.662 | 0.048 | -0.148 | 0.108 | 0.169 | 0.106 | |
| 1 600 | 初始阶段 | 0.992 | 0.988 | 0.980 | 0.981 | 0.930 | 0.953 |
| 第2阶段 | 0.595 | 0.081 | -0.227 | 0.002 | 0.120 | 0.094 | |
2.3 MSLM和SSLM之间的比较
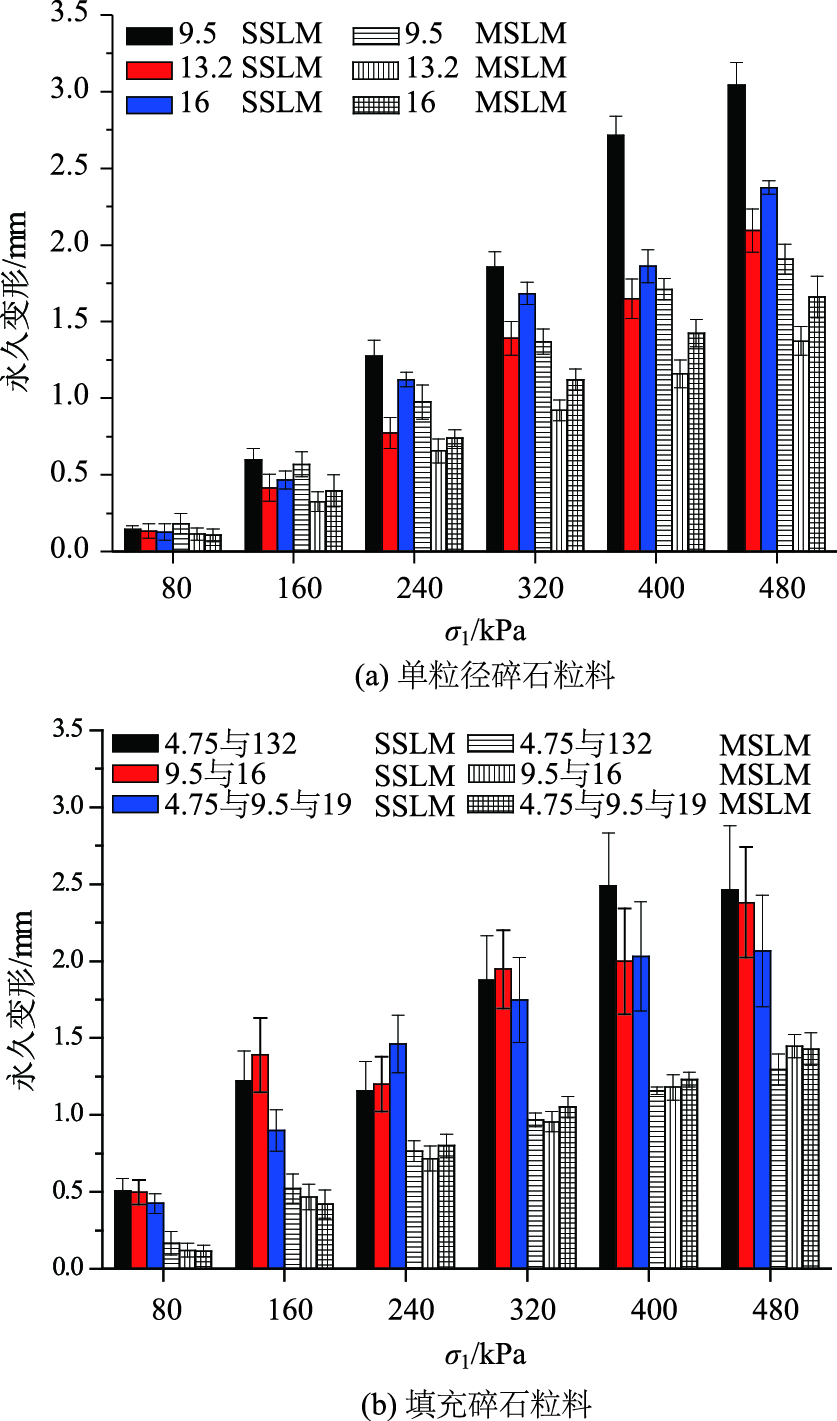
在相同的荷载强度和作用次数下,单粒径碎石粒料和填充碎石粒料在两种加载模式下的永久变形如图 6所示。例如,当荷载强度为240 kPa时,MSLM经历了从80 kPa开始的5个加载阶段,对应的SSLM加载次数为2 000。由图 6(a)可知,SSLM模式下的永久变形大于MSLM的永久变形,加载强度越高,二者之间差异越明显。图 6(b)中填充碎石粒料在两种加载模式下的永久变形与图 6(a)具有相似的情形,相同荷载强度下,SSLM模式的永久变形要明显高于MSLM加载模式;在SSLM加载模式下,除荷载强度为240 kPa外,三档料填充碎石粒料的永久变形均小于两档料填充碎石粒料;而在MSLM加载模式下,3种填充碎石的永久变形大体相近,没有明显的趋势。
|
| 图 6 相同加载次数下SSLM和MSLM的永久变形 Fig. 6 Permanent deformations in SSLM and MSLM with same loading cycles |
| |
SSLM模式下永久变形更大可能有以下几个原因:当加载强度低于240 kPa时,最高荷载强度是初始加载强度的两倍或3倍,对于压实度较高的碎石粒料,结构处于应力承受范围内,在这种情况下主要是由结构的剪切强度抵抗外荷载,两种加载模式的永久变形差异不大;当加载水平超过240 kPa,SSLM模式下,结构层直接承受高级位荷载,此时结构层的承载能力不依赖于其剪切强度,而主要取决于颗粒自身强度,颗粒被压碎的可能性很高,碎石粒料的粒径被改变,细集料增多,倾向于填充结构,产生更大的变形,直到它达到新状态通过结构特性来抵抗荷载[23];对于MSLM模式,荷载强度逐步增加,碎石粒料结构层有一定时间来适应和调整,使其结构特性增强,此时碎石粒料结构层主要依靠剪切作用抵抗外部负荷,破碎颗粒少、粒径变化小,MSLM的永久变形量小。同时,2.2节也说明了永久变形主要集中在初始阶段,SSLM模式下的永久变形在1 000次前线性增长较快,之后变缓;而MSLM模式下各级位400次加载时,该过程使加载结构层逐渐密实稳定,永久变形增长速度却随荷载级位增加而降低。因此,两种模式间的永久变形差异在荷载强度越高时越明显。根据上述,这两种加载模式也解释了路面结构压实3阶段的重要意义,即初压、复压和终压,表明初压时压路机吨位过高不利于结构层,压路机的吨位依次增加有利于提高结构稳定性,降低永久变形,特别是对于粒料类材料。
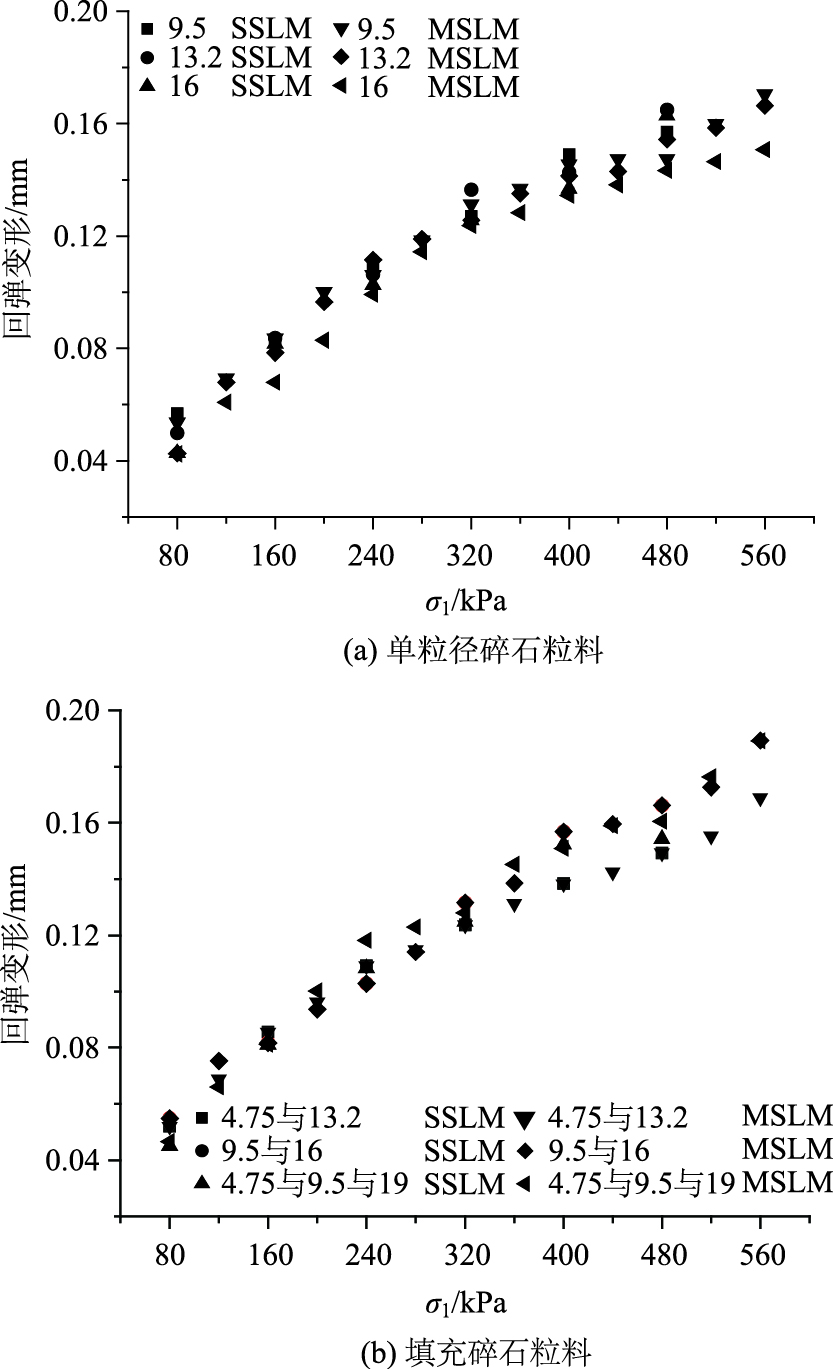
2.4 与重复CBR和三轴试验的模量对比单粒径碎石粒料和填充碎石粒料在MSLM和SSLM两种模式下的回弹变形如图 7所示,它们具有相同的变化范围和趋势,随着荷载水平的增长而近似线性增加。相比较而言,填充碎石粒料的回弹变形比单粒径碎石粒料略大,且三档料填充碎石的回弹变形比两档料填充碎石的大,表明集料颗粒之间的填充关系越明显,粒料材料的弹性恢复能力更强。
|
| 图 7 初始400次加载下SSLM和MSLM的回弹变形 Fig. 7 Resilient deformations in MSLM and SSLM with initial 400 loading cycles |
| |
Opiyo等人[24]针对CBR试验提出了完全摩擦(Full-friction)和无摩擦(No-friction)两种模型对等效模量的方法计算,见式(1)~ (2),Molenaar等人[12]对不同加载强度下100次荷载的重复CBR试验,利用该方法对等效模量进行计算。
完全摩擦:
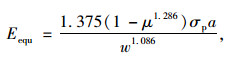
|
(1) |
无摩擦:
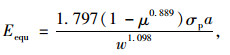
|
(2) |
式中,Eequ为等效模量,μ为UGM的泊松比,取值为0.45,σp为轴向荷载强度,a为贯入压头的半径,w为回弹变形。
根据文献[10, 12]中的方法,重复三轴试验的弹性模量可以用常围压CCP和变围压VCP模型计算,如式(3)~ (4)所示。
常围压CCP模型:
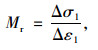
|
(3) |
变围压VCP模型:
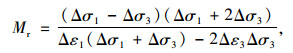
|
(4) |
式中,Δσ1为轴向应力; Δσ3为径向应力; Δε1为弹性轴向应变; Δε3为弹性径向应变。
利用式(1)~ (2),两类粒料的等效模量如图 8所示,完全摩擦模型的等效模量小于无摩擦模型的等效模量。当不考虑摩擦时,等效模量将增加10~20 MPa,可知这两种模型差异不大。在实际情况下,摩擦不能被消除,且粒料材料的模量倾向于小值,故全摩擦模型可以更恰当地描述等效模量。文献[12]中的等效模量在完全摩擦模型下,贯入应力范围为7~12 MPa时,其等效模量为400~1 100 MPa;本研究中轴向荷载强度从80 kPa增加到560 kPa时,计算等效模量从120~330 MPa不等。文献中的等效模量与本研究的计算等效模量之间具有一定的差异,主要原因之一为二者试验的边界条件略有不同。因为CBR试验筒是固定的整体,其提供围压约束作用趋向无限大,而PUMA试模提供的围压在有限范围内可变,故而重复CBR试验的等效模量大于PUMA,但二者具有相同的趋势和规律。
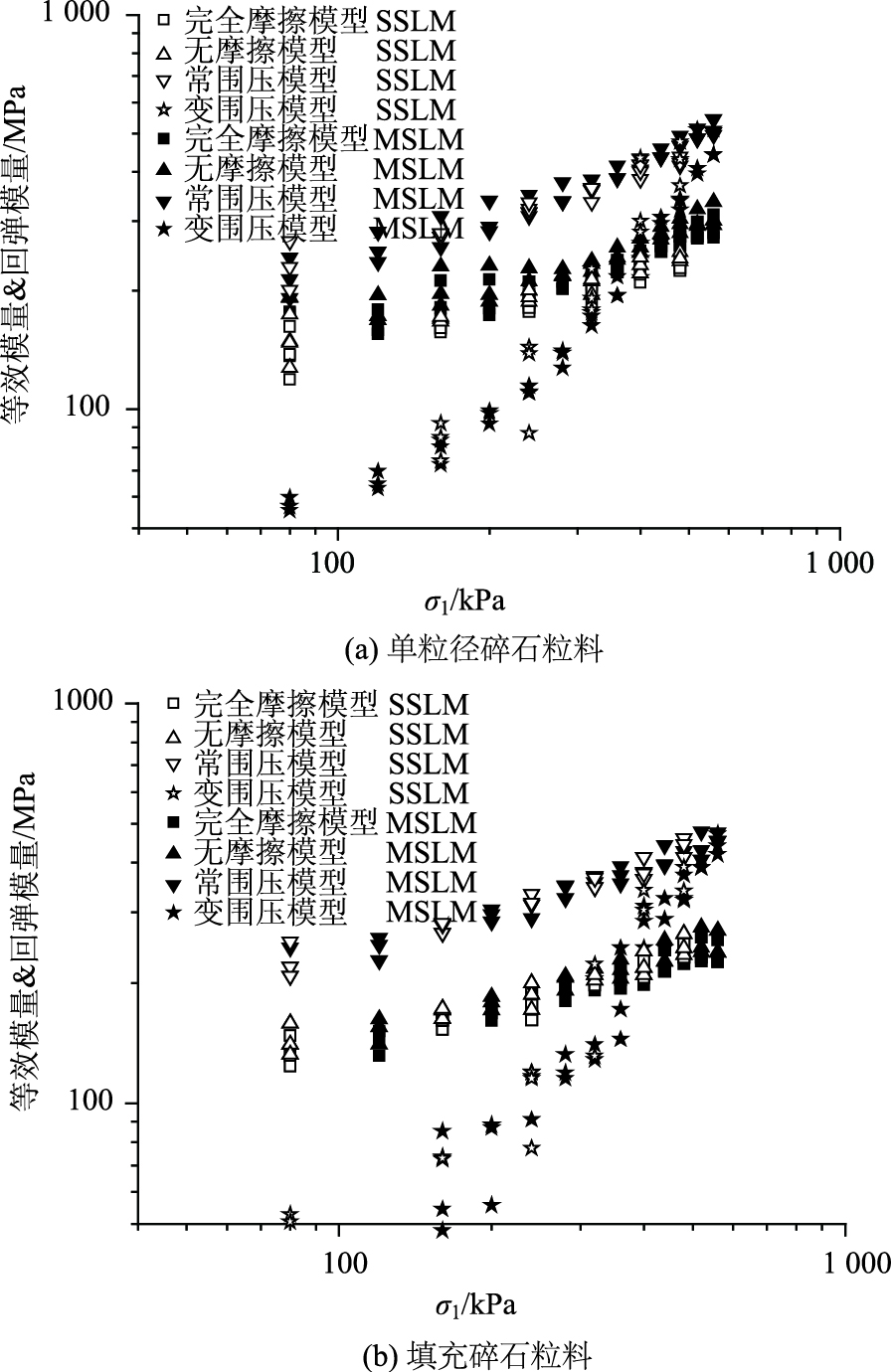
|
| 图 8 初始400次加载下四种模型的计算模量 Fig. 8 Calculated moduli of 4 models with initial 400 loading cycles |
| |
根据CCP模型和VCP模型,两类粒料的计算弹性模量如图 8所示,可知CCP模型的弹性模量大于VCP模型的弹性模量,CCP模型的弹性模量在190~550 MPa,VCP模型的弹性模量在40~520 MPa;随轴向荷载强度增大,VCP模型的弹性模量增长率大于CCP模型,表明轴向荷载增大时,围压对弹性模量的影响也增大。
已有研究成果表明[10, 14],材料整体的密实程度越高,材料的刚度越大,弹性模量越大,然而本研究的试验结果与已有结果之间存在不同,图 8中单粒径碎石粒料的等效模量比填充碎石粒料的等效模量略大。由于等效模量或弹性模量与回弹变形紧密相关,图 7中的回弹变形结果表明填充碎石粒料的回弹变形较大,根据4种模型计算方法可知两类材料模量的变化。
如图 8所示,等效模量或弹性模量与轴向荷载强度在双对数坐标轴内均呈现出近似线性关系,采用线性回归时,其相关系数见表 3,所有的Adjusted-R2均大于0.8,表明模量与轴向荷载线性关系相当好。其中,VCP模型的相关系数低于其他模型,且VCP模型的计算弹性模量与其他模型的计算模量有明显的差异,这与计算模型是否考虑围压有较大关系。在VCP模型中,径向应力是动态计算量,随着加载循环而改变,其他模型中的模量虽然受到被动围压的限制作用,但计算中将其视为恒定值,故这3种模型的计算模量变化幅度相对较小。此外,4个模型中CCP模型的计算模量最大,其通常被用作路面设计中碎石粒料模量取值的代表参数,而实际路面结构中的围压限制是有限的,VCP模型更接近实际状况[25-26],故而采用CCP模型可能过高估计了碎石粒料的弹性模量。
| 加载模式 | 粒料类别/ mm | 重复CBR | 重复三轴 | |||
| 完全摩擦 | 无摩擦 | CCP | VCP | |||
| MSLM | 9.5 | 0.980 | 0.979 | 0.995 | 0.914 | |
| 13.2 | 0.956 | 0.952 | 0.998 | 0.893 | ||
| 16 | 0.939 | 0.934 | 0.991 | 0.936 | ||
| SSLM | 9.5 | 0.962 | 0.961 | 0.970 | 0.895 | |
| 13.2 | 0.956 | 0.953 | 0.970 | 0.921 | ||
| 16 | 0.914 | 0.905 | 0.954 | 0.965 | ||
| MSLM | 4.75 & 13.2 | 0.986 | 0.985 | 0.989 | 0.967 | |
| 9.5&16 | 0.895 | 0.89 | 0.944 | 0.933 | ||
| 4.75&9.5&19 | 0.949 | 0.944 | 0.971 | 0.907 | ||
| SSLM | 4.75&13.2 | 0.998 | 0.998 | 0.999 | 0.929 | |
| 9.5&16 | 0.882 | 0.876 | 0.916 | 0.843 | ||
| 4.75&9.5&19 | 0.928 | 0.92 | 0.965 | 0.894 | ||
与文献[12]中的模量相比,本研究的计算模量偏小,主要原因有以下几方面:加载400次的回弹变形与加载100次的回弹变形有较大差异,由图 3和图 4表明了相同荷载强度、不同加载次数时永久变形存在较大差异,可知回弹变形也会存在较大差异,加载100次或200次时粒料结构的塑性变形占据主要成分,此时的弹性变形较小,故而计算的回弹模量相对较大;单粒径碎石粒料和填充碎石粒料与粒料材料的级配组成有所不同,对结果有一定程度影响,试样不含填料, 最大干密度小, 空隙较多, 结构承载能力低;另外,试验条件也有所不同,PUMA的围压边界条件与重复CBR和重复三轴试验的围压不同。然而,单粒径碎石和填充碎石粒料是组成粒料材料的基础,该结果用作分析单粒径和填充材料对粒料材料整体结构的影响,为进一步探究粒料材料性能研究提供参考。
3 结论基于SSLM和MSLM加载模式,通过PUMA对单粒径碎石和填充碎石粒料进行重复荷载试验,分析和讨论了加载初始阶段的永久变形和弹性模量,可得以下结论:
(1) 在MSLM加载模式下,单粒径碎石的永久变形随荷载强度增加而呈双峰曲线变化,荷载强度小于340 kPa时,永久变形快速增长;随后,永久变形的增速降低,表明永久变形累计到一定程度后,荷载强度对永久变形的影响程度降低。填充碎石粒料在荷载强度200 kPa以下时永久变形就可能达到最大值,填充碎石粒料更易达到密实状态;集料粒径越大,永久变形增量越趋向于单峰变化。
(2) 在SSLM加载模式下,初始阶段永久变形占整个加载过程永久变形的主要部分,且轴向荷载强度越高,初始阶段永久变形所占比例越大;在荷载强度小于240 kPa时,单粒径碎石和填充碎石粒料的永久变形差别不大,当超过240 kPa后,单粒径碎石粒料的永久变形快速增长。
(3) 对比两种加载模式下的永久变形,轴向荷载强度相同时,SSLM加载模式的永久变形均大于和MSLM加载模式,填充碎石粒料在两种加载模式下的永久变形差异更明显。表明MSLM加载模式可以减少碎石粒料的颗粒破碎、增加密实度、改善结构稳定性、提高结构层的承载能力,填充碎石粒料更适用于MSLM模式的压实,为揭示粒料材料3阶段压实过程的原因和重要性提供依据。
(4) 通过4种模型计算碎石粒料的弹性模量,完全摩擦模型可以更好地描述等效模量,PUMA试验的等效模量小于文献中的重复CBR试验结果,但它们呈现相同的变化趋势和规律;CCP模型计算的模量是4种模型中的最大值,因未考虑围压的影响,可能过高估计了碎石粒料的模量代表值。
| [1] |
高启聚, 姚祖康. 粒料基层设计指标和控制模型研究[J]. 公路交通科技, 2016, 33(5): 39-45. GAO Qi-ju, YAO Zu-kang. Study on Design Index and Model for Controlling Permanent Deformation of Granular Base Course[J]. Journal of Highway and Transportation Research and Development, 2016, 33(5): 39-45. |
| [2] |
李绍辉, 郭忠印. 级配碎石本构模型弹性变形适用性及验证[J]. 同济大学学报:自然科学版, 2016, 44(8): 1227-1233. LI Shao-hui, GUO Zhong-yin. Applicability and Verification of Unbound Granular Material Elastic Deformation Constitutive Model[J]. Journal of Tongji University:Natural Science Edition, 2016, 44(8): 1227-1233. |
| [3] |
ERLINGSSON S, RAHMAN M S. Evaluation of Permanent Deformation Characteristics of Unbound Granular Materials by Means of Multistage Repeated-load Triaxial Tests[J]. Transport Research Record, 2013, 2369: 11-19. |
| [4] |
RAHMAN M S, ERLINGSSON S. Predicting Permanent Deformation Behaviour of Unbound Granular Materials[J]. International Journal of Pavement Engineering, 2015, 16(7): 587-601. |
| [5] |
王龙, 孟书涛, 徐全亮. 级配碎石基层的设计参数研究[J]. 公路交通科技, 2006, 23(8): 22-27. WANG Long, MENG Shu-tao, XU Quan-liang. Study on the Design Parameter of Graded Macadam Base[J]. Journal of Highway and Transportation Research and Development, 2006, 23(8): 22-27. |
| [6] |
LEKARP F, ISACSSON U, DAWSON A. State of the Art. Ⅱ:Permanent Strain Response of Unbound Aggregates[J]. Journal of Transportation Engineering, 2000, 126(1): 76-83. |
| [7] |
HUANG Y H. Pavement Analysis and Design[M]. 2nd ed. Upper Saddle River, USA: Pearson Education, 2004.
|
| [8] |
CERNI G, CARDONE F, VIRGILI A, et al. Characterisation of Permanent Deformation Behaviour of Unbound Granular Materials under Repeated Triaxial Loading[J]. Construction and Building Materials, 2012, 28(1): 79-87. |
| [9] |
HORNYCH P, ABSAMAD A E. Selection and Evaluation of Models for Prediction of Permanent Deformations of Unbound Granular Materials in Road Pavements[R]. Paris: Competitive and Sustainable Growth Programme, 2004.
|
| [10] |
金刚.级配碎石三轴试验研究[D].大连: 大连理工大学, 2007. JIN Gang. Laboratory Study of Triaxial Test on Graded Broken Stone[D]. Dalian: Dalian University of Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10141-2007210266.htm |
| [11] |
陈庆村, 王龙, 王德印. 石灰粉煤灰微粘结级配碎石路用性能研究[J]. 公路交通科技, 2009, 26(11): 31-35. CHEN Qing-cun, WANG Long, WANG De-yin. Study on Pavement Performance of Lime-flyash Micro-bonded Graded Aggregates[J]. Journal of Highway and Transportation Research and Development, 2009, 26(11): 31-35. |
| [12] |
ARAYA A, MOLENAAR A, HOUBEN L. Characterization of Unbound Granular Materials Using Repeated Load CBR and Triaxial Testing[J]. GeoShanghai 2010 International Conference.[S. l.]:American Society of Civil Engineers, 2010, 355-363. |
| [13] |
MOHAJERANI A, BAO T N, GLAVACEVIC L. Estimation of Resilient Modulus of Unbound Granular Materials Using Clegg Impact Value and Field Stress Levels[J]. Transportation Geotechnics, 2016(7): 115-129. |
| [14] |
刘星.级配碎石的级配与模量研究[D].西安: 长安大学, 2007. LIU Xing. Research on Grading Method and Resilient Modulus of Unbound Aggregate Base[D]. Xi'an: Chang'an University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-11941-2009257110.htm |
| [15] |
XIAO Yuan-jie, TUTUMLUER E. Performance Checks for Unbound Aggregate Base Permanent Deformation Prediction Models under Dynamic Stress States Induced by Moving Wheel Loading[J]. Procedia Engineering, 2016, 143: 979-990. |
| [16] |
THOM N H, COOPER A, GRAFTON P, et al. A New Test for Base Material Characterisation[C]//Proceedings of the International Symposium on Heavy Duty Asphalt Pavements and Bridge Deck Pavements.[S. l.]: International Society for Asphalt Pavements, 2012: 12-097.
|
| [17] |
田尔布, 马骉, 路学敏, 等. 嵌锁密实型水泥混凝土粗集料级配振动分析[J]. 混凝土, 2008(3): 77-79. TIAN Er-bu, MA Biao, LU Xue-min, et al. Vibration Analysis on Coarse Aggregate Gradation of Interlocking-dense Cement Concrete[J]. Concrete, 2008(3): 77-79. |
| [18] |
马骉, 田尔布, 路学敏, 等. 水泥混凝土粗集料嵌锁密实结构试验分析[J]. 中外公路, 2008, 28(6): 217-220. MA Biao, TIAN Er-bu, LU Xue-min, et al. Experimental Analysis on Coarse Aggregate Interlocking-dense Structure of Cement Concrete[J]. Journal of China & Foreign Highway, 2008, 28(6): 217-220. |
| [19] |
JTG E42-2005, 公路工程集料试验规程[S]. JTG E42-2005, Test Methods of Aggregate for Highway Engineering[S]. |
| [20] |
EN 13286-7. Unbound and Hydraulically Bound Mixtures-Part 7: Cyclic Load Triaxial Test for Unbound Mixtures[S].
|
| [21] |
WERKMEISTER S, DAWSON A R, WELLNER F. Permanent Deformation Behaviour of Granular Materials[J]. Road Materials and Pavement Design, 2005, 6(1): 31-51. |
| [22] |
EL-BASYOUNY M M, WITCZAK M, KALOUSH K. Development of the Permanent Deformation Models for the 2002 Design Guide[C]//The Annual Meeting of the Transportation Research Board. Washington, D.C.: TRB, 2005.
|
| [23] |
黄宝涛, 张敏思, 雍军. 振动压实下不规则颗粒细观响应的离散元模拟[J]. 公路交通科技, 2009, 26(7): 7-12. HUANG Bao-tao, ZHANG Min-si, YONG Jun. Numerical Simulation of Irregular Particle Micro-response under Vibrating Compressive Load by DEM[J]. Journal of Highway and Transportation Research and Development, 2009, 26(7): 7-12. |
| [24] |
OPIYO T O. A Mechanistic Approach to Laterite-based Pavements[D]. Delft, Netherlands: International Institute for Infrastructure, 1995.
|
| [25] |
SIMONSEN E, ISACSSON U. Soil Behavior during Freezing and Thawing Using Variable and Constant Confining Pressure Triaxial Tests[J]. Canadian Geotechnical Journal, 2001, 38(4): 863-875. |
| [26] |
RONDON H A, WICHTMANN T, TRIANTAFYLLIDIS T, et al. Comparison of Cyclic Triaxial Behavior of Unbound Granular Material under Constant and Variable Confining Pressure[J]. Journal of Transportation Engineering, 2009, 135(7): 467-478. |
 2019, Vol. 36
2019, Vol. 36
