扩展功能
文章信息
- 程耀飞, 蒋勇, 孙大权, 孙国强
- CHENG Yao-fei, JIANG Yong, SUN Da-quan, SUN Guo-qiang
- 不同类型沥青胶浆自愈合行为方程
- Self-healing Behavior Equation of Different Types of Asphalt Mastic
- 公路交通科技, 2019, 36(3): 42-48
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 42-48
- 10.3969/j.issn.1002-0268.2019.03.007
-
文章历史
- 收稿日期: 2017-10-26
2. 同济大学道路与交通工程教育部重点实验室, 上海 201804
2. Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China
早在1967年,Bazin和Saunierd[1]就通过试验证实了沥青混凝土具有自愈合行为,并被证明对提高沥青路面的抗疲劳能力具有重要作用。随后,在认知沥青自愈合行为宏观表象与微观形成过程的基础上,研究学者针对沥青材料自愈机理、自愈表征和增强技术等做了大量研究[2-5],而得到明确有效的自愈合行为方程是愈合研究中的最终落脚点。
Lytto和Little等[6-8]基于裂缝表面能理论认为愈合动力为裂缝自由能的降低,并从断裂力学的角度建立了沥青混凝土自愈合行为方程,该理论模型可预测沥青混凝土的愈合速率,但无法揭示裂缝愈合过程,且试验参数繁多,难以标定。Kringos等[9]提出了相场愈合模型,以沥青为多相结构(基质相和蜂状微结构),解释了随着温度的变化而产生的愈合过程。Wool和Shen等[10-11]从分子扩散的角度解释了沥青的自愈合过程,并将其归结为裂缝界面的润湿及分子的扩散纠缠,但该理论难以考虑黏附强度的动态增长过程,且润湿速率方程参数难以通过试验准确测得,现有研究中鲜有得到沥青宏观愈合方程。Álvaro García[11-13]在分子扩散理论的基础上结合毛细力学理论分析了沥青愈合过程,但该模型要求沥青牛顿流体状态,因而低温下的沥青愈合不再适用。
本研究在前人研究基础上,基于扩散理论,将自愈合分为润湿愈合和扩散黏聚愈合两部分,建立了考虑温度影响的沥青胶浆自愈合行为方程,定量描述了沥青胶浆愈合强度随愈合时间变化的过程,对量化沥青材料的自愈合过程具有重要价值。此外,通过在不同温度条件下对各种沥青胶浆进行疲劳愈合试验,并结合对愈合行为方程参数的分析,验证了该理论方程对沥青材料的适用性和可靠性。
1 基于扩散理论的愈合行为方程沥青疲劳裂缝主要为细长的微观裂缝,长径比很大,因此可将每条裂缝看作是曲折的毛细管,而沥青的润湿过程则是沥青的毛细作用引起。润湿后的裂缝由于沥青分子的扩散与随机化形成扩散愈合强度。从而,可将沥青愈合过程分为由毛细力引起的润湿愈合过程和分子扩散形成的扩散愈合过程,进而建立基于扩散理论的自愈合行为方程。
(1) 润湿愈合
根据Washburn毛细模型[14],假设裂缝的半径为r,对于任意长度及形状的裂缝,通过毛细管某一截面的液体体积为:
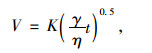
|
(1) |
式中,K为独立于液体材料性能的参数;γ为液体的表面张力;η为液体的黏度;t为愈合时间。
沥青在毛细作用驱动下润湿裂缝界面获得强度,从而润湿愈合强度指数为:
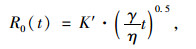
|
(2) |
式中符号同式(1)。
(2) 扩散黏聚愈合
沥青在裂缝界面润湿后,由于分子间的扩散,分子链的纠缠、随机化过程,逐渐形成愈合强度[7]。Wool和O'Conner[7]研究得到聚合物的静态愈合行为方程:
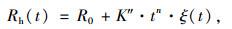
|
(3) |
式中,ξ(t)为聚合物界面分子重排列的影响;R0为聚合物的润湿愈合;K″为扩散快慢,与温度有关;t为愈合时间;n的大小与扩散分子大小有关,取值为0.25~0.5。沥青分子重排列的影响小[15],式(3)可简化为:
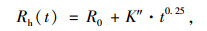
|
(4) |
从而根据式(4)中的静态愈合函数,沥青的扩散愈合强度指数可表示为:
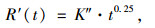
|
(5) |
式中符号同式(3)。
(3) 宏观愈合方程
宏观愈合过程分为润湿和分子扩散两个主要步骤。假设裂缝润湿的时间为τ,则分子扩散时间为(t-τ),综合式(2)、式(5)可得到沥青的宏观愈合方程:
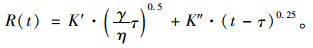
|
(6) |
由式(6)可看出自愈合的两部分都与时间有关,由于自愈合润湿和扩散过程的时间起点不同,沥青裂缝产生后即存在润湿,而扩散需润湿过程完成后才经过分子扩散。与分子的随机化时间相比,润湿过程很短,可看作瞬间强度,这一过程往往在裂缝产生瞬间就已经完成。因此,愈合时间(间歇时间)的起点可作为分子扩散的时间起点,从而润湿愈合可简化成常数项,而且沥青的自愈合还与温度相关,因而,考虑温度和愈合时间影响的行为方程为:
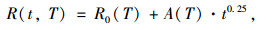
|
(7) |
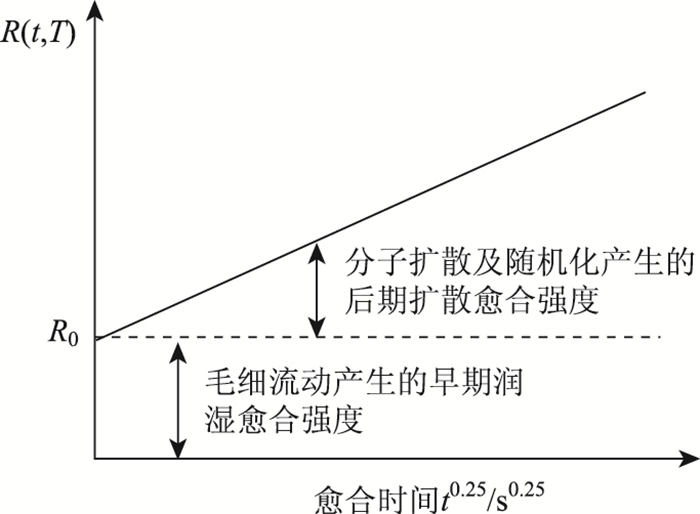
式中,R(t, T)为宏观愈合强度指数;R0(T)为润湿愈合强度指数;t为愈合时间;A(T)为温度T条件下R(t, T)随t0.25的比变化斜率。早期愈合随着裂缝的毛细流动主要形成润湿愈合强度,后期随着沥青分子扩散及随机化主要形成扩散愈合强度,图 1为愈合强度与愈合时间的关系示意图。
|
| 图 1 沥青愈合强度形成过程 Fig. 1 Formation process of asphalt healing strength |
| |
2 原材料与试验方法 2.1 原材料
本研究所用材料包括某沥青(泰州)有限责任公司提供的70#道路石油沥青,新疆克拉玛依乌尔禾区提供的黑色块状岩沥青(粉碎后作为沥青改进剂),北京某石化公司提供星型SBS(4303)聚合物,荷兰某公司提供的表面活性剂(下面简称WMX)。此外,沥青胶浆的填料主要有石灰石矿粉、水泥、消石灰。各改性沥青基本技术性质如表 1所示。
| 样品 类型 |
材料组成 | 软化点/ ℃ |
25 ℃针入度/ (0.1 mm) |
延度 (5 ℃)/cm |
| NA | 70#沥青 | 47.9 | 69.8 | >100 |
| RA | NA+8%岩沥青 | 60.2 | 42.5 | 26.8 |
| SBS | NA+5%SBS改性沥青 | 94 | 50.8 | 31 |
| WMX | NA+0.7%WMX | 44.9 | 56.1 | 6.2 |
| SK | SK高黏沥青 | 86.5 | 45.3 | 32.9 |
2.2 试验方法
为模拟沥青胶浆在混合料中的状态,采用短期老化后的沥青与填料以一定比例混合。按《公路工程沥青及沥青混合料试验规程》(JTG E20—2011)要求,对沥青进行TFOT短期老化,再将填料在175 ℃条件下保温4~5 h,最后将填料按一定的用量加入到流动状态下的沥青中,用剪切机在175 ℃条件下剪切45 min。
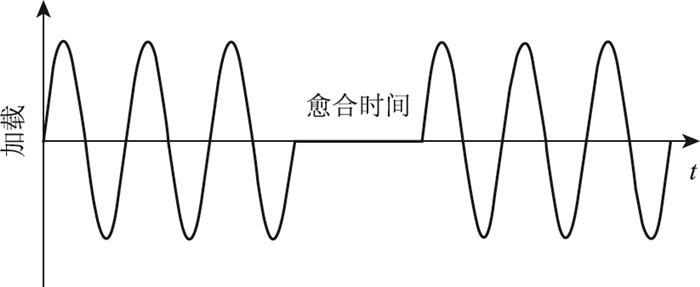
考虑间断交通流对于沥青路面的荷载特点,如图 2所示,经过一段时间的连续交通流荷载后,路面有一段较长时间的间歇。采用间断型疲劳自愈合加载模式研究沥青胶浆的长期自愈合性能,使用动态剪切流变仪(DSR,AR1500EX,美国TA仪器公司生产),以应力控制模式对沥青胶浆进行重复剪切,采用8 mm平行板,沥青厚度2 mm,加载频率10 Hz。
|
| 图 2 间歇型疲劳自愈合加载波 Fig. 2 Intermittent loading wave of fatigue self-healing |
| |
3 试验结果分析 3.1 自愈合评价指标
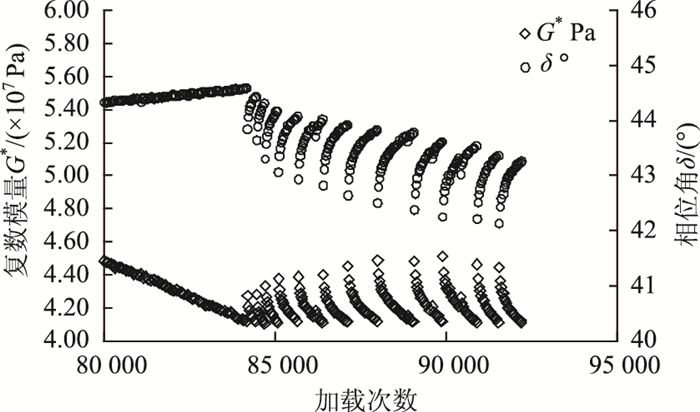
沥青胶浆自愈合过程可视为疲劳开裂的逆过程。在重复剪切疲劳过程中,随着加载次数的增加,沥青胶浆的复数模量降低、相位角增大,引入间歇期后,材料的复数模量和相位角表现为反方向的恢复,具体变化如图 3所示。
|
| 图 3 沥青胶浆在自愈合过程中复数模量与相位角的变化 Fig. 3 Changes of complex modulus and phase angle in asphalt mastic self-healing process |
| |
从图 3可以看出,随着自愈合时间的增加,沥青胶浆的复数模量不断恢复增大,而相位角则不断降低,从表象上看自愈合过程与疲劳过程相反,此结果与已有研究一致[16-18]。因此,现有研究常将复数模量的恢复作为评价宏观自愈合能力的指标,但不同研究者的表征形式各异,Little[7]和单丽岩[19]分别采用式(8)、式(9)评价沥青的自愈合。
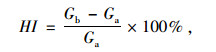
|
(8) |
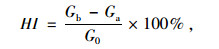
|
(9) |
式中,Ga, Gb分别为愈合前后沥青胶浆的复数模量;G0为沥青胶浆的初始复数模量。
根据沥青材料疲劳过程中的复数模量变化,基于模量衰减率的损伤度为:
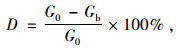
|
(10) |
式中各符号意义同式(8)、式(9)。分析式(8)可发现,损伤程度越小的情况下,间歇前的复数模量越大,而自愈合的模量(式(8)分子部分)增长幅度较小,得到的愈合指数越小,这样得到的结论为损伤度越小愈合性能越小,与实际情况不符合,而式(9)也存在同样的问题,均难以合理考虑损伤度的影响。因此,提出损伤恢复程度作为宏观愈合强度指数,即自愈合恢复的损伤程度占疲劳损伤程度的比例,如式(11),简称损伤恢复度。
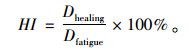
|
(11) |
当以复数模量的衰减量表征沥青胶浆疲劳损伤程度时,式(11)可以变换为:
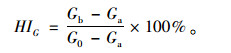
|
(12) |
基于扩散理论的愈合行为方程,将自愈合分为润湿愈合与扩散愈合两部分,宏观愈合强度指数与愈合时间t0.25成线性关系。为了验证这一理论对不同材料类型与条件(温度、损伤度)下沥青胶浆的适用性,采用DSR设备进行疲劳自愈合试验,经测试分析得到不同损伤度、填料类型、粉胶比(F/B)、沥青类型的胶浆在不同愈合时间下的宏观愈合值HIG,结果见表 2,并拟合得到HIG与t0.25的自愈合行为方程,结果见表 3。
| 材料类型 | 温度/℃ | 愈合时间/s | ||||||||
| 30 | 60 | 300 | 600 | 900 | 1 200 | 1 800 | 2 700 | 3 600 | ||
| NA+Lime D=0.3, F/B=0.8 |
15 | 0.089 | 0.093 | 0.131 | 0.148 | 0.153 | 0.165 | 0.189 | 0.209 | 0.209 |
| 20 | 0.14 | 0.15 | 0.194 | 0.207 | 0.233 | 0.215 | 0.242 | 0.262 | 0.276 | |
| 17 | 0.246 | 0.247 | 0.314 | 0.331 | 0.325 | 0.334 | 0.350 | 0.356 | 0.372 | |
| 23 | 0.248 | 0.254 | 0.274 | 0.298 | 0.290 | 0.293 | 0.299 | 0.310 | 0.322 | |
| NA+Lime D=0.3, F/B=1.0 |
15 | 0.026 | 0.094 | 0.089 | 0.131 | 0.161 | 0.188 | 0.195 | 0.204 | 0.223 |
| 23 | 0.235 | 0.253 | 0.286 | 0.310 | 0.314 | 0.319 | 0.340 | 0.351 | 0.354 | |
| NA+Lime D=0.15, F/B=1.0 |
15 | 0.194 | 0.182 | 0.248 | 0.278 | 0.315 | 0.307 | 0.352 | 0.381 | 0.373 |
| NA+Lime D=0.45, F/B=1.0 |
15 | 0.056 | 0.059 | 0.082 | 0.089 | 0.097 | 0.100 | 0.109 | 0.116 | 0.126 |
| NA+Lime D=0.3, F/B=1.2 |
23 | 0.217 | 0.234 | 0.316 | 0.332 | 0.342 | 0.346 | 0.348 | 0.371 | 0.379 |
| NA+Slaked lime D=0.3, F/B=1.0 |
23 | 0.143 | 0.160 | 0.221 | 0.257 | 0.253 | 0.272 | 0.300 | 0.296 | 0.293 |
| NA+Cement D=0.3, F/B=1.0 |
23 | 0.092 | 0.135 | 0.166 | 0.193 | 0.240 | 0.239 | 0.270 | 0.309 | 0.291 |
| SBS+Lime D =0.3, F/B=1.0 |
20 | 0.193 | 0.257 | 0.380 | 0.463 | 0.521 | 0.557 | 0.600 | 0.651 | 0.680 |
| RA+Lime D=0.3, F/B=1.0 |
20 | 0.166 | 0.193 | 0.314 | 0.379 | 0.422 | 0.447 | 0.479 | 0.500 | 0.519 |
| WMX+Lime D=0.3, F/B=1.0 |
20 | 0.101 | 0.154 | 0.191 | 0.204 | 0.232 | 0.233 | 0.252 | 0.268 | 0.276 |
| SK+Lime D=0.3, F/B=1.0 |
20 | 0.228 | 0.309 | 0.460 | 0.522 | 0.565 | 0.584 | 0.531 | 0.450 | 0.414 |
| 沥青类型 | 填料类型 | 粉胶比F/B | 温度/℃ | 损伤度/% | 方程 | R2 |
| NA | Lime | 1.0 | 15 | 15 | y=0.036 2x+0.093 2 | 0.975 4 |
| NA | Lime | 1.0 | 15 | 30 | y=0.023 5x+0.030 8 | 0.989 9 |
| NA | Lime | 1.0 | 15 | 45 | y=0.012 7x+0.026 0 | 0.987 1 |
| NA | Lime | 0.8 | 15 | 30 | y=0.023 3x+0.031 4 | 0.986 5 |
| NA | Lime | 0.8 | 17 | 30 | y=0.024 3x+0.085 8 | 0.949 6 |
| NA | Lime | 0.8 | 20 | 30 | y=0.026 1x+0.187 2 | 0.922 0 |
| NA | Lime | 1.0 | 23 | 30 | y=0.021 1x+0.196 2 | 0.980 3 |
| NA | Slaked lime | 1.0 | 23 | 30 | y=0.036 8x+0.060 6 | 0.980 4 |
| NA | Cement | 1.0 | 23 | 30 | y=0.037 2x+0.019 4 | 0.964 4 |
| NA | Lime | 0.8 | 23 | 30 | y =0.023 1x+0.198 4 | 0.931 0 |
| NA | Lime | 1.2 | 23 | 30 | y=0.026 1x+0.181 2 | 0.908 6 |
| 5%SBS+NA | Lime | 1.0 | 20 | 30 | y=0.084 5x+0.029 7 | 0.982 6 |
| 8%RA+NA | Lime | 1.0 | 20 | 30 | y=0.063 2x+0.043 8 | 0.951 7 |
| 0.7%WMX+NA | Lime | 1.0 | 20 | 30 | y=0.019 8x+0.145 9 | 0.971 7 |
| SK | Lime | 1.0 | 20 | 30 | y=0.099 3x+0.021 1 | 0.980 7 |
从表 3可看出,在不同温度条件下,不同损伤度、填料类型、粉胶比、沥青类型胶浆的宏观愈合强度指数与愈合时间t0.25均具有很好的相关性,相关系数(R2)均在0.9以上,最高达到了0.989 9,从而验证了提出的毛细扩散理论对沥青胶浆自愈合的适用性。
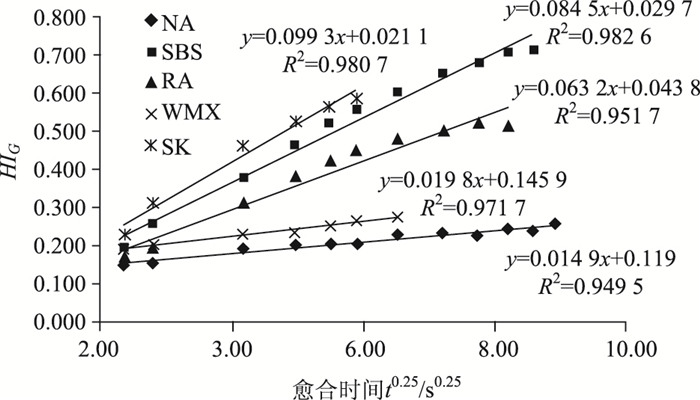
3.3 自愈合方程参数分析根据毛细扩散愈合机理,不同沥青由于分子的差异,其润湿、扩散过程有所不同。不同沥青类型胶浆的愈合曲线如图 4所示,沥青胶浆的自愈合曲线在愈合时间内存在交点,说明同一影响因素,对沥青胶浆的润湿愈合、扩散愈合的影响趋势不同。根据式(7)将愈合曲线与纵坐标的截距作为早期润湿愈合强度指数HI0。扩散愈合主要与分子的扩散和随机化过程有关,其愈合强度随着时间的增长而提高,故可根据愈合曲线的斜率来评价不同沥青胶浆的扩散愈合速率。
|
| 图 4 不同沥青类型胶浆自愈合曲线(D=0.3, 20 ℃) Fig. 4 Self-healing curves of different types of asphalt (D=0.3, 20 ℃) |
| |
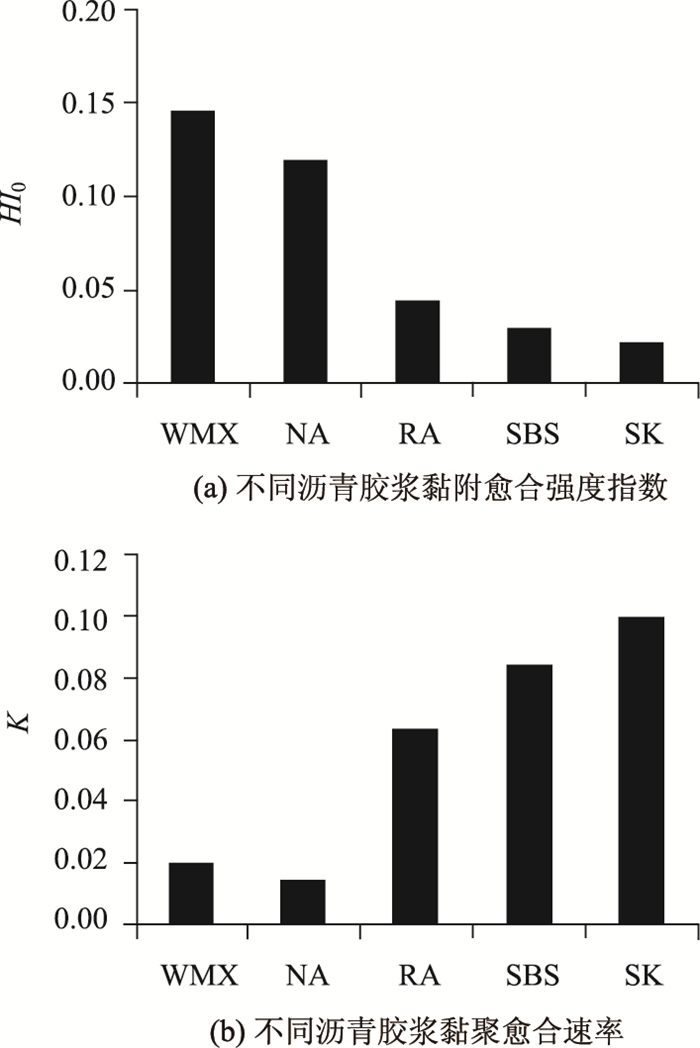
从而可分别确定不同沥青胶浆润湿愈合强度指数与扩散愈合速率大小,如图 5所示,发现不同沥青胶浆的润湿愈合及扩散愈合变化趋势相反。
|
| 图 5 不同沥青胶浆粘附愈合强度指数与黏聚愈合速率 Fig. 5 Adhesion healing strength indexes and cohesion healing rates of different asphalt mastics |
| |
(1) 由图 5(a)可知聚合物及天然岩沥青的润湿黏附愈合HI0小于基质沥青,而加入表面活性剂的温拌沥青的润湿黏附愈合HI0大于基质沥青。润湿是液体沿固体表面扩散的现象,裂缝愈合过程中可将润湿表征为黏度为η的沥青沿着半径为R、长度为l的毛细管扩散,用Poliseuille黏度方程和毛细管上升方程,计算沥青润湿长度l所需要时间:
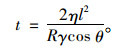
|
(13) |
式(13)表明,沥青的润湿速度主要取决于沥青的黏度和接触角。聚合物及天然岩沥青的加入,提高了沥青的黏度,故润湿速度慢,润湿愈合值小。表面活性剂加入沥青中,不但可以降低沥青的黏度,还能提高沥青的极性,从而有效降低了沥青表面张力,提高润湿速率[20],润湿愈合值大。
(2) 由图 5(b)可知聚合物及天然岩沥青的扩散愈合速率大于基质沥青,而加入表面活性剂的温拌沥青愈合速率稍大于基质沥青。扩散愈合强度的形成与裂缝宽度、分子间作用力及分子扩散速率(或扩散分子数量)有关,聚合物分子间的作用力主要由单体分子间的作用力构成,分子量越高,作用力越大,强度越高[21],从而聚合物和天然岩沥青的愈合速率高于基质沥青。且在相同损伤度条件下,改性沥青颗粒具备更高的强度,可起到阻止裂纹扩散的作用,疲劳损伤以细小裂纹为主,裂缝界面相对于基质沥青更大,因此参与扩散的分子更多,反应速率越快。而在沥青中加入表面活性剂后,不仅可加快分子扩散速率,还能增强分子间作用力,但增强能力有限,效果并不明显。
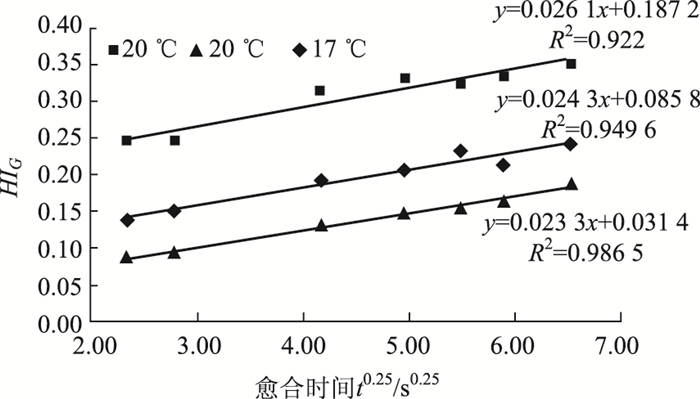
另外,沥青是黏弹性材料,因而胶浆自愈合能力与温度密切相关,不同温度下,粉胶比为0.8,损伤度为0.3的沥青胶浆宏观愈合指数HIG与愈合时间t0.25的关系曲线如图 6所示,根据愈合曲线的截距与斜率大小可知,温度越高,沥青的润湿愈合指数越高、扩散愈合速率也越高,其他沥青胶浆亦存在类似规律。这是由于温度越高,沥青的毛细流动作用越强,从而润湿愈合越强。而且,根据热力学原理,温度越高,分子内能越高,分子扩散速率越大,从而沥青胶扩散愈合速率越大[15]。
|
| 图 6 不同温度下的沥青胶浆自愈合曲线(D=0.3, F/B=0.8) Fig. 6 Self-healing curves of asphalt at different temperatures (D=0.3, F/B=0.8) |
| |
综上分析,愈合方程曲线的截距和斜率分别表征沥青胶浆的润湿愈合强度与扩散愈合速率,截距值越大,表明沥青胶浆润湿愈合能力越强,斜率越大,表明沥青胶浆的扩散愈合速率越大。
4 结论(1) 基于扩散理论提出了不同类型沥青胶浆的宏观愈合行为方程,将沥青胶浆的愈合过程分为润湿愈合和扩散愈合两部分。由于润湿时间很短,沥青的润湿愈合强度在裂缝开裂后的瞬间得以完成,进入间歇期后主要进行扩散愈合,且扩散愈合强度与愈合时间t0.25成线性关系。
(2) 在不同温度条件下对不同损伤度、填料类型、粉胶比、沥青类型的沥青胶浆进行疲劳自愈合试验,拟合得到自愈合行为方程,发现损伤恢复度HIG与愈合时间t0.25具有较强的线性相关性(R2大于0.9)。
(3) 通过对不同沥青类型与温度条件下的胶浆疲劳愈合试验结果进行分析,发现可用愈合方程曲线的截距和斜率分别表征沥青的润湿愈合强度与扩散愈合速率,进一步验证了提出的理论方程的可靠性。
| [1] |
BAZIN P, SAUNIER J B. Deformability, Fatigue and Healing Properties of Asphalt Mixes[C]//International Conference on the Structural Design of Asphalt Pavements. Ann Arbor, US: International Society for Asphalt Pavements, 1967: 553-569.
|
| [2] |
KIM Y R, LITTLE D N, LYTTON R L. Evaluation of Micro-damage, Healing, and Heat Dissipation of Asphalt Mixtures, Using a Dynamic Mechanical Analyzer[J]. Transportation Research Record, 2001, 176: 60-66. |
| [3] |
HOU Y, WANG L B, PAULI T, et al. Investigation of the Asphalt Self-healing Mechanism Using a Phase-field Model[J]. Journal of Materials in Civil Engineering, 2015, 27(3): 04014118. |
| [4] |
SUN D Q, HU J L, ZHU X Y. Size Optimization and Self-healing Evaluation of Microcapsules in Asphalt Binder[J]. Colloid and Polymer Science, 2015, 293(12): 3505-3516. |
| [5] |
徐辰.沥青自愈合特性及影响因素研究[D].重庆: 重庆交通大学, 2013. XU Chen. Study on Characteristics of Asphalt Self-healing and Its Influencing Factors[D]. Chongqing: Chongqing Jiaotong University, 2013. |
| [6] |
ROBERTSON R E, BRANTHAVER J F, HARNSBE-RGER P M, et al. Fundamental Properties of Asphalts and Modified Asphalts, Vol Ⅱ: Final Report, New Methods, FHWA-RD-99-213[R]. McLean, US: Turner-Fairbank Highway Research Center, 2001.
|
| [7] |
LITTLE D N, LYTTON R, WILLIAMS D, et al. An Analysis of the Mechanism of Micro-damage Healing Based on the Application of Micromechanics First Principles of Fracture and Healing[J]. Journal of the Association of Asphalt Paving Technologists, 1999, 68: 501-542. |
| [8] |
SCHAPERY R A. On the Mechanics of Crack Closing and Bonding in Linear Viscoelastic Media[J]. International Journal of Fracture, 1989, 39(1-3): 163-189. |
| [9] |
KRINGOS N, PAULI T, ROBERT R, et al. A Thermodynamic Approach to Healing in Bitumen[C]//7th RILEM Conference on Advanced Testing and Characterization of Bituminous Materials. London: Taylor and Francis Group, 2009: 123-132.
|
| [10] |
WOOL R P, O'CONNOR K M. A Theory Crack Healing in Polymers[J]. Journal of Applied Physics, 1981, 52(10): 5953-5963. |
| [11] |
SHEN S H, SUTHARSAN T. Quantification of Cohesive Healing of Asphalt Binder and Its Impact Factors Based on Dissipated Energy Analysis[J]. Road Materials and Pavement Design, 2011, 12(3): 525-546. |
| [12] |
GARCÍA Á. Self-healing of Open Cracks in Asphalt Mastic[J]. Fuel, 2012, 93(1): 264-272. |
| [13] |
孙大权, 张立文, 梁果. 沥青混凝土疲劳损伤自愈合行为研究进展(1):自愈合行为机理与表征方法[J]. 石油沥青, 2011, 25(5): 7-11. SUN Da-quan, ZHANG Li-wen, LIANG Guo. Review on Self-healing Behavior of Asphalt Concrete(1) Mechanism and Characterization Methods of Self-healing Behavior[J]. Petroleum Asphalt, 2011, 25(5): 7-11. |
| [14] |
WASHBURN E W. The Dynamics of Capillary Flow[J]. Physical Review, 1921, 17(3): 273-283. |
| [15] |
SUN D Q, LIN T B, ZHU X Y, et al. Calculation and Evaluation of Activation Energy as a Self-healing Indication of Asphalt Mastic[J]. Construction & Building Materials, 2015, 95: 431-436. |
| [16] |
QIU J, WU S P, YU J Y, et al. Investigating Self Healing Behaviour of Pure Bitumen Using Dynamic Shear Rheometer[J]. Fuel, 2011, 90(8): 2710-2720. |
| [17] |
姜睆.沥青胶浆自愈合能力研究[D].武汉: 武汉理工大学, 2011. JIANG Huan. Research on Seal-healing Capacity of Bitumen Mastics[D]. Wuhan: Wuhan University of Technology, 2011. |
| [18] |
崔亚楠, 赵琳, 孙广宁. 两种沥青胶浆的疲劳及自愈合性能试验[J]. 复合材料学报, 2018, 35(3): 699-705. CUI Ya-nan, ZHAO Lin, SUN Guang-ning. Experimental Study on Fatigue and Self-healing Performance of Two Kinds of Asphalt Mortar[J]. Acta Materiae Compositae Sinica, 2018, 35(3): 699-705. |
| [19] |
单丽岩.基于粘弹特性的沥青疲劳流变机理研究[D].哈尔滨: 哈尔滨工业大学, 2010. SHAN Li-yan. Study on Asphalt Fatigue Rheological Mechanism Based on Viscoelastic Properties[D]. Harbin: Harbin Institute of Technology, 2010. |
| [20] |
肖庆一.沥青混合料油石界面研究[D].南京: 东南大学, 2004. XIAO Qing-yi. Study on Asphalt-aggregate Interface of Asphalt Mixture[D]. Nanjing: Southeast University, 2004. |
| [21] |
何曼君, 陈维孝, 董西侠. 高分子物理[M]. 修订版. 上海: 复旦大学出版社, 2000. HE Man-jun, CHEN Wei-xiao, DONG Xi-xia. Polymer Physics[M]. Rev.ed. Shanghai: Fudan University Press, 2000. |
 2019, Vol. 36
2019, Vol. 36
