扩展功能
文章信息
- 关伟, 李先通
- GUAN Wei, LI Xian-tong
- 一种基于K近邻和多元回归的传感器缺失值预测算法
- A KNN and Multiple Regression Based Sensor Missing Value Estimation Algorithm
- 公路交通科技, 2019, 36(3): 14-21
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 14-21
- 10.3969/j.issn.1002-0268.2019.03.003
-
文章历史
- 收稿日期: 2018-06-04
2. 哈尔滨工业大学 交通科学与工程学院, 黑龙江 哈尔滨 150001
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin Heilongjiang 150001, China
目前,传感器作为一种成熟的技术已被广泛应用于公路系统内环境感知与设施监控领域,成为公路监控系统的重要数据来源[1]。虽然传感器分布于公路系统内某特定区域,并且具有一定的计算、存储和通信能力,但其自身固有特点决定其在感知数据过程中不可避免地存在数据缺失问题,如数据采集失败、数据失真、数据无意义等[2],尤其是应用环境发生变化时,如网络拥堵、突发性电磁辐射加剧等问题会使这种数据缺失现象更为严重[3]。
在传感器监控过程中,如果出现了缺失值,将严重影响数据分析算法对当前公路状态的计算。例如,传感器Si用于监测公路平整度,其采集到的数值的取值范围不超出[0.1, 0.5],若某时刻t时,传感器Si采集到的数据值为0.01,那么使用者将无法判断这个数值的出现是由于公路平整度发生了变化,还是传感器失效产生的异常值,抑或是其他原因。
感知数据的缺失问题,是影响传感器进一步深入应用的主要原因,给各种基于传感器的应用带来了困难,更严重的是,当缺失值出现后,传感器所感知数据集的可用性将急剧降低,甚至不再可用。
因此,如何对缺失的感知数据进行有效预测是亟待解决的问题。
针对传感器监测数据中的缺失值问题,已有相关研究工作被发表,如Batista等于2003年提出的最近填充算法(KNN)[4],该算法通过经典的K近邻(K-Nearest Neighbor,KNN)方法解决了缺失值的预测,但该算法在预测缺失值时,重点侧重了空间上数据的相关问题,却未考虑数据的时间相关性。Liu等提出一种基于自适应参数选取的算法LWLA[5],预测的准确度较高,但局限于预测缺失值较少的情况。当某数据集缺失值较多时,该算法准确度有所下降。DMI算法同样关注于此问题[6],在DMI算法中引入了数据集相似度的概念,通过数据集的相似度拟定参数,从而获得较高的预测精度。然而该算法引入了多数据集,是一种通过空间换时间的策略,在数据集规模较大时,对算法的效率影响较大。Pan等研究人员针对无线传感器网络丢失数据估计方法进行了较深人的研究,其提出的算法基于感知数据时空相关性建立缺失值估计模型[7-9],并通过多元回归的方法得出预测结果,但该算法主要应用于无线传感器网络之中,由于无线传感器网络独特的电源与计算能力问题等,导致该算法具有一定的局限性。同样应用于无线传感器网络的算法还包括许可等提出的插值法预测缺失值[10],算法的效率较高。上述给出部分针对传感器缺失值问题的研究成果,然而公路交通领域内传感器缺失值问题的研究成果还比较少,其中包括基于RBF神经网络的传感器缺失值预测算法[11-16]等,但算法对于缺失值的预测过程简单,而且研究者并未对算法的效率给出讨论。
上述算法都提出了传感器缺失值预测算法或模型,且均能在数据缺失时通过预测得出比较真实的结果,即使数据环境的变化并不平稳也能得出相应地预测结果。然而,这些算法或模型仅考虑了空间相关性或者时间相关性。事实上,如果同时从时-空两个角度入手,对传感器的缺失值进行预测,能得到更好的效果。
此外,在非传感器缺失值的预测中,也提出了一些有效的算法。例如刘钊等提出的算法用于预测交通状态并取得了准确的结果[17]。显然,类似算法虽然不能直接应用于传感器缺失值的预测问题,但有一定借鉴作用。
基于上述原因,本研究在充分考虑感知数据的时-空相关性基础上提出一种基于K近邻多元回归方法KMRA的缺失值预测算法,用于公路状态监测过程中传感器缺失值的预测。该方法利用K近邻方法通过产生缺失值传感器相邻传感器数据形成空间相关性分析,同时采用多元回归方法计算该传感器本身所生成的时间序列以完成时间相关性分析,最终通过时、空结合的方式对缺失值进行预测,以此提高算法的预测精度[18]。算法在真实数据集上进行了大量试验,试验结果得出,本研究提出的预测方法分别构建基于时间维度和空间维度状态向量的预测模型,这种将两种方式结合的预测方式具有较高的准确性。
1 传感器的缺失值本研究提出的算法,用于解决数据集出现缺失值时的数据预测,尤其是针对传感器等感知硬件的采集数据。因此,在给出算法及相关理论之前,首先要给出数据集中缺失值的定义。
1.1 问题定义定义缺失值。设某传感器网络中节点ni,由于ni持续采集数据,因此得到的数据是1个时间序列,该序列可通过Si=(< vi1, T1>,…,< vin, Tn>)表达,其中vik是该节点在时刻Tk的监测值。当时刻Tk (其中k∈{1,…,n})时,节点ni的监测值采集失败或该监测值不可用,则称节点ni在时刻Tk产生缺失值[9]。
定义缺失值预测。当传感器节点产生缺失值时,需要对缺失值进行预测,设预测值ṽik且使|ṽik-vik|最小的问题称为缺失值预测问题。
1.2 预备算法当传感器出现监测数据缺失时,最简单的做法是发出指令命令其重新传送数据,但这样的处理办法在采集数据量大、网络通讯能力有限等限制下不能被满足,甚至有些传感器本身没有数据存储能力,并不能重新提供缺失数据。因此,人们往往需要通过数据的相关性,对缺失值进行预测。数据之间的相关性通常表现在两个方面,即时间与空间。时间相关性是指,传感器节点v采集的数据是1个时间序列,而该序列上的数据取值存在一定的相关性。空间相关性则指,在某个空间内的传感器的监测值彼此之间存在某种关联。因此,对于传感器缺失值的预测问题,常常通过空间相关性或时间相关性两个角度进行预测。
1.2.1 空间相关性预测当传感器缺失值存在空间相关性时,可通过K近邻算法预测缺失值。预测算法可通过如下步骤实现。
(1) 确定传感器节点间的相关性
设传感器vi, vj之间存在空间相关性,可通过式(1)计算量化其相关性的值域(即[0, 1]规范)。
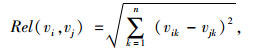
|
(1) |
式中,Rel(vi, vj)为其相关性;vik为节点vi的第k个样本。
由式(1)可知,Rel(vi, vj)的取值越小,vi, vj间相关性越大。然而,这种相关性不仅限于vi与其近邻节点vj之间,同样存在于与vj相临近的其他节点监测值之间,即∀vj, vk ∈ Vneighb(i),vj与vk间同样存在数据的相关性。因此,在这个基于空间的监测值序列中,为了能够准备预测时刻t的缺失值,降低由单个节点进行缺失值估计引发的误差,必须将监测时间序列中1个时间段内的感知数据联合预测,这种联合的方式,可采用非参数回归模型来统一不同时刻监测值对预测结果的影响。因此,引入相关系数的概念。
(2) 确定节点vj与存在缺失值传感器节点v的相关系数
与节点v的相关性不同,则其对v缺失值的预测结果影响也不同。由式(1)选取与v具有高相关度样本数m,并由式(2)分别给出m个节点v1, v2, …, vm的相关系数。
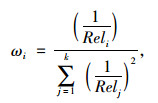
|
(2) |
式中,Reli为与节点vi与v的相关性。在此基础上,形成对节点v的预测值。
(3) 预测v的缺失值
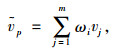
|
(3) |
式中,ωi为式(2)所计算近邻传感器相关系数;ṽp为地点p的预测值。
通过上述计算,利用与节点v空间相关的m个节点的监测值可对v某时刻t的缺失值vt进行预测。
1.2.2 时间相关性预测事实上,数据相关性不仅存在于节点v与其空间上的邻居节点,同样存在于节点v不同时刻的监测数据序列中。不失一般性,设节点v监测数据所形成的序列在时刻t存在缺失值,且满足时刻t在节点v的监测序列中存在至少q/2个邻近时间节点,记为v(t-1), …, v(t-q), v(t+1), …, v(t+q), 记Vt-serial(i) = { v(t-1), …, v(t-q), v(t+1), …, v(t+q)}是邻居集合。因此,对于v在时刻t的缺失值,可通过式(4)计算。
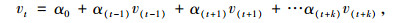
|
(4) |
式中,vt为节点v在时刻t的监测数据,v(t-k), v(t+k), k={1, 2, …, q/2}是节点v在时刻t相邻近时刻的实际监测数据。在式(4)中,称vt为被解释变量,v(t-k), v(t+k), k={1, 2, …, q/2}可2k个解释变量,而式(4)中的系列α值是偏相关系数,它的取值大小反映了该项监测数据对预测值的影响程度。
当时刻t时节点v出现缺失值,监测值可通过式(4)进行预测。在多元回归模型理论中,应用式(4)前,必须选取h(h-q≥2)组已知数据作为样本数据对式(4)中的系列α值进行回归计算,从而得到式(5):
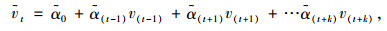
|
(5) |
式中,ṽt为vt的预测值,v(t-k), v(t+k), k={1, 2, …, q/2}是节点v与时刻t邻近时刻实际监测值。通过式(5)对节点v任意时刻t的缺失值进行预测,我们称式(5)为节点v的缺失值预测方程,而预测值与实测值之间的差称为“残差”,记为et,即et=ṽt-vt。残差et的值越小,则预测结果越准确。
在算法的设计过程中,还要考虑如何得到使残差et最小的偏相关系数。此时,在不失一般性的情况下,可对这q组样本数据所形成的矩阵进行处理,从而得出偏相关系数的值。
算法通过时间序列构造缺失值的估计方程中,需要对q值进行确定。算法中用于计算回归系数的样本容量与它的K邻居个数相关。此时,不妨设v的邻居个数为k,因此,可以最多选择k作为其样本容量。在引入多元回归模型后,考虑其统计特性,本研究将样本数定义为k,然而,由于缺失值的预测方程中包含的解释变量个数与k的关系为k/3,因此,最终在式(5)中的q取值为k/3。
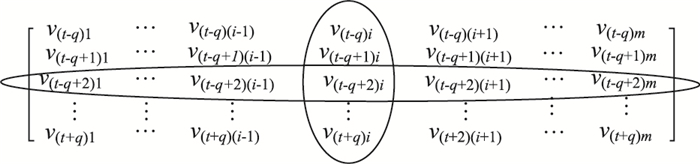
2 基于K近邻多元回归算法KMRA空间相关性与时间相关性并不是独立存在的。如图 1所示,当传感器节点v产生缺失值vt时,与vt存在相关性的数据形成数据空间m。因此,通过空间相关性对vt预测时,对应于图 1中的某1行,刻画了传感器节点之间的相关性。通过时间相关性对vt预测时,对应于图 1中的某1列,它刻画了传感器节点v在不同时刻取值之间的相关性。
|
| 图 1 相关数据空间m Fig. 1 Space of related data m |
| |
正是由于它们在相关数据空间中表达行或列,通过时间相关性和空间相关性对某1时刻t的缺失值预测结果并不一致。遗憾的是,在传感器的实际使用环境中,无法通过理论分析得出哪种预测方式得到的结果更接近实际值。因此,为减小误差以逼近真实结果,本研究在充分考虑感知数据的时-空相关性基础上提出一种基于K近邻多元回归方法(KMRA)的缺失值预测算法,提出在实际应用中采用时空协同计算的方式,降低由单一缺失值预测算法所能引起的系统误差。
2.1 算法的计算过程KMRA算法将时空相关性整合为一体,减小由单一相关性预测引起的误差。
首先,当t时刻位于位置p的传感器产生了缺失值,则分别通过式(3)和式(5)计算ṽp和ṽt,即空间相关性预测与时间相关性预测。
其次,将ṽp和ṽt通过加权平均的方法整合为一体,如式(6)所示。
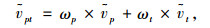
|
(6) |
式中,ωp为空间相关性权重系数; ωt为时间相关性权重系数,且0<ωp, ωt<1。
最后,通过式(6)将ṽp和ṽt简单地整合起来并不能使得预测值变得更准确。理论上,取值越接近监测值的分量越应该得到更高的权重。因此,引入样本决定系数μ来反映回归方程对样本数据的拟合程度,其值越大说明拟合优度越好,反之越差。容易得出,样本数据的拟合程度越高,估计值越准确,因此,式(6)中的权重值将通过样本决定系数计算,式(7)是该系统的计算方法。
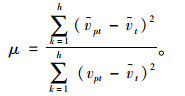
|
(7) |
式(7)给出了样本决定系数,其中ṽt为节点p感知所获得样本的平均值。然而,通过对式(6)的分析可以得出,解释变量个数增加的同时,会导致μ的增大。同时,样本个数与容量对μ的影响与解释变量基本相同。这种影响会导致算法整体效率的下降明显,因此需要对μ进一步修正,并将修正后的值用于计算式(6)中的权值。
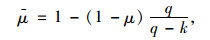
|
(8) |
式中,μ与μ均为决定系数,分别为修正前与修正后的决定系数。同时,q与k分别表示在计算μ的过程中引入的样本容量和解释变量个数。通过式(8)的校正,可得空间与时间相关性最终的权重如式(9)所示。
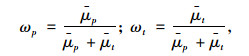
|
(9) |
式中, μp为修正后的空间决定系数; μt为修正后的时间决定系数。
通过式(9)自适应地优化拟合权重系数,并将之应用于空间与时间相关性计算之中,因此算法KMRA能更准确地预测缺失值。
3 试验 3.1 试验设置试验的实现语言是Python3,试验集中于来自交通部足尺环道试验场地的数据,集中选择了2017年4月10日的两个数据集进行了下述试验。
试验在PC机上实现,其操作系统为Windows 10并已经更新到最新补丁,内存为DDR3 8GB,硬盘为机械硬盘2TB,CPU为Intel Core I5,并采用了PyCharm为代码编写环境。
为评价算法KMRA预测的准确程度,本研究将KMRA算法应用于非缺失数据,即对非缺失数据预测得出的结果与已知结果进行比较,使得试验结果客观真实。为达到这个目的,试验选定的数据集不应存在缺失值,或使得缺失值数量尽量小。在选定试验数据集后,依照试验要求随机选定若干个监测值作为缺失值。
为客观地评价算法的预测结果,采用根均方误差RMSE作为预测结果准确性的度量。
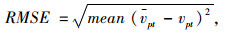
|
(10) |
式中,vpt为真实的数据值,并设定vpt为当vpt已经缺失后的预测值,mean意义为求平均值,即对所有缺失值及其预测结果求平均。
在设置了试验数据集的基础上,我们分别与其他2个算法进行了比较。
STM算法。该算法用于预测无线传感器网络的缺失值。无线传感器由于独特的电源问题,在数据传输与采集过程中出现缺失值的情况比较普遍,尤其是连续出现缺失值的情况多。STM算法在发现缺失值时,通过采用回归方法对缺失值预测。算法同时考虑了时间与空间两个角度,并分别从这两个角度出发回归得到预测值。算法的详细描述可参考文献[8]。
KNN-BP算法。该算法通过2个阶段进行预测。第1个阶段是通过KNN算法处理缺失值,属于预处理阶段,而第2个阶段则采用BP神经网络进行,将第1阶段的结果作为输入项进行处理,进一步逼迫缺失值。文献[12]给出了详细算法。
在试验中,主要考察了影响算法效率的邻居结点数和连续缺失数等因素,这些因素将是试验验证的主要内容。邻居节点个数K(算法中的m)对算法影响较大。与节点v相关性高的节点被遗漏或相关性小的节点被包括,都将对算法的准确性产生较大影响。鉴于数据来源的足尺环道传感器设计布局,本研究在试验中仅考察了6~14个节点的规模,默认值为10个节点。另外,在实际应用中,当发生干扰磁场或其他连续性影响因素时,会在一个时间段内持续产生缺失值,本研究的试验包含了连续缺失值预测问题,并设置缺失值连续发生次数达到10次及以上时为连续预测问题。后续试验中,如无特殊提及,m值取默认值,而缺失值为单独缺失值。
此外,本研究的试验结果,为算法多次运行的预测结果均值,以尽力避免算法的偶然性或突发性,做到客观与公正。
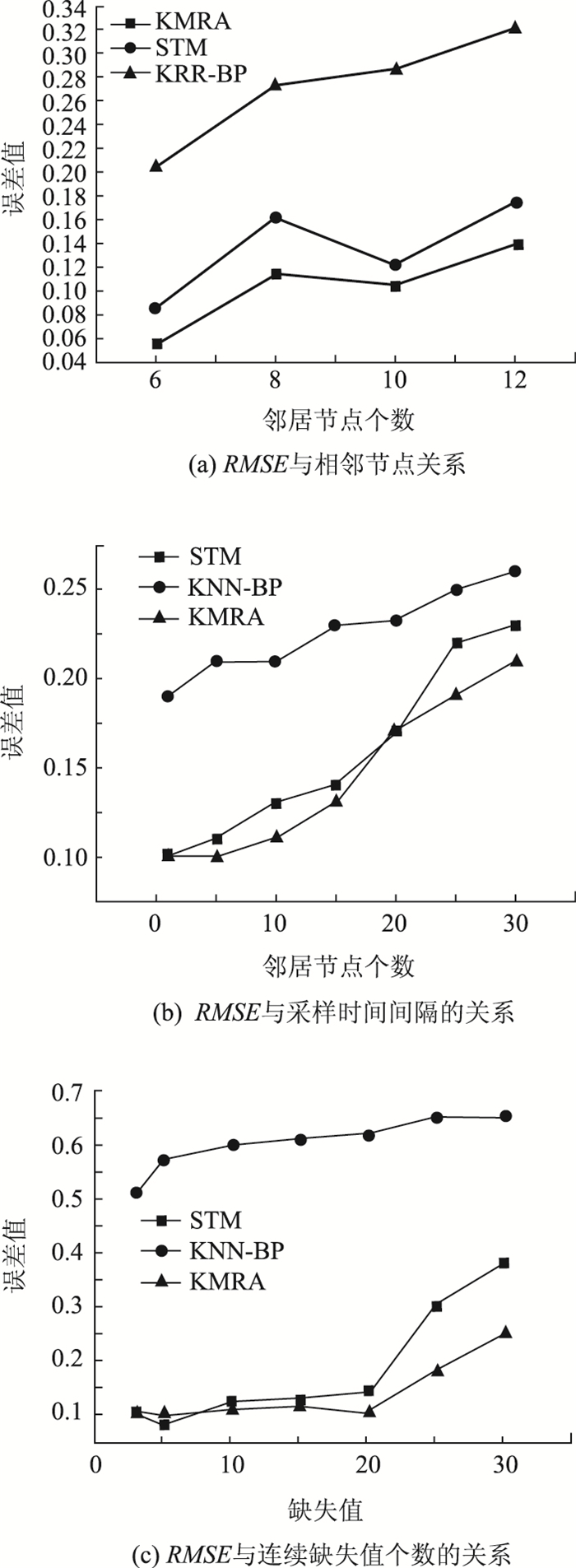
3.2 应力数据集试验结果与分析图 2的试验数据为足尺环道监测数据中的应力数据部分,而与STM算法和KNN-BP算法的比较在邻居点个数、采样间隔时间大小及连续预测问题等3方面展开。
|
| 图 2 足尺环道应力数据集上的试验 Fig. 2 Experiments on stress dataset of full-scale track |
| |
在图 2(a)中,STM算法的预测误差随邻居节点的增加而增加,这是由于多元回归方式特征引起的,而KMRA中采用的K近邻方法对于空间相关性的描述更准确。因此,算法在邻居节点小于10个时,误差水平比较接近,而在超过10个节点后,KMRA算法的误差水平增加幅度更小。
图 2(b)所示为节点采样时间间隔对算法的影响。由图中可以看出,随着节点采样时间间隔的增加,预测结果的误差值均有增加。得到这样的结果并不意外,因为算法STM和KMRA均引入了数据的时间序列概念,而时间序列中存在的数据相关性会随时间间隔的增加而变小,从而引发了预测误差值的增加。此时KNN-BP算法所受的影响最小,由于该算法并未引入传感器节点监测值时间序列的计算。然而,KMRA算法通过K近邻回归的方式计算空间相关性,因此KMRA算法得到的预测值更接近真实结果。通过此试验可以看出,KMRA算法通过m个邻居节点协同预测缺失值,得到准确的结果,而且算法也更稳定。
图 2(c)所示为连续出现缺失值个数增加时,算法预测结果的误差率情况。与图 2(b)类似,当连续出现缺失值时,依赖于时间相关性的分量准确度会随之下降,相反地,空间相关性所受影响较小。但连续出现缺失值时,与时间间隔的增加还有所不同,即算法可通过数据较全的一侧逐步形成预测值,但这样单侧预测仍然存在较大的误差。此时,通过K近邻算法更多依赖于空间相关性的KMRA算法则取得了更好的效果,甚至与完全以空间相关性计算预测值的KNN-BP算法相同。
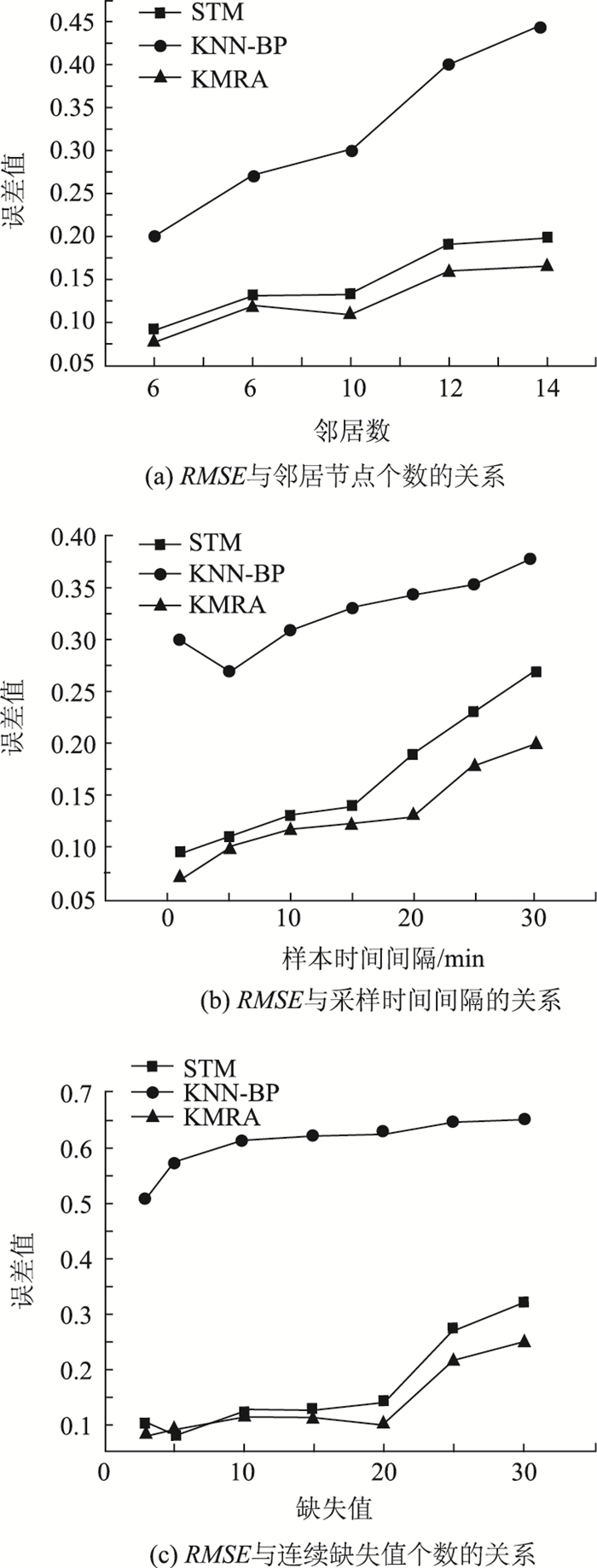
3.3 其他传感器数据集试验结果与分析3.2节中针对应力传感器的数据展开了实验及结果分析,在本小节中,将采用试验场中其他数据采集传感器的数据集进行试验,试验同样包括邻居点个数、节点采样时间间隔、连续缺失数据个数等内容,试验结果如图 3所示。
|
| 图 3 足尺环道应变数据集上的试验 Fig. 3 Experiments on strain dataset of full-scale track |
| |
从图 3(a)可以看出,具有一定相关性的邻居节点个数的增加,使3个算法的误差均出现增大趋势,其中,KNN-BP算法由于其复杂程度与m相关,因此增长速度最快。相应地,KMRA与STM算法在效率上比较接近,增长速度也较慢,但由于KMRA算法中训练过程简便,使得算法整体效率高于STM算法。
图 3(b)所示试验内容为针对不同采样时间间隔对算法效率的影响。由图中结果显示可以得出,STM与KMRA算法均受时间间隔大小影响,算法效率随时间间隔的增加而降低,这是由于上述算法中时间序列中数据相关性随时间间隔增加而降低,而这种相关性的降低引起了算法预测值的准确度。另外,虽然KNN-BP算法受影响小是由于其未采用时间序列的相关性展开预测,但算法整体效率较另2种算法为低。
图 3(c)的试验为测试缺失值连续出现时算法预测值的准确性。相应地,当连续出现缺失值时,相对于稳定的空间相关性而言,基于时间的相关性预测精度下降,而空间相关性相对保持不变,因此,在预测结果上,STM与KMRA算法同时考虑时间与空间的算法在精度上受到较大影响,尤其是在连续缺失20个值时,算法的精度急剧下降,这与q值相关,当达到20个缺失值的时候,算法只能展开单侧预测,从而影响了算法精度。虽然KNN-BP算法受到的影响不大,但算法整体精度较低。
4 结论传感器在采集监测数据时,不可避免地会产生缺失值,而缺失值地出现也极大地影响了传感器的应用,甚至使传感器的监测数据不再可用。本研究针对这种情况,提出了一种基于K近邻回归及多元回归方法的传感器缺失值预测算法KMRA,适用于传感器网络出现缺失值时进行预测。KMRA算法采用K近邻回归用于空间相关数据的预测,采用多元回归实现基于该传感器本身时间序列的预测,并通过加权平均的方法将时间与空间相关数据有机整合形成最终结果。由于算法综合考察了时-空特征,因此具有高度的有效性和准确性。KMRA利用交通部足尺环道数据进行了真实数据为基础的测试,结论表明,算法能准确预测传感器出现的缺失值,且相比其他相关算法提高了效率和预测结果的准确率,从而增强了传感器的应用范围。
| [1] |
敖道朝, 李国维, 李临生, 等. 基于传感器和无线模式的高速公路边坡自动化监测系统[J]. 公路交通科技, 2015, 32(11): 41-47. AO Dao-zhao, LI Guo-wei, LI Lin-sheng, et al. Auto-monitoring System of Expressway Slope Based on Sensor and Wireless Modes[J]. Journal of Highway and Transportation Research and Development, 2015, 32(11): 41-47. |
| [2] |
张倍阳, 张谢东, 陈卫东, 等. 基于嵌套层迭遗传算法的大跨桥梁传感器优化布置[J]. 武汉理工大学学报:交通科学与工程版, 2016, 40(4): 745-749. ZHANG Bei-yang, ZHANG Xie-dong, CHEN Wei-dong, et al. Sensor Location Optimization of Large Span Bridge Based on Nested-stacking Genetic Algorithm[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2016, 40(4): 745-749. |
| [3] |
YI C, KIM L P. An Accurate and Robust Missing Value Estimation for Microarray Data: Least Absolute Deviation Imputation[C]//2006 5th International Conference on Machine Learning and Applications. Orlando, USA: IEEE, 2006: 1-5.
|
| [4] |
BATISTA G E A P A, MONARD M C. An Analysis of Four Missing Data Treatment Methods for Supervised Learning[J]. Applied Artificial Intelligence, 2003, 17(5/6): 519-533. |
| [5] |
LIU C C, DAI D Q, YAN H. The Theoretic Framework of Local Weighted Approximation for Microarray Missing Value Estimation[J]. Pattern Recognition, 2010, 43(8): 2993-3002. |
| [6] |
ZHANG R, XU Z B, HUANG G B, et a1. Global Convergence of Online BP Training with Dynamic Learning Rate[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(2): 330-341. |
| [7] |
PAN L, GAO H, LIU Y. A Spatial Correlation Based Adaptive Missing Data Estimation Algorithm in Wireless Sensor Networks[J]. International Journal of Wireless Information Networks, 2014, 21(4): 280-289. |
| [8] |
PAN L Q, LI J Z, LUO J Z. A Temporal and Spatial Correlation Based Missing Values Imputation Algorithm in Wireless Sensor Networks[J]. Chinese Journal of Computers, 2010, 33(1): 1-11. |
| [9] |
潘立强, 李建中. 传感器网络中一种基于多元回归模型的缺失值估计算法[J]. 计算机研究与发展, 2009, 46(12): 2101-2110. PAN Li-qiang, LI Jian-zhong. A Multiple-regression-model-based Missing Values Imputation Algorithm in Wireless Sensor Network[J]. Journal of Computer Research and Development, 2009, 46(12): 2101-2110. |
| [10] |
许可, 雷建军. 基于属性相关性的无线传感网络缺失值估计方法[J]. 计算机应用, 2015, 35(12): 3341-3343, 3347. XU Ke, LEI Jian-jun. Estimating Algorithm for Missing Values Based on Attribute Correlation in Wireless Sensor Network[J]. Journal of Computer Applications, 2015, 35(12): 3341-3343, 3347. |
| [11] |
袁媛, 邵春福, 林秋映, 等. 基于RBF神经网络的交通流数据修复研究[J]. 交通运输研究, 2016, 2(5): 46-52. YUAN Yuan, SHAO Chun-fu, LIN Qiu-ying, et al. Repair of Traffic Flow Data Based on RBF Neural Network[J]. Transport Research, 2016, 2(5): 46-52. |
| [12] |
LEE B, KIM K, CHUNG E Y. Replacement Policy Adaptable Miss Curve Estimation for Efficient Cache Partitioning[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2017, 37(2): 445-457. |
| [13] |
ASIF M T, MITROVIC N, DAUWELS J, et al. Matrix and Tensor Based Methods for Missing Data Estimation in Large Traffic Networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(7): 1816-1825. |
| [14] |
陈光平. 基于时间序列数据特性的缺失值估计算法[J]. 计算机工程与应用, 2012, 48(12): 135-138. CHEN Guang-ping. Missing Value Estimating Algorithm Based on Time Series Data Properties[J]. Computer Engineering and Applications, 2012, 48(12): 135-138. |
| [15] |
许可, 雷建军. 基于属性相关性的无线传感网络缺失值估计方法[J]. 计算机应用, 2015, 35(12): 3341-3343. XU Ke, LEI Jian-jun. Estimating Algorithm for Missing Values Based on Attribute Correlation in Wireless Sensor Network[J]. Journal of Computer Applications, 2015, 35(12): 3341-3343. |
| [16] |
李珊, 俞瑛, 胡康华, 等. 基于制造云服务QoS序列特性的缺失值估计算法[J]. 计算机集成制造系统, 2016, 22(12): 2930-2936. LI Shan, YU Ying, HU Kang-hua, et al. Missing Value Estimating Algorithm Based on Cloud Manufacturing Services QoS Time Series Data Properties[J]. Computer Integrated Manufacturing Systems, 2016, 22(12): 2930-2936. |
| [17] |
刘钊, 杜威, 闫冬梅, 等. 基于K近邻算法和支持向量回归组合的短时交通流预测[J]. 公路交通科技, 2017, 34(5): 122-128. LIU Zhao, DU Wei, YAN Dong-mei. Short-term Traffic Flow Forecast Based on Combination of K Nearest Neighbor Algorithm and Support Vector Regression[J]. Journal of Highway and Transportation Research and Development, 2017, 34(5): 122-128. |
| [18] |
陈飞彦, 田宇驰, 胡亮, 等. 物联网中基于KNN和BP神经网络预测模型的研究[J]. 计算机应用与软件, 2015, 32(6): 127-130. CHEN Fei-yan, TIAN Yu-chi, HU Liang. STUDY on KNN and BP Neural Network-based Prediction Model in IOT[J]. Computer Applications and Software, 2015, 32(6): 127-130. |
 2019, Vol. 36
2019, Vol. 36
