扩展功能
文章信息
- 周兴业, 蒋勇, 王旭东, 张建国
- ZHOU Xing-ye, JIANG Yong, WANG Xu-dong, ZHANG Jian-guo
- 基于温度与应变参数的沥青混合料动态模量依赖模型研究
- Study on Dynamic Modulus Dependent Model of Asphalt Mixture Based on Temperature and Strain Parameters
- 公路交通科技, 2019, 36(3): 7-13
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(3): 7-13
- 10.3969/j.issn.1002-0268.2019.03.002
-
文章历史
- 收稿日期: 2018-05-25
2. 哈尔滨工业大学 交通科学与工程学院, 黑龙江 哈尔滨 150090;
3. 中国路桥工程有限责任公司, 北京 100011
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin Heilongjiang 150090, China;
3. China Road & Bridge Corporation, Beijing 100011, China
结构层模量是路面力学分析的关键参数,它的取值直接影响着受力分析结果,是新建路面设计和在役路面寿命评估必须面对的问题,也是世界各国路面设计存在差异的主要原因之一。沥青混合料劲度模量主要反映材料在外力作用下的应力-应变关系[1],由于它是一种典型的黏弹性材料,不同试验温度、加载方式、应变水平和试验频率下的劲度模量存在显著差异。
目前沥青混合料劲度模量主要有2种表达形式。第1种是直接采用与时间有关的模量依赖模型,代表性的有凌天清[2-3]以加荷时间和温度表征的回弹模量应力依赖模型等。第2种是根据线黏弹的时温等效原理,将不同频率和温度下的动态模量转化为广泛频率内、基准温度下的模量主曲线,代表性的有Witczak等[4]采用S形曲线描述的动态模量主曲线、Hirsch[5]和Christensen[6]等根据混合料法则提出的沥青混合料动态模量预测模型等,这类模型是基于线黏弹原理构造的,模量只与时间和温度有关,与应力应变无关,目前美国MEPDG设计指南和我国2017版公路沥青路面设计规范中[7]均要求按此进行参数取值。然而,大量的试验结果表明[8-9],不同应变水平下沥青混合料动态模量具有不同的变化规律,特别是在高应变水平下,沥青混合料会表现出明显的非线性性质,材料模量对荷载水平具有明显的依赖性。目前基于线性黏弹性假设构造的沥青混合料动态模量主曲线,由于未考虑荷载作用下的非线性问题,不能如实反映材料在结构中的真实响应状态[10-17],会引起结构分析结果的不合理问题,有必要重新构建一个基于非线性黏弹性的沥青混合料劲度模量依赖模型。
为了表征沥青混合料的非线性黏弹性以及温度、荷载依赖性,使得路面结构分析中的参数取值更加合理和客观地反映实际情况,本研究采用法国梯形梁二点弯曲试验方法研究了不同沥青混合料的弯拉动态模量,通过不同应变水平、不同温度、不同加载频率下的试验结果,建立基于温度与应变参数的沥青混合料动态模量依赖模型。
1 动态模量依赖模型构建 1.1 模型构建方法众所周知,沥青混合料是一种典型的黏弹性材料,力学性质受温度、荷载模式、加载时间的影响最为显著,它对荷载的响应强烈地依赖于温度。在低应变范围时,沥青混合料可视为线性黏弹性材料,其性状与应变水平无关,根据时温等效原理,可将温度、频率对劲度模量的影响进行相互等效和转换。已有研究[4]据此开展了大量的研究工作,并得到了式(1)中以S形曲线表征的动态模量主曲线。
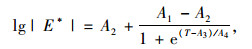
|
(1) |
式中,A1,A2为与模量有关的回归参数;T为温度;A3,A4为与曲线形状有关的回归参数。
然而,在高应变范围时,沥青混合料的黏弹性性状不仅与温度有关,而且与应变水平高度相关,且材料的应力应变关系会表现出明显的非线性性质,此时,必须将其作为非线性黏弹性材料来看待。由于高应变下的沥青混合料性状受温度与荷载影响较大,劲度模量相应也具有明显的温度与荷载依赖性,显然式(1)并不能表达这一特性,有必要重新构建一个基于非线性黏弹性的沥青混合料劲度模量依赖模型。笔者通过不同应变水平下沥青混合料动态模量试验发现,式(1)中A1和A2与应变水平间具有明显的非线性关系,可引入非线性算子A1=a·eb·ε,A2=a·ec·ε,代入式(1)中构造一个基于温度与应变的沥青混合料动态模量依赖模型,见式(2)。
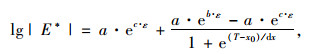
|
(2) |
式中,a,b,c为与模量有关的回归参数;ε为应变;x0,dx为与曲线形状有关的回归参数。
1.2 模型参数的获取方法由于沥青混合料劲度模量的影响因素较多,在模型参数获取过程中,应根据不同试验条件下的沥青混合料动态模量试验结果进行回归分析。需要考虑的试验条件应包括:加载方式、应变水平、环境温度和试验频率。模型参数的具体获取方法如下:
(1) 根据沥青混合料在路面结构层中的实际受力状态,选择与之对应的动态模量试验加载方式,包括但不限于:压缩、剪切、弯曲、拉伸等测试方法。
(2) 在选定加载方式下,开展不同应变水平εi(i=1,…,n)、不同加载频率fj(j=1,…,m)、不同试验温度Tk(k=1,…,p)下的沥青混合料动态模量试验。
(3) 以某一频率fj为基准频率,建立不同应变水平εi下、基于温度参数的沥青混合料复模量主曲线表达式。
(4) 将(3)中结果整理成自变量为温度和应变水平、因变量为动态模量的数据格式,采用式(2)进行多元回归分析,即可获得基于温度和应变的沥青混合料动态模量依赖模型中各个参数的回归结果。
2 试验设计如前所述,由于不同受力状态和加载方式下沥青混合料的性状差异较大,为了全面研究沥青混合料动态模量依赖模型,本研究选择弯拉加载方式开展相关试验研究。试验材料选择RIOHTRACK足尺环道路面结构STR1使用的沥青混合料AC13(SBS)、AC20(AH-30),以及结构STR19使用的沥青混合料SMA13(SBS)、AC25(AH-30)[18]。4种材料的级配组成、马歇尔试验结果和路用性能如表 1~表 3所示。
| 混合料类型 | 各筛孔尺寸(mm)下通过率/% | |||||||||||
| 26.5 | 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| AC25(AH-30) | 99.7 | 77.9 | — | 56.8 | 42.8 | 25.9 | 18.5 | 12.9 | 10.4 | 8.2 | 6.6 | 5.0 |
| AC20(AH-30) | — | 100.0 | 95.3 | 72.9 | 52.6 | 30.4 | 21.1 | 14.7 | 12.0 | 9.5 | 7.7 | 5.9 |
| AC13 (SBS) | — | — | 100.0 | 98.0 | 60.6 | 34.8 | 25.4 | 17.7 | 13.4 | 9.9 | 8.8 | 7.1 |
| SMA13 (SBS) | — | — | 100.0 | 97.7 | 54.7 | 24.9 | 16.7 | 14.0 | 12.5 | 11.4 | 11.0 | 9.7 |
| 马歇尔试验指标 | AC25 (AH-30) |
AC20 (AH-30) |
AC13 (SBS) |
SMA13 (SBS) |
| 最佳油石比/% | 4.1 | 4.6 | 5.1 | 5.5 |
| 毛体积相对密度 | 2.537 | 2.514 | 2.554 | 2.470 |
| 空隙率/% | 3.8 | 4.5 | 4.0 | 4.5 |
| 沥青饱和度/% | 71.4 | 67.8 | 75.8 | 73.4 |
| 矿料间隙率/% | 13.3 | 14.0 | 15.8 | 17.3 |
| 路用性能 | 指标 | AC25 (AH-30) |
AC20 (AH-30) |
AC13 (SBS) |
SMA13 (SBS) |
| 水稳定性 | 残留稳定度/% | 97.7 | 116.2 | 95.3 | 106.9 |
| 60 ℃车辙试验 | 动稳定度/(次·mm-1) | 6 869 | 7 144 | — | — |
| 相对变形/% | 1.3 | 1.9 | — | — | |
| 70 ℃车辙试验 | 动稳定度/(次·mm-1) | — | — | 3 646 | 4 081 |
| 相对变形/% | — | — | 3.3 | 2.5 |
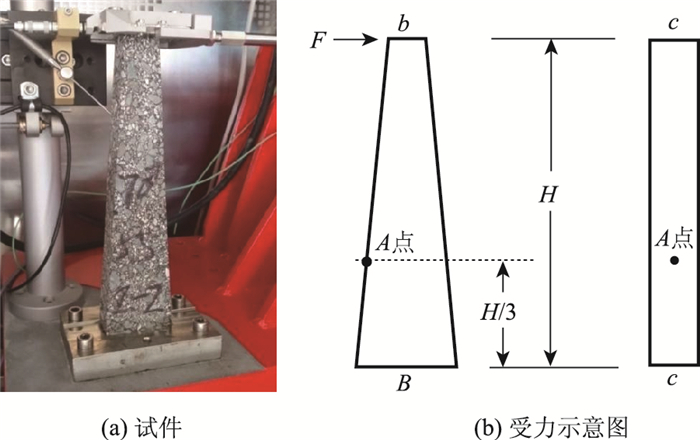
弯拉荷载模式下沥青混合料动态模量采用如图 1所示的法国梯形梁二点弯曲试验进行研究。梯形梁试件的正视图是上底为b、下底为B、高为H的等腰梯形,侧视图是宽为c、高为H的正方形;试验荷载F施加在梯形梁上底处,以距下底H/3高度处A点的应变值作为弯曲试验的控制指标。根据图 1中所示,梯形梁试件H/3高度处的弯拉模量可以采用式(3)进行计算。
|
| 图 1 法国梯形梁二点弯曲试验 Fig. 1 Two-point bending test of French trapezoid beam |
| |
本研究在开展沥青混合料梯形梁试验时,根据1.2节中所述方法选择5种应变水平、7个加载频率、10个试验温度,每个应变水平下平行试验的梯形梁试件数量为4个。试验的基本参数如下。
(1) 应变水平:30,60,90,120,150 με;
(2) 加载频率:10,15,20,25,30,35,40 Hz;
(3) 试验温度:0,5,10,15,20,25,30,35,40,45 ℃。
试验中,首先在同一应变水平、同一试验温度下,对梯形梁试件从高频到低频进行频率扫描,记录不同频率下的动态模量;然后保持应变水平不变,变化试验温度,对同一梯形梁试件再次进行频率扫描,直至完成10个试验温度为止。通过笔者前期大量的试验研究发现,相同试验条件下4个梯形梁试件的动态模量试验结果平行性较好,且温度低时的平行性略优于温度高时。表 2中4种沥青混合料在0 ℃时动态模量变异系数均值约为2.5%,45 ℃时动态模量变异系数均值约为6.2%,本研究10个试验温度下动态模量变异系数均值约为4%。可见,文中的试验方法属于低变异水平、误差较小,具有十分良好的平行性和可靠性。
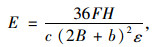
|
(3) |
式中,E为梯形梁试件A点处弯拉模量;F为试验荷载;H为梯形梁试件高度;B为梯形梁试件下底宽度;b为梯形梁试件上底宽度;c为梯形梁试件厚度;ε为应变水平。
3 试验结果与分析 3.1 AC13(SBS)沥青混合料弯拉动态模量依赖模型表 4为不同试验条件下AC13(SBS)沥青混合料梯形梁动态模量试验结果,本研究按照1.1节中所述方法建立动态模量依赖模型。
| 应变/ με |
温度/ ℃ |
不同频率(Hz)下的动态模量试验结果/MPa | ||||||
| 40 Hz | 35 Hz | 30 Hz | 25 Hz | 20 Hz | 15 Hz | 10 Hz | ||
| 30 | 0 | 21 261 | 21 043 | 21 030 | 20 582 | 20 193 | 19 761 | 18 843 |
| 5 | 18 616 | 18 430 | 18 312 | 18 068 | 17 547 | 16 800 | 15 932 | |
| 10 | 15 635 | 15 178 | 14 901 | 14 682 | 14 188 | 13 627 | 12 650 | |
| 15 | 12 571 | 12 229 | 11 946 | 11 586 | 10 955 | 10 243 | 9 323 | |
| 20 | 9 399 | 9 100 | 8 766 | 8 374 | 7 818 | 7 152 | 6 272 | |
| 25 | 6 844 | 6 520 | 6 071 | 5 837 | 5 461 | 4 819 | 4 119 | |
| 30 | 4 567 | 4 368 | 4 108 | 3 880 | 3 530 | 3 020 | 2 523 | |
| 35 | 3 173 | 3 011 | 2 842 | 2 601 | 2 378 | 1 943 | 1 596 | |
| 40 | 2 173 | 2 087 | 1 893 | 1 797 | 1 510 | 1 288 | 1 051 | |
| 45 | 1 447 | 1 318 | 1 242 | 1 266 | 1 096 | 916 | 756 | |
| 60 | 0 | 20 874 | 20 848 | 20 598 | 20 463 | 20 015 | 19 604 | 18 955 |
| 5 | 18 563 | 18 343 | 18 068 | 17 718 | 17 207 | 16 682 | 15 799 | |
| 10 | 15 339 | 15 092 | 14 863 | 14 475 | 13 956 | 13 277 | 12 363 | |
| 15 | 12 287 | 12 016 | 11 675 | 11 169 | 10 610 | 9 946 | 9 037 | |
| 20 | 8 993 | 8 720 | 8 287 | 7 934 | 7 435 | 6 813 | 5 956 | |
| 25 | 6 388 | 6 072 | 5 778 | 5 442 | 5 039 | 4 499 | 3 808 | |
| 30 | 4 196 | 3 952 | 3 666 | 3 477 | 3 130 | 2 743 | 2 290 | |
| 35 | 2 769 | 2 600 | 2 414 | 2 260 | 2 017 | 1 733 | 1 416 | |
| 40 | 1 781 | 1 622 | 1 517 | 1 386 | 1 247 | 1 051 | 839 | |
| 45 | 1 158 | 1 015 | 1 035 | 965 | 807 | 719 | 580 | |
| 90 | 0 | 20 831 | 20 741 | 20 439 | 20 263 | 19 868 | 19 388 | 18 668 |
| 5 | 18 413 | 18 140 | 17 790 | 17 362 | 16 975 | 16 330 | 15 545 | |
| 10 | 15 134 | 14 896 | 14 410 | 14 186 | 13 614 | 12 906 | 12 038 | |
| 15 | 11 979 | 11 512 | 11 118 | 10 727 | 10 130 | 9 501 | 8 604 | |
| 20 | 8 679 | 8 394 | 7 998 | 7 676 | 7 116 | 6 507 | 5 691 | |
| 25 | 6 028 | 5 691 | 5 411 | 5 071 | 4 688 | 4 188 | 3 540 | |
| 30 | 3 943 | 3 712 | 3 474 | 3 198 | 2 920 | 2 549 | 2 109 | |
| 35 | 2 538 | 2 381 | 2 171 | 2 038 | 1 819 | 1 561 | 1 285 | |
| 40 | 1 588 | 1 480 | 1 341 | 1 245 | 1 096 | 948 | 760 | |
| 45 | 1 043 | 946 | 870 | 808 | 707 | 619 | 474 | |
| 120 | 0 | 20 297 | 20 066 | 20 032 | 19 769 | 19 443 | 19 026 | 18 318 |
| 5 | 17 985 | 17 670 | 17 491 | 17 192 | 16 643 | 16 079 | 15 222 | |
| 10 | 14 883 | 14 485 | 14 148 | 13 758 | 13 191 | 12 574 | 11 654 | |
| 15 | 11 613 | 11 177 | 10 792 | 10 359 | 9 785 | 9 111 | 8 209 | |
| 20 | 8 369 | 7 968 | 7 605 | 7 219 | 6 731 | 6 143 | 5 350 | |
| 25 | 5 755 | 5 390 | 5 046 | 4 741 | 4 367 | 3 895 | 3 313 | |
| 30 | 3 711 | 3 446 | 3 234 | 2 990 | 2 710 | 2 374 | 1 962 | |
| 35 | 2 399 | 2 229 | 2 054 | 1 872 | 1 690 | 1 443 | 1 167 | |
| 40 | 1 478 | 1 347 | 1 242 | 1 158 | 1 032 | 873 | 693 | |
| 45 | 994 | 881 | 798 | 746 | 640 | 554 | 447 | |
| 150 | 0 | — | — | — | — | — | — | — |
| 5 | 17 817 | 17 511 | 17 148 | 16 793 | 16 271 | 15 629 | 14 741 | |
| 10 | 14 546 | 14 210 | 13 782 | 13 371 | 12 813 | 12 152 | 11 202 | |
| 15 | 11 164 | 10 699 | 10 305 | 9 802 | 9 260 | 8 591 | 7 730 | |
| 20 | 8 011 | 7 606 | 7 212 | 6 830 | 6 348 | 5 766 | 5 020 | |
| 25 | 5 389 | 5 069 | 4 780 | 4 452 | 4 076 | 3 637 | 3 078 | |
| 30 | 3 515 | 3 291 | 3 087 | 2 825 | 2 555 | 2 218 | 1 837 | |
| 35 | 2 256 | 2 077 | 1 912 | 1 794 | 1 608 | 1 358 | 1 101 | |
| 40 | 1 394 | 1 294 | 1 203 | 1 072 | 939 | 806 | 645 | |
| 45 | 1 073 | 822 | 729 | 671 | 591 | 507 | 404 | |
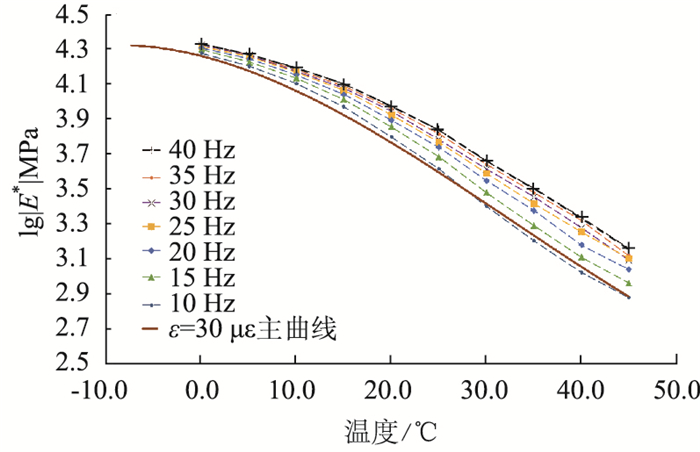
研究中,选择10 Hz作为基准频率,首先以应变水平30 με的试验结果为基础,根据时温等效原理计算每个加载频率下的移位因子,如表 5所示。试验结果经过平移后,得到如图 2所示的应变水平为30 με,基于温度参数的沥青混合料动态模量主曲线,对其进行回归分析后的主曲线表达式见式(4)。
| 频率/Hz | 40 | 35 | 30 | 25 | 20 | 15 | 10 |
| 移位因子 | 7.402 1 | 6.586 0 | 5.785 5 | 5.375 2 | 4.139 6 | 2.188 2 | 0 |
|
| 图 2 AC13(SBS)弯拉动态模量主曲线(ε=30 με) Fig. 2 Principal curves of flexural-tensile dynamic modulus of AC13(SBS) asphalt mixture (ε=30 με) |
| |

|
(4) |
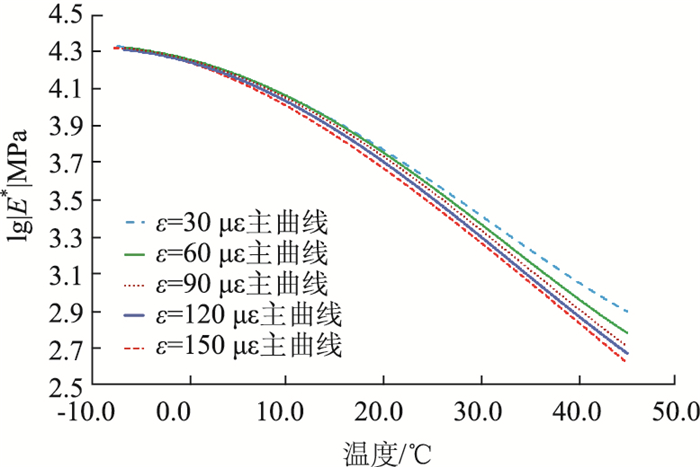
同理,可得到其他应变水平下的动态模量主曲线簇,如图 3所示。每个应变水平下动态模量主曲线表达式的各个回归参数如表 6所示。
|
| 图 3 AC13(SBS)弯拉动态模量主曲线簇 Fig. 3 Principal curve cluster of flexural-tensile dynamic modulus of AC13(SBS) asphalt mixture |
| |
| 回归参数/με | 30 | 60 | 90 | 120 | 150 |
| A1 | 4.485 4 | 4.482 9 | 4.501 3 | 4.495 9 | 4.565 6 |
| A2 | 2.373 3 | 2.167 7 | 1.986 8 | 1.986 5 | 1.765 3 |
| A3 | 29.507 1 | 30.969 1 | 32.058 0 | 31.256 2 | 32.268 9 |
| A4 | 14.172 3 | 14.007 3 | 14.584 9 | 14.400 2 | 16.097 0 |
将图 3中的动态模量主曲线簇,整理成自变量为温度和应变水平、因变量为动态模量的数据格式,采用式(2)对其进行多元回归分析,最终得到基准频率为10 Hz下,AC13(SBS)沥青混合料基于温度和应变的沥青混合料弯拉动态模量依赖模型,如式(5)所示。
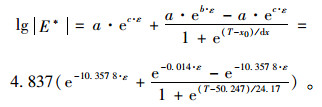
|
(5) |
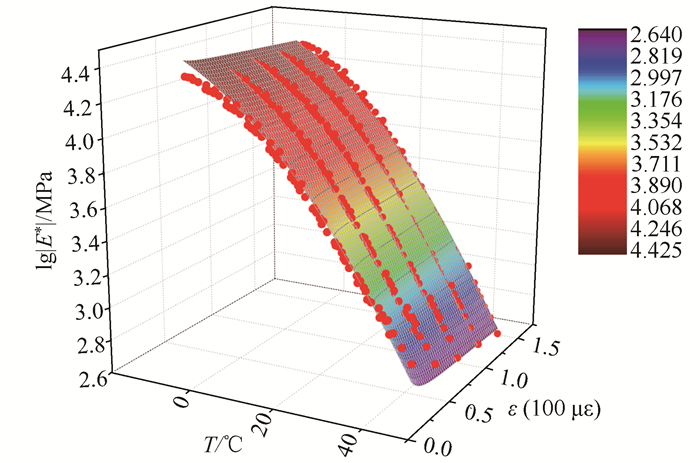
由式(5)可知,动态模量是温度和应变两个参数的函数,在三维空间中可以采用曲面的形式进行表示,因此式(5)也可以称为沥青混合料动态模量主曲面表达式,曲线形式如图 4所示。
|
| 图 4 AC13(SBS)弯拉动态模量主曲面 Fig. 4 Principal surface of flexural-tensile dynamic modulus of AC13(SBS) asphalt mixture |
| |
采用相关系数检验和方差分析检验(F检验)对式(5)中的动态模量依赖模型进行综合评价,结果如表 7所示。从表 7中可以看出,动态模量依赖模型的相关系数R较高、决定系数R2能够达到0.994 3,而且F检验的P值为0<0.01,这表明式(5)中的动态模量依赖模型对试验结果的拟合效果非常好,动态模量与温度、应变水平之间具有十分显著的相关关系,可以采用该模型描述AC13(SBS)沥青混合料弯拉动态模量。
| 相关系数检验 | F检验 | ||||||
| 决定系数R2 | 差异来源 | 自由度DF | 离差平方和SS | 均方MS | F值 | P值 | |
| 0.994 3 | SS组间(处理因素) | 5 | 5 817.79 | 1 163.56 | 874 314.68 | 0 | |
| SS组内(抽样误差) | 415 | 0.552 29 | 0.001 33 | — | — | ||
| 总和 | 420 | 5 818.34 | — | — | |||
3.2 其他沥青混合料弯拉动态模量依赖模型
采用上述方法,可以获得足尺环道结构STR1和STR19中SMA13(SBS),AC25(AH-30),AC20(AH-30)等沥青混合料的梯形梁弯拉动态模量依赖模型。模型的回归参数和检验评价结果如表 8所示。从表 8中可以看出,每种沥青混合料弯拉动态模量依赖模型的决定系数R2均能够达到0.99以上、F检验的P值均为0,这表明所构造的依赖模型能够较好地拟合试验结果,可以用于描述几种沥青混合料的弯拉动态模量随温度和应变水平的变化规律。
| 混合料类型 | a | b | c | x0 | dx | R2 | P值(F检验) |
| AC13(SBS) | 4.837 0 | -0.014 0 | -10.357 8 | 50.247 | 24.170 | 0.994 3 | 0 |
| SMA13(SBS) | 4.793 9 | -0.014 8 | -9.885 1 | 51.023 | 25.454 | 0.994 1 | 0 |
| AC25/20 (AH-30) | 4.677 1 | -0.012 4 | -11.232 1 | 62.248 | 20.007 | 0.996 9 | 0 |
由表 8中的结果可知,SMA13(SBS)弯拉动态模量依赖模型可以写成式(6),AC25(AH-30)和AC20(AH-30)弯拉动态模量依赖模型可以写成式(7)。
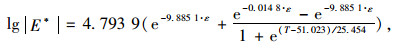
|
(6) |
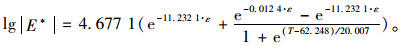
|
(7) |
为了更好地表征沥青混合料的非线性黏弹性,本研究基于劲度模量的温度、荷载依赖性,构建了以温度与应变参数表达的沥青混合料动态模量依赖模型,提出了模型参数获取的试验方法。针对足尺环道用沥青混合料,采用法国梯形梁二点弯曲试验研究了其弯拉动态模量,并给出了相应的模量依赖模型表达式。通过相关系数检验和方差分析检验发现,所构建的动态模量依赖模型对试验结果的拟合效果非常好,动态模量与温度、应变水平之间具有十分显著的相关性,可以采用该模型描述沥青混合料弯拉动态模量。在路面结构分析中使用该模型,可更加客观地反映实际路面中的非线性响应现象,有效避免了结构分析中由于模量取值不合理,所造成的计算结果失真等问题。
| [1] |
姚祖康. 沥青路面结构设计[M]. 北京: 人民交通出版社, 2011. YAO Zu-kang. Structural Design of Asphalt Pavements[M]. Beijing: China Communications Press, 2011. |
| [2] |
凌天清, 王士杰, 许志鸿. 考虑材料非线性性能的沥青路面位移与应力分析[J]. 中国公路学报, 1999, 12(1): 1-6. LING Tian-qing, WANG Shi-jie, XU Zhi-hong. Study of Nonlinear Analysis of Flexible Pavements[J]. China Journal of Highway and Transport, 1999, 12(1): 1-6. |
| [3] |
凌天清, 王士杰, 许志鸿. 柔性路面非线性分析中的几个问题[J]. 重庆交通大学学报:自然科学版, 1994, 13(5): 35-40. LING Tian-qing, WANG Shi-jie, XU Zhi-hong. Some Problem in Nonlinear Analysis Flexible Pavement[J]. Journal of Chongqing Jiaotong Institute:Natural Science Edition, 1994, 13(5): 35-40. |
| [4] |
WITCZAK M W, ANDREI D, MIRZA W.Development of Revised Predictive Model for the Dynamic(Complex) Modulus of Asphalt Mixtres, Inter-team Technical Report, NCHRP 1-37A[R]. Washington, D.C.: University of Maryland, 1999.
|
| [5] |
HIRSCH T J. Modulus of Elasticity of Concrete Affected by Elastic Moduli of Cement Paste Matrix and Aggregate[J]. Journal of the American Concrete Institute, 1962, 59(3): 427-452. |
| [6] |
CHRISTENSEN D W Jr, PELLINEN T, BONAQUIST R F. Hirsch Model for Estimating the Modulus of Asphalt Concrete[J]. Journal of Association of Asphalt Paving Technologists, 2003, 72: 97-121. |
| [7] |
JTG D50-2017, 公路沥青路面设计规范[S]. JTG D50-2017, Specifications for Design of Highway Asphalt Pavement[S]. |
| [8] |
KIM Y R, LITTLE D, SONG I. Effect of Mineral Fillers on Fatigue Resistance and Fundamental Material Characteristics:Mechanstic Evaluation[J]. Trans-portation Research Road, 2003, 1832: 1-8. |
| [9] |
周兴业, 王旭东, 苏波. 路面实体结构模型力学响应试验方法研究[J]. 公路交通科技, 2017, 34(6): 23-29. ZHOU Xing-ye, WANG Xu-dong, SU Bo. Study on Mechanical Response Test Method for Real Pavement Structure Model[J]. Journal of Highway and Transpor-tation Research and Development, 2017, 34(6): 23-29. |
| [10] |
张鹏, 国兴玉, 王旭光, 等. 足尺路面加速加载试验设备技术研究[J]. 山东交通学院学报, 2011, 19(4): 41-45. ZHANG Peng, GUO Xing-yu, WANG Xu-guang, et al. Research on Experiment Equipment Technology of Full-size Road Surface Loading[J]. Journal of Shandong Jiaotong University, 2011, 19(4): 41-45. |
| [11] |
METCALF J B. Application of Full-scale Accelerated Pavement Testing[M]. Washington, D.C.: Nation Academy Press, 1996.
|
| [12] |
HUANG Y H. Pavement Analysis and Design[M]. Upper Saddle River, NJ: Prentice Hall, 1993.
|
| [13] |
PRIEST A L, TIMM D H. A Full-scale Pavement Structural Study for Mechanistic-empirical Pavement Design[J]. Journal of the Association of Asphalt Paving Technologists, 2005, 74: 519-556. |
| [14] |
韦金城, 王林, 杨永顺, 等. 永久性沥青路面试验路力学响应分布的数值仿真[J]. 公路交通科技, 2010, 27(6): 15-19, 33. WEI Jin-cheng, WANG Lin, YANG Yong-shun, et al. Numerical Simulation of Mechanical Response of Perpetual Road Test Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 15-19, 33. |
| [15] |
董泽蛟, 柳浩, 谭忆秋, 等. 沥青路面三向应变响应现场实测研究[J]. 华南理工大学学报:自然科学版, 2009, 37(7): 46-51. DONG Ze-jiao, LIU Hao, TAN Yi-qiu, et al. Field Measurement of Three-Direction Strain Response of Asphalt Pavement[J]. Journal of South China University of Technology:Natural Science Edition, 2009, 37(7): 46-51. |
| [16] |
田泽峰, 范兴华, 刘云全. 足尺沥青路面加速加载试验实践导论[M]. 沈阳: 东北大学出版社, 2012. TIAN Ze-feng, FAN Xing-hua, LIU Yun-quan. Introduction of Full Scale Accelerated Pavement Test on Asphalt Pavement Practice[M]. Shenyang: Northeastern University Press, 2012. |
| [17] |
郭大智, 冯德成. 层状弹性体系力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001. GUO Da-zhi, FENG De-cheng. Layered Elastic System Mechanics[M]. Harbin: Harbin Institute of Technology Press, 2001. |
| [18] |
王旭东. 足尺路面试验环道路面结构与材料设计[J]. 公路交通科技, 2017, 34(6): 30-37. WANG Xu-dong. Design of Pavement Structure and Material for Full-scale Test Track[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 30-37. |
 2019, Vol. 36
2019, Vol. 36
