扩展功能
文章信息
- 胡宝雨, 赵琥, 孙祥龙, 王弟鑫, 刘宁
- HU Bao-yu, ZHAO Hu, SUN Xiang-long, WANG Di-xin, LIU Ning
- 城市公交与农村客运同步换乘模型
- A Model of Synchronous Transfer between Urban Bus Line and Rural Passenger Line
- 公路交通科技, 2019, 36(2): 144-150
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 144-150
- 10.3969/j.issn.1002-0268.2019.02.019
-
文章历史
- 收稿日期: 2017-09-18
2. 哈尔滨工业大学 交通科学与工程学院, 黑龙江 哈尔滨 150090;
3. 东北林业大学 土木工程学院, 黑龙江 哈尔滨 150040;
4. 成都市规划设计研究院, 四川 成都 610081;
5. 哈尔滨电气国际工程有限责任公司, 黑龙江 哈尔滨 150000
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin Heilongjiang 150090, China;
3. School of Civil Engineering, Northeast Forestry University, Harbin Heilongjiang 150040, China;
4. Chengdu Planning and Design Institute, Chengdu Sichuan 610081, China;
5. Harbin Electric International Co., Ltd., Harbin Heilongjiang 150000, China
随着城乡经济的发展,城乡之间的客运需求日益增加。因此,研究城市公交与农村客运线路之间的换乘不仅能提高城乡客运线路的运营效率,满足城乡客运需求,同时有助于城乡客运一体化的发展。目前国内外关于换乘等待时间、公交方式协同以及公交路径选择等方面已有相关研究[1-11]。在公交同步换乘方面,A.Ceder等[12]以车辆相遇次数最大为目标建立了公交最大协同换乘模型,并提出了求解该模型的启发式算法;周雪梅等[13]基于ITS获取公交信息的条件下,以换乘总时间最短为目标建立公交发车时刻的优化模型;石琴等[14]以车辆相遇次数最大、多车相遇的机会最大为目标建立了公交最大同步换乘的多目标规划模型。国外有一些学者[15-18]通过采用时间窗等方法来限制换乘线路车辆到达换乘站点的时间差等方法建立了最大化同步到达换乘次数模型,并设计了启发式算法对模型进行求解。本研究借鉴公交同步换乘的研究方法,结合城市公交与农村客运的换乘形式,考虑了乘客出行对换乘路径的选择,建立了城市公交与农村客运同步换乘的双层优化模型,并运用启发式算法求解该模型。
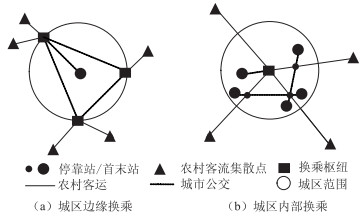
1 同步换乘分析考虑城市公交与农村客运换乘枢纽的功能和布局,以及城市规模形态,城市公交与农村客运的换乘形式分为城区边缘换乘形式(如图 1(a)所示)和城区内部换乘形式(如图 1(b)所示)。城区边缘换乘形式是农村客运只到达城市边缘,在城市边缘地区建设换乘枢纽;其优点是农村客运避开城市中心区,对城市内部交通干扰小,缺点是乘客换乘需求大;一般适合于城市形态为团块式的大城市和特大城市。城区内部换乘形式是农村客运利用城区内部的主干道进入城市中心区,合用部分城市公交站点,在城市中心区或穿越的另一侧建设换乘枢纽;其优点是提高农村客运的直达率,增加中心城区的可达性与吸引力,缺点是增加了城市中心区的交通压力;一般适合于城区交通量较小且城区道路交通条件允许的中小城市[7]。
|
| 图 1 城市公交与农村客运换乘形式示意图 Fig. 1 Schematic diagram of urban public transport and rural passenger transfer |
| |
城市公交与农村客运同步换乘是指通过优化发车时刻和发车间隔,使得换乘线路间车辆尽可能地同时到达,以实现城乡线路“无等待”换乘,按照换乘的形式可分为城区边缘换乘和城区内部换乘。城区边缘换乘是指农村客运线路与城市公交线路在换乘枢纽处换乘,同时通过城市公交线路与其他农村客运线路换乘;城区内部换乘是指农村客运线路与城市公交线路在共用站点处换乘,同时通过城市公交线路实现与其他农村客运线路换乘,并且在客运换乘枢纽与城市公交及其他农村客运换乘。
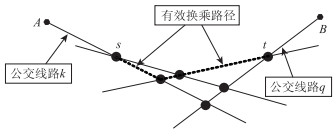
2 同步换乘模型及算法 2.1 模型构建若公交线路k上A点到公交线路q上B点存在多条换乘路径(如图 2所示),则称使得从A点到B点出行时间最短且换乘次数不大于2次的换乘路径为有效换乘路径,在该换乘路径上的换乘站点称为有效换乘站点。把离A点最近的换乘站点称为换乘初始点,记作s,离B点最近的换乘站点称为换乘终止点,记作t,则寻找A点到B点之间的有效换乘路径问题转换为在线路k或线路q上寻找换乘站点j,使得路径s→j→t的出行时间最短。当线路k与线路q都经过换乘站点j时,换乘次数为1,否则换乘次数为2。
|
| 图 2 有效换乘路径示意图 Fig. 2 Schematic diagram of effective transfer path |
| |
为实现城市公交与农村客运线路间的同步换乘,应使得线路在有效换乘站点处相遇的次数尽可能多。因此,城市公交与农村客运同步换乘模型是双层优化模型,上层优化模型以乘客在换乘路径上的出行时间最短为目标,确定有效换乘路径;下层优化模型在有效换乘路径上,以线路在有效换乘站点处相遇的次数最多为目标,优化城市公交线路与农村客运线路的发车时刻。
城市公交与农村客运换乘网络G= {N, E},N为换乘站点的集合;E为换乘站点间有向弧的集合;n为换乘站点数量;m为线路总数量。
上层优化模型为:
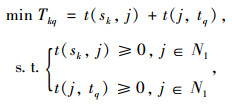
|
(1) |
式中,Tkq为第k条线路换乘初始点sk到第q条线路换乘终止点tq的出行时间;N1为线路k和线路q上的换乘站点集合;t(sk, j)为第k条线路换乘初始点sk直达换乘站点j的出行时间,j∈N1;t(j, tq)为换乘站点j直达第q条线路换乘终止点tq的出行时间,j∈N1。
下层优化模型为:
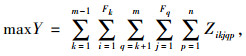
|
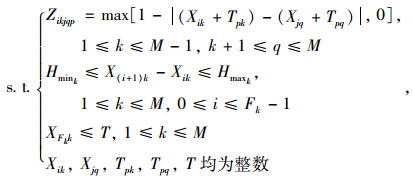
|
(2) |
式中,Zikjqp为0-1变量,Zikjqp=1为线路k的第i个发车时刻所发车辆与线路q的第j个发车时刻所发车辆相遇,Zikjqp=0为线路k的第i个发车时刻所发车辆与线路q的第j个发车时刻所发车辆没有相遇;Y为网络中的总相遇次数;Fk为规划周期内线路k的发车次数;XFkk为线路k规划周期内最后一次发车时刻;Xik为第k条线路上第i个发车时刻,i=0时Xik为规划周期的初始时刻;Xjq为第q条线路上第j个发车时刻,j=0时Xjq为规划周期的初始时刻;Tpk为第k条线路从起点到换乘站点p的行车时间;Tpq为第q条线路从起点到换乘站点p的行车时间;Hmaxk为第k条线路上两次相邻发车之间允许的最大发车间隔,1≤k≤M;Hmink为第k条线路上两次相邻发车之间的最小发车间隔,1≤k≤M;T为规划周期(发车时刻离散分布在区间[0, T]之间)。
下层优化模型中,目标函数为所有换乘站点处线路相遇次数总和最大;第1个约束条件定义了目标函数中的0-1变量;第2个约束条件表示所有线路的每次发车间隔均在最小发车间隔与最大发车间隔之间;第3个约束条件表示最后一次发车时刻能在规划的时段内完成;第4个约束条件表示该模型为整数优化模型。
为使下层优化模型更符合实际,对每条线路应满足以下约束条件:
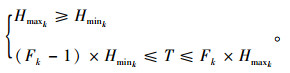
|
(3) |
上层优化模型是一个最短路问题,下层优化模型是一个混合整数线性规划问题,求解模型最优解计算复杂,本研究设计了一种启发式算法求解该双层优化模型,具体步骤如下。
步骤1:建立城市公交与农村客运线路换乘网络,执行数据初始化模块,分别对线路和换乘站点进行编号、对每条线路进行初始数据整理,建立包括Hmin,Hmax,Fk等数据的线路数据表,并验证数据是否满足约束条件式(3)。
步骤2:执行有效换乘模块。选取某条线路的行驶方向作为优化方向,沿优化方向确定该线路与其他线路的换乘站点,根据上层优化模型,确定该线路与其他线路的有效换乘路径,从而确定有效换乘站点。对有效换乘站点建立站点数据表,包括2个元素:(1)经过该换乘站点的换乘线路;(2)到达该换乘站点行驶时间最长的线路。
步骤3:逐次判断所有的有效换乘站点是否为同步换乘站点。若是同步换乘站点则执行同步换乘模块;若不是同步换乘站点,则执行非同步换乘模块。其中,同步换乘站点为:在所有未确定车辆达到时间的有效换乘站点中,通过的换乘线路最多,且距离换乘初始点最近的站点;同步模块为:按车辆尽可能早到达同步换乘站点来设置经过该同步换乘站点的发车时刻,并根据线路的Hmin和Hmax连续产生车辆同时到达;非同步模块为:按车辆到达非同步换乘站点的最小时间来设置经过非同步换乘站点的线路的发车时刻,若该站点没有其他同时到达的车辆,将其记为不可能同步换乘站点。
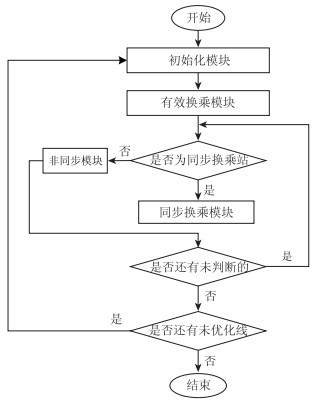
步骤4:选取其他线路的行驶方向作为优化方向,转到步骤2对该优化方向的线路进行发车时刻优化,直到所有线路的所有行驶方向都完成优化。算法流程图如图 3所示。
|
| 图 3 算法流程图 Fig. 3 Flowchart of algorithm |
| |
3 案例分析
运用以上模型和算法,分别对城区边缘同步换乘和城区内部同步换乘进行案例分析,验证模型算法过程。
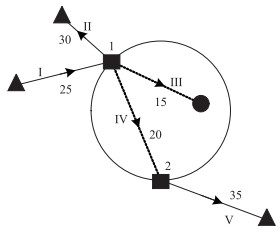
3.1 城区边缘同步换乘(1) 某市城市公交与农村客运在城区边缘换乘,一共5条线路,其中3条农村客运线路,2条城市公交线路,线路编号、换乘站点编号、站点间行驶时间如图 4所示,取规划周期T=60。建立线路数据表(如表 1所示),经验证数据满足约束条件式(3)。
|
| 图 4 边缘换乘形式下的换乘网络图 Fig. 4 Transfer network in edge transfer form |
| |
(2) 选取优化方向,如图 4中箭头所示方向。根据上层模型可确定,线路Ⅰ换乘线路Ⅱ,Ⅲ,Ⅳ的有效换乘站点为1,换乘线路Ⅴ的有效换乘站点为1和2。建立节点数据表,如表 2所示。
| 站点编号 | 换乘线路对数 | 换乘线路 | tmax | tmax对应的线路 |
| 1 | 4 | Ⅰ→Ⅱ | 25 | Ⅰ |
| Ⅰ→Ⅲ | 25 | Ⅰ | ||
| Ⅰ→Ⅳ | 25 | Ⅰ | ||
| Ⅰ→Ⅴ | 25 | Ⅰ | ||
| 2 | 1 | Ⅰ→Ⅴ | 45 | Ⅰ |
(3) 从表 2中可确定换乘站点1为同步换乘站点,执行同步换乘模块,结果如表 3所示。
由表 3可知,线路Ⅱ发车次数为2次满足要求,而线路Ⅰ,Ⅲ,Ⅳ的发车次数还未达到要求。一般根据最小发车间隔,结合相遇时刻确定其余发车时刻。线路Ⅰ的其余发车时刻为40,线路Ⅲ的其余发车时刻为10,15,20,30,35,40,线路Ⅳ的其余发车时刻为9,17,33,53。站点2属于非同步换乘站点,根据非同步模块可确定线路Ⅴ的发车时刻为45(与线路Ⅰ在时刻0的发车同步换乘,与线路Ⅳ在时刻25的发车相遇)。根据线路Ⅴ的最小发车间隔可确定其余发车时刻为15。所有有效换乘站点检查结束,得到该优化方向上的结果,如表 4所示。
| 线路发车时刻 | 相遇时刻 | 相遇次数 | ||||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | 站点1 | 站点2 | ||
| 10, 15, 20 | 9, 17 | 15 | ||||||
| 0 | 25 | 25 | 25 | 45 | 25 | 45 | ||
| 30, 35, 40 | 33 | 3 | ||||||
| 20 | 45 | 45 | 45 | 45 | ||||
| 40 | 53 | |||||||
(4) 同理选取其他优化方向,计算得该优化方向上的发车时刻,依次可计算出每条线路的2个行驶方向的发车时刻。
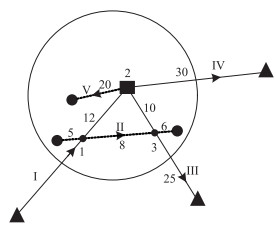
3.2 城区内部同步换乘(1) 某市城市公交与农村客运的换乘形式为内部换乘,一共5条线路,其中3条农村客运线路,2条城市公交线路,线路编号、换乘站点编号、站点间行驶时间如图 5所示,取规划周期T=60。建立线路数据表(如表 5所示),经验证数据满足约束条件式(3)。
|
| 图 5 内部换乘形式下的换乘网络 Fig. 5 Transfer network in internal transfer form |
| |
(2) 选取优化方向,如图 5中箭头所示方向。根据上层模型确定,线路Ⅰ换乘线路Ⅱ的有效换乘站点为1;换乘线路Ⅲ的有效换乘站点是1和3;换乘线路Ⅳ,Ⅴ的有效换乘站点为2。建立节点数据表,如表 6所示。
| 站点编号 | 换乘线路对数 | 换乘线路 | tmax | tmax对应的线路 |
| 1 | 2 | Ⅰ→Ⅱ | 20 | Ⅰ |
| Ⅰ→Ⅲ | 20 | Ⅰ | ||
| 2 | 2 | Ⅰ→Ⅳ | 32 | Ⅰ |
| Ⅰ→Ⅴ | 32 | Ⅰ | ||
| 3 | 1 | Ⅰ→Ⅲ | 28 | Ⅰ |
(3) 从表 2中可确定换乘站点1为同步换乘站点,执行同步换乘模块,结果如表 7所示。
由表 3可知,线路Ⅰ发车次数为3次满足要求,而线路Ⅱ的发车次数还未达到要求。根据最小发车间隔确定线路Ⅱ的其余发车时刻为7,23,43。站点2属于非同步换乘站点,根据非同步模块可确定线路Ⅳ的发车时刻为32(与线路Ⅰ在时刻0的发车相遇),线路Ⅴ的发车时刻为32,52(分别与线路Ⅰ在时刻0和时刻20的发车相遇)。根据线最小发车间隔可确定线路Ⅳ的其余发车时刻为2,线路Ⅴ的其余发车时刻为8,14,20,26,38,44。站点3也属于非同步换乘站点,根据非同步模块可确定线路Ⅲ的发车时刻为18,38,58(分别与线路Ⅰ在时刻0,20,40的发车同步换乘,与线路Ⅱ在时刻15,35,55的发车相遇),发车次数为3次满足要求。所有有效换乘站点检查结束,得到该优化方向上的结果,如表 8所示。
| 线路发车时刻 | 相遇时刻 | 相遇次数 | |||||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | 站点1 | 站点2 | 站点3 | ||
| 7 | 2 | 8, 14, 20, 26 | |||||||
| 0 | 15 | 18 | 32 | 32 | 20 | 32 | 28 | ||
| 23 | 38, 44 | 8 | |||||||
| 20 | 35 | 38 | 52 | 40 | 52 | 48 | |||
| 43 | |||||||||
| 40 | 55 | 58 | 60 | 68 | |||||
(4) 同理选取其他优化方向,计算得该优化方向上的发车时刻,依次可计算出每条线路的2个行驶方向的发车时刻。
4 结论城市公交与农村客运同步换乘能够使得城市公交与农村客运客流便捷、高效交换,是实现城乡客运一体化的重要组成,通过以上研究得到如下结论:
(1) 分析了城市公交与农村客运的换乘形式,在此基础上描述了城区边缘同步换乘和城区内部同步换乘2种同步换乘形式。
(2) 以乘客在换乘路径上的出行时间最短为上层优化目标,以车辆在有效换乘站点相遇次数最多为下层优化目标,建立了城市公交与农村客运同步换乘的双层优化模型,该模型考虑了乘客出行对换乘路径的选择,实现了在有效换乘路径上城乡线路“无等待”换乘。
(3) 设计了启发式算法对所建立的双层优化模型进行求解,得到基于同步换乘的城乡线路发车时刻表。并通过案例进行了检验,该算法能够求解得到模型的满意解。
| [1] |
HALL R, DESSOUKY M, LU Q. Optimal Holding Times at Transfer Stations[J]. Computers and Industrial Engineering, 2001, 40(4): 379-397. |
| [2] |
CHOWDHURY S M, CHIEN S I. Intermodal Transit System Coordination[J]. Transportation Planning and Technology, 2002, 25(4): 257-287. |
| [3] |
李文勇, 王炜, 陈学武. 公交出行路径蚂蚁算法[J]. 交通运输工程学报, 2004, 4(4): 102-105. LI Wen-yong, WANG Wei, CHEN Xue-wu. Bus Travel Transit Path Based on Ant Algorithm[J]. Journal of Traffic and Transportation Engineering, 2004, 4(4): 102-105. |
| [4] |
戴帅, 姜华平, 陈海泳, 等. 公共交通换乘时间可靠度研究[J]. 公路交通科技, 2007, 24(9): 124-126. DAI Shuai, JIANG Hua-ping, CHEN Hai-yong, et al. Study on Transfer Reliability of Integrated Public Transport[J]. Journal of Highway and Transportation Research and Development, 2007, 24(9): 124-126. |
| [5] |
李铭, 李旭宏, 吕慎. 基于城市TOD发展模式的客运换乘枢纽布局规划研究[J]. 公路交通科技, 2006, 23(11): 100-104. LI Ming, LI Xu-hong, LÜ Shen. Research on Layout of Passenger Transit Hub Based on Urban TOD Development Pattern[J]. Journal of Highway and Transportation Research and Development, 2006, 23(11): 100-104. |
| [6] |
谷金晶, 杨艳, 张敬东. 考虑到站时间差的多层级常规公交时刻表[J]. 公路交通科技, 2016, 33(6): 128-133. GU Jin-jing, YANG Yan, ZHANG Jing-dong. Timetable of Multi-level Transit Considering Arrival Time Difference[J]. Journal of Highway and Transportation Research and Development, 2016, 33(6): 128-133. |
| [7] |
杜建波.城市公交智能调度算法研究[D].杭州: 浙江工业大学, 2017. DU Jian-bo.Research on Intelligent Scheduling Algorithm for Urban Public Transport[D].Hangzhou: Zhejiang University of Technology, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10337-1017247166.htm |
| [8] |
魏明, 陈学武, 孙博. 多模式区域公交协调调度模型和算法[J]. 公路交通科技, 2015, 32(4): 136-142. WEI Ming, CHEN Xue-wu, SUN Bo. A Model and an Algorithm of Schedule Coordination for Multi-mode Regional Bus Transit[J]. Journal of Highway and Transportation Research and Development, 2015, 32(4): 136-142. |
| [9] |
柏海舰, 董瑞娟, 张敏, 等. 基于同步多样性的公交时刻优化方法[J]. 交通运输工程学报, 2013, 13(3): 79-85. BAI Hai-jian, DONG Rui-juan, ZHANG Min, et al. Optimization Method of Bus Time Based on Synchronization Diversity[J]. Journal of Traffic and Transportation Engineering, 2013, 13(3): 79-85. |
| [10] |
熊杰, 关伟, 黄爱玲. 社区公交接驳地铁路径优化研究[J]. 交通运输系统工程与信息, 2014, 14(1): 166-173. XIONG Jie, GUAN Wei, HUANG Ai-ling. Research on Optimal Routing of Community Shuttle Connect Rail Transit Line[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(1): 166-173. |
| [11] |
苏彩艳.基于运行时间可靠性的公交线网协同调度问题研究[D].长沙: 中南大学, 2012. SU Cai-yan.Research on Synchronization of Bus Networks Based on Running Time Reliability[D].Changsha: Central South University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10533-1012476494.htm |
| [12] |
CEDER A, GOLANY B, TAL O. Creating Bus Timetables with Maximal Synchronization[J]. Transportation Research Part A:Policy and Practice, 2001, 35(10): 913-928. |
| [13] |
周雪梅, 杨晓光. 基于ITS的公共交通换乘等待时间最短调度问题研究[J]. 中国公路学报, 2004, 17(2): 82-84. ZHOU Xue-mei, YANG Xiao-guang. Study of Dispatching at Minimum Waiting Time of Public Transportation Transfer under the Condition of ITS[J]. China Journal of Highway and Transport, 2004, 17(2): 82-84. |
| [14] |
石琴, 覃运梅, 黄志鹏. 公交区域调度的最大同步换乘模型[J]. 中国公路学报, 2007, 20(6): 90-94. SHI Qin, QIN Yun-mei, HUANG Zhi-peng. Maximal Synchronous Transfer Model of Bus Regional Dispatching[J]. China Journal of Highway and Transport, 2007, 20(6): 90-94. |
| [15] |
IBARRA-ROJAS O J, RIOS-SOLIS Y A. Synchronization of Bus Timetabling[J]. Transportation Research Part B:Methodological, 2012, 46(5): 599-614. |
| [16] |
NESHELI M M, CEDER A, GONZALEZ V A. Real-time Public-transport Operational Tactics Using Synchronized Transfers to Eliminate Vehicle Bunching[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(11): 3220-3229. |
| [17] |
LIU T, CEDER A, CHOWDHURY S. Integrated Public Transport Timetable Synchronization with Vehicle Scheduling[J]. Transportmetrica A:Transport Science, 2017, 13(10): 932-954. |
| [18] |
NESHELI M M, CEDER A. Improved Reliability of Public Transportation Using Real-time Transfer Synchronization[J]. Transportation Research Part C:Emerging Technologies, 2015, 60: 525-539. |
 2019, Vol. 36
2019, Vol. 36
