扩展功能
文章信息
- 李高盛, 彭玲, 李祥, 吴同
- LI Gao-sheng, PENG Ling, LI Xiang, WU Tong
- 基于LSTM的城市公交车站短时客流量预测研究
- Study on Short-term Traffic Forecast of Urban Bus Stations Based on LSTM
- 公路交通科技, 2019, 36(2): 128-135
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 128-135
- 10.3969/j.issn.1002-0268.2019.02.017
-
文章历史
- 收稿日期: 2017-05-03
2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
随着国家和各级政府对智慧城市建设关切度的提升,智慧城市作为一项国家战略已然成为“两会”的高频词,代表了国家和人民的殷切期盼。智慧交通是智慧城市的重要组成部分,而智慧公交的建设也将助力智慧城市的发展。城市公交车站是人口密集区,也是人口流量较大的区域,成为社会治安和环境维护的重要监测点。公交车站客流量的监控和预测不但对公交运营决策和综合管理提供及时准确的数据参考,而且能够聚焦安保监管范围,为社会治安提供支持,保障城市的公共安全。
目前,国内外学者已经将很多成熟的模型应用于车流量和客流量预测领域,如传统的移动平均法、KNN算法、ARMA及其改进版本ARIMA等。具体如下,李琦[1]应用移动平均法进行物流需求;J. Rice[2]和J. Myung[3]采用KNN方法找到与当前最相似的历史K天,并将前K天的序列数据作为当前时间的预测数据;但是这2种方法预测的结果为未来一段时间的大致趋势,并且该方法对数据具有平滑效应,因此不能保证预测结果的准确性。Ahmed M S等[4]采用ARIMA方法进行短时间高速公路交通客流量预测;宋子房[5]运用灰色系统理论预测模型和时间序列的ARIMA预测模型分别对车流量状况进行预测;这些方法具有模型简单,同时具有较强的解释性,但是由于交通流的非线性和随机性,使得该参数模型不能很好地描述其特有的性质,导致预测误差比非参数模型更大。唐秋生[6]建立一种新的GSO-BPNN方法,该方法在BP网络的基础上植入萤火虫优化算法(Glowworm Swarm Optimization, GSO),优化网络的初始权值和阈值,但是该方法只能应对较短的时间序列数据,对于长时间的序列将会导致前面记忆遗忘的现象。为了改善上述状况, Yongxue Tian[7],Zheng Zhao[8]等研究发现,LSTM(Long Short-term Memory)能够克服“遗忘”现象,拥有较强的“记忆”能力,并将其应用于长时间序列的短期交通流预测。在2015年,Ma[9-10]等在RNN的提出之后,将LSTM运用于交通流量预测,研究成果表明LSTM网络由3层组成,其中隐藏层由记忆块组成,LSTM的长时间学习优势在交通流预测中得以体现。除此之外,Hongxin Shao等[11]研究发现LSTM能够学习到单站点长时间序列客流量数据的非线性关系,从而将其应用于短期客流量预测。Wu Yuankai等[12]基于LSTM与CNN研究交通流的时间-空间相关性。但是,上述方法的更迭都只是针对某一特定站点进行时间序列的观测而并未考虑多站点的相关性,即忽略了各站点之间的相互影响。本研究在前辈学者研究的基础上,将LSTM应用于多个公交车站点长时间序列的客流量预测。
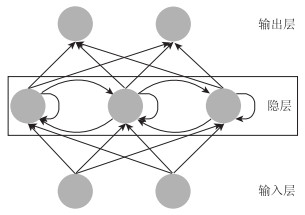
1 LSTM 1.1 RNN人工神经网络(Artificial Neural Network, ANN)是人脑的简洁化和抽象化的表示,它是由大量的神经元相互连接而形成的[13]。1985年,David Rumelhart等[14]提出了神经网络的误差反向传播算法,即BP神经网络(Back Propagation Neural Network),为神经网络的研究掀开崭新的一页。为了解决各类新问题,科学界在原有BP神经网络的基础上进行改进,从而涌现出大量的衍生算法,其中循环神经网络(Recurrent Neural Networks, RNN)被常用作处理序列数据,完成序列数据的预测或者分类任务。循环神经网络,如图 1所示,它是同时兼备前向反馈和后向反馈链路的神经网络,这种网络能够有效分析序列数据的上下文信息,诸如语音识别领域[15-16]、电子学传感器[17]等。该算法较传统的BP神经网络的优点在于,隐层之间的神经元不再是无连接而是有连接,这种改进使得网络能够对前面的信息进行记忆保留,并应用于当前的输出计算中,计算结束再将记忆传递给下一个神经元。因此,RNN在自然语言处理领域[18](Natural Language Processing, NLP)中取得了巨大成功以及广泛应用。
|
| 图 1 RNN隐层的前向反馈、后向反馈及神经元互连 Fig. 1 Forward feedback, backward feedback and neuronal interconnection of RNN hidden layer |
| |
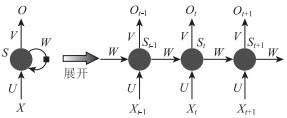
图 2中{xt-1, xt, xt+1, …}为输入集(Input units),{St-1, St, St+1…}为隐藏单元(Hidden units),{Ot-1, Ot, Ot+1, …}为输出集(Output units),t代表序列(Step),而U, V, W是一组共享参数。
|
| 图 2 时间序列数据的信息流的传递过程 Fig. 2 Transfer process of information flow of time series data |
| |
1.2 LSTM
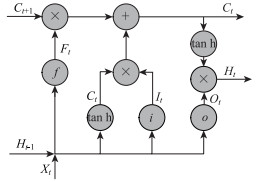
研究发现[19],RNN具备的记忆能力周期较短,只能记忆短时期的上下文信息,而面对长序列的信息随着学习量的增多或者学习周期的增长将会导致梯度消失或者梯度爆炸的现象。长短期记忆网络(Long Short Term Memory, LSTM)是一种特殊类型的RNN网络结构,可以学习长期依赖信息。LSTM由Hochreiter等[20]于1997年提出并在近期被Alex Graves[21]进行了改良和推广。该模型可以记忆长序列中的规律,并且有效规避梯度消失现象[20]。如图 2所示,相较于传统的RNN,LSTM的隐层单元(Hidden units)被记忆块(Memory blocks)代替,这些记忆块中的记忆单元(Memory cell)能够存储前面的序列信息,同时增加3种门:输入门(Input gate)、输出门(Output gate)、忘记门(Forget gate)用于控制记忆的序列信息。记忆块中有2条主线,分别为记忆线和输入输出线,其中,记忆线在t时刻所完成的运算为其前一时刻的记忆状态Ct-1经过忘记门状态Ft和输入门状态It的不同处理后得到该时刻的记忆线输出Ct;而输入输出线的运算过程为在t时刻输入一组新的变量值Xt与前一时刻的隐层输出状态Ht-1共同通过输出门状态Ot的运算后,参考记忆线在该时刻的输出Ct,得到隐层的输出结果Ht。LSTM中t时刻所得的Ct和Ht将被传递到下一时刻参与计算。具体流程如图 3所示。
|
| 图 3 LSTM记忆单元结构 Fig. 3 LSTM memory cell structure |
| |
为了得到目标Ct和Ht,计算步骤如下:
(1) 式(1)~式(4)分别为计算输入门It、忘记门Ft、输出门Ot及记忆单元的输入状态Ct。
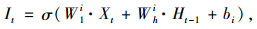
|
(1) |
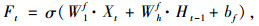
|
(2) |
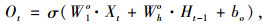
|
(3) |
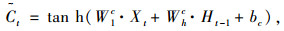
|
(4) |
式中,W1i,W1f,W1o,W1c为Xt的权重;Whi,Whf,Who,Whc为Ht-1的权重;bi,bf,bo,bc为偏置条件;σ为sigmoid函数;tanh为双曲正切函数。
(2) 计算LSTM记忆线的t时刻输出Ct,如式(5)所示:
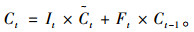
|
(5) |
(3) 计算LSTM的t时刻隐层输出Ht,如式(6)所示:
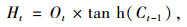
|
(6) |
(4) 计算t+1时刻的序列值,依据输入网络的固定长度的历史序列数据和模型训练结果,得到t+1时刻的预测值xt+1。计算方式如式(7)所示:
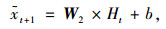
|
(7) |
式中,W2为输出层和隐层之间的权重矩阵;b为输出层的偏项。
2 试验及结论分析 2.1 试验数据本研究的试验数据来自于中新天津生态城的4条公交线路,数据内容包括从2015年8月5日至2016年1月31日的54个公交车站上下车乘客数,总记录数超过77万条。经过数据异常值、空值的去除等预处理和线性归一化之后,最终挑选“城管中心”、“服务中心”、“公安分局”等13个时间序列完备的公交车站点作为研究目标。最终数据内容如表 1所示。
| 站点数 | 日期区间 | 每日起终时间 | 统计时间间隔/min |
| 13 | 2015.8.5- 2016.1.31 | 7:00:00- 20:30:00 | 30 |
原始数据展示如图 4所示。
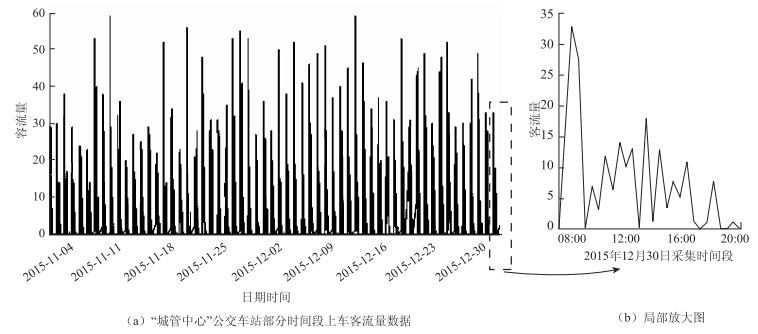
|
| 图 4 “城管中心”公交车站部分时间段上车客流量数据及局部放大图 Fig. 4 "Urban management center"bus station getting on traffic volume and partial magnification in a time period |
| |
2.2 数据相关性分析
鉴于生态城的公交线路具有较强的地域性,绝大多数乘客为生态城居民或从业人员,采用皮尔逊相关系数的绝对值度量各公交站点客流量的相关性,计算结果如表 2所示。
| 站点名称 | 上/下车 | 城管中心 | 服务中心 | 公安分局 | 航母公园 | 和畅园 | 和风路派出所 | 季景新城 | 鲲玺园 | 芦花庄园 | 仁副营炮台站 | 商业街 | 维护中心 | 运河中路 |
| 城管中心 | 上 | 1.000 | 0.597 | 0.530 | 0.569 | 0.589 | 0.566 | 0.581 | 0.530 | 0.559 | 0.490 | 0.493 | 0.551 | 0.563 |
| 下 | 1.000 | 0.556 | 0.545 | 0.526 | 0.525 | 0.510 | 0.572 | 0.565 | 0.529 | 0.551 | 0.570 | 0.542 | 0.572 | |
| 服务中心 | 上 | 0.597 | 1.000 | 0.549 | 0.558 | 0.633 | 0.622 | 0.582 | 0.638 | 0.562 | 0.583 | 0.740 | 0.578 | 0.556 |
| 下 | 0.556 | 1.000 | 0.607 | 0.596 | 0.655 | 0.578 | 0.551 | 0.604 | 0.548 | 0.583 | 0.789 | 0.642 | 0.612 | |
| 公安分局 | 上 | 0.530 | 0.549 | 1.000 | 0.518 | 0.518 | 0.542 | 0.526 | 0.554 | 0.529 | 0.562 | 0.538 | 0.541 | 0.538 |
| 下 | 0.545 | 0.607 | 1.000 | 0.555 | 0.536 | 0.522 | 0.517 | 0.523 | 0.522 | 0.544 | 0.581 | 0.579 | 0.541 | |
| 航母公园 | 上 | 0.569 | 0.558 | 0.518 | 1.000 | 0.526 | 0.518 | 0.524 | 0.538 | 0.532 | 0.526 | 0.537 | 0.530 | 0.542 |
| 下 | 0.526 | 0.596 | 0.555 | 1.000 | 0.539 | 0.520 | 0.511 | 0.522 | 0.512 | 0.540 | 0.577 | 0.542 | 0.598 | |
| 和畅园 | 上 | 0.589 | 0.633 | 0.518 | 0.526 | 1.000 | 0.748 | 0.733 | 0.718 | 0.551 | 0.524 | 0.556 | 0.554 | 0.529 |
| 下 | 0.525 | 0.655 | 0.536 | 0.539 | 1.000 | 0.569 | 0.608 | 0.689 | 0.513 | 0.556 | 0.659 | 0.583 | 0.528 | |
| 和风路派出所 | 上 | 0.566 | 0.622 | 0.542 | 0.518 | 0.748 | 1.000 | 0.715 | 0.690 | 0.534 | 0.540 | 0.559 | 0.549 | 0.528 |
| 下 | 0.510 | 0.578 | 0.522 | 0.520 | 0.569 | 1.000 | 0.528 | 0.507 | 0.503 | 0.518 | 0.529 | 0.560 | 0.521 | |
| 季景新城 | 上 | 0.581 | 0.582 | 0.526 | 0.524 | 0.733 | 0.715 | 1.000 | 0.679 | 0.524 | 0.524 | 0.531 | 0.524 | 0.524 |
| 下 | 0.572 | 0.551 | 0.517 | 0.511 | 0.608 | 0.528 | 1.000 | 0.672 | 0.494 | 0.548 | 0.585 | 0.516 | 0.526 | |
| 鲲玺园 | 上 | 0.530 | 0.638 | 0.554 | 0.538 | 0.718 | 0.690 | 0.679 | 1.000 | 0.540 | 0.571 | 0.629 | 0.552 | 0.546 |
| 下 | 0.565 | 0.604 | 0.523 | 0.522 | 0.689 | 0.507 | 0.672 | 1.000 | 0.507 | 0.550 | 0.660 | 0.563 | 0.501 | |
| 芦花庄园 | 上 | 0.559 | 0.562 | 0.529 | 0.532 | 0.551 | 0.534 | 0.524 | 0.540 | 1.000 | 0.534 | 0.541 | 0.551 | 0.537 |
| 下 | 0.529 | 0.548 | 0.522 | 0.512 | 0.513 | 0.503 | 0.494 | 0.507 | 1.000 | 0.515 | 0.529 | 0.524 | 0.521 | |
| 仁副营炮台站 | 上 | 0.490 | 0.583 | 0.562 | 0.526 | 0.524 | 0.540 | 0.524 | 0.571 | 0.534 | 1.000 | 0.565 | 0.546 | 0.567 |
| 下 | 0.551 | 0.583 | 0.544 | 0.540 | 0.556 | 0.518 | 0.548 | 0.550 | 0.515 | 1.000 | 0.572 | 0.542 | 0.539 | |
| 商业街 | 上 | 0.493 | 0.740 | 0.538 | 0.537 | 0.556 | 0.559 | 0.531 | 0.629 | 0.541 | 0.565 | 1.000 | 0.562 | 0.536 |
| 下 | 0.570 | 0.789 | 0.581 | 0.577 | 0.659 | 0.529 | 0.585 | 0.660 | 0.529 | 0.572 | 1.000 | 0.628 | 0.586 | |
| 维护中心 | 上 | 0.551 | 0.578 | 0.541 | 0.530 | 0.554 | 0.549 | 0.524 | 0.552 | 0.551 | 0.546 | 0.562 | 1.000 | 0.544 |
| 下 | 0.542 | 0.642 | 0.579 | 0.542 | 0.583 | 0.560 | 0.516 | 0.563 | 0.524 | 0.542 | 0.628 | 1.000 | 0.570 | |
| 运河中路 | 上 | 0.563 | 0.556 | 0.538 | 0.542 | 0.529 | 0.528 | 0.524 | 0.546 | 0.537 | 0.567 | 0.536 | 0.544 | 1.000 |
| 下 | 0.572 | 0.612 | 0.541 | 0.598 | 0.528 | 0.521 | 0.526 | 0.501 | 0.521 | 0.539 | 0.586 | 0.570 | 1.000 |
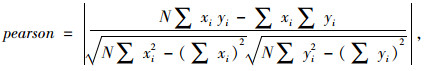
|
(8) |
式中,xi为公交车站点x在时间段i的上/下车客流量;yi为公交车站点y在时间段i的上/下客流量;N为参与计算的时间段总数。
由表 2可见,98%公交站点客流量之间的皮尔逊相关系数绝对值大于0.5。
2.3 基于LSTM的神经网络模型的客流量预测(1) 神经网络模型构建及参数选择
由于模型的输出为t时段全部站点的上/下车客流量,而其输入特征为这些站点t时段前的r个连续时间序列的上/下车客流量值。模型的输入输出如图 5所示,其中虚线矩形为模型输入,虚线箭头代表输出目标,3种线型为3次不同的训练,xt为t时段全部站点的上/下车客流量。为了使模型的表现更为良好,需要使用交叉验证方式选择合适时间步长、网络层数、各层节点数。
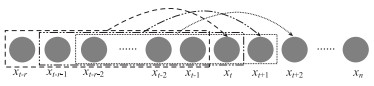
|
| 图 5 模型的训练方式 Fig. 5 Training mode of model |
| |
为了使模型具有较强的泛化能力,在每次做时间步长调整过后,需要对训练集利用随机函数将数据块完全打乱,使得最大化地降低块与块之间的关联性,增强预测的合理性和准确性,最终将整个数据集分为2个部分:训练集(80%)和测试集(20%)。试验中的网络构建采用Keras框架实现LSTM模块。在时间步长、网络层数、各层节点数的参数优选时采用6折交叉验证,通过交叉验证的试验发现,采用2层LSTM构建的循环神经网络,每层包含的节点数为350,时间步长为5时,模型具有良好的表现力。模型采用随机梯度下降(Stochastic Gradient Descent, SGD)的方法进行优化,学习率为0.001,批处理大小为128,迭代次数为10,最大迭代次数为300,激活函数为ReLU,损失函数选择平均绝对误差(Mean Absolute Error, MAE)。网络结构如图 6所示。
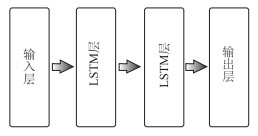
|
| 图 6 试验构建的神经网络结构 Fig. 6 Neural network structure used in experiment |
| |
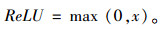
|
(9) |
(2) 模型评估
为了评估LSTM神经网络预测结果的表现力,本研究采用均方误差(Mean Squared Error, MSE)和平均绝对误差(Mean Absolute Error, MAE)2个标准去评估预测误差[22]。
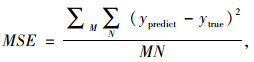
|
(10) |
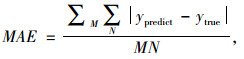
|
(11) |
式中,ypredict为预测值;ytrue为真实值;N为预测总条目数;M为站点数。
(3)试验结果
本试验预测方式为利用前5个时间序列的公交车站客流量数据,预测第6个时间段的客流量。
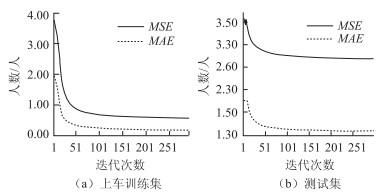
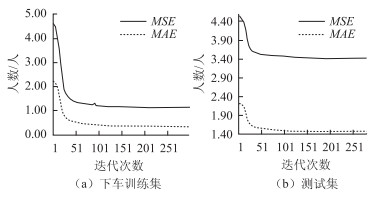
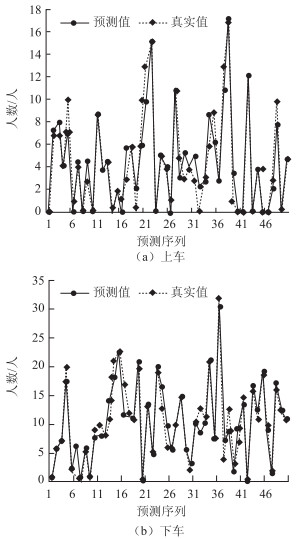
本试验中所构建的LSTM模型在上车客流量训练集和下车客流量训练集中的平均MSE和平均MAE分别可以达到0.84人和0.26人,由此可以看出该模型能够对训练集完成较好的学习。在测试集中,由于生态城内部公交车带有较强的区域性,因此在分时间段统计客流量时会存在较多的0值,也就是说,在高峰时间段上下车乘客会数量较多,而在其他时间段客流量会体现出稀疏型。因此,在预测数据中,上车和下车客流量的平均MSE和平均MAE会有所上升,分别为3.18人和1.43人,模型训练和测试结果为图 7和图 8。图 9中为在“鲲玺园站”随机抽取的50个预测时段的预测值和真实值进行对比,可以看出,模型的预测值与真实值有较高的吻合程度且平均误差为0.9人。
|
| 图 7 上车训练集和测试集中随着迭代次数的增加,MAE与MSE值的变化 Fig. 7 Changes of MAE and MSE as number of iterations increases in training set and test set of getting on bus |
| |
|
| 图 8 下车训练集和测试集中随着迭代次数的增加,MAE与MSE值的变化 Fig. 8 Changes of MAE and MSE as number of iterations increases in training set and test set of getting off bus |
| |
|
| 图 9 “鲲玺园站”随机抽取50个预测序列的上车和下车预测值和真实值对比 Fig. 9 Comparison of randomly selected 50 prediction sequences of predicted traffic values and true traffic values of getting on and getting off bus at Kunxiyuan station |
| |
(4) 对比试验
另外,为了比较LSTM神经网络模型在单站点输入和多站点输入时的预测精度,本研究将LSTM神经网络模型分别用于单站点预测和多站点同时预测。试验中模型的训练和测试数据集总体相同,只是在LSTM神经网络的单站点预测时,需要分别将单个站点的客流量输入模型,同时以全部站点的平均MSE和平均MAE作为预测精度的衡量标准。试验结果如表 3所示,可以看出,多站点的LSTM神经网模型的预测精度优于单站点的LSTM模型,说明考虑站点客流量之间的相关性能够提高建模精度。
| LSTM模型的输入 | 数据方式 | 平均MSE/人 | 平均MAE/人 |
| 单站点输入 | 上车 | 3.56 | 2.18 |
| 下车 | 3.68 | 2.19 | |
| 多站点同时输入 | 上车 | 2.97 | 1.38 |
| 下车 | 3.40 | 1.47 |
另外,本研究将多站点输入时的LSTM神经网络模型与传统SVR,ARMA进行了对比试验。这些模型同样使用相同的训练集和测试集,但是模型输入略有不同。对于SVR和ARMA模型,由于其无法学习站点之间的相互影响关系,需要采用对每个站点进行单独的建模预测,并将得到的MSE和MAE取均值。预测精度见表 4。从表中可以看出,LSTM神经网络模型在多站点输入时的预测精度较2种传统的时间序列模型(ARMA和SVR)高,说明在长时间序列的公交车站客流量预测中,LSTM具有更高的精度。
| 方法 | 总体平均MSE/人 | 总体平均MAE/人 |
| LSTM(多站点同时输入) | 3.18 | 1.43 |
| ARMA | 10.87 | 8.13 |
| SVR | 8.51 | 6.22 |
综上,LSTM神经网络模型在长时间序列的公交车站客流量预测时具有优秀的表现力,并且,多站点同时输入能够提高其预测精度。
3 结论本研究实现了一种基于LSTM的神经网络模型的公交车站点客流量预测方法,该模型能够学习传统时间序列预测算法所不能发现的多个站点间的相关性,并且拥有较长时间的记忆功能,可对多站点的长时间序列客流量数据进行有效学习。通过对比发现,该模型较传统的单站点时间序列预测模型有较好的预测效果和泛化能力。证明了基于LSTM的神经网络模型在多个站点的客流量预测中的有效性,并且通过对实际的客流量监测数据方面分析可以得出,多个公交车站的客流量数据间存在相关关系。因此,对于公交车站客流量预测和调度等时效性较强的问题具有十分重要的意义。在未来的研究中,可以比较细致地考虑站点之间的距离或者站点所处的地理空间位置,进一步细致地研究站点之间客流量的影响程度,从而逐步提高模型预测的表现力。
| [1] |
李琦. 物流需求预测中移动平均法应用分析[J]. 中国商贸, 2011(2): 139-140. LI Qi. Analysis on Application of Moving Average Method in Logistics Demand Forecasting[J]. China Business & Trade, 2011(2): 139-140. |
| [2] |
RICE J, ZWET E V. A Simple and Effective Method for Predicting Travel Times on Freeways[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(3): 200-207. |
| [3] |
JIWON M, KIM D K, KHO S Y, et al. Travel Time Prediction Using k Nearest Neighbor Method with Combined Data from Vehicle Detector System and Automatic Toll Collection System[J]. Transportation Research Record, 2011, 2256: 51-59. |
| [4] |
AHMED M S, COOK A R. Analysis of Freeway Traffic Time-series Data by Using Box-Jenkins Techniques[J]. Transportation Research Record, 1979, 722: 116. |
| [5] |
宋子房. 公路短时车流量预测模型研究[J]. 科学决策, 2014(4): 83-94. SONG Zi-fang. Study on Short-term Traffic Volume Prediction Model[J]. Scientific Decision Making, 2014(4): 83-94. |
| [6] |
唐秋生, 程鹏, 李娜. 基于GSO-BP神经网络的城市轨道交通客流量短时间预测[J]. 交通科技与经济, 2017, 19(1): 1-4. TANG Qiu-sheng, CHENG Peng, LI Na. Short Time Forecasting of Passenger Flow in Urban Railway Using GSO-BPNN Method[J]. Technology & Economy in Areas of Communications, 2017, 19(1): 1-4. |
| [7] |
RUMELHART D E, HINTON G E, WILLIAMS R J.Learning Internal Representations by Error Propagation[D].San Diego: University of California San Diego, 1985. http://www.researchgate.net/publication/243743707_Learning_Internal_Representations_through_Error_Propagation
|
| [8] |
ZHAO Z, CHEN W, WU X, et al. LSTM Network:A Deep Learning Approach for Short-term Traffic Forecast[J]. IET Intelligent Transport Systems, 2017, 11(2): 68-75. |
| [9] |
MA X, YU H, WANG Y, et al. Large-scale Transportation Network Congestion Evolution Prediction Using Deep Learning Theory[J]. Plos One, 2015, 10(3): 40-44. |
| [10] |
MA X, TAO Z, WANG Y, et al. Long Short-term Memory Neural Network for Traffic Speed Prediction Using Remote Microwave Sensor Data[J]. Transportation Research Part C:Emerging Technologies, 2015, 54(5): 187-197. |
| [11] |
SHAO H, SOONG B H.Traffic Flow Prediction with Long Short-term Memory Networks (LSTMs)[C]//2016 IEEE Region 10 Conference (TENCON).Singapore[s.n.], 2016: 2986-2989. http://www.researchgate.net/publication/313585973_Traffic_flow_prediction_with_Long_Short-Term_Memory_Networks_LSTMs
|
| [12] |
WU Y K, TAN H C.Short-term Traffic Flow Forecasting with Spatial-temporal Correlation in a Hybrid Deep Learning Framework[D].Beijing: Beijing Institute of Technology, 2016. https://www.researchgate.net/publication/311430647_Short-term_traffic_flow_forecasting_with_spatial-temporal_correlation_in_a_hybrid_deep_learning_framework
|
| [13] |
高隽. 人工神经网络原理及仿真实例[M]. 北京: 机械工业出版社, 2003. GAO Jun. Principles of Artificial Neural Network and Simulation Examples[M]. Beijing: China Machine Press, 2003. |
| [14] |
RUMELHART D, MCCLELLAND J. Learning Internal Representations by Error Propagation[M]. Cambridge: MIT Press, 1988: 318-362.
|
| [15] |
朱小燕, 王昱, 徐伟. 基于循环神经网络的语音识别模型[J]. 北京:计算机学报, 2001, 24(2): 213-218. ZHU Xiao-yan, WANG Yu, XU Wei. Speech Recognition Model Based on Recurrent Neural Networks[J]. Beijing:Chinese Journal of Computers, 2001, 24(2): 213-218. |
| [16] |
TEBELSKIS J.Speech Recognition Using Neural Networks[D].Berlin: Siemens AG, 1995. https://www.researchgate.net/publication/2415744_Speech_Recognition_Using_Neural_Networks
|
| [17] |
沈文炜, 施惠昌. 基于循环神经网络的传感器漂移补偿方法[J]. 计算机工程与科学, 2005, 27(12): 95-96. SHEN Wen-wei, SHI Hui-chang. An RNN-based Approach to Compensating Sensor Drift[J]. Computer Engineering & Science, 2005, 27(12): 95-96. |
| [18] |
BENGIO Y, DUCHARME R, VINCENT P, et al. A Neural Probabilistic Language Model[J]. Journal of Machine Learning Research, 2003, 3(2): 1137-1155. |
| [19] |
FU R, ZHANG Z, LI L.Using LSTM and GRU Neural Network Methods for Traffic Flow Prediction[C]//201631st Youth Academic Annual Conference of Chinese Association of Automation (YAC).Wuhan: IEEE, 2016: 324-328. https://www.researchgate.net/publication/312402649_Using_LSTM_and_GRU_neural_network_methods_for_traffic_flow_prediction
|
| [20] |
HOCHREITER S, SCHMIDHUBER J. Long Short-term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780. |
| [21] |
GRAVES A. Supervised Sequence Labelling with Recurrent Neural Networks[M]. Berlin: Springer-Verlag, 2012.
|
| [22] |
沈家军, 王炜, 陈峻. 基于灰色马尔可夫模型的近期公交客流量预测[J]. 公路交通科技, 2007, 24(9): 120-123. SHEN Jia-jun, WANG Wei, CHEN Jun. Short-term Urban Public Transit Volume Forecast Based on Gray-Markov Model[J]. Journal of Highway and Transportation Research and Development, 2007, 24(9): 120-123. |
 2019, Vol. 36
2019, Vol. 36
