扩展功能
文章信息
- 陈朝慰, 梁巍
- CHEN Chao-wei, LIANG Wei
- 横向分段施工预应力混凝土斜箱梁极限承载能力研究
- Study on Ultimate Bearing Capacity of Transversely Segmental Constructed PC Skew Box Girder
- 公路交通科技, 2019, 36(2): 103-111
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 103-111
- 10.3969/j.issn.1002-0268.2019.02.014
-
文章历史
- 收稿日期: 2018-05-25
横向分段施工预应力混凝土斜箱梁结构(以下简称分段合成斜箱梁),指将箱梁分解为预制工字梁和湿接缝两个组成部分,通过采用分片预制工字梁→预应力张拉→吊装→现浇合成箱梁的施工方式进行混凝土斜弯箱梁桥的组合施工。该施工方式可以显著降低吊装要求,减少桥梁设计和施工的难度,加快施工进度,并且节约工程的造价。但由于其“化整为零、集零为整”的施工步骤,与整体预制(或现浇)施工的箱梁相比,受力性能存在一定的差异[1-6],如在弹性受力阶段,外力作用时分段合成斜箱梁底板湿接缝受到预制工字梁的预应力作用,受力有异于普通钢筋混凝土,此重分布应力对湿接缝混凝土的受拉产生了抑制作用[2-3]。
当前国内外学者对箱梁的极限承载能力均有一定的研究,严圣友[7]对30 m部分预应力混凝土箱梁的极限承载能力进行了试验研究,得到结构极限承载力及裂缝分布规律; 余波等[8]对左家堡大桥进行了破坏试验,将测点应力和裂缝分布与有限元计算结果进行对比,吻合较好; 罗振先[9]等研究了偏心荷载下薄壁箱梁的极限承载力分析方法; 余晓琳[10]等对大悬臂展翅预应力混凝土宽箱梁桥极限承载力分析; 葛继平[11]等对重复荷载下高速铁路32 m箱梁模型受力全过程试验进行了研究,得到箱梁已经达到承载力极限状态(破坏)的标志是弯曲挠度达到跨度的1/30,受拉主筋处最大裂缝宽度达到1.8 mm;张逸[12]等对箱型截面齐次广义屈服函数的数值拟合及极限承载力进行了分析;M.Samaan, S.T.Song等[13-14]建立了多座不同几何尺寸的箱梁桥有限元模型,考察不同跨径、箱梁数量和车道数对其在荷载作用下应力、支反力以及挠度的影响; Miller等[15]对挪威Smestua桥进行破坏性试验,最终桥梁受剪破坏,试验说明几何外形和边界条件对桥梁的受力性能有很大影响; ROSCHKE等[16]利用足尺模型对I-295公路桥梁进行破坏性试验,结果表明该桥的极限承载能力大于设计值。但以上文献的研究对象均为整体浇铸及预制的箱梁结构,其结论对于分段浇注的箱梁是否适用仍未可知,而对于后者的极限承载能力研究,截至目前仍未见相关报道。
为此,本研究以东莞厚街水道大桥为工程背景,研究分段施工合成斜箱梁桥的极限承载能力。该桥是一座长为3×(5×40)m=600 m,斜交角为30°~40°的预应力混凝土单箱多室等截面箱梁桥,箱高2.2 m,桥面单幅宽度为17.5 m;预制单跨40 m的最大弦弧高为13 cm,采用分段合成斜箱梁施工方式。设计荷载:城-A级;抗震设计的基本烈度为6度,按7度设防。为了便于分析其受力性能,取跨径40 m、斜交角为40°的标准跨分别制作分段合成斜箱梁和整体浇注斜箱梁的两个模型,对其进行混凝土模型试验[17]。其后对整体浇注斜箱梁有限元模型进行改进,通过利用生死单元的功能在块体模型上施加等效荷载的方式完善了分段合成斜箱梁的有限分析模型,在此基础上分析比较了两者极限承载能力试验和有限元模型之间的差异,进一步通过参数分析研究了横向分段施工预应力混凝土斜箱梁的极限承载能力的影响因素,最后系统总结了横向分段施工斜箱梁的极限承载能力。
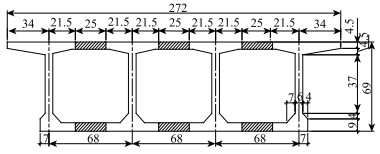
1 模型试验 1.1 试验模型设计试验模型的制作方式与文献[2]所述一致,根据斜箱梁实桥的原型,按照1: 3.2的比例设计整体浇注斜箱梁和分段合成斜箱梁模型,模型梁跨度均为12.38 m,宽度均为2.72 m,斜交角均40°,预应力筋和普通钢筋布置均相同,截面如图 1所示,施工方式分别采用整体浇注方式和分段施工再合成的方式。
|
| 图 1 试验模型的横截面(单位:cm) Fig. 1 Cross-section of test model(unit:cm) |
| |
1.2 试验加载
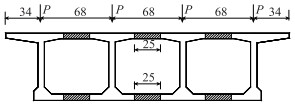
考虑到作用于顶板上荷载需通过腹板传递到底板以及便于加载的需要,模型的加载布置如图 2所示,将4个集中荷载分别施加于跨中横断面梁的腹板顶端。试验的加载系统采用成都市某液压设备有限公司的4台100 t稳压液压千斤顶,利用分配梁对斜箱梁模型进行同步加载。
|
| 图 2 横向4个加载点(单位:cm) Fig. 2 Loading points in transverse direction (unit:cm) |
| |
试验主要器材有:千斤顶、应变片、挠度计、WBD-30百分表、WBD-50百分表、裂缝显微镜,以及IBM数字采集系统和DH3816数字采集系统。
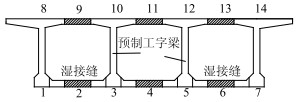
位移和应变的测点布置于梁肋底部、顶部和湿接缝中心位置,如图 3所示,图中所示的数字即为位移和应变测试工具所处的位置。
|
| 图 3 测点布置 Fig. 3 Layout of measuring points |
| |
1.3 加载过程
在试验过程中,采用分级加载的方式进行,先按每级60 kN加载,每级荷载稳定10 min后,采集数据。当发现监控点的数据有突变时,按每级40 kN加载。在加载过程中观测结构开裂情况,用裂缝显微镜检测裂缝大小,并用白笔画出裂缝长度开展情况。
1.3.1 整体浇注斜箱梁当施加的荷载为420 kN左右时,发现监控点5的采集数据曲线发生突变,挠度和应变值增长加快,随后按每级40 kN加载,并观测裂缝宽度。继续加载,在结构跨中截面的各梁肋底部发现裂缝,随着荷载增加,裂缝向两边发展。当加载至约660 kN时,梁底裂缝宽度为0.08;当加载至约700 kN时,梁底裂缝宽度为0.12 mm。经计算得出荷载为680 kN时,最大的裂缝宽度已达到《公路钢筋混凝土及预应力混凝土桥涵设计规范》容许的最大裂缝宽度值0.1 mm。当加载到920 kN左右时,结构的挠度增长迅速时,进行连采数据,直至结构破坏。
1.3.2 分段合成斜箱梁当加载至300 kN左右时,发现监控点4的采集数据曲线发生突变,随后按每级40 kN加载,并观测裂缝宽度。继续加载,在结构跨中截面的各湿接缝混凝土处发现裂缝,随着荷载增加,裂缝向两边的预制工字梁发展,直到预制工字梁肋底处开裂;随着荷载继续增加,裂缝沿着各腹板斜向增长,此时对每级加载后裂缝的开展实行标记。当施加的荷载增至540 kN时,最大的裂缝宽度为0.08 mm,增至580 kN时为0.11 mm。经计算得出荷载为564 kN时,最大的裂缝宽度已达到《公路钢筋混凝土及预应力混凝土桥涵设计规范》容许的最大裂缝宽度值0.1 mm。当加载到880 kN左右时,结构的挠度增长迅速,进行连采数据,直至结构破坏。
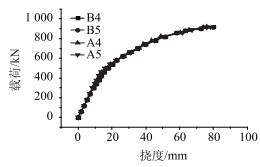
1.4 试验结果分析破坏工况荷载作用下,分段合成斜箱梁和整体浇注斜箱梁跨中截面一些测点的挠度和应变如图 4~图 6所示,图中的A和B分别代表的是整体浇注斜箱梁和分段合成斜箱梁,A和B后的数字表示测点的位置,如B4代表分段合成斜箱梁测点4的结果。由于加载后期,挠度增长速度过快,为了仪器安全,挠度数据只测至920 kN。
|
| 图 4 荷载-挠度曲线 Fig. 4 Curves of load vs. deflection |
| |
|
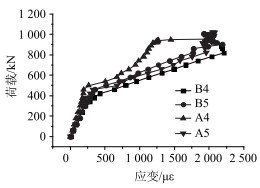
| 图 5 荷载-钢筋应变曲线 Fig. 5 Curves of load vs. strain of steel bar |
| |
|
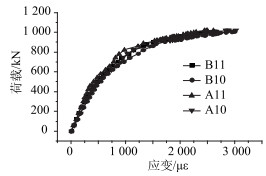
| 图 6 荷载-混凝土应变曲线 Fig. 6 Curves of load vs. strain of concrete |
| |
从图 4~图 6可以看出,对于整体浇注预应力混凝土斜箱梁,当施加的荷载为420 kN左右时,挠度和应变值增长加快,荷载-挠度曲线以及荷载-应变曲线的斜率减小,表明跨中截面的混凝土开裂;对于分段合成斜箱梁,当施加的荷载为300 kN时,4点的钢筋应变值曲线突变,荷载-挠度曲线以及荷载-应变曲线的斜率减小,此时可见其跨中截面湿接缝处产生裂缝;当施加的荷载为460 kN时,4点和5点的钢筋应变值曲线突变,荷载-挠度曲线以及荷载-应变曲线的斜率显著减小,此时可见跨中截面处预制工字梁也产生了裂缝;当荷载增至800 kN时,荷载-混凝土应变曲线和荷载-挠度曲线变得更加平缓,现场的裂缝观测表明,结构跨中截面处出现梁体裂缝。
从图 5~图 6可以看出,对于整体浇注预应力混凝土斜箱梁,当施加的荷载达到986 kN左右时,测得钢筋的应变值处于不稳定状态,混凝土应变值急剧增长,表明受力钢筋达到屈服;当施加的荷载达到1 020 kN左右时,结构达到其极限荷载,荷载-混凝土应变曲线图趋向于水平,此时混凝土的最大压应变值已超过3 000 με,表明跨中截面顶板的混凝土被压碎,施加的荷载达到结构的极限承载力值。因此整体浇注预应力混凝土斜箱梁极限承载力为1 020 kN。
从图 5~图 6可以看出,对于分段合成斜箱梁,当荷载增至937 kN时,可发现钢筋应变不稳定,而混凝土应变快速增长,表明受力钢筋达到屈服。当施加的荷载达到1 008 kN时,结构即达到了其极限承载能力,荷载-混凝土应变曲线图趋向于水平,混凝土的最大压应变值达到3 000 με,跨中截面顶板的混凝土被压碎,施加的荷载达到结构的极限承载力值。因此分段合成斜箱梁的极限承载力为1 008 kN。
因此整体浇注斜箱梁和分段合成斜箱梁的破坏过程既有相同点,也有不同点。两者的共同点是:当结构最后破坏时,受拉钢筋先达到屈服,然后混凝土被压碎,结构再也不能承载,施加的荷载达到结构的极限承载力值;且整体浇注斜箱梁的极限承载力为1 020 kN,分段合成斜箱梁为1 008 kN,两者相差仅为1.18%,可以认为两者的极限承载力基本相等。
两者的不同点为:当施加荷载达到300 kN时,分段合成斜箱梁跨中截面湿接缝的混凝土开裂,达到460 kN时,预制工字梁的混凝土开裂,所以湿接缝的混凝土先于预制工字梁开裂。从图 4可以看出,对于整体浇注斜箱梁,当荷载达到420 kN时,整体浇注斜箱梁5点所处主梁混凝土开裂,达到460 kN时,4点所处的主梁混凝土开裂。因此分段合成斜箱梁的混凝土开裂荷载(300 kN)低于后者(420 kN);另外,前者达到《规范》容许的最大裂缝宽度值0.1 mm时的荷载为564 kN,后者为680 kN,所以前者最大裂缝宽度的荷载也小于后者。
2 整体浇注斜箱梁分析建立整体浇注斜箱梁的有限元模型,进行有限元分析,并与试验加载结果进行比较,得到其极限承载能力。
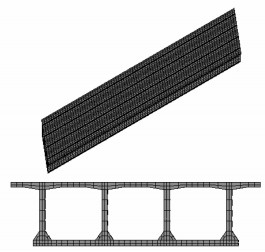
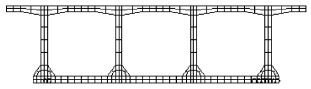
2.1 有限元模型建立应用ANSYS程序对整体浇注斜箱梁进行建模分析[18-21],模型采用分离式的有限元模型,混凝土采用Solid65单元模拟,预应力钢筋与普通钢筋用Link8单元模拟,假定普通钢筋与混凝土之间不存在滑移,通过耦合两者节点的全部自由度来实现联结;预应力钢筋与混凝土只在张拉处耦合两者节点的全部自由度,其余则放松纵向的自由度,全桥共有23 142个块体单元和736个link8线单元,模型如图 7所示。
|
| 图 7 有限元模型图 Fig. 7 FE model |
| |
分析时混凝土的受拉本构关系为双直线的模型,如式(1)所示。式中ft为混凝土的抗拉强度;εl0=ft/Et;εt为混凝土的应变;σt为混凝土的应力;Et为混凝土的弹性模量。对预应力钢筋和普通钢筋采用弹性强化模型,屈服前为完全弹性的,屈服后的应力-应变关系简化为很平缓的斜直线(E′s=0.01Es)见式(2)。其中εs为钢筋的应变;σs为钢筋的应力;Es为钢筋的弹性模量。采用弧长法进行非线性静力计算,L2规范进行非线性计算的收敛核查。
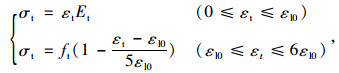
|
(1) |

|
(2) |
式中,fy为钢筋的屈服强度;εy为钢筋的屈服应变。
应用上述模型,输入工况的荷载,计算整体浇注箱梁的位移和应变,并查看结构的裂缝。
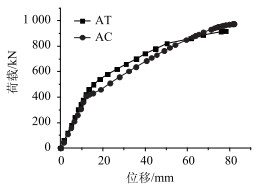
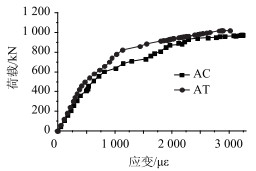
2.2 位移和应变比较分析在有限元分析过程中,随着荷载的逐步增加,构件由弹性开始转化为塑性。当荷载施加到800 kN左右时,跨中单元的应变已经达到了混凝土应变极限,构件完全进入塑性工作状态。随着荷载的逐渐增大,混凝土继续开裂,钢筋开始屈服,承载能力下降。当荷载进一步增大,在较小的荷载增量下,产生较大的竖向变形,程序计算出现不能收敛,此时认为对应的荷载值即为该斜箱梁的极限荷载。加载过程中测点5的荷载-挠度曲线图如图 8所示,测点10的荷载-应变如图 9所示,其中AC表示整体浇注斜箱梁的有限元计算值,AT表示整体浇注斜箱梁的试验实测值。
|
| 图 8 整体浇注斜箱梁测点5的荷载-挠度曲线 Fig. 8 Curves of load vs. deflection at 5th measuring point of ICPCSBG |
| |
|
| 图 9 整体浇注斜箱梁测点10的荷载-应变曲线 Fig. 9 Curves of load vs. strain at 10th measuring point of ICPCSBG |
| |
从图 8~图 9可以看出,在荷载为0~400 kN时,计算值和试验值误差较小,符合较好,这是由于混凝土还处于线弹性阶段。此后加载,明显显示出材料的非线性特点,荷载-挠度和荷载-应变关系呈曲线状态;当荷载施加到975 kN时,挠度计算值达到82.8 mm,此时荷载-挠度和荷载-应变曲线都出现转弯点,计算不能收敛,可以认为此时的挠度对应的荷载值975 kN为整体浇注斜箱梁的极限荷载。
从图 8~图 9还可以看出,计算与实测的荷载-挠度和荷载-应变关系相对吻合良好。当挠度为79.2 mm,试验荷载约为919.7 kN时,计算荷载为948.6 kN,两者相差为3.1%;此时试验对应的应变为1 920 με左右,计算值为2 140 με,两者相差为10.2%;且计算出的整体浇注斜箱梁的极限承载力为975 kN,虽低于实测值,但与之相差只有4.4%,两者基本吻合。
2.3 裂缝分析从图 4可以看出,当荷载施加到420 kN左右时,荷载-位移曲线发生突变,表明结构产生开裂。结构的跨中截面底部首次出现裂缝,如图 10所示,此与试验测试结果一致;当荷载施加800 kN时,梁体的应变明显增大,竖向位移增长幅度也加大,梁体已经出现了裂缝,梁体下缘的混凝土单元已经退出工作,其拉应力全部由钢筋来承担。梁体的裂缝如图 11所示。
|
| 图 10 跨中截面底部首条裂缝 Fig. 10 First crack at bottom of midspan section |
| |

|
| 图 11 整体浇注斜箱梁梁体裂缝图 Fig. 11 Cracks of ICPCSBG |
| |
从上述的位移、应变和裂缝分析可见,有限元分析与试验结果基本一致,说明有限元模型中参数的取值是正确的,可以用上述的参数对整体浇注斜箱梁的极限承载力进行分析。
3 分段合成斜箱梁的有限元分析及数据比较 3.1 分析思路由于分段合成斜箱梁在施加预应力时各片预制工字梁还未浇注成一个整体,各片预制工字梁是单独承受预加力和自重作用,因此在有限元模型上施加预应力时,可通过生死单元来实现,即先“杀死”各片湿接缝梁和虚横梁的单元,然后施加预应力和自重。待预应力加载求解后,在下一个载荷步重新激活被“杀死”的单元,再施加其他的荷载求解运算。若采用生死单元考虑结构的施工过程,利用上述模型分析分段合成斜箱梁极限承载力,则将无法实现结构截面上的应力重分布。参考文献[22]的做法,并根据文献[2]和文献[3]湿接缝应力计算的思路,预制梁对湿接缝贡献力可等效为均布荷载q和梁端部弯矩M0的联合作用,因此可以利用生死单元的功能,在块体模型上通过施加等效荷载来实现湿接缝获得的贡献应力,并可利用上述整体浇注斜箱梁的有限元模型计算分段合成斜箱梁的极限承载力。由于这只是预先在湿接缝混凝土上施加其开裂前所获得协调应力值,并扣除掉预制工字梁的贡献应力,所以分段合成斜箱梁的开裂荷载将不会改变,结构的极限承载力值也不会改变。
应用整体浇注斜箱梁模型,按照上述思路,输入各阶段的荷载,计算分段合成斜箱梁的位移和应变,并查看结构的裂缝。
3.2 位移和应变比较分析对于分段合成斜箱梁,在试验计算过程中,随着荷载的逐步增加,构件由弹性开始转化为塑性。当荷载施加到780 kN左右时,跨中单元的应变已经达到了混凝土应变极限,构件完全进入塑性工作状态。随着荷载的逐渐增大,混凝土继续开裂,钢筋开始屈服,承载能力下降。当荷载进一步增大,在较小的荷载增量下,产生较大的竖向变形,程序计算出现不能收敛,此时认为对应的荷载值即为该斜箱梁的极限荷载。
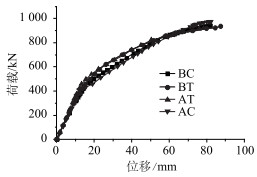
加载过程中5点荷载-挠度曲线图如图 12所示,10点混凝土荷载-应变如图 13所示,4点和5点处的钢筋荷载-应变如图 14所示,其中BC表示分段合成斜箱梁的有限元计算值,BT表示分段合成斜箱梁的试验实测值,AC和AT表示的含义与之前一样。
|
| 图 12 测点5的荷载-挠度曲线 Fig. 12 Curves of load vs. deflection at 5th measuring point |
| |
|
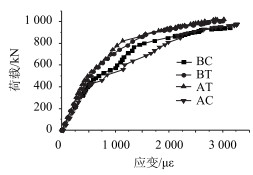
| 图 13 测点10的荷载-混凝土应变曲线 Fig. 13 Curves of load vs. strain of concrete at 10th measuring point |
| |
|
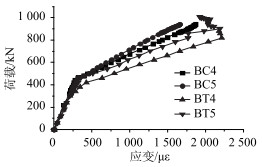
| 图 14 分段合成斜箱梁荷载-钢筋应变曲线 Fig. 14 Curves of load vs. strain of steel bar of TSCPCSBG |
| |
从图 12~图 14可以看出,在荷载为0~420 kN时,计算值和试验值误差较小,符合较好。此后加载,明显显示出材料的非线性特点,荷载-挠度关系和荷载-应变呈曲线状态。当计算荷载施加到941 kN时,计算挠度值达到81.8 mm,混凝土应变达到达3 200 με左右,钢筋的拉应变1 900 με左右,此时荷载-挠度曲线出现转弯点,计算不能收敛,认为已经达到斜箱梁的极限状态了。因此有限元计算得到分段合成斜箱梁的极限荷载为941 kN。
从图 12~图 14还可以看出,分段合成斜箱梁的有限元计算值与试验的实测值吻合良好。试验实测的极限承载力为1 008 kN,有限元计算值为941 kN,两者只相差6.7%。当荷载为937 kN时,试验实测出5点挠度为87.4 mm,有限元计算值为80.0 mm,两者只相差8.5%。
此外,分段合成斜箱梁的极限承载力的有限元计算值为941 kN,整体浇注斜箱梁是975 kN,两者只相差3.5%,可以认为两者的极限承载力基本相等。综上所述,分段合成斜箱梁与整体浇注斜箱梁的极限承载力相差甚微,可认为两者基本相等。
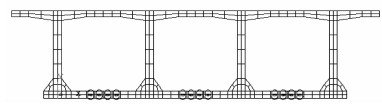
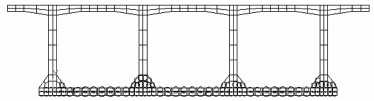
3.3 裂缝分析当荷载施加至315 kN时,结构的跨中截面底部湿接缝出现裂缝,如图 15所示;荷载施加至450 kN时,预制工字梁的跨中截面底部出现裂缝,如图 16所示;荷载施加780 kN时,梁体的竖向位移明显增大,已经出现了裂缝,下缘的混凝土单元已经退出工作,其拉应力全部由钢筋来承担。梁体的裂缝如图 17所示。
|
| 图 15 跨中截面底部湿接缝开裂 Fig. 15 Cracks at wet joint of bottom of midspan section |
| |
|
| 图 16 跨中截面底部混凝土开裂 Fig. 16 Concrete cracks at bottom of midspan section |
| |

|
| 图 17 分段合成斜箱梁梁体裂缝图 Fig. 17 Cracks of TSCPCSBG |
| |
分段合成斜箱梁跨中截面下缘湿接缝开裂荷载、预制工字梁跨中截面下缘开裂荷载和梁体出现裂缝荷载的有限元计算值与试验实测值比较如表 1所示。从表 1可以看出,有限元计算出分段合成斜箱梁各重要阶段的荷载与试验测试结果相差较小,最大不超过7%,所以有限元计算值与试验值吻合良好。
| 类型 | 湿接缝开裂荷载 | 预制工字梁开裂荷载 | 梁体裂缝荷载 | 极限承载力 |
| 计算值C/kN | 315 | 450 | 780 | 941 |
| 实测值T/kN | 300 | 460 | 800 | 1 008 |
| (1-C/T)/% | -5.0 | 2.2 | 2.5 | 6.7 |
从上述的位移、应变和裂缝分析可以看出,有限元分析的结果与试验结构吻合良好,本研究提出关于分析分段合成斜箱梁极限承载力的思路可行。
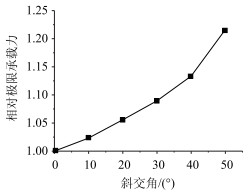
4 参数分析 4.1 斜交角的影响分析分别取斜交角φ为0°,10°,20°,30°,40°和50°建立有限元模型,按照上述的分析过程,计算各模型的极限承载力,计算结果如图 18所示。其中纵坐标采用相对极限承载力。相对极限承载力指的是以箱梁斜交角为0°时的极限承载力为分母,任何斜交角的极限承载力为分子得到的比值。
|
| 图 18 斜交角对极限承载力的影响 Fig. 18 Influence of skew angle on ultimate bearing capacity |
| |
从图 18可以看出,当在跨中作用集中荷载时,随着斜交角的增大,斜箱梁的极限承载力增大。在斜交角φ分别为0°和10°时,其相对极限承载力仅相差2.2%,认为斜交角小于10°的斜桥可以按正桥进行计算。
4.2 抗弯抗扭刚度比的影响分析通过增加横梁实现抗弯抗扭刚度比k的变化,每根横梁的厚度为20 cm,共分析以下4种斜箱梁模型的极限承载力。
模型1:试验模型;
模型2:在试验模型的基础上,在梁的端部截面各增加一根横梁;
模型3:在模型2的基础上,在梁的跨中截面增加一根横梁;
模型4:在模型3的基础上,在梁的L/4截面各增加一根横梁。
从模型1变化到模型4,其横梁数目逐渐增加,因此它们的抗弯抗扭刚度比k不断减小。通过计算得到4个模型的极限承载力如表 2所示。
| 模型 | 1 | 2 | 3 | 4 |
| 极限承载力 | 975 | 987 | 998 | 1 002 |
从表 2可以看出,随着抗弯抗扭刚度比k的减小,即横梁数目的增加,斜箱梁的极限承载力逐渐增大,但增大幅度较小,如模型4只比模型1增大2.8%。由此可见,由于斜箱梁的抗扭刚度大,增加横梁数目对结构的受力性能影响很小。因此设计斜箱梁结构时,可以不设横梁或设少量的横梁。
5 结论通过对整体浇注斜箱梁和分段合成斜箱梁的极限承载力有限元分析,并与试验结果进行比较,以及相应的的参数分析,得到以下结论。
(1) 试验测试和有限元分析结果均表明了分段合成与整体浇注斜箱梁的极限承载力相差甚微(在研究设计的条件下,模型试验仅相差1.18%,有限元分析仅相差3.5%),可认为两者基本相等。
(2) 试验测试和有限元分析结果均表明了两种形式的斜箱梁在荷载作用下,其破坏过程不同,前者跨中湿接缝混凝土先于预制工字梁混凝土开裂,后者梁肋底部混凝土开裂先于湿接缝处的混凝土,且前者的开裂荷载低于后者。
(3) 分段合成斜箱梁有限元分析的极限承载力结果与试验测试结果基本吻合,表明提出把预制梁对湿接缝的贡献力等效为均布荷载q作用和梁端部弯矩M0的联合作用,利用生死单元的功能,在块体模型上通过施加等效荷载,实现湿接缝获得贡献力,然后再计算结构极限承载力的思路是可行的。
(4) 整体浇注(或分段合成)斜箱梁的极限承载力随着斜交角的增加而增大;而斜交角小于10°的斜桥可以按正桥进行简化计算,其误差仅为2.2%。
(5) 整体浇注(或分段合成)斜箱梁的极限承载力随着抗弯抗扭刚度比的减小而增大,但增大幅度较小(研究中最大与最小抗弯抗扭刚度比所对应的极限承载力仅相差2.8%), 因此在设计斜箱梁结构时,可以不设横梁或设少量的横梁。
(6) 文中提出的分片预制工字梁→预应力张拉→吊装→现浇合成箱梁的施工方式,不仅能大幅减小施工和设计难度,节省工程造价,而且在受力性能方面与整体浇注的混凝土斜箱梁相比相差不多,因此在宽度较大的大中跨径混凝土斜交箱梁桥建设当中具有较为显著的优势。
(7) 文中研究了分段合成简支斜箱梁的极限承载力,对于分段合成连续斜箱梁的极限承载力应该如何计算,以及其与整体浇注斜箱梁的极限承载力有多大的差距,有待于进一步研究。
| [1] |
陈朝慰.横向分段施工预应力混凝土斜箱梁受力性能研究[D].福州: 福州大学, 2007. CHEN Chao-wei.Study on Loading Behavior of Transversely Segmental Constructed Prestressed Concrete Skew Box Girder[D].Fuzhou: Fuzhou University, 2007. http://www.cnki.com.cn/Article/CJFDTotal-FJJC201605006.htm |
| [2] |
陈朝慰. 横向分段施工预应力箱梁的湿接缝受力性能研究[J]. 四川理工学院学报:自然科学版, 2016, 29(2): 61-64. CHEN Chao-wei. Study on the Mechanical Performance of the Wet-joint of the Prestressed Concrete Box Girder with Transversely Segmental Construction[J]. Journal of Sichuan University of Science Engineering, 2016, 29(2): 61-64. |
| [3] |
陈朝慰, 彭大文. 横向分段施工预应力混凝土斜箱梁的模型试验研究[J]. 公路交通科技, 2009, 26(3): 87-93. CHEN Chao-wei, PENG Da-wen. Study on the Model Experiment of the Prestressed Concrete Skewed Box Girder with Transversely Segmental Construction[J]. Journal of Highway and Transportation Research and Development, 2009, 26(3): 87-93. |
| [4] |
郭德群.考虑剪切变形效应的单跨斜梁桥受力特性研究[D].湖南: 长沙理工大学, 2015. GUO De-qun.Mechanical Analysis of Single-span Skew Bridges Considering Shear Deformation Effect[D].Hunan: Changsha University of Science & Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10536-1016262616.htm |
| [5] |
余钱华, 杨晓超. 剪力柔性梁格理论在弯箱梁桥中的应用[J]. 中外公路, 2013, 33(5): 206-209. YU Qian-hua, YANG Xiao-chao. Application of Shear-flexible Grillage Theory in Curved Box Girder Bridge[J]. Journal of China & Foreign Highway, 2013, 33(5): 206-209. |
| [6] |
方志, 曹清, 郑辉. 钢筋混凝土箱梁顶板横向受力有效分布宽度的塑性分析[J]. 中国公路学报, 2017, 30(10): 45-52. FANG Zhi, CAO Qing, ZHENG Hui. Plastic Analysis of Transverse Effective Width of Top Slabs in Reinforced Concrete Box-girders[J]. China Journal of Highway and Transport, 2017, 30(10): 45-52. |
| [7] |
严圣友. 30 m部分预应力混凝土箱梁极限承载能力试验研究[J]. 公路工程, 2012, 37(1): 87-90. YAN Sheng-you. The Test Study of the Ultimate Bearing Capacity for the 30 m PPC Box Girder[J]. Highway Engineering, 2012, 37(1): 87-90. |
| [8] |
余波, 李勇, 孙晓红, 等. 左家堡大桥实桥承载力破坏试验及分析[J]. 公路交通科技, 2011, 28(7): 100-105, 112. YU Bo, LI Yong, SUN Xiao-hong, et al. Destructive Test and Analysis of Bearing Capacity of Zuojiabao Bridge[J]. Journal of Highway and Transportation research and Development, 2011, 28(7): 100-105, 112. |
| [9] |
罗振先.偏心荷载下薄壁箱梁的剪力滞、畸变及极限承载力分析[D].南宁: 广西大学, 2016. LUO Zhen-xian.Analysis on Shear Lag, Distortion and Ultimate Bearing Capacity of Box-section Beam under Eccentric Load[D].Nanning: Guangxi University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10593-1016199783.htm |
| [10] |
余晓琳, 贾布裕, 杨铮, 等. 大悬臂展翅预应力混凝土宽箱梁桥极限承载力分析[J]. 铁道科学与工程学报, 2015, 12(6): 1379-1386. YU Xiao-lin, JIA Bu-yu, YANG Zheng, et al. Analysis of Ultimate Bearing Capacity of Prestressed Concrete Box-girder Bridge with Large-cantilever-wing[J]. Journal of Railway Science and Engineering, 2015, 12(6): 1379-1386. |
| [11] |
葛继平, 王志强, 张旭, 等. 重复荷载下高速铁路32 m箱梁模型受力全过程试验[J]. 建筑科学与工程学报, 2013, 30(1): 49-54, 65. GE Ji-ping, WANG Zhi-qiang, ZHANG Xu, et al. Experiment on Full-range Static Performance of Model of 32 m High-speed Railway Box Girder under Repeated Loading[J]. Journal of Architecture and Civil Engineering, 2013, 30(1): 49-54, 65. |
| [12] |
张逸, 欧伟, 周强, 等. 箱型截面齐次广义屈服函数的数值拟合及极限承载力分析[J]. 钢结构, 2018, 33(3): 44-49, 103. ZHANG Yi, OU Wei, ZHOU Qiang, et al. Homogeneous Generalized Yield Function Fitting and Ultimate Bearing Capacity Analysis of Structures with Box Section[J]. Journal of Steel Structure, 2018, 33(3): 44-49, 103. |
| [13] |
SAMAAN M, SENNAH K M, KENNEDY J B. Distribution of Wheel Loads on Continuous Steel Spread-box Girder Bridges[J]. Journal of Bridge Engineering, 2002, 7(3): 175-183. |
| [14] |
SONG S T, CHAI Y H, HIDA S E. Live-load Distribution Factors for Concrete Box-girder Bridges[J]. Journal of Bridge Engineering, 2003, 8(5): 273-280. |
| [15] |
MILLER R A, AKTAN A E, SHAHROOZ B M. Destructive Testing of Decommissioned Concrete Slab Bridge[J]. Journal of Structural Engineering, 1994, 120(7): 2176-2198. |
| [16] |
ROSCHKE P N, PRUSKI K R. Overload and Ultimate Load Behavior of Posttensioned Slab Bridge[J]. Journal of Bridge Engineering, 2000, 5(2): 148-155. |
| [17] |
章关永. 桥梁结构试验[M]. 北京: 人民交通出版社, 2010. ZHANG Guan-yong. Experiment of Bridge Structure[M]. Beijing: China Communications Press, 2010. |
| [18] |
马驰, 刘世忠, 冀伟, 等. 单箱多室波形钢腹板PC组合箱梁剪力滞效应研究[J]. 公路交通科技, 2018, 35(2): 62-71. MA Chi, LIU Shi-zhong, JI Wei, et al. Study on Shear Lag Effect of Single-box Multi-cell PC Composite Box Girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2018, 35(2): 62-71. |
| [19] |
王景全, 丁峰, 戴嘉平, 等. 钢-混凝土连续组合梁桥施工全过程监测及数值分析[J]. 公路交通科技, 2006, 23(12): 91-94. WANG Jin-quan, DING Feng, DAI Jia-ping, et al. Monitoring and Numerical Analysis for Construction Phase of a Steel-concrete Composite Continuous Box Girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2006, 23(12): 91-94. |
| [20] |
姜基建, 杨婧, 王文龙. 斜交箱梁桥静动力特性试验研究[J]. 交通科技, 2015, 268(1): 1-4. JIANG Ji-jian, YANG Qian, WANG Wen-long. Experimental Study on Dynamic and Static Behavior of Skew Box Girder[J]. Transportation Science & Technology, 2015, 268(1): 1-4. |
| [21] |
任红伟, 刘保东, 李鹏飞. 考虑剪切滑移的波纹钢腹板预应力箱梁抗弯承载力计算[J]. 公路交通科技, 2012, 29(3): 86-91. REN Hong-wei, LIU Bao-dong, LI Peng-fei. Calculation of Flexural Capacity for Prestressed Box Girder with Corrugated Steel Webs Considering Shear Slip[J]. Journal of Highway and Transportation Research and Development, 2012, 29(3): 86-91. |
| [22] |
刘杰, 叶见曙, 陈娟娟. 节段接缝剪切变形对PC箱梁变形影响试验[J]. 中国公路学报, 2015, 28(2): 77-86. LIU Jie, YE Jian-shu, CHEN Juan-juan. Experiment on Effect of Shearing Deformation at Segmental Joint on Deformation of PC Box Girder[J]. China Journal of Highway and Transport, 2015, 28(2): 77-86. |
 2019, Vol. 36
2019, Vol. 36
