扩展功能
文章信息
- 颜全哲, 魏津昌, 上官萍, 卓卫东, 黄新艺
- YAN Quan-zhe, WEI Jin-chang, SHANGGUAN Ping, ZHUO Wei-dong, HUANG Xin-yi
- 公路混凝土梁桥寿命期养护优化策略分析
- Analysis on Optimal Maintenance Strategy for Highway Concrete Girder Bridges during Service Life
- 公路交通科技, 2019, 36(2): 95-102, 150
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 95-102, 150
- 10.3969/j.issn.1002-0268.2019.02.013
-
文章历史
- 收稿日期: 2018-05-04
2. 福建省公路管理局, 福建 福州 350004
2. Fujian Highway Administrative Bureau, Fuzhou Fujian 350004, China
早期道路系统预防性养护主要针对路面。1999年美国联邦公路管理局(FHWA)对预防性养护定义为[1]:一种在路面状况良好的情况下采取的基于费用-效益的养护策略。预防性养护在没有提高路面结构能力的情况下延迟路面的损坏, 通过延长原有路面的使用寿命来推迟昂贵的大修和重建活动。
20世纪90年代, 美国密西根运输部(MDOT)率先对密西根州路网中路面质量进行预防性养护试验; 试验结果发现, 对于质量合格的道路, 路面经历75%的设计寿命, 其质量降低40%, 此时预防性养护的成本假设为1美元; 若没有及时养护, 在之后12%的使用时间内, 质量再次降低40%, 此时通过纠正性养护(如大修或重建)所得到与进行预防性养护所得到相同的路况所需的费用就为4~5美元或更多[2]。美国密西根运输部的试验结果表明, 推迟路面养护将会面临着路面的大修和重建, 不仅使路面长期处于低服务水平, 而且还会造成寿命期的高成本。因此, 预防性养护具有可观的经济效益和社会效益。
近年来, 孙马等[3]提出了以桥梁预防性养护经济性、安全性及耐久性为目标的层次评价分析模型, 并建立一套关于桥梁预防性养护的模糊综合评价体系。张春霞和王巍等[4-6]初步建立了桥梁预防性养护全寿命费用与优化方法以及桥梁预防性养护实施效果后评估体系等理论框架, 并应用微粒群算法, 构建了综合养护效果最大化、使用寿命最大化和养护成本最小化等多目标的优化模型。黄天立等[7]基于Gamma过程和Matlab遗传算法工具箱, 提出锈蚀钢筋混凝土桥梁结构检查养护策略优化分析方法, 并得到可提供在不同结构使用寿命期望和检查养护成本预算下收益最大的检查养护策略的Pareto优化解集。Qaradhawi等[8]提出了桥梁预防性养护计划的优化方法。白山云等[9]结合实际工程, 对公路悬索桥的预防性养护措施和预防性养护作业等进行了探讨。
尽管预防性养护概念自提出以来, 已在许多发达国家和我国部分省市的路面养护中得到了实践应用[10-12]。然而, 当前在桥梁预防性养护研究和应用方面仍存在两个主要问题:
(1) 国内外预防性养护研究主要针对路面, 桥梁预防性养护并未形成完整的体系。
(2) 对桥梁预防性养护的最佳介入时机还没有一个普遍认同的方法。
我国公路桥梁建设自改革开放以来进入高峰期, 迄今已建成的公路桥梁总数超80万座。随着在役桥梁存量的增加、结构的老化和性能的衰退, 桥梁养护任务日益艰巨, 已逐渐成为我国公路管理部门的工作重心。因此, 研究在役公路桥梁寿命期的养护优化策略, 特别是预防性养护的介入时机等, 无疑具有重要的现实意义。本研究以公路混凝土梁桥为研究对象, 以桥梁寿命期养护活动总成本最小为优化目标, 利用Matlab软件的遗传算法, 研究探讨混凝土梁桥的养护优化策略; 通过案例分析, 得到了混凝土梁桥寿命期内主梁和桥墩的最佳养护时间和养护方法。研究结果可为我国在役公路混凝土梁桥养护提供参考。
1 混凝土梁桥寿命期养护优化决策模型 1.1 混凝土梁桥寿命期养护类型划分混凝土梁桥在服役一段时间后, 由于各种原因会产生裂缝、钢筋锈蚀和混凝土剥蚀等病害, 如果任凭病害发展, 将会使得结构的性能指标降低, 甚至危及桥梁的使用寿命和承载能力; 因此, 需要对混凝土梁桥进行正常养护。按照养护效果, 可将混凝土梁桥养护措施划分为预防性养护(PM—Preventive Maintenance)和纠正性养护(CM—Corrective Maintenance)两大类, 两类养护措施的判断标准如表 1所示; 其中, "预防性养护"对应我国现行公路桥涵养护规范(JTG H11—2004)[13]的"正常保养"和"小修", "纠正性养护"对应"中修、大修"及"加固改造"。
| 养护类型 | 判断标准 | 养护措施 |
| 预防性养护 | 基于时间的养护或定期养护, 为了延缓或推迟结构退化而采取的养护 | 正常保养、小修 |
| 纠正性养护 | 基于性能的养护, 为了提高结构性能而采取的养护 | 中修、大修; 改建、重建 |
1.2 模型假设
由于混凝土梁桥养护优化决策涉及的不确定因素众多, 为量化优化模型, 本研究作以下假设。
(1) 在建模中不考虑特定的养护措施, 仅将养护措施分为预防性养护和纠正性养护两大类, 且假定养护期间结构性能不会恢复到初始的性能指标值。
(2) 养护的开始时间和周期均为随机变量, 养护后结构退化率下降值和性能指标增量也均为随机变量。
(3) 各个养护行为之间是相互独立的, 预防性养护行为只降低结构的退化速率, 不能提高结构性能指标。纠正性养护行为只提高结构性能指标, 不能降低结构的退化速率。
(4) 桥梁结构性能指标采用现行公路桥涵养护规范[13]的全桥结构技术状况评分值。
根据美国科罗拉多大学Frangopol教授等的研究成果[14-15], 确定了如表 2和表 3所示的预防性养护和纠正性养护各随机变量的分布函数。参考文献[16], 通过调查统计福建省内81座公路混凝土梁桥的历史养护记录数据, 确定了如表 2和表 3所列的各随机变量的特征值; 其中, t1, tP, tPD, tn的单位为年; SCn的单位为万元; BDIn (n≥1), ΔBDIn(n≥1), [BDI]为评分值; α为指数退化模型的系数, 在没有可靠统计数据可用时, 一般可根据历史桥梁评定数据, 通过回归分析方法确定。
| 随机变量 | 含义 | 分布类型 | 随机变量特征值描述 |
| t1 | 初始性能退化到第一次养护的时间间隔 | 三角分布 | 桥墩:T(2, 3, 4), 主梁:T(4, 5, 6) |
| θn(n≥1) | 第n次养护时结构性能退化率 | 对数正态分布 | 均值:2/3α, 方差:0.001 |
| tP | 周期性养护时间间隔 | 三角分布 | 桥墩:T(3, 4, 5), 主梁:T(6, 8, 9) |
| tPD | 养护效果的持续时间 | 三角分布 | T(7.5, 10, 12.5) |
| SCn(n≥1) | 每次养护活动的成本 | 三角分布 | T(3, 24, 68) |
| 随机变量 | 含义 | 分布类型 | 随机变量特征值描述 |
| BDI1 | 第一次养护时结构的性能指标 | 三角分布 | T(50, 55, 65) |
| t1 | 初始性能退化到第一次养护的时间间隔 | 三角分布 | 桥墩:T(0, 10, 20);主梁:T(10, 25, 30) |
| BDIn(n≥2) | 第n次养护时结构的性能指标 | 均匀分布 | T(40, 48, 60) |
| △BDIn(n≥1) | 第n次养护后结构性能指标增量 | 对数正态分布 | 均值:20;标准差:0.2 |
| tn(n≥2) | 第n次与第n-1次养护的时间间隔 | 三角分布 | 桥墩:T(10, 17, 25);主梁:T(10, 25, 30) |
| SCn(n≥1) | 每次养护活动的成本 | 三角分布 | T(100, 200, 300) |
1.3 寿命期养护优化决策的数学模型
本研究以寿命期养护活动总成本最低为公路混凝土梁桥养护策略的优化目标, 故优化目标函数可以表示为Minimize(LCMC)。寿命期养护活动总成本按式(1)计算:
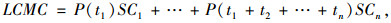
|
(1) |
式中, LCMC为桥梁寿命期养护活动总成本; SCn(1≤n≤10)为第n次养护活动的成本, 通过抽样得到; P(t)为工程经济中的一次支付现值系数, 由式(2)计算:
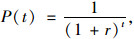
|
(2) |
式中r为折现率, 根据桥梁所在地银行公布确定。
在进行公路混凝土梁桥养护策略优化时, 要保证结构的服役时间te不小于设计使用年限, 且结构的性能指标不低于性能指标限值, 所以, 有以下的2个约束条件:
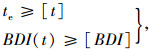
|
(3) |
式中, [t]为设计使用年限, 按现行公路桥涵设计通用规范[17]的规定取值; [BDI]为结构性能指标的最低限值, 本研究参考现行公路桥涵养护规范[13]取为40。
影响桥梁结构长期性能的因素众多, 线性退化模型往往不能反映结构长期性能的变化规律, 本研究采用如下指数形式的非线性退化模型[16]:
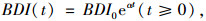
|
(4) |
式中, t为桥梁服役时间; BDI0为桥梁结构的初始性能指标。
1.4 优化算法传统的优化算法主要有目标加权法、主要目标法、极大极小值法和分层排序法等; 传统优化算法运算便捷简单, 适用于数学复杂程度低的问题。随着数学、运筹学和系统论等相关科学的发展, 近年来逐渐出现了一些新的优化算法, 如粒子群优化算法(PSO)、遗传算法(GA)等。由于在桥梁养护策略优化过程中带有大量的随机数, 因此, 本研究优先考虑使用遗传算法。
利用Matlab遗传算法实现桥梁养护优化的基本步骤包括[18]:编码、设定初始种群N、设计适应度函数、设定遗传参数(交叉概率、变异概率和代沟)、选择操作、交叉操作和变异操作。
2 案例分析 2.1 工程背景本研究选取的分析案例为一座在役的公路混凝土简支梁桥, 该桥位于福建省泉州市漳东线, 桥梁全长209.5 m, 桥面总宽24.5 m; 上部结构为钢筋混凝土空心板梁, 桥跨组合为10×20 m; 下部结构为多柱框架桥台、多柱式墩; 伸缩缝类型为毛勒橡胶伸缩缝, 水泥混凝土桥面铺装, 板式橡胶支座。该桥设计日均交通量为2 184辆/天, 设计时速为40 km/h, 设计荷载等级为汽车-20级, 桥梁环境为海洋氯化物环境。该桥于2004年11月建成投入使用, 建成至今无维修记录。表 4为该桥的历次桥梁检测结果。
| 性能指标 | 不同检测年份的评分值 | |||
| 2005 | 2008 | 2011 | 2014 | |
| BDIpier | 95 | 80 | 69 | 62 |
| BDIgirder | 97 | 91 | 85 | 80 |
利用表 4所列的历次桥梁检测数据, 根据式(4), 采用灰色系统预测方法[19], 得到了该桥在无养护情况下的混凝土主梁和桥墩的性能退化近似公式:
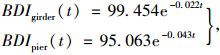
|
(5) |
式中, BDIgirder为主梁的结构性能指标随时间变化的函数; BDIpier为桥墩的结构性能指标随时间变化的函数。
由式(5)通过简单计算即可发现, 在没有采取任何养护措施时, 该桥混凝土主梁在使用约41 a后, 其性能已无法满足最低要求, 即出现安全性问题; 其混凝土桥墩在使用约20 a后, 即已出现安全性问题。可见, 若不及时采取适当的养护措施, 该桥在2024年后即可能出现结构安全问题。
2.2节以该桥主梁和桥墩为研究对象进行案例分析, 分别探讨仅预防性养护、纠正性养护以及预防性与纠正性组合的综合养护条件下的优化策略。
2.2 仅预防性养护条件下的养护优化结果如果在桥梁寿命期内仅进行预防性养护, 则可采用基于时间的维护模型, 即预防性维护模型进行优化。该模型将结构的维护行为视为按一定时间周期有规律地进行的, 并假定养护后结构在养护效果持续时间tPD时段内退化速率变慢且呈线性退化, 在(tP-tPD)时段内退化速率恢复为指数退化模型(tP为维护周期), 故每次预防性养护开始时的性能指标BDI(t)可由式(5)确定。
一般情况下, 预防性养护效果的持续时间tPD小于周期性养护时间间隔tP; 根据预防性维护模型假定, 经推导可得如下的桥梁寿命期内性能指标的表达式:
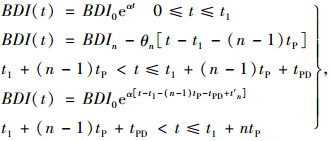
|
(6) |
式中, n为预防性养护次数, 其他参数由式(7)计算:
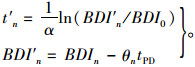
|
(7) |
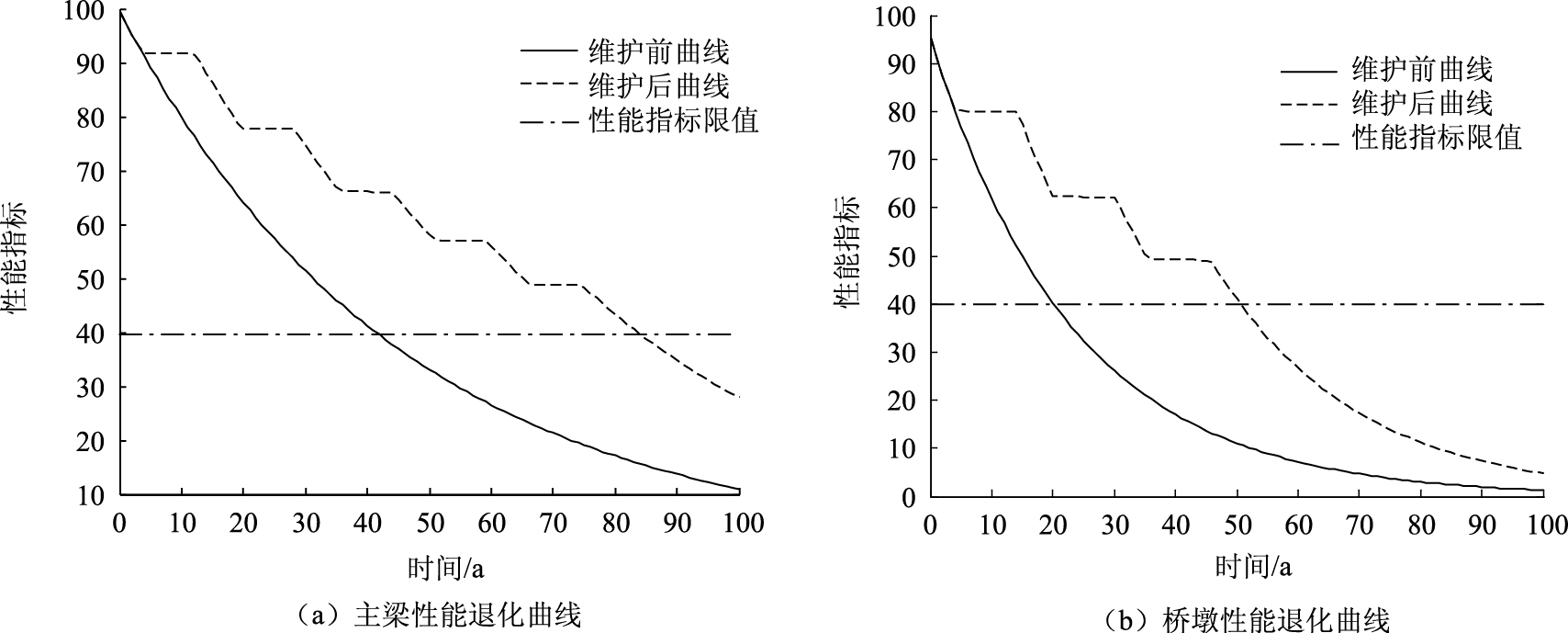
利用Matlab遗传算法, 进行仅预防性养护下养护策略的优化计算; 设定初始种群N=100, 迭代次数50次, Monte-Carlo生成随机数200次。图 1为计算得到的仅预防性养护条件下、采用最优养护方案后主梁和桥墩的性能退化曲线。从图 1中可见, 仅仅采用预防性养护, 主梁和桥墩均在其设计使用年限前即达到性能指标的最低限值, 而且即使后续继续进行预防性养护, 也无法使其性能提高到安全的水平。计算结果表明, 主梁在第5次预防性养护8.60 a后, 其性能指标已经降低到最低限值以下, 表明此时主梁已出现安全性问题, 其使用寿命仅为83.67 a; 桥墩在第3次预防性养护10.25 a后, 其性能指标也已降低到最低限值以下, 表明此时桥梁已出现安全性问题, 其使用寿命仅为50.55 a。
|
| 图 1 仅预防性养护条件下构件性能退化曲线 Fig. 1 Deterioration curves of component performance under PM condition |
| |
2.3 仅纠正性养护条件下的养护优化结果
如果在桥梁寿命期内仅进行纠正性养护, 则可采用基于性能的维护模型, 即纠正性维护模型进行优化。该模型将结构的维护行为视为当性能指标下降到某一预定值(本研究假定为40)时进行的, 并假定养护后结构仍满足指数退化模型, 故每次的维护时间tn可由退化模型和预定的性能指标计算确定。
根据纠正性维护模型假定, 经推导可得如下的桥梁寿命期内性能指标的表达式:
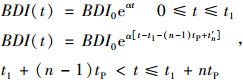
|
(8) |
式中, n为纠正性养护次数, 其他参数由式(9)计算:
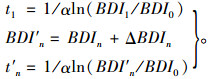
|
(9) |
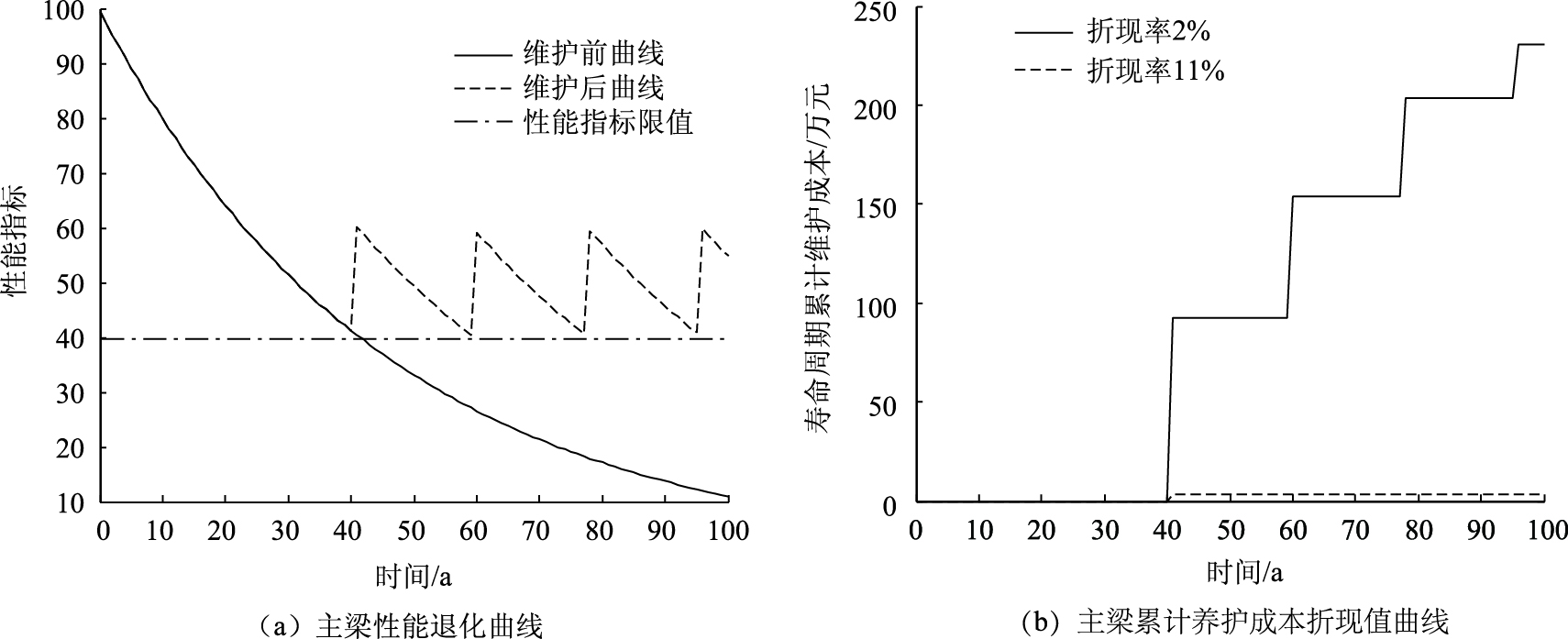
利用Matlab遗传算法, 进行仅纠正性养护下养护策略的优化计算; 设定初始种群N=100, 迭代次数50次, Monte-Carlo生成随机数200次。图 2为计算得到的仅纠正性养护条件下、采用最优养护方案后主梁的性能退化曲线及累计养护成本折现值曲线。从图 2中可见, 仅通过4次纠正性养护, 主梁即可在其设计使用年限内不出现安全性问题; 计算结果表明, 通过4次纠正性养护后, 主梁在其性能指标不低于最低性能指标的条件下, 使用年限可达113.60年。表 5列出了仅纠正性养护条件下主梁养护的优化结果, 从表 5中可见, 第1次进行纠正性养护的时间为桥梁建成后约41 a; 之后, 每次纠正性养护的时间间隔约为18 a; 此外, 每次纠正性养护的成本均有所不同。优化分析结果表明, 在r=2%折现率下, 寿命期内主梁累计总养护成本为230.70万元; 在r=11%折现率下, 累计总养护成本仅为3.47万元; 而且在主梁性能指标接近最低限值时进行纠正性养护, 可使寿命期总养护成本显著减小。
|
| 图 2 仅纠正性养护下主梁性能退化和累计养护成本折现值曲线 Fig. 2 Curves of performance deterioration and accumulative maintenance cost discount value of girder under CM condition |
| |
| 养护次数 | tn/a | SCn/万元 | BDIn |
| 1 | 40.69 | 207.78 | 40.63 |
| 2 | 18.37 | 197.39 | 40.41 |
| 3 | 18.45 | 227.93 | 40.24 |
| 4 | 17.89 | 181.56 | 40.56 |
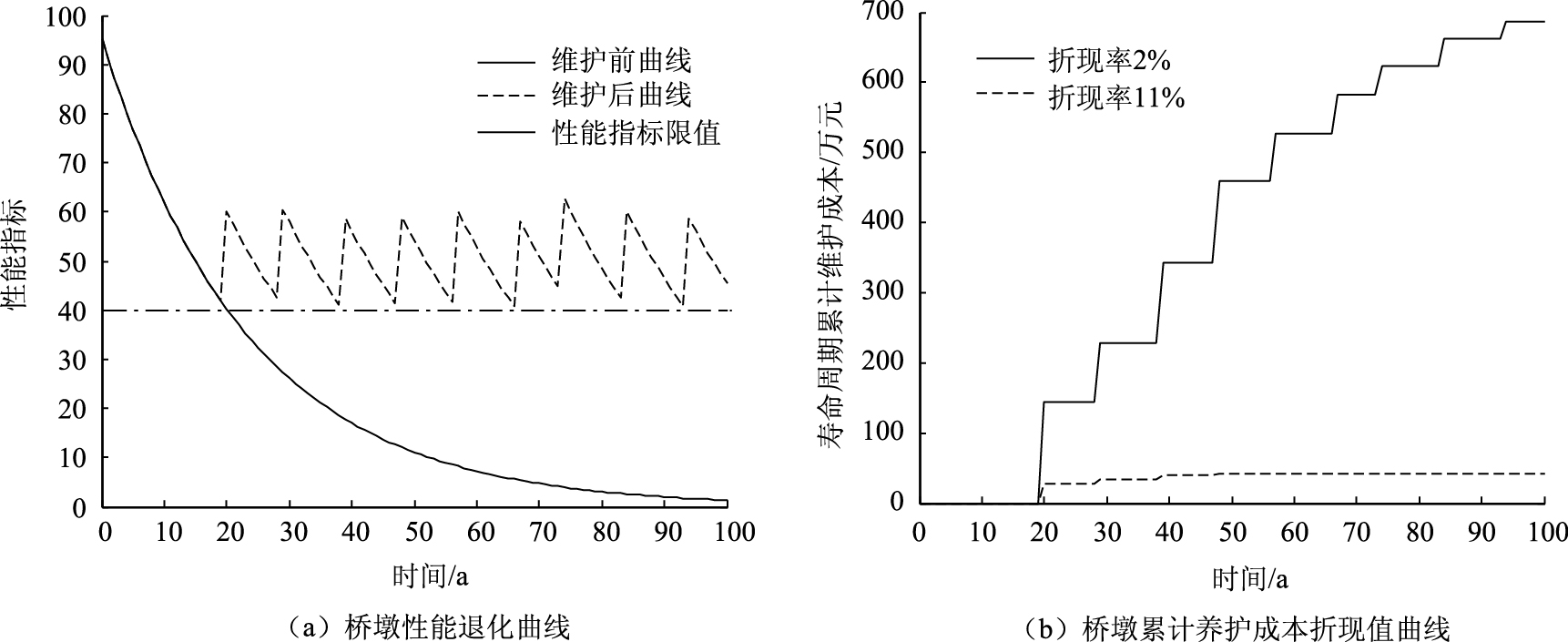
图 3为计算得到的仅纠正性养护条件下、采用最优养护方案后桥墩的性能退化曲线及累计养护成本折现值曲线; 从图 3中可见, 由于该桥的桥墩处于干湿循环环境中, 性能退化速度很快, 寿命周期内需要9次纠正性养护, 才能保持其性能满足最低要求; 计算结果表明, 通过9次纠正性养护后, 桥墩的使用年限可达102.94 a。表 6列出了仅纠正性养护条件下桥墩养护的优化结果, 从表 6中可见, 第1次进行纠正性养护的时间为桥梁建成后约20 a; 之后, 每次纠正性养护的时间间隔约为8~10 a。此外, 在r=2%折现率下, 寿命期内桥墩累计总养护成本为685.86万元; 在r=11%折现率下, 累计总养护成本仅为42.05万元。优化分析结果表明, 在桥墩性能指标接近最低限值时进行纠正性养护, 也可使寿命期总养护成本显著减小。
|
| 图 3 仅纠正性养护下桥墩性能退化和累计养护成本折现值曲线 Fig. 3 Curves of performance deterioration and accumulative maintenance cost discount value of piers under CM condition |
| |
| 养护次数 | tn/a | SCn/万元 | BDIn |
| 1 | 19.77 | 214.84 | 40.62 |
| 2 | 9.13 | 146.63 | 40.96 |
| 3 | 9.26 | 246.72 | 40.79 |
| 4 | 9.27 | 294.29 | 40.76 |
| 5 | 9.20 | 209.34 | 40.68 |
| 6 | 9.40 | 205.13 | 40.68 |
| 7 | 7.70 | 174.30 | 43.40 |
| 8 | 9.38 | 199.23 | 42.46 |
| 9 | 10.26 | 154.82 | 40.24 |
2.4 预防性与纠正性养护组合条件下的养护优化决策
如果在桥梁寿命期内既进行预防性养护, 同时又进行纠正性养护, 则可采用基于时间和性能的维护模型、即预防性与纠正性养护组合条件下的综合养护决策模型进行优化。该模型将结构的维护行为视为按一定时间周期有规律地进行, 并在性能指标下降到某一预定值(本研究假定为40)时, 立刻采取纠正性养护措施以提高结构的性能。该模型假定在采取预防性养护后, 在维护效果持续时间tPD时段内退化速率变慢且呈线性退化, 在(tP-tPD)时段内退化速率恢复为指数退化模型(tP为维护周期); 在采取纠正性养护后, 并假定养护后结构仍满足指数退化模型, 故每次的维护时间tn可由退化模型和预定的性能指标计算确定。
通常情况下预防性养护总是在纠正性养护之前进行的。为了简化问题, 这里假定预防性养护和纠正性养护不是随机任意组合的, 而是先进行预防性养护, 直到预防性养护无法维持结构最低性能指标时, 再进行纠正性养护; 并假定进行纠正性养护后, 就不再进行预防性养护。根据模型假定及综合养护方案假定, 经推导可得如下的桥梁寿命期内性能指标的表达式:
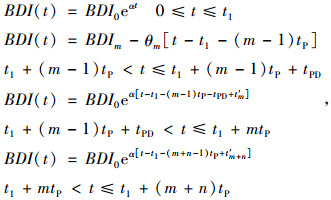
|
(10) |
式中, m和n分别为前期预防性养护及后期纠正性养护的次数, 其他参数由式(11)计算:
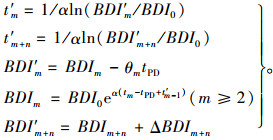
|
(11) |
利用Matlab遗传算法, 进行预防性与纠正性养护组合条件下养护策略的优化计算; 设定初始种群N=100, 迭代次数50次, Monte-Carlo生成随机数200次。根据2.2节和2.3节优化分析结果可知, 仅预防性养护条件下, 主梁和桥墩在寿命期内性能指标不能一直保持在最低限值之上; 仅纠正性养护条件下, 主梁和桥墩分别需要4次和9次养护, 其性能指标在寿命期内才能保持在最低限值之上。因此, 在考虑预防性与纠正性养护组合的综合养护优化策略时, 主梁和桥墩纠正性养护次数分别不应超过4次和9次; 此外, 由于预防性养护通常在纠正性养护之前进行, 且要保证寿命期性能指标在限值之上, 故主梁和桥墩预防性养护次数分别应小于5次和3次, 且预防性养护和纠正性养护的总次数应小于10次。由此, 确定了预防性与纠正性养护组合条件下主梁和桥墩可选的综合养护方案, 并分别见表 7和表 8; 表中PM和CM分别为预防性养护和纠正性养护。
| PM次数 | 1 | 1 | 2 | 1 | 2 | 3 | 1 | 2 | 3 | 4 |
| CM次数 | 4 | 3 | 3 | 2 | 2 | 2 | 1 | 1 | 1 | 1 |
| PM次数 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 |
| CM次数 | 9 | 8 | 7 | 6 | 8 | 7 | 6 | 5 | 7 | 6 | 5 | 4 |
根据表 7和表 8, 分别对主梁和桥墩进行综合养护方案寻优, 各可选综合养护方案的优化分析结果分别见表 9和表 10中, 表中LCMC均为r=2%时的计算值(单位为万元), 而且没有列出不满足约束条件的综合养护方案。从表 9和表 10中可见, 桥梁寿命期总养护成本与结构使用寿命和结构性能均不成正相关关系; 采用4次预防性养护+1次纠正性养护的综合养护优化方案, 主梁在寿命期内累计总养护成本最小, 为109.82万元; 采用4次纠正性养护的优化方案, 主梁使用年限最长, 可达113.6 a, 但其寿命期内累计总养护成本为230.7万元, 在所有可选综合养护优化方案中费用最高; 采用3次预防性养护+6次纠正性养护的综合养护优化方案, 桥墩在寿命期内累计总养护成本最小, 为339.18万元; 采用3次预防性养护+7次纠正性养护的综合养护优化方案, 桥墩使用年限最长, 可达108 a, 但其寿命期内累计总养护成本为398.98万元。
| 综合养护方案 | te/a | BDI | LCMC |
| 1PM+3CM | 101.37 | 41.22 | 185.66 |
| 2PM+3CM | 113.49 | 54.30 | 202.79 |
| 3PM+2CM | 101.20 | 41.07 | 160.16 |
| 4PM+1CM | 105.39 | 45.04 | 109.82 |
| 综合养护方案 | te/a | BDI | LCMC |
| 1PM+9CM | 104.91 | 49.41 | 559.27 |
| 2PM+8CM | 106.81 | 53.10 | 543.54 |
| 3PM+7CM | 108.00 | 56.41 | 398.98 |
| 2PM+7CM | 104.06 | 47.64 | 451.69 |
| 3PM+6CM | 102.93 | 45.38 | 339.18 |
2.5 不同养护方案优化结果比较
根据2.2节~2.4节的优化分析结果, 表 11和表 12分别给出了主梁和桥墩不同养护方案优化结果的比较, 表中LCMC均为r=2%时的计算值(单位为万元)。另外, 由于仅预防性养护无法使主梁和桥墩达到设计使用年限, 故表中没有列出其对应的LCMC值。从表 11和表 12可以发现, 优化的综合养护方案寿命期内累计总养护成本最小; 仅预防性养护, 无法使主梁和桥墩满足在设计使用年限内正常使用的要求; 仅纠正性养护, 可使主梁和桥墩的使用年限最长, 但寿命期内累计总养护成本相对较高。
| 养护方案 | 养护次数 | te/a | BDI | LCMC |
| 仅预防性养护 | 5 | 83.67 | <40 | — |
| 仅纠正性养护 | 4 | 113.60 | 54.78 | 230.70 |
| 综合养护 | 4PM+1CM | 105.39 | 45.04 | 109.82 |
| 养护方案 | 养护次数 | te/a | BDI | LCMC |
| 仅预防性养护 | 3 | 50.55 | <40 | — |
| 仅纠正性养护 | 9 | 102.94 | 45.39 | 685.86 |
| 综合养护 | 3PM+6CM | 102.93 | 45.38 | 339.18 |
3 结论
(1) 对公路混凝土梁桥, 综合预防性与纠正性养护的优化方案寿命期内累计总养护成本最小; 仅预防性养护, 无法使结构满足在设计使用年限内正常使用的要求; 仅纠正性养护, 可使结构的使用寿命最长, 但寿命期内累计总养护成本相对较高。
(2) 桥梁寿命期总养护成本与结构寿命和结构性能均不成正相关关系。
(3) 在结构性能指标接近最低限值时进行纠正性养护, 可使寿命期总养护成本显著减小。
(4) 本研究优化分析仅考虑预防性养护与纠正性养护的一般组合方案, 未考虑两者的随机任意组合。
| [1] |
FHWA. Insights into Pavement Preservation: A Compendium, FHWA-IF-00-011[R]. Washington, D.C.: Federal Highway Administration, 2000.
|
| [2] |
JOHNSON A M. Best Practices Handbook on Asphalt Pavement Maintenance, MN/RC 2000-04[R]. Minneapolis: University of Minnesota, 2000.
|
| [3] |
孙马, 刘庆阳, 向程龙. 桥梁预防性养护综合评估指标体系研究[J]. 重庆交通大学学报:自然科学版, 2013, 32(增1): 899-902. SUN Ma, LIU Qing-yang, XIANG Cheng-long. Comprehensive Evaluation Index System of Bridge Preventive Maintenance[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2013, 32(S1): 899-902. |
| [4] |
张春霞, 王巍. 基于费用效益最优的桥梁预防性养护时机确定方法研究[J]. 公路, 2013(7): 259-262. ZHANG Chun-xia, WANG Wei. Study on Determining Preventive Maintenance Time for Bridges Based on Best Cost-benefit[J]. Highway, 2013(7): 259-262. |
| [5] |
王巍, 张春霞, 乔国栋. 基于灰色模糊综合评判的桥梁预防性养护后评估体系研究[J]. 公路, 2014(1): 153-157. WANG Wei, ZHANG Chun-xia, QIAO Guo-dong. Study on Post Evaluation System of Bridge Preventive Maintenance Based on Grey Fuzzy Synthetic Evaluation[J]. Highway, 2014(1): 153-157. |
| [6] |
王巍, 张春霞, 邢佳鹏, 等. 桥梁预防性养护效果-成本-寿命集成优化[J]. 重庆交通大学学报:自然科学版, 2014, 33(4): 24-28. WANG Wei, ZHANG Chun-xia, XING Jia-peng, et al. Integrated Optimization Research on Effect-cost-life of Bridge Preventive Maintenance[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2014, 33(4): 24-28. |
| [7] |
黄天立, 周浩, 王超, 等. 基于伽马过程的锈蚀钢筋混凝土桥梁检测维护策略优化[J]. 中南大学学报:自然科学版, 2015, 46(5): 1851-1861. HUANG Tian-li, ZHOU Hao, WANG Chao, et al. Optimization Inspection and Maintenance Strategy for Corrosive Reinforced Concrete Girder Bridges Based on Gamma Process[J]. Journal of Central South University:Science and Technology Edition, 2015, 46(5): 1851-1861. |
| [8] |
YUNIARTO H A, QARADHAWI Y. Optimization in Indonesia's Bridge Preventive Maintenance Programme:A Proposal[J]. Applied Mechanics and Materials, 2016, 845: 299-304. |
| [9] |
白山云, 陈开利, 陈杰, 等. 公路悬索桥预防性养护技术[J]. 桥梁建设, 2014, 44(2): 101-106. BAI Shan-yun, CHEN Kai-li, CHEN Jie, et al. Preventive Maintenance Techniques for Highway Suspension Bridges[J]. Bridge Construction, 2014, 44(2): 101-106. |
| [10] |
凌建明, 官盛飞, 赵鸿铎, 等. 公路沥青路面预养护多层次模糊决策模型[J]. 公路交通科技, 2008, 25(6): 25-29, 34. LING Jian-ming, GUAN Sheng-fei, ZHAO Hong-duo, et al. Multi-hierarchy Fuzzy Decision-making Model for PPM Treatment Selection of Highway Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2008, 25(6): 25-29, 34. |
| [11] |
苏卫国, 赵慧芳. 路面预防性养护效益评估方法[J]. 公路交通科技, 2009, 26(1): 16-20, 25. SU Wei-guo, ZHAO Hui-fang. Pavement Preventive Maintenance Benefits Evaluation[J]. Journal of Highway and Transportation Research and Development, 2009, 26(1): 16-20, 25. |
| [12] |
樊旭英, 高凤春, 王海龙, 等. 基于改进EW-AHP的沥青路面预防性养护评价模型[J]. 公路交通科技, 2017, 34(9): 8-13. FAN Xu-ying, GAO Feng-chun, WANG Hai-long, et al. A Model for Asphalt Pavement Preventive Maintenance Evaluation Based on Improved EW-AHP[J]. Journal of Highway and Transportation Research and Development, 2017, 34(9): 8-13. |
| [13] |
JTG H11-2004, 公路桥涵养护规范[S]. JTG H11-2004, Code for Maintenance of Highway Bridges and Culverts[S]. |
| [14] |
FRANGOPOL D M, KONG J S, GHARAIBEH E S. Reliability-based Life-cycle Management of Highway Bridges[J]. Journal of Computing in Civil Engineering, 2001, 15(1): 27-34. |
| [15] |
FRANGOPOL D M, KONG J S. Life-cycle Safety and Costing for Maintenance of Aging Bridges[C]//Proceedings of the 2001 Structures Congress and Exposition. Washington, D.C.: Structural Engineering Institute of ASCE, 2001: 1-6.
|
| [16] |
彭建新, 邵旭东. 混凝土桥梁结构性能退化可靠性评估及全寿命设计方法[M]. 北京: 人民交通出版社, 2014. PENG Jian-xin, SHAO Xu-dong. Reliability Assessment of Performance Deterioration and Whole-life Design Method for Concrete Bridge Structures[M]. Beijing: China Communications Press, 2014. |
| [17] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [18] |
雷英杰, 张善文. MATLAB遗传算法工具箱及应用[M]. 2版. 西安: 西安电子科技大学出版社, 2014. LEI Ying-jie, ZHANG Shan-wen. MATLAB Genetic Algorithm Toolbox and Its Application[M]. 2nd ed. Xi'an: Xidian University Press, 2014. |
| [19] |
邓聚龙. 灰预测与灰决策[M]. 武汉: 华中科技大学出版社, 2002. DENG Ju-long. Grey Prediction and Grey Decision[M]. Wuhan: Huazhong University of Science and Technology Press, 2002. |
 2019, Vol. 36
2019, Vol. 36
