扩展功能
文章信息
- 常柱刚, 张红显
- CHANG Zhu-gang, ZHANG Hong-xian
- 悬臂施工材料时变效应对PC箱梁桥的影响研究
- Influence of Material Time-dependent Effect on Cantilever Construction of PC Box Girder Bridge
- 公路交通科技, 2019, 36(2): 67-73
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 67-73
- 10.3969/j.issn.1002-0268.2019.02.010
-
文章历史
- 收稿日期: 2017-06-27
PC箱梁桥以其独特的受力条件以及跨越能力大的优点, 广泛应用于大跨度桥梁, 多采用悬臂浇注法施工。悬臂浇注法施工工艺成熟, 受到广大施工单位的青睐, 但在施工过程中, PC箱梁桥混凝土强度、弹性模量随着时间的变化而变化, 随着施工阶段的增加, 结构由短悬臂阶段变化为长悬臂, 合龙过程中伴随着体系转换, 并且由于浇注时间的差异, 各节段材料性能有较大差别[1]。对一特定节段, 当预应力钢筋张拉后, 由于强度、弹性模量的持续增长, 预应力筋的锚固、约束作用, 必然对结构挠度、应力产生影响。针对PC箱梁桥材料时变效应对桥梁施工的影响问题, 许多学者从混凝土配合比、混凝土养护方式、不同龄期混凝土本构模型等角度进行了试验和理论研究[2-3], 取得了一定的研究成果:其中, 对于材料时变效应对PC箱梁桥悬臂施工的影响研究[4], 主要集中在混凝土强度、弹性模量的发展规律, 以及二者关系上[5-6], 而较少涉及材料时变效应对结构应力、位移的影响。
本研究拟在混凝土试块主桥同养条件下, 对C55高强混凝土进行试验研究, 依靠混凝土材料性能随时间变化的趋势, 拟合实际工程中混凝土强度、弹性模量时变变化规律, 并根据实测数据, 通过有限元计算分析施工过程中结构受力、位移情况, 验证材料时变效应对结构的影响作用。
1 原材料及试件制备 1.1 试件试验水泥:普通硅酸盐水泥, 强度等级为P.O52.5, 材料符合《通用硅酸盐水泥》(GB 175—2007)[7]要求。砂:当地料场、采用天然砂。碎石:当地料场, 5~20 mm合成连续级配(20~10 mm: 10~5 mm=7: 3)。水:云南省怒江州天然水。外加剂:吉源JY-PC聚羧酸高性能减水剂。粉煤灰:某粉煤灰有限责任公司Ⅰ级F类。经各材料设计与计算[8], 实验室C55混凝土配合比见表 1。
1.2 试验制备及试验方法
由于桥梁结构为纵向受力构件, 因此, 若采用立方体试件, 则与结构受力性能不符, 因此本研究采用棱柱体试件进行试验。为了使试验结果更加切合实际, 本研究设计制作的24组棱柱体混凝土试件与主桥同步养生, 分别选取养护龄期为3, 5, 7, 14, 28, 60 d的混凝土试件进行轴心抗压强度与弹性模量试验。
(1) 棱柱体混凝土强度试验:在混凝土浇注现场制作150 mm×150 mm×300 mm标准棱柱体试件, 与主桥同步养生, 按照《公路工程水泥及水泥混凝土试验规程》(JTG E30—2005)[9], 利用TYE—2000E型压力试验机, 在各龄期对试件进行棱柱体抗压试验。
(2) 混凝土弹性模量试验:利用TM-Ⅱ型混凝土弹性模量测定仪, 在实验室对各龄期的试件进行混凝土弹性模量试验。
2 试验结果 2.1 数据统计整理试验所得结果, 分别对弹性模量Ec、轴心抗压强度fc结果进行分析, 部分试验值如表 2所示。
| 龄期/d | fc/MPa | Ec/(×104MPa) | ||||
| 3 | 34.3 | 36.6 | 35.3 | 3.27 | 3.18 | 3.19 |
| 5 | 49.5 | 49.8 | 50.2 | 3.56 | 3.54 | 3.62 |
| 7 | 51.7 | 51.0 | 52.1 | 3.85 | 3.89 | 3.83 |
| 14 | 52.9 | 54.4 | 54.2 | 4.06 | 4.03 | 3.98 |
| 28 | 56.6 | 54.8 | 54.4 | 4.41 | 4.45 | 4.50 |
| 60 | 59.7 | 61.0 | 60.1 | 5.06 | 5.02 | 5.08 |
试验测试值有时会出现个别异常数据(与其他数据差异过大或过小的数据), 如果将混有异常数据的试验数据进行试验结果分析, 将增大试验误差[10-11]。目前判断异常数据应用较为广泛的有格拉布斯准则和肖维勒准则, 由于本试验选取试块个数n=144<185, 因此, 本研究采用格拉布斯准则来判断试验数据[12]。
选定置信区间为α=95%, Xi为第i个试验值; X为数学期望; S为标准差; Ti为统计系数; T(n, a)为统计临界系数, 则3 d龄期:
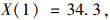
|
(1) |
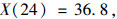
|
(2) |
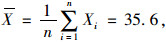
|
(3) |
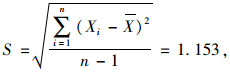
|
(4) |
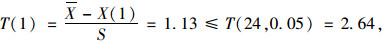
|
(5) |
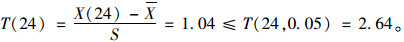
|
(6) |
可知T (1), T (24)均满足要求, 无可疑数据, 同理可检验5, 7, 14, 28, 60 d试验数据, 经格拉布斯准则检验, 主桥同养下早龄期混凝土抗压强度与弹性模量试验测试值为有效值。
2.2 混凝土轴心抗压强度为了减小试验数据误差, 本研究分析某一龄期混凝土抗压强度时, 根据格拉布斯检验, 剔除异常数据, 对有效数据取平均值, 作为养护该龄期t时, 混凝土轴心抗压强度值。[13]。
由试验所得各龄期对应的轴心抗压强度值, 对数据进行科学处理后, 可回归分析龄期与试验结果二者之间关系。本研究采用在数据处理方面功能强大的matlab软件进行非线性回归分析, 为选取最优回归方程, 本研究选取4种函数形式进行回归拟合, 函数表达式见表 3。
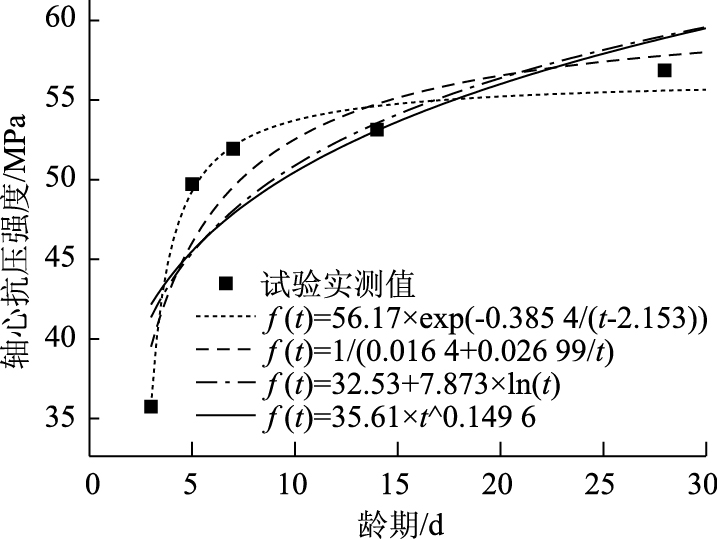
| 函数类型 | 函数形式 | 回归系数a | 回归系数b | 回归系数c | 确定系数R-square | 和方差SSE |
| 指数函数 | fc(t)=a×exp(b/(t-c)) | 56.17 | -0.385 4 | 2.153 | 0.984 7 | 3.955 |
| 双曲函数 | fc(t)=1/(a+b/t) | 0.016 42 | 0.026 99 | — | 0.859 3 | 36.55 |
| 对数函数 | fc(t)=a+b×ln(t+c) | 32.53 | 7.873 | 0 | 0.733 3 | 69.28 |
| 幂函数 | fc(t)=a×(t+b)c | 35.61 | 0 | 0.149 6 | 0.696 8 | 78.75 |
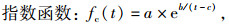
|
(7) |
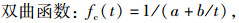
|
(8) |
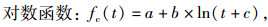
|
(9) |
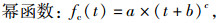
|
(10) |
式中, a, b, c为回归系数; t为养护龄期, 在PC箱梁桥施工过程中, 由于刚浇注的混凝土尚未成型, 本研究暂不考虑养护龄期0~3天的混凝土强度, 假定混凝土养护3天后才开始承受荷载, 因此本研究仅考虑t∈ (3, 28)范围内混凝土材料性能的变化情况。
C55混凝土轴心抗压强度随龄期变化的拟合曲线如图 1所示。
|
| 图 1 早龄期混凝土轴心抗压强度随时间的变化 Fig. 1 Axial compressive strength of early-age concrete varying with time |
| |
对比分析不同函数表达式下轴心抗压强度变化规律, 根据确定系数(拟合度)R-square最大, 和方差SSE最小的原则, 使用指数型函数来表示早龄期混凝土轴心抗压强度与养护龄期的关系最为准确。
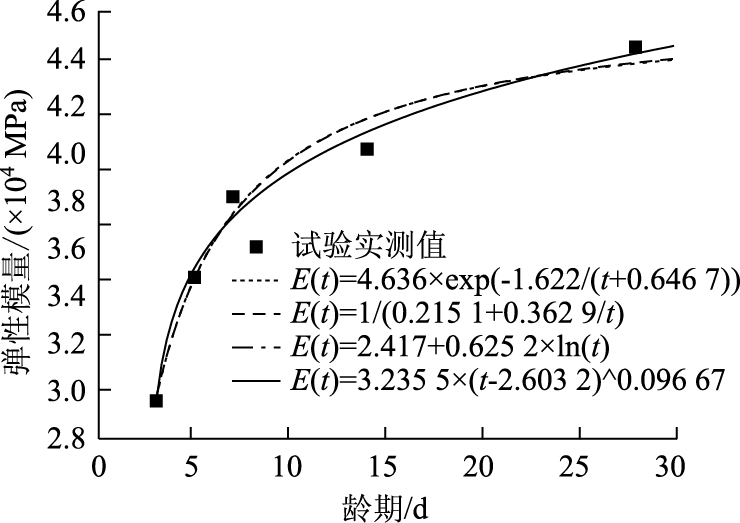
2.3 混凝土弹性模量为了减小试验数据误差, 本研究分析某一龄期混凝土弹性模量时, 根据格拉布斯检验, 剔除异常数据, 对有效数据取平均值, 作为养护该龄期t时, 混凝土弹性模量值。由试验所得各龄期对应的弹性模量值, 对数据进行科学处理后, 可回归分析龄期与试验结果二者之间关系。本研究采用在数据处理方面功能强大的matlab软件进行非线性回归分析, 为选取最优回归方程, 本研究选取4种函数形式进行回归拟合, 拟合图如图 2所示。
|
| 图 2 弹性模量时变规律 Fig. 2 Time varying rule of elastic modulus |
| |
对比分析不同函数表达式下轴心抗压强度变化规律, 根据确定系数(拟合度)R-square最大, 和方差SSE最小的原则, 使用幂函数来表示早龄期混凝土弹性模量与养护龄期的关系最为准确。
2.4 早龄期混凝土fc (t)与Ec (t)的关系早龄期混凝土弹性模量与轴心抗压强度有关, 为比较fc (t)与Ec (t)随养护时间变化的增长情况, 现将C55混凝土养护28天作为基准, 计算混凝土各龄期轴心抗压强度值、弹性模量值与28天龄期fc (28)与Ec (28)的百分比值: 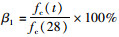
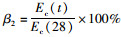
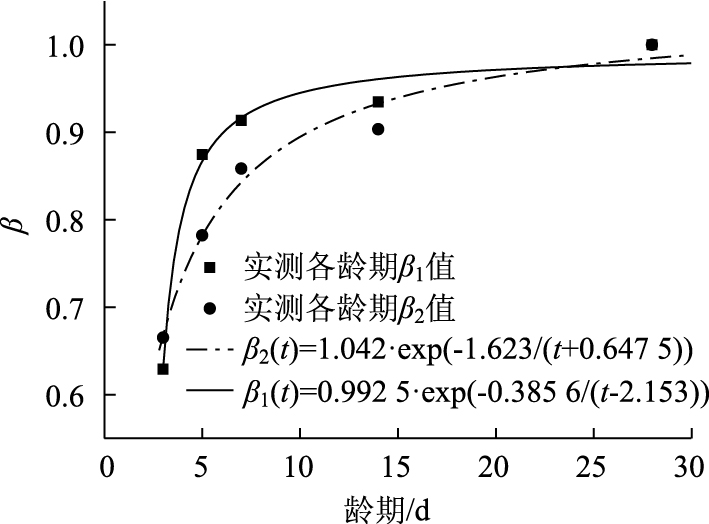
|
| 图 3 C55混凝土力学性能相对值随龄期的变化 Fig. 3 Mechanical property relative value of C55 concrete varying with age |
| |
由图 3可知, C55混凝土轴心抗压强度、弹性模量随龄期单调增加, 增长速度渐减并趋向收敛; 混凝土3 d强度达到28天强度的64.1%, 弹性模量达到28天弹性模量的72.1%, 证明在养护混凝土最初期, 相比弹性模量的发展, C55混凝土强度发展较为缓慢; 在养护3~7 d龄期时, 混凝土强度增长迅速, 5 d强度即超过28天强度的90%, 而同期5 d弹性模量试验值为28 d弹性模量的80.2%, 7 d弹性模量试验值为28 d弹性模量的86.7%, 混凝土龄期达到14 d时, 弹性模量达到28 d弹性模量的90.3%, 此时C55混凝土强度为28 d强度值的96.6%, 即在3~28 d养护龄期内, C55混凝土弹性模量增长滞后于混凝土强度的增长。
混凝土结构设计规范(GB50010—2010)中对混凝土弹性模量与其强度等级值(fcu, k为代表)的关系定义为[14]:
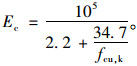
|
(11) |
根据试验结果, 采用该式进行弹性模量计算有较大误差。由于混凝土在实际施工过程中, 采用的是混凝土施工配制强度Rp, 因此, 利用matlab、Originlab分别对混凝土弹性模量与其强度进行非线性关系拟合, 取最优方程, 有E (t)=31 799.5+294.2e[(f(t)-35.4)/5.281 1], 函数拟合图形如图 4所示, 该函数关系式进行弹性模量与强度分析, 确定系数R-square为0.991 7, 相关性较好。
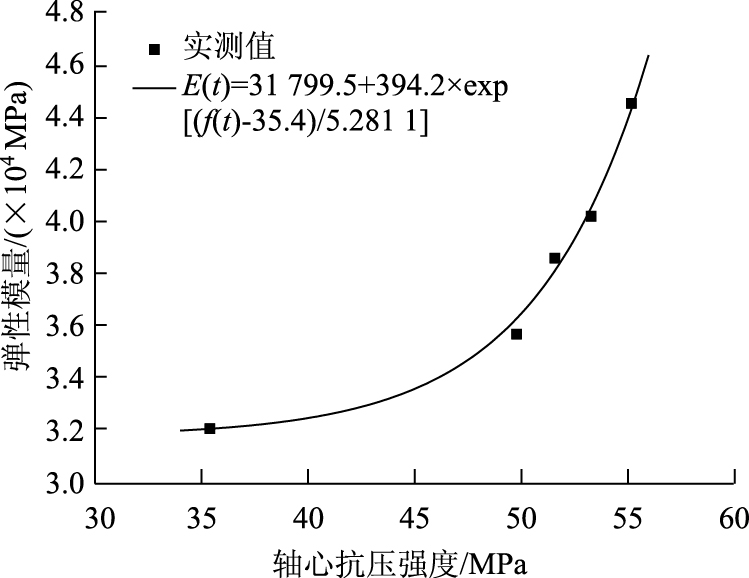
|
| 图 4 C55混凝土弹性模量与轴心抗压强度的关系 Fig. 4 Relationship between elastic modulus of C55 concrete and axial compressive strength |
| |
3 时变效应对PC箱梁桥施工的影响 3.1 时变效应的分析方法
目前分析混凝土结构徐变方法主要有RCM法、IDM法、EMM法等, 在混凝土结构施工过程中, 混凝土加载应力σc≤0.4~0.5fc, 此时徐变行为为线性[15], 因此本研究在分析徐变作用时采用RCM法。在叠加原理及徐变应变的作用下, 结构总应变可表示为:
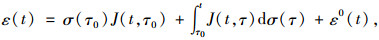
|
(12) |
其中:
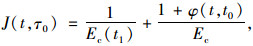
|
(13) |
式中, J(t, τ0)为柔度函数(也称徐变函数), 表示从时间τ0起一直作用的单位常应力在时间t所产生的应变(即单位应力产生的弹性应变和徐变应力之和); ε(t)为t时刻的总应变; ε0 (t)为与应力无关的应变(包括收缩应变和温度应变等); t, t1为计算龄期; t0为加载龄期。
3.2 有限元模型建立Midas civil在模拟结构施工过程中内力分析上具有独特的优势, 因此, 本研究依据该有限元分析软件进行施工阶段悬臂结构内力、挠度分析[16]。
分别以应力、挠度为主要判断指标, 建立以悬臂结构应力控制下的有限元模型A, 以悬臂结构挠度控制下的有限元模型B, 利用有限元软件中自定义强度、弹性模量板块功能, 自定义2.2, 2.3节混凝土早龄期强度、弹性模量变化函数。
采用Midas civil有限元软件对云南省六丙公路一期工程兑房河特大桥进行梁单元建模, 如图 5所示。兑房河特大桥主桥桥跨布置为(100+180+100)m连续刚构, 主梁混凝土强度等级为C55混凝土, 主梁单元划分依据实际结构施工过程中节块浇注顺序, 并依次施加预应力。

|
| 图 5 有限元模型 Fig. 5 Finite element model |
| |
3.3 数值结果分析
PC刚构桥施工过程中, 最大悬臂状态结构最不稳定, 因此本研究以单个"T"构最大悬臂状态作为主要研究对象。
(1) 悬臂状态应力差异
PC刚构桥施工过程中, 悬臂状态下根部的压应力储备是悬臂浇注过程中的关键性参数, 直接决定了结构合龙及运营过程中的应力水平及分布合理性[17]。因此本研究选取箱梁根部应力状态作为研究对象。按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)[18], 即"时不变效应"计算结构应力状态, 并与3.2节时变效应计算结果进行对比。有限元计算应力沿墩顶位置对称分布, 以下仅列出单侧应力值, 如图 6所示。
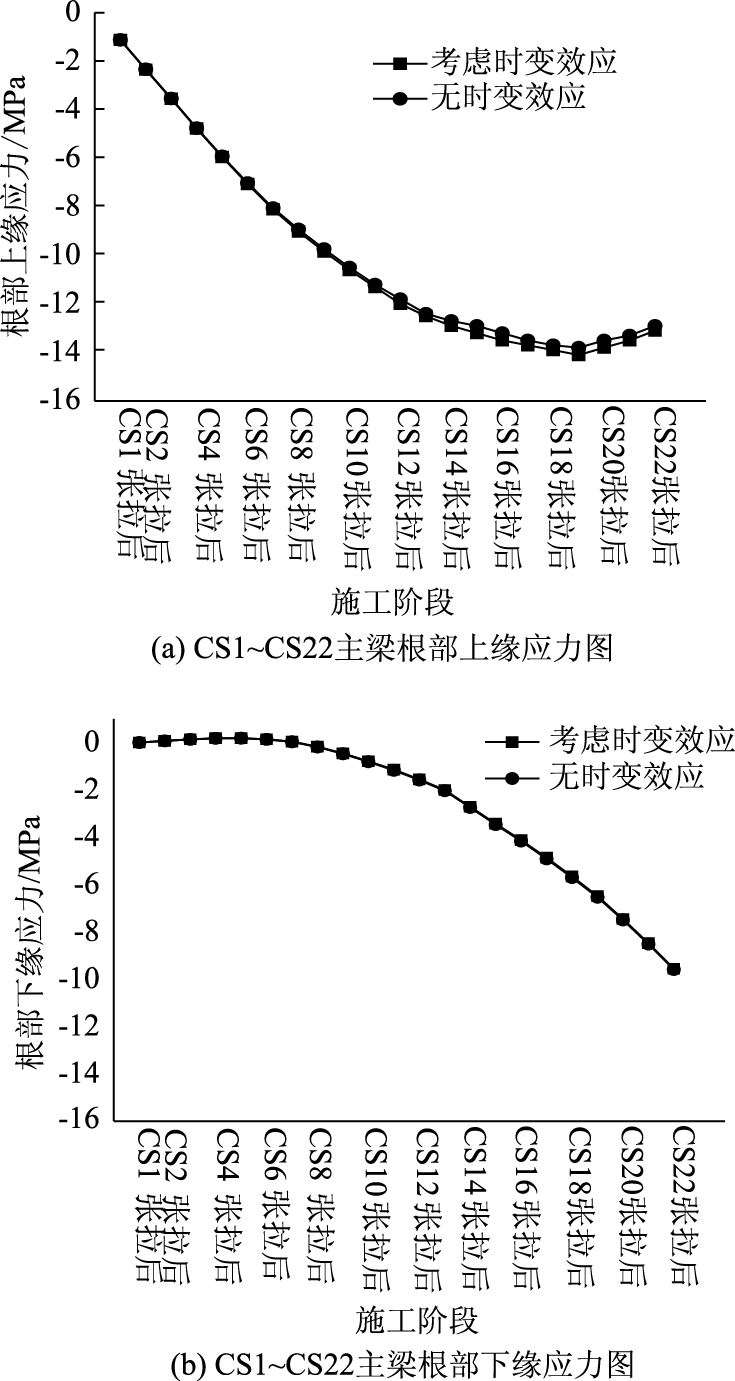
|
| 图 6 施工过程中主梁根部应力图 Fig. 6 Curves of stress at main beam root in construction |
| |
由图 6(a)可见, 随着施工过程的发展, 悬臂结构上缘压应力逐渐增大, 考虑材料时变效应, 与采用规范计算的结构根部压应力最大差值为0.3 MPa, 应力变化2.22%, 时变效应对结构应力影响较小; 由图 6(b)可见, 悬臂施工过程中, 相比结构上缘压应力, 下缘应力较小, 考虑材料时变效应, 与采用规范计算的结构根部压应力最大差值为0.05 MPa, 应力变化1.02%。可以看出, 材料时变效应对采用悬臂浇注结构根部压应力储备影响较小。
(2) 悬臂状态挠度差异
张拉完双悬臂施工最后一个节块, 计算各关键节点挠度值。按照公桥规, 即"时不变效应"计算结构位移状态, 并与3.2节时变效应计算结果进行对比, 分别读取张拉最后一个施工阶段后"T"构各节点当前步骤位移(即由于张拉最后一个悬臂段引起的各节点挠度变化)与该施工阶段后累加位移(即张拉最后一个悬臂段后悬臂结构的实际位移), 如图 7所示。
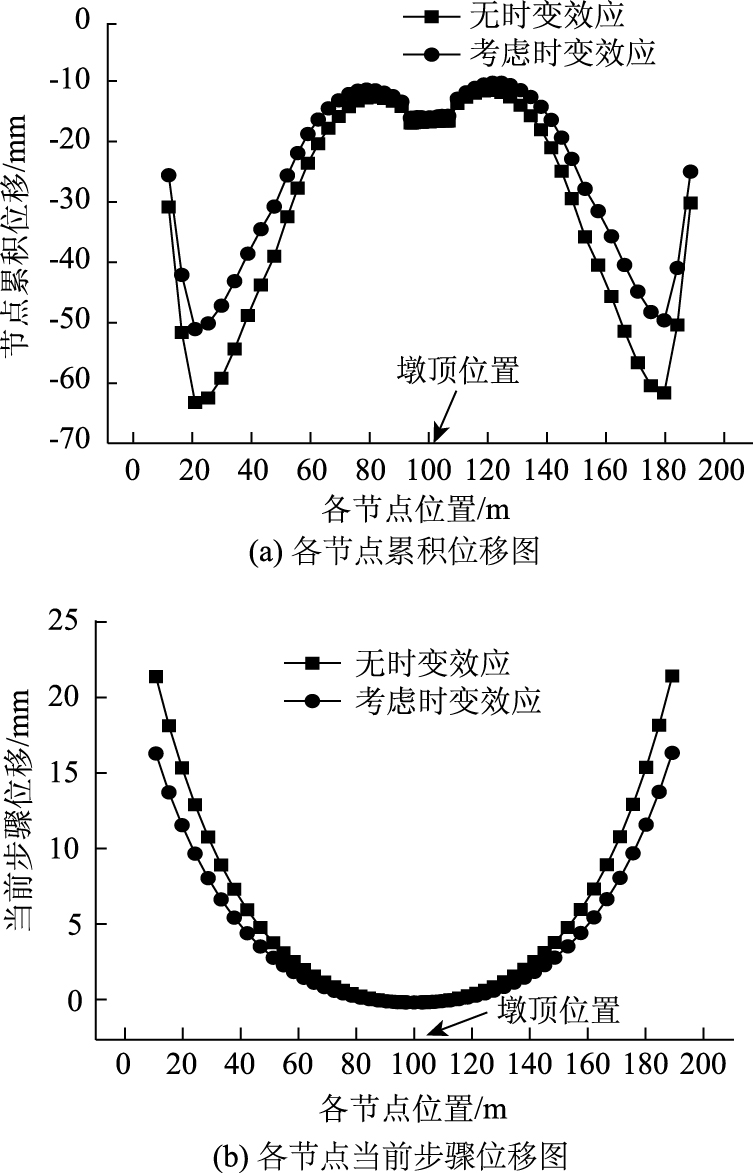
|
| 图 7 最大悬臂阶段张拉后节点位移图 Fig. 7 Curves of nodal displacement at maximum cantilever stage after tensioning |
| |
由图 7(a)可知, 最大悬臂阶段张拉预应力后, 考虑材料时变效应, 与采用规范计算的各节点累积位移相差较大, 在0~L/4倍桥梁跨度处, 挠度差异为0.7~5.6 mm, 最大位移变化21.01%, 在L/4~L/2倍桥梁跨度处, 挠度差异达到5.6~12.3 mm, 最大位移变化24.45%。由图 7(b)可知, 最大悬臂阶段张拉预应力后, 考虑材料时变效应, 与采用规范计算的各节点当前步骤位移在最大悬臂端时差异最大, 为5.1 mm, 位移变化30.96%。
4 结论(1) 主桥同养状态下, 混凝土轴心抗压强度与龄期之间的关系呈指数函数发展, 在养护3~7 d间, 混凝土强度发展迅速, 7 d强度超过28天强度的90%;混凝土弹性模量较于轴心抗压强度增长较为缓慢, 与龄期之间的关系呈幂函数发展, 在养护5~7 d时, 弹性模量超过28天的80%。
(2) 混凝土强度与弹性模量之间的关系式应以试验为基础, 在主桥同养状态下, 混凝土轴心抗压强度与弹性模量呈指数函数。
(3) 考虑材料时变效应对悬臂结构进行应力分析, 按照规范计算, 上、下缘应力变化最大值分别为0.3, 0.05 MPa, 变化幅度为2.22%, 1.02%, 即考虑材料时变效应对PC刚构桥悬臂施工期压应力储备影响较小。
(4) 考虑材料时变效应对悬臂结构进行挠度分析, 按照规范计算, 悬臂结构累积位移最大变化发生在最大悬臂阶段, 位移变化34.45%, 当前步骤位移变化30.96%, 即材料时变效应对PC刚构桥悬臂施工期挠度影响较大, 特别在合龙前挠度控制中, 不可忽略材料时变效应的影响。
| [1] |
刘扬.混凝土斜拉桥施工期时变可靠性研究[D].长沙: 湖南大学, 2005. LIU Yang. Research on Time-dependent Reliability of Concrete Cable-stayed Bridges during Construction[D]. Changsha: Hunan University, 2005. http://cdmd.cnki.com.cn/article/cdmd-10532-2006040541.htm |
| [2] |
金贤玉, 田野, 金南国. 混凝土早龄期性能与裂缝控制[J]. 建筑结构学报, 2010, 31(6): 204-212. JIN Xian-yu, TIAN Ye, JIN Nan-guo. Early Age Properties and Cracking Control of Concrete[J]. Journal of Building Structures, 2010, 31(6): 204-212. |
| [3] |
吕毅刚, 韩伟威, 吕健鸣, 等. 基于暴露试验的桥梁混凝土长期弹性模量试验研究[J]. 公路交通科技, 2016, 33(5): 78-84. LÜ Yi-gang, HAN Wei-wei, LÜ Jian-ming, et al. Experimental Study on Long-term Elastic Modulus of Bridge Concrete Based on Exposure Experiment[J]. Journal of Highway and Transportation Research and Development, 2016, 33(5): 78-84. |
| [4] |
GUO Tong, CHEN Zhe-heng, LIU Tie, et al. Time-dependent Reliability of Strengthened PSC Box-girder Bridge Using Phased and Incremental Static Analyses[J]. Engineering Structures, 2016, 117: 3584371. |
| [5] |
陈萌.混凝土结构收缩裂缝的机理分析与控制[D].武汉: 武汉理工大学, 2006. CHEN Meng. Analysis on Mechanism and Control of Shrinkage Cracking of Concrete Structure[D]. Wuhan: Wuhan University of Technology, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10497-2006169080.htm |
| [6] |
胡晓鹏.早龄期混凝土结构性能时变规律研究[D].西安: 西安建筑科技大学, 2011. HU Xiao-peng. Time-varying Law of Early Age Concrete Structure Properties[D]. Xi'an: Xi'an University of Architecture & Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10703-1011297343.htm |
| [7] |
GB 175-2007, 通用硅酸盐水泥[S]. GB 175-2007, Common Portland Cement[S]. |
| [8] |
金贤玉, 沈毅, 李宗津, 等. 混凝土早龄期受力对后期性能的影响[J]. 混凝土, 2003(7): 35-37. JING Xian-yu, SHEN Yi, LI Zong-jin, et al. Influence of Preload Concrete on Its Latter Performance[J]. Concrete, 2003(7): 35-37. |
| [9] |
JTG E30-2005, 公路工程水泥及水泥混凝土试验规程[S]. JTG E30-2005, Test Methods of Cement and Concrete for Highway Engineering[S]. |
| [10] |
刘渊.误差理论与数据处理[D].大连: 大连理工大学, 2008. LIU Yuan. Error Theory and Data Processing[D]. Dalian: Dalian University of Technology, 2008. |
| [11] |
熊艳艳, 吴先球. 粗大误差四种判别准则的比较和应用[J]. 大学物理试验, 2010, 23(1): 66-68. XIONG Yan-yan, WU Xian-qiu. The Generalizing Application of Four Judging Criterions for Gross Errors[J]. Physical Experiment of College, 2010, 23(1): 66-68. |
| [12] |
林丽芬, 肖化, 吴先球. 肖维勒准则和格拉布斯准则的比较[J]. 大学物理试验, 2012, 25(6): 86-88. LIN Li-fen, XIAO Hua, WU Xian-qiu. Comparison between Chauvenet's Criterion and Grubbs Criterion[J]. Physical Experiment of College, 2012, 25(6): 86-88. |
| [13] |
田明革.钢筋混凝土框架结构施工期性能研究[D].长沙: 湖南大学, 2008. TIAN Ming-ge. Research on Performance of Reinforced Concrete Frame Structure during Construction[D]. Changsha: Hunan University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10532-2009083797.htm |
| [14] |
GB 50010-2010, 混凝土结构设计规范[S]. GB 50010-2010, Code for Design of Concrete Structures[S]. |
| [15] |
周敉, 宋一凡, 赵小星. 预应力混凝土桥梁悬臂浇筑的施工控制[J]. 长安大学学报:自然科学版, 2005, 25(6): 43-48. ZHOU Mi, SONG Yi-fan, ZHAO Xiao-xing. Control Technique for Construction of Pre-stressed-concrete Cantilever Casting Bridge[J]. Journal of Chang'an University:Natural Science Edition, 2005, 25(6): 43-48. |
| [16] |
丁欣海.大跨度连续刚构桥主梁施工仿真分析及可靠度研究[D].长沙: 长沙理工大学, 2012. DING Xin-hai. Simulation Analysis and Reliability Research on Large Span Continuous Rigid Frame Bridge Girder Construction[D]. Changsha: Changsha University of Science & Technology, 2012. http://cdmd.cnki.com.cn/article/cdmd-10536-1012348434.htm |
| [17] |
张方.大跨度预应力混凝土梁桥时变性能及分析方法研究[D].成都: 西南交通大学, 2011. ZHANG Fang. Research on Time-dependent Performance and Analytical Method for Long-span Prestressed Concrete Girder Bridge[D]. Chengdu: Southwest Jiaotong University, 2011. http://cdmd.cnki.com.cn/article/cdmd-10613-1011233301.htm |
| [18] |
JTG D62-2004, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG D62-2004, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
 2019, Vol. 36
2019, Vol. 36
