扩展功能
文章信息
- 唐利民
- TANG Li-min
- 基于区间分析理论的变形监测数据处理方法
- A Method for Deformation Monitoring Data Processing Based on Interval Analysis Theory
- 公路交通科技, 2019, 36(2): 61-66, 73
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 61-66, 73
- 10.3969/j.issn.1002-0268.2019.02.009
-
文章历史
- 收稿日期: 2016-10-30
2. 长沙理工大学 公路养护技术国家工程实验室, 湖南 长沙 410004;
3. 长沙理工大学 交通运输工程学院, 湖南 长沙 410004
2. State Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science & Technology, Changsha Hunan 410004, China;
3. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha Hunan 410004, China
区间分析理论是美国数学家R.E.Moore在20世纪60年代第一次系统提出的[1-2]。在数值计算、误差分析、不确定性分析、结构工程上的应用非常广泛[3-8]。区间变形监测在边坡, 路基、桥梁、隧道等工程的变形监测与灾害预警中, 有3个重要的应用。一是监测数据的区间取值基本方法, 二是多源监测数据的融合, 三是区间变量[3-4]变形分析理论与方法。
工程变形监测数据处理中, 由于变形观测数据的近似或扰动, 跟真实形变存在一定误差, 在一定的观测手段和方法下, 这类误差导致目标函数的变化并不大, 但其所求的理论分析模型参数却会存在巨大差异。
目前一般采用点变量来表达变形体某一位置在某一时空的变形信息[9]。然而, 点变量表达的变形点的信息, 没有区间变量表达的信息全面。所以, 在变形监测领域中, 利用区间变量来研究变形体的变形规律和特征, 要比点变量更能反映变形体的复杂性。
基于此, 本研究探讨了利用区间变量来表达变形监测数据处理与分析模型中的参数, 借鉴区间分析理论, 讨论了基于区间变量的变形监测数据分析过程与相关法则, 为进一步深入理解变形体及变形监测数据处理的复杂性质, 探索一种新的方式。
1 区间分析基本理论与方法 1.1 监测参数区间取值方法 1.1.1 概率统计取值法按照概率统计理论, 可以取平行监测参数的平均值与其3倍标准差的组合确定其取值区间。设某监测参数x的平行监测平均值为μ, 其三倍标准差为3θ, 则此参数的区间取值为:
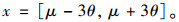
|
(1) |
若监测参数x满足正态分布规律, 可以认为此区间取值以0.997 4的概率出现在整个监测过程中。也即x取值在此区间之外的概率为0.002 6, 按照小概率事件的含义, 是不可能发生的。
某些变形体监测参数的统计和分析结果可能符合T分布或其他概率统计分布规律, 此时可按其符合的分布规律, 取合适的概率确定其区间取值。
1.1.2 仪器精度法一般变形监测用设备, 均有精度范围, 如GPS、测量机器人、InSAR等。设某监测设备的精度为±β, 观测值为x, 则区间变量取值可为:
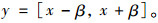
|
(2) |
在某一时空对同一监测点观测多次, 总可以找到其最大值xmax和最小值xmin, 则此监测参数的区间变量可取值为:
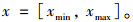
|
(3) |
变形监测数据的区间取值, 有其自身的特点。比如, 在特定情形下, 某种监测数据的取值区间, 应该综合考虑各方面因素, 使得此取值区间大于或小于监测数据本身的误差区间。
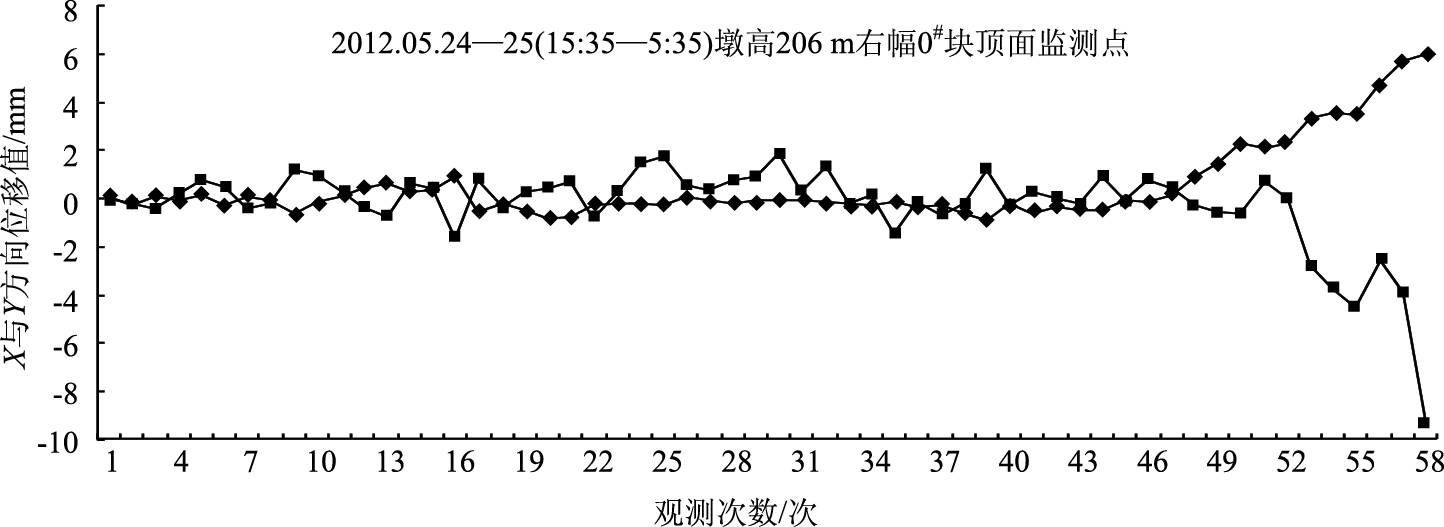
例如, 采用测量机器人对结构物的形变进行实时监测时, 由于各种因素包括仪器在一定距离内的精度等, 使得观测到的原始数据存在误差区间[10-11]。图 1为贵州毕威高速赫章特大桥11#高墩(T型刚构同类桥梁中, 目前为世界第一高墩)施工过程中, 2012年5月24至25日, 离地面206 m高的11#墩右幅0号块顶面处的观测数据[10]。
|
| 图 1 右幅0号块顶面处的观测数据 Fig. 1 Observation data of top of block No.0 on right |
| |
若考虑测量机器人所获得监测数据本身的综合误差区间为[-2, 2]mm, 则意味着前50次观测时间段内(10 min间隔1次, 500 min内), 不考虑此监测点的位移。考虑到观测当天的天气(晴, 温度:10~16 ℃, 风力1级), 可以设定当天观测数据的误差区间为[-2, 2]mm。
1.2 区间分析计算基础及区间扩展函数理论 1.2.1 区间分析计算基础区间分析, 又称区间数学, 是一门用区间变量代替点变量进行运算的数学分支, 最初是从计算数学的误差理论研究发展起来的。区间数学是定义在区间集合上的数学理论。
实数集R上的一个连续子集X= [X, X]称为实区间。所有实区间的集合记作IR= { [X, X]:X, X ∈R, X ≤X }。区间X上下端点分别记做sup(X)和inf(X)。区间X的中点, 宽度, 半径和绝对值, 分别定义如下。
中点:
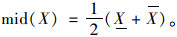
|
(4) |
宽度:
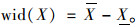
|
(5) |
半径:
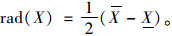
|
(6) |
绝对值:
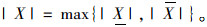
|
(7) |
为符号简洁计, 记m(X)=mid (X), w (X)=wid(X), r (X)=rid (X)。
设X= [X, X], Y= [Y, Y]∈IR。区间四则运算法则为:
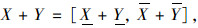
|
(8) |
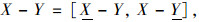
|
(9) |
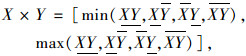
|
(10) |
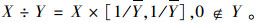
|
(11) |
区间向量和区间矩阵运算规则分别是实向量和实矩阵运算规则的推广, 只是分量或元素间运算采用区间运算规则, 具体运算规则可见文献[1-2]。
1.2.2 区间扩展函数理论区间扩展函数的概念在区间分析理论中非常重要。区间扩展函数包括基本函数、自然扩展函数、中值区间扩展函数、Taylor区间扩展函数等。设f:Rn→R若存在区间值映射F:I (Rn)→I (R), 它对任意xi∈Xi (i=1, 2, …, n), 有:
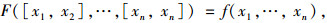
|
(12) |
则称F为函数f的区间扩展。由区间运算的性质, 易知实函数f (x1, x2, …, xn)的区间扩展F (X1, X2, …, Xn)不是唯一的。进一步考察f与其区间扩展F之间的关系, 特别是f的值域与其区间扩展F之间的关系, 是一个很重要的问题。因为它可以导出确定函数值域的计算方法, 是有实用价值的[2]。
2 改善区间计算超宽度的原则 2.1 改写监测数据处理的表达式文献[2]证明, 如果在函数f(x1, x2, …, xn)的表达式中, 每个自变量只出现一次, 则其超宽度恒等于0。此结论意味着, 在区间分析变形监测数据处理中, 理论公式若满足每个自变量只出现一次的情况, 则其超宽度恒等于0。比如, 令x= [-2, 2], 求f(x)=x2-x。
(1) 直接利用f (x)=x2-x计算, 得f(x)= [-2.00, 6.00];
(2) 将f(x)改写为f(x)=x(x-1), 得f(x)= [-6.00, 6.00];
(3) 将f(x)改写为f(x)=(x-1/2)2-1/4, 得f(x)= [-0.25, 6.00]。
(1)~ (3)这3种不同方式的同一表达式, 其区间计算结果完全不同。如果按照计算结果的区间长度来说, 第2种改写最长, 第3种改写最短。
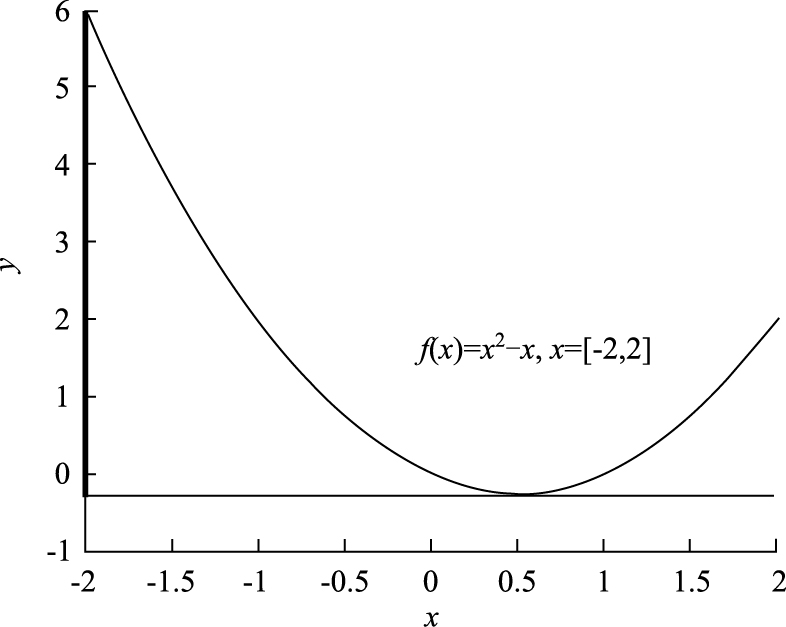
实际上, f(x)=x2-x在x= [-2, 2]内的值域为[-0.25, 6.00], 最小值点在x=0.5处, f(x)=-0.25, 见图 2。可见, 由于第3种表达式中, 自变量x只出现了一次, 其区间计算结果等于实际值域, 超宽度为0。
|
| 图 2 函数f(x)=x2-x, x∈ [-2, 2]的值域 Fig. 2 Value range of function f(x)=x2-x, x∈ [-2, 2] |
| |
图 2也说明, 区间运算法则的计算结果与采用自变量左右端点值计算获得的函数值组合后的区间是不一致的。比如函数f(x)=(x-1/2)2-1/4, 当求x∈[0, 1]时的区间值时, 采用左右端点值计算, f(0)=0.52-0.25=0, f(1)=0.52-0.25=0, 则左右端点值计算结果的函数值的组合区间为[0, 0]。
显然, x∈[0, 1]时, f(x)= (x-1/2)2-1/4的值域并不是[0, 0], 而是[-0.25, 0]。
按区间分析四则运算法则, x∈[0, 1], 得f(x)=-0.25, 0] (Matlab代码:»x=infsup (0, 1);»(x-0.5)^2-0.25= [-0.250 1, 0.000 0])。所以, 不能简单采用直接按自变量左右端点值的计算结果来获得函数值的区间结果。
2.2 缩小监测参数的区间宽度方法根据区间四则运算法则, 可以知道, 缩小监测参数本身的区间取值, 可以有效减小区间超宽度。此结论的成立, 再次突出了监测数据本身的质量和精度的重要性。比如, f(x)=x2-x, x∈ [0, 1]时, f(x)= [-1, 1];x∈ [0.4, 0.6]时, f(x)= [-0.44, -0.04]。
2.3 选择合理的数据处理理论模型根据区间四则运算法则以及区间超宽度相关理论, 理论模型的选择, 以尽可能减少计算结果的超宽度为准。如f (x)=x2-x, 采用f(x)= (x-1/2)2-1/4计算获得的实际值域为[-0.25, 6.00], 区间宽度为6.25;当采用f(x)=x×(x-1)计算得f(x)= [-6.00, 6.00], 其区间宽度为12。而12较6.25大了5.75, 故必须重视合理的数据处理理论模型。
3 区间分析数据处理实例 3.1 时间序列模型某边坡的序列变形观测数据(填方边坡上某点的沉降量)共8个, 采用AR(4)模型进行观测数据的时间序列分析[9]。对于AR(n)模型, 有
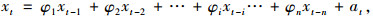
|
(13) |
式中, n为自回归模型阶数, xt-i为观测数据序列, φi为观测数据序列, φi为回归系数, at为观测数据噪声。
X1N为边坡变形观测数据, 采点变量处理, 基于最小二乘原理, 建立矩阵X和Y后, 可得最小二乘解:
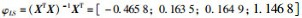
以表 1中点变量为监测平均值, 设观测数据的3倍标准差为0.3 mm, 根据第1节的式(1), 表 1点变量可写成表 2区间变量。
| x1N | 9.79 | 11.44 | 13.00 | 14.68 |
| x1N | 16.29 | 17.90 | 19.56 | 21.21 |
| X1N | [9.76, 9.82] | [11.41, 11.47] | [12.97, 13.03] | [14.65, 14.71] |
| x1N | [16.26, 16.32] | [17.87, 17.93] | [19.53, 19.59] | [21.18, 21.24] |
可知:

|
(14) |

|
(15) |
此时, Xval, Yval为区间矩阵[2]。后续的计算, 需要根据区间矩阵的运算法则及最小二乘法原理进行。
由于区间矩阵求逆算法的复杂性, 很多文献对此进行了研究[12-13]。德国汉堡科技大学Siegfried M. Rump教授及其团队开发的基于Matlab平台的区间计算工具箱INTLAB[14-15], 还不能有效地计算区间矩阵的逆, 导致计算结果出错。同时, 由于时间序列AR(n)模型的严重病态性, INTLAB命令verifylss(a, b)也不能计算出结果。
但是, 由于计算模型矩阵的病态性(条件数达到1.761 3e+06), 数值计算上会产生很大的困难。verifylss(a, b)命令也不能获得正确的结果。为获得有意义的φLS值, X采用中点值的点矩阵, Y采用区间矩阵计算, AR (4)模型φLS的区间参数值为([-0.966 7, 0.035 2]; [-0.507 7, 0.834 8]; [-0.882 3, 1.212 2];[0.499 0, 1.794 7]), 基于区间运算法则, 预测出第9个数据区间值为[-31.595 1, 77.408 9], 中点值为22.91 cm。
φLS的区间参数中点值为[-0.465 8;0.163 5;0.164 9;1.146 8], 与完全采用点变量计算得到的结果φLS= (XTX)-1XTY= [-0.465 8;0.163 5;0.164 9;1.146 8]相等。第9个数据中点值为22.91 cm与点变量预测结果22.89 cm接近。
3.2 灰色系统模型试采用GM (1, 1)灰色预测模型时, 计算灰参数a。
由点变量计算得[16]:
a= [-0.035 4;4.886 4]。预测得x(1)(6)=32.218 4, x(1) (7)=38.353 2, x(0)(6)=5.918 4, x(0)(7)=6.134 8。
以表 3中点变量为监测平均值, 现设观测数据的3倍标准差为0.5 mm, 根据第1节的式(1), 表 3可写成表 4。
| 序号 | 1 | 2 | 3 | 4 | 5 |
| x(0) | 4.6 | 5.2 | 5.3 | 5.4 | 5.8 |
| x(1) | 4.6 | 9.8 | 15.1 | 20.5 | 26.3 |
| 序号 | 1 | 2 | 3 | 4 | 5 |
| x(0) | [4.55, 4.65] | [5.15, 5.25] | [5.25, 5.35] | [5.35, 5.45] | [5.75, 5.85] |
| x(1) | [4.55, 4.65] | [9.70, 9.90] | [14.95, 15.25] | [20.3, 20.7] | [26.05, 26.55] |
试计算GM (1, 1)模型的灰参数â。
易知:

|
(16) |
经计算, GM (1, 1)模型的灰参数区间值â= ([-1.827 2, 1.756 4]; [-23.334 2, 33.107 0])。区间值â中点值为[-0.035 4; 4.886 4], 与采用点变量计算得到的结果â= (BTB)-1BTyN= [-0.035 4;4.886 4]相等。此例中, B1的中点值点矩阵转置后互乘, 点矩阵B1TB1条件数为788.210 2。对于GM (1, 1)模型信息矩阵的病态问题的解决, 很多文献提出了自己的方法。本研究提出的调整计量单位法[17], 有效降低了信息矩阵的条件数, 且调整实测数据计量单位不会影响模型的相对残差、平均残差以及预测精度。
当采用区间灰参数进一步预测x(1) (6), x(1)(7)的区间值时, 由于INTLAB软件无法计算, 可以采用区间灰参数的中点值, 利用此中点值进行预测。
由区间预测值x(1)(6)= [32.158 6, 32.278 1], x(1) (7)= [38.291 4, 38.415 1], 得到x(0)(6)= [5.608 5, 6.228 2], x(0)(7)= [6.013 3, 6.256 6]。x(0)(6)的中点值为5.918 4, x(0) (7)的中点值为6.134 9, 与点变量预测值相同。
3.3 一定时间段内的变形信息预测在现实生产要求中, 需要提前预测工程实体在某一定时间段内的变形信息[18]。比如在高墩桥梁施工中, 需要根据当天及以前的墩顶位移监测数据, 预测后天白天施工期间(8 :00-18 :00)墩顶的大致形变值, 以便进行结构力学分析及施工放样的调整。对于墩顶施工放样工作, 由于墩顶的位移造成理论放样点与实际位置的偏差, 必须考虑根据墩顶变形值来修正施工放样点的准确位置。
一定时间段内的变形信息预测, 可以视为区间时段的变形分析。假如3天的墩顶X(或Y)方向的区间变形观测值为:前2天[2.5, 6.8]cm, 前1天[2.4, 7.5]cm, 当天[2.3, 7.8]cm, 即可选择合适的预测函数模型, 按照3.1节, 3.2节的方法进行后1天墩顶X(或Y)方向的变形区间值预测。
预测值为区间值, 较点数值的优点在于, 一般点参数预测模型的预测值, 由于变形体变形规律的复杂性, 就是与变形规律拟合程度很好的数学模型, 也很难与实测变形值符合。但对于区间值, 实测变形值落在预测值的区间内, 概率是较大的。区间预测值较点预测值能进一步提高理论预测模型的预测准确性, 也能更好地反映工程实体变形的复杂特点。
4 结论本研究就区间分析理论的变形监测数据处理方法进行了研究, 得到了以下结果。
(1) 以区间变量来表达数据处理模型中的参数, 建立起了基于区间变量和区间分析理论的变形监测数据处理方法;
(2) 结合4种参数区间变量取值方法, 讨论减小计算结果的区间超宽度措施。
基于区间变量和区间分析理论的变形监测数据处理方法, 对变形监测的理论分析、数值计算、预测结果将产生重要的影响。本研究旨在抛砖引玉, 希望以后有更多的研究加入进来, 更系统和全面地深入研究区间变形监测数据处理理论与方法。
| [1] |
MOORE R E. Interval Arithmetic and Automatic Error Analysis in Digital Computing[D]. Stanford: Stanford University, 1962. https://www.researchgate.net/publication/34342841_Interval_arithmetic_and_automatic_error_analysis_in_digital_computing
|
| [2] |
MOORE R E. Interval Analysis[M]. Englewood Cliffs: Prentice-Hall, 1966.
|
| [3] |
苏永华, 何满潮, 赵明华, 等. 基于区间变量的响应面可靠性分析方法[J]. 岩土工程学报, 2005, 27(12): 1408-1413. SU Yong-hua, HE Man-chao, ZHAO Ming-hua, et al. Reliability Analysis of Response Surface Method Based on Interval Variables[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(12): 1408-1413. |
| [4] |
王朝晖, 王选仓, 马士宾. 基于区间数逼近法的路面使用性能综合评价[J]. 公路交通科技, 2009, 26(1): 21-25. WANG Chao-hui, WANG Xuan-cang, MA Shi-bin. An Approximation Method of Interval Numbers for Comprehensive Evaluation of Pavement Performance[J]. Journal of Highway and Transportation Research and Development, 2009, 26(1): 21-25. |
| [5] |
朱向平, 颜可珍, 刘杰. 沥青路面预养护方案的区间关联模糊优化决策[J]. 中南林业科技大学学报, 2011, 31(11): 166-170. ZHU Xiang-ping, YAN Ke-zhen, LIU Jie. Pre-maintenance Measure of Asphalt Pavement Interval Related Fuzzy Optimization Decision-making[J]. Journal of Central South University of Forestry & Technology, 2011, 31(11): 166-170. |
| [6] |
于生飞, 陈征宙, 张明瑞, 等. 基于区间不确定分析方法的边坡稳定性分析[J]. 工程地质学报, 2012, 20(2): 228-233. YU Sheng-fei, CHEN Zheng-zhou, ZHANG Ming-rui, et al. Interval Analysis Model of Geomaterial Parameters for Uncertainties in Slope Stability Assessment[J]. Journal of Engineering Geology, 2012, 20(2): 228-233. |
| [7] |
唐利民, 郑健龙. 基于区间适定和区间不适定性理论的参数反演方法[J]. 土木工程学报, 2016, 49(11): 91-96. TANG Li-min, ZHENG Jian-long. Parametric Inversion Method Based on Interval Well-posedness and Interval Ill-posedness Theory[J]. China Civil Engineering Journal, 2016, 49(11): 91-96. |
| [8] |
唐利民, 郑健龙. 区间分析岩土工程理论与方法[M]. 北京: 科学出版社, 2017. TANG Li-min, ZHENG Jian-long. Interval Analysis Theory and Method of Geotechnical Engineering[M]. Beijing: Science Press, 2017. |
| [9] |
黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2010. HUANG Sheng-xiang, YIN Hui, JIANG Zheng. Deformation Monitoring Data Processing[M]. Wuhan: Wuhan University Press, 2010. |
| [10] |
唐利民.贵州省毕节至威宁高速公路赫章特大桥11#高墩施工过程中的形变规律研究[R].长沙: 长沙理工大学, 2013. TANG Li-min. Study on Deformation Law of Construction of 11th High Pier of Hezhang Bridge of Bijie-Weining Expressway in Guizhou Province[R]. Changsha: Changsha University of Science and Technology, 2013. |
| [11] |
唐利民.贵州省赤水至望谟高速公路仁赤段二郎河特大桥主桥施工测量控制研究[R].长沙: 长沙理工大学, 2014. TANG Li-min. Research on Construction Survey Control of Main Bridge of Erlanghe Bridge in Renchi Section of Chishui-Wangmo Expressway in Guizhou Province[R]. Changsha: Changsha University of Science and Technology, 2014. |
| [12] |
REVOL N, THÉVENY P. Parallel Implementation of Interval Matrix Multiplication[J]. Reliable Computing, 2013(19): 91-106. |
| [13] |
HASHEMI B, TAVAKOLIPOUR H. A Non-induced Interval Matrix Norm[J]. Reliable Computing, 2013(18): 144-146. |
| [14] |
RUMP S M. INTLAB: INTerval LABoratory[M]//CSENDES T. Developments in Reliable Computing. Dordrecht: Kluwer Academic Publishers, 1999: 77-104.
|
| [15] |
RUMP S M. The Matlab/Octave Toolbox for Reliable Computing[EB/OL]. (2013-01-14)[2017-06-09]. http://www.ti3.tu-harburg.de/rump/intlab/.
|
| [16] |
邓聚龙. 灰色控制系统[M]. 1版. 武汉: 华中工学院出版社, 1985: 293-360. DENG Ju-long. Grey Control System[M]. 1st ed. Wuhan: Huazhong Institute of Technology Press, 1985: 293-360. |
| [17] |
唐利民. GM(1, 1)病态问题求解的调整计量单位法[J]. 武汉大学学报:信息科学版, 2014, 39(9): 1038-1042. TANG Li-min. Adjust Measurement Unit Algorithm for Ill-posed Problem of GM(1, 1) Model[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1038-1042. |
| [18] |
肖大海, 谢全敏, 杨文东. 基于多变量的集成预测模型在隧道拱顶沉降变形预测中的应用[J]. 公路交通科技, 2017, 34(12): 119-121. XIAO Da-hai, XIE Quan-min, YANG Wen-dong. Application of Integrated Forecasting Model Based on Multivariable in Tunnel Vault Settlement Forecasting[J]. Journal of Highway and Transportation Research and Development, 2017, 34(12): 119-121. |
 2019, Vol. 36
2019, Vol. 36
