2019, Vol. 36
表 1(Table 1)
钢板-橡胶吸能圈的设计方法
扩展功能
文章信息
- 王君杰, 涂凌峰, 殷永高, 郑伟峰
- WANG Jun-jie, TU Ling-feng, YIN Yong-gao, ZHENG Wei-feng
- 钢板-橡胶吸能圈的设计方法
- A Method for Designing Steel Plate-rubber Energy Absorption Ring
- 公路交通科技, 2019, 36(2): 50-60
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 50-60
- 10.3969/j.issn.1002-0268.2019.02.008
-
文章历史
- 收稿日期: 2017-04-05
王君杰, 涂凌峰, 殷永高, 郑伟峰. 钢板-橡胶吸能圈的设计方法[J]. 公路交通科技, 2019, 36(2): 50-60.
WANG Jun-jie, TU Ling-feng, YIN Yong-gao, ZHENG Wei-feng.
A Method for Designing Steel Plate-rubber Energy Absorption Ring[J]. Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 50-60.
钢板-橡胶吸能圈的设计方法
1. 同济大学 土木工程学院, 上海 200092;
2. 安徽省交通控股集团有限公司, 安徽 合肥 230088
2. 安徽省交通控股集团有限公司, 安徽 合肥 230088
摘要: 钢材和橡胶是两种常见的工程材料，两者组合起来具有较好的吸能和回弹性能。为了综合两种材料的优异性能用于工程设计，提出了一种由外钢板、橡胶圈和内钢板组成的钢板-橡胶吸能圈（简称钢板-橡胶圈）以用于防撞设计，并由此开展了基于钢板-橡胶圈的设计方法研究：使用有限元软件建立了外径为1 m的25个具有不同结构参数（钢板厚度、环壁厚）的钢板-橡胶圈有限元模型，其中钢板厚度选取的尺寸为0，5，10，15，20，25 mm，环壁厚选取的尺寸是0.05，0.1，0.15，0.2，0.25 m。定义无量纲比值：钢板厚、环壁厚、圈的径向相对变形比。通过数值仿真和统计分析，建立了圈的性能参数（吸能量）与这3个无量纲比值的经验公式，并进行了相应的误差分析，确定了经验公式具有一定的可信度。同时，基于工程设计优化需要，定义了基于回弹率的优化筛选原则，用于筛选掉满足耗能要求但不满足回弹率要求的钢板-橡胶圈。参照结构试验的相似理论，将1 m外径的钢板-橡胶圈的经验公式推广到更多不同外径钢板-橡胶圈中。最后，提出了一种较为实用的用于桥梁防撞结构的钢板-橡胶圈的设计流程，并依照设计流程给出了相关的设计算例。
关键词:
桥梁工程
防撞设计方法
统计分析
钢板-橡胶圈
性能参数
A Method for Designing Steel Plate-rubber Energy Absorption Ring
1. School of Civil Engineering, Tongji University, Shanghai 200092, China;
2. Anhui Transportation Holding Group Co., Ltd., Hefei Anhui 230088, China
2. Anhui Transportation Holding Group Co., Ltd., Hefei Anhui 230088, China
Abstract:
Steel and rubber are 2 common engineering materials, which have good energy absorption and rebound performance. To integrate the excellent properties of the 2 materials for engineering design, a steel plate-rubber energy absorption ring (hereafter called steel plate-rubber ring) composed of outer steel plate, rubber ring and inner steel plate is designed for anti-collision design, and a design method based on steel plate-rubber ring is conducted. Twenty-five finite element models of steel plate-rubber ring with 1 m outer diameter and different structural parameters (steel plate thickness, ring wall thickness) are established by using finite element software. Among which, the thicknesses of the steel plate are 0, 5, 10, 15, 20, 25 mm, and the thicknesses of ring wall are 0.05, 0.1, 0.15, 0.2, 0.25 m. The dimensionless ratios (relative deformation ratios of steel plate thickness, ring wall thickness, ring radial dimension) are defined. The empirical formulas of the ring's performance parameters (energy absorption) and these dimensionless ratios are established through numerical simulation and statistical analysis, and the corresponding errors are analyzed. Meanwhile, based on the optimization of engineering design, the optimal screening principle based on rebound rate is defined to screening out the steel plate-rubber ring which meets the requirement of energy absorption but does not meet the requirement of rebound rate. Referring to the similarity theory of structure test, the empirical formula of steel plate-rubber ring with 1 m outer diameter is extended to steel plate-rubber rings with different diameters. Finally, a practical design procedure of steel plate-rubber ring for bridge anti-collision structure is proposed, and the relevant design example is given according to the design procedure.
Key words:
bridge engineering
anti-collision design method
statistical analysis
steel plate-rubber ring
performance parameter
0 引言
5.2 设计算例
中国很多桥梁跨越通航船舶的河流或海湾, 面临船舶撞击的风险。河流或海湾的水位随季节或年份有很大的变化, 因此最近一些年工程师开发了多种可以随水位浮动的桥梁防船舶撞击结构, 以保证桥梁的运行安全。其中应用较为广泛的是由钢-橡胶材料构成的浮动防撞装置, 如黄石桥长江公路大桥防船撞装置[1]和湛江海湾大桥防撞装置[2]。在这类钢-橡胶材料构成的浮动防撞装置中, 一般都采用橡胶吸能组件, 但目前橡胶吸能组件的设计并没形成一般化的设计方法。
本研究首先提出一种钢板-橡胶吸能圈的设计方案, 然后采用数值模拟方法, 进行了大量的计算分析, 通过数理统计建立了该种吸能圈的一般设计方法。
1 钢板-橡胶吸能圈的构造设计对于浮动防船撞装置, 耗能(吸能)组件的性能是一个重要问题。从现有的工程实践来看, 耗能(吸能)组件多采用橡胶或钢材增强橡胶[3-11], 这种组件大多利用橡胶来吸收能量, 利用钢材来耗散能量。基于此原理, 本研究提出了一种钢板-橡胶吸能圈, 见图 1。吸能圈主要由3部分组成, 分别是外层钢板、橡胶圈以及内层钢板, 钢板与橡胶圈之间采用粘合剂高温硫化制成钢板-橡胶圈。
|
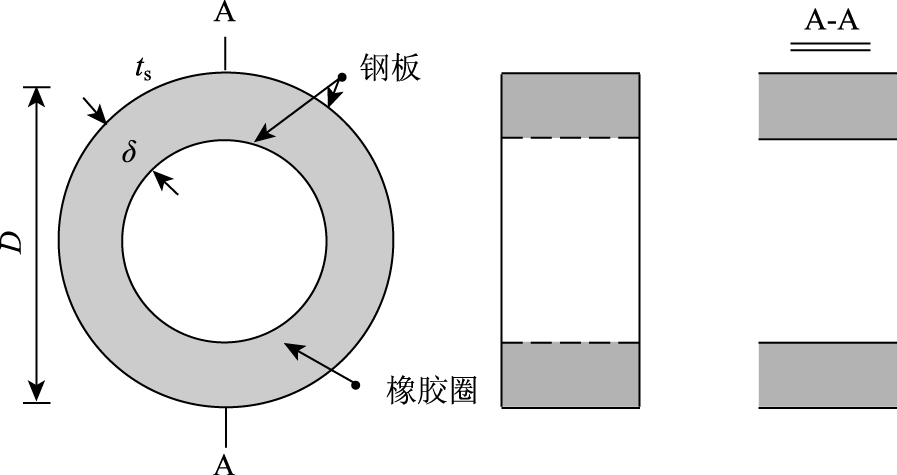
| 图 1 钢板-橡胶圈示意图 Fig. 1 Schematic diagram of steel plate-rubber ring |
| |
橡胶自身弹性模量较低, 但是具有较好的回弹性能。在橡胶圈的基础上设置内钢板和外钢板, 目的是对橡胶圈进行约束加强, 同时钢板也能提供一定的耗能。
定义比值:
|
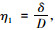
(1) |
|
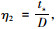
(2) |
式中, ts为钢板厚度; δ为环壁厚; D为圈的外径。
2 钢板-橡胶圈的特性分析 2.1 钢板-橡胶圈的有限元模型分析及结构参数采用有限元软件Hypermesh建立钢板-橡胶圈的有限元计算模型, 具体构造如图 2所示, 钢板-橡胶圈中的橡胶采用实体单元模拟, 钢板单元采用壳单元模拟, 假定各材料层之间的连接是理想的, 在撞击过程中不发生破坏和相对滑移[12-13], 下侧钢板采用3方向自由度固定, 钢板-橡胶圈与下侧钢板连接处采用共节点连接, 上侧钢板在数值模拟过程中均匀下压。
|
| 图 2 有限元模型 Fig. 2 Finite element model |
| |
在本研究中体、壳单元混合建模中采用的连接方式为直接耦合, 即对板、体单元节点共节点处理。根据文献对比结果[14], 采用共节点处理方法得到的计算结果与解析解极为接近, 因此在钢板橡胶圈有限元模型中并未考虑壳、体单元节点转动自由度变形协调问题的影响。
橡胶采用不可压缩的Mooney-Rivlin模型, 即LS-DYNA软件提供的MAT27材料模型, 其材料本构方程为:
|
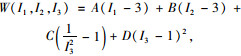
(3) |
式中, W为材料的应变能函数; C=A/2+B, D= [A (5ν-2)+B (11ν-5)]/ [2 (1-2ν)], G=2 (A+B)。由于需要充分检验钢板-橡胶圈耗能能力, 本研究采用常见的硬度为70的橡胶[15], 质量密度为1 100 kg/m3, ν=0.499 9, A=1.039 6 MPa, B=0.020 8 MPa, I2和I3为应变不变量。
由于钢材在初始屈服以后, 材料应变强化明显, 可以考虑采用弹-线性强化模型, 应力应变曲线及参数见图 3。
|
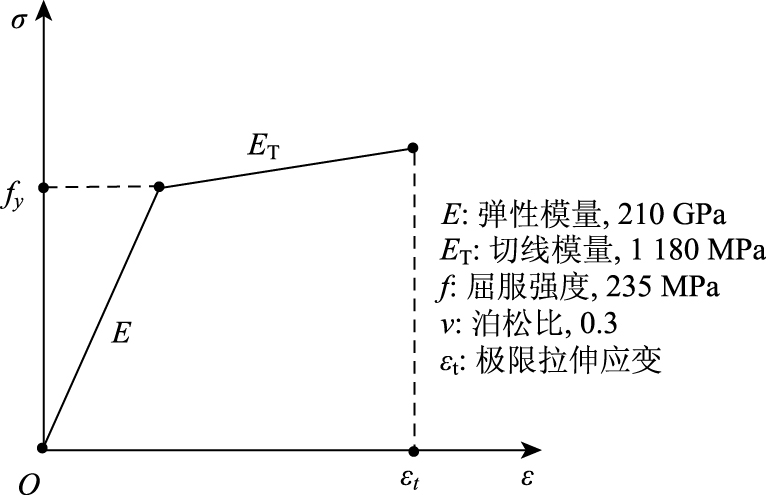
| 图 3 钢板的本构模型及参数 Fig. 3 Constitutive model and parameters of steel plate |
| |
需要指出的是, 加载速率会引起材料的应变率效应, 试验表明[16], 橡胶材料在低应变速率下的应变率效应不明显; 因此在本研究中主要考虑钢板的应变率效应, 2.3小节中将重点探讨加载速率对钢板-橡胶圈吸能能力的影响。
2.2 吸能与回弹特性为研究钢板-橡胶圈的吸能特性, 以外径1 m, 环壁厚0.25 m, 钢板厚度0 m和0.01 m的钢板-橡胶圈为例进行分析。在2.0 m/s的匀速加载下, 得到的反应曲线见图 4、图 5。其中, 定义了无量纲比值, 圈的径向相对变形比:
|
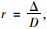
(4) |
|
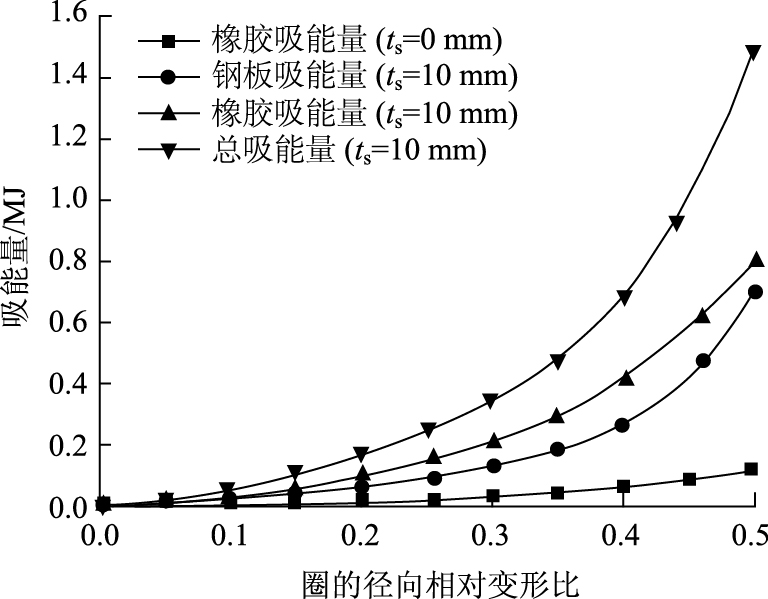
| 图 4 能量曲线 Fig. 4 Energy curve |
| |
|
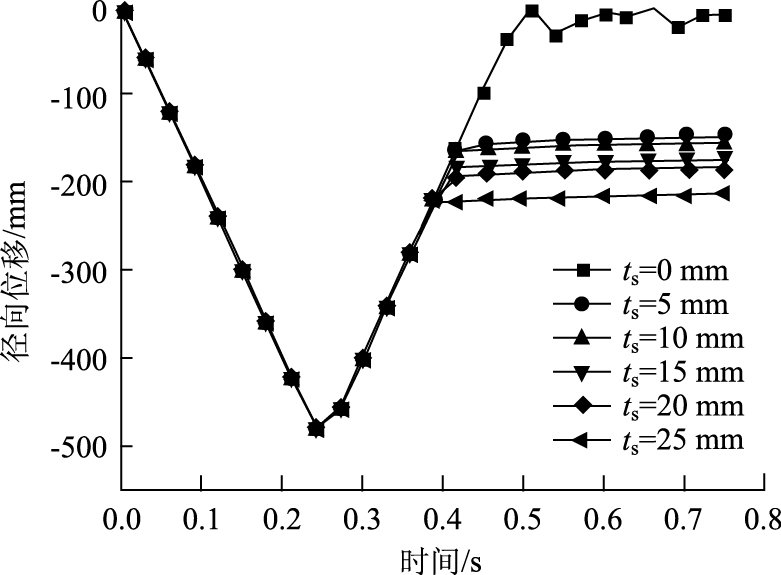
| 图 5 径向位移曲线 Fig. 5 Radial displacement curve |
| |
式中Δ为圈的径向位移。
从图 4的能量曲线来看, 纯橡胶圈(钢板厚度0 mm)吸能量与钢板-橡胶圈(钢板厚度10 mm)的橡胶吸能量差异明显, 这说明钢板自身具有较好的耗能能力, 同时钢板对橡胶施加了一定的约束作用, 可以增加橡胶的耗能能力, 橡胶在内外钢板之间, 可以保证两层钢板能够协同工作增加耗能能力。
从图 5的钢板-橡胶圈的径向位移曲线可以看出:当钢板厚度增加时, 回弹率下降, 但仍具有60%以上的回弹率, 说明钢板-橡胶圈具有较好的回弹性能, 同时钢板厚度越厚, 回弹率越小。
以上可以说明, 钢板-橡胶圈的吸能作用及回弹性能良好, 有用于设计防撞装置的潜力[17]。
2.3 几何参数变化的影响(1)环壁厚δ
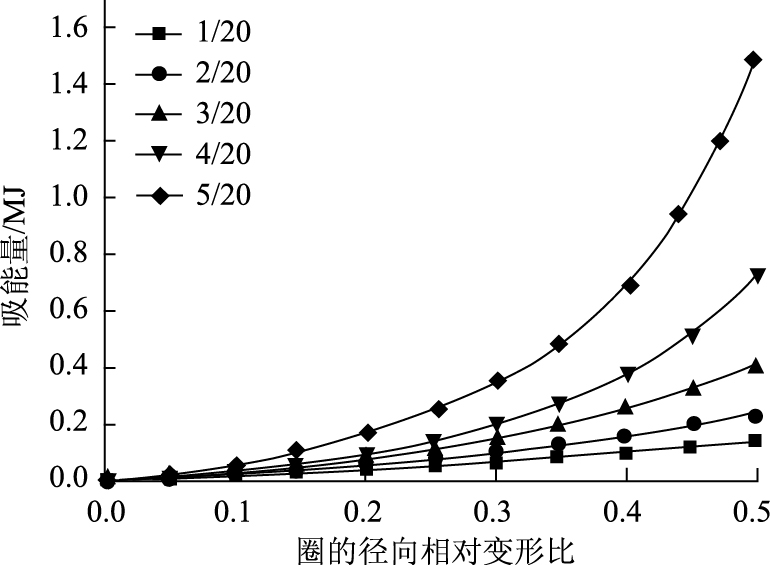
为观察环壁厚δ对圈性能的影响, 选取有限元模型:外径为1 m, 钢板厚度为10 mm, η1取5个值, 分别为1/20, 2/20, 3/20, 4/20, 5/20的情况下, 橡胶层的厚度分别为0.05, 0.1, 0.15, 0.2, 0.25 m。在2.0 m/s匀速加载下, 得到的反应曲线见图 6。
|
| 图 6 改变η1的圈的总吸能量曲线 Fig. 6 Total energy absorption curves of ring when changing η1 |
| |
从图 6可以看到, 环壁厚对圈性能有较大影响。在钢板厚度和外径给定的情况下, 随η1的增大, 吸能曲线向上、向左方移动, 原因是, 随η1的增大圈的内径变小, 圈径向接触挤压阶段对应的径向变形变小。
(2)钢板厚度ts
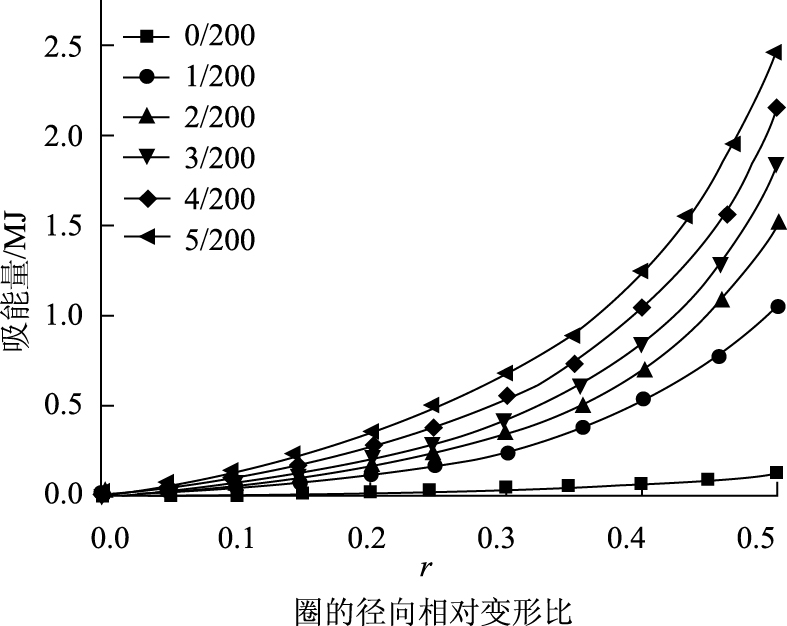
为观察钢板厚度ts对圈性能的影响, 选取有限元模型:外径D为1 m, 环壁厚为0.25 m, η2取6个值, 分别为0/200, 1/200, 2/200, 3/200, 4/200, 5/200, 对应的钢板厚度分别为0, 5, 10, 15, 20, 25 mm。在2.0 m/s匀速加载条件下, 计算得到的力与能量曲线见图 7。
|
| 图 7 改变η2的圈的总吸能量曲线 Fig. 7 Total energy absorption curves of ring when changing η2 |
| |
从图 7可看出, 由于钢板厚度不同导致径向压力和能量值有所不同。以上两图说明在圈的其他参数(外径、壁厚等)给定之后, 增加钢板厚度可以在一定程度上改变钢板-橡胶圈的吸能量。
(3)外径D
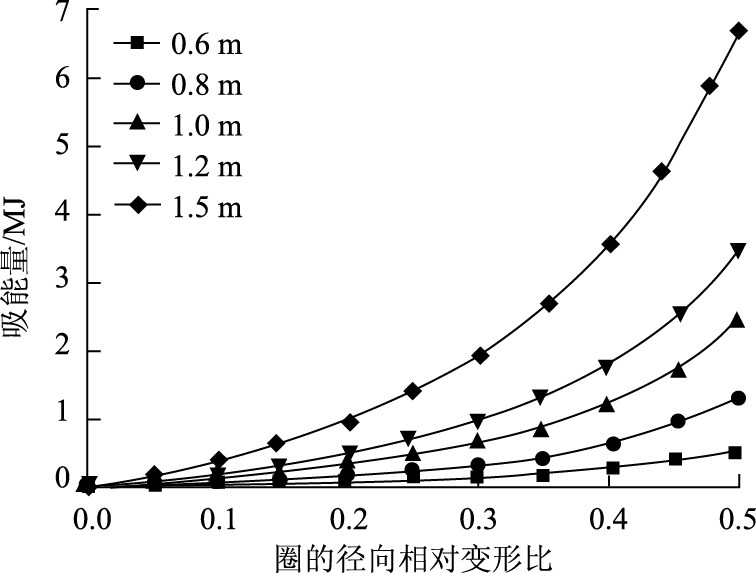
为了讨论圈外径D的影响, 选取有限元模型:η1=5/20, η2=5/200, 外径D取0.6, 0.8, 1.0, 1.2, 1.5 m, 在加载速度2.0 m/s下, 得到的反应曲线见图 8。可以看到, 在η1和η2给定的情况下, 随D的增大, 吸能能力都在增加。
|
| 图 8 改变D的圈的总吸能量曲线 Fig. 8 Total energy absorption curves of ring when changing D |
| |
(4)加载速率v
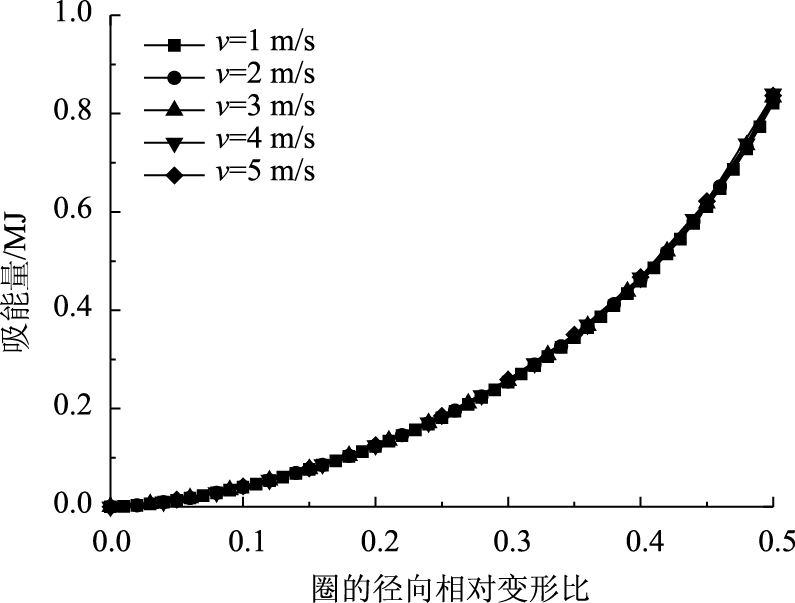
为了研究加载速率的影响, 选取有限元模型:外径为1 m、钢板厚度为12 mm, η1=4/20, 选取5种加载速率:1, 2, 3, 4, 5 m/s进行加载, 求得不同加载速率下钢板-橡胶圈的吸能量如图 9所示, 说明在低速率下, 改变加载速率对钢板-橡胶圈吸能结果影响很小。从而, 可以认为在低速率下(本研究假定为5 m/s以下), 钢板-橡胶圈材料应变率效应不明显。
|
| 图 9 改变v的圈的总吸能量曲线 Fig. 9 Total energy absorption curves of ring when changing loading speed v |
| |
对以上4种因素进行分析发现:环壁厚δ、钢板厚度ts、外径D等参数改变对钢板-橡胶圈耗能能力影响较大, 而在加载速率较低时, 改变加载速率对钢板-橡胶圈耗能能力影响不大。
3 钢板-橡胶吸能圈的设计方法要建立钢板-橡胶圈的设计方法, 首先需要确定设计所需圈的性能参数与圈的结构参数之间的关系。圈的性能参数指吸能量E, 结构参数指环壁厚与外径之比η1、钢板厚度与外径之比η2、外径D、径向变形比r。
3.1 圈参数取值及组合由第2节讨论可知, 钢板-橡胶圈的几何参数取不同值, 它的吸能量值不同。为了研究它们之间的关系, 简化起见, 本研究首先针对外径D=1 m的钢板-橡胶圈, 橡胶圈加载速率取2 m/s, 环壁厚δ和钢板厚度ts分别取5个值, 进行排列组合, 由此, 可以得到25个结构参数不同的有限元模型。
3.2 参数统计对于外径D=1 m的钢板-橡胶圈有限元模型, 当η1, η2确定时, 径向变形比r与吸能量E之间存在一一对应的关系。
从工程设计角度来考虑, 为保证钢板-橡胶圈的回弹性能, 规定钢板-橡胶圈的径向变形比r的最大值为0.5, 设为rc。由2.3节可知, 吸能量E随着r的增大而增大, 因此rc对应的吸能量也是钢板-橡胶圈的吸能量峰值, 记为Ec, Ec的取值与η1, η2有关。
通过参数拟合发现Ec与η1, η2的经验公式的函数类型均可以表达为:
|
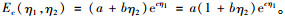
(5) |
根据统计得到的参数a, b, c的经验值见表 1。
表 1 a, b, c的经验统计值
Tab. 1 Empirical statistics values of a, b, c
| 系数 | 公式类型 |
| Ec(η1, η2) | |
| a | 0.04 |
| b | 142.50 |
| c | 8.28 |
为考察式(5)的精度, 计算并统计了模型计算值与式(5)预测值的误差, 见图 10。可见25个相对误差绝大部分集中在(-30%, 30%)以内, 说明拟合效果较好。
|
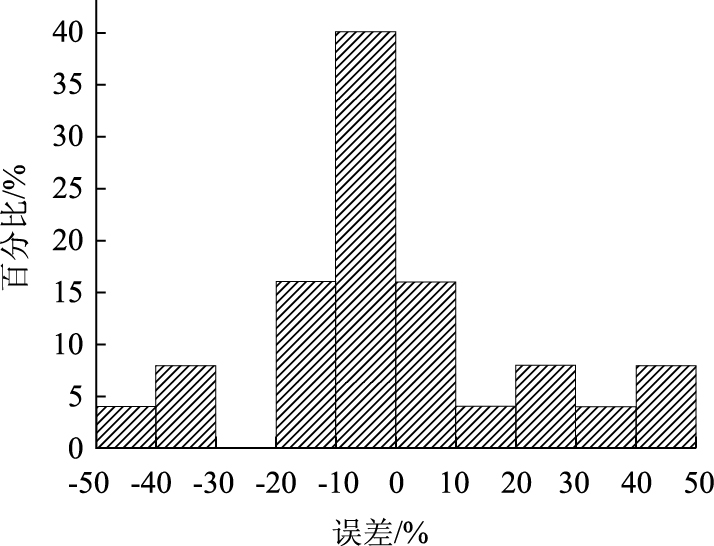
| 图 10 Ec模型计算值与预测值的相对误差 Fig. 10 Relative error of Ec between model calculated value and predicted value |
| |
求得Ec值后, 还需要获得r所对应的E(r), 基于工程需要, r可限定范围为[0.2, 0.5], 本研究定义无量纲比值:
|
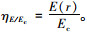
(6) |
对两者分别进行拟合。在拟合时发现, ηE/Ec的函数类型均可表示为:
|
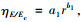
(7) |
式中, 系数a1, b1均可用η1, η2表示出来, 求得:
|
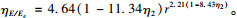
(8) |
为检验上述拟合公式的准确性, 将ηE/Ec在拟合公式中的值与在模型计算的值进行误差分析, 统计图如图 11所示, 发现相对误差绝大部分可以控制在(-20%, 20%)以内, 说明拟合精度满足要求, 具体数值见图 11。
|
| 图 11 ηE/Ec样本值与预测值的相对误差 Fig. 11 Relative error of ηE/Ec between sample value and predicted value |
| |
这样, 对于任意变形比r所对应的E(r)可表示为:
|
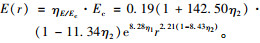
(9) |
由式(9)可知, 如果E(r)的值确定, η1, η2, r存在着很多不同组合, 基于工程设计优化, 这里引入回弹量指标作为优化指标。
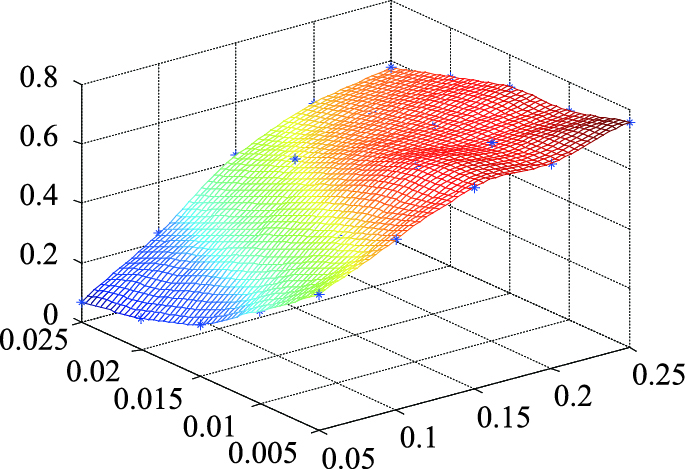
3.3 优化原则对于同一外径的钢板-橡胶圈, 环壁厚及钢板厚度取不同值时, 橡胶圈的回弹率会有差异。一般情况下, 环壁厚越厚, 钢板厚度越薄, 橡胶圈的回弹率越大, 因此, 可以人为指定一个回弹率指标作为优化指标, 认为低于这一指标的环壁厚、钢板厚度的组合不满足工程设计需要。提取外径D=1 m的25个有限元模型的回弹率值如表 2所示。
表 2 不同η1和η2对应的回弹率
Tab. 2 Rebounding rates corresponding to different values of η1 and η2
| η1 | η2 | ||||
| 0.005 | 0.01 | 0.015 | 0.02 | 0.025 | |
| 0.05 | 0.46 | 0.31 | 0.18 | 0.10 | 0.07 |
| 0.1 | 0.58 | 0.49 | 0.41 | 0.32 | 0.23 |
| 0.15 | 0.68 | 0.66 | 0.58 | 0.50 | 0.42 |
| 0.2 | 0.69 | 0.67 | 0.63 | 0.58 | 0.53 |
| 0.25 | 0.76 | 0.70 | 0.69 | 0.64 | 0.58 |
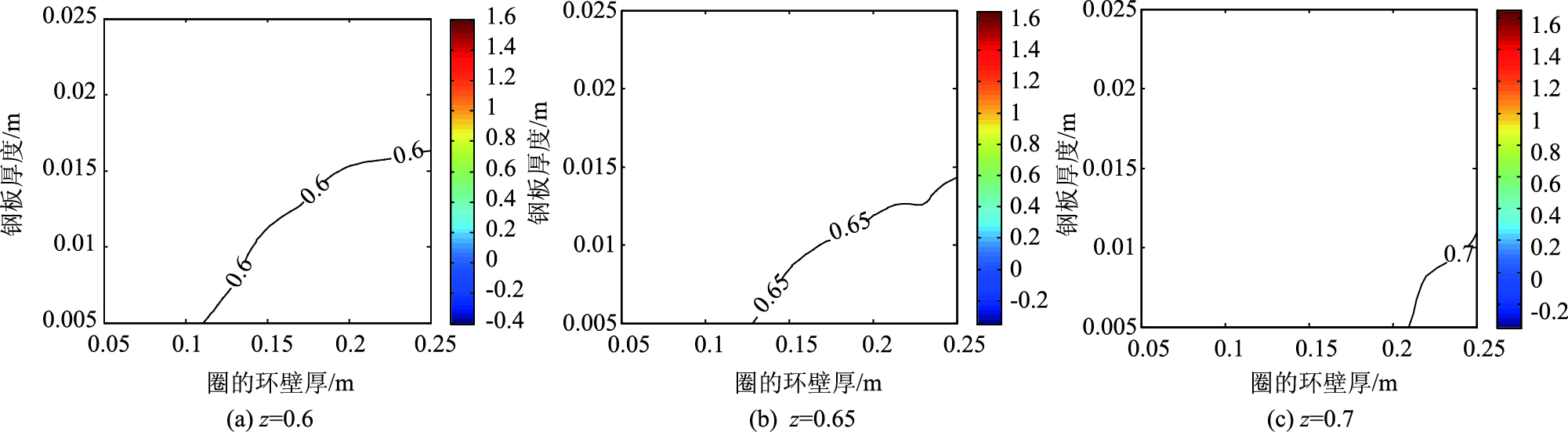
采用MATLAB将表 2数据绘制成曲面图, 见图 12。z表示回弹率, 满足工程设计的钢板-橡胶圈的回弹率一般应不小于0.5, 同时考虑回弹率大于0.7的钢板厚度取值有限, 因此z取值一般为0.5~0.7, 本研究取z=0.5, 0.55, 0.6, 0.65, 0.7, 利用等高面z去截断曲面, 部分图示见图 13, 获得满足相关回弹率的η1, η2的大致范围, 再使用origin进行相关拟合, 获得不小于相应回弹率时η1, η2需要满足的条件。
|
| 图 12 回弹率曲面 Fig. 12 Curued surface of rebound rate |
| |
|
| 图 13 回弹率曲面 Fig. 13 Curued surface of rebound rate |
| |
对满足z=0.5, 0.55, 0.6, 0.65, 0.7的曲线进行拟合, 得到满足z的函数表达式如下:
|
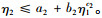
(10) |
根据统计得到的参数a2, b2, c2的经验值见表 3。
表 3 a2, b2, c2的经验统计值
Tab. 3 Empirical statistics parameters of a2, b2, c2
| 系数 | 回弹率z | ||||
| 0.5 | 0.55 | 0.6 | 0.65 | 0.7 | |
| a2 | -0.02 | -0.80 | -0.98 | -0.29 | -0.17 |
| b2 | 0.15 | 0.86 | 1.03 | 0.34 | 0.22 |
| c2 | 0.78 | 0.03 | 0.02 | 0.07 | 0.15 |
对于z值取0.5~0.7范围内其他值时, 可以近似采用表 3进行线性插值, 这样就可以利用回弹率指标, 对具有相同径向压力或吸能量钢板-橡胶圈的不同η1, η2组合进行筛选, 达到优化设计的目的。
4 尺度扩展 4.1 相似关系第2和第3节都是针对外径D=1 m的钢板-橡胶圈来研究, 但在实际工程设计中, 钢板-橡胶圈的外部尺寸并不能人为直接指定。这样, 对于钢板-橡胶圈吸能量的讨论, 就需要引入外径D这个变量。在结构试验中, 常应用相似关系将足尺试件按特定相似比缩减或扩大至适当尺寸, 通过缩小或扩大得到的试件可以全部或部分反映足尺试件的特征[18]。故本研究借鉴这一原理对钢板-橡胶圈进行放缩。其中, 基本缩尺比为:Sρ, SE, SL。导出吸能量E缩尺比SE=SL3。
因此, 对于不同外径D的钢板-橡胶圈, 其吸能量E可以表示为:
|
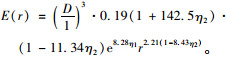
(11) |
对于钢材来说, 由于钢是线弹性材料, 可以直接进行相应缩减或扩大, 而对于橡胶这种各向异性的非线性材料, 如果进行尺寸放缩后的误差在可接受范围内, 也可认为其近似满足相似关系。
4.2 相似关系误差分析由4.1小节可知, 如果在误差允许范围内, 以外径1 m的钢板-橡胶圈为足尺模型直接进行放缩建立的相应相似模型(记为M1)与以实际放缩尺寸建立的模型(记为M2)力学性能参数值应该接近。下面分别取外径D=0.6 m, 1.2 m进行误差分析。
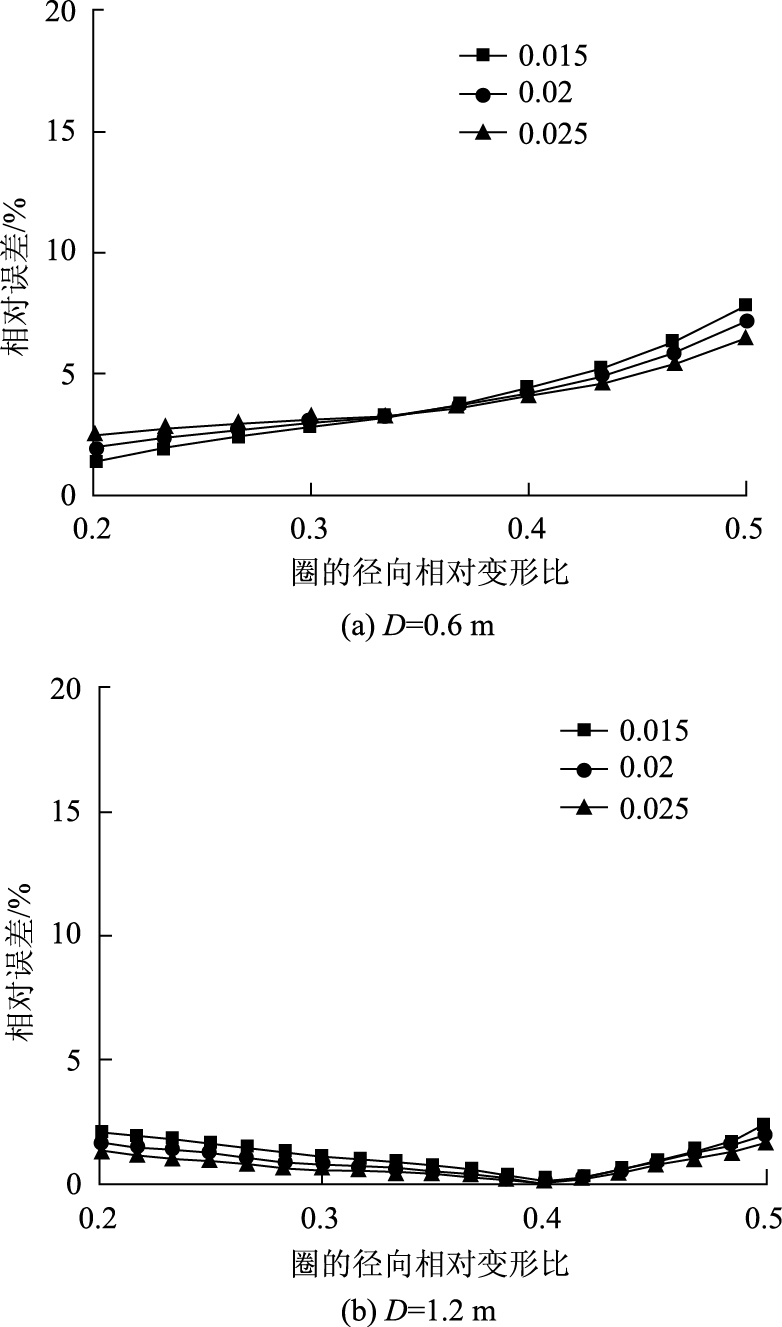
取外径D=0.6 m, 环壁厚η1=0.2, 钢板厚度η2=0.015, 0.02, 0.025, M1和M2吸能量的相对误差如图 14(a)所示; 取外径D=1.2 m, 环壁厚η1=0.2, 钢板厚度η2=0.015, 0.02, 0.025, M1和M2的径向压力与吸能量的相对误差如图 14(b)所示。
|
| 图 14 径向吸能量E相对误差 Fig. 14 Relative error curves of radial energy absorption E |
| |
由图 14可知, 吸能量E的相对误差值基本能在10%以内, 误差在可接受范围内, 说明由相似关系建立的缩尺模型M1可以近似替代实际建立的模型M2, 式(9)可以应用到不同外径中。
5 钢板-橡胶吸能圈的设计流程与设计算例 5.1 设计流程对于钢板-橡胶圈, 如果能知道其最大允许径向变形比和最大吸能量的值, 我们就可以根据构造要求及拟合公式确定钢板-橡胶圈的尺寸(外径、钢板厚度、环壁厚), 同时, 根据筛选原则, 剔除回弹率不满足要求的圈, 从而完成钢板-橡胶圈的设计。
本研究采用的设计原则(可选择的设计控制量)如下:
(1) 根据桥墩需耗散能量E0和吸能筒的布置方案初步确定单个钢板-橡胶圈承受的最大吸能量E (r);
(2) 根据几何方面的要求, 初步确定单个圈的最大允许径向变形比r。
由上一节可知:E(r)的值可以由吸能量峰值Ec与无量纲比值ηE/Ec的乘积获得, 即:
|
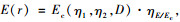
(12) |
式中, Ec, ηE/Ec均与η1, η2, D, r有关, 现在已知E(r)和r, 并根据防撞装置构造要求指定外径D值, 根据钢板加工的可行性将钢板厚度控制在3~25 mm之间的整数值, 从而得到钢板厚对应环壁厚的数值, 再根据筛选原则筛选掉一部分数值, 具体流程图如图 15所示。
|
| 图 15 钢板-橡胶圈设计流程 Fig. 15 Flowchart of desiging steel plate-rubber ring |
| |
5.2 设计算例
根据图 15钢板-橡胶圈的设计流程, 下面结合算例来实现这一过程。
对某航道桥桥墩进行防撞装置设计, 桥墩横断面尺寸是20 m×6 m, 设防代表船舶为3 000 t货船, 撞击速度选用实际工程中比较常见的速度:4 m/s。设计要求规定:钢板-橡胶圈需耗散能量E0=4 MJ, 同时规定橡胶圈最大径向位移不超过其外径的0.4倍, 即r=0.4。
为防止船舶直接碰撞桥墩, 根据水平延展要求确定钢板-橡胶圈直径D=1.8 m; 桥墩宽度6 m, 拟定定橡胶圈数量n=6, 假定单圈最大吸能量E (0.4)=0.8 MJ, 则n·E=6×0.8=4.8 MJ>4 MJ, 满足吸能要求。
在3~25 mm范围内拟定钢板厚度ts, 根据式(2)可确定参数η2, 将η2与r=0.4, D=1.8 m一起代入式(11), 可解得η1值如表 4所示; 最后采用回弹率作为优化筛选指标, 选出满足回弹率要求的η1, η2值如表 4所示。
表 4 满足不同回弹率的η1、η2值
Tab. 4 Values of η1 and η2 which meeting different rebounding rates
| 序号 | ts/m | η2 | η1 | η1最小值(60%) | 是/否 | η1最小值(65%) | 是/否 | η1最小值(70%) | 是/否 |
| (1) | 0.003 | 0.001 7 | 0.175 3 | 0.083 1 | 是 | 0.111 9 | 是 | 0.191 3 | 否 |
| (2) | 0.004 | 0.002 2 | 0.167 4 | 0.090 4 | 是 | 0.114 9 | 是 | 0.195 5 | 否 |
| (3) | 0.005 | 0.002 8 | 0.160 0 | 0.093 0 | 是 | 0.118 1 | 是 | 0.199 7 | 否 |
| (4) | 0.006 | 0.003 3 | 0.153 0 | 0.095 7 | 是 | 0.121 3 | 是 | 0.204 0 | 否 |
| (5) | 0.007 | 0.003 9 | 0.146 3 | 0.098 4 | 是 | 0.124 7 | 是 | 0.208 4 | 否 |
| (6) | 0.008 | 0.004 4 | 0.140 0 | 0.101 3 | 是 | 0.128 1 | 是 | 0.212 9 | 否 |
| (7) | 0.009 | 0.005 0 | 0.133 9 | 0.104 2 | 是 | 0.131 6 | 是 | 0.217 5 | 否 |
| (8) | 0.01 | 0.005 6 | 0.128 1 | 0.107 1 | 是 | 0.135 2 | 否 | 0.222 1 | 否 |
| (9) | 0.011 | 0.006 1 | 0.122 6 | 0.110 2 | 是 | 0.138 8 | 否 | 0.226 9 | 否 |
| (10) | 0.012 | 0.006 7 | 0.117 2 | 0.113 4 | 是 | 0.142 6 | 否 | 0.231 7 | 否 |
| (11) | 0.013 | 0.007 2 | 0.112 1 | 0.116 6 | 否 | 0.146 5 | 否 | 0.236 6 | 否 |
| (12) | 0.014 | 0.007 8 | 0.107 2 | 0.119 9 | 否 | 0.150 4 | 否 | 0.241 6 | 否 |
| (13) | 0.015 | 0.008 3 | 0.102 4 | 0.123 3 | 否 | 0.154 5 | 否 | 0.246 6 | 否 |
| (14) | 0.016 | 0.008 9 | 0.097 8 | 0.126 9 | 否 | 0.158 7 | 否 | 0.251 8 | 否 |
| (15) | 0.017 | 0.009 4 | 0.093 4 | 0.130 5 | 否 | 0.162 9 | 否 | 0.257 1 | 否 |
| (16) | 0.018 | 0.010 0 | 0.089 1 | 0.134 2 | 否 | 0.167 3 | 否 | 0.262 4 | 否 |
| (17) | 0.019 | 0.010 6 | 0.084 9 | 0.138 0 | 否 | 0.171 8 | 否 | 0.267 9 | 否 |
| (18) | 0.02 | 0.011 1 | 0.080 9 | 0.141 9 | 否 | 0.176 4 | 否 | 0.273 4 | 否 |
| (19) | 0.021 | 0.011 7 | 0.077 0 | 0.146 0 | 否 | 0.181 1 | 否 | 0.279 1 | 否 |
| (20) | 0.022 | 0.012 2 | 0.073 2 | 0.150 1 | 否 | 0.185 9 | 否 | 0.284 8 | 否 |
| (21) | 0.023 | 0.012 8 | 0.069 5 | 0.154 4 | 否 | 0.190 8 | 否 | 0.290 6 | 否 |
| (22) | 0.024 | 0.013 3 | 0.065 9 | 0.158 8 | 否 | 0.195 9 | 否 | 0.296 6 | 否 |
| (23) | 0.025 | 0.013 9 | 0.062 4 | 0.163 3 | 否 | 0.201 1 | 否 | 0.302 6 | 否 |
| 注:ts表示钢板厚度; η1表示圈的环壁厚与圈外径的比径; η2表示钢板厚度与圈外径的比值。 | |||||||||
由表 4可以看出, 按回弹率60%, 65%与75%的指标进行优化筛选, η1, η2存在多个解满足吸能要求, 且回弹率越大, 满足要求的解答越少, 工程设计人员可根据自身要求进行筛选。
桥墩所处航道为单向通航, 主要考虑迎水面的撞击情形, 背水面可不设钢板-橡胶圈。本例确定的防撞装置设计参数为:D=1.8 m, ts=12 mm, η1=0.117 2, 如表 4序号(10)所示, 迎水面布置6个钢板-橡胶圈。
下文通过碰撞数值仿真分析验证本研究建立的设计方法的可靠性:
3 000 t货船船艏结构与有限元模型如图 16与图 17所示, 满载排水量3 962 t, 型宽16.2 m, 空载吃水1.6 m, 满载吃水3.3 m。
|
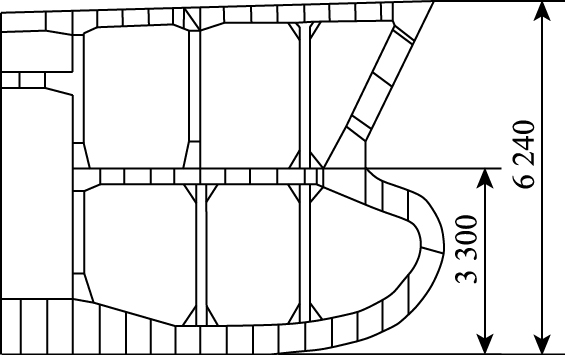
| 图 16 船艏构造(单位:mm) Fig. 16 Structure of ship bow(unit:mm) |
| |
|
| 图 17 船艏有限元模型 Fig. 17 Finite element model of ship bow |
| |
采用LS-DYNA, 首先进行3 000 t船舶以4 m/s正撞刚性墙面的数值仿真, 获得的撞击力如图 18所示。
|
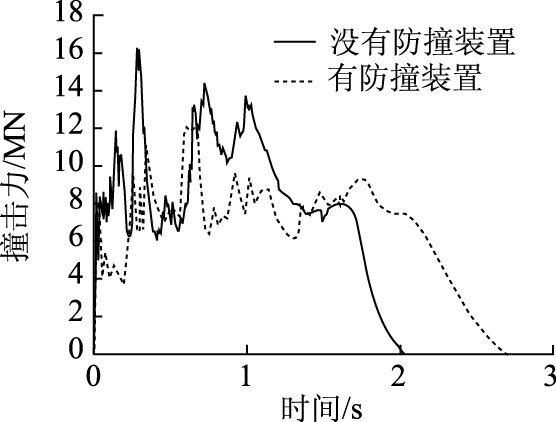
| 图 18 正向撞击碰撞力时程曲线 Fig. 18 Time history curve of positive collision force |
| |
本研究设计的防撞装置由钢板-橡胶圈、外钢围、防爬升柱等部分构成。为发挥钢板-橡胶圈的吸能性能, 外钢围具有足够的整体刚度和强度。橡胶圈与外钢围内壁牢靠连接, 为满足自浮要求, 橡胶圈沿桥墩表面可自由滑动。钢板-橡胶圈采用表 4解答序号(10)的参数, 装置具体构造如图 19所示。
|
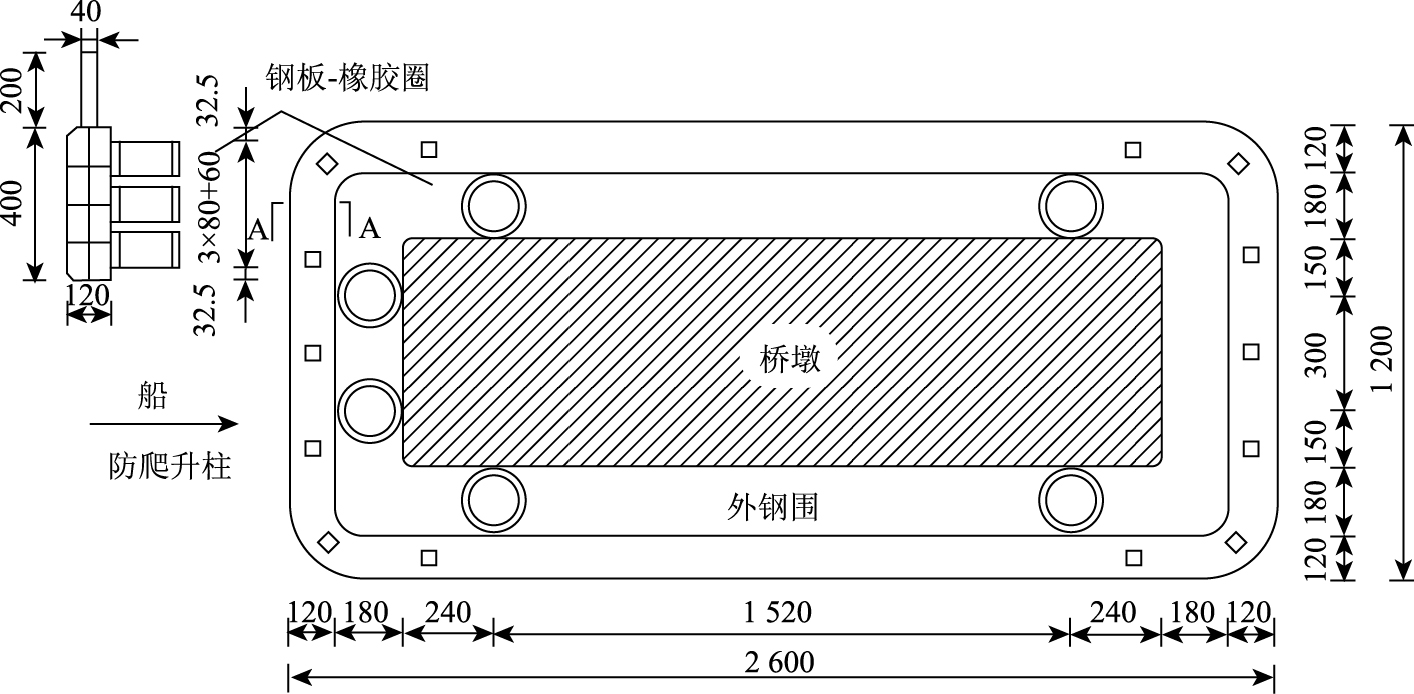
| 图 19 防撞装置平面尺寸图(单位:cm) Fig. 19 Plane dimensions of anti-collision device(unit:cm) |
| |
为简化建模, 钢板-橡胶圈与外钢围采用共节点连接; 由于外钢围和防爬伸柱刚度较大, 在本研究中处理成刚体。钢材、橡胶本构参数见第2节, 船舶、外钢围、钢板-橡胶圈与桥墩之间定义面面接触, 碰撞有限元模型如图 20所示。船舶撞击速度为4 m/s。撞击过程中的应力云图如图 21所示。
|
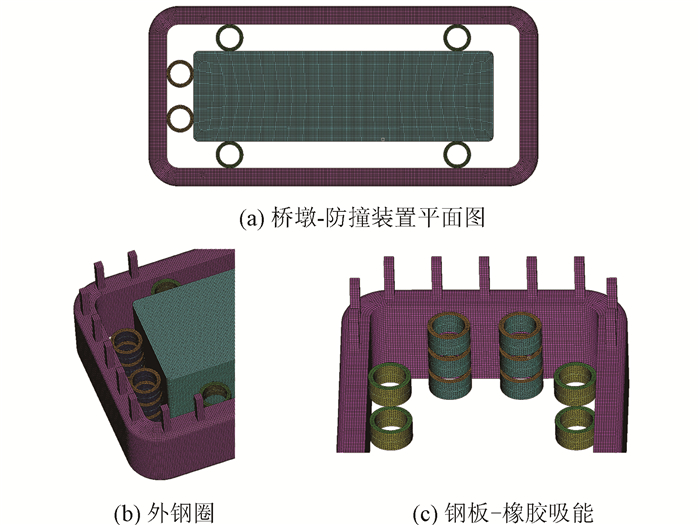
| 图 20 防撞装置有限元模型 Fig. 20 Finite element model of anti-collision device |
| |
|
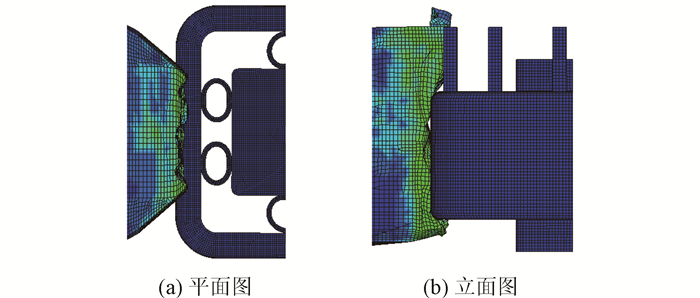
| 图 21 正向撞击变形应力 Fig. 21 Positive collision deformation stress |
| |
设置防撞装置时, 得到的撞击力如图 18所示。与撞击刚性墙面相比, 设置防撞装置时船舶撞击力峰值削减比例约为25%, 具有明显的防护效果。
迎撞面钢板-橡胶圈与船舶吸能时程, 变形比r的时程如图 22与图 23所示。
|
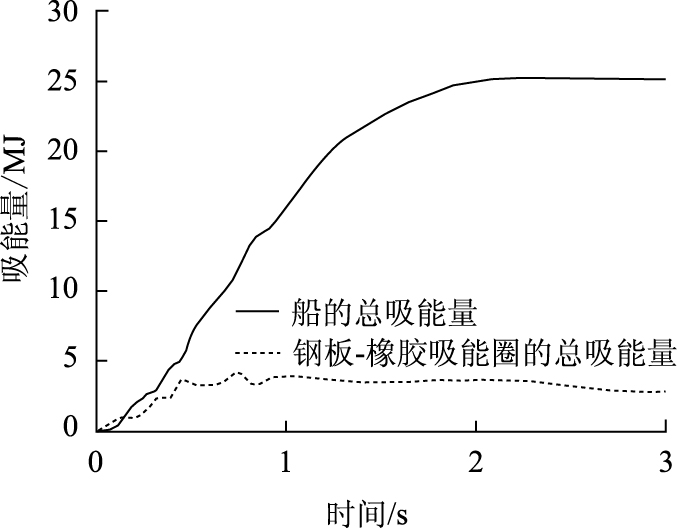
| 图 22 迎撞面钢板-橡胶圈与船舶吸能 Fig. 22 Energy absorption of steel rubber-ring and ship on impact face |
| |
|
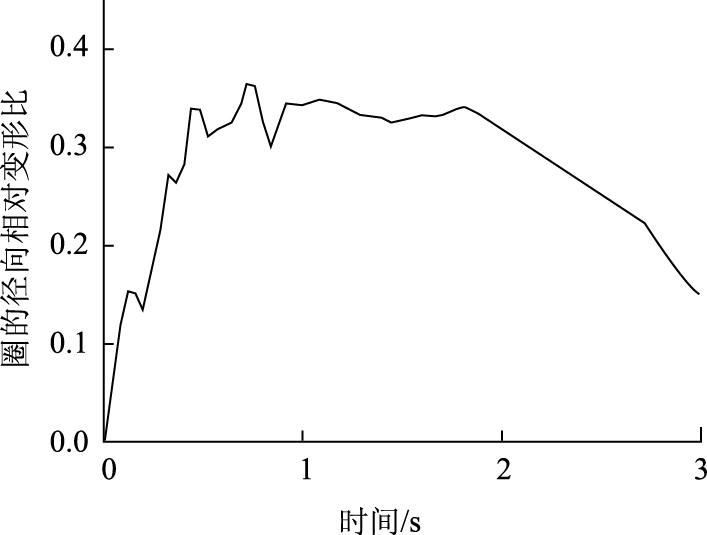
| 图 23 正向钢板-橡胶圈变形比 Fig. 23 Deformation ratio r of positive steel plate-rubber ring |
| |
从图 22可以看出, 迎撞面钢板-橡胶圈最大总吸能量约4.22 MJ, 与设计值4.8 MJ相对误差为12.08%, 从工程设计角度来看, 这种误差是可以接受的。
数值仿真得到的变形比r、钢板-橡胶圈总吸能E与设计值的误差如表 5所示。
表 5 r和E值相对误差
Tab. 5 Relative errors of r and E
| 参数 | 设计值 | 数值模拟值 | 相对误差/% |
| r | 0.4 | 0.37 | 9.25 |
| E/MJ | 4.8 | 4.22 | 12.08 |
由表 5可知, r和E相对误差均在15%以内, 表明本研究建立设计流程的误差在可接受范围内。同时钢板-橡胶圈在撞击过程中能耗散13.31%的船舶初始动能; 撞击力峰值削减幅度约25%, 表明将钢板-橡胶圈应用于防撞装置设计具有较好的潜力。
6 结论(1) 设计了一种钢板-橡胶吸能圈。该装置为圆圈形式, 由外钢板、橡胶圈、内钢板3部分组合而成。
(2) 采用数值模拟方法, 针对1 m外径的钢板-橡胶圈建立了25个(5种不同钢板厚度、5种不同环壁厚)有限元模型, 进行了参数分析; 表明钢板-橡胶圈的性能参数(吸能量)与钢板厚度、环壁厚、圈外径、径向相对位移量有关。
(3) 定义了无量纲比值, 通过对数值模拟得到的样本进行拟合, 得到了1 m外径的钢板橡胶圈的经验设计公式和参数, 同时基于回弹率确定了初步筛选原则, 可以用于钢板-橡胶圈设计。
(4) 根据模型相似律, 将适用于1 m外径的钢板-橡胶圈的经验公式推广到不同外径的钢板-橡胶圈中。
(5) 建立了基于设计最大吸能量和径向允许最大相对变形比的设计流程, 并通过数值仿真进行了验证, 结果表明本研究建立的设计流程具有较好的求解精度和实际应用价值。
参考文献
| [1] |
史元熹, 金允龙, 徐骏.黄石长江大桥主墩防撞设施设计[C]//第十四届全国桥梁学术会议论文集.上海: 中国土木工程学会桥梁及结构工程分会, 2000. SHI Yuan-xi, JIN Yun-long, XU jun. Design of Anti-collision Facilities for Main Pier of Huangshi Yangtze River Bridge[C]//Proceedings of the Fourteenth National Conference on Bridge. Shanghai: Bridge and Structural Engineering Branch of China Civil Engineering Society, 2000. |
| [2] |
曹映泓.湛江海湾大桥主墩柔性消能防撞设施研究实践[C]//第四届全国公路科技创新高层论文集.北京: 中国公路学会, 2008. CAO Ying-hong. Study on Flexible Energy Dissipation Anti-collision Facilities for Main Piers of Zhanjiang Bay Bridge[C]//Proceedings of the Fourth National Highway Science and Technology Innovation. Beijing: China Highway and Transportation Society, 2008. |
| [3] |
张海明, 曹映泓, 段乃民, 等. 湛江海湾大桥主墩防撞设施结构设计[J]. 中外公路, 2006, 26(5): 82-84. ZHANG Hai-ming, CAO Ying-hong, DUAN Nai-min, et al. Structural Design of Anti-collision Facilities for Main Piers of Zhanjiang Bay Bridge[J]. Journal of China & Foreign Highway, 2006, 26(5): 82-84. |
| [4] |
曹映泓, 左智飞, 罗林阁. 湛江海湾大桥柔性吸能防撞装置研究[J]. 中外公路, 2006, 26(5): 72-75. CAO Ying-hong, ZUO Zhi-fei, LUO Lin-ge. Study on Flexible Energy Absorbing Anti-collision Device of Zhanjiang Bay Bridge[J]. Journal of China & Foreign Highway, 2006, 26(5): 72-75. |
| [5] |
倪步友, 倪士强.有外钢围的桥梁柔性防船撞装置与复合材料消能防撞装置对比研究[C]//国际船桥相撞及其防护学术研讨会论文集.北京: 国际船桥相撞及其防护学术研讨会学术委员会, 2014. NI Bu-you, NI Shi-qiang. A Comparative Study on Flexible Ship Anti-collision Device with Steel Fence and the Composite Ship Energy Dissipation and Anti-collision Device[C]//Proceedings of International Symposium on Ship-bridge Collision and Its Protection. Beijing: Academic Committee of International Symposium on Ship-bridge Collision and Its Protection, 2014. |
| [6] |
吕忠达, 杨黎明.象山港公路大桥桥墩抗船撞柔性防护技术及实船撞击试验[C]//国际船桥相撞及其防护学术研讨会论文集.北京: 国际船桥相撞及其防护学术研讨会学术委员会, 2014. LÜ Zhong-da, YANG Li-ming. Bridge Pier Anti-collision Flexible Protection Technology and Ship Impact Test for Xiangshan Port Highway Bridge[C]//Proceedings of International Symposium on Ship-bridge Collision and Its Protection. Beijing: Academic Committee of International Symposium on Ship-bridge Collision and Its Protection, 2014. |
| [7] |
刘慈军.桥墩抗大吨位船舶撞击柔性装置耐久性设计研究[C]//国际船桥相撞及其防护学术研讨会论文集.北京: 国际船桥相撞及其防护学术研讨会学术委员会, 2014. LIU Ci-jun. Study on Durability Design of Flexible Device for Large Tonnage Ship Impact against Bridge Pier[C]//Proceedings of International Symposium on Ship-bridge Collision and Its Protection. Beijing: Academic Committee of International Symposium on Ship-bridge Collision and Its Protection, 2014. |
| [8] |
倪步友, 倪士强.黏滞性高耗能柔性防撞圈的研制和试验[C]//国际船桥相撞及其防护学术研讨会论文集, 北京: 国际船桥相撞及其防护学术研讨会学术委员会, 2014. NI Bu-you, NI Shi-qiang. Development and Test of Viscosity and High Energy Dissipation Flexible Anti-collision Ring[C]//Proceedings of International Symposium on Ship-bridge Collision and Its Protection. Beijing: Academic Committee of International Symposium on Ship-bridge Collision and Its Protection, 2014. |
| [9] |
陈国虞. 从能量吸收评价玻纤复合材料桥梁防船撞装置[J]. 玻璃钢, 2014(4): 22-28. CHEN Guo-yu. Evaluation of Glass Fiber Composite Bridge Anti-collision Device from Energy Absorption[J]. Glass Fiber Reinforced Plastics, 2014(4): 22-28. |
| [10] |
张南, 许琦, 刘钊, 等. 缓冲器对钢筋混凝土桥墩撞击性能影响的试验研究[J]. 公路交通科技, 2009, 12(26): 83-90. ZHANG Nan, XU Qi, LIU Zhao, et al. Experimental Research on Effect of Buffer on Impact Performance of Reinforced Concrete Pier[J]. Highway Traffic Technology, 2009, 12(26): 83-90. |
| [11] |
胥睿.钢板-橡胶混凝土复合覆层应用于桥墩防撞的研究[D], 北京: 北京交通大学, 2017. XU Rui. Research on Steel Plate-rubber Concrete Composite Coating Applied to Bridge Pier Anti-collision[D].Beijing: Beijing Jiaotong University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10004-1017086620.htm |
| [12] |
孙霁.桥梁防撞设施数值仿真研究[D].上海: 同济大学, 2005. SUN Ji. Study on Numerical Simulation of Bridge Anti-collision Facilities[D].Shanghai: Tongji University, 2005. |
| [13] |
朱政, 基于组合式耗能筒的浮式防撞结构研究[D].上海: 同济大学, 2015. ZHU Zheng. Study on Floating Anti-collision Structure Based on Combined Energy Dissipation Tube[D]. Shanghai: Tongji University, 2015. |
| [14] |
郑明军, 王文静, 陈政南, 等. 橡胶Mooney-Rivlin模型力学性能常数的确定[J]. 橡胶工业, 2003, 50(8): 462-465. ZHENG Ming-jun, WANG Wen-jing, CHEN Zheng-nan, et al. Determination for Mechanical Constants of Rubber Mooney-Rivlin Model[J]. China Rubber Industry, 2003, 50(8): 462-465. |
| [15] |
刘卫卫.多类型单元混合建模方法研究[D].成都: 电子科技大学, 2013. LIU Wei-wei. Research on Multi-type Unit Mixed Modeling Method[D]. Chengdu: University of Electronic Science and Technology of China, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10614-1013334047.htm |
| [16] |
吴长河, 冯晓伟, 叶培, 等. 应变率对硫化橡胶压缩力学性能的影响[J]. 功能材料, 2013, 44(8): 1098-1101. WU Chang-he, FENG Xiao-wei, YE pei, et al. Effect of Strain Rate on Mechanical Properties of Vulcanized Rubber[J]. Journal of Functional Materials, 2013, 44(8): 1098-1101. |
| [17] |
秦严严.管道接口橡胶密封圈力学性能研究及应用[D].天津: 河北工业大学, 2011. QIN Yan-yan. Research and Application of Mechanical Properties of Rubber Seal for Pipeline Interface[D].Tianjin: Hebei University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10463-1012461693.htm |
| [18] |
周明华. 土木工程结构试验与检测[M]. 南京: 东南大学出版社, 2008: 72-79. ZHOU Ming-hua. Civil Engineering Structure Test and Detection[M]. Nanjing: Southeast University Press, 2008: 72-79. |