公路交通科技  2019, Vol. 36 Issue (2): 43−49

扩展功能

文章信息

陈小雨, 唐茂林
CHEN Xiao-yu, TANG Mao-lin
悬索桥主缆钢丝腐蚀速率计算方法
A Method for Calculating Corrosion Rate of Main Cable Steel Wires of Suspension Bridge
公路交通科技, 2019, 36(2): 43-49
Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 43-49
10.3969/j.issn.1002-0268.2019.02.007

文章历史

收稿日期: 2018-04-24
引用本文 0
陈小雨, 唐茂林. 悬索桥主缆钢丝腐蚀速率计算方法[J]. 公路交通科技, 2019, 36(2): 43-49.
CHEN Xiao-yu, TANG Mao-lin. A Method for Calculating Corrosion Rate of Main Cable Steel Wires of Suspension Bridge[J]. Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 43-49.
悬索桥主缆钢丝腐蚀速率计算方法
陈小雨 , 唐茂林     
西南交通大学 土木工程学院, 四川 成都 610031
收稿日期: 2018-04-24
基金项目: 国家自然科学基金项目（51478391）
作者简介: 陈小雨 (1986-),女,云南昭通人,工学博士.
摘要: 悬索桥主缆钢丝的腐蚀严重影响着主缆的安全服役，缆内钢丝的腐蚀与其所处的缆内微环境有密切的关系，为预测悬索桥主缆内各区域中钢丝的腐蚀发展和剩余承载力，需建立主缆钢丝区域化腐蚀环境与腐蚀速率之间的计算关系。采用正交试验原理将影响钢丝腐蚀的：温度、相对湿度、NaCl浓度、pH值、钢丝拉力5个主要因素分为两组，分别采用极化电阻腐蚀传感器和电化学工作站三电极体系两种测量手段对正交工况下的钢丝腐蚀速率进行测量。试验分析数据表明：在试验因素的取值范围内相对湿度和pH值各为两组因素中的主要因素，NaCl浓度和pH值两个因素之间存在交互效应，温度、相对湿度、钢丝拉力之间相互独立；通过最小二乘法分别拟合得到5个因素与钢丝腐蚀速率之间的拟合计算关系；将实测的主缆内各区域的腐蚀环境统计为腐蚀环境年谱，并代入腐蚀速率与环境因素的计算关系，得到主缆各区域内钢丝的腐蚀速率和直径损失，其中主缆顶部区域腐蚀速率最高为0.010 8 mm/a，服役20年后直径损失约为0.02 mm即镀锌层耗损完毕，与实际桥梁检测情况吻合，服役100年直径损失将达到约1.1 mm，将不能满足主缆的设计要求。建立的腐蚀速率计算方法为计算钢丝腐蚀量提供参考。
关键词: 桥梁工程     主缆腐蚀预测     正交试验     缆用高强钢丝     悬索桥    
A Method for Calculating Corrosion Rate of Main Cable Steel Wires of Suspension Bridge
CHEN Xiao-yu, TANG Mao-lin    
School of Civil Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China
Abstract: The corrosion of the main cable of suspension bridge seriously affects the safe service of the main cable, the corrosion of the steel wire inside the cable is closely related to the inside microenvironment. In order to predict the corrosion stage of steel wires in different parts of the main cable of suspension bridge, it is necessary to establish the calculation relation between the corrosive environment and the corrosion rate of the main cable steel wires. Dividing the 5 main factors affecting steel corrosion, including temperature, relative humidity, NaCl concentration, pH value and steel wire tension into 2 groups by orthogonal test principle, the corrosion rates of steel wires are measured by polarization resistance corrosion sensor and electrochemical workstation 3-electrode system. The analysis of experimental data shows that (1) the main factors among the 2 groups within the range of experimental factors are relative humidity and pH value respectively; (2) there is an interaction between NaCl concentration and pH value, while temperature, relative humidity and steel wire tension are independent of each other. The fitting calculation relationships between the 5 factors and the corrosion rate of steel wire are obtained by least squares fitting. The corrosion environment of each part in the measured main cable is counted as the corrosion environment aging spectrum, which is put into the calculation relationship between the corrosion rate and the environmental factors. Thus, the corrosion rate and the diameter loss of each part of the main cable are obtained. The corrosion rate in the top part of the main cable is up to 0.010 8 mm/a, the diameter loss after 20 years of service is about 0.02 mm, i.e., the galvanized layer is worn out, which is consistent with the actual bridge detection. After 100 years of service, the diameter loss is about 1.1 mm, which will not meet the design requirements. The established corrosion rate calculation method provides a reference for calculating the corrosion amount of steel wire. The proposed calculation method of corrosion rate will provide a reference for calculating corrosion amount of steel wire.
Key words: bridge engineering     corrosion prediction of main cable     orthogonal test     high strength steel wires for cable     suspension bridge    
0 引言

缆索承载桥梁中缆索系统的腐蚀严重威胁着整个桥梁结构的运营寿命, 对缆索系统中钢丝腐蚀的预测就成了评估桥梁运营安全的重点[1-4]。悬索桥主缆中沿着纵向位置不同的截面处钢丝的腐蚀程度并不一致, 相同截面处的不同位置腐蚀位置也有较大差别[5-8], 例如文献[5-6]中对塞文桥的腐蚀检测可以看出, 中心区域腐蚀程度较轻, 外围区域腐蚀程度相对较重, 且顶部和底部区域以及左右两侧区域的腐蚀分布也不完全相同。导致这一现象的主要原因是截面内在受到外环境影响下发生了不同的温度、相对湿度分布, 进而产生了不同程度的钢丝腐蚀[9], 因此为了能够更准确地评估主缆内钢丝的腐蚀, 必须分区域对主缆截面进行腐蚀环境的统计。除了温度和相对湿度外, 环境中的污染气体、酸雨、钢丝拉力等都是影响缆索钢丝腐蚀的主要因素。文献[9-14]分别对酸雨、温度、拉力等因素对钢丝腐蚀的影响进行了试验, 得到了这些因素对腐蚀起到加速的作用, 但是并没有建立起确切的计算关系。因此想要预测缆索系统的腐蚀, 就必须建立钢丝在各因素共同作用下的腐蚀速率计算关系, 并对主缆进行纵向分节段, 截面分区域, 对每个区域内的腐蚀环境值和持续时间进行详细统计。文献[15-16]对足尺的主缆节段模型进行了温度和相对湿度的测量, 得到了珍贵的资料。本研究首先依据桥梁服役环境中温度、相对湿度、NaCl浓度、pH值、钢丝拉力5个因素的取值, 分两组进行正交试验, 建立其钢丝腐蚀与5个因素之间的计算关系, 然后对主缆跨中截面分5个区域分别统计其腐蚀环境和持续作用时间, 最后将区域化的腐蚀环境代入建立的高强钢丝的腐蚀速率计算关系中, 以算例的形式给出主缆钢丝的腐蚀计算方法。

1 温度、相对湿度腐蚀速率谱 1.1 试验设计及结果

在建立腐蚀速率的过程中, 能满足5个因素同时测量的设备必须耐腐蚀, 能精确控制5个因素的试验值, 但现在的腐蚀设备中并没有合适的设备, 只能将5个因素分为两组进行正交试验。温度和相对湿度是导致金属腐蚀的最主要因素, 因此将此因素作为一组进行试验。试验时采用恒温恒湿试验箱(温度精度在±2 ℃, 相对湿度在低于80%时精度为±5%, 大于80%时精度为±10%。)控制腐蚀环境中温度和相对湿度值。将极化电阻腐蚀传感器(腐蚀速率测量精度为0.000 1 mm/a)贴于试件钢丝表面进行腐蚀速率的测量。试件钢丝采用强度为1 770 MPa直径为5.1 mm的未镀锌高强钢丝(没有合适的测量设备对镀锌高强钢丝测量温度和相对湿度组合下的腐蚀速率进行测量)。每个工况测量3个试件, 每个试件测量3次腐蚀速率, 即每个工况取9个试验值的均值作为该工况下的腐蚀速率, 测量结果如表 1所示。

表 1 温度和相对湿度正交工况下腐蚀速率试验值 Tab. 1 Experimental values of corrosion rate under orthogonal condition of temperature and relative humidity
温度/℃ 各相对湿度(%)下腐蚀速率试验值/(mm·a-1)
45 55 70 80 99
10 0.000 1 0.000 2 0.001 4 0.008 3 0.010 8
20 0.002 1 0.004 0 0.005 8 0.007 8 0.013 6
30 0.003 9 0.004 2 0.004 6 0.007 1 0.019 7
40 0.002 3 0.002 8 0.004 5 0.015 1 0.036 2
50 0.001 1 0.001 4 0.004 3 0.022 9 0.045 5
表选项

依据文献[15-16]中实桥温度、相对湿度监控资料, 夏季主缆内最高温度可达到50 ℃以上, 因此取试验的最高温度为50 ℃; 考虑到0 ℃为冰点, 钢丝结冰冻融与腐蚀的交叠效应复杂, 因此最低温度取10 ℃。主缆除了被浸泡的局部钢丝外, 最大相对湿度是99%, 因此相对湿度上限为99%。由主缆除湿系统的相对湿度设置可知, 在相对湿度为60%以下的环境中可以忽略钢丝的腐蚀。为了得到更宽范围的相对湿度影响, 为安装除湿系统后的腐蚀速率提供参考, 将最低相对湿度取为40%。各因素分别取5个水平值, 两两正交的试验结果如表 1所示。

1.2 因素主次关系分析

为明确两者之间的主次关系, 对试验结果进行方差分析:把总的变差平方和分解为因素的变差平方与误差平方两个部分, 并计算出因素及误差的平均平方和, 然后用F检验法对因素进行显著性检验[17], 如表 2所示。

表 2 方差分析显著性计算表 Tab. 2 Calculation table of variance analysis significance
方差来源 变差
平方和		 自由度 均方 F值 临界值
Fa		 显著性
温度
因素		 SA=
0.000 4		 4 0.000 1 2.34 F0.05(4, 24)=
5.77		 不显著
湿度
因素		 SB=
0.002 0		 4 0.000 5 11.63 F0.05(4, 24)=
5.77		 非常显著
误差e Se=
0.000 7		 16 0.000 043 — — —
总和 ST=
0.003 1		 24 — — — —
表选项

ST为所有数据的总变差和; SA, SB分别为温度、相对湿度因素各自的变差平方和; Se为误差的变差和, 具体的计算方法见文献[17]。由表中计算的F值与临界值Fa统计量结果的对比可以判断, 温度在置信度为95%的概率下, F值小于Fa, 因此A因素是不显著的。而因素B在置信度为95%的概率下其F值远大于Fa, 因此对腐蚀速率的影响显著, 这种显著的可靠性有95%的概率, 即相对湿度因素为主要因素, 温度因素为次要因素。

1.3 计算关系拟合

正交试验数据点较少, 为了拟合曲面计算公式, 使用样条插值对结果进行拟合。由试验数据可以看出在相对湿度大于60%以后, 与低相对湿度情况下的腐蚀速率出现了较大差异, 为了得到更好的拟合公式, 将温度和相对湿度-腐蚀速率谱进行分段拟合, 采用最小二乘法回归分析对插值后的数据进行回归拟合, 得到如下的分段计算式(1)所示:

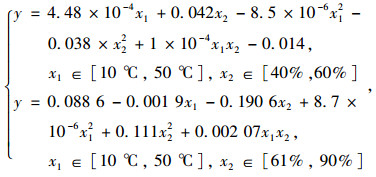
(1)

式中, y为腐蚀速率; x1为温度; x2为相对湿度, 拟合结果的可信度指标如表 3所示。

表 3 拟合回归统计值 Tab. 3 Fitting regression statistics values
拟合式 复相关系数
Multiple R		 复测定系数
R Square		 标准差 离差平方和Q
(1)式 0.952 0.906 0.039 0.006
(2)式 0.937 0.878 0.031 0.009
表选项

由表 3可以看出, 复相关系数RM用来衡量自变量x1, x2与y之间的相关程度大小, 复相关系数分别为0.952, 0.937, 表明它们之间的关系为高度正相关; 复测定系数RS用来说明自变量解释因变量y变差的程度, 以测定因变量y的拟合效果, 复测定系数分别为0.906, 0.878表明可用自变量解释因变量变差的90.6%, 87.8%;标准误差用来衡量拟合程度的大小, 也用于计算与回归相关的其他统计量, 本研究中标准差分别为0.039, 0.031, 此值越小说明拟合程度越好; 离差平方和Q用来描述拟合回归公式与测量数据之间的偏离程度, 该值为0.006和0.009, 值越小说明拟合程度越高。

2 NaCl浓度、pH值、拉力腐蚀速率谱 2.1 试验工况及结果

将NaCl浓度、pH值、拉力作为一组影响因素, 试验时自制钢丝拉力自平衡支架并采用千斤顶进行张拉(为了使得拉力值稳定, 达到设计应力后, 稳定10 min后对其进行张力补充, 直至拉力值再次稳定3 min后撤去千斤顶)。自制电解池中加入工业用NaCl调制试验工况设定浓度的NaCl溶液(0.1 g/L), 并使用HCl和NaOH调节溶液pH值(pH测试仪精度0.1)。测试设备采用电化学工作站CS320(0.000 1 mm/a)的三电极体系, 在25 ℃的环境中进行Tafel曲线外推法测定。试件钢丝采用强度为1 770 MPa直径为5.1 mm的未镀锌高强钢丝。每个工况测量3个试件, 每个试件测量3次腐蚀速率。试验时的温度由恒温恒湿箱控制在常温25 ℃, 测量结果如表 4所示。

表 4 三因素正交试验腐蚀速率值(单位:mm·a-1) Tab. 4 Corrosion rates obtained by three-factor orthogonal test (unit:mm·a-1)
序号 NaCl浓度 pH值/
%		 NaCl+
pH值		 拉力/
MPa		 试验均值/
(mm·a-1)
1 0.3 4 1 400 0.075 4
2 0.3 5 2 500 0.042 8
3 0.3 6 3 600 0.015 9
4 0.3 7 4 700 0.008 7
5 0.3 8 5 800 0.019 1
6 0.9 4 2 600 0.108 9
7 0.9 5 3 700 0.054 8
8 0.9 6 4 800 0.048 6
9 0.9 7 5 400 0.020 1
10 0.9 8 1 500 0.013 7
11 1.8 4 3 800 0.147 2
12 1.8 5 4 400 0.070 3
13 1.8 6 5 500 0.050 1
14 1.8 7 1 600 0.035
15 1.8 8 2 700 0.031 3
16 2.6 4 4 500 0.207 2
17 2.6 5 5 600 0.134 2
18 2.6 6 1 700 0.064 6
19 2.6 7 2 800 0.045 5
20 2.6 8 3 400 0.026 4
21 3.5 4 5 700 0.274 8
22 3.5 5 1 800 0.184 9
23 3.5 6 2 400 0.078 6
24 3.5 7 3 500 0.060 3
25 3.5 8 4 600 0.048 7
表选项

试验参数的取值参考实际缆索桥梁的服役环境, NaCl浓度(g/L)主要考虑跨海大桥所处环境的盐雾浓度值, 最高浓度为海水盐度3.2%~3.75%, 最低为沿海大气中的含量约0.1%~0.7%;pH值, 海水中为8.1~8.3, 重度酸雨pH值为4.5左右(酸性电解液用HCl调制, 碱性电解液用NaOH调制)。拉力以2.0的安全系数计算, 采用1 770 MPa的钢丝, 最大拉力设为800 MPa。

2.2 因素间耦合分析

采用同样的方差分析方法, 分析NaCl浓度、pH值、拉力这3个因素对未镀锌钢丝腐蚀速率的主次关系和耦合效应, 如表 5所示。

表 5 方差分析显著性计算表 Tab. 5 Calculation table of variance analysis significance
方差
来源		 变差平方和 自由度 均方 F值 临界值Fa 显著性
A SA=0.030 5 4 0.007 6 10.86 F0.05(4, 24)=
5.77		 非常显著
B SB=0.064 2 4 0.0161 23.00 F0.01(4, 24)=
13.93		 非常显著
AB SAB=0.004 4 4 0.001 1 1.57 F0.2(4, 24)=
2.4		 不显著
C SC=0.003 8 4 0.000 9 1.28 F0.2(4, 24)=
2.4		 不显著
e Se=0.005 9 8 0.000 7
总和 ST=0.108 8 24
表选项

由表 5中计算的F值与临界值Fa的结果对比可以判断, NaCl浓度因素(A)在置信度为95%的概率下其F值大于临界值Fa, 因此A因素对试验考察值是显著的。pH因素(B)在置信度为99%的概率下其F值大于临界值Fa, 因此对腐蚀速率的影响显著, 这种显著的可靠性有99%的概率。而因素NaCl+ pH的交互作用(AB), 以及因素C在置信度为80%的概率下其F值小于临界值Fa, 因此因素AB以及因素C对试验考察值的影响不显著, 但是AB因素的F值大于C因素的F值, 因此认为AB因素之间有交互效应。

2.3 计算关系拟合

同理对试验数据进行插值, 并对插值后的数据进行置信度为95%的三元二次函数的回归拟合, 由于其中NaCl浓度值变化范围较大, 为达到更好的拟合精度, 将拟合函数按NaCl浓度 < 1和≥1分段拟合, 得到的拟合结果如式(2)所示。

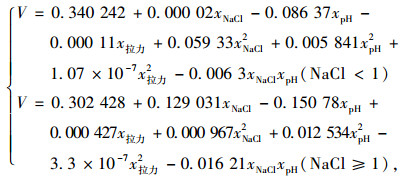
(2)

式中, V为未镀钢丝腐蚀速率; xNaCl为NaCl浓度; xpH为pH值; x拉力为拉力值, 拟合结果的可信度指标如表 6所示。

表 6 拟合回归统计值 Tab. 6 Fitting regression statistics values
拟合式 复相关系数
Multiple R		 复测定系数
R Square		 标准差 离差平方和Q
NaCl < 1 0.948 3 0.978 5 0.004 8 0.023
NaCl≥1 0.983 2 0.921 3 0.003 2 0.016
表选项

由表 6可以看出, 复相关系数RM用来衡量自变量xNaCl, xpH, x拉力与因变量V之间的相关程度, 分别为0.948 3, 0.983 2, 表明它们之间的关系为高度正相关; 复测定系数RS用来说明自变量解释因变量y变差的程度, 以测定因变量y的拟合效果, 复测定系数为0.978 5, 0.921 3表明可用自变量解释因变量变差的97.8%, 92.1%;标准误差用来衡量拟合程度的大小, 也用于计算与回归相关的其他统计量, 本研究中标准差均小于0.005, 此值越小, 说明拟合程度越好; 离差平方和Q用来描述拟合回归公式与测量数据之间的偏离程度, 该值为0.023和0.16说明拟合程度高。

3 主缆区域化腐蚀计算算例分析

实际工程中悬索桥主缆钢丝使用锌高强钢丝, 在实桥检查和试验中均发现其腐蚀的发生分为镀锌层腐蚀和钢丝基体腐蚀两个不同的阶段。通常在运营30 a后出现镀锌层的耗损完毕, 进入到钢丝基体腐蚀阶段, 本研究中的腐蚀速率谱就是对高强钢丝在镀锌保护失效后其基体腐蚀的发展进行预测。

由于目前没有对主缆内5个因素的实桥测量数据, 在此仅给出一个假设算例作为主缆区域化腐蚀计算方法的参考。考虑到我国几乎都位于中到重度酸雨区, 而悬索桥大多是位于长江流域, 因此取中度酸雨pH值5。NaCl浓度在沿海大气中浓度为0.1%~0.7%, 考虑到主缆的密封性, 会使得NaCl进入主缆后产生一定的富集, 保守取为0.5%。钢丝拉力值取桥梁成桥状态下的恒载值, 参考马鞍山长江大桥的主缆参数单根钢丝的恒载值约为630 MPa。主缆跨中截面缆内的温度和相对湿度分布参考文献[16]。

主缆跨中截面各个区域的温度相对湿度分布并不一致, 大致可分为中心区域, 顶部区域, 左右两个侧面区域以及底部区域, 对各个区域文献[16]仅给出了主缆跨中截面温度、相对湿度在3个日期内的最大、最小值的分布云图, 而并没有给出各个温度、相对湿度组合持续的时间, 在进行统计时为了得到最恶劣的环境条件下的腐蚀情况, 仅取该区域内各个季节的温度和相对湿度最大值代替该区域在3个季节中的温度、相对湿度分布和持续时间, 统计结果如表 7所示。

表 7 主缆跨中节段各区域腐蚀环境统计 Tab. 7 Corrosion environment statistics of each part of main cable mid-span segment
区域划分 温度/
℃		 湿度/
%		 pH值 NaCl浓
度/%		 拉力/
MPa		 持续
时间/d
中心区春季 12 95 5 0.5 630 180
中心区夏季 36 65 5 0.5 630 95
中心区冬季 0 85 5 0.5 630 90
顶部区春季 12 85 5 0.5 630 180
顶部区夏季 40 45 5 0.5 630 95
顶部区冬季 0 65 5 0.5 630 90
底部区春季 12 65 5 0.5 630 180
底部区夏季 35 75 5 0.5 630 90
底部区冬季 0 40 5 0.5 630 95
左侧区春季 12 65 5 0.5 630 180
左侧区夏季 36 60 5 0.5 630 95
左侧区冬季 0 40 5 0.5 630 90
右侧区春季 11 75 5 0.5 630 180
右侧区夏季 36 55 5 0.5 630 95
右侧区冬季 0 40 5 0.5 630 90
表选项

将pH=5, NaCl=0.5%, 拉力=630 MPa代入式(2)得到在该环境下未镀锌高强钢丝的腐蚀速率为0.026 7 mm/a, 考虑到在进行第3节试验时的温度和相对湿度条件为25 ℃, 100%相对湿度, 因此将温度=25 ℃, 相对湿度=100%代入式(1)计算得到在该温度和相对湿度组合下的未镀锌高强钢丝腐蚀速率为0.019 7, 则0.026 7-0.019 7=0.007 mm/a即为NaCl浓度、pH值、拉力因素单独作用下的腐蚀速率; 将各区域的环境统计值(表 7)代入式(1)分别计算得到各个区域温度、相对湿度组合工况下的腐蚀速率, 再将两组因素的计算值线性相加(由拟合的计算关系判断可以看出, 各因素间主要以线性关系为主, 耦合效应的显著性较低)得到下述各区域的年腐蚀量计算结果, 如表 8所示。

表 8 主缆跨中节段各区域年腐蚀速率表 Tab. 8 Annual corrosion rates of each part of main cable mid-span segment
截面区域
划分		 春秋季/
(mm·a-1)		 夏秋季/
(mm·a-1)		 冬季/
(mm·a-1)		 年腐蚀量(半
径损失)/mm
顶部区域 0.013 4 0.009 3 0.007 3 0.010 8
中心区域 0.016 7 0.009 9 0.011 8 0.013 7
底部区域 0.007 6 0.013 6 0 0.007 3
左侧区域 0.007 2 0.008 8 0 0.005 8
右侧区域 0.012 3 0.011 8 0 0.009 1
表选项

其中年腐蚀量为各个季节的腐蚀速率乘以各季节的持续时间占全年天数之和, 而底部、左侧、右侧区域在冬季的腐蚀量认为等于"0", 是因为由相对湿度统计可见上述三区域在冬季的相对湿度均低于40%, 认为其不发生腐蚀。由表 8可以看出, 在各区域各季节的腐蚀速率中, 冬季的腐蚀速率都相对较小, 夏季的腐蚀速率反而没有春季的腐蚀速率高, 这是因为冬季温度较低, 而夏季的相对湿度由于缆内的高温条件, 使得水分容易蒸发, 所以相对湿度分布明显小于春季和冬季。同时还可以看出, 中心区域的腐蚀量大于其他区域, 顶部和右侧区域的年腐蚀量次之, 底部和左侧区域腐蚀量最小。以其中腐蚀速率最大的顶部区域值0.010 8 mm来看, 10 a后腐蚀量为0.11 mm, 100 a腐蚀量约为1.1 mm。这一结论虽然环境值参考的足尺模型内测量的环境分布, 但是按照本研究的计算方法得到的腐蚀量与文献[3]中实桥检验的结果大致相符。有了这一主缆直径损失的预测, 就可以依据文献[18]来判断不同服役时间, 主缆钢丝的抗力变化过程。上述算例的结果针对文中分析的算例成立, 各个桥位处的环境才是决定其腐蚀速率的关键。

4 结论

(1) 文章利用恒温恒湿箱和极化电阻传感器测量了温度、相对湿度两个因素正交作用下, 悬索桥主缆用未镀锌高强钢丝腐蚀速率的变化, 并建立了腐蚀速率与温度和相对湿度之间的计算关系。

(2) 文章利用自制的电解池和带拉力平衡支架测量了NaCl浓度、pH值、拉力3因素正交作用下, 悬索桥主缆用未镀锌高强钢丝腐蚀速率的变化, 并建立了腐蚀速率与3个因素之间的计算关系。

(3) 利用已建立的5因素与腐蚀速率之间的计算关系, 以算例的形式给出了将主缆截面分5个区域分别统计其腐蚀环境, 并计算各区域内钢丝腐蚀量的方法, 这种方法对主缆钢丝的腐蚀预测提供了新的思路。

参考文献
[1]
陈小雨, 沈锐利, 唐茂林. 悬索桥主缆检测及承载力评估现状与发展[J]. 重庆交通大学学报:自然科学版, 2013, 32(增1): 760-763, 831.
CHEN Xiao-yu, SHEN Rui-li, TANG Mao-lin. Current Situation and Development for Detection and Bearing Capacity Evaluation of Main Cable of Suspension Bridge[J]. Journal of Chongqing Jiaotong University:Natural Science, 2013, 32(S1): 760-763, 831.
[2]
陈小雨, 沈锐利, 张培炎. 悬索桥主缆的内部检测[J]. 世界桥梁, 2013, 41(1): 86-90.
CHEN Xiao-yu, SHEN Rui-li, ZHANG Pei-yan. Internal Detection of Main Cable of Suspension Bridge[J]. World Bridges, 2013, 41(1): 86-90.
[3]
BETTI R, YANEV B. Conditions of Suspension Bridge Cables:New York City Case Study[J]. Transportation Research Record, 1999, 1654: 105-112.
[4]
周克忠, 李颖. 悬索桥主缆防护技术及应用[J]. 电镀与涂饰, 2017, 36(22): 1227-1231.
ZHOU Ke-zhong, LI Ying. Protection Technologies for Main Cable of Suspension Bridge and Their Applications[J]. Electropating & Finishing, 2017, 36(22): 1227-1231.
[5]
COCKSEDGE C, HUDSON T, URBANS B. M48 Severn Bridge:Main Cable Inspection and Rehabilitation[J]. Bridge Engineering, 2010, 163(4): 181-195.
[6]
YOUNG J S, LYNCH M J. Inspection and Maintenance of Severn Bridge Suspension Cables[J]. Bridge Engineering, 2010, 163(4): 173-180.
[7]
CHRISTODOULOU C. Humber Bridge Suppressing Main Cable Corrosion by Means of Dehumidification[C]//Proceedings of the 18th International Corrosion Congress. Perth, Australia: International Corrosion Council, 2011: 1-12.
[8]
CLARK C A, COLFORD B R. Forth Road Bridge Main Cables:Replacement/Augmentation Study[J]. Bridge Engineering, 2010, 163(2): 79-89.
[9]
陈小雨, 唐茂林, 沈锐利. 主缆高强钢丝腐蚀速率影响因素分析[J]. 重庆交通大学学报:自然科学版, 2015, 34(1): 25-29, 47.
CHEN Xiao-yu, TANG Mao-lin, SHEN Rui-li. Influencing Factors of Main Cable Wires Corrosion Rate of Suspension Bridge[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2015, 34(1): 25-29, 47.
[10]
黎学明, 陈大华, 陈建文, 等. 模拟酸雨溶液中温度对桥梁缆索镀锌高强钢丝腐蚀行为影响[J]. 腐蚀科学与防护技术, 2010, 22(1): 14-17.
LI Xue-ming, CHEN Da-hua, CHEN Jian-wen, et al. Effect of Temperature on Corrosion Behavior of Galvanized Steel Bridge Wires in Simulated Acid Rain[J]. Corrosion Science and Protection Technology, 2010, 22(1): 14-17.
[11]
杨文静, 施衍奇, 黎学明, 等. 大跨度桥梁缆索模拟酸雨加速腐蚀行为研究[J]. 腐蚀科学与防护技术, 2011, 23(1): 65-68.
YANG Wen-jing, SHI Yan-qi, LI Xue-ming, et al. Corrosion Behavior of Galvanized Steel Wires of Long-span Bridge Cables in Simulated Acid Rain[J]. Corrosion Science and Protection Technology, 2011, 23(1): 65-68.
[12]
EL HALEEM S M A, EL AL E E A, EL WANEES S A, et al. Environmental Factors Affecting the Corrosion Behaviour of Reinforcing Steel:I. The Early Stage of Passive Film Formation in Ca(OH)2 Solutions[J]. Corrosion Science, 2010, 52(12): 3875-3882.
[13]
黎学明, 刘强, 孔令峰, 等. 模拟酸雨溶液中应力对镀锌钢绞线腐蚀行为影响[J]. 腐蚀科学与防护技术, 2008, 20(1): 44-49.
LI Xue-ming, LIU Qiang, KONG Ling-feng, et al. Corrosion Behavior of Galvanized Steel under Stress in Simulated Acid Rain Solution[J]. Corrosion Science and Protection Technology, 2008, 20(1): 44-49.
[14]
陈小雨, 唐茂林. 温度和湿度环境下未镀锌高强钢丝的腐蚀速率谱[J]. 西南交通大学学报:自然科学版, 2018, 53(2): 253-259.
CHEN Xiao-yu, TANG Mao-lin. Corrosion Rate of Non-Galvanized High-strength Steel Wires under Different Temperature and Humidity Conditions[J]. Journal of Southwest Jiaotong University:Natural and Science Edition, 2018, 53(2): 253-259.
[15]
俞明德, 沈锐利, 唐茂林, 等. 西堠门大桥主缆横断面温度场研究[J]. 建筑科学与工程学报, 2010, 27(3): 53-58.
YU Ming-de, SHEN Rui-li, TANG Mao-lin, et al. Research on Temperature Field of Main Cable Section of Xihoumen Bridge[J]. Journal of Architecture and Civil Engineering, 2010, 27(3): 53-58.
[16]
陈小雨. 基于无损腐蚀监测系统的悬索桥主缆腐蚀试验及数据分析[J]. 中外公路, 2016, 35(1): 72-76.
CHEN Xiao-yu. Experimental Analysis of Main Cables of Suspension Bridge Based on Nondestructive Corrosion Monitoring System[J]. Journal of China & Foreign Highway, 2016, 35(1): 72-76.
[17]
何为, 薛为东, 唐斌. 优化试验设计方法与数据分析[M]. 北京: 化学工业出版社, 2012.
HE Wei, XUE Wei-dong, TANG Bin. Optimization Experimental Design Method and Data Analysis[M]. Beijing: Chemical Industry Press, 2012.
[18]
陈小雨, 唐茂林. 悬索桥主缆钢丝全寿命腐蚀程度及剩余抗力变化试验研究[J]. 桥梁建设, 2018, 48(1): 60-64.
CHEN Xiao-yu, TANG Mao-lin. Experimental Study of Corrosion Process and Resistance Changes of Galvanized Steel Wires for Main Cable of Suspension Bridge[J]. Bridge Construction, 2018, 48(1): 60-64.