扩展功能
文章信息
- 谢涛, 罗强, 张良, 连继峰
- XIE Tao, LUO Qiang, ZHANG Liang, LIAN Ji-feng
- 降雨渗流下路基坡面稳定性和空心砌块优化
- Stability of Subgrade Slope Surface and Optimization of Hollow Block under Rainfall Infiltration
- 公路交通科技, 2019, 36(2): 28-35, 49
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 28-35, 49
- 10.3969/j.issn.1002-0268.2019.02.005
-
文章历史
- 收稿日期: 2017-09-22
空心砌块是一种主要用于植被不易生长的砂类土、碎石类土、软质岩及改良土路基边坡的坡面防护结构[1],可与植被防护结合使用或单独铺设,以防止路基边坡表层土体被雨水冲刷侵蚀,进而保证整个路基边坡的稳定性。在实际工程中,普遍采用的空心砌块外轮廓形状为正六边形,即正六棱空心砌块。该种空心砌块常常因构造尺寸不合理、砌块内土体松散,在降雨引起的渗流作用下,块内土体被逐渐掏空而造成砌块相互错动甚至翻转,使得砌块成片塌陷,水流直接侵蚀坡面土体,严重影响边坡浅层稳定性,如图 1所示。因此,寻求一种更加合理的砌块尺寸设计方法和更优的砌块形状,对保证路基坡面土体稳定性和降低材料成本具有现实意义。

|
| 图 1 空心砌块防护失稳[2] Fig. 1 Instability of hollow block protection |
| |
岩土工程边坡在开挖或填筑过程中产生的裸露坡面如果不加以治理,会对边坡稳定性及环境造成不利影响。在人们对环境日益要求严格的今天,加强对边坡坡面的防护显得越来越重要。当前,人们在工程实践中越来越多地将工程技术与植被防护相结合。在岩土边坡上进行植被防护,其设计、施工都与一般园艺技术不同[3-4]。首先,必须使用一定的工程措施保证坡体整体的稳定性;其次,斜坡上表层松散土体会在自重作用下产生滑动剥落,特别是在持续的降雨或强降雨作用下,坡面土体极易产生侵蚀、冲刷流失,对坡面的植被及边坡稳定性造成不良影响[5-6]。
为解决上述问题,空心砌块防护被广泛运用于铁路及公路的边坡坡面防护工程,其防护效果主要取决于砌块高度。高度越高防护效果越好,然而材料用量也就越多,高度低了又难以起到防护作用。除了空心砌块本身尺寸对其内土体的影响外,影响空心砌块内土体稳定性的另一重要因素就是降雨[7-10],其作用主要体现在两个方面:一方面雨水的浸入使土发生一定程度的软化,土的强度降低[11-12];另一方面降雨形成的渗透力作用对土体的稳定性具有负面作用,增加了土体的下滑力[10, 13]。为探究降雨引起的渗流作用对坡面表层土体稳定性的影响规律,对路基边坡表层土体在降雨导致的不同渗流方向条件下的稳定性进行分析,并结合空心砌块防护结构,以其内土体为分析对象,探讨降雨渗流作用下砌块内土体稳定性与砌块尺寸之间的合理匹配关系,在此基础上对空心砌块进行优化,寻求一种更加合理、经济的空心砌块形状。
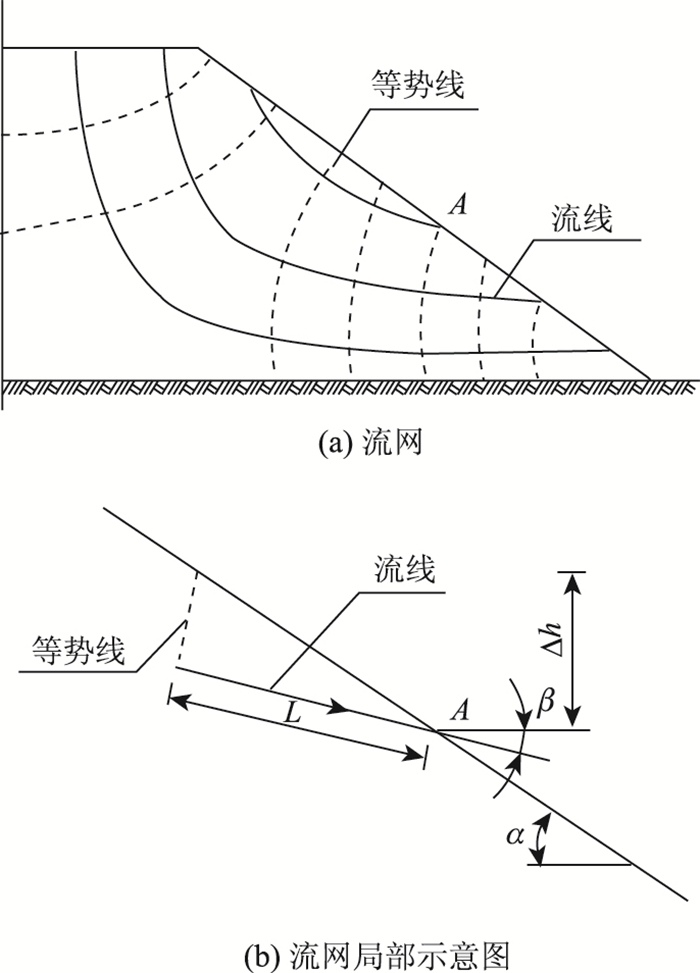
1 降雨渗流下坡面土体稳定性 1.1 降雨作用下路基坡面的水力坡降路基边坡表层土体由于长期受到降雨、蒸发、干湿循环等环境因素长期作用而处于松散状态[11],其渗透性明显高于深部土体及地基。降雨时,雨水通过路基顶面及上部斜坡进入路基,并通过下部斜坡自路基流出,斜坡顶面部分渗流接近竖向渗流,斜坡中部接近顺坡渗流,斜坡底部接近水平渗流[14],其流网示意图如图 2(a)所示。
|
| 图 2 降雨作用下路基边坡流网 Fig. 2 Infiltration net of subgrade slope under rainfall condition |
| |
由于路基边坡具有一定坡度且设有相应的排水设施,降雨时路基坡面能很快将表面雨水排走而不会形成积水。因此,认为在路基坡面上雨水下渗时的水力坡降仅由其自身的重力势能引起。在降雨持续作用下,路基边坡内部逐渐形成稳定渗流,如图 2(b)所示。坡角为α的路基边坡坡面某处的渗流方向与水平线成β角,β的取值范围为0°~90°。雨水流经长度L损失的水头Δh按式(1)计算,水力坡降i按式(2)计算。
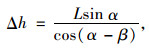
|
(1) |
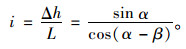
|
(2) |
从式(2)可知,在降雨引起的渗流作用下,水力坡降不仅与渗流方向相关,还受边坡坡角α的影响。当β=0°时,为水平渗流,对应水力坡降i=tan α;当β=α时,为顺坡渗流,对应水力坡降i=sin α;当β=90°时,为竖向渗流,对应水力坡降i=1。
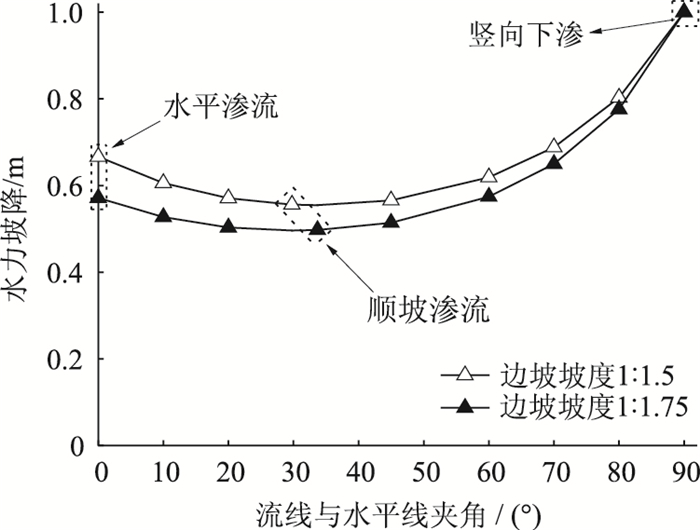
为了更为直观地呈现路基边坡渗流逸出点的水力坡降随渗流方向的变化规律,图 3描绘了通过式(2)求得的坡度为1: 1.5和1: 1.75的路基边坡水力坡降随渗流方向的变化曲线。计算表明,水力坡降随流线与水平线夹角的增加呈现先减小后增大的变化规律。顺坡渗流时,水力坡降最小;竖向下渗时水力坡降最大。
|
| 图 3 水力坡降与渗流方向关系 Fig. 3 Relationship between hydraulic gradient and infiltration direction |
| |
1.2 降雨作用下路基坡面表层土体稳定性
如图 4所示,以路基坡面上土体单元为隔离体[5, 15],该土体单元受到重力W=γ′、渗透力J=iγw、垂直于坡面的正压力N、抗滑力R的作用。
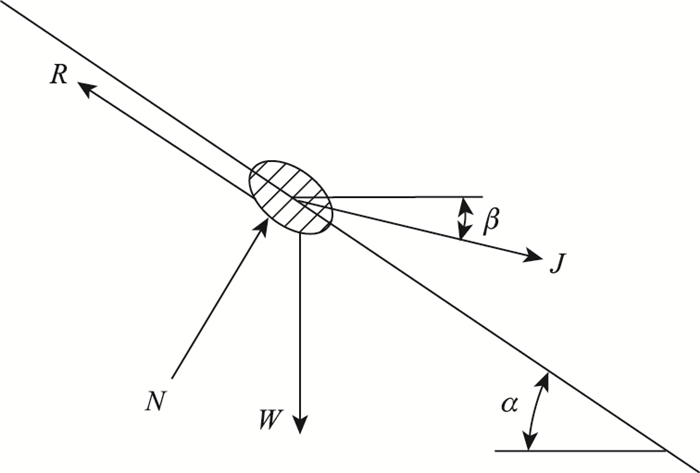
|
| 图 4 路基坡面土体单元受力图 Fig. 4 Force diagram of soil element on subgrade slope surface |
| |
根据平衡关系,支持力N的计算式为:
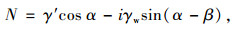
|
(3) |
式中,γ′为浮重度;γw为水的重度。
土体沿顺坡向滑动的下滑力T、抗滑力R的计算式为:
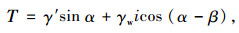
|
(4) |
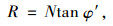
|
(5) |
式中φ′为土的有效内摩擦角。
土体的安全系数Fs等于抗滑力与下滑力之比。实际边坡中的土都不是理想的无黏性土,即使是理想的砂土,在毛细水作用下也会呈现出一定的黏聚力,称为“假黏聚力”[14]。考虑到这部分黏聚力对坡面表层土体稳定性所做的贡献,通常在取值时以土体的综合内摩擦角φ0代替土的有效内摩擦角φ′进行[16],并结合式(2)可推导出路基边坡表层土体在任意渗流方向时的安全系数Fs:
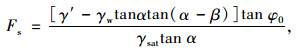
|
(6) |
式中,γsat为土的饱和重度。分别令β等于90°,α,0°代入式(5),得到竖向、顺坡及水平渗流的安全系数计算式:
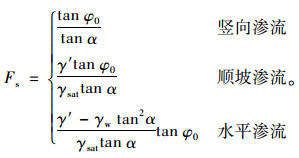
|
(7) |
其中,竖向下渗时坡面土体的安全系数与无渗流条件下的安全系数相同。这是因为竖向下渗时渗透力的方向竖直向下,且对于无黏性土不存在黏聚力,竖向下渗时抗滑力与下滑力之比相对于没有渗流时并没有变化。
根据式(6),土的饱和重度γsat=20 kN/m3、φ0=34°、边坡坡度为1: 1.5和1: 1.75的路基边坡在不同方向渗流作用下的安全系数如图 5所示。两种坡度的边坡表层土体安全系数Fs均随着β的增大而逐渐减小。其中水平渗流时安全系数最小,竖向下渗时安全系数最大,且在同样的土质条件下,渗流方向相同时边坡越陡安全系数越小。以图 5中的路基边坡为例,边坡坡度为1: 1.5时,水平、顺坡、竖向渗流时表层土体的安全系数分别为0.30,0.52,1.01;边坡坡度为1: 1.75时,对应的安全系数分别为0.41,0.60,1.18。由此可见,水力坡降小时土体的稳定性并不一定好。当渗流方向竖直向下时,水力坡降最大,而土体稳定性最好;当渗流为顺坡向时,水力坡降最小,土体稳定性比水平渗流作用下的高。这主要是因为渗流方向越接近水平,垂直于坡面的支撑力就越小,土体的抗滑力就越低,从而导致安全系数减小。
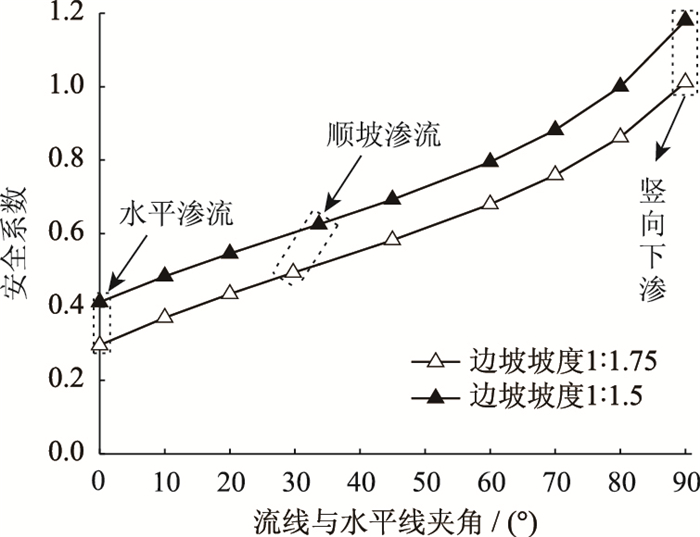
|
| 图 5 安全系数与渗流方向的关系曲线 Fig. 5 Relationship between safety factor and infiltration direction |
| |
结合路基边坡在不同渗流方向作用下的分析可知,路基边坡表层土体的稳定性自上而下不断降低,坡脚处最低,其结果与文献[17]的模型试验现象一致。因此,在边坡坡面防护中,应加强对坡角处的防护,从而保证在降雨导致的渗流作用下坡角处土体不被雨水侵蚀掏空。
2 渗流作用下砌块内土体的稳定性工程上常用空心砌块来防止路基边坡表层土体在持续降雨或强降雨作用下的失稳破坏,其作用主要体现在:一方面空心砌块和块内土体相互约束、组合在一起铺设于坡面上,形成相互嵌固、类似于蜂窝的网状结构,防护整体性较好;另一方面,砌块把整个坡面土体分割成众多小块,并把各小块土体置于空心砌块内,使得来自坡顶的水流需越过空心砌块逐级向下渗流,避免了雨水的直接冲刷。通过在路基坡面铺设空心砌块,从而将坡面冲刷问题转变成砌块内土体的渗流稳定问题。因此,对于空心砌块这种坡面防护措施,防护的关键在于保证砌块内土体的渗流稳定性。
因雨水竖向下渗时坡面土体稳定性较好,能够满足稳定性要求,故坡面防护时主要考虑水平渗流和顺坡渗流作用下铺有空心砌块的路基坡面土体稳定性。
2.1 砌块内土体临界稳定坡角的确定空心砌块将路基坡面分隔成许多小土块,这些小土块在降雨引起的渗流作用下逐渐形成如图 6所示坡度为θ的斜坡AB。
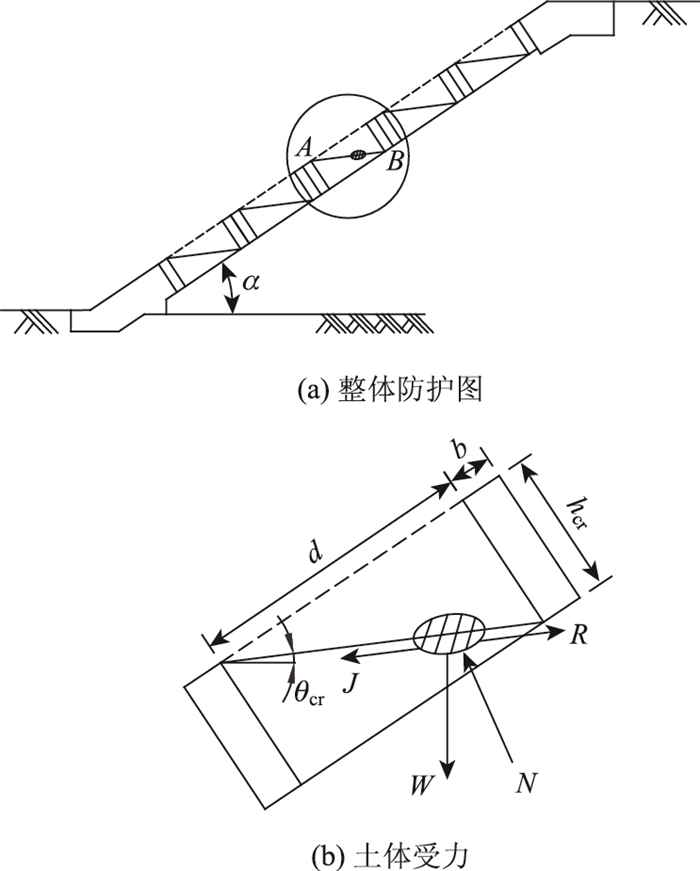
|
| 图 6 砌块内土体受力图 Fig. 6 Force diagram of soil in hollow block |
| |
以砌块内斜坡AB的坡角θ替代式(5)中的坡角α,求得铺有空心砌块的路基边坡坡面表层土体的安全系数F′s为:
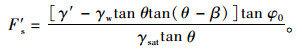
|
(8) |
当F′s=1时,对应θ为土体临界稳定坡角θcr的计算式为:
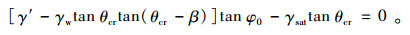
|
(9) |
分别令式(11)中β为0°,α,90°,即可求得水平、顺坡及竖直向下渗流时土体的临界坡角:
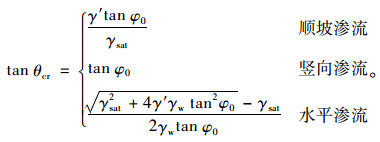
|
(10) |
通过式(10),求得不同φ0对应的水平、顺坡及竖直向下渗流时的临界坡角,如表 1所示。可见,水平及顺坡渗流作用使得土体的临界坡角比没渗流时的天然休止角大幅度减小,且水平渗流时比顺坡渗流的临界坡角更小。表 1中,土体的饱和重度γsat=20 kN/m3。
| 有效内摩擦 角/(°) |
临界坡角/(°) | ||
| 水平渗流 | 顺坡渗流 | 竖向下渗 | |
| 34 | 17.3 | 19.0 | 34 |
| 36 | 18.3 | 20.3 | 36 |
| 38 | 19.4 | 21.7 | 38 |
2.2 砌块高度的确定
空心砌块的几何参数中,高度h对砌块内土体的稳定性起决定作用,合理设计空心砌块高度是防护的核心。
图 6为铺有空心砌块的路基边坡横断面图。边坡坡度为α,空心砌块沿顺坡向内距为d,定义土体刚好被掏空至砌块底部所对应的砌块高度为临界高度hcr,其计算式为:
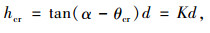
|
(11) |
式中
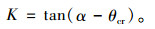
|
(12) |
为保证一定的安全余度,设计高度h的计算式为:
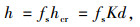
|
(13) |
式中fs为安全储备系数,fs=2时允许被掏空土体的最大深度为空心砌块高度的一半。
按式(13)确定的空心砌块高度,在满足稳定性前提下,将用料降低到最低限度,避免了工程上为增加稳定性而盲目增加空心砌块高度的做法。
3 空心砌块的几何形状优化以控制空心砌块内土体稳定性为出发点,建立砌块尺寸与土性、边坡坡度的合理匹配关系,从几何尺寸的角度对空心砌块进行优化。为探求更加经济、合理的空心砌块形状,对不同形状的空心砌块用于路基坡面防护的适用性及经济性进行分析。
3.1 砌块几何形状选择为确保空心砌块在路基坡面的可拼接性,相邻空心砌块必须满足棱边与棱边之间完全接触而不出现空隙,满足该条件的常见空心砌块形式有三角形、平行四边形及正六边形,如图 7所示。然而,通缝的存在使得前两种空心砌块并不适合于坡面防护工程。以图 7中三角形和平行四边形空心砌块为例,由于存在通缝,铺设在路基坡面的空心砌块不能形成砌块之间相互嵌固、具有良好整体性的蜂窝状结构。当某空心砌块破裂后,其他砌块会随之发生滑动,并且在降雨作用下,雨水会沿着砌块与砌块之间形成的细长通缝CD和MN流动,使得接触处的土体逐渐流失掏空,砌块松动变形,防护结构失稳,对整个边坡坡面土体的稳定性造成不利影响。因此,六棱空心砌块是比较理想的选择。
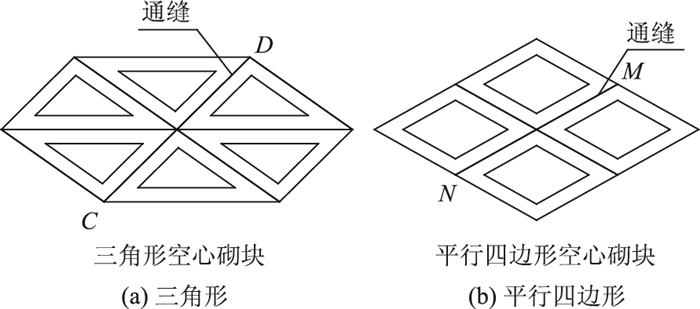
|
| 图 7 空心砌块防护中的通缝 Fig. 7 Continous seams in hollow block |
| |
3.2 六棱空心砌块形状优化分析
为评定不同尺寸及形状空心砌块的经济性,在保证砌块内土体处于同样稳定的情况下,以单位铺设面积所需预制空心砌块的混凝土体积λ为评价指标,即:
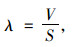
|
(14) |
式中,V为单块空心砌块所需的混凝土体积;S为砌块所占用的平面面积。
如图 8所示的空心砌块的外轮廓边长l及壁厚b保持不变,将其沿纵向压扁成左右两个内角为a的新型六棱空心砌块,a的取值范围为0~120°。
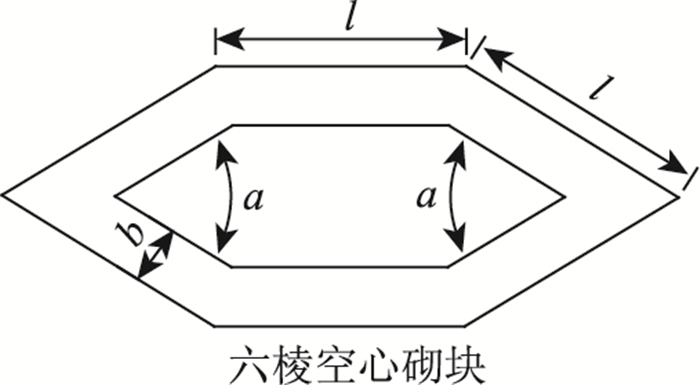
|
| 图 8 空心砌块平面图 Fig. 8 Plane of hollow block |
| |
当a=120°时,即正六棱空心砌块。压扁后砌块沿顺坡向内距变短,在相同水力坡降条件下,砌块内水流的渗流路径变短,从而使得达到相同防护效果时所需砌块高度降低。将压扁后空心砌块内距d=2 [l·sin (a/2)-b]代入式(13),得到尺寸减小后的六棱空心砌块高度计算式:
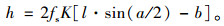
|
(15) |
从式(15)可知,在相同防护效果条件下,砌块高度随内角a的减小而降低。
尺寸压扁后的新型六棱空心砌块单位铺设面积所需的混凝土体积λ为:
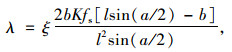
|
(16) |
式中的系数ξ按式(17)确定:
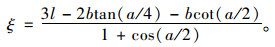
|
(17) |
以边长l=20 cm、壁厚b=5 cm的正六棱空心砌块为例,保持边长l及壁厚b不变,左右两个内角由原来的120°逐渐压缩减小,砌块单位铺设面积所需混凝土体积λ、高度h随内角a的变化规律如图 9所示。图中φ0=34°、γsat=20 kN/m3,边坡坡度1: 1.5,雨水渗流方向为顺坡向下,安全储备系数fs=2。
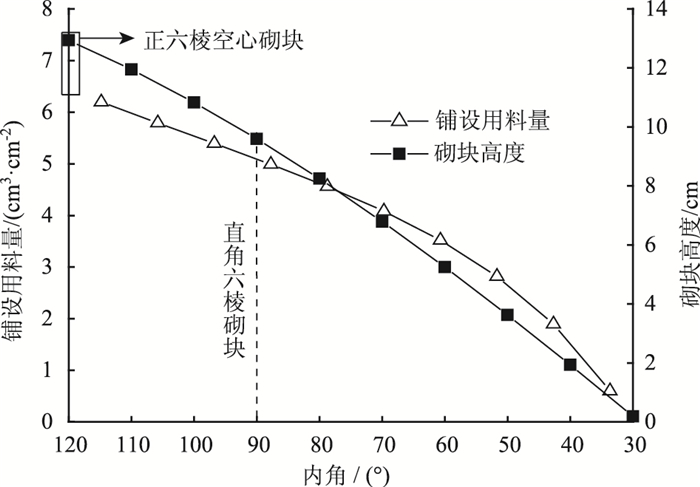
|
| 图 9 砌块内角与用料量及高度的关系曲线 Fig. 9 Relation curves of interior angle with material dosage and height of hollow block |
| |
从图 9可知,空心砌块单位铺设面积所需混凝土用料量λ随内角a的减小而逐渐降低,即砌块越扁平用料越省。这是因为空心砌块内径随着a的减小而变短,从式(13)可知,内径d越短,保持砌块内土体稳定所需的砌块高度就越低,从而使单位铺设面积所需混凝土用量λ减少。图 9中l=20 cm, b=5 cm的空心砌块,当a=30°时,砌块高度近乎为0,空心砌块接近一张薄板,从而使用料λ接近0。然而,现有空心砌块的构筑材料为混凝土,砌块太薄无法满足结构强度要求。
单纯从空心砌块用料角度分析,在保持砌块内土体具有同样安全系数的稳定性条件下,砌块内角a越小(即越扁平),用料越省。但是,砌块除了保证其内土体在渗流作用下的稳定性外,还必须满足自身结构具有足够的强度,以确保在施工过程中及施工后降雨、蒸发、干湿循环等环境因素长期作用下,砌块不出现结构破坏。内角a越小,在砌块左右两个尖角处越容易形成应力集中,导致砌块两端在搬运及施工过程中容易产生脆性断裂,破坏砌块结构的整体性。
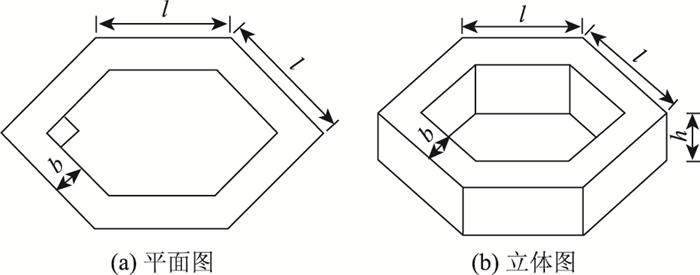
综合用料和砌块本身结构强度两方面因素,选择左右两个内角a=90°的直角六棱空心砌块作为新的结构形式,如图 10所示。一方面,直角六棱空心砌块相对于现有正六棱空心砌块,在相同的防护效果条件下单位铺设面积所需混凝土用料减少了20%左右,降低了材料成本;另一方面,对于空心砌块这种防护结构,为保证砌块转角处不出现过大的应力集中,应避免形成锐角,直角六棱空心砌块相对于锐角六棱空心砌块,砌块本身结构强度更高,且左右两个内角为直角的空心砌块相对于其他形式的空心砌块制模更方便。
|
| 图 10 直角六棱空心砌块示意图 Fig. 10 Schematic diagram of regular 6-edge hollow block |
| |
4 空心砌块的设计及算例 4.1 直角六棱空心砌块的设计
空心砌块作为一种边坡防护结构,除了保证砌块内土体在渗流作用下的稳定性外,还必须满足施工方便、快捷的要求。空心砌块几何尺寸较大,铺设时因单块空心砌块太重而造成施工搬运不便;空心砌块平面尺寸较小,使得铺设同样边坡面积需耗费更多的铺设时间。因此,空心砌块外棱边长l的合理范围为10~25 cm。
空心砌块除了满足砌块内土体的稳定性外,还需保证自身结构强度,以确保在施工过程及施工后空心砌块不发生破坏。通过查阅相关设计资料[1, 7-9]发现,现有空心砌块的壁厚b的取值范围为0.2l~0.25l,且基本能够满足自身强度要求。基于安全考虑,直角六棱空心砌块壁厚取较大值b=0.25l。
将直角六棱空心砌块沿顺坡向内距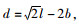
水平渗流:
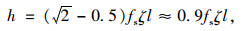
|
(18) |
式中系数ζ按式(19)计算:
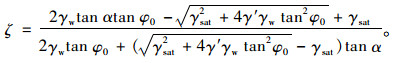
|
(19) |
顺坡渗流:
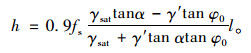
|
(20) |
表 2为现有的正六棱空心砌块与直角六棱空心砌块的几何尺寸[1, 7-9]。坡面土体的综合内摩擦角φ0=28°,γsat=20 kN/m3,边坡坡度1: 1.5,并假定渗流方向为顺坡渗流,安全储备系数均取fs=2。
| 边长 | 壁厚 | 高度 | |
| 正六棱空心砌块 | 直角六棱空心砌块 | ||
| 10 | 2.5 | 8.3 | 6.1 |
| 12 | 3.0 | 9.9 | 7.3 |
| 14 | 3.5 | 11.6 | 8.6 |
| 16 | 4.0 | 13.2 | 9.8 |
| 18 | 4.5 | 14.9 | 11.0 |
| 20 | 5.0 | 16.5 | 12.2 |
| 22 | 5.5 | 18.2 | 13.5 |
| 24 | 6.0 | 19.8 | 14.7 |
从表 2可知,在相同安全系数条件下,直角六棱空心砌块所需的高度比正六棱空心砌块低2.2~5.1 cm,用料更省。图 11为表 2所列的两种空心砌块单位铺设面积所需混凝土用量λ的对比图。通过图 11及计算可知,fs=2时,直角六棱空心砌块比正六棱空心砌块混凝土用量减少20.9%。
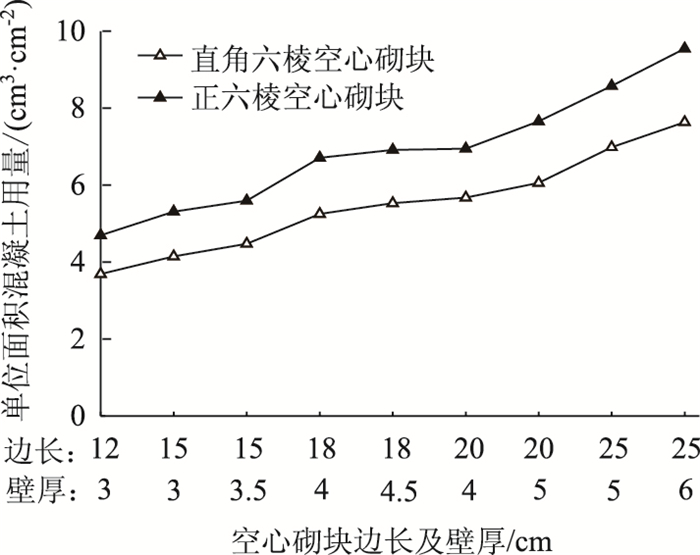
|
| 图 11 混凝土用量对比图 Fig. 11 Comparison of concrete useages |
| |
4.3 影响空心砌块高度的因素及尺寸推荐
通过对空心砌块内土体的分析可知,影响空心砌块高度的因素主要有边坡坡度、土体性质及渗流方向。为探求这3种因素对砌块高度的影响,将不同边坡坡度、土体性质(综合内摩擦角)、渗流方向情况下同样维持fs=2,砌块高度如图 12所示。
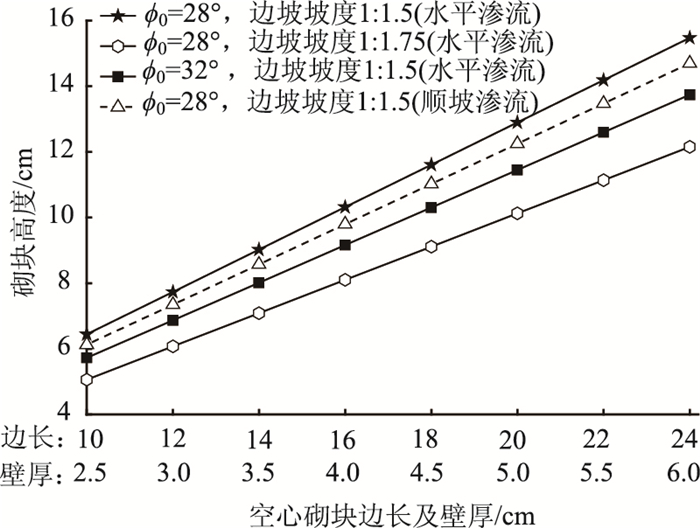
|
| 图 12 不同因素对砌块高度的影响 Fig. 12 Influence of different factors on block height |
| |
从图 12可知,对砌块高度影响最大的是边坡坡度,坡度越陡,维持坡面土体同样安全系数所需的砌块高度越高;影响最小的是渗流方向,对于同样的边坡和土体,顺坡渗流和水平渗流得到的砌块高度差异不会超过1 cm。因此,在通过水平渗流和竖向渗流确定无明显差异的空心砌块尺寸时,为使防护偏于安全,可对整个边坡都按水平渗流条件确定砌块高度。
文献[18]中,路基边坡空心砌块内土体的φ0=28°~32°,γsat=20 kN/m3,常见的边坡坡度为1: 1.5和1: 1.75。为便于工程直接选用,表 3列出了对应于坡度较陡、土体有效内摩擦角较小(坡比1: 1.5、φ0=28°)及坡度较缓、土体有效内摩擦角较大(坡比1: 1.75、φ0=32°)的路基边坡,分别考虑水平渗流和顺坡渗流情况下的直角六棱空心砌块尺寸。
| 棱长 | 壁厚 | 顺坡渗流高度 | 水平渗流高度 | |||
| 有效内摩 擦角28°, 坡比1:1.5 |
有效内摩 擦角32°, 坡比1:1.75 |
有效内摩 擦角28°, 坡比1:1.5 |
有效内摩 擦角32°, 坡比1:1.75 |
|||
| 10 | 2.5 | 6.1 | 3.9 | 6.4 | 4.4 | |
| 12 | 3.0 | 7.3 | 4.7 | 7.7 | 5.2 | |
| 14 | 3.5 | 8.6 | 5.5 | 9.0 | 6.1 | |
| 16 | 4.0 | 9.8 | 6.3 | 10.3 | 7.0 | |
| 18 | 4.5 | 11.0 | 7.0 | 11.6 | 7.9 | |
| 20 | 5.0 | 12.2 | 7.8 | 12.9 | 8.7 | |
| 22 | 5.5 | 13.5 | 8.6 | 14.2 | 9.6 | |
| 24 | 6.0 | 14.7 | 9.4 | 15.5 | 10.5 | |
需要指出的是,本研究的空心砌块防护主要针对边坡表层稳定性,其设置对整体稳定性不会产生实质性影响。因此,边坡的整体稳定性依然可根据现有分析方法予以评估。
5 结论以路基边坡在降雨渗流作用下的坡面表层土体稳定性分析为出发点,结合坡面防护结构空心砌块尺寸与坡面土体稳定性之间的相互关系,对空心砌块进行了设计及优化,得到以下结论:
(1) 建立了降雨渗流作用下坡面表层无黏性土安全系数Fs与渗流方向β、土性、边坡坡度的函数关系。发现坡面土体随着流线方向β由边坡上部竖直入渗逐渐过渡到下部水平溢出的过程,将导致Fs逐渐减小,在坡脚附近降到最低。这与相关文献所述在坡脚附近首先发生破坏的试验现象一致。
(2) 以保持空心砌块内土体稳定为控制目标,建立了水平及顺坡渗流条件下的砌块设计高度h表达式,讨论了边坡坡度、土性及渗流方向对砌块设计高度h的影响,主次顺序依次为边坡坡度、土体强度、渗流方向。为保证防护设计的可靠性,砌块高度宜采用水平渗流条件下的设计值。所建立的设计方法促进了空心砌块从构造设计向基于力学原理结构分析的转变。
(3) 直角六棱空心砌块比现有常用的正六棱空心砌块在相同防护效果下具有更好的经济性。在相同的边长、壁厚及安全储备系数的条件下,直角六棱空心砌块较现有的正六棱空心砌块节省用料约20.9%。
| [1] |
中铁第三勘察设计院集团有限公司.铁路路基边坡防护(冻土地区)[R].北京: 铁道部经济规划研究院, 2014. China Railway Third Survey and Design Institute Group Co., Ltd.Protection of Railway Subgrade Slope (Permafrost Region)[R].Beijing: China Railway Economic and Planning Research Institute, 2014. |
| [2] |
陈锋.戈壁区不良填料路基设计施工技术研究[D].北京: 中国铁道科学研究院, 2011: 3-5. CHEN Feng.Study on Design and Construction Technology of Non-performing Filling Subgrade in Gobi Area[D].Beijing: China Academy of Railway Sciences, 2011: 3-5. http://cdmd.cnki.com.cn/Article/CDMD-83801-1012566709.htm |
| [3] |
孔嵘.边坡生态防护的雨水入渗及设计优化研究[D].长沙: 长沙理工大学, 2012: 1-8. KONG Rong.Study of Slope Ecological Protection against Rainwater Infiltration and Design Optimization[D].Changsha: Changsha University of Science & Technology, 2012: 1-8. http://cdmd.cnki.com.cn/Article/CDMD-10536-1012348633.htm |
| [4] |
李海光. 新型支挡结构设计与工程实例[M]. 2版. 北京: 人民交通出版社, 2014: 486-489. LI Hai-guang. Designing New Type of Retaining Structure and Engineering Example[M]. 2nd ed. Beijing: China Communications Press, 2014: 486-489. |
| [5] |
陈祖煜. 土质边坡稳定分析[M]. 北京: 中国水利水电出版社, 2002: 2-15. CHEN Zu-yu. Analysis on Stability of Soil Slope[M]. Beijing: China Water & Power Press, 2002: 2-25. |
| [6] |
张永兴. 边坡工程学[M]. 北京: 中国建筑工业出版社, 2008: 5-13. ZHANG Yong-xing. Slope Engineering[M]. Beijing: China Architecture & Building Press, 2008: 5-13. |
| [7] |
中铁第一勘察设计院集团有限公司.铁路路基边坡防护(风沙地区)[R].北京: 铁道部经济规划研究院, 2014. China Railway First Survey and Design Institute Group Co., Ltd.Protection of Railway Subgrade Slope (Sandy Region)[R].Beijing: China Railway Economic and Planning Research Institute, 2014. |
| [8] |
中铁第四勘察设计院集团有限公司.铁路路基边坡防护(浸水地区)[R].北京: 铁道部经济规划研究院, 2014. China Railway Fourth Survey and Design Group Co., Ltd.Protection of Railway Subgrade Slope (Flooded Region)[R].Beijing: China Railway Economic and Planning Research Institute, 2014. |
| [9] |
中国中铁二院工程集团有限公司.一般地区铁路路基边坡防护[R].北京: 铁道部经济规划研究院, 2013. China Railway Second Engineering Group Co., Ltd.Protection of Railway Subgrade Slope at General Region[R].Beijing: China Railway Economic and Planning Research Institute, 2013. |
| [10] |
钱家欢, 殷宗泽. 土工原理与计算[M]. 2版. 北京: 中国水利水电出版社, 1994: 122-125. QIAN Jia-huan, YIN Zong-ze. Geotextile Principle and Calculation[M]. 2nd ed. Beijing: China Water & Power Press, 1994: 122-125. |
| [11] |
曾胜, 李振存, 韦慧, 等. 降雨渗流及干湿循环作用下红砂岩顺层边坡稳定性分析[J]. 岩土力学, 2013, 34(6): 1536-1540. ZENG Sheng, LI Zhen-cun, WEI Hui, et al. Stability Analysis of Red Sandstone Bedding Slope under Rainfall Infiltration and Dry-wet Cycling[J]. Rock and Soil Mechanics, 2013, 34(6): 1536-1540. |
| [12] |
王军, 蔡袁强, 徐长节, 等. 循环荷载作用下饱和软黏土应变软化模型研究[J]. 岩石力学与工程学报, 2007, 26(8): 1713-1719. WANG Jun, CAI Yuan-qiang, XU Chang-jie, et al. Study on Strain Softening Model of Saturated Soft Clay under Cyclic Loading[J]. Beijing:Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1713-1719. |
| [13] |
钱建固, 吕玺琳, 黄茂松. 平面应变状态下土体的软化特性与本构模拟[J]. 岩土力学, 2009, 30(3): 617-621. QIAN Jian-gu, LÜ Xi-lin, HUANG Mao-song. Softening Characteristics of Soils and Constitutive Modeling under Plane Strain Condition[J]. Rock and Soil Mechanics, 2009, 30(3): 617-621. |
| [14] |
TERZAGHI K. Theoretical Soil Mechanics[M]. New York: John wiler & Sons, Inc, 1984: 265-264.
|
| [15] |
陈仲颐, 周景星, 王洪瑾. 土力学[M]. 北京: 清华大学出版社, 1994: 241-244. CHEN Zhong-yi, ZHOU Jing-xing, WANG Hong-jin. Soil Mechanics[M]. Beijing: Tsinghua University Press, 1994: 241-244. |
| [16] |
黄广军, 刘昌清, 彭胤宗. 土压力计算中综合内摩擦角取值探讨[J]. 西南交通大学学报, 1996, 31(1): 86-92. HUANG Guang-jun, LIU Chang-qing, PENG Yin-zong. Research of the Equivalent Friction Angle for Cohesive Soil[J]. Journal of Southwest Jiaotong University, 1996, 31(1): 86-92. |
| [17] |
林鸿州, 于玉贞, 李广信, 等. 降雨特性对土质边坡失稳的影响[J]. 岩石力学与工程学报, 2009, 28(1): 198-204. LIN Hung-chou, YU Yu-zhen, LI Guang-xin, et al. Influence of Rainfall Characteristics on Soil Slope Failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 198-204. |
| [18] |
杨烨. 宝中线路堤边坡整治:浆砌片石拱形骨架护坡[J]. 甘肃科技纵横, 2009, 38(1): 155-156. YANG Ye. Control of Embankment Slope in Baoji-Zhongwei Railway:Stone Arch Skeleton Slope Protection[J]. Architectural design, 2009, 38(1): 155-156. |
 2019, Vol. 36
2019, Vol. 36
