扩展功能
文章信息
- 程国勇, 王肖江, 冯长峰
- CHENG Guo-yong, WANG Xiao-jiang, FENG Chang-feng
- 飞机临界荷位的道面板内最大弯矩和板边弯矩分析
- Analysis on Maximum Bending Moment of Pavement and Bending Moment of Pavement Slab Edge at Aircraft's Critical Loading Position
- 公路交通科技, 2019, 36(2): 14-18
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(2): 14-18
- 10.3969/j.issn.1002-0268.2019.02.003
-
文章历史
- 收稿日期: 2017-04-10
2. 南开大学, 天津 300350;
3. 天津大学, 天津 300072
2. Nankai University, Tianjin 300350, China;
3. Tianjin University, Tianjin 300072, China
机场水泥混凝土道面板的内力是道面结构设计、安全性能评估的重要依据,温克尔地基上的半无限大板是上述内力分析的理论依据。一般认为,飞机主起落架的外边缘与半无限大板的自由边水平或竖向相切时为临界荷位,相应的板边弯矩峰值作为内力计算的依据。实际上板边并非最大弯矩位置。当飞机重量较小、起落架构型比较简单时,这种近似足够精确,但随着机型越来越大及起落架构型的复杂化,上述近似导致的误差越来越不可忽视。
李巧生等[1]分析了某大型飞机主起落架作用在9块5 m×5 m道面板上的位置与板底最大弯拉应力的关系以及影响因素。郑飞等[2]基于足尺道面结构有限元模型并考虑接缝传荷能力,得到了单轮、双轮、双轴双轮飞机荷载临界荷位作用下道面板内最大弯拉应力的回归公式。张献民等[3]基于温克尔地基上半无限大板的有限元模型分析了最大主拉应力与起落架构型的关系,发现最大应力位置不在板的自由边板底,并指出在单轴双轮型的起落架荷载作用下,道面板最大主拉应力产生于两机轮中心处;在双轴双轮型起落架荷载作用下,面板最大主拉应力在以4个机轮为顶点组成的矩形中心处;在三轴双轮型起落架荷载作用下,道面板最大主拉应力产生于中间轴上机轮的中心位置。凌建明等[4]基于9块5 m×5 m道面板的足尺三维有限元模型分析了伊尔76运输机作用于板边的荷载应力情况,指出最大弯拉应力位于相切于板边的板底。屈允永等[5]运用中国民用航空局现行的刚性道面设计方法与美国FAA的刚性道面设计方法进行数据对比,发现我国现行民航机场刚性道面设计方法趋于保守,并且计算繁琐,受制于板边弯矩影响图,精确度受到一定影响。程国勇等[6]基于统计原理,使用excel自带的VBA功能和用相关程序,计算出各种机型一个主起落架的轮印覆盖格数, 使得板边弯矩的计算精度得以提高。
从上述研究成果可以看出,飞机临界荷位条件下板边弯矩与最大弯矩的概念比较模糊,二者之间的差异以及这种差异与起落架构型之间的关系缺乏定量描述,无法为道面的设计及结构安全评估提供明确指导。
本研究根据弹性地基板理论并采用有限元方法,对不同起落架构型的民航客机在临界荷位板边弯矩与板内最大弯矩的差异及规律进行研究。
1 有限元建模为确保分析结果准确,在进行实际机型的分析前,首先探讨合理的有限元建模参数,以解析解作为检验有限元分析结果的依据。温克尔地基无限大板上在圆形均布荷载作用下的解析形式解为:

|
(1) |
式中,M为板底(圆心)最大弯矩;μ为泊松比;q为圆形局部荷载强度;R为圆形局部荷载圆半径;l为相对刚度半径;h为板厚;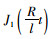
式(1)中含有一阶贝塞尔函数的无穷积分,利用MATLAB提供的自适应于高斯-克朗罗德法的quadgk函数进行计算。
1.1 加载方式为便于道面板网格划分,同时精确模拟机轮加载平面形状,对道面施加均布荷载时采用贴片的方式实现。在道面板上附加一个刚度极小的薄片,薄片材料的弹性模量比道面板材料低6个数量级,薄片厚度取3 mm。荷载取1.47 MPa,加载圆半径取0.2 m,道面板与加载薄片采用abaqus中的Tie连接,道面板的μ取0.15,弹性模量为34.5 GPa。
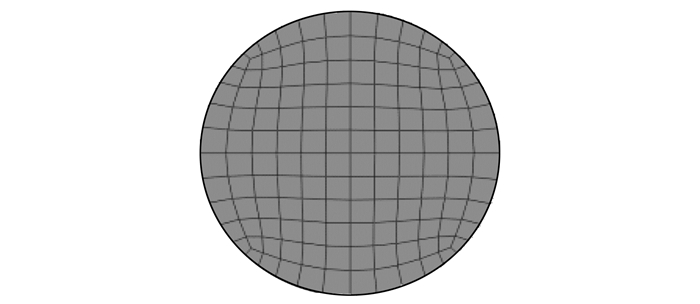
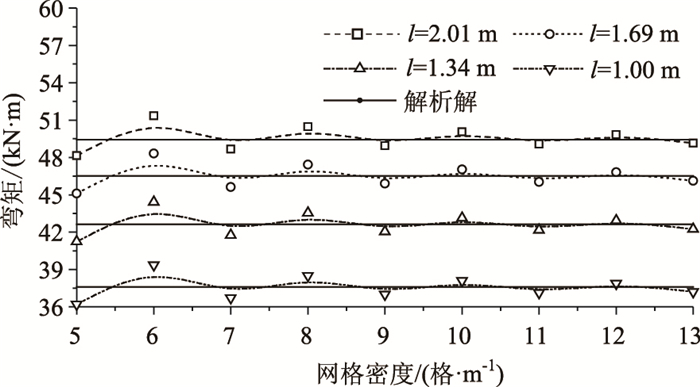
1.2 有限元模型平面尺寸、网格密度确定板的有限元网格划分采用S8R壳单元,加荷薄片网格划分见图 1。道面板划分越精细对弯沉值影响越小,通过尝试发现,在非加载区域,网格划分时单元最大边长小于R/2(0.1 m)时,分析结果已无变化,见图 2。故对非加载区网格划分时,将单元最大边长控制在0.1 m以内。在加载区,为精确判定最大弯矩位置,单元最大边长取R/20(0.01 m)。
|
| 图 1 加载薄片网格划分 Fig. 1 Meshing of loading slice |
| |
|
| 图 2 网格划分对弯矩的影响 Fig. 2 Influence of meshing on bending moment |
| |
为了尽量减弱边界效应,有限元模型中板的平面尺寸应足够大,但同时会增大计算时耗,为此需要尝试确定适合的平面尺寸。由图 3可以看出,随着相对刚度半径的不断加大,板的板底最大弯矩趋于收敛时的板面尺寸呈现线性增大,当混凝土道面板的尺寸在12 m(即荷载作用半径的60倍)以上时,各个相对刚度半径下板底弯矩计算结果已经趋近于无限大板值。故有限元建模中,道面板平面尺寸至少取主起落架作用范围半径的60倍[7-12]。

|
| 图 3 板块尺寸对弯矩计算的影响 Fig. 3 Influence of slab dimension on bending moment calculation |
| |
通过反复计算、对比表明,采用上述建模参数,有限元计算得到的板底最大弯矩与基于式(1)通过数值积分得到的数值解误差可以控制在1%以内。
2 计算结果及分析 2.1 多轴双轮组起落架板底板边最大弯矩的位置分析通过有限元建模分别对双轮、双轴双轮、三轴双轮组进行分析,以A319,A320,A380-800在最大起飞重量下为例,分别计算板底最大弯矩[7-18],具体建模参数见表 1。
| 机型 | 主起落架 构型 |
最大起飞 重量/kN |
主起落架荷载 分配系数 |
主起落架轮距/m | 主起落架轮胎 压力/ MPa |
板面选用尺寸/m | |
| 横向 | 纵向 | ||||||
| A319 | 双轮 | 700 | 0.926 | 0.93 | — | 0.89 | 18×18 |
| A320 | 双轴双轮 | 770 | 0.95 | 0.78 | 1.01 | 1.14 | 16×16 |
| A380-800 | 三轴双轮 | 5 600 | 0.57 | 1.53 | 1.70 | 1.47 | 22×22 |
A319起落架横放时的弯矩数值要大于起落架纵向放置时的弯矩数值,A320和A380-800起落架纵向放置时的弯矩数值要大于起落架横向放置时的弯矩数值,故对A319提取起落架横放时的弯矩数值,对A320和A380-800提取起落架纵向放置时的弯矩数值,得到板边板底最大弯矩靠近板边机轮的中下方位置,见图 4。板底板边最大弯矩处沿着板底向里延伸的距离拟合曲线见图 5。

|
| 图 4 最大弯矩位置示意图 Fig. 4 Schematic diagram of position of maximum bending moment |
| |

|
| 图 5 多轴双轮组板底最大弯矩位置内移距离 Fig. 5 Moving distance of maximum bending position of multi-axle double-wheel sets |
| |
由图 5可观察到,各个机型均出现了随着相对刚度半径的增大,最大弯矩出现位置逐渐内移的情况。随着起落架复杂的程度增加,内移的距离稍有不同,起落架复杂的机型内移的距离会稍大些,内移距离范围为4~14 cm。此后通过对每种双轮组25种常见机型的有限元计算发现,对所有单轴、双轴、三轴双轮组机型,在从空机重量到最大滑行重量范围内都存在这样的规律。
2.2 多轴双轮组起落架板底板边最大弯矩的数值分析通过对各双轮组机型的有限元计算发现,道面板板底最大弯矩与板底板边最大弯矩在数值上的差异随着相对刚度半径的变化也有所变化。现以双轮组代表机型A319,A320,A380-800在最大起飞重量下为例,分析板边弯矩与最大弯矩在数值上的差别,见图 6。

|
| 图 6 弯矩对比 Fig. 6 Comparison of bending moments |
| |
通过以上分析可以看出,3种机型在最大起飞重量下,板底最大弯矩与板底板边最大弯矩的差值都出现随着相对刚度半径的增大逐渐增大的规律,且差值比例均呈现先增大后逐渐减弱的趋势,最大弯矩值高出比例随起落架构型变化略有差异。其中A319最高误差比例达5.06%,A320最高误差比例达3.92%,A380-800最高误差比例达3.51%。
另外,通过对每种双轮组25种常见机型的有限元计算发现,对所有单轴、双轴、三轴双轮组机型,在从空机重量到最大滑行重量范围内都存在这样的规律,即板边弯矩和最大弯矩存在一定的误差,并且该误差不可忽略。
3 结论(1) 从以上的分析和计算中可以看出,采用以解析解为基础的高精度计算模型误差可以控制在1%以内,对于道面板的设计与结果性能的评估提供了便利。
(2) 随着相对刚度半径的增大,最大弯矩出现的位置逐渐内移。同样机型条件下,最大弯矩位置随着相对刚度半径的增大从板边逐渐内移,随着起落架复杂的程度增加,内移的距离会稍有不同,其范围为4~14 cm。
(3) 各机型最大弯矩值高出板边弯矩值的比例随着相对刚度半径的增加均出现先增大后稍微减弱的规律,最大弯矩值最大高出比例达5.06%。最大弯矩值高出比例随起落架构型的变化略有差异。
| [1] |
李巧生, 王德荣. 水泥混凝土道面结构在多轮荷载作用下的响应分析[J]. 振动与冲击, 2010, 29(2): 75-78. LI Qiao-sheng, WANG De-rong. Response Analysis of a Cement Concrete Pavement Structure with Multi-wheel Loading[J]. Journal of Vibration and Shock, 2010, 29(2): 75-78. |
| [2] |
郑飞, 翁兴中. 飞机荷载下水泥混凝土道面板应力计算方法[J]. 交通运输工程学报, 2010, 10(4): 8-14. ZHENG Fei, WENG Xing-zhong. Calculating Methods of Stress for Cement Concrete Pavement Slab under Plane Loads[J]. Journal of Traffic and Transportation Engineering, 2010, 10(4): 8-14. |
| [3] |
张献民, 董倩, 吕耀志. 飞机主起落架构型对道面力学响应的影响[J]. 西南交通大学学报, 2014, 40(4): 675-681. ZHANG Xian-min, DONG Qian, LÜ Yao-zhi. An Adaptive Anisotropic Gaussian Filter for Noise Reduction[J]. Journal of Southwest Jiaotong University, 2014, 40(4): 675-681. |
| [4] |
凌建明, 刘文, 赵鸿铎. 大型军用飞机多轮荷载作用下水泥混凝土道面的结构响应[J]. 土木工程学报, 2007, 40(4): 60-65. LING Jian-ming, LIU Wen, ZHAO Hong-duo. Mechanical Responses of Rigid Airport Pavement to Multiple-gear Military Aircraft Loadings[J]. China Civil Engineering Journal, 2007, 40(4): 60-65. |
| [5] |
屈允永, 邹晓翎. 现行中美民用机场刚性道面设计方法对比分析[J]. 中外公路, 2015, 34(5): 73-77. QU Yun-yong, ZOU Xiao-ling. Contrastive Analysis of Rigid Pavement Design Methods of Civil Airports in China and United States[J]. Journal of China & Foreign Highway, 2015, 34(5): 73-77. |
| [6] |
程国勇, 郭志光. 基于统计原理的板边弯矩计算方法[J]. 中国民航大学学报, 2013, 31(1): 73-75. CHENG Guo-yong, GUO Zhi-guang. Method of Using Excel to Calculating Plate Edge Bending Moment[J]. Journal of Civil Aviation University of China, 2013, 31(1): 73-75. |
| [7] |
王春玲, 黄义. 弹性地基板的分析简化模型[J]. 岩土力学, 2008, 29(1): 52-57. WANG Chun-ling, HUANG Yi. Refined Model for Analysis of Plates on Elastic Foundations[J]. Rock and Soil Mechanics, 2008, 29(1): 52-57. |
| [8] |
AC 150/5320-6D, Airport Pavement Design and Evaluation[S].
|
| [9] |
李松涛.水泥混凝土路面弯沉温度修正试验研究[D].郑州: 郑州大学, 2015. LI Song-tao. Experimental Study on Temperature Correction to Deflection of Cement Concrete Pavement[D]. Zhengzhou: Zhengzhou University, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D646111 |
| [10] |
芦良健.基于实桥的超限车辆荷载模型及其荷载效应研究[D].南昌: 南昌大学, 2014. LU Liang-jian. Research on Over-limited Vehicles Load Model and Load Effect on Existing Bridge[D]. Nanchang: Nanchang University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10403-1014055079.htm |
| [11] |
BALAY J M, CARON C, LERAT P. Adaptation of the French Rational Road Design Procedure to Airfield Pavements[C]//2010 FAA Worldwide Airport Technology Transfer Conference. Atlantic City: Federal Aviation Administration, 2010: 213-221.
|
| [12] |
胡伟.水泥混凝土路面三维数值分析及轴载换算[D].成都: 西南交通大学, 2005. HU Wei. Three-dimensional Numerical Analysis and Axel Load Conversion of Portland Cement Concrete Pavement[D].Chengdu: Southwest Jiaotong University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10613-2005110147.htm |
| [13] |
MH/T 5004-2010, 民用机场水泥混凝土道面设计规范[S]. MH/T 5004-2010, Specifications for Airport Cement Concrete Pavement Design[S]. |
| [14] |
郭稳厚.与机型相关的机场道面相对平整度分析理论研究[D].天津: 中国民航大学, 2015. GUO Wen-hou. Research on Theory of Pavement Relatively Roughness Related to Aircraft Type[D].Tianjin: Civil Aviation University of China, 2015. https://www.ixueshu.com/document/729081c2900b7a467d721b29bfac1625.html |
| [15] |
薛华鑫.飞机滑行状态下刚性道面振动频率响应分析[D].天津: 中国民航大学, 2014. XUE Hua-xin. Analysis on Vibration Frequency Response of Rigid Pavement under Aircraft Taxing Condition[D].Tianjin: Civil Aviation University of China, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10059-1015500306.htm |
| [16] |
周正锋, 凌建明. 基于ABAQUS的机场刚性道面结构有限元模型[J]. 交通运输工程学报, 2009, 9(3): 39-44. ZHOU Zheng-feng, LING Jian-ming. Finite Element Model of Airport Rigid Pavement Structure Based on ABAQUS[J]. Journal of Traffic and Transportation Engineering, 2009, 9(3): 39-44. |
| [17] |
雷亚伟.基于弯沉的道面结构分析系统研究[D].天津:中国民航大学, 2015. LEI Ya-wei. Research of Pavement Structure Analysis System Based on Deflection[D].Tianjin: Civil Aviation University of China, 2015. |
| [18] |
MH/T 5024-2009, 民用机场道面评价管理技术规范[S]. MH/T 5024-2009, Technical Specifications of Aerodrome Pavement Evaluation and Management[S]. |
 2019, Vol. 36
2019, Vol. 36
