扩展功能
文章信息
- 胡亚辉, 董皓, 张君安
- HU Ya-hui, DONG Hao, ZHANG Jun-an
- 整体式梯形转向机构最优区域值计算和优化
- Calculation and Optimization of Optimal Region Value of Integral Trapezoidal Steering Mechanism
- 公路交通科技, 2019, 36(1): 143-149
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 143-149
- 10.3969/j.issn.1002-0268.2019.01.020
-
文章历史
- 收稿日期: 2017-08-28
汽车转向机构的一个主要作用是在转向过程中保持汽车转向的姿态,使得车轮按照一定的角度偏转,为衡量汽车舒适性、操控稳定性提供重要指标。优良的转型机构能使车轮按照一定的关系偏转,大大降低车轮的磨损程度,对汽车的操控性起到很好的保障。很多研究者已经在转向机构优化设计方面做过较多的研究,也形成了一套较为详细的理论,但这些理论研究工作还不完善,因此对转向机构的优化设计完善很有必要。在现有的理论基础上对汽车的梯形转向机构的优化,能够对汽车的生产实践起到指导作用。
国内外许多学者对整体式梯形转向机构的优化设计进行了大量的研究。文献[1]提出了不同于以往的目标优化函数,并与传统的目标函数进行了对比。文献[2]通过对汽车转向系统中的转向梯形机构进行数学建模,得出了整体式转向梯形模型的内、外轮转角的曲线关系,求解得到较好的结果。文献[3]对车辆转向机构的尺寸和定位参数进行优化,进而有效改善了车辆的操纵性能和转向安全性。文献[4]推导出了梯形机构的连杆输入角与输出角计算公式,建立了汽车梯形转向机构优化设计数学模型。文献[5]提出了理想梯形的概念,通过用理想转向梯形横拉杆与实际转向机构横拉杆的偏差作为优化目标,验证了用长度单位作为转向梯形机构校核的评判依据。文献[6]提出了以转角误差平方和的平方根最小为目标的优化目标函数。文献[7]根据阿克曼转角几何原理及前轮定位参数变化规律,用多目标优化方法建立复合加权惩罚函数对转向机构进行了优化设计。文献[8]基于多目标优化理论的综合目标函数,认为优化后,转向机构的综合性能得到明显提高。文献[9-10]建立了梯形转向机构数学模型,以外侧车轮转向角的理想值与实际值的误差作为目标函数进行优化。文献[11]建立了转向拉杆机构空间运动学方程,优化出连杆长度和初始位置。文献[12]针对大学生方程式赛车高速和赛道的特点,设计了一种满足比赛需要且结构简单的赛车转向系统。文献[13]以非独立悬架结构为例,建立空间几何模型进行运动分析,提出了同时满足“与前悬架运动协调”和“左右转向力均匀”两方面要求的转向梯形驱动机构优化设计方法。文献[14-15]以运动精度作为目标,对重型卡车梯形转向机构进行了优化。文献[16]分析了内外转向角间的关系,对转向梯形机构进行了优化。文献[17]以转向角作为输出,揭示了各构件的数学关系。文献[18]以内外车轮转向角与理想转角误差最小最为优化目标并进行了试验验证。以往的研究中给定的优化目标函数以车轮实际转角与理想阿克曼转角曲线误差最小来达到优化梯形机构的目的。然而,传统的目标函数并不能充分说明汽车运动过程瞬心位置的偏差,因此不能更好地判定汽车转向系统的灵活性和良好的操控,也不能充分说明整体式梯形转向机构的工作特性。
因此,本研究在以角度误差为目标函数的基础上,进一步提出以汽车实际瞬心位置与阿克曼瞬心位置的误差为优化目标函数,通过对汽车瞬心位置的确定,更能反映汽车在行驶过程中瞬心位置偏离满足阿克曼定理的理想曲线情况,从而弥补以角度为目标函数的不足。通过建立优化数学模型,采用数值试验法,得到整体式梯形转向机构全局最优解区域。全局最优值组成了一条平面的直线区域带,可以直接在最优解域里寻找最优的机构杆长,大大简化了整体式梯形转向机构的优化与设计。
1 转向机构的数学模型建立为了使梯形结构由弹性变化引起的复杂情况得到简化,需要汽车模型作简化处理[6]。假定:(1)刚性轮胎,忽略弹性轮胎侧偏角对转向梯形的影响;(2)转向梯形为平面运动结构,忽略前后轮定位参数空间结构的影响。阿克曼理论转向特性是全部车轮都必须绕同一个瞬时中心点做圆周纯滚动,而且转向内轮与外轮的转角应满足关系式:
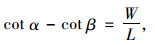
|
(1) |
式中,α和β分别为转向轮的内侧轮转角和外侧车轮转角;W为转向轮销轴延长线与地面交点间的距离;L为汽车轴距。
若以车轮左转动为例,其中α为自变角,根据实际则可以梯形机构推导出因变角度β的数学期望表达式:
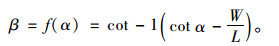
|
(2) |
式(2)是建立在理想的转向梯形机构上的。在实际问题中,梯形机构一旦确定,在车辆转向时,内侧车轮不能严格按照阿克曼转向理论偏转,故会存在误差,只能近似地满足该理论。
按照转向时四连杆机构中的三角形关系推导出实际的因变角度β*:
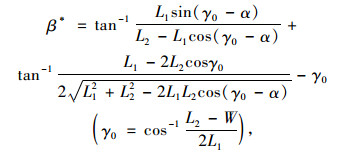
|
(3) |
式中,L1为梯形机构的节臂长度;γ0为梯形机构的底角;L2为梯形机构的拉杆长度;α和β*分别为内侧车轮的转角和外侧车轮的转角。
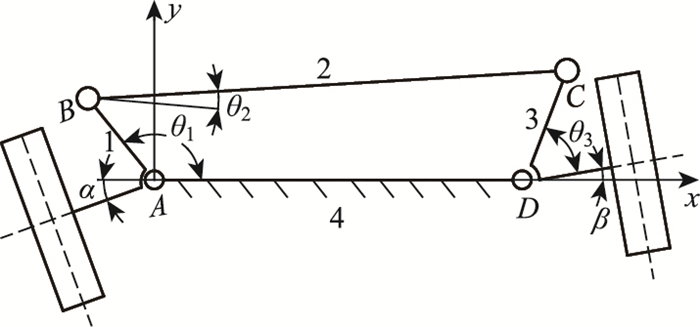
以瞬心位置误差作为目标函数,将四连杆机构简化为梯形机构,如图 1所示。
|
| 图 1 梯形转向机构示意图 Fig. 1 Schematic diagram of trapezoidal steering mechanism 1—梯形节臂L1; 2—转向机构横拉杆L2; 3—梯形节臂L3; 4—主销延长线与地面交点间距离W |
| |
假定以x轴正方向逆时针旋转为正方向,车辆进行左侧偏转,梯形左侧节臂与水平线的夹角为θ1,与初始状态位置相比其转角为α;右侧节臂与水平线的夹角为θ3,其转角为β。其方程的复数形式为:
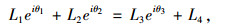
|
(4) |
式中L4即为前轮销轴的延长线与地面交点之间的距离W。
根据数学关系找出两侧节臂与水平线之间夹角θ1和θ3的关系:
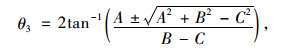
|
(5) |
式中,A=2L1sin θ1;B=2L1L3cos θ1-2L3L4;C=L22-L12-L32-L42+2L1L4cos θ1。
再对梯形四连杆机构进行优化,其中梯形左、右侧节臂长度分别为L1和L3,且L1= L3;横拉杆长度为L2;前轮销轴的延长线与地面交点间的距离为W。
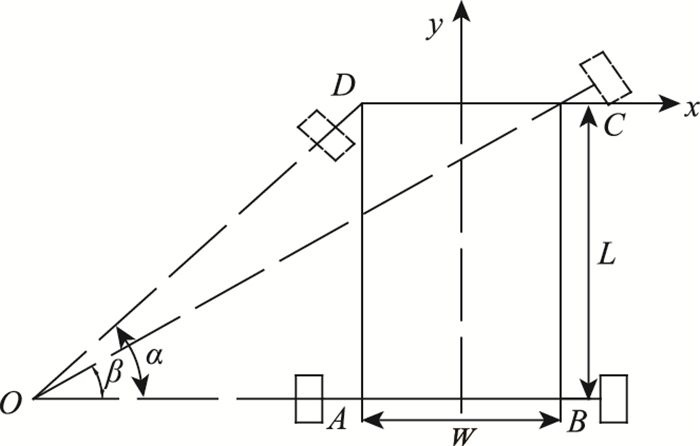
车辆坐标系如图 2所示。选取汽车前轴外车轮方向为x轴正方向;汽车纵向中心线前方为y轴正方向;O点为理想转向瞬心点;前后轮距为L;建立坐标系后得到简化后汽车模型的几个坐标点:A(-w/2, -L),B(w/2, -L),C(w/2, 0),D(-w/2, 0)。
|
| 图 2 车辆坐标系 Fig. 2 Vehicle coordinate system |
| |
车轮转弯时瞬时转向中心为瞬心,其瞬心位置坐标为P(x0,y0),表示为:
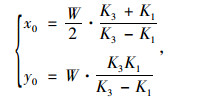
|
(6) |
式中,K1=tan(θ1+γ0);K3=tan(θ3-γ0)。
由于实际存在的梯形机构在转弯时不能严格按照阿克曼转向原理转向,会使转向瞬心在阿克曼转向曲线上下附近波动,使得转向瞬心与理想的转向瞬心有误差,在选取优化目标函数时可考虑将瞬心误差作为优化指标,使得汽车在转弯时有很好的操控性,尽量避免车轮滑动,以减小车轮摩擦、延长使用寿命。
汽车转弯时瞬心位置距离车比较远,体现为瞬心的横坐标绝对值较大。为了满足上述要求,尽量减小瞬心在阿克曼转向瞬心曲线附近的上下波动,即瞬心点在车辆坐标系中平行于x轴且过A和D两点的直线附近波动,点A的纵坐标记为yA,选取目标函数为:
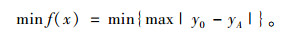
|
(7) |
对于四连杆梯形转向机构,梯形节臂的长度尺寸和横拉杆尺寸一旦确定,则这个梯形就确定了。选择杆长进行优化能够直观反映梯形真实的尺寸大小,这里选取梯形的节臂及横拉杆长度作为优化参数,分别为x1和x2:
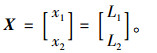
|
(8) |
根据一些现有的设计经验,在选取梯形节臂长度时,为了不至于因节臂太短造成横拉杆轴向力过大,通常对节臂有最小规定:L1≥0.11W;同时又考虑到不能使梯形机构尺寸过大造成机构繁重,通常对梯形节臂做最大规定:L1≤0.15W。由机械原理知道,四连杆机构在运动过程中,需要考虑传动角的变化情况,为了避免四连杆机构在运动过程中发生干涉,通常对传动角δ作相关规定:δ≥40°。
考虑到实际问题,转向轮左转时内侧车轮转角相对外侧车轮较大,车轮只有左转到极限位置时,四连杆机构的传动角最小,此时容易发生运动干涉,但是大多数时候转向都不会到极限位置,大多数转向角α取值都在10°~20°范围内,所以传动角绝大多数都会大于40°。
为使四连杆机构运动中避免此现象发生,根据设计经验,梯形的底角γ0一般取值在60°~80°之间,常取γ0=70°,根据式(3)中的γ0,可确定L2的范围:
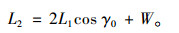
|
(9) |
杆长和传动角的关系为:
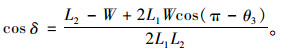
|
(10) |
对约束条件选取的变量X=[x1, x2]T=[L1, L2]T做以下约束:
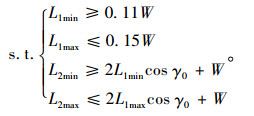
|
(11) |
选取某型号轿车的梯形机构进行优化计算,其轴距为L=2 650 mm,主销轴延长线与地面的交点间距离为W=1 430 mm,用图解法作关于四杆机构杆长度对误差影响的等值线图,从而探究全局最优解。
假定以式(8)作为瞬心误差云图的高H(x,y),L1和L2作为误差云图的因变量,其中:
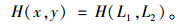
|
(12) |
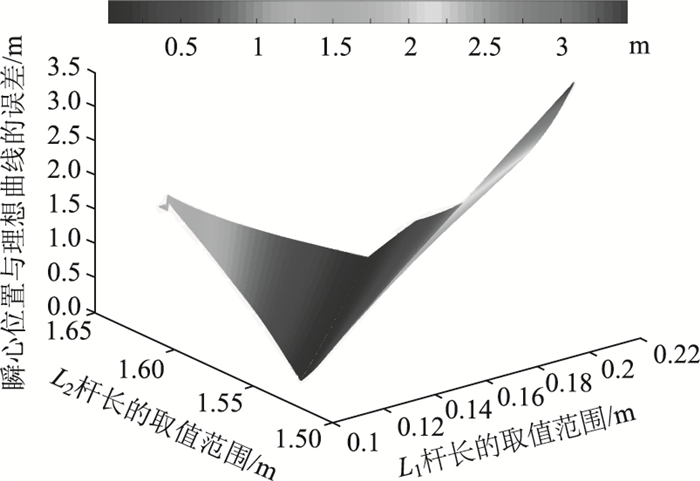
取杆长步长0.5 mm进行计算,得到误差云图,如图 3所示。
|
| 图 3 误差云图H(L1, L2) Fig. 3 Error nephogram H(L1, L2) |
| |
由图 3发现,该图形较为复杂,在图形的“谷底”存在误差最小值。在设定了四连杆机构的连杆长度尺寸后,即对待优化的两个变量L1和L2设定了可行域,两个扭曲的空间面相交在一起,构成云图的低谷区域。
为了探究“谷底”存在的杆长对瞬心位置的影响,得到图 4所示的“谷底”在x-z平面的投影曲线,发现瞬心误差的最大值不超过30 mm。
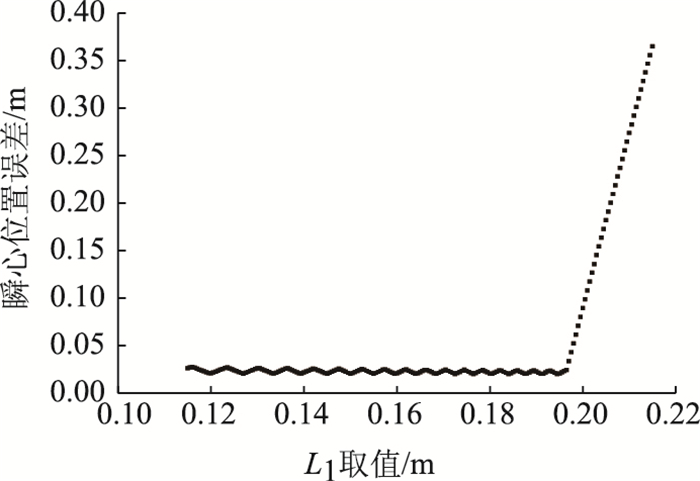
|
| 图 4 “谷底”在x-z平面的投影曲线 Fig. 4 Projection curve of "trough bottom" in x-z plane |
| |
由图 4看出,随着步长的细化,谷底区域几乎平缓,说明在这个平缓区域里杆长非常微小地变化,对瞬心位置的影响甚微,可以忽略。由图 4还发现,“谷底”平时为严格意义上的一条直线,原因在于计算时所取步长稍偏大于0.5 m,若想得到一条严格意义上的直线,则需要把步长设置得更小,但是考虑到实际情况,若把步长设置得太小必定增加计算量,对于工程问题的解决反而没有太大实际意义。
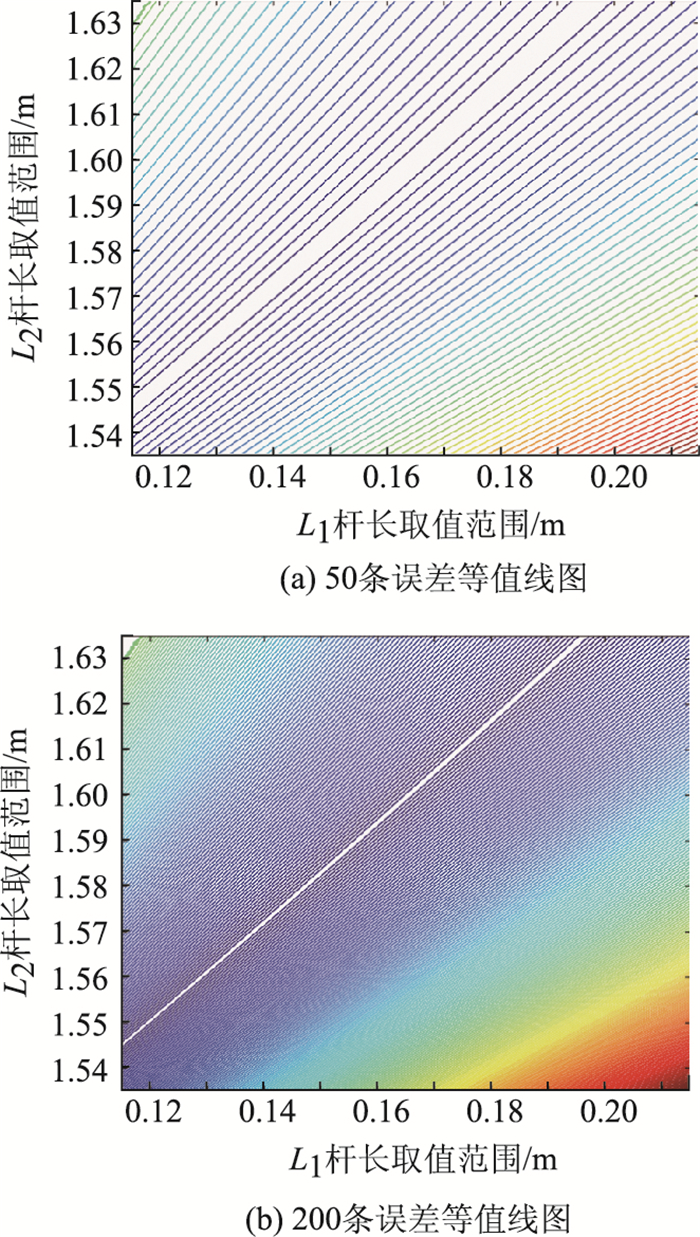
图 5分别给出了50条和200条误差等值线图。
|
| 图 5 等值线图 Fig. 5 Contour lines |
| |
由图 5(a)和5(b)可以看出,“谷底”是一条近似的直线带,并且“谷底”直线带由高度不超过25 mm的直线组成,这些等高线簇的高度表示的是瞬心位置与理想的阿克曼转向曲线的最大误差。一般轿车的转弯半径都在5 000~6 000 mm左右,此直线带上的等值线高度与汽车转弯半径相比微乎其微,几乎可以忽略。所以可认为在满足约束条件的情况下,在直线带区域内点的坐标值代表的杆长都是对L1和L2优化得到的最优值。
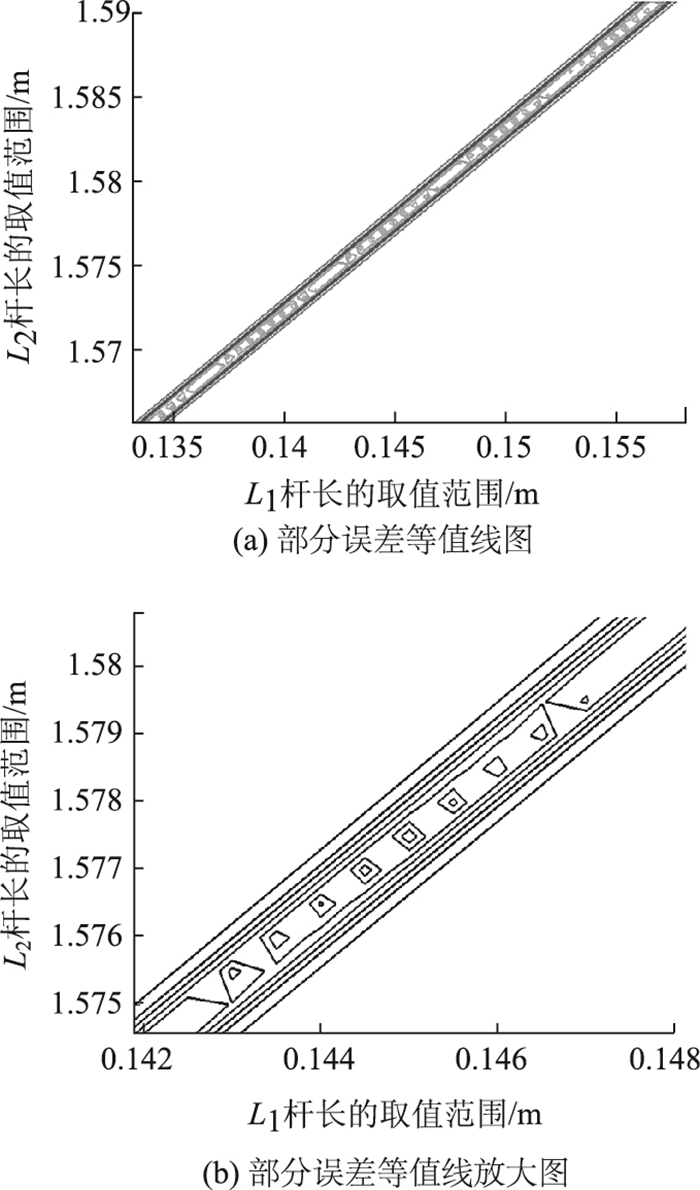
为保证瞬心位置误差能够达到最小状态,需要在“谷底”区域采集数据点,力图能使瞬心位置误差最小,在等值线20 mm与40 mm之间随机采集数据点,等值线图的梯度设置为2.5 mm,得到误差等值线图,如图 6所示。
|
| 图 6 “谷底”区域等值线图 Fig. 6 Contour map of "trough bottom" area |
| |
从图 6(b)发现,在“低谷”地区较为复杂,这一等值线簇的意义在于主销与地面交点距离及轴距确定后,在满足杆长要求的前提下,只要在次区域带选择梯形节臂长度尺寸和横拉杆长度尺寸即可,其瞬心误差最大值为40 mm。按照阿克曼转向原理的描述,车辆进行转向车轮做纯滚动时,转向瞬心在后轴延长线上。由于转向角的大小变化,导致转向半径几米或几十米甚至更大,优化后得到的瞬心误差最大值与转向半径相比,对车辆在转向时造成的位置偏差可以忽略,故可认为得到的结果是最优的。
| L1 | L2 |
| 0.143 0 | 1.575 3 |
| 0.143 5 | 1.575 9 |
| 0.144 2 | 1.576 5 |
| 0.145 1 | 1.577 8 |
| 0.146 0 | 1.578 6 |
| 0.146 7 | 1.579 4 |
| 0.147 3 | 1.580 1 |
| 0.148 0 | 1.580 9 |
| 0.148 7 | 1.581 6 |
| 0.149 6 | 1.582 6 |
| 0.150 6 | 1.583 8 |
| 0.151 6 | 1.584 9 |
| 0.152 6 | 1.585 9 |
| 0.153 7 | 1.587 1 |
| 0.154 6 | 1.588 1 |
| 0.155 6 | 1.589 2 |
| 0.156 5 | 1.590 2 |
| 0.157 3 | 1.591 0 |
| 0.157 9 | 1.591 7 |
| 0.158 7 | 1.592 7 |
| 0.160 1 | 1.594 0 |
| 0.160 9 | 1.595 1 |
| 0.161 5 | 1.595 6 |
| 0.161 9 | 1.596 2 |
| 0.162 6 | 1.597 0 |
| 0.163 2 | 1.597 8 |
| 0.163 9 | 1.598 5 |
|
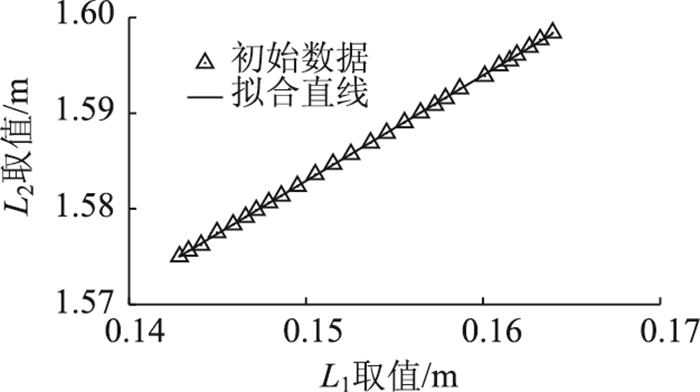
| 图 7 拟合直线 Fig. 7 Fitted straight line |
| |
图 7中,参数a,b分别为a=1.417 4,b=1.103 7,其中相关系数r=0.999 93,说明得到的初始数据有很强的线性关系。从等值线图中仅能看出一条直线带,而非严格意义上的直线,该条直线带上的瞬心误差为20~40 mm,由于最优区域是直线带,故在y轴方向的截距是一系列合适的值。最终得到直线带线性表达式(13):
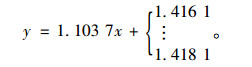
|
(13) |
为了检验上述方程,选取式(2)、式(7)代表的两种目标函数作为检验指标。选取某型号汽车作为验证,其轴距L=2.65 m,主销与地面交点的距离W=1.43 m。假设L1取0.153 3 m,将其代入式(13),得到的L2为1.587 4 m。随后分别得到如图 8所示的瞬心位置误差曲线和图 9所示的角度误差曲线。
|
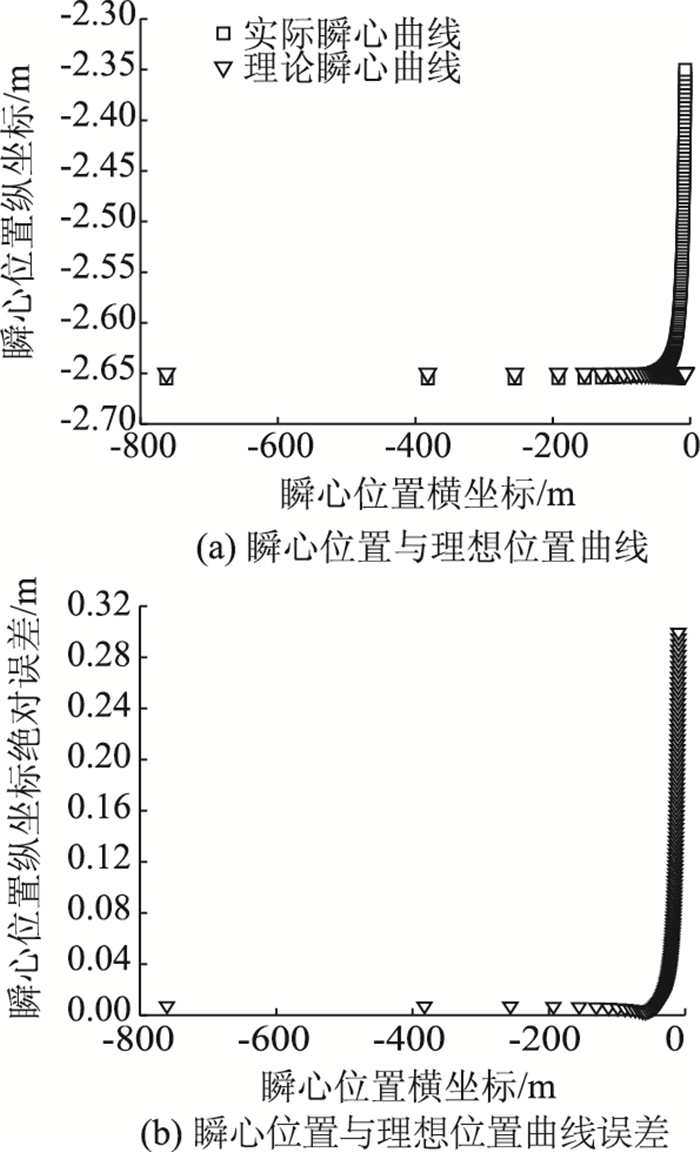
| 图 8 瞬心位置曲线 Fig. 8 Curve of instantaneous position |
| |
|
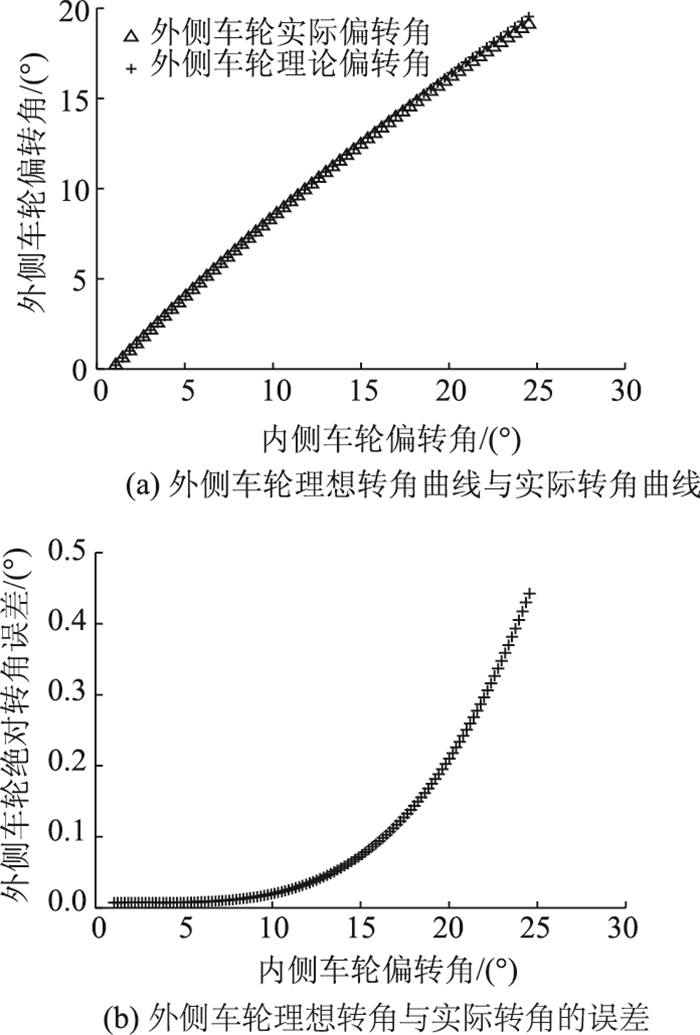
| 图 9 外侧车轮转角曲线 Fig. 9 Curve of outside wheel rotation angle |
| |
从图 8(a)中可以看出,实际瞬心位置在较远处与理想曲线误差较小。从图 8(b)可以看出,在瞬心半径较大时,最大误差比较小,与瞬心半径相比可以忽略。
从图 9(a)看出,转角误差也比较小。从图 9(b)看出,在内侧车轮转角为25°时,外侧车轮出现最大偏差0.45°,也是可以接受的。角度偏差造成的瞬心位置误差不超过40 mm,能够满足设计要求。
4 结论(1) 选取以瞬心位置作为目标函数能清晰定量地判定汽车转向的平稳性。
(2) 通过可视化图像法,能够直观反映梯形转向机构的杆长最优解不是唯一的,构成此最优解的是一条直线带区域。
(3) 瞬心位置误差在20~40 mm的范围内,且此范围内转角误差不超过1°,认为此误差区域内的杆长均为最优解。
最优解域直线带的发现对梯形的优化设计可起到一定的指导作用,为梯形转向机构的设计提供规范性的理论依据。
| [1] |
段亚斌, 董皓, 张君安. 四轮转向梯形机构优化设计及目标函数选取[J]. 汽车实用技术, 2017(14): 79-82. DUAN Ya-bin, DONG Hao, ZHANG Jun-an. Optimum Design of Four Wheel Steering Trapezium and Selection of Objective Function[J]. Automobile Technology, 2017(14): 79-82. |
| [2] |
杜文建, 徐忠四. 基于最小值优化的汽车转向梯形机构优化设计[J]. 机械工程与自动化, 2014(4): 71-73. DU Wen-jian, XU Zhong-si. Optimal Design Based on Nonlinear Minimum Optimization Method for Vehicle Steering Trapezium[J]. Mechanical Engineering & Automation, 2014(4): 71-73. |
| [3] |
刘岭, 闫光荣, 雷毅, 等. 基于改进粒子群算法的车辆转向梯形机构优化[J]. 农业工程学报, 2013, 29(10): 76-82. LIU Ling, YAN Guang-rong, LEI Yi, et al. Optimization Design of Steering Trapezoid Mechanism Based on an Improved Particle Swarm Optimization[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(10): 76-82. |
| [4] |
罗中华, 沈璐瑶, 李奕锋. 汽车梯形转向机构的优化设计[J]. 机械, 2017, 44(12): 41-44. LUO Zhong-hua, SHEN Lu-yao, LI Yi-feng. Optimal Design of Automobile Trapezoid Steering Mechanism[J]. Machinery, 2017, 44(12): 41-44. |
| [5] |
张君, 李恩科, 王伟, 等. 汽车理想转向梯形的研究与横拉杆的优化[J]. 机械设计, 2015(3): 41-45. ZHANG Jun, LI En-ke, WANG Wei, et al. Research on Ideal Steering-trapezium of Vehicle and Optimization for Tie-rod[J]. Journal of Mechanical Design, 2015(3): 41-45. |
| [6] |
张辉, 黄伟. 基于MATLAB的转向梯形机构优化设计[J]. 科协论坛(下半月), 2013(12): 241-242. ZHANG Hui, HUANG Wei. Optimization Design of Turning Trapezoidal Mechanism of MATLAB[J]. Science & Technology Association Forum, 2013(12): 241-242. |
| [7] |
王海涛, 陈哲明. 汽车转向机构仿真及优化设计[J]. 计算机仿真, 2013, 30(3): 162-165, 200. WANG Hai-tao, CHEN Zhe-ming. Simulation and Optimal Design of Automobile Steering Mechanism[J]. Computer Simulation, 2013, 30(3): 162-165, 200. |
| [8] |
姜立标, 刘坚雄, 程铖. 基于正交试验的矿用自卸车转向机构优化设计[J]. 中国机械工程, 2013, 24(15): 2036-2041. JIANG Li-biao, LIU Jian-xiong, CHENG Cheng. Optimization Design of Mining Dump Truck Steering Mechanism Based on Orthogonal Test[J]. China Mechanical Engineering, 2013, 24(15): 2036-2041. |
| [9] |
孔江生, 吴炳胜, 张清年. 轿车转向梯形优化曲线的MATLAB解[J]. 公路交通科技, 2005, 22(7): 139-142. KONG Jiang-sheng, WU Bing-sheng, ZHANG Qing-nian. The Car Turning Trapezium Optimization Curve Simulated with MATLAB[J]. Journal of Highway and Transportation Research and Development, 2005, 22(7): 139-142. |
| [10] |
方志刚, 过学迅, 汪斌, 等. 整体式转向梯形机构优化[J]. 北京汽车, 2010(6): 39-42. FANG Zhi-gang, GUO Xue-xun, WANG Bin, et al. Optimization of Integral Steering Trapezoidal Mechanism[J]. Beijing Automotive Engineering, 2010(6): 39-42. |
| [11] |
查云飞, 钟志华, 闫晓磊. 菱形车转向机构的分析与优化[J]. 中国机械工程, 2010, 21(8): 935-939. ZHA Yun-fei, ZHONG Zhi-hua, YAN Xiao-lei. Analysis and Optimization of Steering Mechanism for Rhombic Vehicle[J]. China Mechanical Engineering, 2010, 21(8): 935-939. |
| [12] |
朱发旺, 尉庆国. 转向梯形机构的设计及优化[J]. 内燃机与配件, 2015(3): 6-10. ZHU Fa-wang, WEI Qing-guo. Design and Optimization of Steering Trapezium[J]. Internal Combustion Engine & Parts, 2015(3): 6-10. |
| [13] |
李玉民, 李旭宏, 过学迅. 转向梯形驱动机构的运动分析及优化设计[J]. 公路交通科技, 2004, 21(8): 124-128. LI Yu-min, LI Xu-hong, GUO Xue-xun. Kinematics Analysis and Optimal Design of Driving Mechanisms of Ackerman Steering Linkage[J]. Journal of Highway and Transportation Research and Development, 2004, 21(8): 124-128. |
| [14] |
ZHANG L, DONG E, XING Y. Steering Trapezoid Mechanism Design Based on Monte Carlo Method[C]//International Conference on Electronic and Mechanical Engineering and Information Technology. Harbin: IEEE, 2011: 2337-2339. https://ieeexplore.ieee.org/document/6023578
|
| [15] |
GUO H, YANG X, CHENG L, et al. Notice of Retraction Reliability-based Robust Optimization of Steering Mechanism of Trucks by Using Evidence Theory[C]//International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering. Harbin: IEEE, 2013: 505-508. https://ieeexplore.ieee.org/document/6625633
|
| [16] |
王志杰.矿用自卸车转向机构优化设计与仿真研究[D].广州: 华南理工大学, 2013. WANG Zhi-jie. Simulation and Optimization of Mining Dump Truck Steering Mechanism[D]. Guangzhou: South China University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10561-1013317530.htm |
| [17] |
古玉锋, 吕彭民, 单增海, 等. 转向杆系空间结构非线性建模与分析[J]. 农业机械学报, 2014, 45(10): 7-14. GU Yu-feng, LÜ Peng-min, SHAN Zeng-hai, et al. Spatial Structural Nonlinear Modeling and Analysis of Steering Linkage[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(10): 7-14. |
| [18] |
史天泽, 王登峰, 陈书明, 等. 基于6σ稳健性的电动汽车断开式转向梯形优化设计[J]. 吉林大学学报:工学版, 2016, 46(3): 700-705. SHI Tian-ze, WANG Deng-feng, CHEN Shu-ming, et al. Robustness Optimization of Divided Steering Linkage for Electric Vehicles Based on 6σ Design[J]. Journal of Jilin University:Engineering and Technology Edition, 2016, 46(3): 700-705. |
 2019, Vol. 36
2019, Vol. 36
