扩展功能
文章信息
- 姚志洪, 蒋阳升, 王逸, 赵斌, 谭宇
- YAO Zhi-hong, JIANG Yang-sheng, WANG Yi, ZHAO Bin, TAN Yu
- 基于动态规划的信号配时滚动优化算法
- A Traffic Signal Timing Rolling Optimization Algorithm Based on Dynamic Programming
- 公路交通科技, 2019, 36(1): 124-130
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 124-130
- 10.3969/j.issn.1002-0268.2019.01.017
-
文章历史
- 收稿日期: 2017-08-23
2. 西南交通大学 综合交通大数据应用技术国家工程实验室, 四川 成都 610031
2. National Engineering Laboratory of Application Technology of Integrated Transportation Big Data, Southwest Jiaotong University, Chengdu Sichuan 610031, China
随着城市社会经济的发展,城市交通愈发拥堵。中国科学院可持续发展战略研究组的研究成果表明,包括北京、上海在内的15个大、中城市每天因交通拥堵造成的经济损失早在2012年就已经接近10亿元人民币[1]。来自中国交通运输部的统计数据资料显示,我国每年由于交通拥堵造成的经济损失占国内生产总值的5%左右。交通拥堵发生时,道路上车辆的平均时速基本在15 km/h以下[2]。而信号控制作为缓解交通拥堵的主要途径之一,发挥着其重要的作用。早在150多年前首次提出了信号控制方法。随着150年的发展,现如今的控制方法主要分为:定时控制、感应控制和自适应控制。
定时控制方法基于交叉口历史流量数据,采用延误模型计算获得交叉口的信号配时方案,其基本假设为在控制期间交叉口的交通需求保持不变,并未考虑实际应用中交通流的波动性。感应控制其基本原理是在交叉口停车线上游设置检测器,通过检测车辆到达调整相位的绿灯时间,其一定程度上解决了固定信号配时的不足;但其基于简单的判断规则,没有优化能力。而自适应控制则是在预测交通需求的基础上,采用优化模型优化交叉口的信号配时方案,最大程度上减少交叉口的延误或排队长度。现有的自适应控制系统[3-4]主要有:澳大利亚的SCATS[5]、英国的SCOOT[6]、法国的PRODYN[7]、意大利的UTOPIA[8]、美国的OPAC[9]、法国的CRONOS[10]和美国的RHODES[11]等。
而在自适应控制系统中,优化算法作为自适应控制系统中不可或缺的部分,起着至关重要的作用。目前自适应控制系统中优化算法可分为以下几类[12]:动态规划算法[13-15],遗传算法[16-17],神经网络[18-19],模糊控制算法[20-21]等。其中动态规划算法应用较为广泛,如自适应控制系统PRODYN[7],UTOPIA[8],OPAC[9]和RHODES[11]中均采用动态规划算法作为其核心优化算法。在RHODES系统中,优化算法为基于动态规划和全数枚举搜索的优化算法;2015年Feng等[14]在其基础上提出了基于双环信号结构的动态规划信号配时优化算法。但其均未考虑优化期间预测流量的时变特征,即预测区间越长,预测效果越差。因此,基于此优化的信号配时方案往往效果不够理想。
随着智能交通技术的发展,预测数据的时间粒度逐渐变小[3]。因此,如何充分利用更细颗粒度的预测数据优化交叉口的信号配时方案是当前研究热点方向之一。为解决COP算法中优化期间未考虑预测区间车流数据动态变化的特性,充分利用更加精细的预测数据,文中提出了基于动态规划的信号配时滚动优化算法。该算法以动态规划算法为基础,引入滚动优化策略。根据实时更新的预测车流数据滚动优化交叉口的信号配时方案,使信号配时方案能适应交叉口的动态车流特征。本研究第2部分为信号配时优化算法。第3部分在实际调查数据的基础上构建仿真环境,对比分析了文中算法和COP算法的控制效果。最后为结论和未来研究方向。
1 信号配时优化算法以典型的四路交叉口为例,根据信号配时手册[22]和Synchro软件手册中的国际交叉口相位定义标准,在不考虑右转车流的情况下,通常一个四路交叉口分为4个方向的左转和直行相位,共8个相位。其中主干路和次干路用栅格隔开,如图 1所示。信号配时优化算法[13]基于预测的到达车辆数量优化交叉口各相位的绿灯时间。其中包括两个层面的优化,上层为采用动态规划算法的思路优化各个相位组的时间,下层为优化每个相位组中相位的绿灯时间的整数优化模型。以下将具体讨论这两层模型算法。
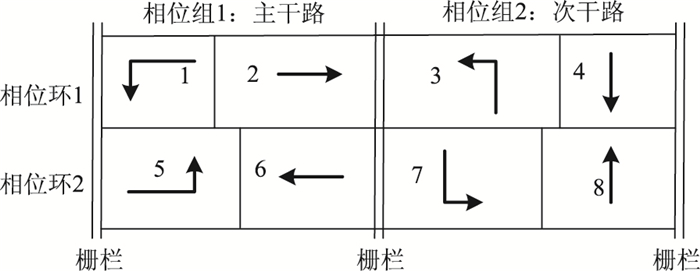
|
| 图 1 交叉口基础相位环图 Fig. 1 Diagram of intersection basic phrase ring |
| |
1.1 动态规划算法
上层模型为动态规划模型,可采用动态规划算法求解。如图 2所示。其中文中与动态规划相关的符号和含义如表 1所示。
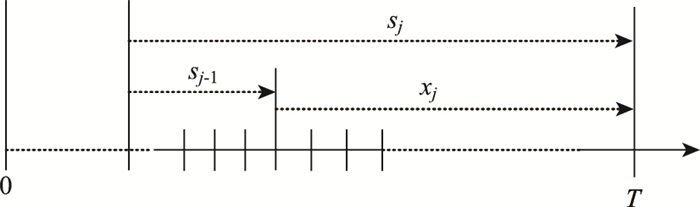
|
| 图 2 动态规划状态、决策变量、离散时间长度示意图 Fig. 2 Relationship among state, decision variable, total number of discrete time-steps |
| |
| 符号 | 含义 |
| p | 相位环和相位组中对应的相位编号,每个相位环和相位组中均有两个相位,所以其取值为1, 2。 |
| r | 相位环编号,取值为1, 2。 |
| j | 动态规划中阶段,与图 1中的相位组编号对应。 |
| J | 动态规划停止时对应的阶段。 |
| xj | 状态j决策变量,表示对应相位组的时间长度。 |
| sj | 状态变量,表示到相位组j的总的离散时间长度。 |
| Sj | 状态变量sj的可能取值。 |
| T | 总的优化时间长度。 |
| Xj(sj) | 给予状态变量sj时控制变量xj的取值集合。 |
| fj(sj, xj) | 给予状态变量sj和控制变量xj时,阶段j的费用(延误或排队)值。 |
| vj(sj) | 开始到阶段j的累计费用(延误或排队)值。 |
| Rr, p | 相位环r中相位p的清空时间,包括黄灯时间和全红时间。 |
| Gr, pmin | 相位环r中相位p的最小绿灯时间。 |
| Gr, pmax | 相位环r中相位p的最大绿灯时间。 |
| Xjmin | 阶段j的最小时间长度,即相位组的最小时间长度。 |
| Xjmax | 阶段j的最大时间长度,即相位组的最小时间长度。 |
| gr, p | 相位环r中相位p的绿灯时间。 |
从图 1可知,当给定每个相位的最小绿灯时间、最长绿灯时间和相位清空时间后,其中,当该相位没有交通需求时,这些参数均可取0。因此,可计算各个阶段(相位组)的最小和最大可能时间长度,即动态规划中决策变量的取值,计算公式如式(1)、式(2)所示。
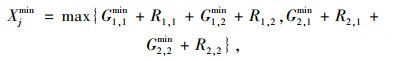
|
(1) |
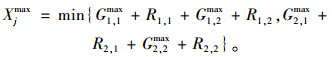
|
(2) |
在获得各个阶段(相位组)的取值后,可计算得出动态规划算法中各个阶段的状态变量取值集合。计算公式如式(3)所示。
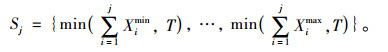
|
(3) |
同时,给定状态变量sj,可计算得到该条件下的决策变量取值范围,计算公式如式(3)~式(5)所示。
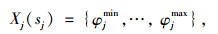
|
(4) |
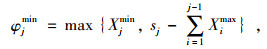
|
(5) |
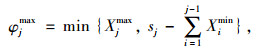
|
(6) |
式中,φjmin和φjmax分别为Xj(sj)集合的最小和最大可能取值。
在得到动态规划算法中相关关键变量取值范围后,可采用前向递归计算获得最优目标函数值,然后采用后向递归获得最优目标函数条件下各个阶段的决策变量取值。其中前向递归和后向递归算法如下。
1.1.1 前向递归算法Step 1:令j=1,sj-1=0,vj(0)=0;
Step 2:根据式(3)计算状态变量集合Sj;
Step 3:遍历方法取集合Sj中状态变量sj;
Step 4:根据式(4)计算给予状态变量sj时控制变量的取值集合Xj(sj);
Step 5:计算vj(sj)=minxj{fj(sj, xj)+vj-1(sj-1)|xj∈Xj(sj)},并记录最优取值xj*(sj);
Step 6:判断集合Sj是否遍历完,若是,转到Step 7,否则转到Step 3;
Step 7:如果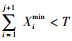
Step 1:令j=J,sj*=T;
Step 2:计算sj-1*=sj*-xj*(sj*);
Step 3:判断j>1是否成立,若成立,令j=j-1,否则结束算法。
1.2 整数优化模型在动态规划算法的前向递归算法Step 5中,需要计算每个阶段的费用值fj(sj, xj),即给定sj和xj,在该阶段费用值(延误或者排队)最小时,各个相位组内相位的最优绿灯时间长度。因此下层是一个整数优化模型,决策变量为相位组(动态规划中的阶段)中相位的绿灯时间长度,目标函数为延误或者排队长度最小。其中延误和排队长度可表示为:
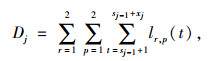
|
(7) |

|
(8) |
式中,Dj和Qj均可表示fj(sj, xj),分别为第j个阶段的总延误和总排队长度;lr, p(t)为第r个环中第p个相位t时刻的排队车辆数;其中sj-1=sj-xj。
各个相位t时刻的排队长度又与前一时刻(t-1)的排队长度、当前时刻的到达车辆数和离去车辆数有关,因此,可由式(9)计算获得。

|
(9) |
式中,ar, p(t)和dr, p(t)分别为第r个相位环中第p个相位t时刻的到达车辆数和离去车辆数。
离去车辆数同时跟当前相位是否为绿灯和离去饱和流率有关,具体计算如式(10)所示。
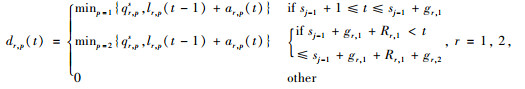
|
(10) |
式中,第1个条件为当前时刻处于第1相位时,该相位的离去车辆数为饱和流率与上一时刻排队车辆数与当前时刻到达车辆数之和的最大值;同理,第2个条件为第2相位绿灯开启时离去车辆的计算条件;第3个条件为2个相位均为红灯或清空时间时,无离去车辆。
同时,各个相位的绿灯时间需要满足最小绿灯、最大绿灯时长和总时长约束,具体如式(11)~式(12)所示。
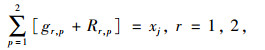
|
(11) |
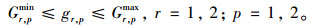
|
(12) |
式(11)为相位组总时长约束,式(12)为相位的最小、最大绿灯时长约束。
因此,下层模型整体上为一个整数优化问题,优化模型如式(13)所示。

|
(13) |
式中,N*为正整数集合。
由式(13)可知,该模型的决策变量为各个相位的绿灯时长,为整数变量,即模型为一个整数规划模型。同时,目标函数为交叉口总延误最小或排队长度最小,可根据实际情况选择对应的控制目标。如流量较小时,选择交叉口总延误最小作为控制目标;流量较大时,可选择排队长度最小作为优化目标。该模型可采用LINGO或者MATLAB中自带的函数求解。
1.3 滚动策略在文献[13-14]中,虽然提出采用动态规划算法去求解信号配时优化模型中,但其并未提及滚动优化。实际应用时,车辆到达预测是实时变化的,即需要根据实时预测的车辆到达数据来动态优化信号配时方案;且随着智能交通技术的发展,预测数据的粒度进一步精细化,这给滚动优化提供了良好的数据条件。文中的滚动思路为,每运行完一个相位组,重新对信号配时方案优化一次。滚动优化示意图如图 3所示。

|
| 图 3 滚动优化示意图 Fig. 3 Schematic diagram of rolling optimization |
| |
由图 3可知,假设每次优化2个相位组(实际最优结果可能不是2个相位组,跟预测区间的长度和动态规划算法的最终优化结果有关),则第1次优化的相位组顺序为相位组1和相位组2;当相位组1运行完后,马上进行第2次优化,此时优化的相位组顺序与第1次相反。依次类推,每运行完1个相位组,马上根据最新的预测数据重新进行一次新的优化。
2 实例分析为证明文中算法的有效性,在实际调查数据的基础上构建微观仿真环境。首先在成都市选取合适的交叉口,该交叉口与周围信号控制交叉口距离均大于1 km,适合单交叉口自适应控制,如图 4所示。现场调查收集交叉口的几何尺寸、车流量、渠化情况和车流转向比例等信息。图 4中交叉口为测试算法交叉口,不考虑右转车流,仅控制该交叉口8个相位的车流。根据调查结果在Vissim中构建仿真路网,仿真路网的相关数据均由调查获得。

|
| 图 4 调查路网图 Fig. 4 Diagram of investigated road network |
| |
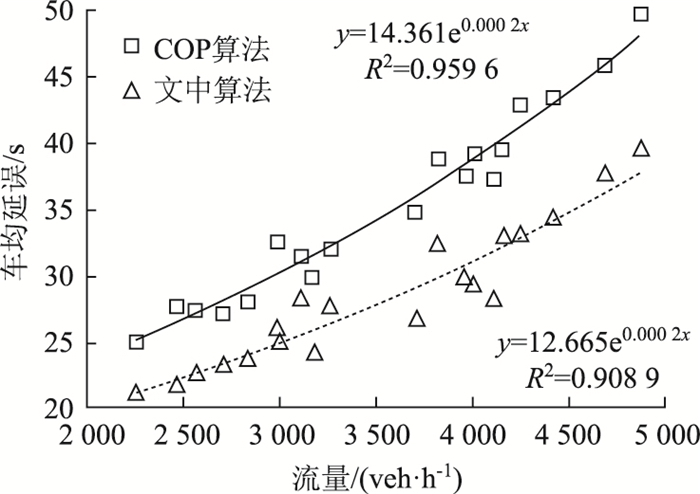
在Vissim中构建仿真路网,采用预测方法对交叉口各个方向的车辆到达进行预测。然后根据预测交通流到达分布采用文中算法对信号配时方案进行优化,再将优化结果实时反馈到VISSIM中实现实时控制。为证明文中算法的控制效果,以车均延误为评价目标,将文中算法和COP算法进行比较分析。通过改变路网输入流量,多次仿真不同流量状态下文中算法和COP算法的交叉口车均延误。2种算法的控制车均延误对比图如图 5所示。
|
| 图 5 文中算法与COP算法效果对比图 Fig. 5 Comparison of calculation results between proposed algorithm and COP algorithm |
| |
由图 5可知,两种算法车均延误与交叉口流量的拟合曲线R2均在0.9以上。这表明车均延误随着交叉口流量呈现指数增长趋势,这与实际情况相符,但文中算法比COP算法效果更好。与COP算法相比,不同流量状态下交叉口的控制延误减少了20%。证明了文中算法适用于各种交通流状态,且均比COP算法控制效果要好。
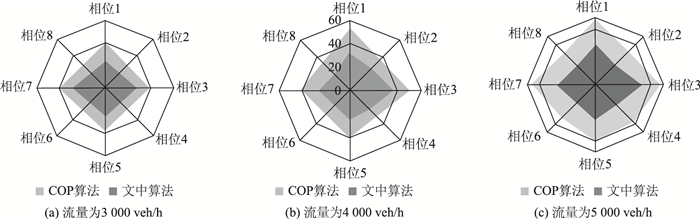
同时,为比较两种控制算法在不同交通流状态下各个相位的车均延误,分别分析了交叉口流量为3 000, 4 000和5 000 veh/h的情况下各个相位的车均延误值,如图 6所示。同时为比较各个相位延误均衡,可计算各个转向的延误标准差值,计算结果如表 2所示。
|
| 图 6 不同流量状态下各个相位车均延误对比图 Fig. 6 Comparison of average vehicle delay of each phase in different traffic volumes |
| |
| 流量/(veh·h-1) | COP算法/s | 文中算法/s |
| 3 000 | 5.85 | 4.07 |
| 4 000 | 7.52 | 5.84 |
| 5 000 | 7.44 | 6.13 |
从图 6可知,文中算法各个相位的车均延误均比COP算法要小。同时根据表 2可知,与COP算法相比,文中算法各个相位的延误的标准差较小,说明文中模型不仅能够优化交叉口的车均延误,还能够保证各个相位的延误均衡。
3 结论为解决COP算法中优化期间未考虑预测区间车流数据动态变化的特性,充分利用细时间颗粒度预测数据,文中提出基于动态规划的单交叉口信号配时滚动优化算法。通过实际调查数据和仿真分析,可得出以下结论:
(1) 在整个交叉口层面,文中算法比COP算法控制延误更小,平均车均延误减少了20%;
(2) 在交叉口相位层面,与COP算法相比,文中算法更能保证各个相位的车均延误均衡。
由于文中采用的滚动优化为基于相位组,即每运行完一个相位组对交叉口的信号配时进行优化一次。滚动优化时间粒度较大,未来可在本研究基础上研究滚动时间粒度更小的滚动优化算法。同时,可考虑研究多交叉口存在相互影响时的协同优化模型。
| [1] |
中国科学院. 2015中国可持续发展报告[M]. 北京: 科学出版社, 2015. Chinese Academy. China Sustainable Development Report 2015[M]. Beijing: Science Press, 2015. |
| [2] |
叶宝林.城市路网交通信号协调控制理论与方法研究[D].杭州: 浙江大学, 2015. YE Bao-lin. Research on Traffic Signal Coordination Control Theories and Methods in Urban Road Networks[D]. Hangzhou: Zhejiang University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015305313.htm |
| [3] |
姚志洪, 蒋阳升, 韩鹏, 等. 基于神经网络的小时间粒度交通流预测模型[J]. 交通运输系统工程与信息, 2017, 17(1): 67-73. YAO Zhi-hong, JIANG Yang-sheng, HAN Peng, et al. Traffic Flow Prediction Model Based on Neural Network in Small Time Granularity[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1): 67-73. |
| [4] |
姚志洪, 沈旅欧, 巫威眺, 等. 基于行程时间分布的异质交通流车队离散模型[J]. 中国公路学报, 2016, 29(8): 134-142, 151. YAO Zhi-hong, SHEN Lü-ou, WU Wei-tiao, et al. Heterogeneous Traffic Flow Platoon Dispersion Model Based on Travel Time Distribution[J]. China Journal of Highway and Transport, 2016, 29(8): 134-142, 151. |
| [5] |
SIMS A G, DOBINSON K W. The Sydney Coordinated Adaptive Traffic (SCAT) System Philosophy and Benefits[J]. IEEE Transactions on Vehicular Technology, 1980, 29(2): 130-137. |
| [6] |
HUNT P B, ROBERTSON D I, BRETHERTON R D, et al. SCOOT: A Traffic Responsive Method of Coordinating Signals, LR 1014 Monograph[R]. Crowthorne: Road Research Laboratory, 1981. https://trid.trb.org/view.aspx?id=179439
|
| [7] |
HENRY J J, FARGES J L, TUFFAL J. The PRODYN Real Time Traffic Algorithm[C]//The 4th IFAC/IFIP/IFORS Conference. Baden-Baden: Elsevier, 1984: 305-310. https://www.sciencedirect.com/science/article/pii/S1474667017625771
|
| [8] |
DONATI F, MAURO V, RONCOLINI G, et al. A Hierarchical-decentralized Traffic Light Control System. The First Realisation:"Progetto Torino"[J]. IFAC Proceedings Volumes, 1984, 17(2): 2853-2858. |
| [9] |
GARTNER N H. OPAC:Strategy for Demand-responsive Decentralized Traffic Signal Control[J]. IFAC Proceedings Volumes, 1990, 23(2): 241-244. |
| [10] |
BOILLOT F, MIDENET S, PIERRELÉE J C. The Real-time Urban Traffic Control System CRONOS:Algorithm and Experiments[J]. Transportation Research Part C:Emerging Technologies, 2006, 14(1): 18-38. |
| [11] |
MIRCJANDANI P, HEAD L. A Real-time Traffic Signal Control System:Architecture, Algorithms, and Analysis[J]. Transportation Research Part C:Emerging Technologies, 2001, 9(6): 415-432. |
| [12] |
ASTHANA R, AHUJA N J, DARBAARI M, et al. A Critical Review on the Development of Urban Traffic Models and Control Systems[J]. International Journal of Scientific and Engineering Research, 2012, 3(1): 1-6. |
| [13] |
SEN S, HEAD K L. Controlled Optimization of Phases at an Intersection[J]. Transportation Science, 1997, 31(1): 5-17. |
| [14] |
FENG Y, HEAD K L, KHOSHMAGHAM S, et al. A Real-time Adaptive Signal Control in a Connected Vehicle Environment[J]. Transportation Research Part C:Emerging Technologies, 2015, 55: 460-473. |
| [15] |
PRIEMER C, FRIEDRICH B. A Decentralized Adaptive Traffic Signal Control Using V2I Communication Data[C]//International IEEE Conference on Intelligent Transportation Systems. Louis: IEEE, 2009: 1-6. https://ieeexplore.ieee.org/document/5309870
|
| [16] |
何兆成, 曾伟良. 变权系数遗传算法在交叉口信号控制中的应用[J]. 公路交通科技, 2011, 28(11): 121-125. HE Zhao-cheng, ZENG Wei-liang. Genetic Algorithm Based on Variable Weighting Coefficient and Its Application in Traffic Signal Control[J]. Journal of Highway and Transportation Research and Development, 2011, 28(11): 121-125. |
| [17] |
CEYLAN H, BELL M G H. Traffic Signal Timing Optimisation Based on Genetic Algorithm Approach, Including Drivers' Routing[J]. Transportation Research Part B:Methodological, 2004, 38(4): 329-342. |
| [18] |
南天伟, 敖梦雅, 魏丽英. 基于模糊神经网络的城市干道信号协调控制[J]. 公路交通科技, 2012, 29(1): 145-149. NAN Tian-wei, AO Meng-ya, WEI Li-ying. Traffic Signal Coordination for Urban Arterial Roads Based on Fuzzy Neural Network[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 145-149. |
| [19] |
SAITO M, FAN J Z. Artificial Neural Network-based Heuristic Optimal Traffic Signal Timing[J]. Computer-aided Civil and Infrastructure Engineering, 2000, 15(4): 293-307. |
| [20] |
杨文臣, 张轮, 张孟, 等. 城市交通信号三级模糊滑动优化控制方法[J]. 同济大学学报:自然科学版, 2014(12): 1846-1853, 1867. YANG Wen-chen, ZHANG Lun, ZHANG Meng, et al. Rolling-horizon Optimization-based Threestage Fuzzy Logic Controller for Urban Traffic Signals[J]. Journal of Tongji University:Natural Science Edition, 2014(12): 1846-1853, 1867. |
| [21] |
TRABIA M B, KASEKO M S, ANDE M. A Two-stage Fuzzy Logic Controller for Traffic Signals[J]. Transportation Research Part C:Emerging Technologies, 1999, 7(6): 353-367. |
| [22] |
URBANIK T, TANAKA A, LOZNER B, et al. Signal Timing Manual[M]. Washington, D.C.: Transportation Research Board, 2015.
|
 2019, Vol. 36
2019, Vol. 36
