扩展功能
文章信息
- 张诗波, 刘澜, 李平飞, 王琰, 肖凌云
- ZHANG Shi-bo, LIU Lan, LI Ping-fei, WANG Yan, XIAO Ling-yun
- 事故再现复合形优化算法及其应用
- A Complex Optimization Algorithm for Accident Reconstruction and Its Application
- 公路交通科技, 2019, 36(1): 117-123
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 117-123
- 10.3969/j.issn.1002-0268.2019.01.016
-
文章历史
- 收稿日期: 2017-08-07
2. 西华大学 汽车与交通学院, 四川 成都 610039;
3. 中国标准化研究院, 北京 100191
2. School of Automobile and Transportation, Xihua University, Chengdu Sichuan 610039, China;
3. China National Institute of Standardization, Beijing 100191, China
事故再现是基于事故的各种信息(例如当事人及证人笔录、事故现场道路状况、车体痕迹、人体损伤、路面痕迹、监控录像、行车记录装置等),运用数学与物理原理或利用相关计算机软件系统,对事故发生过程进行推演与印证,其核心问题是碰撞速度。早期事故再现的研究主要面向的是汽车安全设计,而进入新世纪以来,事故再现的研究已经扩展到了事故分析和鉴定领域,主要面向事故处理和事故成因分析。在具体的事故分析中,由于事故勘查人员认知能力、工具和仪器误差、事故终止状态变化等因素的影响,不可避免地会造成部分事故信息的不可准确测定,以致在事故再现中需要寻找一个最佳碰撞组合条件,使得计算或仿真结果与事故真实后果最大程度吻合或接近,而如何快速、准确地寻找到最佳碰撞组合条件,就是事故再现的优化问题。
最早提出事故再现优化问题的是奥地利的Moser和Hermann[1],由他们开发的事故仿真系统PC-Crash中的车车碰撞优化模块使用了线性算法、遗传算法和蒙特卡洛算法[2]。Dima等人[3]使用PC-Crash的优化工具进行了事故再现优化应用,并用监控视频数据进行了验证。Martins[4]提出了共轭方向法,Costin等人[5]提出了模拟退火法和单纯形法,Guan[6]提出在有限元事故再现优化中使用序列二次规划法,Brach等人[7]提出了非线性优化法。文献中使用较多的是遗传算法,比如Hasija[8],Paulo[9]和黄靖等[10]。孙杰等人[11]将遗传算法优化结合3D激光扫描技术和多刚体动力学应用于人车事故再现模拟与损伤分析中。李一兵等人[12]将事故再现优化问题简化成无约束非线性优化问题,并提出使用改进Gauss-Newton最小二乘法进行优化求解。李江等人[13]在事故再现优化中使用手工调整优化的方法。柴象海等人[14]利用蒙特卡洛法基于摩擦系数进行人车碰撞事故再现。申杰等人[15]提出以汽车碰撞速度或制动延迟时间为优化变量,以人体损伤为约束条件,行人和汽车的停止位置为目标函数,采用序列线性规划算法的优化方法。陈强等人[16]提出了一种基于蒙特卡洛法和随机加权法的改进蒙特卡洛算法。张雷等人[17]将神经网络优化法用于事故再现可靠性分析中。此外,文献中报道过的方法还有对分法、黄金分割法、插值法、最速下降法、牛顿法、共轭梯度法、禁忌搜索算法等。
可以看出,事故再现优化问题的研究在国内外都是一个研究热点,提出了较多算法。这些算法中,有些算法(如对分法和黄金分割法)只针对单变量的一维优化问题;有些算法(如牛顿法、共轭梯度法、最小二乘法等)需对目标函数进行求导,原理较为复杂,不能适用于计算机仿真情况下的事故再现优化;有些算法(如蒙特卡洛法、模拟退火法、遗传算法、禁忌搜索算法、神经网络法等)需要的计算量大,原理不易理解,只能依托计算机程序自动完成。在当前流行的利用事故仿真软件进行的事故再现实践中,优化变量的个数一般只有几个,对软件本身没有内置优化工具的事故再现优化则只能人工试凑,而软件本身内置有优化工具(比如PC-Crash)的事故再现效果也有可能不太理想。基于此,本研究提出一种面向优化变量个数较少(几个)、基于计算机事故仿真的人工调整优化方法,以适应不同事故形态下的事故再现优化需求。
1 复合形优化算法的提出事故再现优化是典型的多变量、多目标、非线性的优化问题,其目标函数一般为事故计算或仿真结果与事故后果(真值)的差值,而目标函数参数(优化变量)为碰撞条件参数,可用式(1)的数学形式描述:

|
(1) |
式中,X为n个优化变量组成的向量,X=[x1, x2, …, xn]T,sil和siu分别为优化变量xi的取值下限和上限;目标函数F(X)是由多个子目标函数{f1(X), f2(X), …, fp(X)}通过加权因子ωk建立起来的总目标函数,
事故再现的优化变量一般为车辆碰撞速度、碰撞角度、行人行走速度以及其他无法精确取值的碰撞前参数(如路面附着系数)等;目标函数和约束函数一般为碰撞参与方停止相对位置、车辆变形、行人抛距或人体损伤等,可根据具体事故的情况确定。Y′k(X)函数可以是显式数学表达式,也可以是隐式仿真模型。文中主要研究基于隐式仿真的事故再现优化问题,这种事故再现优化问题具有如下一些特点。
(1) 优化的目标函数和约束函数是优化变量的隐式函数,无法通过解析关系式显式地表示目标函数和约束函数,同时也很难求解它们的一次偏导。
(2) 事故仿真“正向迭代”流程与事故再现“反向推导”的要求之间存在矛盾,优化的实现需要反复改变仿真参数组合,进而通过比较仿真结果得到最优解。
(3) 事故再现对优化效率有较高的要求。事故碰撞过程仿真涉及高速冲击和长时间的运动分析,要求较小的积分时间步长和较长的仿真时间,需要尽可能控制优化的循环次数,减少优化的总耗时。
随着计算机仿真技术的发展,事故鉴定与分析越来越依赖事故碰撞计算机仿真。在具体的事故仿真建模中,大部分的碰撞条件参数值可以通过事故现场勘查确定,而不确定的参数值往往只有少数几个。在没有实现自动优化的事故仿真中,每组仿真参数值的改变一般只能通过手工调整,这要求优化算法须在最少迭代次数下最快地收敛,基于此,本研究提出将复合形算法应用于事故再现优化中。
2 复合形算法步骤复合形法是求约束优化问题的一种直接搜索算法,它是无约束最优化问题中单纯形法的推广,构思较为直观。复合形法是利用对简单几何图形各顶点的目标函数值作相互比较,在连续改变几何图形的过程中,逐步以目标函数值较小的顶点取代目标函数值最大的顶点,从而进行求优的一种方法[18]。所谓复合形是指n维空间En中具有n+1个以上的顶点组合而成的多面体,比如一维空间中的线段,二维空间中的三角形,三维空间中的四面体等。
复合形法所求解的约束最优化问题的数学形式为:

|
(2) |
式中,X为n个优化变量组成的向量;gi(X)为关于X的约束函数;aj和bj为常量。目标函数为f(X),终止限为ε1>0,ε2>0。
复合形法的迭代步骤如下:
Step1:构成初始复合形
在n维空间中选初始点(离最优点越近越好),从X0出发,沿各坐标方向以步长t移动得k(k≥n)个顶点Xi,i=1, 2, …, k,这样选择顶点可保证向量组X1-X0, X2-X0, …, Xk-X0线性无关。否则,就会使搜索范围局限在较低维的空间内,有可能找不到极小点。在各坐标方向可以移动不同的距离。
各坐标方向上的初始步长可以根据各变量的情况任意指定,或利用随机数生成。各个顶点应该满足约束条件,若不满足,则重新生成。
Step2:计算各顶点的函数值
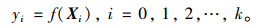
|
(3) |
比较各函数值的大小,确定最好点XL、最差点XH和次差点XG,即:
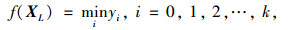
|
(4) |

|
(5) |
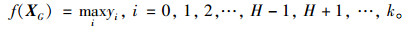
|
(6) |
Step 3:计算XH之外各点的“重心”
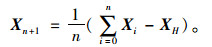
|
(7) |
求出反射点Xn+2=2Xn+1-XH。
Step 4:当f(Xn+2)<f(XL)时,需要扩张,令:
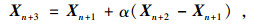
|
(8) |
如果f(Xn+3)<f(Xn+2),则以Xn+3代替XH形成一新复合形;否则,以Xn+2代替XH构成新复合形,然后转Step 8。
Step 5:当f(XL)≤f(Xn+2)≤f(XG)时,以Xn+2代替XH构成新复合形,然后转Step 8。
Step 6:当f(XG)≤f(Xn+2)≤f(XH)时,则需要收缩,即令:
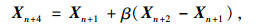
|
(9) |
以Xn+4代替XH得新复合形,并转Step 8。
Step 7:当f(Xn+2)≥f(XH)时,令:
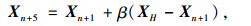
|
(10) |
如果f(Xn+5)≥f(XH),则将复合形缩边,可将向量Xi-XL的长度缩小一半,即:
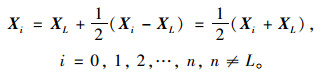
|
(11) |
这样可得一新复合形。否则就以Xn+5代替XH得新复合形。然后转Step 8。
Step 8:收敛性检验
每次迭代得到新复合形后,即应进行收敛性检验,如满足收敛指标,则迭代停止,XL即为所求的近似解。否则,继续进行迭代计算。通常所用的收敛准则是:
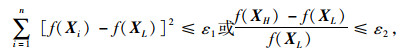
|
(12) |
式中ε1和ε2为预先给定的允许误差。
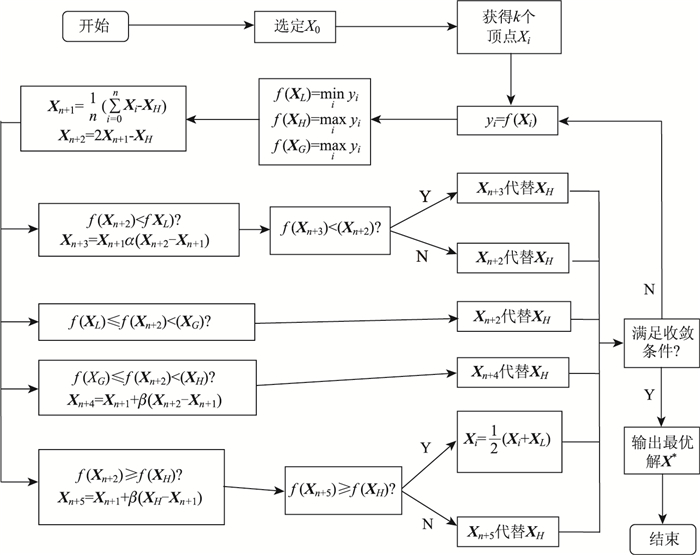
图 1为复合形优化算法的流程图。
|
| 图 1 复合形算法流程图 Fig. 1 Flowchart of complex algorithm |
| |
3 应用案例 3.1 案情简介
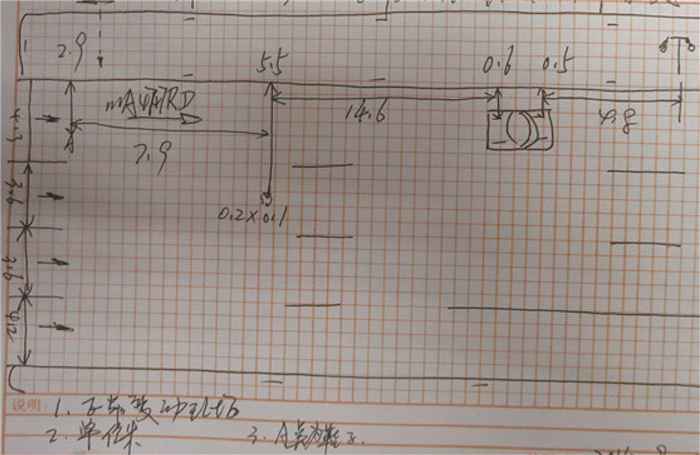
2014年9月22日22时许,在成都市南三环二段主道北侧,一行人在横穿道路时与一红色轿车发生碰撞,行人送医无效后死亡,轿车第一时间停在了原车道内(见图 2)。事故现场遗留有行人的血迹和左鞋,位于轿车后方,距离轿车后轴的距离为14.6 m,22.5 m,轿车后方路面没有制动拖印痕迹(见图 3)。根据事故处理的需要,需要对该事故进行事故再现,分析轿车在事故碰撞时的行驶速度。

|
| 图 2 案例事故现场照片 Fig. 2 Scene photo of case accident |
| |
|
| 图 3 交警绘制的事故现场图(局部) Fig. 3 Accident scene drawing by police (partial) |
| |
本案例事故再现的难点在于:现场痕迹信息无法确定碰撞点具体位置,以致不能确定行人的被抛距离和车辆的制动距离,而现场痕迹中的人车停止纵向相对距离(14.6 m)不仅与碰撞速度强度相关,还与车辆制动强度有很大关系。
3.2 仿真建模通过现场勘查,可以获取事故相关的车辆、行人、道路环境、车辆受损、行人伤情、现场痕迹等信息,可以认为事故的碰撞对应关系及过程为:轿车右前部与行人左侧碰撞,行人小腿与轿车右侧前翼子板最先发生接触,之后行人身体倒向轿车发动机罩盖,其左膝上部至左髋部与右前大灯下方发生碰撞,头部、左肩部与前风窗玻璃右侧边缘和右后视镜发生碰撞,最后行人被抛出落地。
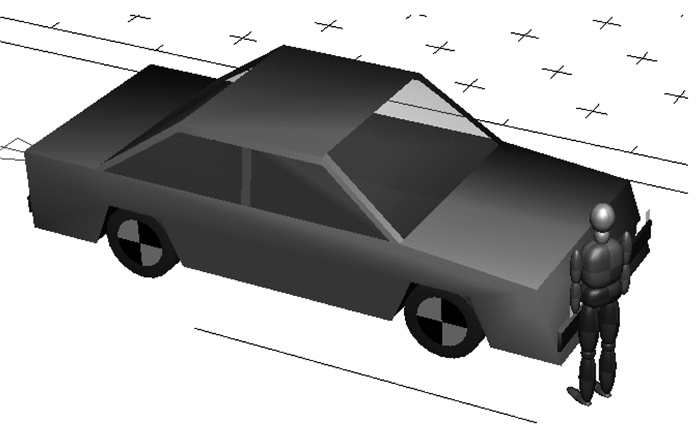
仿真模型构建平台采用多刚体建模系统PC-Crash软件。导入事故现场平面图,选择并设置好行人和车辆多刚体模型的相关参数,调整好碰撞对应关系,设置好车辆制动序列,即完成该起事故的仿真模型构建(见图 4)。
|
| 图 4 事故碰撞仿真模型 Fig. 4 Simulation model of impact accident |
| |
3.3 优化求解过程
由于碰撞对应关系可以确定,可以利用人车停止相对距离作为目标因素,将碰撞速度和车辆制动强度(由车辆纵滑附着系数修正值反映)作为优化变量。因此,本案中要求解事故车辆的碰撞速度,可以描述成如下形式的二维优化问题:
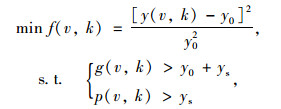
|
(13) |
式中,v和k为优化变量; v为车辆碰撞速度; k为车辆纵滑附着系数修正值;y0为事故现场行人终止位置与车辆终止位置(重心)的距离,y0=14.6+0.5×2.675=15.94 m;y(v, k)为通过仿真得到的行人终止位置与车辆终止位置(后轴)的距离,为关于v和k的隐式函数;ys为事故现场行人左鞋位置与行人终止位置的距离,ys=7.9 m;f(v, k)为目标函数,为人车终止位置之间距离的仿真值与现场测量值的差值;g(v, k)为通过仿真得到的车辆碰撞位置至停止位置的距离,为关于v和k的隐式函数;p(v, k)为通过仿真得到的行人碰撞位置至停止位置的距离,为关于v和k的隐式函数。
取v0=50 km/h, k0=0.8作为初始值X0=(50, 0.8),扩张因子α=2,压缩因子β=0.5,速度步长t1=2,系数步长t2=0.05,允许误差ε=0.000 1。按照复合形法的基本原理和算法步骤,通过表 1的6步迭代获得最优解v*=58.8 km/h,k*=0.55。
| 迭代次数 | XL | XH | XG | f(XL) | f(XH) | f(XG) | ξ | 收敛? |
| 0 | (52, 0.8) | (50, 0.85) | (50, 0.8) | 0.541 885 | 0.601 815 | 0.551 123 | — | — |
| 1 | (52, 0.8) | (53, 0.7) | (50, 0.8) | 0.541 885 | 0.321 813 | 0.551 123 | 0.048 52 | 否 |
| 2 | (53, 0.7) | (57.5, 0.65) | (52, 0.8) | 0.321 813 | 0.133 827 | 0.541 885 | 0.083 77 | 否 |
| 3 | (57.5, 0.65) | (58.8, 0.55) | (53, 0.7) | 0.133 827 | 0.000 022 | 0.321 813 | 0.053 24 | 否 |
| 4 | (58.8, 0.55) | (60.5, 0.55) | (57.5, 0.65) | 0.000 022 | 0.030 308 | 0.133 827 | 0.018 82 | 否 |
| 5 | (58.8, 0.55) | (58.5, 0.6) | (60.5, 0.55) | 0.000 022 | 0.023 813 | 0.030 308 | 0.001 48 | 否 |
| 6 | (58.8, 0.55) | (59.5, 0.562 5) | (58.5, 0.6) | 0.000 022 | 0.003 193 | 0.023 813 | 0.000 58 | 是 |
最优解v*=58.8 km/h,k*=0.55,f(v*, k*)=0.000 022,y(v*, k*)=16.01 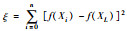 ,ε=0.000 1 ,ε=0.000 1 |
||||||||
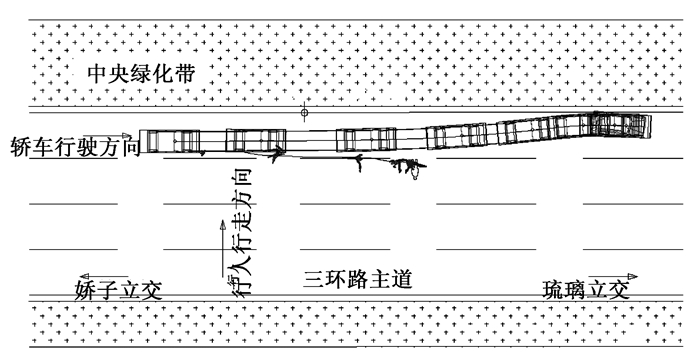
图 5为最优解的仿真结果平面图。
|
| 图 5 事故最优解PC-Crash仿真结果平面图 Fig. 5 PC-Crash simulation plane for accident optimum solution |
| |
3.4 验证
在案例事故的后期资料整理中,交警部门收集到了事发当时记录了事故碰撞发生过程的监控视频(见图 6)。通过对视频进行逐帧检验,在事故碰撞瞬间前10帧时间内,事故轿车的最前端从参考线A运动到参考线B,而参考线A和B对应的路面标线的长度为6.0 m。经过简单计算即可得事故轿车在碰撞前的平均速度约为64.8 km/h。考虑到事故车辆在碰撞前制动反应时间内会有一定的速度损失,因此可以认为基于PC-Crash仿真、利用复合形法优化算法求解出的最优解(58.8 km/h)与车辆实际的碰撞速度(略低于64.8 km/h)拟合度较高,优化方法可行。

|
| 图 6 案例事故监控视频画面(局部放大) Fig. 6 Surveillance video screens of case accident (partial enlarged) |
| |
4 结论
(1) 事故再现的优化实践中,在自动优化工具的效果还不太理想的情况下,人工调整仿真参数组合仍然是一种被广泛使用的方法,需要有方法论的指导才能更高效率、更准确地找到最佳的事故碰撞参数组合。
(2) 复合形优化算法作为一种直接搜索算法,构思较为直观,不需要对目标函数进行求导,对事故碰撞类型也没有限制,对优化变量个数较少的情形可以较为快速地得出最优解,适用于事故鉴定与分析实践中基于事故仿真的人工调整事故再现优化需求。
(3) 复合形优化算法的不足之处是当优化变量个数较多时,事故再现优化的求解效率较低。
| [1] |
MOSER A, STEFFAN H. Automatic Optimization of Pre-impact Parameters Using Post Impact Trajectories and Rest Positions, No. 980373[R]. Warrendale: SAE International, 1998. https://trid.trb.org/view.aspx?id=499593
|
| [2] |
MOSER A, STEFFAN H, SPEK A, et al. Application of the Monte Carlo Methods for Stability Analysis within the Accident Reconstruction Software PC-CRASH, No. 2003-01-0488[R]. Warrendale: SAE International, 2003. https://www.sae.org/publications/technical-papers/content/2003-01-0488/
|
| [3] |
DIMA D S, COVACIU D, CHIRU A. Validation of Simulation and Optimization Reconstruction in PC Crash with Video Recorded Sample[J]. Applied Mechanics & Materials, 2016, 822: 497-502. |
| [4] |
MARTINS G N, NETO M S. Optimization Techniques Applied to the Problem of Ground Vehicles Accidents Reconstruction, No.2005-04-4063[R]. Warrendale: SAE International, 2005.
|
| [5] |
UNTAROIU C D, MEISSNER M U, CRANDALL J R, et al. Crash Reconstruction of Pedestrian Accidents Using Optimization Techniques[J]. International Journal of Impact Engineering, 2009, 36(2): 210-219. |
| [6] |
GUAN F J, BELWADI A, HAN X, et al. Application of Optimization Methodology on Vehicular Crash Reconstruction[C]//Proceedings of the ASME International Mechanical Engineering Congress and Exposition 2009. New York: American Society of Mechanical Engineers (ASME), 2010: 567-573. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1643531
|
| [7] |
BRACH R M, MINK R A. Nonlinear Optimization in Vehicular Crash Reconstruction[J]. SAE International Journal of Transportation Safety, 2015, 3(1): 17-27. |
| [8] |
HASIJA V, TAKHOUNTS E G, RIDELLA S A. Computerized Crash Reconstruction of Real World Crashes Using Optimization Methodology[C]//Proceedings of the 21st(ESV) International Technical Conference on the Enhanced Safety of Vehicles. Washington, D. C.: National Highway Traffic Safety Administration, 2009. https://www.esteco.com/modefrontier/computerized-crash-reconstruction-real-world-crashes-using-optimization-methodology
|
| [9] |
FRANCISCO P. Simulation and Multi-objective Optimization of Road Traffic Accidents[D]. Lisbon: University of Lisbon, 2013.
|
| [10] |
黄靖, 金先龙, 亓文果, 等. 轨迹优化方法在道路交通事故再现中的应用[J]. 农业机械学报, 2005, 36(10): 38-41. HUANG Jing, JIN Xian-long, QI Wen-guo, et al. Application of Trajectories Optimization Method in Accident Reconstruction[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(10): 38-41. |
| [11] |
孙杰, 王涛, 李正东, 等. 基于3D激光扫描、多刚体重建和遗传算法优化的车-人碰撞事故再现模拟与损伤分析[J]. 法医学杂志, 2017, 33(6): 575-580. SUN Jie, WANG Tao, LI Zheng-dong, et al. Reconstruction of Vehicle-human Crash Accident and Injury Analysis Based on 3D Laser Scanning, Multi-rigid-body Reconstruction and Optimized Genetic Algorithm[J]. Journal of Forensic Medicine, 2017, 33(6): 575-580. |
| [12] |
李一兵, 裴剑平, 袁泉. 基于优化思想的事故再现碰撞模型研究[J]. 汽车工程, 2002, 24(4): 279-282. LI Yi-bing, PEI Jian-ping, YUAN Quan. A Study on Impact Models in Accident Reconstruction Based on Optimization[J]. Automotive Engineering, 2002, 24(4): 279-282. |
| [13] |
李江, 张大强, 吴建平, 等. 事故再现中对速度计算结果的调整[J]. 公路交通科技, 2003, 20(2): 104-107. LI Jiang, ZHANG Da-qiang, WU Jian-ping, et al. Optimization of the Result of Velocity Calculation in Traffic Accident Reconstruction[J]. Journal of Highway and Transportation Research and Development, 2003, 20(2): 104-107. |
| [14] |
柴象海, 金先龙, 张晓云, 等. 基于摩擦系数优化的车人碰撞事故再现研究[J]. 摩擦学学报, 2009, 29(2): 168-173. CHAI Xiang-hai, JIN Xian-long, ZHANG Xiao-yun, et al. The Friction Biomechanics Characteristic Analysis for the Car-pedestrian Collision Traffic Accident[J]. Tribology, 2009, 29(2): 168-173. |
| [15] |
申杰, 金先龙, 张晓云, 等. 汽车-行人碰撞事故再现自动优化方法[J]. 机械工程学报, 2009, 45(10): 266-271. SHEN Jie, JIN Xian-long, ZHANG Xiao-yun, et al. Automatic Optimization Method for Vehicle-pedestrian Collision Accident Reconstruction[J]. Journal of Mechanical Engineering, 2009, 45(10): 266-271. |
| [16] |
陈强, 赵航, 姚春德, 等. 一种改进的事故再现蒙特卡罗优化算法[J]. 中国安全科学学报, 2012, 22(5): 31-36. CHEN Qiang, ZHAO Hang, YAO Chun-de, et al. An Improved Accident Reconstruction Optimization Algorithm Based on Monte Carlo Simulation[J]. China Safety Science Journal, 2012, 22(5): 31-36. |
| [17] |
张雷, 梅冰松, 来剑戈, 等. 基于神经网络的冗余信息交通事故再现可靠性分析[J]. 公路交通科技, 2011, 28(2): 121-126. ZHANG Lei, MEI Bing-song, LAI Jian-ge, et al. Reliability Analysis of Traffic Accident Reconstruction with Redundant Information Based on Neural Network[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 121-126. |
| [18] |
郭科, 陈聆, 魏友华. 最优化方法及其应用[M]. 北京: 高等教育出版社, 2007. GUO Ke, CHEN Ling, WEI You-hua. Optimization Method and Its Application[M]. Beijing: Higher Education Press, 2007. |
 2019, Vol. 36
2019, Vol. 36
