扩展功能
文章信息
- 姜学鹏, 张红新, 景安
- JIANG Xue-peng, ZHANG Hong-xin, JING An
- 自然风对射流风机临界风速的影响
- Influence of Natural Wind on Critical Velocity of Jet Fan
- 公路交通科技, 2019, 36(1): 102-108
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 102-108
- 10.3969/j.issn.1002-0268.2019.01.014
-
文章历史
- 收稿日期: 2017-07-12
2. 湖北省工业安全工程技术研究中心, 湖北 武汉 430081;
3. 武汉科技大学 消防安全技术研究所, 湖北 武汉 430081
2. Industrial Safety Engineering Technology Research Center of Hubei Province, Wuhan Hubei 430081, China;
3. Fire Safety Technology Institute, Wuhan University of Science and Technology, Wuhan Hubei 430081, China
对于采用纵向通风隧道,临界风速是隧道排烟系统设计的重要参数。临界风速[1]是隧道中能够阻止烟气发生回流的最小纵向风速。
国内外学者对临界风速进行了诸多研究,Oka等[2]基于无量纲热释放速率提出了无量纲临界风速计算式。Wu等[3]采用隧道水力高度作为特征长度,对无量纲临界风速计算式进行了修正。Li等[4]提出了隧道横截面为特征的临界风速公式。Yi和Weng等[5-6]基于隧道坡度修正了临界风速计算式。Lee和Alva等[7-8]研究了隧道阻塞对临界风速的影响。然而前人研究临界风速问题时,未考虑隧道两端出口具有自然风,且自然风速与风向变化不定。当自然风向与纵向通风同向时,有助于抑制烟气逆流;反之,自然风利于热烟气的逆流,从而影响灭火救援及人员疏散。故隧道火灾发生后,需考虑自然风速与风向对临界风速的影响[9]。
考虑自然风速与风向对射流风机临界风速的影响,通过量纲分析及数值模拟,提出射流风机临界风速与自然风速、火源功率2个影响因素的无量纲计算公式,从而为现有的公路隧道通风排烟提供参考。
1 理论分析影响射流风机临界风速的因素[9-10]有:火源功率Q、空气密度ρ0、空气温度T0、空气定压比热容cp、重力加速度g、隧道几何尺寸、隧道坡度、自然风速V0。因水平隧道高宽比是定值,故隧道几何尺寸及坡度可忽略,只考虑隧道高度H[10]。射流风机临界风速Vc的影响因素表示为:
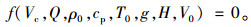
|
(1) |
Ji等[11]认为不存在任何联系的量纲即为所要研究的基本量纲。式(1)的8个物理量中,基本因次数为4,故选择4个基本物理量,即空气密度ρ0、空气温度T0、隧道高度H、重力加速度g。对应的量纲指数行列式不等于零,表明所选的基本物理量是相互独立的[12]。
式(1)中含有[M](质量)、[t](时间)、[L](长度)、[T](温度)4个基本量纲,8个物理量均可由这些基本量纲表示,则式(1)可变为:

|
(2) |
式中
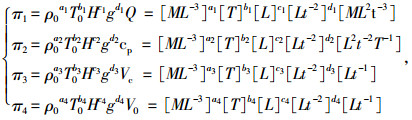
|
(3) |
式中an,bn,cn,dn均为变量系数。
根据相似理论,式(3)可变为:
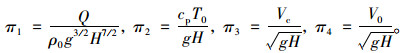
|
(4) |
由式(2)~(4)得:

|
(5) |
式中,Vc*为无量纲射流风机临界风速,
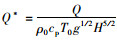

由式(5)表明Vc*取决于Q*和V0*,因此只需确定Vc*与Q*,V0*之间的关系,即可得到射流风机临界风速的无量纲计算公式。
2 数值模拟 2.1 FDS模拟设置采用FDS6[13]模拟隧道火灾,隧道尺寸依据Froude相似准则[14-16]:长度相似比CL=1: 20、时间相似比Ct= (Lm/Lp)1/2、速度相似比Cv= (Lm/Lp)1/2、火源功率相似比Cq= (Lm/Lp)5/2,其中Lm为模型隧道长度,Lp为实体隧道长度。模拟长度10 m、宽度0.6 m、高度0.3 m。墙体在FDS中设为“CONCRETE”属性。
温度测点设置:在距隧道顶板0.01 m高度处设置一系列热电偶,热电偶间距0.1 m。隧道环境气体温度和初始温度均为20 ℃。
射流风机设置:创建一个“0”厚度的障碍物“OBSTRUCTION”,障碍物的表面属性设置“VENT”来模拟射流风机[13]。射流风机直径为0.1 m,设在距离隧道一端出口2 m处。射流风机横向间距L1、射流风机边沿与隧道建筑限界间距L2均对射流风机通风效果有较大影响[17-19],结合规范[9]:L1不小于1倍风机直径, L2不小于0.15 m,根据相似准则L1取0.1 m,L2取0.01 m。
工况设置:选取5种火源功率[9, 20],共设置55组模拟工况,如表 1所示。火源位于隧道中心线上,火源尺寸为0.1 m(长)×0.1 m(宽)×0.06 m(高),整个燃烧过程中火源的热释放速率保持不变。隧道内安全疏散时间不宜小于900 s[21],故模拟运行时间设为200 s。隧道一端开口设置“OPEN”,另外一端设置“SUPPLY”,模拟自然风。根据相似准则得到对应的模拟自然风速约0.5 m/s,故模拟自然风速分别取0,±0.1,±0.2,±0.3,±0.4,±0.5 m/s,其中“+”表示自然风向与射流风机风向同向,“-”表示自然风向与射流风机风向反向(如图 1所示)。

|
| 图 1 隧道火灾模拟(单位:m) Fig. 1 Simulation of tunnel fire(unit:m) |
| |
| 编号 | 实体火源功率/MW | 模拟火源功率/kW | 自然风/(m·s-1) | |
| 同向 | 反向 | |||
| 1 | 5 | 2.8 | 0,-0.1, -0.2,-0.3, -0.4,-0.5 |
0,0.1, 0.2,0.3, 0.4,0.5 |
| 2 | 10 | 5.6 | ||
| 3 | 20 | 11.2 | ||
| 4 | 30 | 16.8 | ||
| 5 | 50 | 28.0 | ||
2.2 网格划分
FDS建模中的网格尺寸是影响计算结果精度的关键参数,其在1/16D*~1/4D*时精度较高[22]。

|
(6) |
式中,D*为火源特征直径;Q为火源功率;T0为环境温度,取T0=293 K;ρ0为空气密度,取ρ0=1.2 kg/m3;cp为空气的定压比热容,取1.02 kJ/ (kg·K);g为重力加速度,取g=9.81 m/s2。
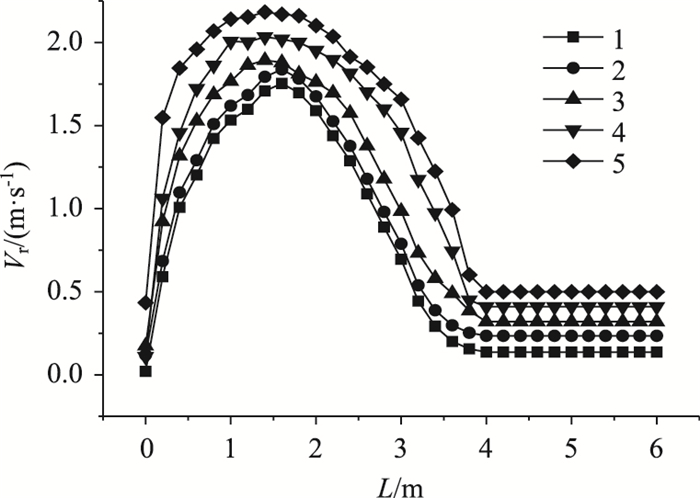
选取2.8 kW代入式(6)中计算得到合适的网格尺寸范围为0.01~0.03 m,网格划分见表 2。图 2显示火源功率为2.8 kW, 自然风速为0 m/s, 射流风机与火源纵向间距为6 m时,随着网格增加,隧道中心线顶棚附近速度Vr曲线逐渐重合。在射流风机与火源纵向间距L为4 m后,其速度逐渐稳定。结果表明,当网格尺寸为0.03 m×0.01 m×0.01 m时,Vr曲线与0.01 m×0.01 m×0.01 m时的Vr曲线基本一致,故网格尺寸选0.03 m×0.01 m×0.01 m。为保证模拟精度的一致性,5种火源功率均取相同的网格尺寸。
|
| 图 2 隧道中心线顶棚附近风速与纵向间距的关系 Fig. 2 Relationship between wind velocity near ceiling of tunnel centre line and longitudinal distance |
| |
| 编号 | x方向网格数/个 | y方向网格数/个 | z方向网格数/个 | 网格总数/个 | 网格尺寸/m |
| 1 | 1 200 | 70 | 40 | 3 360 000 | 0.01×0.01×0.01 |
| 2 | 600 | 70 | 40 | 1 680 000 | 0.02×0.01×0.01 |
| 3 | 300 | 70 | 40 | 840 000 | 0.03×0.01×0.01 |
| 4 | 600 | 35 | 20 | 420 000 | 0.02×0.02×0.02 |
| 5 | 300 | 24 | 14 | 108 000 | 0.03×0.03×0.03 |
2.3 临界风速确定方法
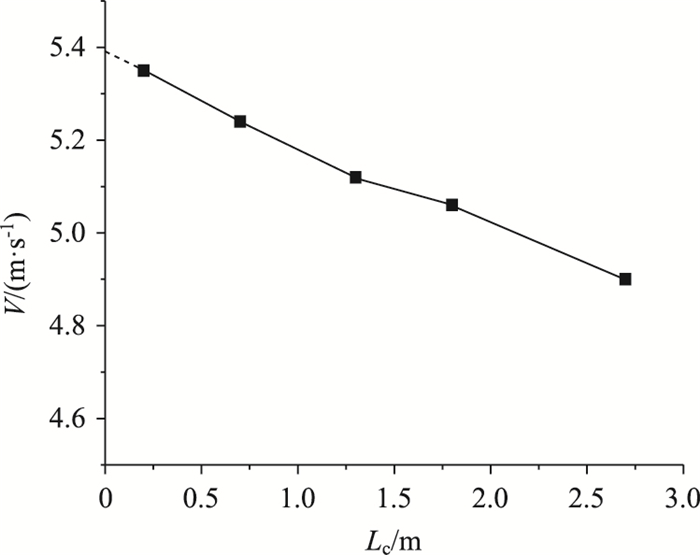
通过烟气逆流长度Lc与风速V曲线确定射流风机临界风速,烟气逆流长度为0 m时所对应的射流风机出口风速,即为临界风速,如图 3所示。随着与火源距离的增加,上游烟气的温度逐渐降低,并在某处温度陡降,该温度陡降处与火源之间的距离即为逆流长度[23-24]。因此,测量隧道顶板附近烟气的纵向温度变化,即可得到烟气逆流长度。
|
| 图 3 风速与烟气逆流长度的关系 Fig. 3 Relationship between wind velocity and smoke backlayering length |
| |
2.4 射流风机与火源纵向间距确定
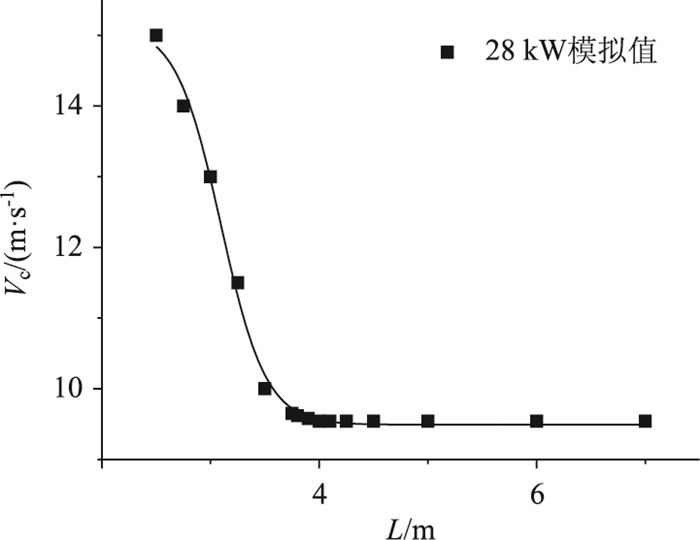
依据文献[25],火源附近风机应停止运行,由于射流风机与火源的纵向间距对隧道排烟影响较大[26],结合Kim等[27]射流风机与火源纵向间距较小时,由于射流风机靠近火源形成的二次流动区导致所需的临界风速增大的结论,故需确定合适的射流风机与火源纵向间距。图 4是火源功率为28 kW、自然风速为0 m/s时,射流风机临界风速Vc与射流风机到火源纵向距离L的拟合曲线,相关系数为0.995 3。Vc随着L增大,逐渐减少至一个常数;L=4 m时,Vc趋于稳定;L较小时,Vc较大。由于热浮力与射流风机出口气流惯性力的相互作用,当L很小时,火源上游流速被射流风机出口气流的惯性力所控制;当L达到一定时,气流的惯性力逐渐减少而热浮力逐渐增大,最终达到平衡状态[28]。最终将L确定为4 m。
|
| 图 4 临界风速与纵向间距的关系 Fig. 4 Relationship between critical wind velocity and longitudinal distance |
| |
3 结果与讨论 3.1 自然风向与射流风机风向同向
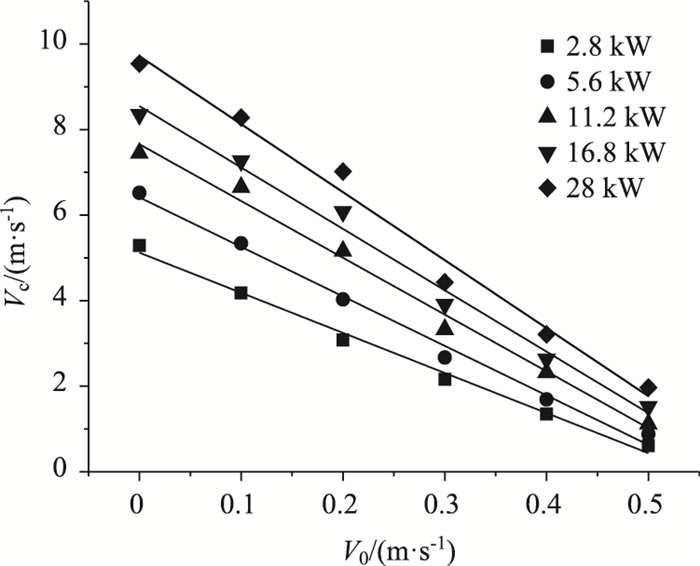
自然风向与射流风机风向同向时,在图 5中,随着自然风速从0 m/s增加到0.5 m/s,对应的射流风机临界风速呈下降趋势。火源功率越大,对应的临界风速下降趋势更显著。由于考虑自然风,射流风机风速与自然风速合流,隧道内部的气流增加,造成射流风机临界风速随着自然风速增大而减小。
|
| 图 5 临界风速与自然风速的关系 Fig. 5 Relationship between critical wind velocity and natural wind velocity |
| |
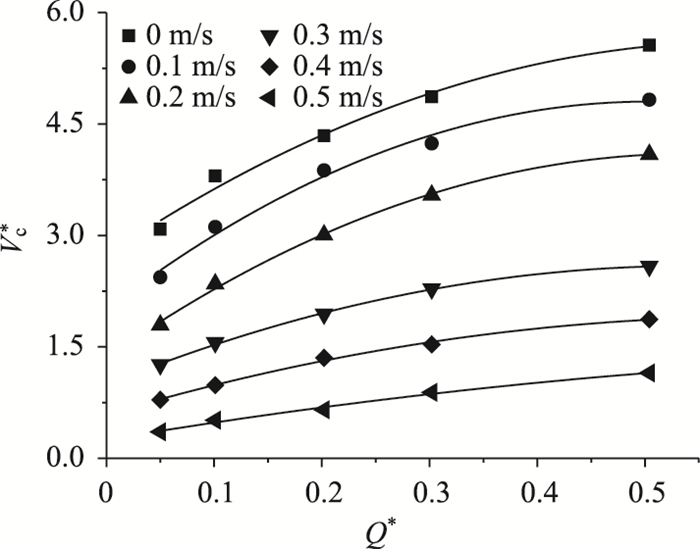
无量纲射流风机临界风速Vc*与无量纲火源功率Q*由式(5)得出。自然风向与射流风机风向同向时,如图 6所示,随着无量纲火源功率从0.05增加到0.504,对应的无量纲临界风速呈先快后慢的上升趋势。自然风速越大,其临界风速上升趋势更缓慢。
|
| 图 6 无量纲临界风速与无量纲火源功率的关系 Fig. 6 Relationship between dimensionless critical wind velocity and dimensionless fire source power |
| |
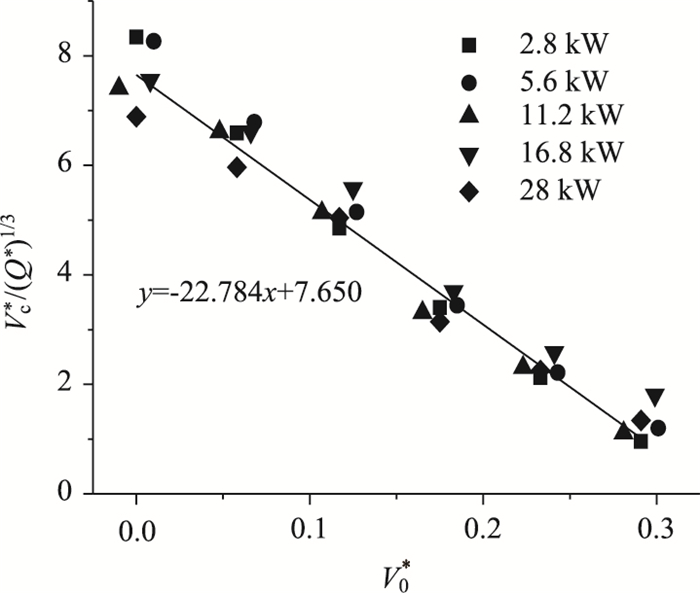
自然风向与射流风机风向同向时,系数Vc*/(Q*)1/3与无量纲自然风经线性拟合(图 7),其相关系数为0.980 3,拟合程度较高。得到无量纲射流风机临界风速的公式为:
|
| 图 7 系数与无量纲自然风速的关系 Fig. 7 Relalonship between coefficient and dimensionless natural wind velocity |
| |
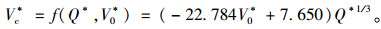
|
(6) |
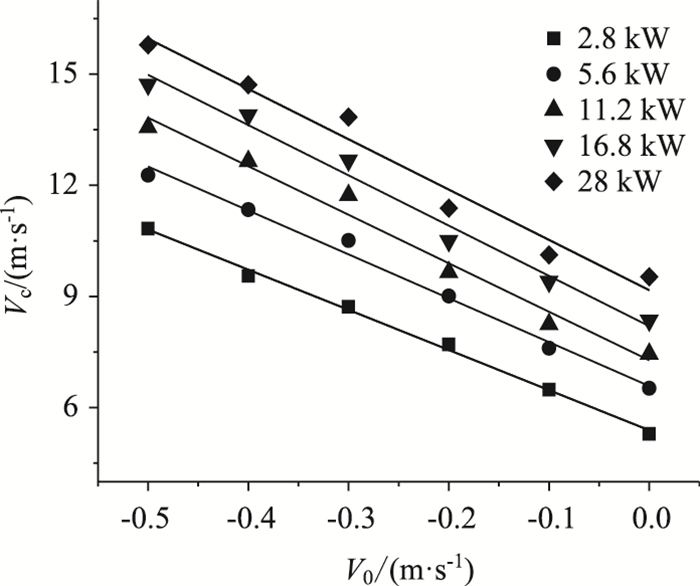
如图 8所示,自然风向与射流风机风向反向时,随着自然风速从-0.5 m/s到0 m/s,对应的临界风速呈下降趋势。由于考虑自然风,下游逆向烟流会受到自然风影响往上游移动,此时射流风机出口风速无法抑制下游烟流,导致所需的射流风机临界风速增大。
|
| 图 8 临界风速与自然风速的关系 Fig. 8 Relationship between critical wind velocity and natural wind velocity |
| |
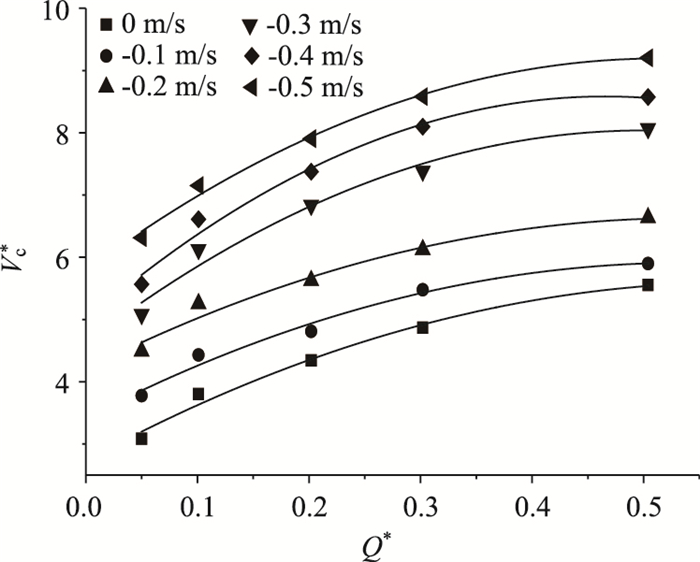
如图 9所示,自然风向与射流风机风向反向时,无量纲火源功率从0.05增加到0.504,对应的无量纲临界风速呈先快后慢的上升趋势。自然风速越大,其临界风速上升趋势越缓慢。
|
| 图 9 无量纲临界风速与无量纲火源功率的关系 Fig. 9 Relationship between dimensionless critical wind velocity and dimensionless fire source power |
| |
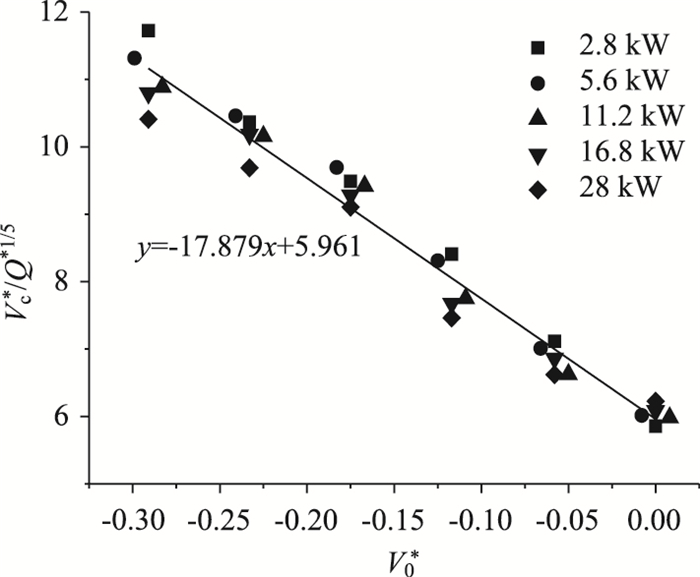
自然风向与射流风机风向反向时,系数V*c/Q*1/5与无量纲自然风经线性拟合(图 10),其相关系数为0.973 7,拟合程度较高。得到无量纲射流风机临界风速公式为:
|
| 图 10 系数与无量纲自然风速的关系S Fig. 10 Relalonship between coefficient and dimensionless natural wind velocity |
| |
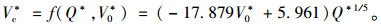
|
(7) |
针对自然风向与射流风机风向同向和反向两种情形,对5种火源功率分别为2.8,5.6,11.2,16.8,28 kW对应的射流风机临界风速进行无量纲分析,并对模拟结果进行拟合。结合式(5),得出无量纲射流风机临界风速。
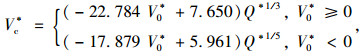
|
(8) |
式中,V0*≥0为自然风向与射流风机风向同向;V0*<0为自然风向与射流风机风向反向。
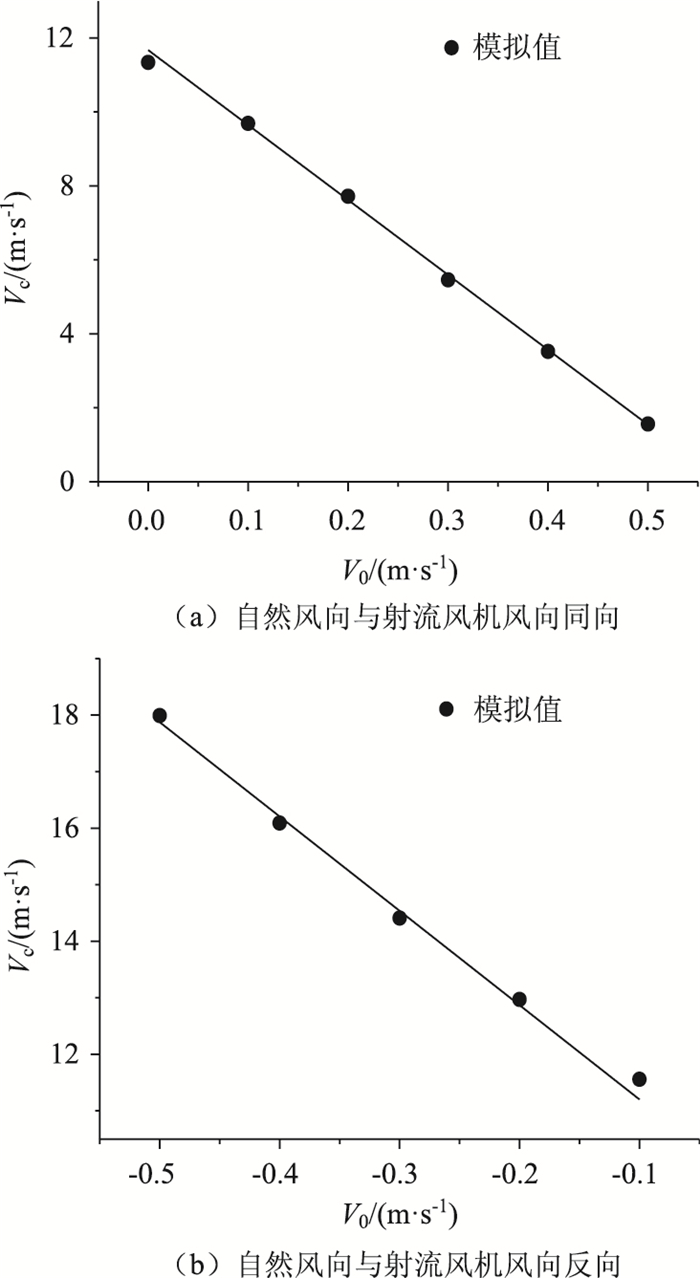
如图 11所示,当火源功率为39.1 kW时,运用式(8)对自然风分别为0,±0.1,±0.2,±0.3,±0.4,±0.5 m/s对应的临界风速进行理论计算,并与模拟值进行比较,其误差率均控制在5%以内。
|
| 图 11 临界风速与自然风速的关系 Fig. 11 Relalonship between critical wind velocity and natural wind velocity |
| |
4 结论
通过理论分析及数值模拟研究了自然风对射流风机临界风速的影响。当射流风机与火源纵向间距不小于4 m时,其临界风速与火源纵向间距无关,提出新的模型预测射流风机临界风速。结论如下:
(1) 当自然风向与射流风机风向同向时,其临界风速与火源功率的1/3次方成正比,这虽与Oka等[2]模型、Wu等[3]模型和Li等模型[10]相似,但实际隧道断面送风是不均匀的,且隧道出入口具有自然风。自然风速越大,临界风速越小。
(2) 当自然风向与射流风机风向反向时,其临界风速与火源功率的1/5次方成正比,且自然风速越大,临界风速越大。
| [1] |
姜学鹏, 张剑高, 丁玉洁. 隧道阻塞比对临界风速影响的模型试验研究[J]. 中国铁道科学, 2015, 36(4): 80-86. JIANG Xue-peng, ZHANG Jian-gao, DING Yu-jie. Model Test Study on Effect of Blockage Ratio on Critical Wind Velocity in Tunnel[J]. China Railway Science, 2015, 36(4): 80-86. |
| [2] |
OKA Y, ATKINSON G T. Control of Smoke Flow in Tunnel Fires[J]. Fire Safety Journal, 1995, 25(4): 305-322. |
| [3] |
WU Y, BAKAR M Z A. Control of Smoke Flow in Tunnel Fires Using Longitudinal Ventilation Systems:A Study of the Critical Velocity[J]. Fire Safety Journal, 2000, 35(4): 363-390. |
| [4] |
LI Y Z, INGASON H. Effect of Cross Section on Critical Velocity in Longitudinally Ventilated Tunnel Fires[J]. Fire Safety Journal, 2017, 91: 303-311. |
| [5] |
YI L, XU Q, XU Z, et al. An Experimental Study on Critical Velocity in Sloping Tunnel with Longitudinal Ventilation under Fire[J]. Tunnelling & Underground Space Technology, 2014, 43(1): 198-203. |
| [6] |
WENG M C, LU X L, LIU F, et al. Study on the Critical Velocity in a Sloping Tunnel Fire under Longitudinal Ventilation[J]. Applied Thermal Engineering, 2016, 94: 422-434. |
| [7] |
LEE Y P, TSAI K C. Effect of Vehicular Blockage on Critical Ventilation Velocity and Tunnel Fire Behavior in Longitudinally Ventilated Tunnels[J]. Fire Safety Journal, 2012, 53(10): 35-42. |
| [8] |
ALVA W U R, JOMAAS G, DEDERICHS A S. The Influence of Vehicular Obstacles on Longitudinal Ventilation Control in Tunnel Fires[J]. Fire Safety Journal, 2017, 87: 25-36. |
| [9] |
JTG/T D70/2-02-2014, 公路隧道通风设计细则[S]. JTG/T D70/2-02-2014, Guidelines for Design of Ventilation of Highway Tunnels[S]. |
| [10] |
LI Y Z, LEI B, INGASON H. Study of Critical Velocity and Backlayering Length in Longitudinally Ventilated Tunnel Fires[J]. Fire Safety Journal, 2010, 45(6): 361-370. |
| [11] |
JI J, GAO Z H, FAN C G, et al. A Study of the Effect of Plug-holing and Boundary Layer Separation on Natural Ventilation with Vertical Shaft in Urban Road Tunnel Fires[J]. International Journal of Heat & Mass Transfer, 2012, 55(21/22): 6032-6041. |
| [12] |
李颖臻.含救援站特长隧道火灾特性及烟气控制研究[D].成都: 西南交通大学, 2010. LI Ying-zhen. Research on Fire Characteristics and Smoke Control of Extra Long Tunnel with Rescue Station[D]. Chengdu: Southwest Jiaotong University, 2010. |
| [13] |
MCGRATTAN K, HOSTIKKA S, MCDERMOTT R, et al. Fire Dynamics Simulator, User's Guide[R]. Gaithersburg: NIST, 2014: 1-268.
|
| [14] |
COSTANTINO A, MUSTO M, ROTONDO G, et al. Numerical Analysis for Reduced-scale Road Tunnel Model Equipped with Axial Jet Fan Ventilation System[J]. Energy Procedia, 2014, 45: 1146-1154. |
| [15] |
MUSTO M, ROTONDO G. CFD Analysis of a Realistic Reduced-scale Modeling Equipped with Axial Jet Fan[J]. Fire Safety Journal, 2015, 74: 11-24. |
| [16] |
袁建平, 方正, 黄海峰, 等. 水平隧道火灾通风纵向临界风速模型[J]. 土木建筑与环境工程, 2009, 31(6): 66-70. YUAN Jian-ping, FANG Zheng, HUANG Hai-feng, et al. Model of Critical Velocity for Fire Ventilation in Horizontal Tunnels[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(6): 66-70. |
| [17] |
孙三祥, 高孟理, 武金明, 等. 双向行车公路隧道射流通风系统优化分析[J]. 公路交通科技, 2006, 23(12): 106-110. SUN San-xiang, GAO Meng-li, WU Jin-ming, et al. Optimization Analysis of Two-direction Road Tunnel Ventilation System with Jet Fan[J]. Journal of Highway and Transportation Research and Development, 2006, 23(12): 106-110. |
| [18] |
王峰, 王明年, 邓园也. 曲线公路隧道射流风机布置方式优化研究[J]. 公路交通科技, 2009, 26(5): 86-90. WANG Feng, WANG Ming-nian, DENG Yuan-ye. Research on Optimal Distribution of Jet Fans in Curvy Tunnel[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 86-90. |
| [19] |
方勇, 兰宇, 曾艳华, 等. 三车道公路隧道射流风机设置位置研究[J]. 现代隧道技术, 2009, 46(2): 90-93. FANG Yong, LAN Yu, ZENG Yan-hua, et al. Study on the Installation of Jet Fans in a Three-lane Highway Tunnel[J]. Modern Tunnelling Technology, 2009, 46(2): 90-93. |
| [20] |
NFPA 502-2004, Standard for Road Tunnels, Bridges, and Other Limited Access Highways[S].
|
| [21] |
DG/TJ08-2033-2008, 道路隧道设计规范[S]. DG/TJ08-2033-2008, Road Tunnel Design Code[S]. |
| [22] |
MCGRATTAN K B, HOSTIKKA S, FLOYD J E. Fire Dynamics Simulator (Version 5):User's Guide[J]. Gaithersburg:NIST, 2007, 206-207. |
| [23] |
李颖臻, 雷波. 隧道火灾模型试验中列车对烟气控制的影响[J]. 铁道学报, 2010, 32(5): 136-139. LI Ying-zhen, LEI Bo. Influence of Train on Control of Smoke Flow in Small-scale Tunnel Fire Experiment[J]. Journal of the China Railway Society, 2010, 32(5): 136-139. |
| [24] |
YI L, XU Q, XU Z, et al. An Experimental Study on Critical Velocity in Sloping Tunnel with Longitudinal Ventilation under Fire[J]. Tunnelling & Underground Space Technology, 2014, 43(1): 198-203. |
| [25] |
DBJ 53-14-2005, 公路隧道消防设计施工管理技术规程[S]. DBJ 53-14-2005, Highway Tunnel Fire Protection Design and Construction Management Technical Regula-tions[S]. |
| [26] |
江平. 移动风机距离对隧道排烟效果的影响研究[J]. 武警学院学报, 2016, 32(8): 28-31. JIANG Ping. A Numerical Study on the Effect of Smoke Ventilation in Tunnel Fires by a Movable Fan[J]. Journal of Chinese People's Armed Police Force Academy, 2016, 32(8): 28-31. |
| [27] |
KIM J Y, YOON S W, YOO J O, et al. A Study on the Smoke Control Characteristic of the Longitudinally Ventilated Tunnel Fire Using PIV[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2006, 21(3/4): 302-302. |
| [28] |
SE C M K, LEE E W M, LAI A C K. Impact of Location of Jet Fan on Airflow Structure in Tunnel Fire[J]. Tunnelling & Underground Space Technology, 2012, 27(1): 30-40. |
 2019, Vol. 36
2019, Vol. 36
