扩展功能
文章信息
- 张兰峰, 庞立果
- ZHANG Lan-feng, PANG Li-guo
- 沥青混凝土小梁开裂损伤影响因素分析
- Analysis on Influencing Factors of Asphalt Concrete Beam Crack Damage
- 公路交通科技, 2019, 36(1): 87-93, 142
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 87-93, 142
- 10.3969/j.issn.1002-0268.2019.01.012
-
文章历史
- 收稿日期: 2017-06-15
2. 广东省南粤交通投资建设有限公司, 广东 广州 510101
2. Guangdong Nanyue Transport Investment & Construction Co., Ltd., Guangzhou Guangdong 510650, China
开裂是沥青路面的主要破坏形式,裂缝严重影响路面的使用功能和寿命,在荷载、温度效应等因素持续作用下,细观尺度的微缺陷(微裂纹、微孔洞等)产生弥散裂隙并进一步增长、扩展、汇合,形成一定尺度的宏观裂纹,导致结构强度下降,以致最终发生破坏。一些学者已经集中研究了含有孔洞、裂纹及任意缺陷材料的裂纹扩展情况和破坏机理。扩展有限元法在标准有限元框架下,在连续区域釆用标准有限元方法,在不连续边界区域对有限元的位移近似函数进行修正,并增加对不连续边界的描述[1]。扩展有限元法利用裂纹富集技术来考虑裂缝尖端奇异应力场和裂缝面两侧位移的不连续性,并引入水平集函数来跟踪裂缝扩展路径和确定裂缝尖端位置[2]。水平集法是一种面向结构界面几何形状描述的数值技术,它采用零水平集函数描述结构界面形状,然后通过分析计算来改变水平集函数值,以得到不断变化的界面形状,特别是水平集在更新时不需重新划分网格[3-4]。扩展有限元技术由于其不依赖网格划分、不需要预知裂缝扩展路径,在裂缝问题的研究中占据明显的优势,可实现对裂缝自由扩展的预测。扩展有限元法在分析断裂问题时克服了常规有限元法要求裂缝面与单元边界一致,裂缝扩展需要重新划分网格及裂缝尖端需要密集网格等缺点,因此得到广泛的应用[5]。程一磊等[6]采用扩展有限元法研究沥青混合料三点弯曲梁裂缝扩展规律,证实了扩展有限元对裂缝扩展模拟与实际裂缝扩展具有良好的符合性。杨涛[7]应用扩展有限元法分析了钢筋混凝土梁裂缝扩展及宽度变化,得到了裂缝处钢筋及混凝土应力的变化及黏结滑移对裂缝模拟的影响程度。金光来[8]采用扩展有限元研究沥青路面疲劳开裂行为,提出了一套能够模拟结构从疲劳损伤到裂缝形成再到裂缝疲劳扩展全过程的有效方法。本研究应用扩展有限元(XFEM),模拟含初始裂纹的沥青混凝土三点弯曲梁的开裂扩展过程,研究沥青混凝土小梁裂缝在荷载作用位置、预设裂缝长度、材料力学参数(抗拉强度、断裂能)等因素变化下的扩展规律。
1 XFEM原理XFEM的基本原理是在裂尖区单元的节点上用奇异函数和在裂纹贯穿区用跃阶函数加强传统有限元的基函数,以模拟由于裂纹存在引起的位移不连续性和裂纹尖端的奇异性[9]。在XFEM中,裂纹完全独立于有限元网格,可以从单元内部开裂,因此裂纹的扩展过程完全无需考虑其形状和走向,可以实现裂纹的真实扩展模拟[10]。扩展有限元位移表达式为[11-12]:
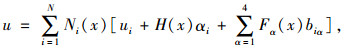
|
(1) |
式中,Ni(x)为通常的形函数;ui为通常的节点位移;αi为被裂纹尖端贯穿的单元节点附加自由度;biα为裂纹尖端嵌入单元的节点附加自由度;H(x)为Heaviside函数,表达式为[13]:
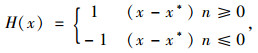
|
(2) |
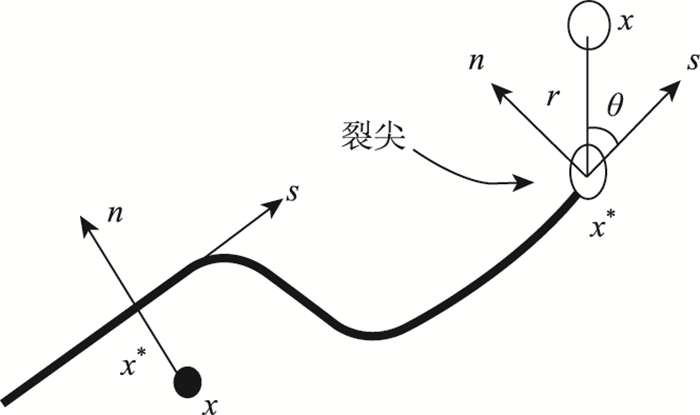
式中,x为高斯积分点;x*为最靠近裂纹尖端的点;n为裂纹在x*的单位外法线分量,如图 1所示, 其中s为裂纹在x*的单位切线分量。
|
| 图 1 XFEM穿越单元内部时各分量示意图 Fig. 1 Schematic diagram of each component when XFEM passing through element interior |
| |
裂纹尖端位移场函数Fα(x)的近似表达式为:
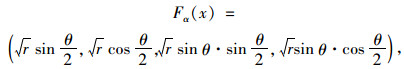
|
(3) |
式中(r, θ)为以裂纹尖端为原点的极坐标。
扩展有限元需要定义材料的弹性模量、损伤准则及破坏准则。软件中提供了5种可供选择的损伤准则,如最大主应力或应变准则、应力比平方和准则等,但是只有最大主应力准则可以实现裂缝的自由扩展,扩展方向为最大主应力方向的正交方向,而其他4种准则只能沿着预先定义好的方向扩展[14]。最大主应力准则为:
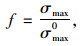
|
(4) |
式中, f为材料所受拉应力最大值与最大允许主应力的比值;σmax为材料所受到的最大拉应力;σmax0为最大允许主应力, 在f=1时材料会出现初始裂缝。
XFEM的建模分为两个部分[15]:
(1) 忽略结构内部细节情况下对材料进行有限元网格划分。
(2) 在单元形函数中增加与内边界相关的附加函数,再通过定义附加自由度即可实现裂纹张开所产生的不连续性。
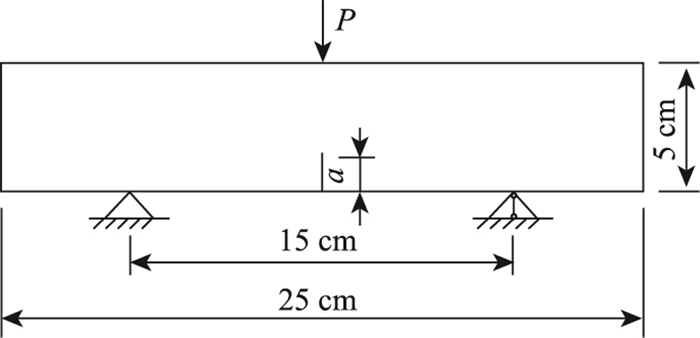
2 小梁模型的建立对沥青混合料的断裂研究主要分为试验研究和数值研究两个方面。试验研究即采用小梁试件、劈裂试件、半圆弯拉试件等不同的结构形式[16]对其加载直到破坏,以获得破坏过程中的各类参数。采用小梁试件模拟沥青混合料开裂行为。模拟沥青混凝土三点弯曲梁的几何尺寸为梁高5 cm,梁长25 cm, 两支座之间的距离为15 cm,采用在梁中点的位移加载方式, 如图 2所示。P为所加荷载,a为初始裂缝长度。裂缝设置时创建一个独立的线单元,并将其实体化来代表裂缝,裂缝独立于XFEM网格, 不需要进行网格划分。网格化分如图 3所示。当裂缝形状比较复杂时,采用XFEM方法定义裂缝可以避免分割实体给网格划分带来的麻烦。模型左端采用固定支座,右端采用滑动支座,并约束除竖向以外的其他自由度。网格划分类型为CPE4R, 在设置Step分析步时,需要在场变量输出中,设置State/Field/User/Time选项选择STATUSXFEM,以观察裂缝扩展。当STATUSXFEM为0时,表示材料没有开裂;当STATUSXFEM为1时,表示完全开裂。当损伤开始以后,材料进入软化阶段,根据已有研究结论[17],沥青混合料适宜采用线性软化模型,并以断裂能作为材料最终破坏的判断依据。数值计算时需要定义断裂能、抗拉强度、弹性模量等参数。所以在模型受力分析中,判断裂缝出现的原则采用最大主拉应力牵引损伤开裂准则和基于能量的线性软化损伤模型。
|
| 图 2 沥青混凝土三点弯曲梁受力模式 Fig. 2 Mechanical mode of asphalt concrete 3-point bending beam |
| |

|
| 图 3 预设裂缝的小梁网格划分 Fig. 3 Meshing of beam with preset crack |
| |
3 材料力学参数选取试验概况 3.1 抗压回弹模量
测定沥青混合料抗压回弹模量采用直径与高度均为100 mm的圆柱形试件,通过单轴压缩试验测得。试验采用AC-16中值级配沥青混合料,结合料采用壳牌70#沥青,试件采用静压法成型,试验温度为0 ℃。取泊松比0.3,加载速率为2 mm/min。试验步骤参照《公路工程沥青及沥青混合料试验规程》(JTG E20—2011)中的沥青混合料单轴压缩试验。沥青混合料的力学参数试验结果如表 1所示。
| 弹性模量/MPa | 泊松比 | 极限抗拉强度/MPa | 断裂能/(J·m-2) |
| 1 250 | 0.3 | 8.5 | 256 |
3.2 间接拉伸试验
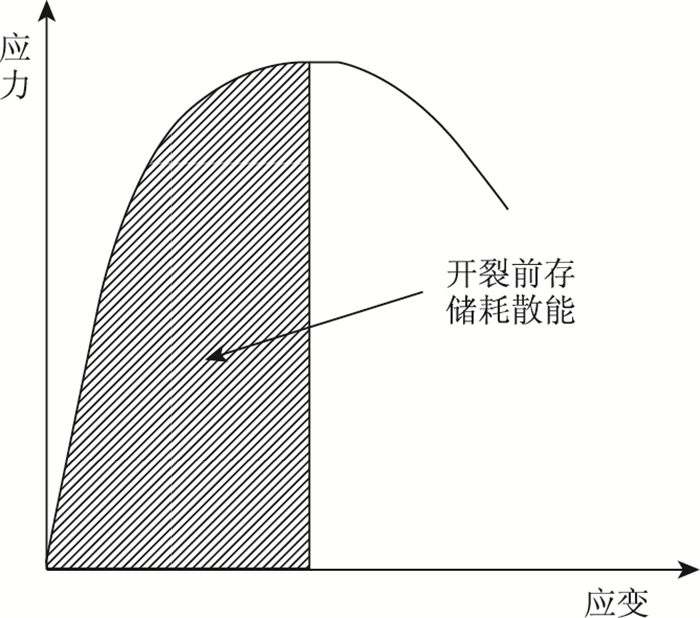
沥青混合料的抗拉强度和断裂能通过间接拉伸试验得到。试验采用的沥青混合料与单轴压缩试验相同,试验采用马歇尔试件,间接拉伸试验步骤参照《公路工程沥青及沥青混合料试验规程》中的沥青混合料劈裂试验,试验温度为0 ℃。取泊松比0.3,加载速率为50 mm/min。抗拉强度取应力-应变曲线的峰值点对应的应力值。断裂能的含义是形成单位面积裂缝所吸收的能量[18]。断裂能密度值就是在间接拉伸试验中,试样断裂时应力-应变曲线下到应力峰值点前曲线的面积(即图 4阴影部分的面积)。根据实测的沥青混合料试件间接拉伸试验应力-应变关系, 拟合应力-应变曲线,建立它们之间的关系式,再代入积分式进行积分,积分式的应变上限是应力峰值点对应的应变值。
|
| 图 4 沥青混合料断裂能密度 Fig. 4 Fracture energy density of asphalt mixture |
| |
断裂能密度计算的公式为:
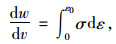
|
(5) |
式中,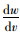
采用与上述相同沥青混合料制备小梁试件,尺寸为高5 cm、长25 cm、宽5 cm,试件采用轮碾法成型,混凝土三点弯曲梁的几何尺寸、受力及边界条件如图 2所示。试验所用试件跨中底部位置设置1条预制裂缝,初始裂缝长度为20 mm, 加载方式采用位移荷载,施加竖向位移荷载s=0.01 m,试验温度为0 ℃,以对比沥青混凝土小梁三点弯曲加载数值模拟与实际试验的符合程度,也就是XFEM对小梁弯曲破坏试验模拟的有效性验证。
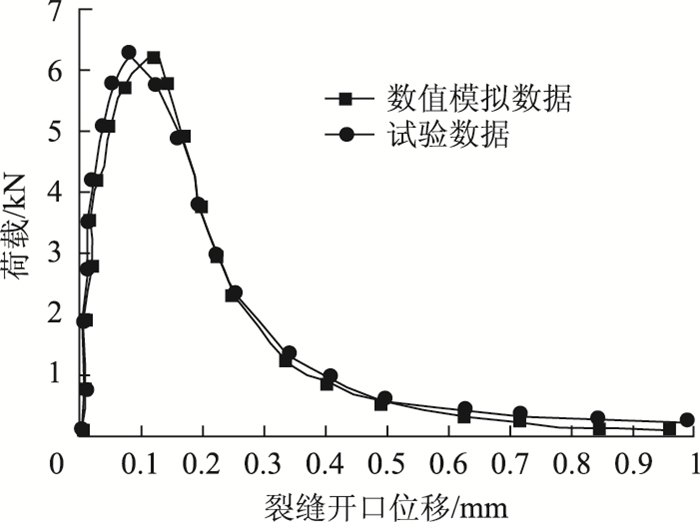
利用所建立的模型对混凝土三点弯曲梁进行工况1数值模拟,将模拟结果与实验室相同尺寸、加载大小和位置的试件试验结果进行对比,如图 5所示。根据图 5,试验曲线和数值模拟曲线基本吻合,说明采用XFEM方法对小梁开裂进行数值模拟是有效的。以下不同状况的小梁弯曲破坏模拟均采用XFEM数值分析。
|
| 图 5 荷载-裂缝开口位移模拟曲线与试验结果 Fig. 5 Simulated Load-crack opening displacement curves and experimental result |
| |
4 小梁裂缝扩展XFEM模拟分析 4.1 裂缝与荷载作用不同位置
在道路实际使用过程中,材料往往处于更加复杂的受力状态,当车辆荷载位于裂缝正上方时,开裂模式为Ⅰ型;当车辆荷载不处于裂缝的正上方时,材料的开裂多为复合型开裂[7]。研究沥青混合料的复合型开裂具有重要的实际意义。利用单边切口梁易于实现Ⅰ-Ⅱ复合型开裂,将荷载作用位置从跨中移开一定距离就可以达到目的。试件跨中底部位置设置预制裂缝,初始裂缝长度为2 cm。设置荷载与裂缝的不同位置关系,分别模拟以下3种工况:(1)在小梁跨中施加位移荷载;(2)距离小梁跨中右侧2 cm处施加位移荷载; (3)距离小梁跨中右侧5 cm处施加位移荷载。施加竖向位移荷载s=0.01 m,研究裂缝扩展规律和施加荷载与裂缝相对位置对裂缝扩展规律的影响。
4.1.1 工况1根据表 1中的参数,在ABAQUS有限元软件中模拟工况1开裂的过程。随着小梁变形的不断增加,跨中处损伤逐渐累积到一定程度后,切缝沿跨中截面竖直向上逐步扩展,直至破坏。软件中输出参数STATUSXFEM可代表损伤带的发展过程,当裂尖的损伤达到STATUSXFEM=1时,表示切缝尖端产生了新的裂缝,宏观上表现为切缝的扩展,破坏形态如图 6所示。工况1的Step分析步共分为100步。

|
| 图 6 裂缝扩展(工况1) Fig. 6 Crack propagation (condition 1) |
| |
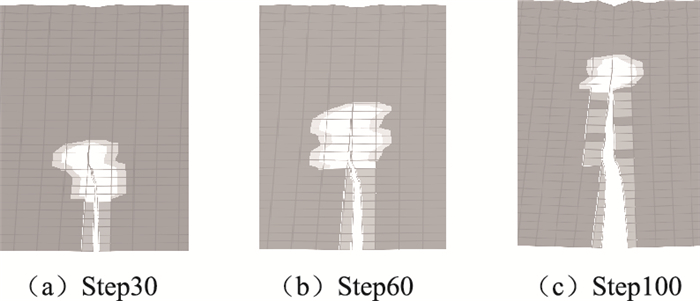
图 7为在小梁模拟分析工况1情况下,在Step30,Step60,Step100时的裂缝状。通过对比发现,裂缝扩展长度随着分析步的增加而增大,而且裂缝扩展路径沿着模型中心线扩展。
|
| 图 7 Step30、Step60、Step100时的裂缝STATUSXFEM图(工况1) Fig. 7 Crack STATUSXFEM diagrams of Step30, Step60 and Step100 (condition 1) |
| |
采用XFEM模拟工况1裂缝扩展情况。裂纹穿过单元时,其两侧的位移场明显出现了不连续的情形。如图 7所示,XFEM在模拟裂纹开裂时引入了非连续的位移模式,使得非连续内边界的描述独立于网格划分,无需调整网格。裂纹路径呈现曲折形状,与所布置网格边界不再保持一致,正体现了XFEM的优势,即可以精确捕捉真实裂纹扩展的形态。
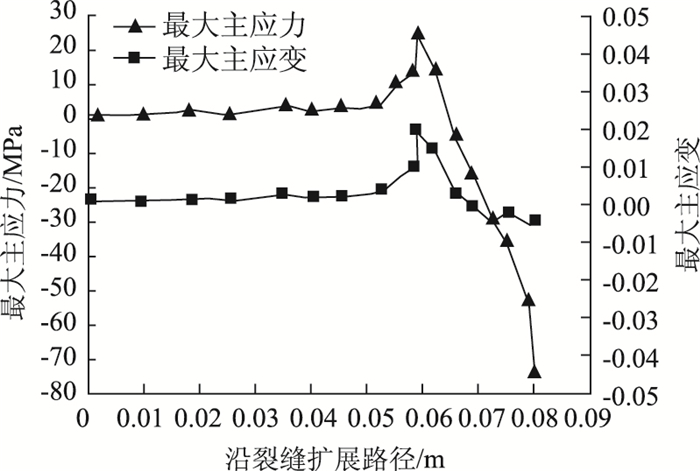
图 8为最大主应力、最大主应变随着裂缝扩展路径的变化。由图 8可知,裂纹扩展过程中,最大主应力、最大主应变沿裂缝路径呈先增大后减小的趋势,裂纹终止时,其尖端应力变小。当最大值应力曲线达到峰值后,裂缝扩展需要的最大主应力迅速减小,小梁的承载能力急速减小。
|
| 图 8 最大主应力、最大主应变随着裂缝扩展路径的变化(工况1) Fig. 8 Maximum principal stress and maximum principal strain varying with crack propagation path (condition 1) |
| |
4.1.2 工况2和工况3
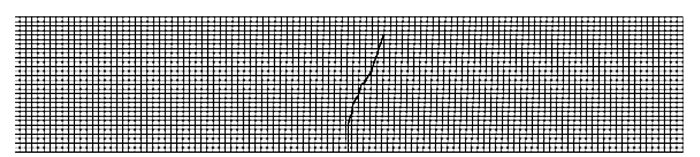
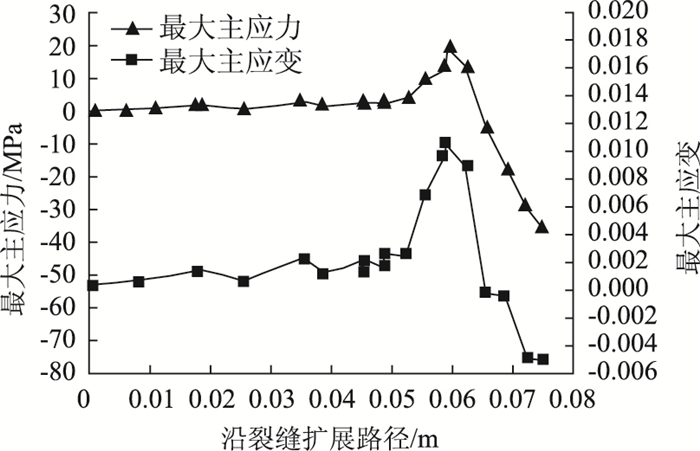
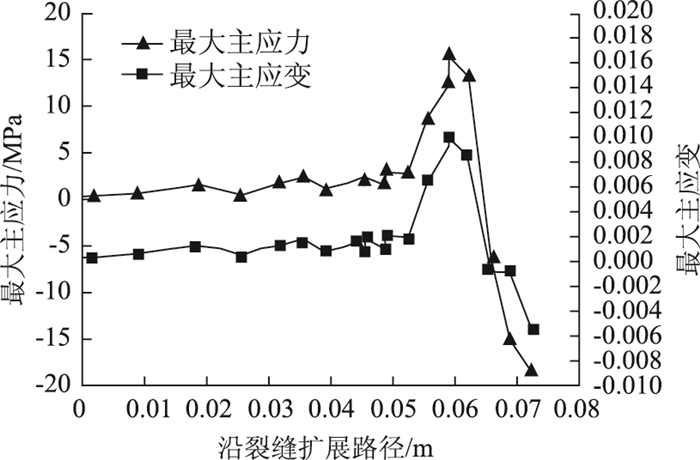
从裂纹扩展图形(图 9、图 11)来看,工况2、工况3由于荷载作用线与裂缝不再重合,在裂缝张开初期,预切口尖端受到拉剪的联合作用,裂缝会偏离切口向加载方向倾斜扩展。复合型开裂的方向为由梁底向上并向跨中加载点处偏移,裂缝偏向一侧,体现出了混合型裂缝的特征。根据图 8、图 10、图 12,得到不同工况最大主应力、最大主应变、裂缝长度数值,如表 2所示。
|
| 图 9 裂缝扩展(工况2) Fig. 9 Crack propagation (condition 2) |
| |
|
| 图 10 最大主应力、最大主应变随着裂缝扩展路径变化图(工况2) Fig. 10 Maximum principal stress, maximum principal strain as the crack propagation path graph (condition 2) |
| |

|
| 图 11 裂缝扩展图(工况3) Fig. 11 Crack propagation graph (condition 3) |
| |
|
| 图 12 最大主应力、最大主应变随着裂缝扩展路径变化(工况3) Fig. 12 Maximum principal stress, the maximum principal strain varying with crack propagation path (condition 3) |
| |
| 荷载-裂缝相对位置 | 最大主应力峰值/MPa | 最大主应变峰值 | 裂缝长度/m |
| 工况1 | 24.22 | 0.019 | 0.080 |
| 工况2 | 18.72 | 0.010 | 0.075 |
| 工况3 | 15.22 | 0.009 9 | 0.072 |
由表 2可知,荷载作用位置离裂缝越远,最大主应力峰值、最大主应变峰值都越小,而且裂缝扩展长度也越小。裂缝与荷载相对位置增大时,裂缝扩展受荷载作用影响减弱。
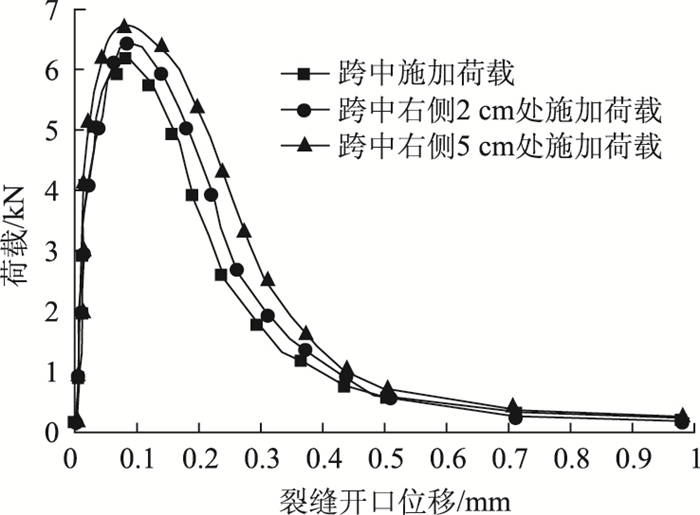
荷载-裂缝开口曲线在研究沥青混合料断裂特性时具有重要的意义。曲线包围的面积可计算材料的断裂能。裂缝荷载相对位置不同时的荷载-裂缝开口位移曲线(图 13)表明,当裂缝与荷载相对位置关系不同但初始裂缝长度和所施加荷载大小不变时,荷载到裂缝距离增大,不仅增大了裂缝扩展需要的荷载,而且使得图 13曲线向右侧扩展,也就是增大了荷载-裂缝开口关系曲线所包围的面积,即增大了裂缝扩展需要的断裂能。
|
| 图 13 裂缝荷载不同相对位置时的荷载-裂缝开口位移曲线 Fig. 13 Load-crack opening curves with different relative positions of load and crack |
| |
4.2 初始裂缝长度不同
基于工况1,设小梁跨中底部的初始裂缝长度分别为2, 2.5, 3 cm,其他力学参数与表 1相同,跨中施加位移荷载s=0.01 m。
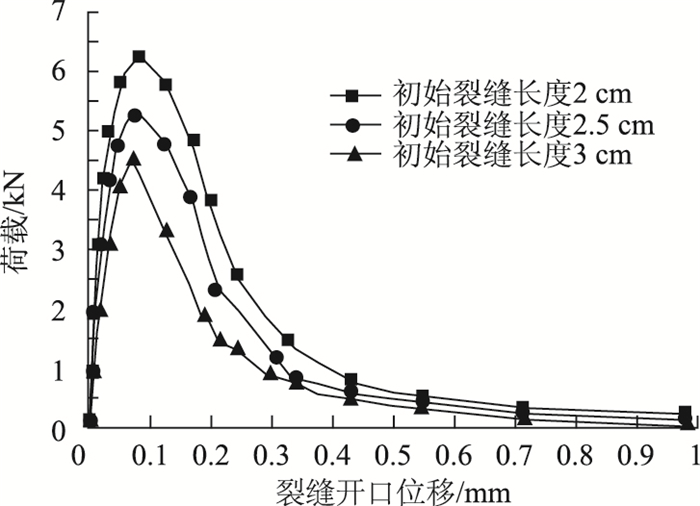
不同初始裂缝长度时的荷载-裂缝开口位移曲线(图 14)表明,当初始裂缝长度增大,但所加荷载位置与大小不变时,裂缝扩展需要的荷载增大,而且荷载-裂缝开口关系曲线包围的面积也增大,说明裂缝扩展需要更大的断裂能,也就是越难开裂。
|
| 图 14 不同初始裂缝长度时的荷载-裂缝开口位移曲线 Fig. 14 Load-crack opening curves with different initial crack lengths |
| |
4.3 力学参数不同
基于工况1,设初始裂缝长度2 cm, 跨中施加位移荷载s=0.01 m。改变材料的抗拉强度为7.5,8.5,9.5 MPa,断裂能为256 J/m2;改变材料的断裂能为225,256,300 J/m2,抗拉强度为8.5 MPa,研究抗拉强度、断裂能变化对裂缝扩展的影响。
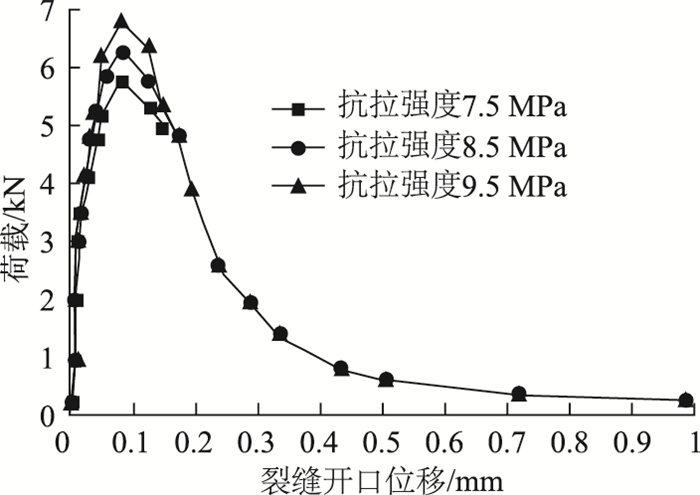
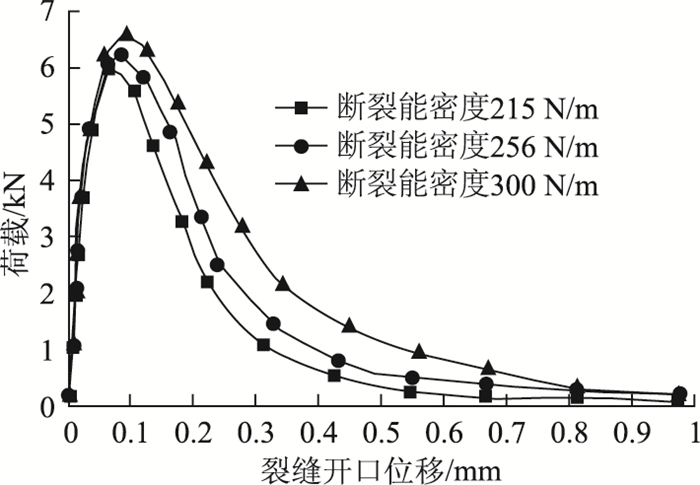
材料不同抗拉强度时的荷载-裂缝开口位移曲线(图 15)表明,当仅改变沥青混合料抗拉强度而断裂能不变时,沥青混合料抗拉强度的增大会导致荷载峰值增大,而荷载-裂缝开口位移曲线线形基本不变,也就是对小梁变形影响较小。根据材料不同断裂能时的荷载-裂缝位移开口曲线(图 16),抗拉强度不变,断裂能增大会导致荷载和变形的同时增大,曲线向右上方外侧扩展偏移,荷载-裂缝开口关系曲线包围面积增大,这说明断裂能更能综合反映荷载和变形,而仅将抗拉强度做为开裂指标是很单一的。
|
| 图 15 材料不同抗拉强度时的荷载-裂缝开口位移曲线 Fig. 15 Load-crack opening curves with different tensile strengths |
| |
|
| 图 16 材料不同断裂能时的荷载-裂缝位移开口曲线s Fig. 16 Load-crack opening curves with different fracture energies |
| |
5 结论
(1) 模拟结果表明,XFEM在模拟裂缝开裂时引入了非连续的位移模式,裂缝扩展路径呈现曲折形状,与所布置网格边界不再保持一致,可以精确捕捉真实裂缝扩展的形态,可以很好地模拟沥青混凝土小梁的裂缝扩展,路径不依赖于单元边界,裂缝从单元内部断开,更符合实际情况。
(2) 裂缝扩展类型与荷载作用位置的关系极大。当荷载作用线与预设裂缝重合时,裂缝主要受到拉应力作用,从预设裂尖沿着荷载作用线向上扩展,体现了Ⅰ型裂缝特征。当荷载作用线与裂缝不再重合时,裂缝尖端受到拉、剪应力的联合作用,裂缝从梁底向上并向跨中加载点处偏移,体现了Ⅰ-Ⅱ型裂缝特征。荷载作用位置离裂缝越远,最大主应力峰值、最大主应变峰值越小,而且裂缝扩展长度也越小。
(3) 改变模拟分析参数抗拉强度和断裂能的数值,发现抗拉强度的增加只是增大开裂需要的荷载,而断裂能改变不只改变开裂需要的荷载数值,而且改变小梁受力产生的变形,所以断裂能更能正确反映材料的抗裂性能。
| [1] |
冯坤.基于扩展有限元法与水平集法的结构裂纹扩展特性研究[D].杭州: 浙江大学, 2013. FENG Kun. Research on Structural Crack Propagation Property Based on Extended Finite Element Method and Level Set Method[D]. Hangzhou: Zhejiang University, 2013. |
| [2] |
胡少伟, 鲁文妍. 基于XFEM的混凝土三点弯曲梁开裂数值模拟研究[J]. 华北水利水电大学学报:自然科学版, 2014, 35(4): 1-2. HU Shao-wei, LU Wen-yan. Numerical Simulation of Concrete Three-point Bending Beam Cracking Based on XFEM[J]. Journal of North China University of Water Resources and Electric Power:Natural Science Edition, 2014, 35(4): 1-2. |
| [3] |
严明星.基于扩展有限元法的沥青混合料开裂特性研究[D].大连: 大连海事大学, 2012. YAN Ming-xing. Study of Cracking Characteristic of Asphalt Mixture Based on Extend Finite Element Method[D]. Dalian: Dalian Maritime University, 2012. |
| [4] |
STOLARSKA M, CHOPP D L, MOES N, et al. Modelling Crack Growth by Level Sets in the Extended Finite Element Method[J]. International Journal for Numerical Methods in Engineering, 2001, 51(8): 943-960. |
| [5] |
冯琦. 基于XFEM的环氧沥青混凝土断裂行为研究[J]. 北方交通, 2014(4): 91-94. FENG Qi. The Fracture Response Analysis of Epoxy Asphalt Mixture Based on XFEM[J]. Northern Communications, 2014(4): 91-94. |
| [6] |
程一磊, 杨新华. 沥青混合料三点弯曲断裂的扩展有限元模拟[J]. 固体力学学报, 2017, 38(3): 282-285. CHEN Yi-lei, YANG Xin-hua. Numerical Simulation for Three-point Bending Fractures of Asphalt Mixture Based on Extended Finite Element Method[J]. Chinese Journal of Solid Mechanics, 2017, 38(3): 282-285. |
| [7] |
杨涛, 邹道勤. 基于XFEM的钢筋混凝土梁开裂数值模拟[J]. 浙江大学学报:工学版, 2013, 47(3): 496-498. YANG Tao, ZOU Dao-qin. Numerical Simulation of Crack Growth of Reinforced Concrete Beam Based on XFEM[J]. Journal of Zhejiang University:Engineering Science Edition, 2013, 47(3): 496-498. |
| [8] |
金光来.基于扩展有限元的沥青路面疲劳开裂行为的数值研究[D].南京: 东南大学, 2015. JIN Guang-lai. Numerical Analysis of Fatigue Cracking Behavior in Asphalt Pavement Based on Extended Finite Element Model[D]. Nanjing: Southeast University, 2015. |
| [9] |
杨擎.扩展有限元法在沥青路面多裂纹扩展分析中的应用[D].武汉: 华中科技大学, 2011. YANG Qing. Application of XFEM in Multiple Crack Propagation Analysis of Asphalt Pavement[D]. Wuhan: Huazhong University of Science & Technology, 2011. |
| [10] |
CHESSA J, BELYTSCHKO T. An Extended Finite Element Method for Two-phase Fluids[J]. Journal of Applied Mechanics, 2003, 70(1): 10-17. |
| [11] |
SONG S H, PAULINO G H, BUTTLAR W G. Cohesive Zone Simulation of Mode Ⅰ and Mixed-mode Crack Propagation in Asphalt Concrete[C]//Geo-frontiers Congress 2005.[S. l.]: ASCE, 2005.
|
| [12] |
BELYTSCHKO T, BLACK T. Elastic Crack Growth in Finite Elements with Minimal Remeshing[J]. International Journal for Numerical Methods in Engineering, 2015, 45(5): 601-620. |
| [13] |
李兴权, 孙晓燕, 尹子燕. 含初始裂缝的素混凝土梁三点弯数值模拟[J]. 公路, 2012(7): 221-224. LI Xing-quan, SUN Xiao-yan, YIN Zi-yan. Three-point Bending Numerical Simulation of Concrete Beam with Initial Crack[J]. Highway, 2012(7): 221-224. |
| [14] |
SUKUMAR N, PREVOST J H. Modeling Quasi-static Crack Growth with the Extended Finite Element Method. Part Ⅰ:Computer Implementation[J]. International Journal of Solids & Structures, 2003, 40(26): 7513-7537. |
| [15] |
李录贤, 王铁军. 扩展有限元法(XFEM)及其应用[J]. 力学进展, 2005, 35(1): 5-10. LI Lu-xian, WANG Tie-jun. The Extended Finite Element Method and Its Applications:A Review[J]. Advances in Mechanics, 2005, 35(1): 5-10. |
| [16] |
李立寒, 曹林涛, 罗芳艳, 等. 沥青混合料劈裂抗拉强度影响因素的研究[J]. 建筑材料学报, 2004, 7(1): 41-45. LI Li-han, CAO Lin-tao, LUO Fang-yan, et al. Research on the Factors Affecting on the Split Tension Strength of Asphalt Mixes[J]. Journal of Building Materials, 2004, 7(1): 41-45. |
| [17] |
金光来, 黄晓明, 梁彦龙. 两种不同模式下的沥青混合料断裂过程研究[J]. 湖南大学学报:自然科学版, 2014, 41(6): 120-124. JIN Guang-lai, HUANG Xiao-ming, LIANG Yan-long. A Numerical Analysis of the Fracture Behavior of Asphalt Concrete under Two Different Modes[J]. Journal of Hunan University:Natural Science Edition, 2014, 41(6): 120-124. |
| [18] |
张晓东. 基于扩展有限元法及虚拟裂缝模型的混凝土断裂过程区分析[J]. 计算机辅助工程, 2016, 25(1): 62-65. ZHANG Xiao-dong. Analysis on Concrete Fracture Process Zone Based on Extended Finite Element Method and Fictitious Crack Model[J]. Computer Aided Engineering, 2016, 25(1): 62-65. |
 2019, Vol. 36
2019, Vol. 36
