扩展功能
文章信息
- 白桦, 姬乃川, 张亮亮, 刘健新, 何晗欣
- BAI Hua, JI Nai-chuan, ZHANG Liang-liang, LIU Jian-xin, HE Han-xin
- 紊流风特性参数对近流线形桥梁表面风压分布影响
- Influence of Turbulent Wind Characteristic Parameters on Wind Pressure Distribution on Approximate Streamlined Bridge Surface
- 公路交通科技, 2019, 36(1): 70-77
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 70-77
- 10.3969/j.issn.1002-0268.2019.01.010
-
文章历史
- 收稿日期: 2017-07-28
2. 山西省交通科学研究院, 山西 太原 030006;
3. 西安建筑科技大学 土木工程学院, 陕西 西安 710055
2. Shanxi Transportation Research Institute, Taiyuan Shanxi 030006, China;
3. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an Shaanxi 710055, China
紊流风特性参数的模拟精度直接决定了桥梁结构风洞试验结果的可靠性。国内外学者针对紊流风参数模拟对风洞试验结果的影响进行了大量研究,如Stathopoulos指出应严格模拟紊流强度,紊流积分尺度在受到条件限制时可以适当放弃,而Hold却认为紊流积分尺度应严格模拟[1]。Tieleman的研究结果支持了Stathopoulos的研究结论[2]。Bearman分析了紊流积分尺度对风洞试验结果影响不大的原因[3]。Lee研究发现紊流积分尺度对钝体桥梁断面的阻力系数有影响,积分尺度与模型特征尺寸比值在1时达到极大,在1.5~2时,达到极小[4]。Schewe与Bucher研究了紊流风参数对悬索桥气动稳定性的影响[5-6],认为紊流强度会降低单个振型的稳定性,紊流降低扭转发散临界风速。张志田教授研究发现紊流强度对西堠门大桥的静风稳定性有明显影响[7-8],Scanlan在紊流场中测得的气动导数比均匀流场稍大[9]。潘韬研究发现紊流强度越大,抖振力功率谱密度能量也越大,紊流积分尺度对顺风向抖振力影响较明显[10]。华旭刚给出了紊流积分尺度对输电塔风洞试验结果的修正系数[11]。卢占斌对CAARC模型进行试验[12],研究了部分紊流参数对矩形建筑结构的影响。但文中缺少单参数变化的影响分析。王利娟研究表明紊流参数对流线形桥梁断面影响更明显[13]。李春光研究表明紊流积分尺度随断面钝化,其影响逐渐减弱[14]。茅建校研究发现随紊流空间相关系数衰减因子增大,位移响应会逐渐减小[15]。白桦、王骑、马文勇研究了风特性参数对不同断面风洞试验结果的影响,指出其影响均不可忽略[16-18]。
以上研究表明紊流风特性参数可能会对桥梁结构的抖振、颤振等试验结果产生影响,为了分析产生这种影响的根本原因,本研究尝试总结桥梁结构表面风压分布受紊流风参数的影响规律。在风洞中采用格栅紊流,形成了紊流强度与积分尺度单参数变化的风场,以此来研究紊流风特性参数对桥梁结构表面风压分布规律的影响。
1 风洞试验 1.1 紊流风特性参数模拟不同格栅形成的局部紊流风场如图 1所示。表 1、表 2给出了不同风场测得的风特性参数。为表述方便,定义格栅10~20表示格栅宽度为10 cm,格栅中心方孔尺寸为20 cm的格栅风场。通过对比格栅10~30与格栅10~60紊流场中的风洞试验结果可得紊流强度单参数变化对结构表面风压分布的影响,对比格栅10~20与格栅10~30可得积分尺度单参数变化对结构表面风压分布的影响。试验风速为15 m/s。

|
| 图 1 格栅风场 Fig. 1 Turbulence field of grilles |
| |
| 格栅宽度/ cm |
不同格栅中心孔尺寸(cm)紊流强度/% | |||
| 60 | 40 | 30 | 20 | |
| 25 | 35.1 | 37.9 | 33.4 | 37.5 |
| 20 | 31.7 | 25.8 | 23.3 | 29.1 |
| 15 | 25.6 | 25.9 | 20.9 | 18.2 |
| 10 | 22.3 | 17.8 | 17.3 | 18.6 |
| 格栅宽度/ cm |
格栅中心孔尺寸(cm)紊流积分尺度/m | |||
| 60 | 40 | 30 | 20 | |
| 25 | 0.12 | 0.29 | 0.25 | 0.38 |
| 20 | 0.11 | 0.40 | 0.20 | 0.77 |
| 15 | 0.10 | 0.30 | 0.29 | 0.28 |
| 10 | 0.10 | 0.07 | 0.10 | 0.23 |
1.2 试验模型
试验模型为缩尺比1: 50的某航道桥近流线形箱梁断面,在模型跨中位置布置一圈测压孔,如图 2所示。风攻角为0°,±5°,±10°共5种。

|
| 图 2 测点布置示意图 Fig. 2 Schematic diagram of measuring points |
| |
1.3 试验结果及分析 1.3.1 紊流强度对平均风压系数的影响
图 3给出了桥梁模型表面不同位置测点在不同紊流强度流场中平均风压系数随风攻角的变化规律,图 3(a)流场的紊流强度为17%,图 3(b)流场的紊流强度为22%,两个流场的紊流积分尺度相同。图中横坐标表示测点编号,可见:对于近流线形桥梁断面,两个流场中各测点的变化趋势基本相同,紊流强度的变化并不会改变平均风压系数随风攻角的变化规律。测点5,7,13,20,35,40均处于模型上表面,当风攻角由负变正,平均风压系数逐渐减小,上表面上游到中间位置处的风压系数(测点5~20)随风攻角的变化幅度较上表面下游位置大(测点35~40)。随风攻角变化,风压系数变化幅度最小的位置在主梁下游尾部位置(测点50~60),变化幅度最大的位置在主梁上游迎风侧,如测点118正对来流,平均风压系数随风攻角变化幅度最大。在同一风攻角,近流线形桥梁断面下表面的风压梯度变化较上表面大。
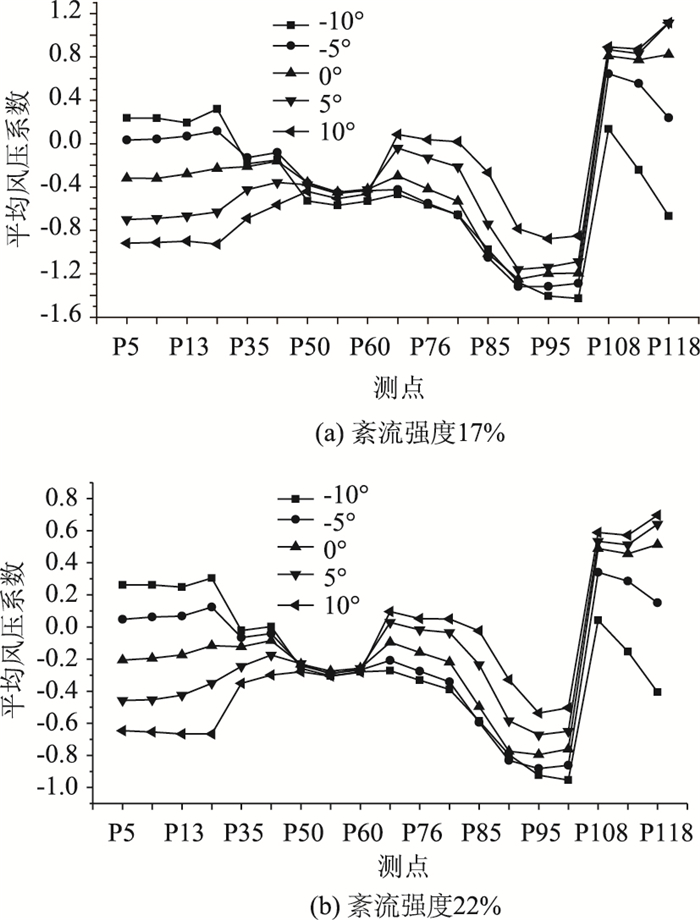
|
| 图 3 局部紊流风场中各测点平均风压随风攻角变化 Fig. 3 Mean wind pressure of different measuring points in local turbulent wind field varying with wind attack angle |
| |
图 4给出了紊流强度对平均风压系数的影响。可见:除了迎风侧各点的风压系数为正,其余位置风压系数均为负。紊流强度由17%增大到22%会导致平均风压系数的绝对值减小。位置不同,平均风压系数随紊流强度变化的幅度也不同,紊流强度增大5%,0°攻角35号测点平均风压系数绝对值减小42%,50号测点减小35%,70号测点减小68%。108,112,118号测点位于正压区,平均风压系数也随紊流强度增大而减小,减小的幅度分别为40%,41%,38%。所以对于近流线形桥梁断面,其表面不同位置平均风压系数随紊流强度变化幅度各不相同,很难定量地进行统一修正。
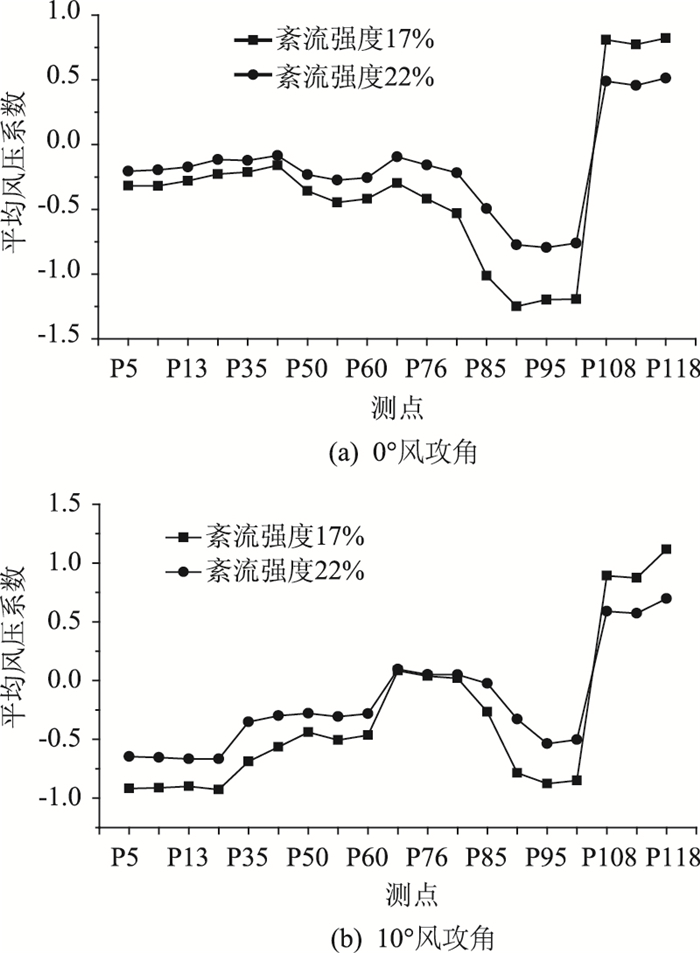
|
| 图 4 紊流强度对不同风攻角各测点平均风压影响 Fig. 4 Influence of turbulence intensity on mean wind pressures of different measuring points at different wind attack angles |
| |
图 5给出了测点35与测点100的平均风压系数随紊流强度与风攻角的变化情况。可见:紊流强度增大会使平均风压系数的绝对值减小,减小的幅度不仅和测点所在的位置有关,还与风攻角有关。不同风攻角下,紊流强度增大导致平均风压系数减小的幅度各不相同,测点35反映得尤为明显。故紊流强度对近流线形桥梁表面平均风压的影响规律比较复杂,受到很多条件影响,为了保证试验精度,需要在风洞中准确模拟桥址处的紊流强度。
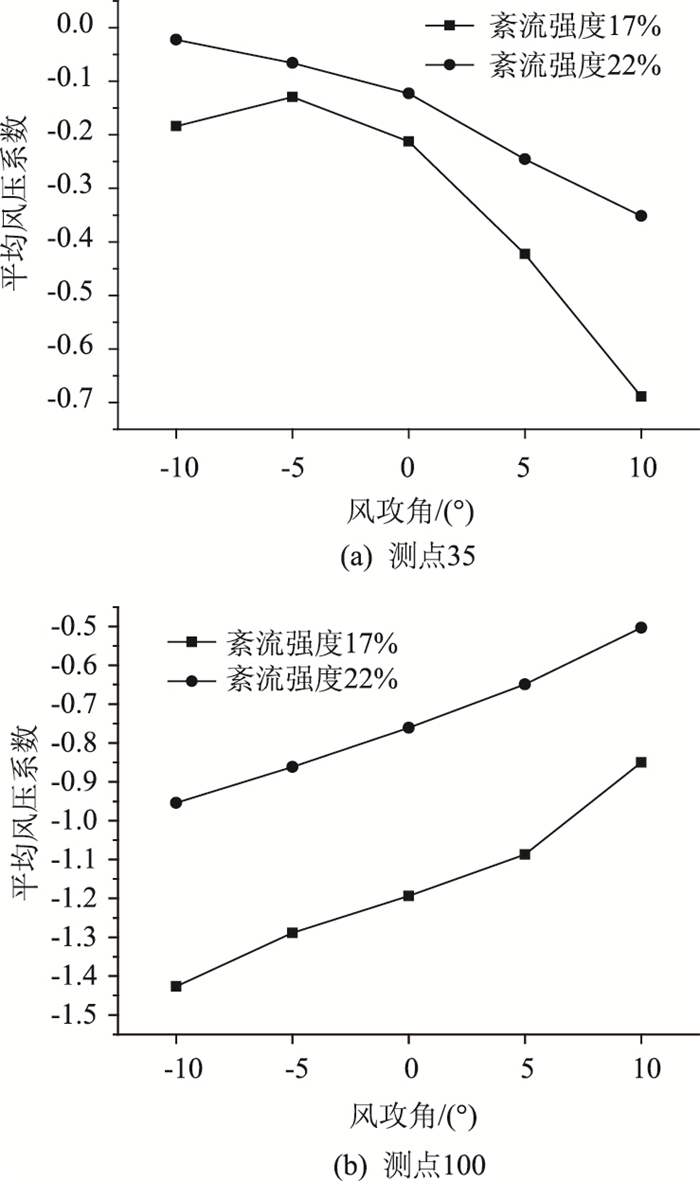
|
| 图 5 不同测点平均风压随风攻角及紊流强度变化图 Fig. 5 Mean wind pressure at different measuring points varying with wind attack angle and turbulence intensity |
| |
1.3.2 紊流强度对脉动风压系数的影响
图 6给出了紊流强度对脉动风压系数的影响。可见:模型表面各测点脉动风压系数基本随紊流强度增大而增大,但是在0°风攻角下,处于尾流区的50号到60号测点脉动风压系数却呈减小趋势,10°风攻角下70号到80号测点也出现了来流紊流强度大,但是脉动风压系数小的趋势,分析原因可能是因为这些位置受栏杆、风嘴、检修车轨道等附属结构影响,这些附属结构在来流作用下会产生特征紊流,这些测点脉动风压系数主要受到特征紊流的影响而不是来流紊流的影响,并没有表现出来流紊流强度越大脉动风压系数也越大的特点。所以对于桥梁断面,表面脉动风压系数基本随来流紊流强度增大而增大,但要考虑栏杆、检修车轨道等带来的影响,较低的来流在某些风攻角下,小部分区域受特征紊流的影响可能产生较大的脉动风压系数。
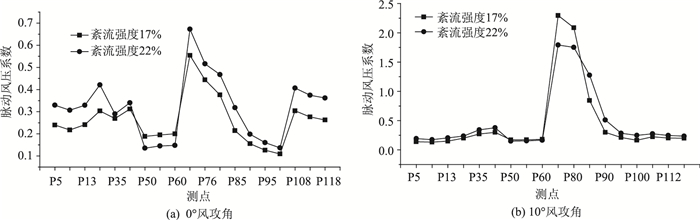
|
| 图 6 紊流强度对不同风攻角各测点脉动风压影响 Fig. 6 Influence of turbulence intensity on fluctuating wind pressure of different measuring points at different wind attack angles |
| |
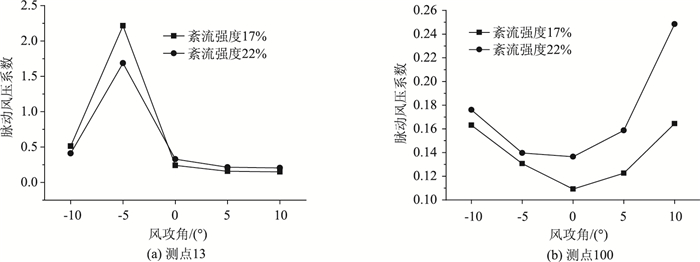
图 7给出了紊流强度对上表面测点13与下表面测点100脉动风压系数影响。可见:测点13在负攻角时,脉动风压系数随紊流强度增大而减小,正攻角时,脉动风压系数随紊流强度增大而增大。测点100在各风攻角下脉动风压系数均随紊流强度增大而增大,风攻角的变化会导致脉动风压系数增大的幅度不同。
|
| 图 7 不同测点脉动风压随风攻角及紊流强度变化图 Fig. 7 Fluctuating wind pressure at different measuring points varying with wind attack angle and turbulence intensity |
| |
对近流线形桥梁断面,受到栏杆、检修车轨道、风嘴、来流紊流强度、测点位置、风攻角等众多因素影响,结构表面脉动风压系数随紊流强度变化的规律比较复杂,不便采用公式统一修正。风洞试验时,这些因素的不当模拟,都会给风洞试验结果带来误差,且不便修正。
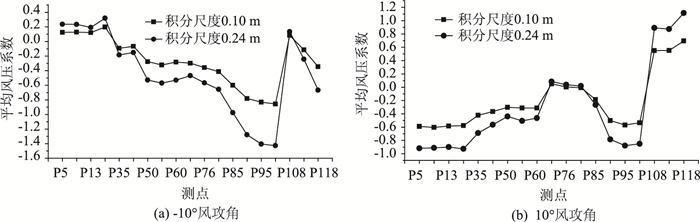
1.3.3 积分尺度对平均风压的影响图 8给出了积分尺度对各测点平均风压系数的影响。可见:积分尺度增大会导致平均风压系数的绝对值也增大,但桥面表面各位置增大的幅度各不相同。同上,近流线形桥梁断面受到来流紊流、特征紊流等诸多因素影响,很难进行修正,只能定性了解积分尺度增大会导致桥梁结构表面平均风荷载增大。
|
| 图 8 紊流积分尺度对不同风攻角各测点平均风压影响图 Fig. 8 Influence of turbulence intensity on mean wind pressure of different measuring points at different wind attack angles |
| |
1.3.4 积分尺度对脉动风压的影响
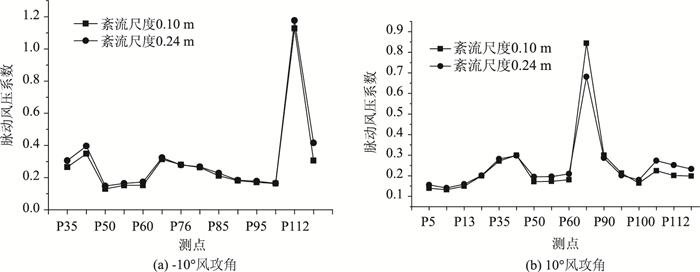
图 9给出了不同风攻角下,积分尺度对各测点脉动风压系数的影响。相比平均风压,脉动风压系数变化的幅度很小,而且不规律。脉动风压主要受来流紊流强度、特征紊流等因素影响,积分尺度对其影响很小。所以进行桥梁气弹模型试验时,应首先保证准确模拟紊流强度,积分尺度可以适当放宽要求。
|
| 图 9 紊流积分尺度对不同风攻角各测点脉动风压影响图 Fig. 9 Influence of turbulence integral scale on fluctuating wind pressure of different measuring points at different wind attack angles |
| |
1.3.5 积分尺度对脉动风压相关系数的影响
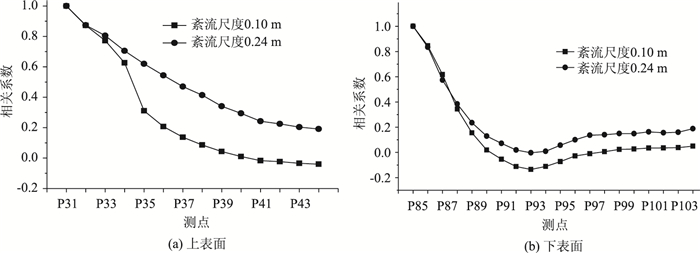
图 10分别在模型上表面连续选择31到44共14个测点,下表面选择85到104共20个测点,分别计算这些测点对31测点与85测点的相关系数。可见:不管是上表面还是下表面,前几个测点在两种紊流积分尺度流场中保持同样的衰减率,与来流的紊流积分尺度无关。如上表面31与32测点、下表面85到87测点衰减率在两种流场中基本相同。上表面从测点33开始,相关系数的衰减率在两种积分尺度流场中发生变化,下表面从88测点开始出现不一致。前面几个测点相关系数衰减率相同说明受来流积分尺度的影响很小,主要受主梁表面涡脱、再附等特征紊流的影响,其后测点才与来流的积分尺度相关。受其影响,来流积分尺寸越小,相关系数衰减越快。紊流积分尺度越大,可以让更大范围内的测点保持较大的相关系数。
|
| 图 10 0°风攻角时主梁表面不同位置相关系数 Fig. 10 Correlation coefficients of different positions of main beam surface at 0° wind attack angle |
| |
图 11给出了10°风攻角,上、下表面测点风压相关系数。可见:与0°攻角相比,上表面衰减率从39测点开始出现差异,差异点的位置推后,说明在10°风攻角,断面外形所产生的特征紊流形成的涡团尺度在上表面较0°攻角大,上表面各测点在特征紊流所形成的较大涡团范围内保持相同的衰减幅度,与来流积分尺度无关。当测点距离增大后,相关系数的衰减幅度才受来流积分尺度影响,积分尺度越小,相关系数衰减速度与幅度越大。下表面出现的差异点较0°攻角提前,说明在10°攻角,来流在下表面产生的特征紊流涡团尺度有所减小。风攻角的变化会导致上、下表面特征紊流的涡团尺度发生变化。与上表面相比,风攻角由0°变为10°,上表面特征紊流所产生的涡团尺度变化较下表面大。
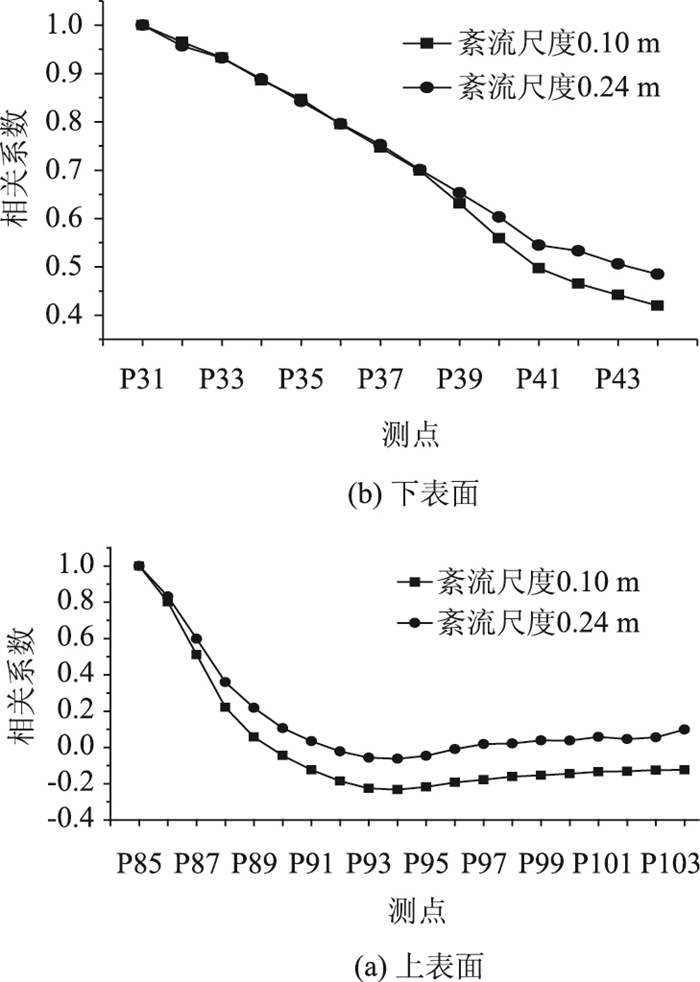
|
| 图 11 10°风攻角时主梁表面不同位置相关系数 Fig. 11 Correlation coefficients of different positions of main beam surface at 10° wind attack angle |
| |
1.3.6 积分尺度对脉动风功率谱的影响
图 12给出了紊流积分尺度对主梁上表面25测点脉动风压功率谱的影响。图中两种积分尺度流场中的测点脉动风功率谱在高频部分均与规范给出的Kaimal谱吻合较好,在低频部分能力低于Kaimal谱。两个流场中的测点脉动风功率谱基本一致,故积分尺度变化对测点脉动风功率谱的影响很小,脉动风功率谱主要与来流紊流相关,不受积分尺度变化的影响。
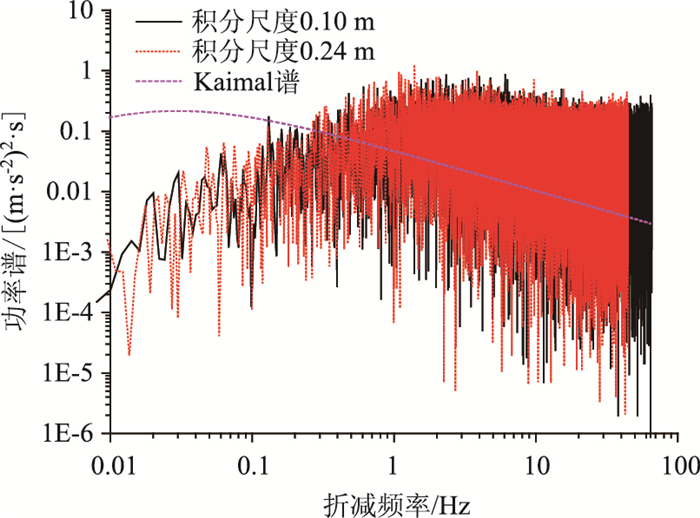
|
| 图 12 积分尺度对脉动风功率的影响 Fig. 12 Influence of integral scale on fluctuating wind power |
| |
2 结论
(1) 对近流线形桥梁断面,紊流强度由17%增大到22%会使结构表面平均风压系数绝对值减小。平均风压系数受结构表面位置、风攻角等因素的影响比较明显,当位置或风攻角发生变化后,紊流强度增大导致平均风压系数绝对值减小的幅度也会发生变化,很难进行定量修正。
(2) 近流线形桥梁表面大部分位置的脉动风压系数会随紊流强度增大而增大,但受栏杆、风嘴、检修车轨道等附属结构影响,这种趋势可能出现相反的变化,即小部分区域受特征紊流的影响可能在较小的紊流强度流场中产生较大的脉动风压系数。
(3) 紊流积分尺度增大会导致近流线形桥梁表面平均风荷载增大。
(4) 紊流积分尺度对脉动风压系数的影响很小。进行桥梁气弹模型试验时,应首先保证准确模拟紊流强度,在条件许可的情况下再准确模拟紊流积分尺度。
(5) 紊流积分尺度越小,桥梁表面压力相关系数衰减的速度与幅度越大。相邻位置的脉动风压相关系数主要受特征紊流影响,与来流的积分尺度无关。
| [1] |
STATHOPOULOS T, SURRY D. Scale Effects in Wind Tunnel Testing of Low Buildings[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1983, 13(1): 313-326. |
| [2] |
TIELEMAN H W. Wind Tunnel Simulation of the Turbulence in the Surface Layer[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1990, 36(1): 1309-1318. |
| [3] |
BEARMAN P W, MOREL T. Effect of Free Stream Turbulence on the Flow around Bluff Bodies[J]. Progress in Aerospace Sciences, 1983, 20(2): 97-123. |
| [4] |
LEE B E. Some Effect of Turbulence Scale on the Mean Forces on a Bluff Body[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1975, 1(4): 361-370. |
| [5] |
SCHEWE G. Reynolds-number Effects in Flow around More-or-less Bluff Bodies[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2001, 89(14): 1267-1289. |
| [6] |
BUCHER C G, LIN Y K. Effects of Wind Turbulence on Motion Stability of Long-span Bridges[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1990, 36(1): 1355-1364. |
| [7] |
张志田, 陈政清, 葛耀君, 等. 紊流中大跨度桥梁的扭转发散特性[J]. 工程力学, 2010, 27(2): 108-116. ZHANG Zhi-tian, CHEN Zheng-qing, GE Yao-jun, et al. Torsional Divergence Characteristics of Long Span Bridge in Turbulence[J]. Engineering Mechanics, 2010, 27(2): 108-116. |
| [8] |
WANG T, HAN W, YANG F, et al. Wind-vehicle-bridge Coupled Vibration Analysis Based on Random Traffic Flow Simulation[J]. Journal of Traffic and Transportation Engineering:English Edition, 2014, 1(4): 293-308. |
| [9] |
SCANLAN R H, LIN W H. Effects of Turbulence on Bridge Flutter Derivatives[J]. Journal of the Engineering Mechanics Division, 1978, 104(4): 719-733. |
| [10] |
潘韬, 赵林, 曹曙阳, 等. 多风扇主动控制风洞类平板断面抖振力识别研究[J]. 振动与冲击, 2010, 29(6): 178-183. PAN Tao, ZHAO Lin, CAO Shu-yang, et al. Buffeting Force Analysis of Thin Plate Section in Multiple Fans Active Control Wind Tunnel[J]. Journal of Vibration and Shock, 2010, 29(6): 178-183. |
| [11] |
华旭刚, 陈政清, 杨靖波, 等. 大缩尺比气弹模型风洞试验紊流积分尺度修正[J]. 建筑结构学报, 2010, 31(10): 55-61. HUA Xu-gang, CHEN Zheng-qing, YANG Jing-bo, et al. Turbulence Integral Scale Corrections to Aeroelastic Wind Tunnel Experimental Results with Large Scale Model[J]. Journal of Building Structures, 2010, 31(10): 55-61. |
| [12] |
卢占斌, 魏庆鼎. 网格紊流CAARC模型风洞实验[J]. 空气动力学学报, 2001, 19(1): 16-23. LU Zhan-bin, WEI Qing-ding. An Experiment on a CAARC Model in Grid Turbulent Flow[J]. Acta Aerodynamica Sinica, 2001, 19(1): 16-23. |
| [13] |
王利娟, 林志兴. 紊流对桥梁颤振特性影响的试验研究[J]. 同济大学学报:自然科学版, 2001, 29(4): 390-395. WANG Li-juan, LIN Zhi-xing. Experimental Study of Turbulence Effects on Bridge Flutter[J]. Journal of Tongji University:Natural Science Edition, 2001, 29(4): 390-395. |
| [14] |
李春光, 张记, 陈政清. 紊流积分尺度对桥梁颤振导数影响的试验研究[J]. 公路交通科技, 2016, 33(11): 69-75. LI Chun-guang, ZHANG Ji, CHEN Zheng-qing. Experimental Study on Influence of Turbulence Integral Scale on Flutter Derivatives of Bridge[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 69-75. |
| [15] |
茅建校, 王浩, 陶天友, 等. 紊流空间相关系数对大跨度三塔悬索桥抖振响应的影响[J]. 振动与冲击, 2016, 35(10): 202-206. MAO Jian-xiao, WANG Hao, TAO Tian-you, et al. Effects of the Turbulent Spatial Correlation Coefficient on Buffeting Responses of a Triple-tower Suspension Bridge[J]. Journal of Vibration and Shock, 2016, 35(10): 202-206. |
| [16] |
白桦.影响桥梁及建筑结构风洞试验结果若干因素研究[D].西安: 长安大学, 2012. BAI Hua. Research on Effect of Several Factors on Wind Tunnel Test Result of Bridge and Building Structure[D].Xi'an: Chang'an University, 2012. |
| [17] |
王骑, 廖海黎, 李明水, 等. 流线型箱梁气动外形对桥梁颤振和涡振的影响[J]. 公路交通科技, 2012, 29(8): 44-50, 70. WANG Qi, LIAO Hai-li, LI Ming-shui, et al. Influence of Aerodynamic Shape of Streamline Box Girder on Bridge Flutter and Vortex-induced Vibration[J]. Journal of Highway and Transportation Research and Development, 2012, 29(8): 44-50, 70. |
| [18] |
马文勇, 邓然然, 卢金玉. D形断面柱体驰振耦合气动力特性试验研究[J]. 振动工程学报, 2017, 30(5): 755-763. MA Wen-yong, DENG Ran-ran, LU Jin-yu. Characteristics of Coupled Aerodynamic Forces of a Galloping Cylinder with D-section[J]. Journal of Vibration Engineering, 2017, 30(5): 755-763. |
 2019, Vol. 36
2019, Vol. 36
