扩展功能
文章信息
- 柳兴成, 蔺鹏臻, 何志刚
- LIU Xing-cheng, LIN Peng-zhen, HE Zhi-gang
- 考虑全截面剪切变形效应的波形钢腹板箱梁挠度计算
- Calculation of Deflection of Box Girder with Corrugated Steel Webs Considering Shear Deformation Effect of Whole Section
- 公路交通科技, 2019, 36(1): 63-69
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 63-69
- 10.3969/j.issn.1002-0268.2019.01.009
-
文章历史
- 收稿日期: 2017-04-10
2. 兰州交通大学 土木工程学院, 甘肃 兰州 730070
2. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou Gansu 730070, China
随着社会的不断进步,传统的预应力混凝土箱梁桥已不能满足社会发展的需求,其中大跨度桥梁的自重大,严重影响着现代桥梁的发展,同时混凝土腹板的开裂给桥梁的后期养护带来了很大的困扰。从第一座波形钢腹板箱梁桥建成到现在的30多年之间,一种采用弯成波折形状的薄壁钢板作为腹板的钢混组合箱梁已渐渐进入广大学者的视线[1]。波形钢腹板箱梁可以减轻恒载20%左右,降低地震力,解决混凝土箱梁的腹板开裂问题,钢腹板的折皱效应可有效地提高腹板的抗剪能力,同时在跨径相同的情况下可缩减下部结构的工程量,而且波形钢腹板像水波一样的曲线形状所产生的视觉效应更具美感[2]。在波形钢腹板箱梁受力时,波形钢腹板承担剪力,混凝土顶底板承担弯矩,结构受力明确,充分利用了材料各自的优势。与混凝土箱梁一样,波形钢腹板箱梁也存在由于翼板的剪切变形而引起的剪力滞效应[3],而且在跨中截面尤为明显[4]。到目前为止,对于波形钢腹板箱梁的抗剪、抗弯等力学性能,国外学者Driver[5]、Luo等[6]、Elgaaly等[7]已通过大量的模型试验进行了系统的研究,国内学者李宏江等[8-12]对波形钢腹板的剪切变形进行了深入研究,但没有考虑剪力滞效应。姚浩[13]研究了考虑腹板剪切变形和一般余弦式的剪力滞翘曲位移函数对挠度的影响,但未深入探究翼板的剪切变形规律。
本研究在合理定义翘曲位移函数的同时,考虑腹板的剪切变形,提出一种考虑波形钢腹板和混凝土顶、底板在其自身平面内的全截面剪切变形的挠度计算方法,并在单箱单室和单箱双室算例中,以ANSYS有限元值为参考,验证其精确性,并分析挠度的组成部分,研究各组成部分对挠度的贡献程度,为波形钢腹板箱梁挠度的简化计算提供必要的理论基础。
1 考虑全截面剪切变形的位移函数 1.1 波形钢腹板箱梁纵向位移表达式波形钢腹板箱梁等薄壁结构在竖向荷载作用下发生弯曲变形时,横截面沿着纵向(梁长方向)的位移包括3部分:
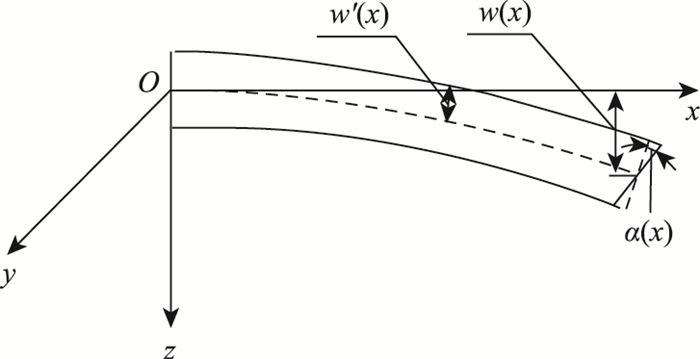
(1) 梁体的竖向挠曲w(x)引起的变形,详见图 1,即欧拉-伯努利梁理论变形,其表达式为:
|
| 图 1 铁木辛柯梁横截面转角 Fig. 1 Cross-section rotation angle of Timoshenko beam |
| |
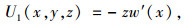
|
(1) |
式中,z为梁上一点的z轴坐标;w′(x)为由竖向位移w(x)引起的纵向位移转角。
(2) 考虑截面横向剪切变形引起的的挠度,详见图 1,即铁木辛柯梁理论变形,其表达式为:
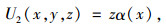
|
(2) |
式中α(x)为箱梁截面的剪切变形转角。
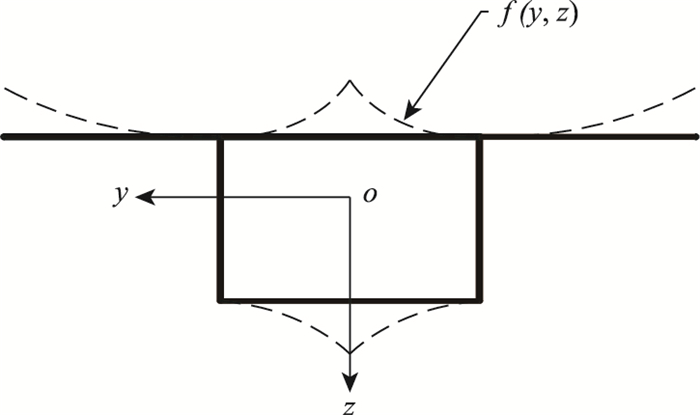
(3) 考虑箱梁翼板(顶、底板)在其自身平面内剪切变形效应的变形,详见图 2,即由剪力滞效应引起的变形,其表达式为:
|
| 图 2 箱梁剪力滞翘曲位移 Fig. 2 Shear lag warping displacement of box girder |
| |
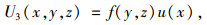
|
(3) |
式中,f(y, z)为箱梁截面的剪力滞翘曲位移函数;u(x)为顶底、板翘曲位移差。
于是,波形钢腹板箱梁的纵向位移可表示为:
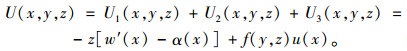
|
(4) |
由式(4)可知,w′(x)和u(x)为待求的变量,α(x)为反映波形钢腹板在其面内剪切变形的位移函数,由式(5)确定[14]:
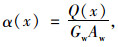
|
(5) |
式中,Q(x)为剪力;Gw为波形钢腹板的有效剪切模量,可用式(6)计算确定[15];Aw为波形钢腹板的横截面面积。
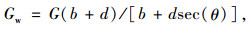
|
(6) |
式中,b,d,θ参数见图 3;G为波形钢腹板的剪切模量。

|
| 图 3 波形钢腹板几何形状 Fig. 3 Geometric shape of corrugated steel web |
| |
f(y, z)为反映顶、底板在其面内剪切变形的翘曲位移函数,是需提前定义的。参考文献[3],定义顶、底板的翘曲位移函数为经典的三次抛物线:
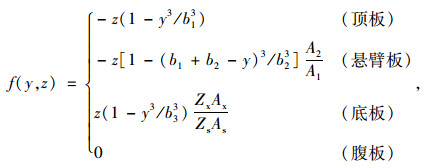
|
(7) |
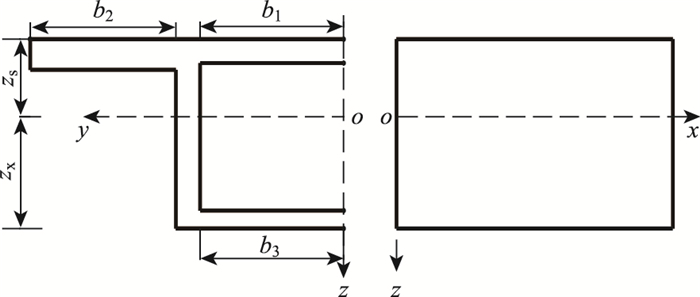
式中,b1和b3分别为内侧顶板和底板的半宽;b2为悬臂板的宽度;A1和A2分别为内侧顶板和悬臂板的面积,As和Ax分别为顶板(内侧顶板和悬臂板)和底板的面积; Zs和Zx分别为上、下缘到截面中性轴的距离(如图 4所示)。
|
| 图 4 箱梁节段及正方向 Fig. 4 Box girder segment and its positive direction |
| |
2 波形钢腹板箱梁挠度计算公式 2.1 基本假定
根据波形钢腹板箱梁在纵向的手风琴效应,在公式推导中采用以下假定[16-17]:
(1) 忽略波形钢腹板的纵向刚度,外荷载产生的剪力全部由波形钢腹板承担,而弯矩均由混凝土顶底板承担。
(2) 忽略顶、底板及翼缘板的竖向应变和横向应变,以及其面外的剪切应变。
(3) 在弯曲荷载作用下,顶底板及翼缘板符合“拟平截面假定”。
(4) 箱梁在弹性工作范围之内,不考虑钢筋的影响。
2.2 基于变分原理的控制微分方程根据波形钢腹板箱梁的纵向位移函数,可得其弹性应变为:
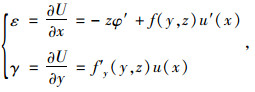
|
(8) |
式中,φ′=w′(x)-α(x),f′y(y, z)为f(y, z)对y的偏微分。
顶底板及翼缘板的应变能可用对梁段体积V积分表示为:
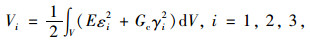
|
(9) |
式中,E为混凝土的弹性模量;Gc为混凝土的剪切模量。
波形钢腹板的应变能为:
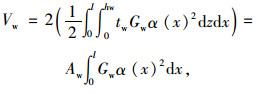
|
(10) |
式中,hw为波形钢腹板竖向高度;tw为波形钢腹板的厚度;l为波形钢腹板箱梁的计算跨径。
引入竖向弯曲惯性矩I、剪滞翘曲惯性矩Iu、剪滞翘曲惯性积If和剪滞翘曲面积Au等广义截面特性[18]后,梁体总的应变能为:
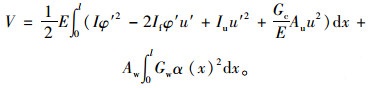
|
(11) |
根据最小势能原理,梁体处于平衡状态的充分必要条件是梁体总势能的一阶变分为零,则:
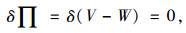
|
(12) |
式中,V为梁体的总应变能;W为梁体的外力势能,采用式(13)计算。
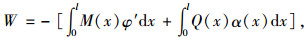
|
(13) |
式中M(x)为外荷载产生的梁段弯矩。
将式(11)和式(13)代入式(12),利用变分原理,得到箱梁的竖向挠曲位移w(x)关系式:
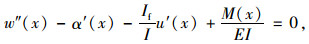
|
(14) |
及边界条件:
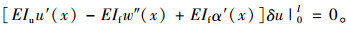
|
(15) |
u(x)可利用微分方程(16)和边界条件(15)求得。
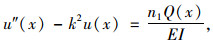
|
(16) |
式中,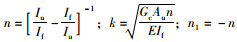
至此,波形钢腹板箱梁挠度的计算可首先根据波形钢腹板箱梁截面的参数和材料的特性值,计算得到k,n;然后根据不同工况下的梁体内力,由式(14)~ (16)联立求解微分方程得到。
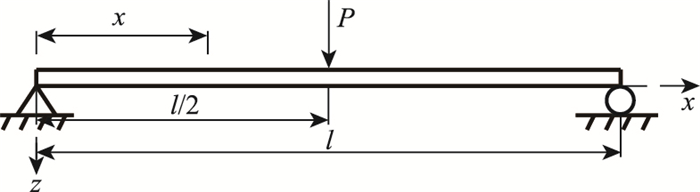
2.3 不同荷载作用下的挠度计算公式 2.3.1 简支梁受跨间集中力作用对于图 5跨间作用集中力P的波形钢腹板简支箱梁,利用式(14)~(16),得到挠度计算公式式(17)。
|
| 图 5 简支波形钢腹板箱梁跨中作用集中荷载 Fig. 5 Simply supported box girder with corrugated steel webs under concentrated load at midspan |
| |
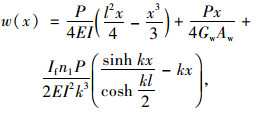
|
(17) |
令x=l/2,可得跨中位置的竖向挠度为:
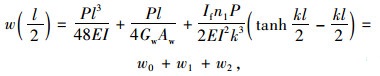
|
(18) |
式中,w0为根据初等梁理论得到的挠度;w1为由腹板剪切变形引起的挠度;w2为由剪力滞效应引起的挠度[13]。
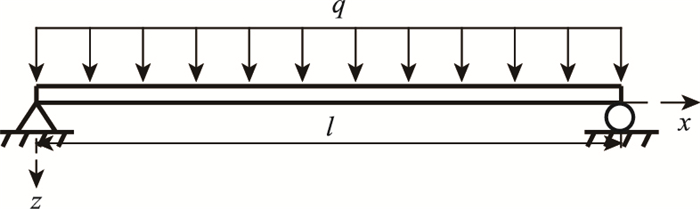
2.3.2 简支梁受满跨均布荷载作用对于如图 6所示的承受满跨均布荷载q的波形钢腹板简支箱梁,利用式(14)~ (16),得到挠度计算公式为:
|
| 图 6 简支波形钢腹板箱梁受均布荷载作用 Fig. 6 Simply supported box girder with corrugated steel webs under uniformly distributed load |
| |
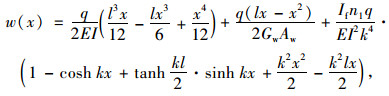
|
(19) |
令x=l/2,可得跨中位置的竖向挠度为:
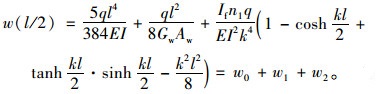
|
(20) |
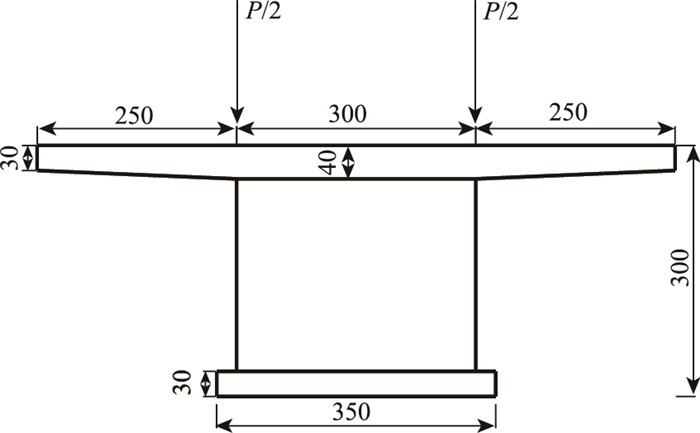
本研究采用文献[8]中的单箱单室波形钢腹板箱梁为模型,其截面尺寸如图 7所示。为了在箱梁横截面上不产生扭转和畸变效应,将集中荷载P施加在波形钢腹板与顶板的相交处。波形钢腹板的截面参数:b=30 mm,d=26 mm,厚度t=1 mm,θ=30°。材料特性:弹性模量为2.7×1010 Pa,剪切模量为8.4×1010 Pa。
|
| 图 7 单箱单室波形钢腹板箱梁截面(单位:mm) Fig. 7 Cross-section of single-box single-cell corrugated box girder (unit:mm) |
| |
利用式(18)计算在集中荷载P=25 kN作用下跨径分别为3,4.5,6,7.5,9 m的箱梁跨中竖向挠度,与文献[8]仅考虑腹板剪切变形而未考虑剪力滞效应的跨中挠度计算值和采用板壳单元的ANSYS有限元值[8]进行对比分析,见表 1。
由于本研究考虑了翼板和腹板的剪切变形,更符合箱梁的受力特点。与板壳有限元解相比,本研究各种跨径下的挠度计算误差均在5%以内,符合波形钢腹板箱梁挠度计算的精度需求。与仅考虑波形钢腹板剪切转角的计算值相比,本研究在7.5 m跨径以内的挠度计算结果精度更高,在不小于7.5 m跨径时的挠度计算结果比有限元值稍大,误差在2%以内。
3.2 挠度规律研究为了研究由初等梁理论得到的挠度w0、由腹板剪切变形引起的挠度w1和由剪力滞效应引起的挠度w2等各挠度值在不同跨径下对总挠度的贡献,定义Δwi,其表达式为:
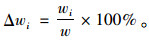
|
(21) |
在集中荷载P=25 kN作用下,取3,4.5,6,7.5,9 m作为基本跨径,计算得到w0,w1,w2以及Δw,见表 2。
| 跨径/m | 变量 | w0 | w1 | w2 | w |
| 3 | 挠度/mm | 0.964 | 0.520 | 0.025 | 1.509 |
| Δwi | 63.88 | 34.46 | 1.66 | — | |
| 4.5 | 挠度/mm | 3.254 | 0.780 | 0.038 | 4.072 |
| Δwi | 79.91 | 19.16 | 0.93 | — | |
| 6 | 挠度/mm | 7.713 | 1.040 | 0.051 | 8.804 |
| Δwi | 87.61 | 11.81 | 0.58 | — | |
| 7.5 | 挠度/mm | 15.064 | 1.300 | 0.063 | 16.427 |
| Δwi | 91.70 | 7.91 | 0.39 | — | |
| 9 | 挠度/mm | 26.030 | 1.560 | 0.077 | 27.667 |
| Δwi | 94.08 | 5.64 | 0.28 | — |
从表 2可以看出,在荷载不变的情况下,初等梁理论计算所得的挠度值对总挠度的贡献最小可达到63.88%,此时腹板剪切变形所引起的挠度对总挠度的贡献为34.46%,剪力滞效应引起的挠度对总挠度的贡献为1.66%。但随着跨度的增加,初等梁理论计算所得的挠度对总挠度的贡献增大,而腹板的剪切变形和剪力滞效应引起的挠度对总挠度的贡献降低。
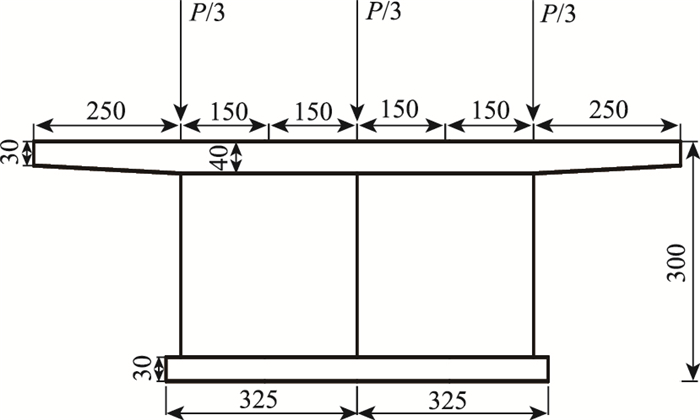
4 单箱双室箱梁的挠度分析 4.1 算例研究本研究采用文献[13]中单箱双室箱梁算例中的截面特性,如图 8所示。为了在箱梁横截面上减少扭转和畸变效应的影响,将集中荷载P或者均布荷载q施加在波形钢腹板与顶板的相交处。其中波形钢腹板的截面参数和材料特性与上述单箱单室箱梁的算例一致。
|
| 图 8 单箱双室波形钢腹板箱梁截面(单位:mm) Fig. 8 Cross-section of single-box double-cell corrugated box girder (unit: mm) |
| |
利用式(18)和式(20)分别计算集中荷载P=25 kN或均布荷载q=5 kN/m作用下跨径分别为3,4.5,6,7.5,9 m的简支箱梁的跨中竖向挠度,并与ANSYS有限元值[13]相比较,见表 3。其中箱梁的横断面尺寸保持不变。
从表 3可以看出,两种荷载作用下,本研究的计算结果比ANSYS有限元值都略大,最大误差在10%以内,但随着桥梁跨度的增加,误差减小,最小误差在5%左右。
4.2 挠度规律研究以3,4.5,6,7.5,9 m为基本跨径,利用式(21)计算分析单箱双室波形钢腹板简支箱梁在集中荷载P=25 kN或均布荷载q=5 kN/m作用下,w0,w1,w2对总挠度的贡献,结果见表 4、表 5。
| 跨径/m | 变量 | w0 | w1 | w2 | w |
| 3 | 挠度/mm | 0.569 | 0.347 | 0.047 | 0.963 |
| Δwi | 59.09 | 36.03 | 4.88 | — | |
| 4.5 | 挠度/mm | 1.920 | 0.520 | 0.070 | 2.510 |
| Δwi | 76.49 | 20.72 | 2.79 | — | |
| 6 | 挠度/mm | 4.552 | 0.693 | 0.094 | 5.339 |
| Δwi | 85.26 | 12.98 | 1.76 | — | |
| 7.5 | 挠度/mm | 8.890 | 0.867 | 0.117 | 9.874 |
| Δwi | 90.04 | 8.78 | 1.18 | — | |
| 9 | 挠度/mm | 15.362 | 1.040 | 0.141 | 16.543 |
| Δwi | 92.86 | 6.29 | 0.85 | — |
| 跨径/m | 变量 | w0 | w1 | w2 | w |
| 3 | 挠度/mm | 0.213 | 0.104 | 0.015 | 0.332 |
| Δwi | 64.16 | 31.33 | 4.51 | — | |
| 4.5 | 挠度/mm | 1.080 | 0.234 | 0.032 | 1.346 |
| Δwi | 80.24 | 17.38 | 2.38 | — | |
| 6 | 挠度/mm | 3.414 | 0.416 | 0.057 | 3.887 |
| Δwi | 87.83 | 10.70 | 1.47 | — | |
| 7.5 | 挠度/mm | 8.334 | 0.650 | 0.089 | 9.073 |
| Δwi | 91.85 | 7.17 | 0.98 | — | |
| 9 | 挠度/mm | 17.282 | 0.936 | 0.128 | 18.347 |
| Δwi | 94.20 | 5.10 | 0.70 | — |
将表 4中的数据与表 2中的数据对比可得,单箱双室和单箱单室的各种挠度变化规律相同,但随着箱室的增加,由全截面剪切变形引起的挠度也增大,最大增幅为4.79%。将表 4中的数据与表 5中的数据对比可得,均布荷载作用下,初等梁理论计算所得的挠度增大,腹板剪切变形引起的挠度变小,最大减幅为4.7%,而剪力滞效应引起的挠度基本不变。
5 结论(1) 本研究的计算结果与ANSYS板壳分析结果吻合良好,在不同跨径下的挠度计算误差均在5%以内,符合波形钢腹板箱梁挠度计算的精度需求。
(2) 将本研究方法进一步推广,通过单箱双室箱梁算例的对比分析得出,本研究的计算公式对于单箱多室箱梁同样适用,而且计算结果略偏大,但随着跨径的增大,误差减小,最小误差在5%左右。同时,全截面剪切变形效应对单箱单室波形钢腹板箱梁挠度的贡献最大为36.12%,对单箱双室波形钢腹板箱梁挠度的贡献最大为40.91%,随着跨径的增大,全截面剪切变形效应对挠度的贡献减小。
(3) 在同一工况下,波形钢腹板箱梁的箱室越多,全截面剪切变形效应对挠度的贡献越大。在不同工况下,波形钢腹板箱梁的箱室越多,集中荷载作用下的全截面剪切变形效应对挠度的贡献越大。
| [1] |
CHEYREZY M, COMBAULT J. Composite Bridges with Corrugated Steel Webs: Achievements and Prospects[C]//IABSE Symposium on Mixed Structures, including New Materials. Brussels: IABSE, 1990.
|
| [2] |
李澎涛.波形钢腹板组合箱梁桥不同阶段的力学特性分析[D].天津: 河北工业大学, 2016: 1-7. LI Peng-tao. Analysis of Mechanical Property of Composite Box Girder Bridge with Corrugated Steel Webs at Different Stages[D]. Tianjin: Hebei University of Engineering, 2016: 1-7. |
| [3] |
蔺鹏臻, 周世军. 基于剪切变形规律的箱梁剪力滞效应研究[J]. 铁道学报, 2011, 33(4): 100-104. LIN Peng-zhen, ZHOU Shi-jun. Analysis on Shear-lag Effect of Box Girders Based on Flange-slab Shear Deformation Law[J]. Journal of the China Railway Society, 2011, 33(4): 100-104. |
| [4] |
任红伟. 波纹钢腹板预应力混凝土箱梁弯曲性能试验研究[J]. 铁道学报, 2008, 30(1): 60-64. REN Hong-wei. Experimental Study on Prestressed Concrete Box-girders with Corrugated Steel Webs under Symmetrical Loads[J]. Journal of the China Railway Society, 2008, 30(1): 60-64. |
| [5] |
DRIVER R G, ABBAS H H, SAUSE R. Shear Behavior of Corrugated Web Bridge Girders[J]. Journal of Structural Engineering, 2006, 132(2): 195-203. |
| [6] |
LUO R, EDLUND B. Shear Capacity of Plate Girders with Trapezoidally Corrugated Webs[J]. Thin-Walled Structures, 1996, 26(1): 19-44. |
| [7] |
ELGAALY M, SESHADRI A, HAMILTON R W. Bending Strength of Steel Beams with Corrugated Webs[J]. Journal of Structural Engineering, 1997, 123(6): 772-782. |
| [8] |
李宏江, 叶见曙, 万水, 等. 剪切变形对波形钢腹板箱梁挠度的影响[J]. 交通运输工程学报, 2002, 2(4): 17-20. LI Hong-jiang, YE Jian-shu, WAN Shui, et al. Influence of Shear Deformation on Deflection of Box Girder with Corrugated Steel Webs[J]. Journal of Traffic and Transportation Engineering, 2002, 2(4): 17-21. |
| [9] |
万水, 李淑琴, 马磊. 波形钢腹板预应力混凝土组合箱梁结构在中国桥梁工程中的应用[J]. 建筑科学与工程学报, 2009, 26(2): 15-20. WAN Shui, LI Shu-qin, MA Lei. Application of Prestressed Concrete Composite Box-girder Structure with Corrugated Steel Webs in Bridge Engineering in China[J]. Journal of Architecture and Civil Engineering, 2009, 26(2): 15-20. |
| [10] |
李立峰, 刘志才, 王芳. 波形钢腹板PC组合箱梁抗弯承载力的理论与试验研究[J]. 工程力学, 2009, 26(7): 89-96. LI Li-feng, LIU Zhi-cai, WANG Fang. Theoretical and Experimental Research on the Flexural Behavior of External Prestressed Composite Beam with Corrugated Webs[J]. Engineering Mechanics, 2009, 26(7): 89-96. |
| [11] |
李立峰, 刘志才, 王芳. 波形钢腹板组合箱梁弹性阶段弯曲理论及模型试验研究[J]. 公路交通科技, 2008, 25(1): 69-73, 78. LI Li-feng, LIU Zhi-cai, WANG Fang. Research on Flexure Theory at Elastic Stage and Model Test of Composite Box-girder with Corrugated Steel Webs[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 69-73, 78. |
| [12] |
徐岳, 朱万勇, 杨岳. 波形钢腹板PC组合箱梁桥抗弯承载力计算[J]. 长安大学学报:自然科学版, 2005, 25(2): 60-64. XU Yue, ZHU Wan-yong, YANG Yue. Calculation of Ultimate Moment Capacity of Prestressed Concrete Box-girder Bridge with Corrugated Steel Webs[J]. Journal of Chang'an University:Natural Science Edition, 2005, 25(2): 60-64. |
| [13] |
姚浩, 程进. 基于变分原理的波形钢腹板箱梁挠度计算解析法[J]. 工程力学, 2016, 33(8): 177-184. YAO Hao, CHENG Jin. Analytical Method for Calculating Deflection of Corrugated Box Girders Based on Variational Principle[J]. Engineering Mechanics, 2016, 33(8): 177-184. |
| [14] |
冯天鹏, 徐向锋, 张峰, 等. 波形钢腹板箱梁剪力滞效应研究[J]. 重庆交通大学学报:自然科学版, 2016, 35(6): 11-16. FENG Tian-peng, XU Xiang-feng, ZHANG Feng, et al. Shear Lag Effect of Box Girder with Corrugated Steel Webs[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2016, 35(6): 11-16. |
| [15] |
JOHNSON R P, CAFOLLA J. Corrugated Webs in Plate Girders for Bridges[J]. Structures and Buildings, 1997, 122(2): 157-164. |
| [16] |
冀伟, 刘世忠, 蔺鹏臻. 均布荷载作用下波形钢腹板简支箱梁的挠度[J]. 公路交通科技, 2012, 29(12): 70-73. JI Wei, LIU Shi-zhong, LIN Peng-zhen. Deflection of Simple-supported Box Girder with Corrugated Steel Webs under Uniform Load[J]. Journal of Highway and Transportation Research and Development, 2012, 29(12): 70-73. |
| [17] |
左志鹏.波形钢腹板组合梁的变形分析研究[D].成都: 西南交通大学: 2015: 6-16. ZUO Zhi-peng. Research and Analysis on Deflection of Composite Beams with Corrugated Steel Webs[D]. Chengdu: Southwest Jiaotong University: 2015: 6-16. |
| [18] |
张元海, 李乔. 箱形梁剪滞效应分析中的广义力矩研究[J]. 铁道学报, 2007, 29(1): 77-81. ZHAN Yuan-hai, LI Qiao. Study on the Generalized Moment in Shear Lag Effect Analysis of the Box Girder[J]. Journal of the China Railway Society, 2007, 29(1): 77-81. |
 2019, Vol. 36
2019, Vol. 36
