扩展功能
文章信息
- 张向东, 李军, 周军霞, 孙汉东, 杨宇婷
- ZHANG Xiang-dong, LI Jun, ZHOU Jun-xia, SUN Han-dong, YANG Yu-ting
- 考虑D-P边界退化的冻风积土蠕变损伤规律研究
- Study on Creep Damage Rule of Frozen Aeolian Soil Considering D-P Boundary Degradation
- 公路交通科技, 2019, 36(1): 55-62, 86
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 55-62, 86
- 10.3969/j.issn.1002-0268.2019.01.008
-
文章历史
- 收稿日期: 2017-01-23
2. 沈阳建筑大学 土木工程学院, 辽宁 沈阳 110168;
3. 辽宁工程技术大学 建筑与交通学院, 辽宁 阜新 123000;
4. 辽宁奥路通科技有限公司, 辽宁 沈阳 110006
2. School of Civil Engineering, Shenyang Jianzhu University, Shenyang Liaoning 110168, China;
3. School of Architecture and Transportation, Liaoning Technical University, Fuxin Liaoning 123000, China;
4. Liaoning Aolutong Science and Technology Co., Ltd., Shenyang Liaoning 110006, China
风积土是由岩石风化作用形成的碎屑经风力搬运作用形成的一类细粒土,在我国东北部及西部地区有着广泛的分布。由于其具有松散的颗粒结构,以风积土作为填土路基在寒冷的冬季较容易发生冻胀现象,且冻结状态下的风积土路基达到稳定的变形为一缓慢的过程,具有明显的流变特征[1-3]。因此,研究受气候变化及工程活动影响的冻风积土蠕变特性对该类路基沉降控制及安全使用具有实际意义。
冻风积土流变模型与流变试验研究是岩土工程领域重要的方向。董连成[4]通过对不同温度、不同加载应力下的冻结兰州黄土、黏土和砂质黏土的蠕变试验获得了3种土的蠕变特性;赵延林[5]通过对分级加载下的岩石蠕变进行黏弹塑性分离以及对西原元件进行改进的方法建立了一种新的蠕变损伤模型;Bray Matthew T[6]采用一个简单的松弛试验获得了冻风积土在蠕变过程中的蠕变参数;赵晓东[7]等通过开展不同温度梯度下的三轴蠕变试验,研究了冻风积土蠕变特征和温度梯度下的冻风积土非均质特征。
在荷载作用下,冻风积土内部裂隙的发展是导致冻风积土在蠕变过程中发生损伤的重要因素。前苏联学者维亚洛夫[8]首次将损伤力学引入到冻风积土领域进行研究,并引入一种冻风积土蠕变破坏程度的描述方法;Kachanov[9]最先提出用连续性变量描述材料连续性受损的变形特征;孙琦[10]通过对不同温度、不同应力下的风积土进行正交蠕变试验,获得了冻结条件下风积土蠕变损伤模型;汪承维[11]等以西原模型为基础,采用改进的Mohr-Coulomb屈服准则,建立了3个阶段的蠕变损伤本构模型。王其虎[12]等考虑天然岩石的初始损伤以及蠕变过程中岩石加载后裂隙扩充产生的新损伤,对岩石的蠕变特性进行描述。
目前,有关蠕变损伤初始时间研究较少,并且大都认为冻风积土蠕变损伤发生在第Ⅲ阶段,建立的损伤模型大多是对元件模型进行改进,并考虑损伤对蠕变参数的影响,但是很少对屈服边界的损伤机理进行深入研究。通过对冻风积土室内蠕变试验所获得的蠕变曲线分析,认为从衰减蠕变过渡到加速蠕变必然存在一个驻点(凹凸曲线的分界点),因此蠕变损伤开始于第Ⅱ阶段的拐点。通过改进的西原模型,以损失时间阈值点和屈服临界点为界限提出了分阶段的蠕变损伤模型。最后,通过屈服边界损伤阐述了冻风积土在蠕变过程中发生屈服的机理。
1 蠕变损伤模型 1.1 蠕变损伤变量对于蠕变损伤过程,Kachanov建议将损伤演化率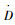
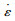
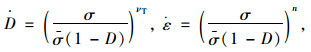
|
(1) |
式中,D为蠕变损伤变量;(·)为变量对时间的一阶导数;σ,νT和n为依赖于温度的材料待测特征参数。
设tD为发生蠕变损伤的初始时间,对式(1)第1式变形,并且两边对时间进行积分可得:
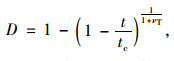
|
(2) |
式中,t为时间;tc为蠕变试验停止的时间,可表示为:
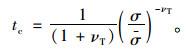
|
(3) |
如图 1所示,冻风积土最先发生的是瞬时变形ε0,此部分变形瞬时即可完成,满足胡克定律。接下来由于土颗粒间位错阻力不断加大,发生具有时间延滞特性的减速蠕变,分别对应着蠕变曲线的第Ⅰ阶段及第Ⅱ阶段前期。由于微裂隙随变形的不断发展,当裂隙间连通出现空洞时开始发生加速蠕变,蠕变曲线上的拐点A(ε″=0)为衰减蠕变和加速蠕变的分界点,则A点对应的时间tD必为损伤时间阈值(初始损伤时间);ε″为应变的二阶导数。
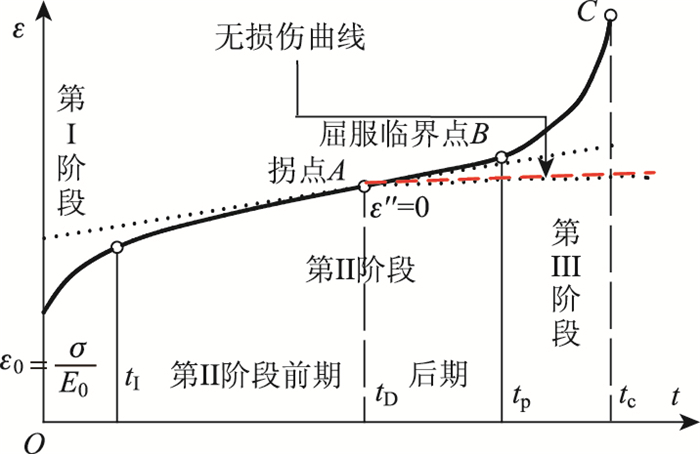
|
| 图 1 蠕变损伤阶段划分图 Fig. 1 Division of creep damage stages |
| |
西原模型能够描述从蠕变第Ⅰ阶段至蠕变第Ⅲ阶段弹-黏弹-黏塑性特征而得到广泛应用,元件模型如图 2所示。当应力σ超过屈服强度σs时,变形由第Ⅱ阶段稳定蠕变进入第Ⅲ阶段加速蠕变。但由于冻风积土内部产生的空洞,σs是随损伤变量D逐渐演化的。因此,将西原模型中黏塑性元件改进成具有损伤特性的非线性黏塑性体,发生屈服时边界服从于Drucker-Prager准则。
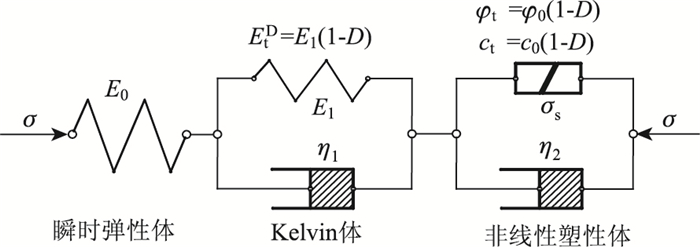
|
| 图 2 改进的西原非线性元件模型 Fig. 2 Modified Nishihara nonlinear element model 注:φt,ct为发生蠕变损伤后的黏聚力和内摩擦角;φ0,c0为初始黏聚力和内摩擦角; EtD为发何时能损伤后的弹性模量。 |
| |
在拐点A之前发生的是衰减蠕变,此部分的蠕变变形εOD (t)可表示为[14]:
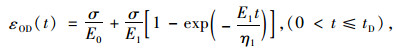
|
(4) |
式中,E0, E1分别为瞬时弹性体和Kelvin体初始弹性模量;η1为Kelvin体初始黏滞系数。
从拐点A到屈服临界点B之间的蠕变εDP (t)可表示为:
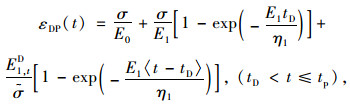
|
(5) |
式中,定义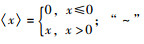
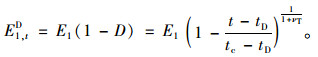
|
(6) |
当进入第Ⅱ阶段后期及第Ⅲ阶段时,若不发生损伤,在超过A点后的最终变形将接近一定值(如图 1的虚线)。但是大量试验结果显示负温较高时冻风积土发生图 1中实线所示的加速蠕变现象[15-16],原因是裂隙连通形成内部裂纹使冻风积土内部结构发生损伤,影响冻风积土继续承载的能力。
当t>tp时,有效应力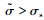
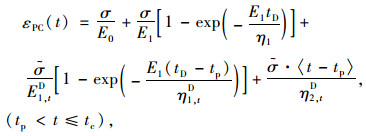
|
(7) |
其中,η2, tD的损伤演化准则为:
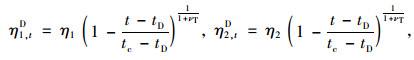
|
(8) |
式中,η1, tD,η2, tD为发生损伤后的黏滞性系数。
2 冻风积土蠕变特性测试 2.1 试样制备与测试装置试验用土取自于辽宁省阜新市境内人民桥填土路堤下的风积砂路基填土。将采集的风积土样品通过风干、碾碎及筛分选取粒径小于2 mm的土样进行土工试验,测得其基本物理参数见表 1。
| 试件编号 | 液限/% | 塑限/% | 塑性指数/% | 含水率/% | 干密度/ (g·cm-3) |
黏聚力/kPa | 内摩擦角/(°) |
| ① | 31.8 | 18.2 | 13.6 | 21.1 | 1.79 | 21.6 | 17.3 |
| ② | 32.5 | 17.8 | 14.7 | 20.8 | 1.73 | 21.9 | 16.9 |
| ③ | 30.6 | 17.6 | 13.0 | 20.6 | 1.82 | 22.3 | 17.2 |
| 平均 | 31.4 | 17.9 | 13.8 | 20.8 | 1.78 | 21.9 | 17.1 |
加入适量的蒸馏水搅拌均匀并利用模具制成圆柱形试件。抽气2 h并饱水24 h,然后放入-30 ℃的制冷箱中静置48 h,然后脱模套上橡胶套,最后放在恒温压力舱中,分别在-2,-5,-10,-15 ℃和-20 ℃的恒温条件下进行蠕变试验[17]。采用英国进口的冻土GDS测试系统进行恒温蠕变测试,并收集数据。围压选取为0.08 MPa,轴向荷载选取为不同负温下三轴抗压强度的60%[18]。在30 s内将轴压均匀增加到预定的荷载,然后保持偏应力稳定。当试样轴向变形速率连续24 h每小时应变小于5×10-4或者发生破坏出现宏观裂纹时停止加载。测得不同负温条件下的蠕变曲线如图 3所示。
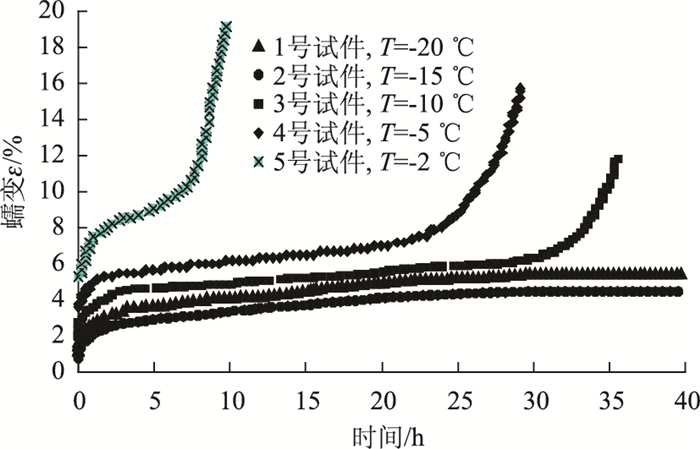
|
| 图 3 不同负温条件下的轴向变形曲线 Fig. 3 Axial deformation curves at different negative temperatures |
| |
2.2 测试结果分析
由图 3可以看出,温度为-20 ℃和-15 ℃时并未出现蠕变第Ⅲ阶段,说明负温较低时冻风积土强度比较大,蠕变损伤发展比较缓慢。轴压达到预定值所产生的瞬时弹性变形会达到最终变形的40%以上。对于-10,-5 ℃和-2 ℃的冻风积土试样,均出现了蠕变第Ⅲ阶段,负温越低对应第Ⅱ阶段的时间越长。所以,温度对冻风积土蠕变损伤发展起直接作用。不同负温条件下的冻风积土初始瞬时变形及单轴抗压强度如图 4所示。特征时间及损伤参数见表 2。不同温度下的损伤变量演化如图 5所示。
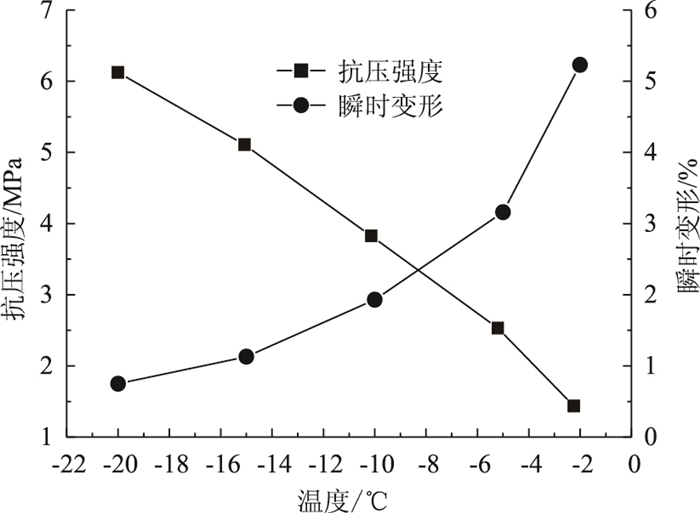
|
| 图 4 不同负温条件下瞬时变形与抗压强度 Fig. 4 Instantaneous deformations and compressive strengths at different negative temperatures |
| |
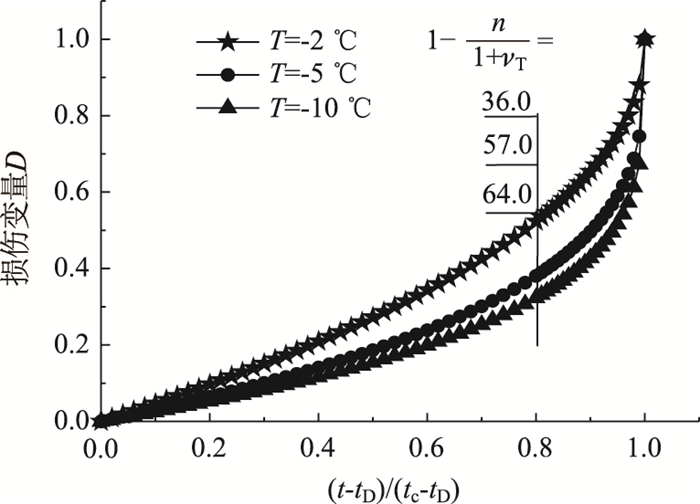
|
| 图 5 损伤变量随时间演化过程 Fig. 5 Damage variable varying with time |
| |
| 试验温度/℃ | tD | tp | tc | n | νT | σ/MPa |
| -10 | 17.61 | 31.72 | 39.53 | 0.76 | 1.12 | 3.65 |
| -5 | 10.69 | 20.68 | 31.41 | 0.84 | 0.97 | 1.64 |
| -2 | 2.85 | 5.87 | 8.23 | 0.92 | 0.43 | 0.83 |
由表 2可以看出温度越高冻风积土发生损伤的时间tD及发生破坏的时间tc越短。由图 5可看出温变参数νT随着温度的升高而减小,νT越小冻风积土内部蠕变损伤发展的越快。
3 屈服边界损伤演化规律 3.1 屈服边界损伤原理当tD < t < tp时,冻风积土的抗剪强度指标c0,φ0随时间逐渐发生损伤,假设抗剪强度指标ct,φt随时间的损伤演化率为:
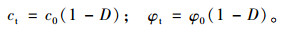
|
(9) |
德鲁克和普拉格考虑了中间主应力影响,通过对Mises条件改进提出了Drucker-Prager(D-P)屈服准则,适用于岩土材料[19]。在主应力空间中,无损伤屈服边界σs方程可表示为:
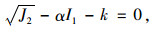
|
(10) |
式中,I1为第一主应力不变量; J2为第二偏应力不变量;α, k为由冻风积土黏聚力和内摩擦角所确定的模型参数,可表示为:
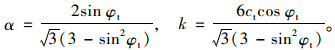
|
(11) |
围压可认为是相等的(σ2=σ3),方程可退化为如式(12)的二维形式,屈服边界Γ所围成的图形为一偏心椭圆(图 6)。
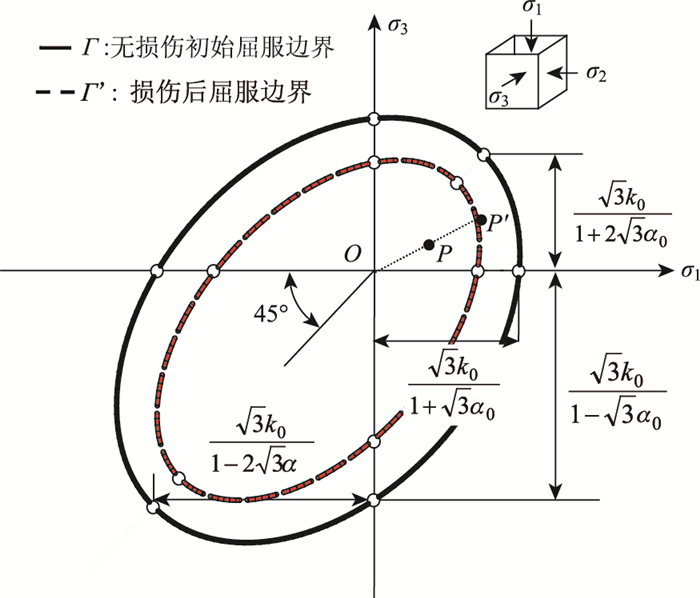
|
| 图 6 屈服边界损伤原理 Fig. 6 Yield boundary damage principle |
| |
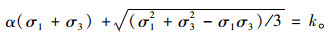
|
(12) |
当时间t < tD时,对于蠕变初期位于未损伤屈服边界Γ内某一应力状态点P (σp, 1, σp, 3)并未发生屈服。随着冻风积土内部裂隙不断发展而产生的空洞致使其产生蠕变损伤,损伤后P点的第一、第三主应力都将变大向右上方扩展,此时的应力状态可用lemaitre有效应力形式来表示[20],即:
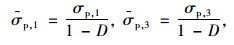
|
(13) |
式中,σp, 1,σp, 3分别为应力点P的横纵坐标。
另一方面,随着蠕变的发展,屈服边界开始发生蠕变损伤而具有收缩趋势,某一时刻扩展后的P′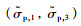
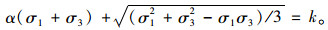
|
(14) |
将点P′的横纵坐标及式(11)中αt,kt的表达式代入式(14),可得点P′进入到损伤屈服边界所需要的时间满足:
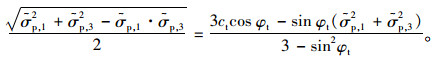
|
(15) |
一般情况下,冻结状态下风积土相对于其他类土体内摩擦角φt较小,sin2 φt在0.1左右,因此式(15)中sin2φt可以近似忽略不计[21]。利用泰勒级数对式中的sin φt,cos φt进行展开并略去高阶无穷小的量,可近似得到:
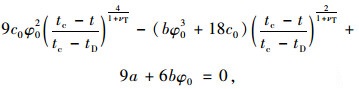
|
(16) |
其中,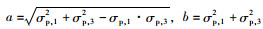
式(16)可转化为一元二次方程,舍弃较大解(该解对应P点到达屈服边界另一侧)该方程的正实数解为:
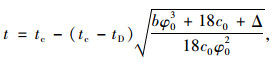
|
(17) |
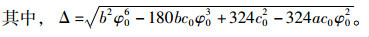
|
(18) |
式(11)给出了屈服边界参数α, k的演化规律,式(17)给出了冻风积土内部某一点进入屈服边界所需时间的近似解,这两个方程确定了冻风积土屈服边界损伤的规律。
3.2 屈服轨迹的初步探讨由图 7,P点与原点O连线OP与横轴Oσ1所夹的角θ0可表示为:
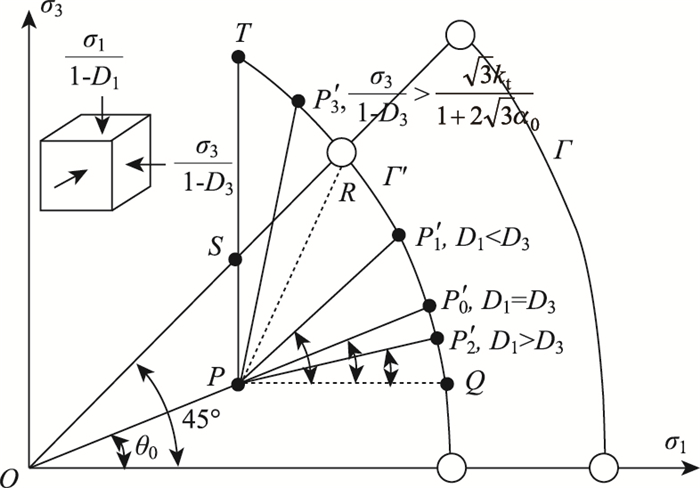
|
| 图 7 应力屈服轨迹示意图 Fig. 7 Schematic diagram of strain yield locus |
| |
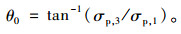
|
(19) |
设D1, D3分别为轴向和围向的损伤变量,对于同性损伤来说D1=D3,蠕变损伤后,P点落在了损伤屈服边界Γ′上P′0点,PP′0与水平轴的夹角θ′0为:
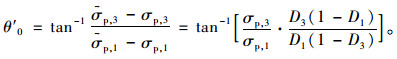
|
(20) |
若D1=D3,发生的是各项同性损伤,θ′0=θ0;若D1 < D3,发生的是各项异性损伤,θ′0=θ1;若D1>D3,发生的是各项异性损伤,θ′0=θ2。
各向同性损伤时,P点的屈服轨迹位移矢量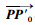
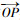
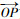
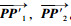
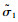
当屈服轨迹角θ′0增大的过程中,屈服轨迹矢量有可能达到PQRT区域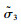
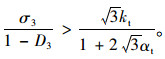
|
(21) |
对于损伤后的屈服强度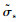
图 2所示的蠕变模型初始蠕变参数可根据图 3所测得试验数据进行拟合确定,结果见表 3。
| 试验温度/℃ | E0/ MPa |
E1/ MPa |
η1/ (MPa·h) |
η2/ (MPa·h) |
α0 | k0/ MPa |
| -20 | 488.8 | 258.3 | 92.3 | 未屈服 | 1.17 | 3.05 |
| -15 | 233.7 | 143.1 | 77.5 | 未屈服 | 2.36 | 4.11 |
| -10 | 117.5 | 86.5 | 54.2 | 97.6 | 1.17 | 4.86 |
| -5 | 78.5 | 35.2 | 37.9 | 72.9 | 2.36 | 5.02 |
| -2 | 15.6 | 2.8 | 18.6 | 51.7 | 3.12 | 7.33 |
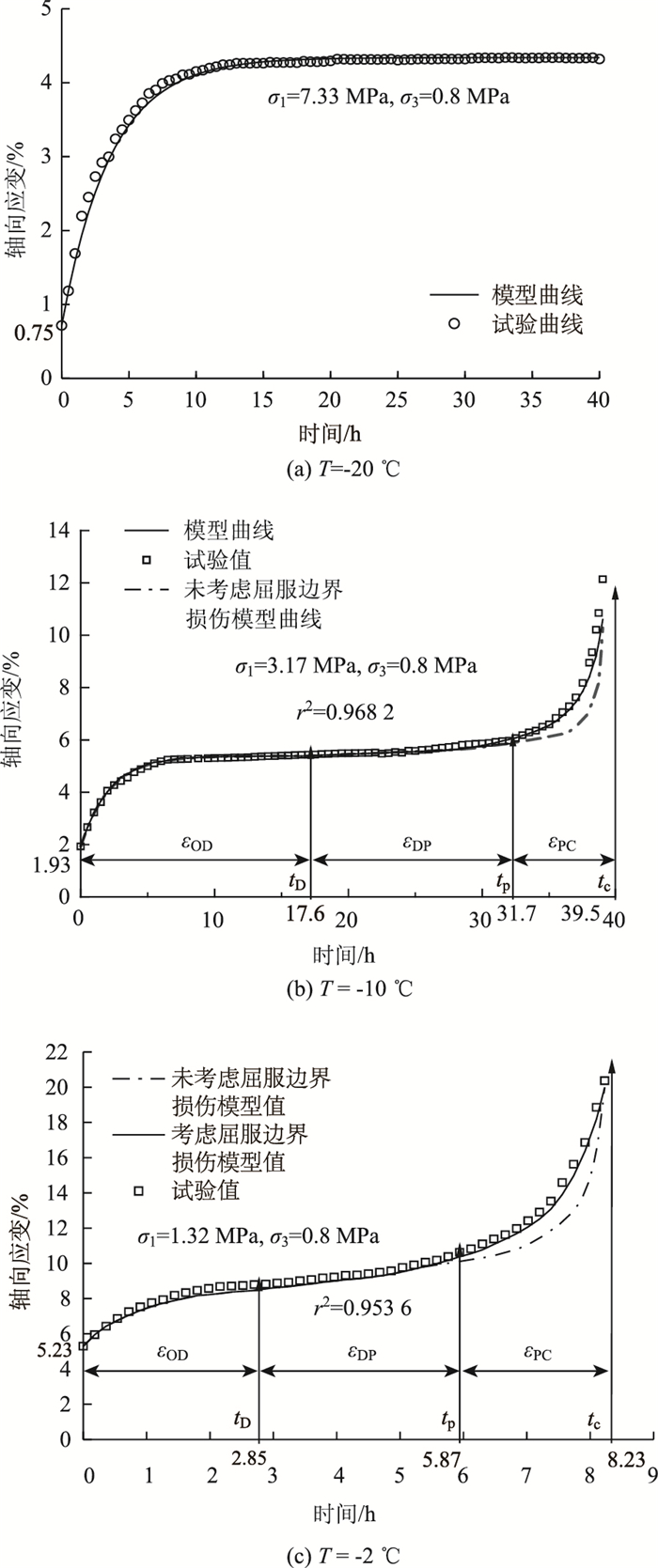
由表 3可知,较低温度下的冻风积土蠕变曲线并未出现第Ⅲ阶段,可认为该温度下的蠕变损伤为零,采用式(9)所给出无损伤蠕变模型来计算该温度下的蠕变变形量。以T=-20 ℃为例,由表 3中的初始蠕变参数E0,E1及η1和式(4)所确定的模型值与试验实测值对比如图 8(a)所示。
|
| 图 8 不同负温条件下模型值与实测值对比图 Fig. 8 Comparison between model calculated values and measured values at different negative temperatures |
| |
温度较高时蠕变曲线出现了第Ⅲ阶段及拐点,从拐点所对应的时间tD开始发生蠕变损伤。以负温-2 ℃和-10 ℃为例,从0到tD采用未损伤蠕变模型εOD;从tD到tp采用损伤蠕变模型εDP;从tp到tc采用非线性D-P损伤蠕变模型εPC。采用分阶段蠕变损伤模型计算值与实测值对比如图 8(b)~(c)所示。若不考虑屈服边界损伤的影响,模型曲线如图中的虚线所示。
由以上对比分析可知,负温为-20 ℃时模型曲线和实测曲线比较接近,相关系数r2可达到0.974 2;而当温度升高时模型值与试验值偏差程度有一定增加,r2可达0.953 6。若不考虑屈服边界的损伤,模型值会与实测值有较大差距,说明所提出的考虑屈服边界损伤的分阶段蠕变损伤模型能够较好地描述冻风积土在不同负温条件下的冻风积土蠕变各阶段特征。负温越高蠕变第Ⅱ阶段越短,出现宏观裂纹时间越短。
从图 8(a)可以看出低温无损伤条件下冻风积土蠕变曲线并未出现拐点,而图 8(b)~(c)中高温冻风积土从开始加载到破坏的蠕变曲线均出现了由凸到凹的变化过程,因此蠕变曲线的拐点是确定蠕变损伤时间阈值的重要依据。
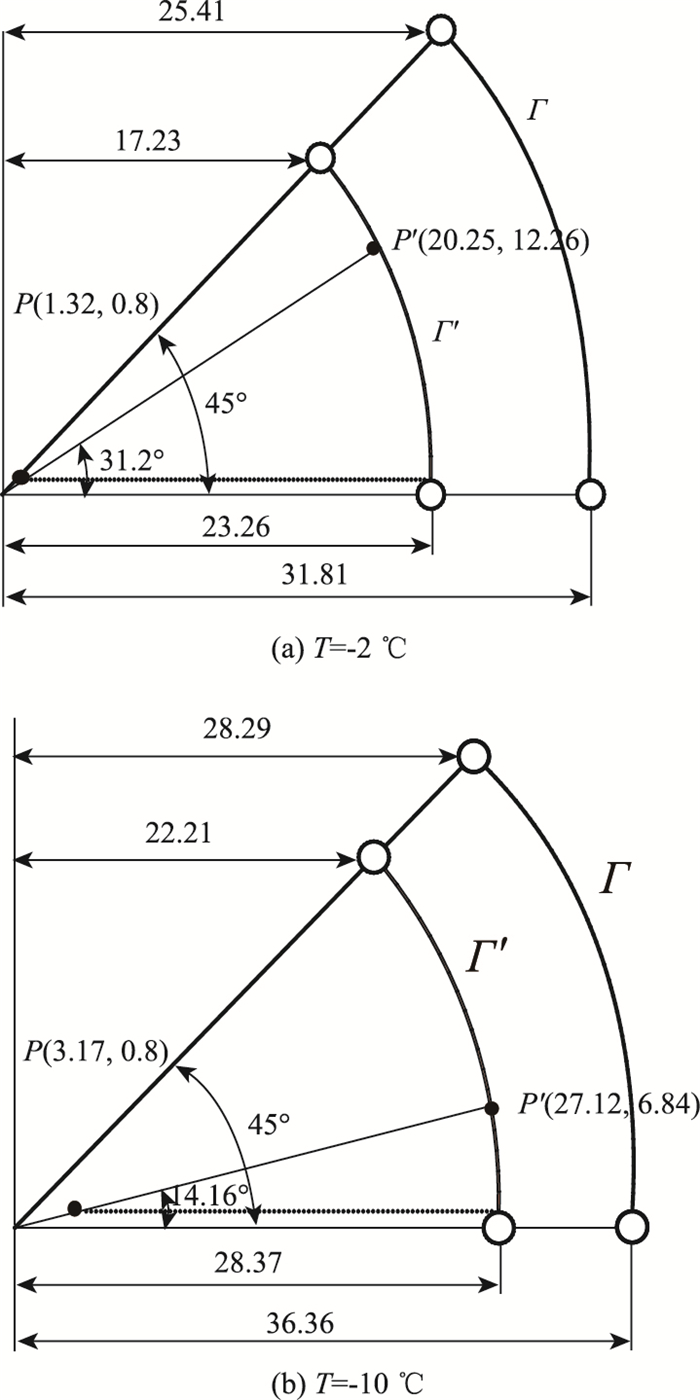
4.2 屈服边界损伤验证本研究主要是研究各项同性损伤的屈服边界损伤特性,假设内部各点的应力状态相同,在-2,-5 ℃,和-10 ℃的σ1分别为0.82,2.27 MPa和3.67 MPa,围压分别为0.05,0.1 MPa和0.2 MPa。屈服边界的损伤参数结果如表 4所示。
| 试验温度/℃ | c0/MPa | φ0/(°) | a/MPa | b/MPa | Δ |
| -2 | 28.3 | 17.1 | 0.57 | 0.337 | 0.12 |
| -5 | 32.8 | 17.8 | 1.14 | 1.32 | 0.37 |
| -10 | 39.6 | 18.2 | 2.55 | 6.55 | 0.48 |
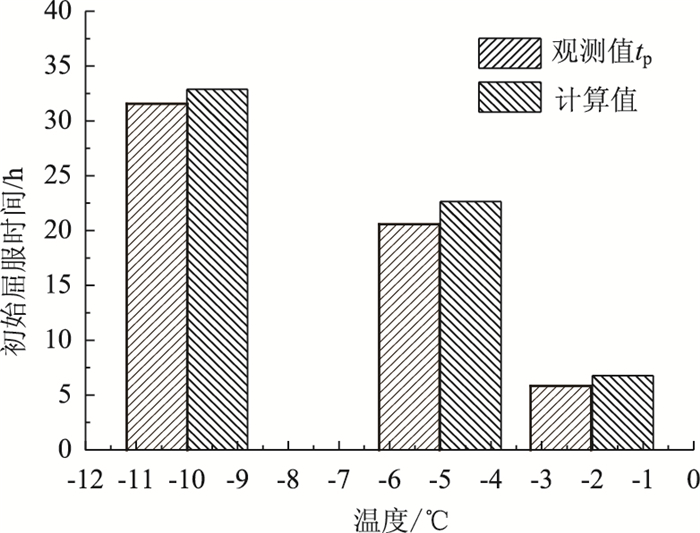
将由式(17)计算得到的屈服时间与试验蠕变曲线观测屈服临界点B所对应的时间进行对比,二者间相对误差如图 9所示。按照第4.1节所述的屈服边界损伤原理并结合图 9确定屈服时间。损伤后的屈服边界与有效应力间的演化关系如图 10所示。
|
| 图 9 初始屈服时间计算值与观测值对比 Fig. 9 Comparison of initial yield time between calculated value and observed value |
| |
|
| 图 10 屈服边界损伤验证演示图(单位:MPa) Fig. 10 Demonstration graph of verifying yield boundary damage (unit:MPa) |
| |
从图 9可看出,由式(12)计算到和观测到的初始屈服时间结果比较接近,最大的相对误差为9.48%;由图 10可看出损伤后的应力点与损伤屈服边界较为接近。因此,式(9)的假设及本研究提出的屈服边界损伤模型具有合理性。
5 结论通过对不同负温条件下的冻风积土进行蠕变试验,给出了冻风积土的初始损伤时间与初始屈服时间的确定方法,研究了损伤变量在不同温度下的演化规律,将其应用到蠕变损伤模型与屈服边界领域研究,得到了如下结论。
(1) 将出现第Ⅲ阶段的蠕变曲线的拐点作为蠕变损伤时间阈值,将第Ⅲ阶段初始时间作为屈服临界点,依据这两个特征时间为分界点提出了分阶段描述的冻风积土蠕变损伤模型,结果表明分阶段蠕变模型可以较好地描述冻风积土发生损伤时的蠕变特征,最小的相关系数可达0.953 6。
(2) 给出了冻风积土分阶段的蠕变损伤模型,将西原模型中黏塑性元件改进成具有损伤特性的非线黏塑性体来描述冻风积土发生蠕变损伤第Ⅲ阶段变形规律,利用试验蠕变曲线反演出模型的蠕变参数,采用损伤后的屈服边界Γ′作为冻土发生屈服的标准,模型可以较好地描述各阶段蠕变特征。
(3) 提出了屈服边界的损伤理论,揭示了冻风积土蠕变过程发生损伤的机理,初步探讨了各项同性损伤与各向异性损伤对冻风积土进入屈服边界的方式,给出了研究冻风积土进入蠕变第Ⅲ阶段发生损伤的一种新方法。
| [1] |
刘世伟, 张建明, 张虎, 等. 青藏高原多年冻土长期蠕变变形试验研究[J]. 岩石力学与工程学报, 2012, 31. LIU Shi-wei, ZHANG Jian-ming, ZHANG Hu, et al. Research on Long-term Creep Test of Permafrost on Qinghai——Tibet Plateau[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S1): 3245-3253. |
| [2] |
张向东, 傅强. 冻土三轴蠕变特性试验研究及平面冻土墙厚度的确定[J]. 岩土力学, 2011, 32(8): 2261-2266. ZHANG Xiang-dong, FU Qiang. Experimental Study of Triaxial Creep Properties of Frozen Soil and Thickness Determination of Flat Frozen Soil Wall[J]. Rock and Soil Mechanics, 2011, 32(8): 2261-2266. |
| [3] |
刘萌心, 姚晓亮, 齐吉琳, 等. 考虑应力历史的冻土一维蠕变模型[J]. 岩土工程学报, 2015, 38(5): 898-903. LIU Meng-xin, YAO Xiao-liang, QI Ji-lin, et al. 1D Creep Model for Frozen Soil Taking Account of Stress History[J]. Chinese Journal of Geotechnical Engineering, 2015, 38(5): 898-903. |
| [4] |
董连成, 张公, 赵淑萍, 等. 冻土蠕变指标试验研究[J]. 冰川冻风积土, 2014, 36(1): 130-136. DONG Lian-cheng, ZHANG Gong, ZHAO Shu-ping, et al. Experimental Study of the Creep Indexes of Frozen Soil[J]. Journal of Glaciology and Geocryology, 2014, 36(1): 130-136. |
| [5] |
赵延林, 唐劲舟, 付成成, 等. 岩石黏弹塑性应变分离的流变试验与蠕变损伤模型[J]. 岩石力学与工程学报, 2016, 35(7): 1297-1308. ZHAO Yan-lin, TANG Jin-zhou, FU Cheng-cheng, et al. Rheological Test of Separation between Viscoelastic-plastic Strains and Creep Damage Model[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1297-1308. |
| [6] |
BRAY M T. Secondary Creep Approximations of Ice-rich Soil and Ice Using Transient Relaxation Tests[J]. Cold Regions Science and Technology, 2013, 88(2): 17-36. |
| [7] |
赵晓东, 周国庆. 温度梯度冻土蠕变变形规律和非均质特征[J]. 岩土工程学报, 2014, 36(2): 390-394. ZHAO Xiao-dong, ZHOU Guo-qing. Creep Deformation and Heterogeneous Characteristics for Frozen Soils with Thermal Gradient[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 390-394. |
| [8] |
维亚洛夫C C.土力学的流变原理[M].杜余培, 译.北京: 科学出版社, 1978. VIALOV C C. Soil Mechanics Rheological Principle[M]. DU Yu-pei, translated. Beijing: Science Press, 1978. |
| [9] |
KACHANOV L M. Introduction to Continuum Damage Mechanics[M]. Dordrecht: Martinus Nijhoff Publishers, 1986.
|
| [10] |
孙琦, 张向东, 杨佳, 等. 冻结条件下风积土蠕变损伤特性及本构模型研究[J]. 公路交通科技, 2015, 32(5): 61-67. SUN Qi, ZHANG Xiang-dong, YANG Jia, et al. Study on Creep Damage Characteristics and Constitutive Model of Aeolian Soil under Freezing Condition[J]. Journal of Highway and Transportation Research and Development, 2015, 32(5): 61-67. |
| [11] |
汪承维, 李栋伟. 深部人工冻土黏弹塑损伤耦合本构模型研究及其验证[J]. 冰川冻风积土, 2013, 35(5): 1219-1223. WANG Cheng-wei, LI Dong-wei. Study and Verification of Laboratory Prepared Frozen Soil Viscoelastic-plastic Damage Coupling Constitutive Model[J]. Journal of Glaciology and Geocryology, 2013, 35(5): 1219-1223. |
| [12] |
王其虎, 叶义成, 刘艳章, 等. 考虑初始损伤和蠕变损伤的岩石蠕变全过程本构模型[J]. 岩土力学, 2016, 37(增1): 57-62. WANG Qi-hu, YE Yi-cheng, LIU Yan-zhang, et al. A Creep Constitutive Model of Rock Considering Initial Damage and Creep Damage[J]. Rock and Soil Mechanics, 2016, 37(S1): 57-62. |
| [13] |
KACHANOV M. Effective Elastic Properties of Cracked Solids:Critical Review of Some Basic Concepts[J]. Applied Mechanics Review, 1992, 45(8): 305-336. |
| [14] |
孙凯, 陈正林, 陈剑, 等. 一种基于修正西原模型的冻土蠕变本构关系[J]. 岩土力学, 2015, 36(增1): 142-146. SUN Kai, CHEN Zheng-lin, CHEN Jian, et al. A Modified Creep Constitutive Equation for Frozen Soil Based on Nishihara Model[J]. Rock and Soil Mechanics, 2015, 36(S1): 142-146. |
| [15] |
彩雷洲.青藏高温高含冰量砂质粉土蠕变试验研究[D].哈尔滨: 哈尔滨工业大学, 2015. CAI Lei-zhou. Study on Creep Test of High Temperature and High Ice Content Sandy Silt[D]. Harbin: Harbin Institute of Technology, 2015. |
| [16] |
王伸远, 李栋伟. 深部人工冻结黏土三轴蠕变试验研究[J]. 冰川冻土, 2014, 36(6): 1479-1483. WANG Shen-yuan, LI Dong-wei. Experimental Study of the Triaxial Creep Features of Deep Artificial Frozen Clay[J]. Journal of Glaciology and Geocryology, 2014, 36(6): 1479-1483. |
| [17] |
路贵林.多年冻风积土区高温冻风积土力学特性试验研究[D].北京: 中国矿业大学, 2015. LU Gui-lin. Experimental Study on Mechanical Characteristics of Frozen Aerated Soil at Multi-year Frozen Aeolian Area[D]. Beijing: China University of Mining and Technology, 2015. |
| [18] |
马小杰, 张建明, 常小晓, 等. 高温-高含冰量冻土蠕变试验研究[J]. 岩土工程学报, 2007, 29(6): 848-852. MA Xiao-jie, ZHANG Jian-ming, CHANG Xiao-xiao, et al. Experimental Study on Creep of Warm and Ice-rich Frozen Soil[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(6): 848-852. |
| [19] |
刘金龙, 栾茂田, 许成顺, 等. Drucker-Prager准则参数特性分析[J]. 岩石力学与工程学报, 2006, 25(增2)): 4009-4015. LIU Jin-long, LUAN Mao-tian, XU Cheng-shun, et al. Study on Parametric Characters of Drucker-Prager Criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 4009-4015. |
| [20] |
LEMAITRE J, SERMAGE J P. One Damage Law for Different Mechanisms[J]. Computational Mechanics, 1997, 20(1/2): 84-88. |
| [21] |
王永忠, 刘雄军, 艾传井, 等. 南方短时冻土抗剪强度指标c、φ值的试验研究[J]. 武汉大学学报:工学版, 2010, 43(2): 198-202. WANG Yong-zhong, LIU Xiong-jun, AI Chuan-jing, et al. Experimental Investigation on Shear Strength Parameters c and φ for a Temporarily Frozen Soil in South China[J]. Engineering Journal of Wuhan University, 2010, 43(2): 198-202. |
 2019, Vol. 36
2019, Vol. 36
