扩展功能
文章信息
- 牛涌, 杨兴振, 赵建林, 季文魁
- NIU Yong, YANG Xing-zhen, ZHAO Jian-lin, JI Wen-kui
- 基于上限分析法的含夹层边坡地震稳定性分析
- Analysis on Seismic Stability of Slope Containing Interlayer Based on Upper Bound Analysis Method
- 公路交通科技, 2019, 36(1): 38-45
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 38-45
- 10.3969/j.issn.1002-0268.2019.01.006
-
文章历史
- 收稿日期: 2018-01-16
我国的滇西南地区地震频发,高边坡分布广泛,由地震诱发的地质灾害层出不穷[1-3]。该地区的高边坡中常分布有软弱夹层,软弱夹层多是由于构造作用和水化作用而形成的泥化夹层,主要成分是黏土,其抗剪强度较低,透水性较差,遇水易软化。在雨水充沛季节,部分含泥化夹层边坡有沿着泥质带滑动的倾向,泥化夹层对边坡的稳定性起着控制作用[4],因此,对含泥化夹层的岩质边坡在地震荷载下的稳定性进行分析,对滇西南地区的高速公路建设具有很高的工程实用价值。
已有大量学者[5-7]在地震荷载下的边坡稳定性研究方面进行了深入地研究,最常见的应用地震稳定性分析的方法有:拟静力法、Newmark有限滑动位移法、有限元法和振动台模型试验法[8]。拟静力法的核心是以一个恒力代替动荷载加载至滑体中心上,然后依据平衡理论建立力和弯矩的平衡方程,并以此来求安全系数的一种方法。这种方法原理简单,计算也不复杂,成为边坡地震稳定性分析的主要方法,但是缺点是没有考虑在地震荷载下安全系数随时间变化的特性,应用该方法分析的结论并不十分合理。有限元法是一种把拟分析边坡离散为无数个单元体,以弹性力学和结构力学为基础,应用计算机进行计算而发展来的一种方法。这种方法计算相对更加直观准确,但是由于在建模过程中网格划分等一些参数的不同往往会对分析结果产生很大的影响。本研究将对极限分析中的上限分析法进行探讨,并研究如何将其应用到地震荷载下的边坡稳定性分析中,最后结合模型试验对这种方法进行验证。
1 极限分析的基本原理与极限平衡法基于应力或位移的角度对边坡的稳定性进行分析不同,极限分析是一种以理想的方式考虑土体的应力应变,基于功率的角度对边坡的稳定性进行评价的方法[9-10]。极限分析法的应用首先假设土体满足理想弹塑性假设,而且假设破坏时的土体体积是不变的,以库伦屈服准则为基础,在满足Drunker塑性公设和流动法则的前提下,基于内部耗散功率(滑面上阻力消耗的功率)和外力(滑体自重、地震力、裂隙静水压力等)做功功率的大小关系来评价边坡的稳定性。极限分析法包括上限分析法和下限分析法,分别是求出精确的上限解和下限解,而真实的解介于两者之间,本研究主要对上限分析法在含夹层边坡中的应用进行研究并将其推广到地震荷载下的边坡稳定性分析中的应用。
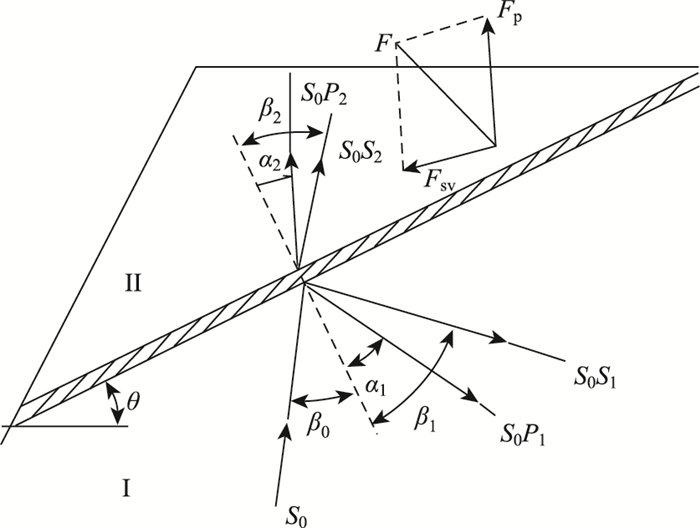
2 上限分析法在边坡地震稳定性分析中的应用 2.1 基于波动理论求地震波对滑体做功功率当一正弦SV波透过边坡中的夹层时,会产生P波和SV波两种形式的透射波(见图 1),其透射系数可以由式(1)求出。
|
| 图 1 波的透-反射及应力波作用力示意图 Fig. 1 Schematic diagram of wave transmit-reflect and stress wave forces |
| |
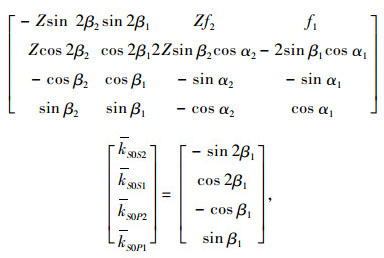
|
(1) |
其中,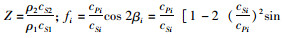
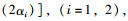
式中,α1, α2分别为P波的反射角和透射角;β1, β2分别为S波的入射角和反射角;ρ1, ρ2分别为Ⅰ,Ⅱ两层岩层的密度;cPi, cSi(i=1, 2)分别为P波和S波在两个岩层中的传播速度;kS0P2, kS0S2即为要求的透射P波和S波的透射系数。
设有一入射波为正弦SV波,周期为T,持时为t,其加速度波方程为:
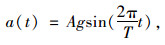
|
(2) |
式中A为调整加速度波幅值的系数。
对式(2)在(0, t)积分,可得速度波方程为:
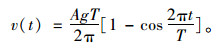
|
(3) |
由于透射应力波的位移、速度和加速度的透-反射系数均相等,则透射SV波和透射P波的波速均可以用入射波的速度方程乘以透射系数进行表示,如式(4)和式(5)所示。
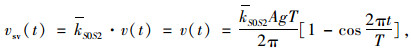
|
(4) |
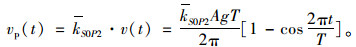
|
(5) |
由速度波和应力波的转换公式可以计算透射SV波和透射P波在Ⅱ滑块体中的应力波公式:
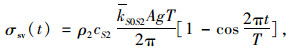
|
(6) |
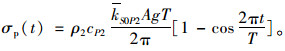
|
(7) |
透射应力波在滑动体Ⅱ中传播时,在滑块体Ⅱ内各层岩体之间产生剪应力,但是这个剪应力对用极限分析法研究边坡在软弱夹层面上的稳定性不产生影响,故只需考虑透射应力波在滑动面上产生的力即可,取边坡宽度为单位宽度,透射应力波在滑动体Ⅱ上产生的力为:

|
(8) |

|
(9) |
则透射应力波对滑体沿夹层滑动时的做功功率为:
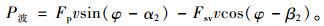
|
(10) |
地震荷载下含夹层边坡的能量系数为:
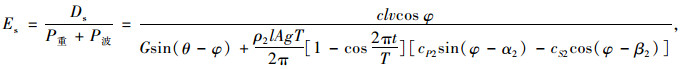
|
(11) |
式中,θ为夹层倾角;φ为夹层土体内摩擦角,也等于滑动速度与夹层的夹角;c为夹层土体的黏聚力;l为滑带的长度。
2.2 能量系数的时程分析在式(11)中求得的能量系数是一个与时间t有关的函数,反映在震动荷载下能量系数随时间的动态变化过程(见图 2),这是由于在地震荷载作用过程中,边坡所受到的外荷载的大小和方向均是实时变化的,而能量系数的动态变化只是反映在动荷载历时过程中的能量系数变化范围,并不能确定一个具体的指标来表征在动荷载下边坡的稳定性。

|
| 图 2 能量系数时程曲线 Fig. 2 Time histry curve of energy coefficient |
| |
在极限平衡法中,将稳定系数时程转换为评价稳定性指标的常见方法有可靠性理论确定的动安全系数法、平均安全系数法、最小安全系数法和最小平均安全系数法。其中刘汉龙[11]参考跨大步迭代法,提出以最小平均安全系数作为评价指标;吴兆营[12]基于边坡动安全系数的非线性分析方法提出以安全系数时程对时间的加权平均作为评价指标的方法。本研究参考在极限平衡法的上述安全系数时程的评价方法后提出极限分析中的最小平均能量系数法,用最小平均能量系数评价边坡的稳定性。
最小平均能量系数法是把地震荷载的平均值施加到滑体上时,滑体的能量系数为Es0,在地震荷载下的最小能量系数为Esmin,取0.65(Es0-Esmin)为能量系数的平均幅值来表示因为地震而导致的能量系数的偏移幅值,则最小平均能量系数可表示为:
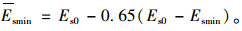
|
(12) |
最小平均能量系数示意图如图 3所示。求得最小平均能量系数后即可依据其值对边坡的稳定性做出评价,当最小平均能量系数Esmin>1时,消耗的功率大于外力做功功率,边坡处于稳定状态;当最小平均能量系数Esmin < 1时,消耗功率小于外力做功功率,边坡发生滑动破坏;当最小平均能量系数Esmin= 1时,边坡处于极限稳定状态。

|
| 图 3 最小平均能量系数示意图 Fig. 3 Schematic diagram of minimum mean energy coefficient |
| |
3 应用上限分析法计算模型破坏
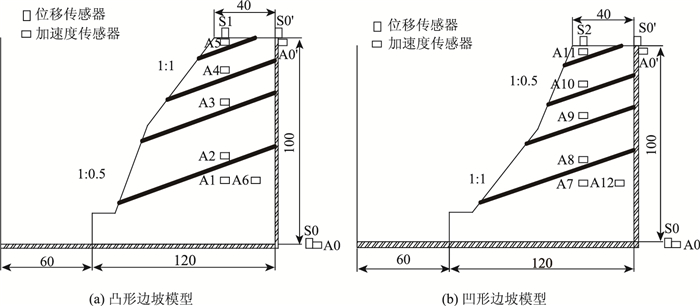
在地震稳定性研究中,由于振动台模型试验能较为真实地模拟地震效应[13],所以该方法成了研究边坡地震稳定性的最为广泛的一种应用方法。本研究综合了滇西南地区的常见边坡形态制作了“凹”形和“凸”形两种边坡,采用西安建筑科技大学结构工程与抗震教育部重点实验室的单向双自由度的振动台(2.2 m×2 m)进行了试验。试验选用的是刚性模型箱,为了减小模型箱的边界效应[14-16],在震动方向的后壁铺垫一层5 cm厚的泡沫板,模型箱底板上随机布设小钢片和钢柱,目的是为了增加模型路堤和模型箱底座之间的摩擦力。同时,本研究基于π定理[17-18],采用量纲分析法对相似判据进行推导,并以此为依据进行试验材料的选取和配置。本试验中基本量纲选为几何长度、密度和加速度,相似常数分别取cl=30, cρ=1, ca=1,其他相似常数可以通过π定理逐步导出,推导结果见表 1。试验以泥岩为典型边坡材料,基于相似理论对模型试验材料进行合理地选取。通过室内三轴试验结合相似关系发现当重晶石粉:石英砂:石膏粉:水按照32: 56: 9: 8的配比制作模型材料时,原型材料和模型材料的材料密度比为1,其他几项物理力学参数也接近满足相似比例关系,两种材料的力学性能较为相似,故此种配合比的材料作为模型材料满足要求。泥岩和模拟材料的主要力学参数指标见表 2。模型设计和加速度传感器布设示意图如图 4所示。
| 物理量 | 相似关系 | 相似常数 |
| 几何尺寸L | CL | 30* |
| 密度ρ | Cρ | 1* |
| 剪切模量G | CG=CLCρCa | 30 |
| 泊松比μ | Cμ | 1 |
| 内聚力c | Cc=CLCρCa | 30 |
| 内摩擦角φ | Cφ | 1 |
| 加速度a | Ca | 1* |
| 重力加速度g | Cg=Ca | 1 |
| 振动频率ω | 
|
0.18 |
| 应力σ | Cσ=CLCρCa | 30 |
| 应变ε | Cε=1 | 1 |
| 时间t | 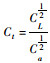
|
5.48 |
| 位移s | Cs=CL | 30 |
| 速度ν |
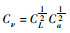
|
5.48 |
| 岩性 | 密度ρ/(g·cm-3) | 剪切模量G/MPa | 泊松比 | 内聚力c/kPa | 内摩擦角φ/(°) | |
| 红层软岩(泥岩) | 原型 | 2.47 | 1 900 | 0.3 | 532 | 24.04 |
| 相似材料 | 模型 | 2.4 | 63.3 | 0.3 | 17.3 | 24.5 |
|
| 图 4 模型设计示意图(单位:cm) Fig. 4 Schematic diagram of model design(unit:cm) |
| |
每个模型都设置了4个夹层,夹层厚度2 cm,倾角15°,试验采用3种地震波共进行了24组加载,具体加载方案如表 3所示。
| 试验序号 | 工况代号 | 地震波类型 | 地震加速度峰值/(×g) |
| 1 | WN-1 | 白噪声 | 0.05 |
| 2 | ELC-1 | EL Centro | 0.1 |
| 3 | SIN-1 | 正弦波5 Hz | 0.1 |
| 4 | SIN-2 | 正弦波7.5 Hz | |
| 5 | SIN-3 | 正弦波10 Hz | |
| 6 | SIN-4 | 正弦波12.5 Hz | |
| 7 | WN-2 | 白噪声 | 0.05 |
| 8 | ELC-2 | EL Centro | 0.2 |
| 9 | ELC-3 | EL Centro | 0.3 |
| 10 | WN-3 | 白噪声 | 0.05 |
| 11 | ELC-4 | EL Centro | 0.4 |
| 12 | ELC-5 | EL Centro | 0.6 |
| 13 | WN-4 | 白噪声 | 0.05 |
| 14 | SIN-5 | 正弦波5 Hz | 0.3 |
| 15 | SIN-6 | 正弦波7.5 Hz | |
| 16 | WN-5 | 白噪声 | 0.05 |
| 17 | ELC-6 | EL Centro | 0.8 |
| 18 | ELC-7 | EL Centro | 1.0 |
| 19 | WN-6 | 白噪声 | 0.05 |
| 20 | SIN-7 | 正弦波10 Hz | |
| 21 | SIN-8 | 正弦波12.5 Hz | 0.3 |
| 22 | SIN-9 | 正弦波14 Hz | |
| 23 | WN-7 | 白噪声 | 0.05 |
| 24 | WN-8 | 白噪声 | 0.05 |
本研究选用SIN-5工况和SIN-9工况进行计算分析。在试验过程中观察到在SIN-5工况下模型边坡呈现出变化,两种类型边坡均在第3个夹层处出现裂缝,存在继续发展产生滑动破坏的趋势,其他各夹层处无明显破坏迹象,故只对第3个夹层进行分析。
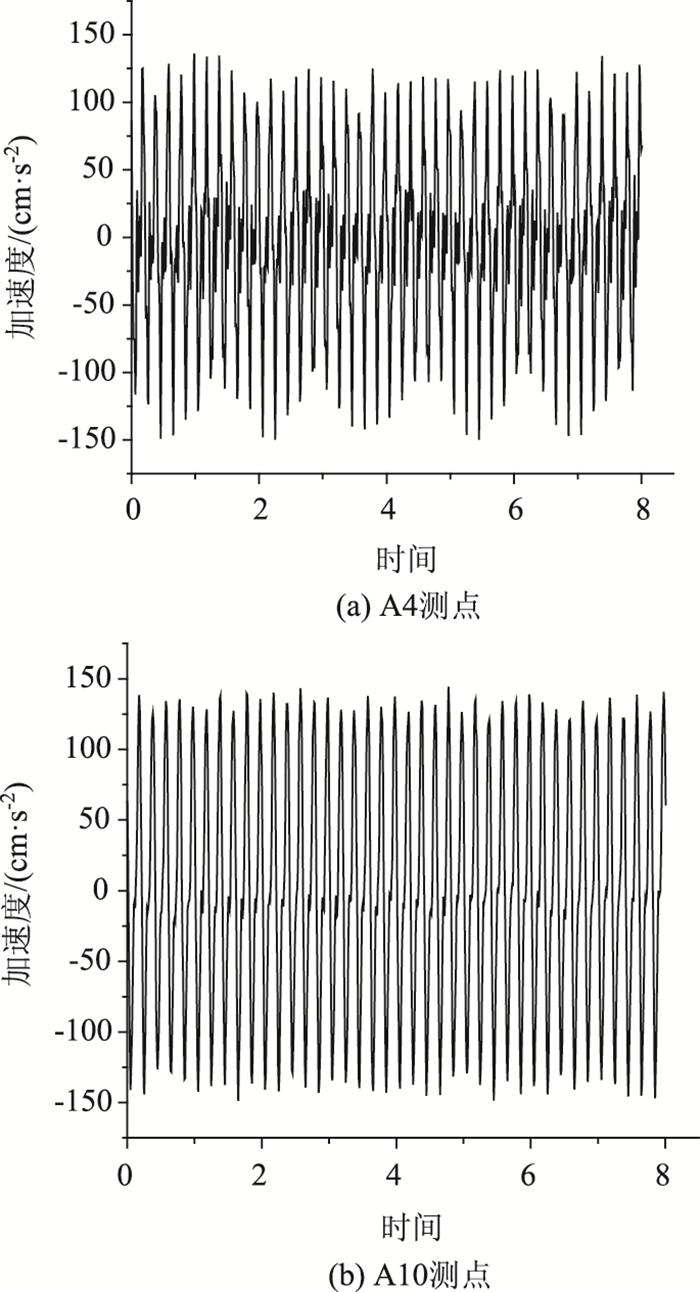
由于振动台加载的地震波为水平向,在计算时也只考虑水平向地震波对边坡稳定性的影响,分别应用A4和A10测得的数据进行计算,其加速度时程曲线如图 5所示。
|
| 图 5 SIN-5工况下A4和A10测点的加速度时程曲线 Fig. 5 Acceleration time history curve of measuring points A4 and A10 under condition SIN-5 |
| |
用函数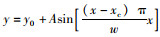
| 测点 | 方程 | 拟合相关系数 | 参数 | 参数值 | 方差 |
| A4 | y=108.3·sin(31.4x) | 0.993 | A | 108.3 | 0.92 |
| w | 0.1 | 3.528 37×10-5 | |||
| A10 | y=119.9·sin(31.4x) | 0.995 | A | 119.9 | 1.61 |
| w | 0.1 | 2.009 09×10-5 |
模型的各计算参数见表 5。
| 坡型 | 密度ρ/(g·cm-3) | 波速Cs/(m·s-1) | 地震波加速度幅值A/(cm·s-2) | 周期T/s | 滑体体积V/m3 | 夹层内摩擦角/(°) | 夹层黏聚力/kPa |
| 凸坡 | 2.4 | 401.5 | 108.3 | 0.2 | 0.102 | 23 | 12 |
| 凹坡 | 2.4 | 401.5 | 119.9 | 0.2 | 0.103 | 23 | 12 |
根据式(2)~(9)应力波做功公式可求得振动台加载的水平向地震波对两种坡面的边坡模型的做功功率,即可求得模型边坡在SIN-5工况下的能量系数,计算过程如下:
对凸型边坡,加速度波方程:
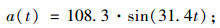
|
应力波对滑体的作用力:
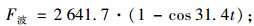
|
应力波做功功率,重力做功功率:
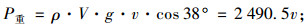
|
滑带消耗能量的功率:

|
夹层处的能量系数:
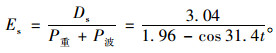
|
由式(12)求得其最小平均能量系数Esmin=1.18,用同种方法可求得凹型模型边坡在第3个夹层处的最小平均能量系数为1.09。
由于振动台加载的地震波在模型中不只有水平向的横波,还会在传播过程中出现纵波等复杂波形,而模型试验中只有水平向加速度传感器,只能基于水平向的地震波产生的力计算夹层处的能量系数忽略了其他波的影响,使得计算的能量系数偏大。求得的两种坡面形式模型的第3个夹层处的能量系数分别为1.18和1.09,接近临界破坏状态时的能量系数1,而由于计算结果偏大,真实状态模型在SIN-5状态下发生轻微破坏现象与极限分析法求得的结果基本一致。
对SIN-9工况进行计算,在试验过程中,SIN-9工况加载结束后,两种类型边坡均在第3个夹层处产生的大幅滑移、崩塌现象,模型发生彻底破坏。
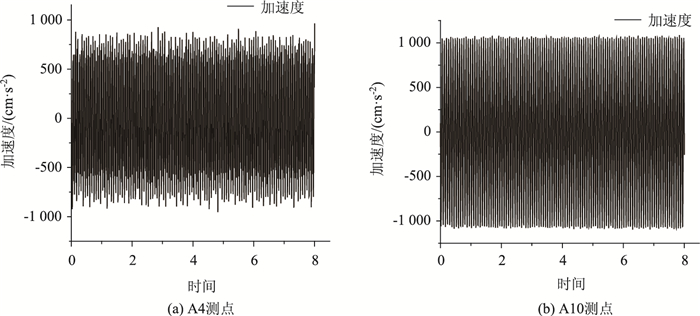
对A4和A10测点测得的加速度时程曲线(图 6)进行拟合处理,处理结果见表 6。
|
| 图 6 SIN-9工况下A4和A10测点的加速度时程曲线 Fig. 6 Acceleration time history curve of measuring points A4 and A10 under condition SIN-9 |
| |
| 测点 | 方程 | 拟合相关系数 | 参数 | 参数值 | 方差 |
| A4 | y=709.5·sin(87.2x) | 0.995 | A | 709.5 | 1.11 |
| w | 0.036 | 2.997×10-7 | |||
| A10 | y=1 037.7·sin(87.2x) | 0.997 | A | 1 037.7 | 1.26 |
| w | 0.036 | 2.136×10-7 |
求凸型边坡第3个夹层处的能量系数:加速度波方程:
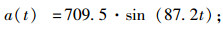
|
应力波对滑体作用力:

|
应力波对滑体做功功率:
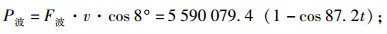
|
重力做功功率:
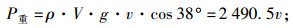
|
滑带消耗能量的功率:
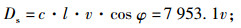
|
夹层处的能量系数:
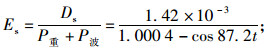
|
求得其最小平均能量系数:
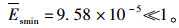
|
同样可求得凹型边坡的最小平均能量系数Esmin=1.21×10-5≪1。由以上两个模型在第3个夹层处的能量系数远远小于1可得边坡处于极度不稳定状态,这与SIN-9工况下边坡出现完全破坏相一致。
4 结论文章对极限分析上限法在含夹层边坡在地震荷载下的稳定性进行了研究,基于波动学理论推导了地震波在透过夹层时产生的透射波对滑体的做功功率,针对地震荷载下能量系数随时间波动的特性,提出了以最小平均能量系数作为边坡稳定性的评价标准,最后通过室内振动台模型试验进行了验证,得出以下结论:
(1) 以正弦波代替地震波,基于波动理论可以求得地震波对边坡滑体的做功功率,该功率可用于计算地震工况下边坡稳定性的能量系数。
(2) 地震工况下边坡稳定性的能量系数为一个与时间t有关的函数,其反映了震动荷载下能量系数随时间的动态变化过程,本研究提出了最小平均能量系数法作为边坡稳定性的评价指标。
(3) 通过模型试验验证基于极限分析上限法求得的最小平均能量系数判定的稳定性结论与实际的破坏状态相一致,证明了以上限分析法求得的最小平均能量系数用于评价含夹层岩质边坡在地震荷载下稳定性是可行的。
| [1] |
何藴龙, 陆述远. 岩石边坡地震作用近似计算方法[J]. 岩土工程学报, 1998, 20(2): 66-68. HE Yun-long, LU Shu-yuan. A Method for Calculating the Seismic Action in Rocks[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(2): 66-68. |
| [2] |
宋玉环.西南地区软硬互层岩质边坡变形破坏模式及稳定性研究[D].成都: 成都理工大学, 2011. SONG Yu-huan. Failure Models and Instability of Slopes with Soft and Hard Rock Interbedded Laminated Structure in Southwest China[D]. Chengdu: Chengdu University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10616-1011236229.htm |
| [3] |
徐冠军.滇西南地区高边坡抗震性能振动台模拟试验研究[D].西安: 长安大学, 2015. XU Guan-jun. Study on Seismic Behavior of High Slope through Shaking Table Test in Southwest Yunnan[D]. Xi'an: Chang'an University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10710-1015803228.htm |
| [4] |
何满朝. 软岩工程力学的理论与实践[M]. 北京: 中国矿业大学出版社, 1996. HE Man-chao. Theory and Practice of Soft Rock Engineering Mechanics[M]. Beijing: China Mining University Press, 1996. |
| [5] |
时少波.地震荷载作用下风积沙高路堤稳定性模型试验研究[D].西安: 长安大学, 2015. SHI Shao-bo. Test Research of Aeolian Sand Embankment Stability under Seismic Load[D]. Xi'an: Chang'an University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10710-1015803225.htm |
| [6] |
冯志仁, 刘红帅, 于龙. 地震作用下含软弱夹层顺层岩质边坡表面放大效应研究[J]. 防灾减灾工程学报, 2014, 34(1): 96-100. FENG Zhi-ren, LIU Hong-shuai, YU Long. Surface Amplification Effect of Bedding Rocky Slope with Weak Interlayer under Earthquake[J]. Journal of Disaster Prevention and Mitigation Engineering, 2014, 34(1): 96-100. |
| [7] |
陈国庆, 黄润秋, 石豫川, 等. 基于动态和整体强度折减法的边坡稳定性分析[J]. 岩石力学与工程学报, 2014, 33(2): 243-256. CHEN Guo-qing, HUANG Run-qiu, SHI Yu-chuan, et al. Stability Analysis of Slope Based on Dynamic and Whole Strength Reduction Methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 243-256. |
| [8] |
宋玉环.西南地区软硬互层岩质边坡变形破坏模式及稳定性研究[D].成都: 成都理工大学, 2011. SONG Yu-huan. Failure Mode and Instability of Slopes with Soft and Hard Rock Interbedded Laminated Structure in Southwest China[D]. Chengdu: Chengdu University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10616-1011236229.htm |
| [9] |
王根龙, 伍法权, 张茂省. 平面滑动型岩质边坡稳定性极限分析上限法[J]. 工程地质学报, 2011, 19(2): 176-180. WANG Gen-long, WU Fa-quan, ZHANG Mao-sheng. Method of Upper Bound Limit Analysis for Plane Sliding of Rock Slopes[J]. Journal of Engineering Geology, 2011, 19(2): 176-180. |
| [10] |
陈祖煜. 土力学经典问题的极限分析上、下限解[J]. 岩土工程学报, 2002, 24(1): 1-11. CHEN Zu-yu. Limit Analysis for the Classic Problems of Soil Mechanics[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(1): 1-11. |
| [11] |
刘汉龙, 费康, 高玉峰. 边坡地震稳定性时程分析方法[J]. 岩土力学, 2003, 24(4): 553-556, 560. LIU Han-long, FEI Kang, GAO Yu-feng. Time History Analysis Method of Slope Seismic Stability[J]. Rock and Soil Mechanics, 2003, 24(4): 553-556, 560. |
| [12] |
吴兆营, 薄景山, 刘红帅, 等. 岩体边坡地震稳定性动安全系数分析方法[J]. 防灾减灾工程学报, 2004, 24(3): 237-241. WU Zhao-ying, BO Jing-shan, LIU Hong-shuai, et al. A Method for Evaluating Dynamic Safety Factor Rock Slope Seismic Stability Analysis[J]. Journal of Disaster Prevention and Mitigation Engineering, 2004, 24(3): 237-241. |
| [13] |
李永靖, 乔朋庆, 邢洋, 等. 地震荷载下煤矸石路基变形室内试验与数值模拟分析[J]. 中国地质灾害与防治学报, 2014, 25(2): 54-59. LI Yong-jing, QIAO Peng-qing, XING Yang, et al. Experimental Study and Numerical Simulation on Deformation Characteristics of Coal Gangue Fill Subgrade under Seismic Loads[J]. The Chinese Journal of Geological Hazard and Control, 2014, 25(2): 54-59. |
| [14] |
方勇, 符亚鹏, 周超月, 等. 公路隧道下穿双层采空区开挖过程模型试验[J]. 岩石力学与工程学报, 2014, 33(11): 2247-2257. FANG Yong, FU Ya-peng, ZHOU Chao-yue, et al. Model Test of Highway Tunnel Construction under Double-deck Mined-out Area[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11): 2247-2257. |
| [15] |
张延杰, 王旭, 梁庆国, 等. 湿陷性黄土模型试验相似材料的研制[J]. 岩石力学与工程学报, 2013, 32(2): 4019-4024. ZHANG Yan-jie, WANG Xu, LIANG Qing-guo, et al. Development of Model Test Similar Material of Collapsible Loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 4019-4024. |
| [16] |
杨俊杰. 相似理论与结构模型试验[M]. 武汉: 武汉理工大学出版社, 2005: 5-11. YANG Jun-jie. Similarity Theory and Structure Model Test[M]. Wuhan: Wuhan University of Technology Press, 2005: 5-11. |
| [17] |
万利军, 单伟, 袁建新. 自锚式悬索桥静力特性模型试验研究[J]. 公路交通科技, 2014, 31(6): 108-114. WAN Li-jun, SHAN Wei, YUAN Jian-xin. Experimental Study on Static Characteristics Model of Self-anchored Suspension Bridge[J]. Journal of Highway and Transportation Research an Development, 2014, 31(6): 108-114. |
| [18] |
关振长, 龚振峰, 陈仁春, 等. 基于正交设计的岩质相似材料配比试验研究[J]. 公路交通科技, 2016, 33(9): 92-98, 111. GUAN Zhen-chang, GONG Zhen-feng, CHEN Ren-chun, et al. Experimental Study on Mix Proportion of Rock Similar Material Based on Orthogonal Design[J]. Journal of Highway and Transportation Research an Development, 2016, 33(9): 92-98, 111. |
 2019, Vol. 36
2019, Vol. 36
