扩展功能
文章信息
- 史笑凡, 杨春风, 王可意
- SHI Xiao-fan, YANG Chun-feng, WANG Ke-yi
- 基于支持向量机和改进BP神经网络的路基边坡稳定性研究
- Study on Stability of Roadbed Slope Based on SVM and Improved BP Neural Network
- 公路交通科技, 2019, 36(1): 31-37
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(1): 31-37
- 10.3969/j.issn.1002-0268.2019.01.005
-
文章历史
- 收稿日期: 2017-08-14
2. 河北工业大学 土木工程重点实验中心, 天津 300401;
3. 河北工程大学, 河北 邯郸 056000
2. Key Lab of Civil Engineering, Hebei University of Technology, Tianjin 300401, China;
3. Hebei University of Engineering, Handan Hebei 056000, China
边坡失稳是一种复杂的地质现象,也是目前世界上3大地质灾害源之一。据统计,全球每年因为边坡失稳造成的公共财产损失达到数亿美元。为了防止和减轻由于边坡失稳造成的破坏,边坡的稳定性分析和预测变得尤为重要。然而,过多的统计不确定性,导致对边坡的稳定性研究变得异常困难。
目前,有关边坡稳定性的预测预报方法主要分为如下两类,一是定性分析法,其中包括地质分析法、工程地质类比法等。这类方法综合考虑影响边坡稳定的各种因素,快速地对边坡的稳定状况及其发展趋势作出评价[1]。我国学者李宁[2]等根据岩质边坡动力稳定性分析的几个要点,定性判断边坡的稳定性;二是定量分析法,定量方法中又包含确定性分析和不确定性分析。定量分析方法是边坡工程稳定性分析和滑坡预测预报的常见方法,在各类边坡工程实践中发挥了重要作用[3]。例如胡厚田[4]采用信息量统计方法和模糊综合评判方法对崩塌落石灾害进行空间预测;邱向荣、袁仁茂[5]等也采用模糊综合评判方法对公路边坡进行了研究;赵洪波等[6]提出了支持向量机在边坡稳定估计中的应用;黄发明等[7]提出采用PSO-SVM法预测滑坡地下水位;周爱红[8]等提出岩质边坡落石运动特征参数分析的支持向量机预测模型。
鉴于边坡岩土体的结构、岩土体构成与物理力学性质的不确定性和非线性的特点,边坡稳定性分析方法应有同时处理不确定性信息和动态非线性的能力,能够根据大量的工程边坡土质参数客观的识别出边坡的稳定状态。而支持向量机和BP神经网络作为非线性预测分析方法具有非线性和不确定性的能力,适合应用于边坡稳定性分析的研究中。纵观国内外研究,对于支持向量机和BP人工神经网络两种在边坡稳定性预测模型上的对比分析,目前鲜有研究。本研究将基于支持向量机和BP人工神经网络原理,对边坡稳定性建立安全系数预测模型,并对模型进行分析对比。
1 支持向量机算法支持向量机是一种基于统计学习理论的智能机器学习方法,通过寻求结构化风险最小来提高学习机的泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的[9]。
本研究中的边坡参数样本属于小样本,且样本值与待预测值非线性相关,因此,考虑利用支持向量机的独特优势,建立各点的支持向量机回归预测模型,并结合凸优化问题对预测结果进行分析。对于文中要研究的边坡稳定性类非线性问题笔者的基本思路是:首先对样本点进行编号i=1,2,3,…,m,其中m为观测点总数,然后建立所要研究样本的序列{x1, x2, x3, …, xm}。假设用前m-1个样本点来预测第m个样本点的值,将样本序列分为训练样本、检验样本、预测样本3个部分,建立回归映射关系。支持向量机就是通过建立前m-1个样本点的训练样本与第m个样本点的训练样本之间的映射关系,并通过检验样本检验其映射精度,最后通过前m-1个样本点的预测样本来预测第m个样本点的预测值。上述直观的映射关系可以转化为数学回归问题,将输入值与输出值之间的关系转化为数学问题。对于线性函数f (x)=y=kx+b的拟合问题,拟合数据{xi,yi},i =1,2,…,m,xi∈Rn,yi∈R,假定存在f函数在ε精度能够估计所有的数据,寻找最小k(k为参数变量)的问题可以表示为凸优化问题:
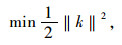
|
(1) |
(注:*为引用公式,下同)。
约束条件为:
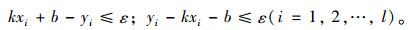
|
(2) |
引入松弛变量ξi,ξi*,此时的优化目标为:
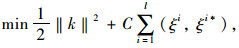
|
(3) |
约束条件为:

|
(4) |
引入Lagrange函数和对偶变量,得到对偶问题:
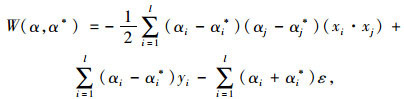
|
(5) |
式中W为对偶问题的目标函数。
约束条件为:
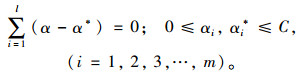
|
(6) |
可得到支持向量机拟合函数为:
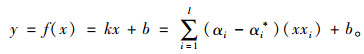
|
(7) |
同理,对于非线性问题可以通过非线性转换将初始问题映射到某高维特征空间中的线性问题进行求解。在高维特征空间中,线性问题中的内积运算可用核函数进行代替,即G(xi, yi)=φ(xi)φ(xj),得到拟合函数见式(8):
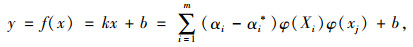
|
(8) |
约束条件为:
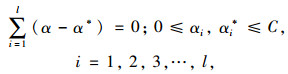
|
(9) |
式中,y为待预测值;α,α*为Lagrange乘子;m为样本点个数;G (xi, yi)为核函数;b为阈值;C为对超出误差ε的样本惩罚程度且大于0。最终求出Lagrange乘子及值,确定回归函数。
2 改进的BP神经网络算法人工神经网络是一种通过模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型[10]。目前,人工神经网络在各个领域应用广泛,其中使用最为普遍的是反向传播(Back Propagation)神经网络。相对于传统的数据处理方法,BP神经网络模型更适合处理模糊的、非线性的预测模拟问题。文中研究的边坡稳定性预测属于非线性问题,符合BP神经网络的算法规则。
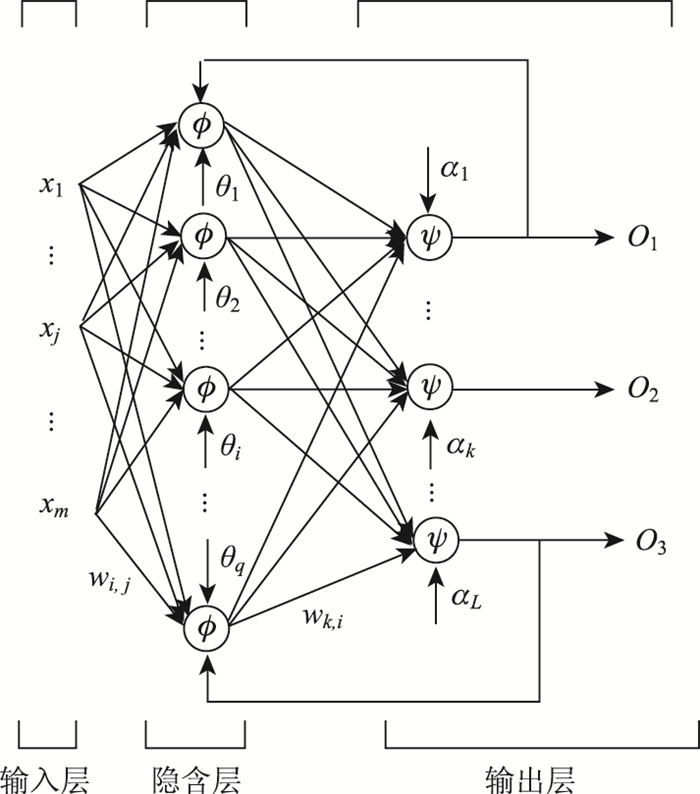
边坡稳定性的模拟、预测是函数的映射与拟合,以三层BP神经网络模型结构(见图 1)能够满足需要。本研究拟采用增加动量因子的方法改进BP算法,该方法能够降低网络对误差曲面的局部敏感性,抑制网络陷于局部极小而不能收敛的问题[11]。增加动量因子的权值计算公式如下:
|
| 图 1 简单BP网络三层结构 Fig. 1 Three-layer structure of simple BP network |
| |

|
(10) |
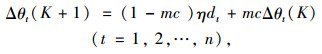
|
(11) |
式中,Wjt为层与层之间的连接权值;K为训练次数;mc为动量因子;η为学习效率;dt为输出层(隐含层)第t个神经元的一般化误差曲面斜率;θt为隐含层、输出层第t个节点的阈值;Oj为神经元的输出;Δ为增量。节点作用函数采用非对称S型函数的形式,ex为指数函数;f(x)本身是一种S型曲线。

|
(12) |
附加动量因子mc依据已有研究[12],其最大误差变化率应大于等于1,一般为1.04。mc的取值判断条件见式(13):
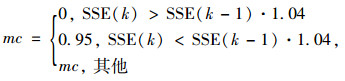
|
(13) |
式中SSE为误差平方和。
3 两种预测模型的综合分析 3.1 边坡稳定性影响因素的确定和样本选取对于边坡稳定性的影响因素众多,针对胶泥湾地区的实际情况,并结合了文献[13]中的45个边坡实例,得到其中的主要因素包括岩土体的内摩擦角φ、重度γ、黏聚力c、边坡角α、边坡高度H以及孔隙水压力γw这6个重要指标[14],而边坡的失稳也正是由于这些主要因素共同作用造成的。通过预测模型算法的演化计算来得到这6项土质参数与边坡安全系数Fs的回归函数,从而得到安全系数的预测值。
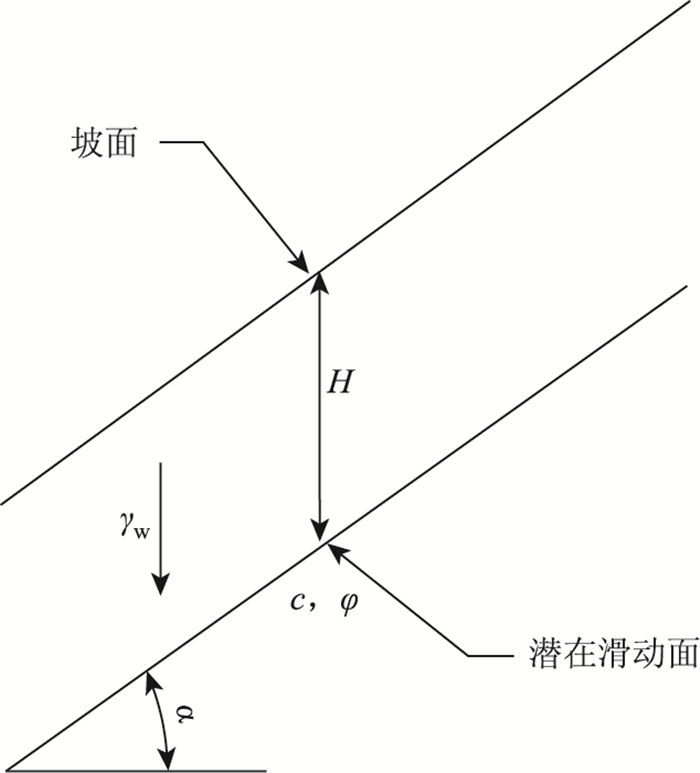
本研究选取的边坡模型为均质岩土边坡,设H为潜在滑动面和坡面间的土层厚度;α为边坡角;γw为孔隙水压力;c,φ为潜在滑动面上土体的有效黏聚力和有效内摩擦角,具体图示见图 2。
|
| 图 2 边坡稳定分析模型 Fig. 2 Slope stability analysis model |
| |
为了讨论孔隙水压力γw的取值,引入变异性概念。参数的变异性指的是,由于试验条件与试验误差的影响,使各次参数的测定值有所不同,这种特性就是参数的变异性。参数的变异性决定了其不确定性,一般用变异系数δ来反映数据的离散程度:
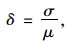
|
(14) |
式中,μ为参数的均值;σ为参数的标准差。变异系数是一量纲量,可用于比较不同参数的离散程度。
自20世纪末以来,中外学者对参数变异性的研究一直都在做不断的努力,以我国学者高大钊[15]为代表,其总结了国内外不同试验方法及不同地域所得岩土参数的变异系数取值范围,主要归纳为3个岩土参数指标:黏聚力c、内摩擦角φ以及孔隙水压力γw。各个参数的变异系数取值范围为:δγw<0.10,δc=0.19~0.55,δφ=0.05~0.40。根据各参数变异系数的取值范围可以看出,δγw取值较小,所以其对边坡稳定性预测结果影响较低,因此本研究不考虑孔隙水压力随土体深度的变化情况而将其设为定值。
本研究选取的学习样本数据共有45组,其中稳定边坡35个,失稳边坡10个。预测样本采用北京—新疆高速公路胶泥湾至冀晋界段的5个边坡工程,位于桩号K4+580~K4+780范围内,这一地段为深路堑土质边坡,部分地区局部土质岩体较厚且松散,在将来施工开挖时,极易使新产生的边坡失稳,形成不稳定斜坡。
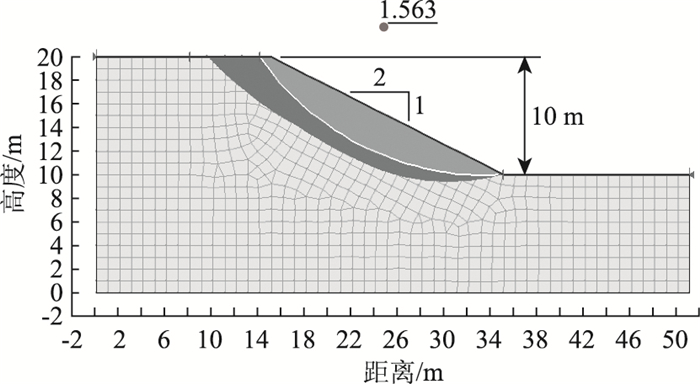
本研究通过Geo-slope软件和Fellenius[16]法计算得到预测边坡样本的安全系数,以样本1为例,计算结果如图 3所示。
|
| 图 3 边坡样本安全系数分析模型 Fig. 3 Slope sample safety factor analysis model |
| |
表 1为预测样本,共5组,其数据如下。
| 样本序号 | 重度/(kN·m-3) | 内聚力/kPa | 内摩擦角/(°) | 边坡角/(°) | 边坡高/m | 孔隙水压力 | 安全系数 |
| 1 | 18.900 | 17.500 | 31.000 | 26.500 | 10.000 | 0.260 | 1.563 |
| 2 | 20.200 | 16.700 | 22.300 | 42.400 | 25.000 | 0.250 | 1.389 |
| 3 | 21.500 | 14.000 | 19.300 | 38.900 | 35.000 | 0.270 | 1.419 |
| 4 | 20.400 | 25.000 | 20.400 | 35.000 | 35.000 | 0.320 | 1.764 |
| 5 | 14.000 | 0.000 | 40.000 | 45.000 | 50.000 | 0.300 | 1.000 |
将学习和预测中的样本数据进行归一化处理,将样本取值限制在[0, 1]区间之中。常用的归一化处理为现行函数转化法,表达式如下:
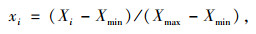
|
(15) |
式中,X,x分别为转换前后的数值;Xmax和Xmin分别为最大值和最小值。
3.2 两种模型的建立本研究采用Matlab[17]的工具箱对胶泥湾边坡实例进行支持向量机和BP神经网络的评价预测,并在其中编制了相应程序。软件版本为Matlab R2016a。
3.2.1 支持向量机模型确定学习样本后,建立支持向量机预测模型,并选择合适的核函数和惩罚系数C [18]。本研究通过对各种核函数测试之后,最终决定以样本的预测值与实际值的平均误差作为衡量标准,其中边坡稳定性支持向量机预测模型中的核函数选用径向基函数且γ取为0.25;采用遗传算法对C值进行测试,最终确定C=0.6;由式(1)~ (7)解得α,α*,b,便得到支持向量机边坡安全系数预测模型。
3.2.2 BP神经网络模型设计神经网络有3层结构,即输入层(Input Layer)、隐含层(Hidden Layer)和输出层(Output Layer),其中输入层与隐含层的传递函数选取tansig函数,隐含层到输出层的传递函数采用logsig函数。将输入层的神经元因子数设置为6个。此外,经过多次试验计算,隐含层单元数采用9,输出层有一个输出节点,所以三层单元数结构为6-9-1,模型样本如图 4所示。动量因子mc为0.60,学习效率η为0.10,在训练过程中模型表现了良好的误差收敛性能。

|
| 图 4 BP神经网络模型 Fig. 4 BP neural network model |
| |
3.3 两种模型预测结果比较
本研究分别采用支持向量机和改进BP神经网络分别对45组样本进行学习,利用建立的模型对余下5组样本进行预测,其样本训练和预测结果见图 5。

|
| 图 5 两种预测模型的预测结果 Fig. 5 Prediction results by 2 prediction models |
| |
从图 5可以看出,在样本学习的过程中两种模型都能较好地拟合实际值曲线,这说明两种模型都具有良好的数据泛化能力。通过计算,支持向量机模型的拟合误差绝对值之和为6.037,BP神经网络模型为4.366,且两者拟合程度都在85%以上,这说明学习效果良好。然而在样本预测阶段情况发生了变化,原本在学习阶段表现更优的BP神经网络却出现大幅度波动的情况,没有更好地拟合真实值曲线,精度较差;相反之下,支持向量机表现优秀,基本拟合了实际值样本曲线,预测精度更高。这是因为支持向量机(SVM)预测模型在处理小样本数据预测时具备独特优势,而BP神经网络受样本规模影响较大,针对样本容量相对较少的数据预测具有一定的限制,因此根据样本规模选取预测方法、建立预测模型是高精度预测的基础。
支持向量机与BP神经网络两种模型与实际值的预测比较见表 2。从表中的数据可以直观的看出,支持向量机模型的最大误差为0.12,小于BP神经网络的0.32;平均误差为0.087 4同样小于BP神经网络的0.214。两种误差分别仅为BP网络的37.5%与40.8%,这说明支持向量机模型与实际值契合的更优,预测结果更贴合实际,精度更高。并且两种模型的绝对误差与相对误差正负都有,表明预测模型对边坡安全系数的预测是均衡的,不会有总是过大或总是过小的情况。
| 序号 | 实际值 | 支持向量机SVM | BP神经网络 | |||||
| 预测值 | 绝对误差 | 相对误差/% | 预测值 | 绝对误差 | 相对误差/% | |||
| 1 | 1.563 | 1.457 | -0.106 | 6.781 | 1.35 | -0.213 | 13.628 | |
| 2 | 1.389 | 1.396 | 0.007 | -0.504 | 1.65 | 0.261 | -18.791 | |
| 3 | 1.419 | 1.325 | -0.094 | 6.624 | 1.54 | 0.121 | -8.527 | |
| 4 | 1.764 | 1.654 | -0.11 | 6.234 | 1.444 | -0.32 | 18.141 | |
| 5 | 1 | 1.12 | 0.12 | -12 | 1.155 | 0.155 | -15.5 | |
| 最大误差 | 0.12 | 0.32 | ||||||
| 平均误差 | 0.087 4 | 0.214 | ||||||
3.4 学习样本容量对两种模型预测结果的影响
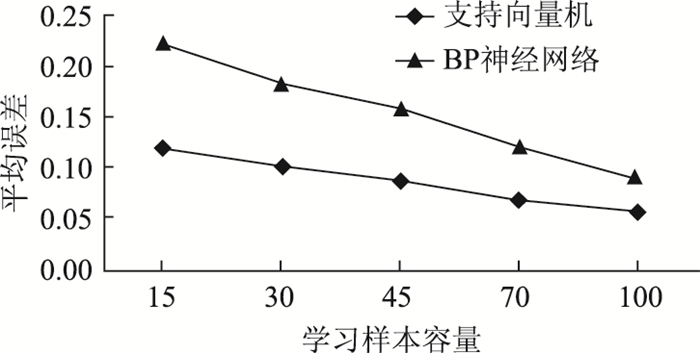
为了研究更具有代表性,本研究选取的各个边坡参数学习样本不具备任何相关性,都是随机挑选的。例如,样本的边坡高度上至200 m,下至5 m。而学习样本容量的大小在一方面决定了两种预测方法最终所得平均误差的结果,为此笔者选择了15,30,45,70,100这5个不同的学习样本容量,按照上文方法步骤计算得到各个样本对应的预测安全系数,然后计算平均误差,最终的比较结果变化曲线见图 6。
|
| 图 6 两种预测结果随样本容量的变化 Fig. 6 Two prediction results varying with sample size |
| |
通过图 6的曲线变化可以得知,支持向量机模型的预测结果在小样本容量时表现出很大优势,BP神经网络模型则与之不同,小样本时预测精度明显低于支持向量机,而当样本容量逐渐增大,平均误差随之减小,精度逐渐提高,与支持向量机相差越来越小。由此可见,支持向量机较之BP神经网络更适用于小样本预测,而BP神经网络在大样本预测时精度会明显提高。
4 结论边坡稳定性受到诸多因素的制约与影响,由于难以在边坡安全系数和影响因素之间建立一种合适、确定的数学模型,所以本研究选取了支持向量机和BP神经网络两种分析方法,对其分别建立了支持向量机模型和BP人工神经网络模型,根据45个样本实例数据,对5个工程边坡实例的安全系数进行预测计算,主要内容有:
(1) 支持向量机模型在边坡稳定性预测上的研究。建立胶泥湾地区高速公路边坡安全系数预测的支持向量机模型,并利用45个不同土质参数的边坡数据对模型的可靠性进行训练,分析预测安全系数,证明预测模型的有效性。
(2) BP神经网络模型在边坡稳定性预测上的研究。通过附加动量因子mc来改进BP神经网络,从而建立了改进后的胶泥湾地区高速公路边坡安全系数预测的BP神经网络模型,同样利用45个不同土质参数边坡数据对模型的可靠性进行验证,得到的预测数据证明了模型的有效性和可靠性,说明改进后的BP神经网络预测模型具有更好的预测效果。
(3) 两种模型都具备只通过学习和误差校正来模拟样本点之间的内在非线性关系的能力,但是BP神经网络受样本规模影响较大,尤其在小样本条件下,支持向量机的泛化能力明显优于BP网络。并且支持向量机模型的训练和预测速度更快,得到的回归式稳定且唯一。
由以上的对比分析可以得出,支持向量机和BP神经网络在进行边坡稳定分析中都是有效的工具,但是相比之下支持向量机预测精度更高,速度更快,更适用于小样本预测,能有效表征复杂条件下边坡安全系数以及与各影响因子之间的非线性关系,具有较强的非线性动态数据处理能力和推广力;并且可以降低分析过程中遇到的不确定性。因此认为,支持向量机为边坡稳定性防治提供了精确的科学依据,为区域滑坡灾害调控决策、预警预报提供了新的科学方法。
| [1] |
胡厚田. 边坡地质灾害的预测预报[M]. 成都: 西南交通大学出版社, 2001. HU Hou-tian. Prediction and Forecast of Slope Geological Hazard[M]. Chengdu: Southwest Jiaotong University Press, 2001. |
| [2] |
李宁, 姚显春, 张承客. 岩质边坡动力稳定性分析的几个要点[J]. 岩石力学与工程学报, 2012, 31(5): 873-881. LI Ning, YAO Xian-chun, ZHANG Cheng-ke. Several Points in Dynamic Stability Analysis of Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 873-881. |
| [3] |
唐小松, 李典庆, 曹子君, 等. 有限数据条件下边坡可靠度分析的Bootstrap方法[J]. 岩土力学, 2016, 37(3): 893-901, 911. TANG Xiao-song, LI Dian-qing, CAO Zi-jun, et al. A Bootstrap Method for Analyzing Slope Reliability Based on Limited Shear-strength Parameter Data[J]. Rock and Soil Mechanics, 2016, 37(3): 893-901, 911. |
| [4] |
胡厚田. 崩塌落石综合预测方法的研究[J]. 铁道工程学报, 1996, 6(2): 182-190. HU Hou-tian. Synthetical Prediction of Landfall and Rockfall[J]. Journal of Railway Engineering Society, 1996, 6(2): 182-190. |
| [5] |
邱向荣, 袁仁茂, 许伟文. 公路边坡灾害危险性预测模糊综合评判法[J]. 水土保持研究, 2003, 10(3): 26-28, 36. QIU Xiang-rong, YUAN Ren-mao, XU Wei-wen. Fuzzy Mathematics Method for Evaluation of Slope Stability[J]. Research of Soil and Water Conservation, 2003, 10(3): 26-28, 36. |
| [6] |
赵洪波, 冯夏庭. 支持向量机函数拟合在边坡稳定性估计中的应用[J]. 岩石力学与工程学报, 2003, 22(2): 241-245. ZHAO Hong-bo, FENG Xia-ting. Application of Support Vector Machines Function Fitting in Slope Stability Evaluation[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 241-245. |
| [7] |
黄发明, 殷坤龙, 张桂荣, 等. 多变量PSO-SVM模型预测滑坡地下水位[J]. 浙江大学学报:工学版, 2015, 49(6): 1193-1200. HUANG Fa-ming, YIN Kun-long, ZHANG Gui-rong, et al. Prediction of Groundwater Level in Landslide Using Multivariable PSO-SVM Model[J]. Journal of Zhejiang University:Engineering Science Edition, 2015, 49(6): 1193-1200. |
| [8] |
周爱红, 王帅伟, 袁颖, 等. 岩质边坡落石运动特征参数分析及SVM预测模型[J]. 公路交通科技, 2017, 34(3): 20-25. ZHOU Ai-hong, WANG Shuai-wei, YUAN Ying, et al. Analysis on Characteristic Parameters of Rock Slope Rockfall Movement and SVM Prediction Model[J]. Journal of Highway and Transportation Research and Development, 2017, 34(3): 20-25. |
| [9] |
赵志刚, 左仕, 李清. 基于支持向量机与神经网络法的路基沉降预测对比研究[J]. 路基工程, 2015(4): 15-19. ZHAO Zhi-gang, ZUO Shi, LI Qing. Comparative Study on Prediction of Subgrade Settlement Based on Support Vector Machine and Neural Network Methods[J]. Subgrade Engineering, 2015(4): 15-19. |
| [10] |
肖大海, 谢全敏, 杨文东. 基于多变量的集成预测模型在隧道拱顶沉降变形预测中的应用[J]. 公路交通科技, 2017, 34(12): 90-96. XIAO Da-hai, XIE Quan-min, YANG Wen-dong. Application of Integrated Forecasting Model Based on Multivariable in Tunnel Vault Settlement Forecasting[J]. Journal of Highway and Transportation Research and Development, 2017, 34(12): 90-96. |
| [11] |
于国强, 张茂省, 王根龙, 等. 支持向量机和BP神经网络在泥石流平均流速预测模型中的比较与应用[J]. 水力学报, 2012, 43(增2): 105-110. YU Guo-qiang, ZHANG Mao-sheng, WANG Gen-long, et al. Application and Comparison of Prediction Models of Support Vector Machines and Back-propagation Artificial Neural Network for Debris Flow Average Velocity[J]. Journal of Hydraulic Engineering, 2012, 43(S2): 105-110. |
| [12] |
NILSSON P, UVO C B, BERNDTSSON R. Monthly Runoff Simulation:Comparing and Combining Conceptual and Neural Network[J]. Models Journal of Hydrology, 2006, 321(1): 344-363. |
| [13] |
王超.工程高边坡稳定性预测方法研究[D].北京: 北京交通大学, 2009. WANG Chao.Study on Prediction Methods for High Engineering Slope[D].Beijing: Beijing Jiaotong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10004-2009204797.htm |
| [14] |
XUE Xin-hua, YANG Xing-guo, CHEN Xin. Application of a Support Vector Machine for Prediction of Slope Stability[J]. Science China:Technological Sciences, 2014, 57(12): 2379-2386. |
| [15] |
高大钊. 关于岩土设计参数标准值计算公式的讨论[J]. 工程勘察, 1996, 24(3): 5-8. GAO Da-zhao. Discussion on Calculation Formula of Standard Value of Geotechnical Design Parameters[J]. Geotichnical Investigation and Surveying, 1996, 24(3): 5-8. |
| [16] |
杨建民, 张丹蕾, 秦军. 考虑渗流作用的土坡稳定分析Fellenius法和简化Bishop法[J]. 工业建筑, 2017, 47(12): 111-120. YANG Jian-min, ZHANG Dan-lei, QIN Jun. Fellenius Method and Simplified Bishop Method for Slope Stability Analysis Considering Seepage Effect[J]. Industrial Construction, 2017, 47(12): 111-120. |
| [17] |
唐高朋, 赵炼恒, 李亮, 等. 基于MATLAB的边坡稳定性极限上限分析程序开发[J]. 岩土力学, 2013, 34(7): 2091-2098. TANG Gao-peng, ZHAO Lian-heng, LI Liang, et al. Program Development for Slope Stability Using MATLAB Software and Upper Bound Limit Analysis[J]. Rock and Soil Mechanics, 2013, 34(7): 2091-2098. |
| [18] |
ZHANG Chun-hua, TIAN Ying-jie, DENG Nai-yang. The New Interpretation of Support Vector Machines on Statistical Learning Theory[J]. Science China Mathematics, 2010, 53(1): 151-164. |
 2019, Vol. 36
2019, Vol. 36
