扩展功能
文章信息
- 卢才武, 赵海, 江松, 刘茹玥
- LU Cai-wu, ZHAO Hai, JIANG Song, LIU Ru-yue
- 基于新陈代谢——GM(1, N)马尔科夫的轨道交通客运量预测方法
- A Prediction Method of Rail Transit Passenger Volume Based on Metabolism-GM(1, N) Markov Model
- 公路交通科技, 2018, 35(12): 141-150
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(12): 141-150
- 10.3969/j.issn.1002-0268.2018.12.020
-
文章历史
- 收稿日期: 2017-08-14
随着中国城市化水平不断提高,大量的人口涌向城市,城市人口数量越来越多,机动车数量的不断增长,城市基础设施建设的滞后性就日益严重,如何有效解决城市人口出行问题以及交通拥堵问题是城市发展的关键。城市轨道交通具有载客量大、速度快和节约城市用地等特点,是今后城市交通发展的主要方向。预测轨道交通客运量可以作为轨道交通科学管理的基础数据,对提高轨道交通管理水平和建立高效轨道交通线路网起指导作用。其中,宏观层面的轨道交通客运量预测可为区域整体线路规划和轨道交通专项规划提供直接和有效的基础数据,微观层面的某条轨道交通线路客运量预测是对车型进行选择、确定配车数量、站点规划以及对已建成的线路进行优化调整的主要依据。因此,对轨道交通客运量的发展规律进行分析,对于提高轨道交通的管理水平和轨道交通营运效率具有非常重要的现实意义,同时可以促进轨道交通事业的可持续发展。但由于轨道交通客运需求受地方经济水平、人口数量、城市交通结构、轨道交通服务水平等众多因素影响,对其客运量准确预测较为困难,目前国内外学者一般采用神经网络法、灰色系统理论和指数平滑法等进行研究。
Vlahogianni等基于有限的知识网络结构优化原则,通过提供先进的基于遗传算法的多层结构优化战略可以优化客运量数据的时空分布特征[1];Suryani等通过建立系统动力学框架模型对客运需求进行预测,根据系统动力学的物理特性和信息流反馈控制连续决策和行动,可用来模拟、分析和仿真,以提高模型的预测精度[2];Fernandez等研究了客运系统的运输能力问题,解释了客运量的概念并且分析了到目前为止关于客运量模型的工作,讨论各模拟方法以及优缺点[3];国内学者刘昱岗针对公路客运量的影响因素复杂的特点,在预测公路客运量时,首次提出灰色综合弹性系数的概念,并建立灰色关联弹性模型。实证检验,发现该模型比使用传统弹性系数的方法,预测精度较高,具有一定的实用性[4];考虑到影响客运量的因素众多,且数据具有小样本贫信息的特点,王洁采用基于最小二乘法改进的GM(1,1)模型,对上海市的客运量进行短期预测[5]。王玉刚对传统灰色模型的紧邻均值生成序列做出改进,发现改进后的灰色预测模型要比传统的灰色预测模型的拟合精度更高,更适用于重庆市的常规公交客运量的预测[6]。杨琦等针对2004—2009年西安市公交客运量应用灰色系统理论进行初步预测分析,之后采用马尔科夫理论对预测结果进行修正,发现马尔科夫灰色模型在理论与实际方面都有较好的实用性[7];芮海田等采用二次曲线拟合的方法计算指数平滑的初始值和平滑系数,之后应用指数平滑法对安徽省2010—2011年公路客运量进行预测,最后采用马尔科夫模型对预测结果进行修正,所得结果相对误差较小,有较强的实用性[8];曹尧谦等为全面考量客运专线的客运量情况,采用四阶段法构建模型,并用灰色模型替代原有重力模型进行优化,预测结果精度较高,具有重要的参考意义[9];孙可朝建立基于灰色模型、一元回归和指数平滑3种预测方法,建立了以历年预测值加权之和与实际值的差值的绝对值之和最小为目标函数,选取“百城百站”旅客发送量为基础数据,对未来道路旅客发送量进行预测,从而证明该组合预测模型操作方便,可减少单个模型预测的不确定性[10]。李俊芳等将人口距车站远近划分为不同圈层,通过多元变量偏相关系数计算,综合选取道路网密度等11个变量建立圈层人口与BP神经网络预测模型,实证分析表明以圈层人口为变量的BP神经网络模型的预测精度明显优于其他模型[11];冯冰玉等根据客运量数据小样本和非线性的特点,利用RBF神经网络超强的学习能力对传统灰色GM(1,1)模型进行优化,提高预测精度[12];吴华稳等针对客货运量具有混沌时间序列的特性,在Takens相空间重构的基础上,对该混沌时间序列进行识别,构建RBF神经网络预测模型,得到预测结果与实际值及BP神经网络预测结果相对比,可知混沌RBF神经网络模型具有更高的预测精度[13];李晓晖等针对中国客运量的特点,建立了以因子分析法为基础的Logistic模型,消除了由于影响因素较多而产生的多重共线性对预测结果的影响,经实际验证该模型预测精度高,有较好的实用性[14];刘钊等针对短时交通流,建立了综合考虑预测路段和与其邻近路段交通流的混合预测模型(KNN-SVR), 该模型优于传统的单一预测方法[15];何南等考虑交通运输方式之间的替代性,建立了考虑铁路、航空影响的公路客运交通需求预测模型,经预测结果与实际结果比较分析,表明公路、铁路、航空间存在竞和关系[16];胡彦蓉等针对人工神经网络在预测时训练速度慢等特点,利用KPCA法对2000-2008年杭州市公路客运量数据的特征进行提取,并建立KPCA-SVM预测模型,结果表明该模型具有较高的预测精度和可靠性,为公路客运量预测研究提供了一种新方法[17]。梁小珍等针对时间序列包含噪声以及单一模型可能存在预测不准确的问题,提出一种基于奇异谱分析(SSA)的集成预测模型,对我国2014-2016年度航空客运量进行了预测[18]。
以上大多是针对客货运量进行研究预测的,虽然与城市轨道交通客运量预测在预测思想上大体一致,但由于城市轨道交通客运量预测有其一定的特殊性,尤其是城市轨道交通受众多因素影响,其自身变化动态性较强,相关影响因素自身规律也难以准确表达,要达到较高的预测精度,现有的研究方法仍存在较大的难度。本研究应用灰色理论(GM(1,n)模型)对城市轨道交通客运量进行初步预测,并对预测结果的残差进行修正。在此基础上,进一步利用马尔科夫理论,构建状态转移概率矩阵,二次修正预测结果,之后融入新陈代谢的思想,根据时间序列删除已陈旧的或价值不大的信息,加入已得到的预测结果作为新的预测数据源,之后对下一时刻进行预测,以提高模型预测的精度。最后,利用2008-2013年上海市以及北京市轨道交通客运量数据进行仿真研究,对2014-2016年客运量进行预测,预测结果证明,该组合模型比GM(1,n)模型、传统马尔科夫GM(1,n)有更高的预测精度,因此具有较高的实际应用价值。
1 新陈代谢——GM(1,N)马尔科夫模型的建立 1.1 建模思想本研究以GM(1,n)模型预测的结果作为研究基础,将灰色理论、马尔科夫理论与新陈代谢3种方法的思想相融合[7-9, 16],从而提出一种全新的轨道交通客运量预测模型:新陈代谢——GM(1,n)马尔科夫模型。此预测方法首先使用传统GM(1,n)预测模型计算得出的预测值作为背景,利用残差修正对预测结果进行一次修正,再利用马尔科夫理论原理构建状态转移概率矩阵对GM(1,n)预测模型的结果进行二次修正优化,此后对此过程融入新陈代谢的思想,将已预测得的信息作为新信息加入,剔除旧信息,然后对下一时刻进行预测,从而提高了模型对未来较远时刻的预测精准度。整体建模过程如图 1所示,具体建模步骤如下文所述。
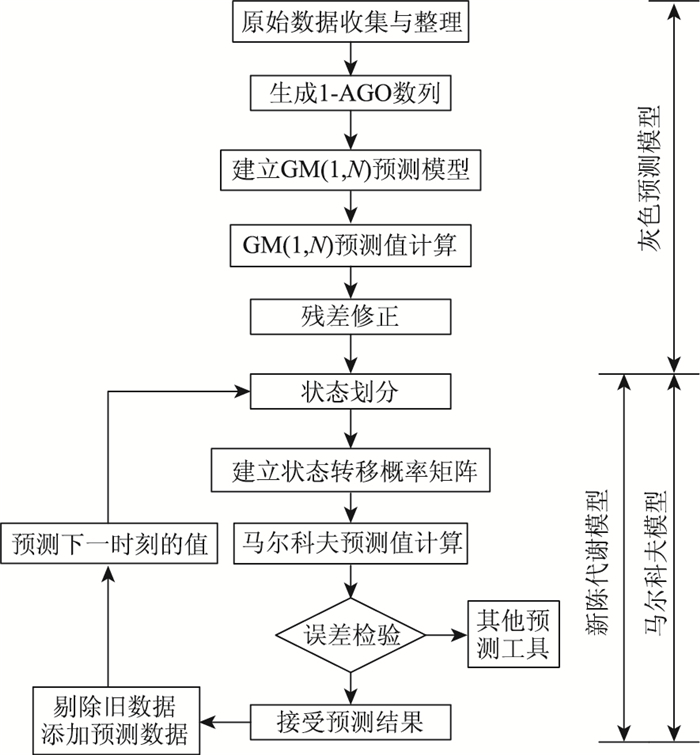
|
| 图 1 建模流程 Fig. 1 Modeling process |
| |
1.2 GM(1,n)模型
GM(1,n)是我国学者邓聚龙在1982年提出的灰色理论中表示n个变量、一阶微分的预测模型,主要适用于数据少和状态波动小的短期预测,是农业、经济、交通、物流领域预测模型中最基本的一种[19]。其原理是通过累加生成,将一组原本杂乱无章、毫无规律的数列生成为呈现出指数增长变化规律的数列,从而减弱了原始数据自身的随机性和波动性,并将其视为基于原始序列关于时间的函数,建立GM(1,n)模型,即建立一阶线性微分方程,求解该微分方程,从而得到累加数列的灰色预测值,最后通过累减还原得到原始数列的预测值。
其具体建模过程如下:
(1) GM(1,n)模型建立
设有N个含有n个元素的数据序列:
Xi(0)=[xi(0)(1), xi(0)(2), …, xi(0)(n)] i=1, 2, …, n,对Xi(0)做一次累加,得到1次累加生成数列(简称1-AGO):Xi(1)=[xi(1)(1), xi(2)(2), …, xi(3)(n)] i=1, 2, …, n,其中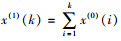
对Xi(1)作紧邻均值生成,得到Z(1)=(z(1)(2), z(1)(3), …, z(1)(n)),
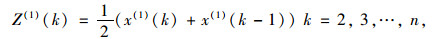
|
(1) |
最后构建关于Xi(1)的GM(1,n)灰微分方程:
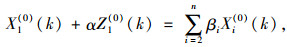
|
(2) |
将数列Xi(1)视为基于原始序列关于时间t的函数Xi(1)=Xi(1)(t),则可得到GM(1,n)白化微分方程:
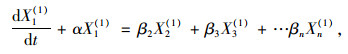
|
(3) |
式中α, β1, β2, …, βn均为参数。
(2) 求解参数
设数列Yn=[xi(0)(1),xi(0)(2),…,xi(0)(n)]T,参数列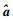
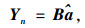
|
(4) |
从而可解得:
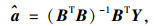
|
(5) |
其中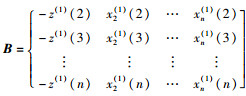
(3) 计算微分方程的解
将参数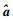
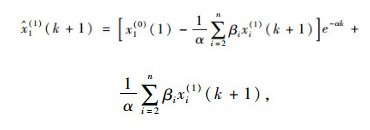
|
(6) |
式中α,βi均为参数。
(4) 累减还原
通过式(6)得到的解为原始数列累加生成数列X i(0)的预测值,因此需通过累减还原得到原始数列在GM(1,n)模型下的预测值:
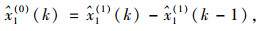
|
(7) |
综上所述,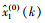
(5) 残差计算
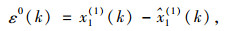
|
(8) |
根据式(8)可计算得残差值,残差表示原始数据和预测数据之间的偏离程度,残差越小,说明偏离程度越小,预测精度越好。
(6) 残差修正
记生成的原始残差为ε0=(ε1, ε2, …, εn),其中ε0为X1(0)的残差序列。对残差序列建立GM(1, n)模型,求出其参数P=[αε,βε]T, 根据式(8)计算出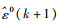
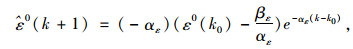
|
(9) |
式中αε,βε均为参数。则式(6)修正成:
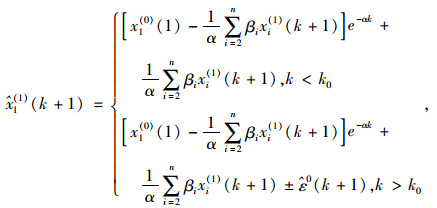
|
(10) |
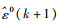
上述GM(1,n)预测模型是通过将原始数据累加生成为具有准指数规律的序列,分析挖掘该序列潜在的规律,从而获得预测值,通常只适合原始数据变化接近指数规律变化。同时数据的获得具有偶然性,以及轨道交通客运量的自身动态波动性,会导致预测结果产生较大误差。
马尔科夫模型是指一个随机变量序列,它与某个系统的状态相对应,而此系统在某个时刻的状态只依赖于它在前一时刻的状态。该模型是通过各状态之间的转移概率来预测一个系统的发展变化的数学方法,适合应用于随机波动性较大的预测问题,具有较高的科学性、适用性。
因此针对GM(1,n)模型预测精度一般的实际情况,以及轨道交通客运量自身波动性大的特点,本研究基于灰色GM(1,n)对预测结果进行状态划分,构建轨道交通客运量状态转移概率矩阵,同时采用马尔科夫模型对GM(1,n)预测结果进行二次修正优化,以弥补GM(1,n)模型的局限性,提高预测的精度。具体建模过程如下:
(1) 状态区间划分
基于灰色GM(1,n)的马尔科夫模型状态划分方法是以GM(1,n)模型预测结果的相对误差分布情况,作出其相应散点图,以及n条与x轴平行的直线,每2条相邻直线之间的区域可视为一种状态,记为状态Ei。
状态区间划分的个数一般来说取决于原始数据的容量。由于原始数据容量较小时,状态转移的总次数相应的也较少,因此为了更客观地反映出原始数据在各状态间的转移情况,状态个数应划分的较少。相反当原始数据容量较大时,为了便于从状态转移概率矩阵中挖掘出更多的信息来提高预测精度,状态个数应划分的较多。
(2) 建立状态转移概率矩阵
由状态Ei转移到状态Ej的次数为ni→j,以状态Ei为起点转向另一个状态的次数为Ni,则状态Ei转移到状态Ej的状态转移概率为:
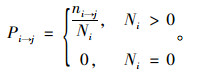
|
(11) |
根据式(11)可计算状态转移概率矩阵为:
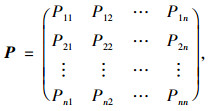
|
(12) |
式(12)中,Pn1+Pn2+…+Pnn=1。(其中0≤Pij≤1,(i, j=0, 1, 2, …, n)矩阵中每个元素都非负)。
(3) 计算马尔科夫预测值
建立状态转移概率矩阵P后,设n时刻对象处于Ei状态,若P中的第k行满足maxPij=Pkl,则认为n+1时刻(预测时刻)最有可能从状态Ei转移到状态Ej,从而也就确定了预测值的变动区间[E1i, E2i],可取该区间的中位数为n+1时刻的预测值:
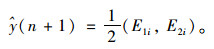
|
(13) |
(4) 误差检验
计算相对误差:
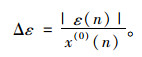
|
(14) |
一般将GM(1,n)预测模型与马尔科夫模型相组合进行预测时,计算状态转移概率矩阵的数据来源是固定不变的,也就是说该模型不能为预测所应用的数据序列提供新的信息源,将前面己预测出的最新结果加入到数据序列中,使用这种固定不变的数据源对未来较远的时刻进行预测时,预测结果必然会产生很大误差。
因此本研究在建模过程中融入新陈代谢的思想,即在预测n+2时刻的预测值时,加入预测数据作为新信息,然后删除最早的数据信息,来对一般GM(1,n)马尔可夫模型进行改进。其具体过程如下述:
在原始数据序列Xi(0)=[xi(0)(2), xi(0)(3), …, xi(0)(n)] i=1, 2, …, n中,加入预测数据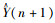
影响城市轨道交通客运量的因素较多,如城市经济发展水平,居民出行频率,常住人口数量,城市交通水平等,但目前在交通运输管理相关理论中未形成准确的数学模型对轨道交通客运量进行预测,以分析其发展规律。由于影响轨道交通客运量的各个影响因素自身的发展状况较为模糊,同时GM(1,n)预测模型与多元回归预测模型不同,选取的相关因素越多对预测精度的影响越大,因此将众多因素综合起来预测未来轨道交通客运量必然会产生较大的误差。
综合本研究所建立模型的特点以及国内外学者研究成果,在各影响因素中,从区域宏观角度出发,本研究选取常住人口、轨道交通运营里程、公共汽电车客运总量、出租汽车载客里程和个人民用车辆拥有量作为预测轨道交通客运量的相关因素。主要是因为,常住人口是反映某区域人口数量的主要指标,而人口数量与城市交通发展水平是呈线性关系,一般来说某地区的人口越多,该地区的交通基础设施建设水平就越高。同时人口数量对居民出行频率具有较强的解释作用,而城市轨道交通作为今后城市居民出行的重要组成部分,与居民出行频率有着直接的关系;轨道交通运营里程作为反映轨道交通自身的运营情况的指标,与轨道交通线路数量,运营车辆数量,以及运营线路长度有关,该指标可以体现轨道交通的建设水平,运营水平以及载客水平。一般可认为轨道交通运营里程越多,该地区轨道交通数量越多,轨道交通运营更活跃,其客运量就越大;公共汽电车客运总量、出租汽车载客里程和个人民用车辆拥有量作为衡量城市区域机动化程度的重要因素,与居民出行方式选择、城市拥堵情况等都具有很强的关联性,组成了居民交通出行的重要选择方式,一定程度上与轨道交通客运量有替代关系。故本研究从城市人口基数、轨道交通自身发展以及替代品3个方面综合考虑选取常住人口、轨道交通运营里程、公共汽电车客运总量、出租汽车载客里程和个人民用车辆拥有量作为研究轨道交通客运量的相关因素。
2.2 GM(1,n)模型建立根据上述因素分析,依据上海市统计局统计年鉴进行数据收集整理,得到2008—2013年上海市轨道交通客运量及相关因素值如表 1所示。
| 指标 | 年份 | |||||
| 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | |
| 轨道交通客运量/万人 | 112 798 | 131 837 | 188 407 | 210 105 | 227 573 | 250 628 |
| 常住人口/万人 | 2 141 | 2 210 | 2 303 | 2 347 | 2 380 | 2 415 |
| 轨道交通运营里程/(万列·公里) | 2 516 | 2 871 | 4 778 | 5 406 | 5 570 | 5 872 |
| 公共汽电车客运总量/万人 | 266 000 | 270 600 | 281 100 | 280 400 | 280 800 | 271 000 |
| 出租汽车载客里程/万公里 | 412 700 | 377 300 | 395 400 | 397 900 | 398 400 | 405 900 |
| 个人民用车辆拥有量/万辆 | 196.03 | 210.42 | 229.83 | 245.88 | 182.57 | 203.64 |
2.2.1 数据处理
将2008—2013年轨道交通客运量数列X1(0)=(112 798, 131 837, 188 407, 210 105, 227 573, 250 628),常住人口数列X2(0)=(2 141, 2 210, 2 303, 2 347, 2 380, 2 415)等相关因素数列进行累加生成,可得1-AGO数列X1(1)=(112 798.00, 244 635.00, 433 042.00, 643 147.00, 870 720.00, 1 121 348.00),X2(1)=(2 141.00, 4 351.00, 6 654.00, 9 001.00, 11 381.00, 13 796.00)。在轨道交通客运量数据1-AGO基础上的紧邻均值生成为Z1(1)=(178 716.50, 338 838.50, 538 094.50, 756 933.50, 996 034.00)。
2.2.2 矩阵构造及参数计算

|
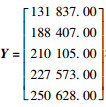
根据式(6),代入上述计算得出的参数值可得轨道交通客运量预测模型: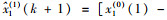
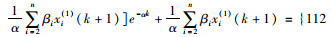
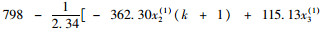
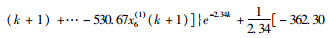
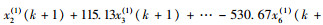
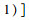
| 年份 | 实际值/万人 | GM(1,n)模型 | 残差GM(1,n)模型 | |||
| 预测值/万人 | 相对误差/% | 预测值/万人 | 相对误差/% | |||
| 2008 | 112 798 | 112 798 | — | 188 407 | — | |
| 2009 | 131 837 | 140 783.26 | 6.79 | 140 783.26 | 6.79 | |
| 2010 | 188 407 | 213 758.86 | 13.46 | 189 583.591 | 0.62 | |
| 2011 | 210 105 | 229 575.25 | 9.27 | 208 568.986 | -0.73 | |
| 2012 | 227 573 | 244 993.24 | 7.65 | 226 740.572 | -0.37 | |
| 2013 | 250 628 | 267 850.92 | 6.87 | 251 990.895 | 0.54 | |
| 平均相对误差 | 8.81 | 1.37 | ||||
由表 2可知GM(1,n)模型的预测平均相对误差为8.81%,误差较大,因此说明GM(1,n)模型有待进一步改进和优化,使其能符合实际应用需求,现对该模型进行一次修正,即对预测结果的残差进行修正。
2.2.4 残差修正根据式(5)、式(9)、式(10)可得残差序列预测值为ε0=(-8 946.26, -24 175.30, -21 006.30, -18 252.70, -15 860.00)以及基于残差修正得到的GM(1,n)模型的预测修复值见表 2。
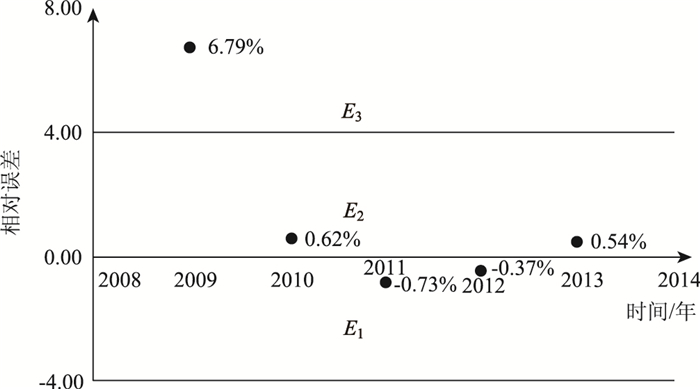
2.3 马尔科夫模型建立 2.3.1 状态划分由表 2可得轨道交通客运量残差GM(1,n)模型的相对误差散点图(见图 2),可将其按等距划分(间距为4%)为3个状态E1,E2,E3,分别为[-4%,0%],[0%,4%],[4%,8%]。
|
| 图 2 状态划分图 Fig. 2 State partition |
| |
根据相对误差散点图以及状态划分情况,轨道交通客运量残差GM(1,n)模型预测结果所在区间状态情况如表 2所示。
2.3.2 转移概率矩阵计算根据式(10)、式(11)以及表 3可计算一步状态转移概率矩阵为:
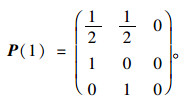
|
| 年份 | 相对误差/% | 所在状态 |
| 2009 | 6.79 | E3 |
| 2010 | 0.62 | E2 |
| 2011 | -0.73 | E1 |
| 2012 | -0.37 | E1 |
| 2013 | 0.54 | E2 |
2.3.3 计算预测值
根据表 3可知,2013年轨道交通客运量的状态处于E2,由maxPij=Pkl可知经过1年的转换,系统状态转为E1的概率为1,则2014年的轨道交通客运量最有可能处于状态E1。由式(10)得GM(1,n)模型预测值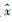
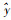
预测2015年的轨道交通客运量需建立二步、三步状态转移矩阵: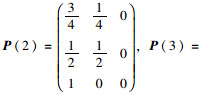
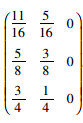
把2008年到2013年的轨道交通客运量所组成的时间序列中2008年的轨道交通客运量数据去掉,增加2014年马尔科夫GM(1,n)模型预测值288 255.17万人,用2009年到2014年的轨道交通客运量的6个数据构造一组新的数据序列:
X1(0)=(131 837, 188 407, 210 100, 227 000, 250 600, 288 255.17)。对此序列建立新的GM(1,n)模型,得到预测结果,针对预测结果的相对误差重新划分状态区间构造新的状态转移矩阵,计算新陈代谢——GM(1,n)马尔科夫模型下2015年轨道交通客运量的预测值为314 724.28万人。同理可计算出2016年轨道交通客运量为349 397.59万人。综合比较本研究应用的各预测方法对2014—2016年上海市轨道交通客运量预测结果情况比较如表 4,图 3所示。
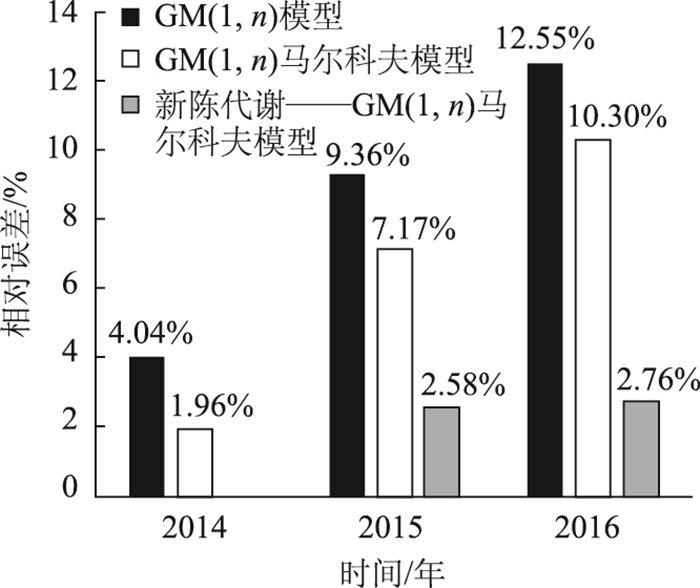
| 方法 | 年份 | 实际值/万人 | 预测值/万人 | 相对误差/% |
| GM(1,n)模型 | 2014 | 282 727 | 294 137.93 | 4.04 |
| 2015 | 306 798 | 335 501.91 | 9.36 | |
| 2016 | 340 000 | 382 682.82 | 12.55 | |
| GM(1,n)马尔科夫模型 | 2014 | 282 727 | 288 255.71 | 1.96 |
| 2015 | 306 798 | 328 791.87 | 7.17 | |
| 2016 | 340 000 | 375 029.16 | 10.30 | |
| 新陈代谢——GM(1,n)马尔科夫模型 | 2014 | 282 727 | — | — |
| 2015 | 306 798 | 314 724.28 | 2.58 | |
| 2016 | 340 000 | 349 397.59 | 2.76 |
|
| 图 3 上海市轨道交通客运量各预测方法预测结果比较 Fig. 3 Comparison of predicted passenger volumes of urban rail transit in Shanghai obtained by different prediction methods |
| |
由表 4和图 3可知:应用新陈代谢思想对GM(1,n)马尔科夫模型进行优化后,预测2015,2016年上海市轨道交通客运量分别为314 724.28万人、349 397.59万人,与实际值的相对误差分别为2.58%,2.76%。
为了验证模型的普适性,本研究采用北京市2008年到2013年的相关数据进行近一步的验证计算。北京作为中国第一个拥有城市轨道交通系统的城市,其历史可以追溯到1969年,目前北京市共拥有19条轨道交通线路(含京港地铁线路),运营里程554 km,其轨道交通发展在我国具有较强的代表性。北京市轨道交通客运量及相关因素值如表 5所示。
| 指标 | 年份 | |||||
| 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | |
| 轨道交通客运量/万人 | 121 660 | 142 268 | 184 645 | 219 280 | 246 162 | 320 469 |
| 常住人口/万人 | 1 771 | 1 860 | 1 961.9 | 2 018.6 | 2 069.3 | 2 114.8 |
| 轨道交通运营里程/(万列·km) | 2 565 | 3 102 | 3 594 | 4 817 | 5 390 | 6 920 |
| 公共汽电车客运总量/万人 | 470 863 | 516 517 | 505 144 | 503 272 | 515 416 | 484 306 |
| 出租汽车载客里程/万km | 69 000 | 68 000 | 69 000 | 69 600 | 69 862 | 69 946 |
| 个人民用车辆拥有量/万辆 | 244.27 | 296.56 | 371.51 | 387.29 | 405.55 | 424.95 |
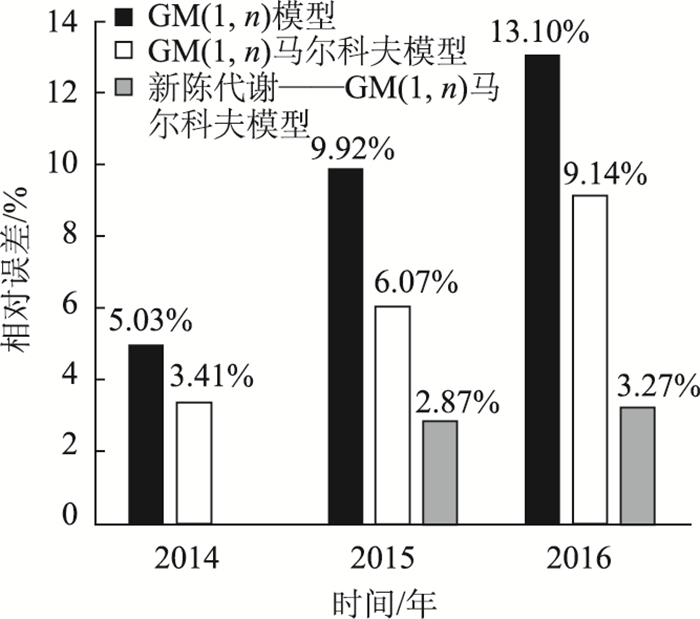
根据上述建模过程及相关数据,由表 6和图 4可知:应用新陈代谢——GM(1,n)马尔科夫模型预测2015,2016年北京市轨道交通客运量分别为35 025.14万人、386 639.02万人,与实际值相对误差分别为2.87%,3.27%,精度较高。可见,本研究提出的新陈代谢——GM(1,n)马尔科夫模型预测精度较高,具有较好的普适性,满足实际需求。
| 方法 | 年份 | 实际值/万人 | 预测值/万人 | 相对误差/% |
| GM(1,n)模型 | 2014 | 338 668 | 355 718.06 | 5.03 |
| 2015 | 340 436 | 374 197.87 | 9.92 | |
| 2016 | 374 381 | 423 407.68 | 13.10 | |
| GM(1,n)马尔科夫模型 | 2014 | 338 668 | 350 213.79 | 3.41 |
| 2015 | 340 436 | 361 100.95 | 6.07 | |
| 2016 | 374 381 | 408 588.41 | 9.14 | |
| 新陈代谢——GM(1,n)马尔科夫模型 | 2014 | 338 668 | — | — |
| 2015 | 340 436 | 350 205.14 | 2.87 | |
| 2016 | 374 381 | 386 639.02 | 3.27 |
|
| 图 4 北京市轨道交通客运量各预测方法预测结果比较 Fig. 4 Comparison of predicted passenger volumes of urban rail transit in Beijing obtained by different prediction methods |
| |
3 结论
(1) 轨道交通建设作为未来城市交通发展的主要趋势,其客运量预测对于建设规划具有重要意义。同时轨道交通客运量变化情况复杂,具有显著的随机波动特征以及有效信息不明确的情况,属于典型的灰色系统。
(2) 由于轨道交通客运量中有消息不明确以及影响因素难以确定,传统的GM(1,n)预测模型对轨道交通客运量预测误差较大,但对预测结果进行残差修正后,预测精度已可满足实际应用需求。
(3) 应用马尔科夫模型对轨道交通客运量GM(1,n)模型进行二次修正,结合2种方法的自身特点,预测结果与2014,2015,2016年上海市以及北京市轨道交通客运量实际数据进行对比,相对误差分别为1.96%,7.17%,10.30%;3.41%,6.07%,9.14%。可知模型有效性较高,但同时可得知该模型对较近年份预测精度更高。
(4) 将新陈代谢思想融入到GM(1,n)马尔科夫预测模型中,对2015,2016年上海市以及北京市轨道交通客运量进行再预测,相对误差分别为2.58%,2.76%;2.87%,3.27%,最终预测结果精度较高,可得基于新陈代谢GM(1,n)马尔科夫的轨道交通客运量预测方法能反映轨道交通客运量变化规律,实用性较强。
(5) 在后续的研究中,为了更加准确地预测轨道交通客运量,在相关因素以及数据分析上,需加入外部因素(如线路新建,相关政策的变化等)定性分析,以弥补预测模型自身的缺陷。
| [1] |
VLAHOGIANNI E I, KARLAFTIS M G, GOLIAS J C. Optimized and Meta-optimized Neural Networks for Short-term Traffic Flow Prediction:A Genetic Approach[J]. Transportation Research Part C:Emerging Technologies, 2005, 13(3): 211-234. |
| [2] |
SURYANI E, CHOU S Y, CHEN C H. Air Passenger Demand Forecasting and Passenger Terminal Capacity Expansion:A System Dynamics Framework[J]. Expert Systems with Applications, 2010, 37(3): 2324-2339. |
| [3] |
FERNANDEZ R, PLANZER R. On the Capacity of Bus Transit Systems[J]. Transport Reviews, 2002, 22(3): 267-293. |
| [4] |
刘昱岗, 董道建. 灰色关联弹性模型在公路客运量预测中的运用[J]. 公路工程, 2015, 40(1): 253-256. LIU Yu-gang, DONG Dao-jian. The Application of Grey Correlation-elastic Model in the Prediction of Road Passenger Transport Volume[J]. Highway Engineering, 2015, 40(1): 253-256. |
| [5] |
王洁, 王波. 上海未来短期客运量的预测分析——基于最小二乘法改进的GM(1, 1)模型[J]. 数学的实践与认识, 2017, 47(13): 67-74. WANG Jie, WANG Bo. Forecast Analysis of Short-term Passenger Traffic in Shanghai:Based on the Improved GM(1, 1) Model of Least Square Method[J]. Mathematics in Practice and Theory, 2017, 47(13): 67-74. |
| [6] |
王玉刚, 姚红云, 李英帅, 等. 基于灰色理论的重庆市常规公交客运量影响因素分析及预测[J]. 交通信息与安全, 2014, 32(6): 89-94. WANG Yu-gang, YAO Hong-yun, LI Ying-shuai, et al. The Influence Factors and Prediction Model of Bus Passenger Volume in Chongqing Based on Grey Theory[J]. Journal of Transport Information and Safety, 2014, 32(6): 89-94. |
| [7] |
杨琦, 杨云峰, 冯忠祥, 等. 基于灰色理论和马尔科夫模型的城市公交客运量预测方法[J]. 中国公路学报, 2013, 26(6): 169-175. YANG Qi, YANG Yun-feng, FENG Zhong-xiang, et al. Prediction Method for Passenger Volume of City Public Transit Based on Grey Theory and Markov Model[J]. China Journal of Highway and Transport, 2013, 26(6): 169-175. |
| [8] |
芮海田, 吴群琪, 袁华智, 等. 基于指数平滑法和马尔科夫模型的公路客运量预测方法[J]. 交通运输工程学报, 2013, 13(4): 87-93. RUI Hai-tian, WU Qun-qi, YUAN Hua-zhi, et al. Prediction Method of Highway Passenger Transportation Volume Based on Exponential Smoothing Method and Markov Model[J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 87-93. |
| [9] |
曹尧谦, 李夏苗. 基于改进四阶段法的武广客运专线客流预测[J]. 铁道科学与工程学报, 2010, 7(3): 109-113. CAO Yao-qian, LI Xia-miao. Improved Four-stage Flow Forecast Method for Wuhan-Guangzhou Passenger Dedicated Line[J]. Journal of Railway Science and Engineering, 2010, 7(3): 109-113. |
| [10] |
孙可朝. 基于规划求解的组合预测模型在道路客运量预测中的应用[J]. 公路交通科技, 2017, 34(12): 103-107, 114. SUN Ke-chao. Application of Combination Forecasting Model Based on Planning Solving in Road Passenger Transport Volume[J]. Journal of Highway and Transportation Research and Development, 2017, 34(12): 103-107, 114. |
| [11] |
李俊芳, 杨冠华, 邹江源, 等. 基于圈层人口变量的城市轨道交通车站客流预测[J]. 同济大学学报:自然科学版, 2015, 43(3): 423-429. LI Jun-fang, YANG Guan-hua, ZOU Jiang-yuan, et al. Forecasting Method of Urban Rail Transit Ridership at Station-level Based on Population Variable in Circle Group[J]. Journal of Tongji University:Natural Science Edition, 2015, 43(3): 423-429. |
| [12] |
冯冰玉, 鲍学英, 王起才. 基于灰色和神经网络的铁路客运量预测研究[J]. 铁道科学与工程学报, 2015(5): 1227-1231. FENG Bing-yu, BAO Xue-ying, WANG Qi-cai. Research of Railway Passenger Volume Forecast Based on Grey and Neural Network[J]. Journal of Railway Science and Engineering, 2015(5): 1227-1231. |
| [13] |
吴华稳, 甄津, 王宇, 等. 基于径向基神经网络的铁路客货运量预测研究[J]. 铁道科学与工程学报, 2014(4): 109-114. WU Hua-wen, ZHEN Jin, WANG Yu, et al. Railway Passenger and Freight Prediction Based on RBF Neural Network Theory[J]. Journal of Railway Science and Engineering, 2014(4): 109-114. |
| [14] |
李晓晖, 谭清美, 赵爱文. 基于因子分析和Logistic模型的中国客运量预测[J]. 系统管理学报, 2014, 23(3): 444-450. LI Xiao-hui, TAN Qing-mei, ZHAO Ai-wen. China's Passenger Traffic Forecast Based on Factor Analysis and Logistic Model[J]. Journal of Systems & Management, 2014, 23(3): 444-450. |
| [15] |
刘钊, 杜威, 闫冬梅, 等. 基于K近邻算法和支持向量回归组合的短时交通流预测[J]. 公路交通科技, 2017, 34(5): 122-128. LIU Zhao, DU Wei, YAN Dong-mei, et al. Short-term Traffic Flow Forecast Based on Combination of K Nearest Neighbor Algorithm and Support Vector Regression[J]. Journal of Highway and Transportation Research and Development, 2017, 34(5): 122-128. |
| [16] |
何南, 李季涛. 考虑运输方式间影响关系的公路客运交通需求预测[J]. 公路交通科技, 2017, 34(7): 153-158. HE Nan, LI Ji-tao. Highway Passenger Trasport Demand Forecasting Considering Relationship among Transport Modes[J]. Journal of Highway and Transportation Research and Development, 2017, 34(7): 153-158. |
| [17] |
胡彦蓉, 吴冲, 刘洪久. 基于KPCA-SVM的公路客运量预测研究[J]. 技术经济与管理研究, 2012(1): 8-12. HU Yan-rong, WU Chong, LIU Hong-jiu. Prediction of Highway's Passenger Traffic Based on KPCA-SVM[J]. Technoeconomics & Management Research, 2012(1): 8-12. |
| [18] |
梁小珍, 乔晗, 汪寿阳, 等. 基于奇异谱分析的我国航空客运量集成预测模型[J]. 系统工程理论与实践, 2017, 37(6): 1479-1488. LIANG Xiao-zhen, QIAO Han, WANG Shou-yang, et al. An Integrated Forecasting Model for Air Passenger Traffic in China Based on Singular Spectrum Analysis[J]. System Engineering-Theory & Practice, 2017, 37(6): 1479-1488. |
| [19] |
刘思峰, 杨英杰, 吴利丰. 灰色系统理论及其应用[M]. 7版. 北京: 科学出版社, 2014. LIU Si-feng, YANG Ying-jie, WU Li-feng. Grey System Theory and Its Application[M]. 7th ed. Beijing: Science Press, 2014. |
 2018, Vol. 35
2018, Vol. 35
