扩展功能
文章信息
- 许金良, 景立竹, 韩跃杰, 燕孟华
- XU Jin-liang, JING Li-zhu, HAN Yue-jie, YAN Meng-hua
- 基于MOVES的小半径圆曲线路段载重柴油车碳排放预测模型
- A Carbon Emission Prediction Model for Heavy-duty Diesel Trucks in Small-radius Curves Based on MOVES
- 公路交通科技, 2018, 35(12): 124-131, 158
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(12): 124-131, 158
- 10.3969/j.issn.1002-0268.2018.12.018
-
文章历史
- 收稿日期: 2018-07-30
根据我国“十三五”发展规划的要求, 控制二氧化碳排放是各行业现阶段的核心目标之一。交通运输行业作为碳排放的重要来源[1-2], 需进一步研究节能减排的新思路、新技术、新举措。目前交通运输行业的碳排放主要来自机动车尾气, 尤其是载重柴油车[3], 由于其载重量大、动力性能强, 且部分车辆存在使用年限较长、尾气排放不达标的问题, 油耗水平和碳排放水平远高于小客车[4-5], 已然成为道路碳排放中不可忽视的一部分。除了发动机性能与燃油品质, 道路条件和交通状况亦是影响载重柴油车行驶速度、加减速状态的重要因素, 对其燃油消耗及尾气排放水平也有着决定性作用[6-7]。明确不同因素对载重汽车碳排放水平的影响规律, 提出准确可靠的碳排放预测方法, 对于预判车辆污染水平、有的放矢地采取污染控制策略有着重要意义。
目前, 国内外学者已经在微观、中观、宏观层面上, 针对不同变量条件建立了载重汽车碳排放预测模型。贾洪飞等人采用实证对比分析法提出了不同纵坡条件、不同运行速度下的柴油油耗调整系数[8]。章后忠等人以及彭勃分别采用不同的数据收集方法, 实地采集了大量载重汽车油耗数据, 分析了车速、道路纵坡、路面平整度等因素对碳排放水平的影响程度[9-10]。刘真基于现场实测数据, 建立了车速与道路线形之间的定量关系, 提出了基于行车速度和路面摩阻力系数的燃油消耗量估算方法[11]。孙文圃等人运用MOVES模型对载重柴油车在纵坡路段的碳排放情况进行了模拟, 建立了高速公路纵坡段非线性碳排放回归模型[12]。Ko等人提出了一种针对不同纵断面线形的可计算多种污染气体排放量的模型[13]。Jiao等人得到了以机动车行驶速度、机动车类型、交通状态、道路纵坡为自变量的机动车碳排放影响因子确定模型, 并推导出最小碳排放因子所对应的最佳道路纵坡设计方案[14]。Abou-Senna等人、Huisingh等人分别通过实地数据采集和软件仿真的方法, 考虑了气象条件、车辆类型、公路等级、路线线形、交通流状态等因素, 建立了车辆尾气排放率预测模型以及公路空气污染状况综合评价模型[15-16]。
总结上述文献可以得知, 相比国内学者, 国外学者针对不同层次的碳排放预测模型的研究更为全面。宏观层面上, 提出了综合天气状况、交通流条件、道路平纵线形等多种因素的碳排放估算方法; 中微观层面上, 着重研究了道路纵断面设计要素对车辆碳排放水平的影响规律, 但是缺少对平面线形指标影响作用的分析。国内学者对碳排放预测模型的研究多于早年开展, 且研究成果集中于中微观层面上, 着重关注道路纵断面线形及路面平整程度对碳排放的影响, 忽视了平面线形条件的作用。
为解决上述道路平面设计要素对车辆碳排放影响作用尚不明确的问题, 本研究将从微观视角出发, 探究道路平面线形指标与车辆碳排放水平的相关关系。国内外研究成果已经证明, 相比于直线路段, 车辆在圆曲线路段的加减速行为更为频繁, 尤其是当圆曲线半径小于等于550 m时, 半径对行驶速度及加减速过程的影响将非常显著[17-19], 且车辆发动机动力输出也将明显区别于一般路段, 车辆油耗和碳排放水平普遍较高。由此可以推断, 圆曲线路段, 尤其是半径小于等于550 m的小半径圆曲线路段是车辆易产生高碳排的路段。此外, 考虑到载重柴油车污染气体的排放水平远高于小客车, 故将以载重柴油汽车作为研究对象, 首先对国外已有碳排放预测模型的参数做必要校准, 使之能够适用于我国实际的道路交通条件及车辆条件; 之后, 采用软件仿真的方法研究载重汽车在小半径圆曲线路段的碳排放变化规律, 建立碳排放预测模型, 实现在无需借助软件计算的情况下方便、快速地预测小半径圆曲线路段车辆碳排放水平的目的。
1 模拟参数修正及数据库建立美国国家环保局于2004年开发的MOVES机动车尾气排放模型预测结果精度较高, 可以实现对小客车、摩托车、载重汽车、公共汽车等不同车型的碳排放水平预测, 在机动车尾气排放水平预测及空气质量评估等方面得到了广泛应用[20-22]。本研究将以符合我国实际情况的本地化参数作为MOVES的基础模拟参数, 通过仿真模拟建立碳排放数据库, 作为后续回归分析的数据基础。
1.1 模型参数的本地化MOVES模型的原始数据库是以美国各个州县机动车排放数据为基础而建立的, 直接用来预测我国机动车碳排放水平是不合理的。为了减小软件参数设置对本研究结果的影响程度, 保证预测精度, 文中在分析MOVES模型主体结构及计算原理的基础上, 调查了我国现阶段的车辆分类标准、燃油特性、载重汽车尾气排放控制标准、车辆检测与维护情况等, 并与美国的具体情况相对比, 应用符合我国实际情况的道路、交通、车辆、燃油等信息合理修正了MOVES微观层次上模拟机动车排放水平所需输入的一系列参数。从合理修正原始参数和正确设计模拟情景两方面进行考虑, 本地化的参数设置汇总如下:
(1) 模拟规模:微观层次;
(2) 模型计算年份:相比于美国, 我国在柴油排放检测及控制标准制定方面有一定程度的落后。将我国第五阶段机动车污染物排放标准以及现阶段主要供应的柴油品质与美国进行对比, 如表 1所示, 确定2009年为MOVES模型的计算年份。
| 参数名称 | 中国(2017年标准, -20#柴油) | 美国(2009年标准) |
| 硫含量(质量分数)/(mg·kg-1) | ≤10 | ≤10 |
| 10%蒸余物残炭(质量分数)/% | ≤0.3 | ≤0.3 |
| 灰分(质量分数)/% | ≤0.01 | ≤0.01 |
| 多环芳烃含量(质量分数)/% | ≤11 | ≤10 |
| 十六烷指数 | ≥46 | 50 |
| 运动黏度(20 ℃)/(mm2·s-1) | 2.5~8.0 | 2.0~7.0 |
| 密度(20 ℃)/(kg·L-1) | 790~840 | 800~840 |
(3) 道路类型:非限制出入的乡村道路, 对应MOVES模型中代码为3的道路类型;
(4) 地理信息: MOVES模型提供了美国50个州3 000余个地理区域供用户匹配建模所需的地理信息, 本研究从影响模型计算值的经纬度、海拔、平均气温、年均降水量、相对湿度等方面对照了陕西省和美国各州的具体情况, 最终确定以密苏里州作为软件中的模拟地理区域;
(5) 排放源类型:参考《机动车类型术语和定义》(GA 802—2014)对陕西省内省道107、省道108进行车型分布情况调查和统计, 结果表明, 车身长度大于等于6 000 mm且最大允许总质量大于12 000 kg的重型载货汽车在载货汽车中所占比例最大, 为40.8%;与此同时, 通过随机抽样调查112辆重型载货汽车的生产厂家、车型、车龄分布情况,车龄在3~6年范围内的一汽解放悍威某重型载货汽车所占比例最大。综合上述分析并考虑我国车型现状及未来发展趋势, 文中选择以一汽解放悍威某重型载货汽车作为载重柴油车的代表车型, 即主要碳排放源, 对应MOVES模型中代码为53的排放源类型;
(6) 燃油类型: -20#柴油, 对应MOVES模型中代码为20043的燃油;
(7) 车龄:平均车龄4.5年, 对应MOVES模型中代码为405的车龄组合;
(8) 机动车检测和维修状况:采用MOVES模型缺省值;
(9) 车辆运行工况: MOVES模型共设置有77种车辆运行工况, 每种运行工况对应不同的碳排放速率和调整系数。为了实现对车辆排放水平的估算, 需要首先根据机动车瞬时速度和瞬时比功率VSP值来查找运行工况代码, 将车辆逐秒运行状态匹配到相应的运行工况中, 然后由MOVES模型计算每个运行工况下的碳排放量, 并将所有运行工况下的碳排放量相加, 即可得到车辆在行驶过程中的累积碳排放量。VSP的数值与车辆瞬时速度和瞬时加速度有关, 计算公式如式(1)所示。
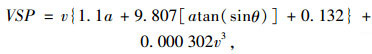
|
(1) |
式中, VSP为机动车瞬时比功率; v为车辆瞬时速度; a为车辆加速度; θ为道路纵坡, 在本研究模拟计算过程中, 由于不考虑纵断面线形对车辆碳排量的影响, 因此取θ=0。v和a的数值与圆曲线半径、进入圆曲线路段时的初始速度、和圆曲线起点或中点的距离、在圆曲线路段行驶的时间等因素有关, 在对比了多种速度和加速度预测模型各自的适用范围及优缺点, 并采用实测数据验证预测精度之后, 最终采用了Fitzpatrick等人在文献[23]中提出的取值和计算方法。
1.2 MOVES碳排放数据库的建立完成对MOVES中不变参数的设置后, 还需要设置可变参数。影响圆曲线路段机动车碳排放水平的可变参数有很多, 包括运行速度、圆曲线半径、圆曲线长度、超高、纵坡、竖曲线、路面条件、驾驶员驾驶技术、天气条件、风阻力等。其中, 速度以及平面线形指标是本研究的重点研究要素。由于道路超高的设置是以圆曲线半径和运行速度为基础的, 因此它并非一个独立的自变量。综上, 在分析载重柴油车在圆曲线路段上的碳排放规律时, 以车辆进入圆曲线路段的初速度V0、圆曲线半径R、圆曲线长度L这3个因素为自变量, 建立载重柴油车的碳排放数据库及模型。
根据对陕西省内几条主要国省干线重型载重柴油车行驶速度的测量统计结果, 以车辆进入圆曲线路段初始速度的第10分位和第90分位数值分别作为建立数据库时V0取值的上限和下限, 即V0取值范围为30~80 km/h, 变化步长10 km/h。根据线形资料收集整理结果, 圆曲线长度取值范围设置为0~600 m, 变化步长50 m。另外, 为了保证行车安全, 实际道路条件下的圆曲线半径通常不会太小, 为减小计算量, 这里取圆曲线半径200 m作为MOVES模型计算的下限值, 550 m为上限值, 变化步长50 m。为避免平纵线形组合的影响, 这里将路段信息中的纵坡坡度均设置为0%, 且不设置竖曲线。车道宽度、中央分隔带设置、路肩宽度等数据则参考路线设计类规范, 尽量取上限值或不影响车辆运行速度的数值。
根据式(1)计算不同线形组合条件下车辆的瞬时比功率数值。在计算过程中, 注意将上述3个自变量中的2个设置为固定值, 另1个按照变化步长依次取值。之后, 将对应的线形指标作为路段信息输入MOVES模型中, 将运行工况分布情况作为运行工况信息输入MOVES模型中, 计算得出所有运行工况下的累积碳排放量数据。将3因素依次作为变化量, 模拟计算所有的累积碳排量数据, 即可建立MOVES碳排放数据库。
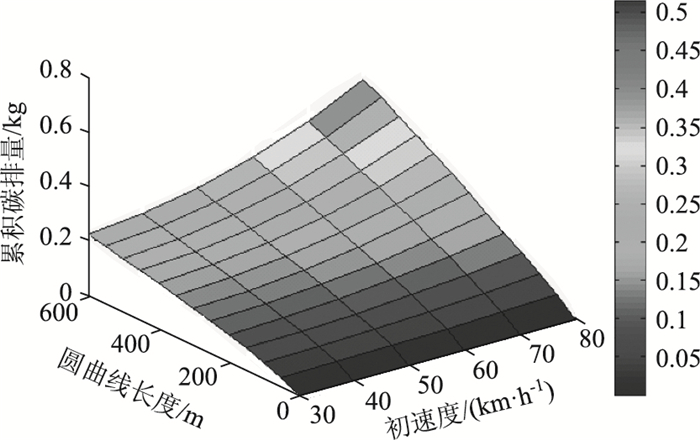
图 1以坐标图的形式展示了圆曲线半径固定200 m时所建立的累积碳排放量数据库文件。
|
| 图 1 圆曲线半径等于200 m时累积碳排放量数据库 Fig. 1 Accumulated carbon emission database when curve radius is 200 m |
| |
2 载重柴油车碳排放预测模型建立 2.1 一元回归模型
完成数据库建立后, 即可应用其中数据展开回归分析。
为了直观地展示3个自变量对于车辆碳排量的影响规律, 首先分别分析它们对碳排量的独立影响作用。这里以单位圆曲线长的碳排量为因变量, 其计算方法如式(2)所示, 分别建立圆曲线半径、圆曲线长度、车辆初速度与这一因变量的关系模型。
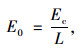
|
(2) |
式中, E0为单位圆曲线长车辆碳排放量; Ec为圆曲线长度范围内车辆的累积碳排放量; L为圆曲线长度。
(1) 圆曲线半径R与单位圆曲线长碳排量E0关系模型
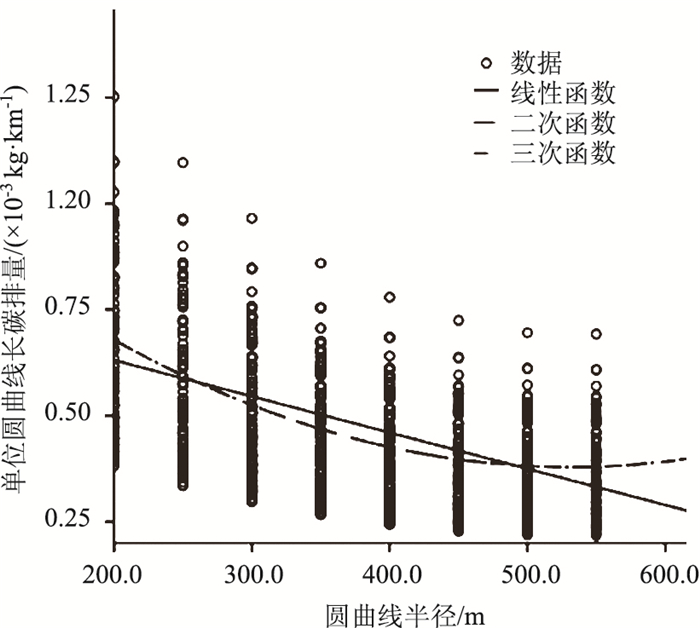
以MOVES碳排放数据库为数据来源, 绘制圆曲线半径R与单位圆曲线长碳排量E0散点图, 对数据做数理统计分析, 确定没有需要剔除的异常或可疑数据。利用SPSS软件对散点进行曲线拟合, 如图 2所示。从判定系数R2、赤池信息量AIC、贝叶斯信息量BIC、F检验、显著性检验这几个方面对不同形式函数的拟合效果做出评价, 如表 2所示。
|
| 图 2 R与E0拟合曲线 Fig. 2 R-E0 fitting curves |
| |
| 函数形式 | R2 | AIC | BIC | F | Sig. |
| 线性函数 | 0.705 | 1 240.595 1 | 1 249.307 3 | 251.317 | 0.000 |
| 二次函数 | 0.736 | 1 205.411 2 | 1 214.130 4 | 144.850 | 0.000 |
| 三次函数 | 0.736 | 1 206.808 3 | 1 218.900 7 | 96.398 | 0.000 |
从表中各指标的大小来看, 3种函数的显著性水平都小于0.05, 说明在95%置信水平下方程回归显著。采用二次函数和三次函数拟合的判定系数相同, 但二次函数对应的F值更大, AIC和BIC值更小, 能够在保证拟合精度的同时避免回归方程中参数的冗余。因此选择二次函数作为拟合函数, 建立的回归方程如式(3)。
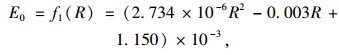
|
(3) |
式中, E0为单位圆曲线长车辆碳排放量; R为圆曲线半径。
(2) 车辆进入圆曲线路段的初始速度V0与单位圆曲线长碳排量E0关系模型
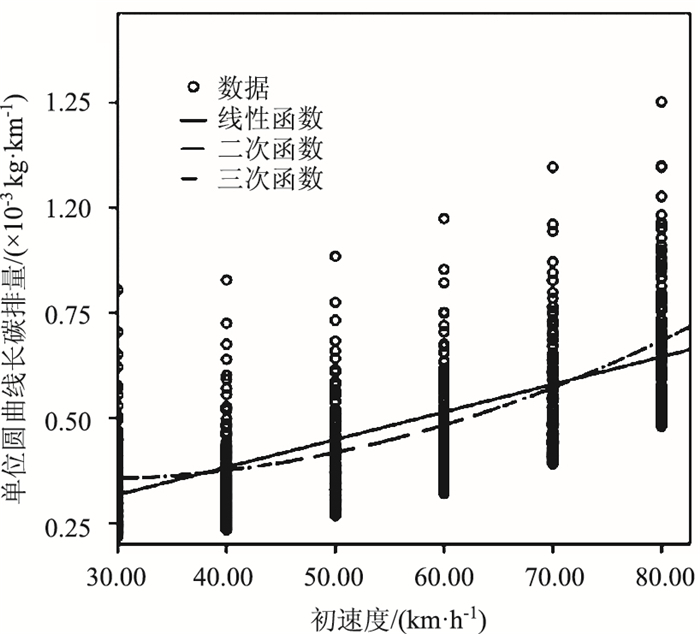
图 3所示为依据MOVES碳排放数据库所绘制的车辆初速度V0与单位圆曲线长碳排量E0散点图及SPSS拟合曲线。拟合函数各项参数的对比见表 3。
|
| 图 3 V0与E0拟合曲线 Fig. 3 V0-E0 fitting curves |
| |
| 函数形式 | R2 | AIC | BIC | F | Sig. |
| 线性函数 | 0.700 | 1 376.003 6 | 1 384.715 8 | 383.420 | 0.000 |
| 二次函数 | 0.727 | 1 345.320 4 | 1 357.454 2 | 213.564 | 0.000 |
| 三次函数 | 0.727 | 1 349.881 6 | 1 358.593 8 | 142.128 | 0.000 |
由表 3可以看出, 在95%置信水平下, 3种回归方程都表现出良好的显著性。采用二次函数拟合效果最好, 由此得到的车辆初速度与单位圆曲线长碳排量回归关系表达式为式(4)。
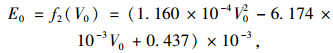
|
(4) |
式中, E0为单位圆曲线长车辆碳排放量; V0为车辆驶入圆曲线时的初始速度。
(3) 圆曲线长度L与单位圆曲线长碳排量E0关系模型
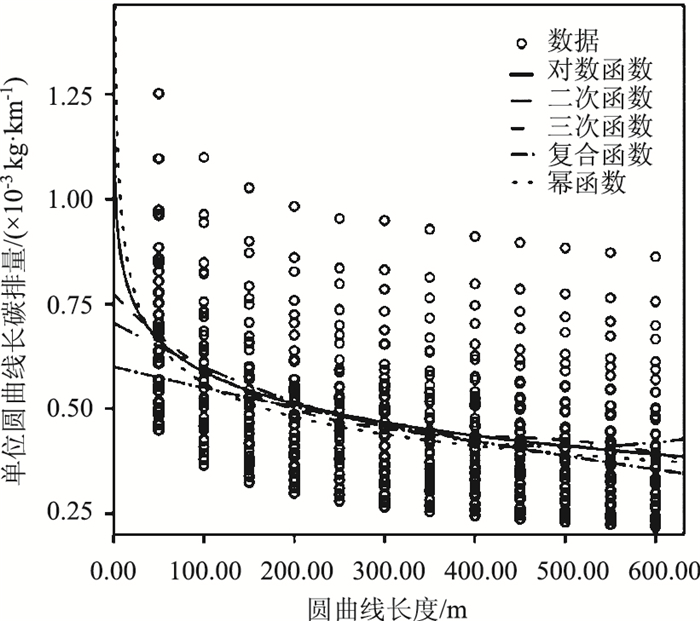
运用SPSS对圆曲线长度L与单位圆曲线长碳排量E0数据散点做曲线拟合, 如图 4所示。几种函数形式拟合效果对比见表 4。
|
| 图 4 L与E0拟合曲线 Fig. 4 L-E0 fitting curves |
| |
| 函数形式 | R2 | AIC | BIC | F | Sig. |
| 对数函数 | 0.735 | 1 541.162 8 | 1 549.875 1 | 144.738 | 0.000 |
| 二次函数 | 0.727 | 1 545.817 2 | 1 554.529 4 | 69.347 | 0.000 |
| 三次函数 | 0.726 | 1 540.243 4 | 1 548.955 7 | 48.452 | 0.000 |
| 复合函数 | 0.709 | 1 555.793 8 | 1 564.506 0 | 127.775 | 0.000 |
| 幂函数 | 0.738 | 1 520.216 6 | 1 528.928 8 | 151.041 | 0.000 |
采用幂函数拟合时对应的判定系数R2值最大而AIC,BIC值最小, 且F检验、显著性检验均满足要求, 因此选择幂函数作为圆曲线长度与单位圆曲线长碳排量相关关系的拟合函数, 具体表达式如式(5)所示。
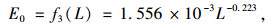
|
(5) |
式中, E0为单位圆曲线长车辆碳排放量; L为圆曲线长度。
2.2 多元回归模型为了明确3个变量对载重柴油车在小半径圆曲线路段碳排放水平的综合影响作用, 建立三参数协同作用下的累积碳排量预测模型, 这里采用多元回归的方法进行模型建立。以2.1节的3个一元模型的基本函数形式作为参考, 以圆曲线半径、圆曲线半径平方、车辆初速度、车辆初速度平方、圆曲线长度、圆曲线长度幂次方作为自变量, 其系数分别取α1,α2,β1,β2,γ1,γ2, 另外在模型中加入常数项ε。借助SPSS软件进行多元非线性迭代计算, 建立形式如式(6)所示的车辆累积碳排量Ec计算模型。
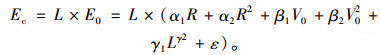
|
(6) |
将上述自变量系数及常数项的初始值设定为1.000, 置信水平设置为95%, SPSS迭代历程见表 5(因篇幅有限, 其中若干过程在表格中以省略号表示), 参数估计结果及T检验见表 6。
| 迭代次数 | 残差平方和 | ε | α1 | α2 | β1 | β2 | γ1 | γ2 |
| 0.1 | 18 688 496 583 346.190 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 1.1 | 4 051 795 406.509 | 1.000 | 0.998 | -0.020 | 1.000 | 0.983 | 0.998 | 0.990 |
| 2.1 | 53 745 812.526 | 1.000 | 0.973 | 4.179E-5 | 0.987 | -0.065 | 0.950 | 0.698 |
| 3.1 | 44 599 631.249 | 1.000 | 0.972 | -6.501E-5 | 0.986 | -0.074 | 0.954 | 0.724 |
| 4.1 | 37 404 862.809 | 0.991 | -0.686 | 0.003 | 0.751 | -0.035 | 0.907 | 0.737 |
| 5.1 | 21 316 207.663 | 0.988 | -0.758 | 0.003 | 0.690 | -0.032 | -0.371 | 0.950 |
| …… | …… | …… | …… | …… | …… | …… | …… | …… |
| 40.1 | 1.175 | 1.255 | -2.910E-3 | 2.681E-6 | -6.620E-3 | 1.160E-4 | -1.122E-3 | 0.830 |
| 41.1 | 1.161 | 1.267 | -2.905E-3 | 2.774E-6 | -6.167E-3 | 1.160E-4 | -1.209E-3 | 0.815 |
| 42.2 | 1.146 | 1.269 | -2.905E-3 | 2.753E-6 | -6.167E-3 | 1.160E-4 | -1.479E-3 | 0.801 |
| 43.1 | 1.141 | 1.270 | -2.904E-3 | 2.737E-6 | -6.167E-3 | 1.160E-4 | -1.707E-3 | 0.787 |
| 44.2 | 1.126 | 1.274 | -2.904E-3 | 2.741E-6 | -6.167E-3 | 1.160E-4 | -2.019E-3 | 0.766 |
| 45.1 | 1.114 | 1.276 | -2.904E-3 | 2.738E-6 | -6.167E-3 | 1.160E-4 | -2.173E-3 | 0.761 |
| 46.1 | 1.114 | 1.276 | -2.904E-3 | 2.738E-6 | -6.167E-3 | 1.160E-4 | -2.180E-3 | 0.761 |
| 47.1 | 1.114 | 1.276 | -2.904E-3 | 2.738E-6 | -6.167E-3 | 1.160E-4 | -2.180E-3 | 0.761 |
| 48.1 | 1.114 | 1.276 | -2.904E-3 | 2.738E-6 | -6.167E-3 | 1.160E-4 | -2.180E-3 | 0.761 |
| 注:主迭代数在小数左侧显示, 次迭代数在小数右侧显示。 | ||||||||
| 参数 | 估计值 | 标准误差 | 95%置信区间 | T值 |
| ε | 1.276 | 0.034 | [1.210, 1.341] | 37.529 |
| α1 | -2.904E-3 | 0.000 | [-0.003, -0.003] | ∞ |
| α2 | 2.738E-6 | 0.000 | [2.422E-6, 3.054E-6] | ∞ |
| β1 | -6.167E-3 | 0.001 | [-0.008, -0.005] | 7.520 |
| β2 | 1.160E-4 | 0.000 | [0.000, 0.000] | ∞ |
| γ1 | -2.180E-3 | 0.001 | [-0.005, 0.000] | 2.121 |
| γ2 | 0.761 | 0.081 | [0.602, 0.920] | 9.395 |
根据迭代结果, 建立圆曲线线形指标及初速度与载重柴油汽车累积碳排放量的多元非线性回归模型, 如式(7)所示。经验证, 该回归方程中各参数的显著性水平都小于预设值0.05, 满足显著性检验要求。方程判定系数R2等于0.938, 接近1, 拟合优度较高。
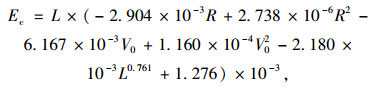
|
(7) |
式中, Ec为小半径圆曲线路段载重柴油车的累积碳排量; R为圆曲线半径; V0为进入圆曲线路段时车辆的初始速度; L为圆曲线长度。
3 多元回归模型验证为了验证本研究建立的碳排放量预测模型是否能真实反映车辆的实际碳排放水平, 这里需要对预测结果的精确度做出检验。为此, 本研究开展了实地测试试验, 将实测数据与模型计算结果进行对比。
3.1 试验方案考虑到现有的柴油车尾气测试方法对检测仪器的技术水平以及外界环境条件的要求都较为苛刻, 本研究选择以更方便测定、且测量精度易于控制的油耗量作为直接观测量, 间接获得二氧化碳排放量数据。实地测试若干小半径圆曲线路段载重柴油车的实际油耗量, 利用目前国际上广泛使用的、由联合国政府间气候变化专门委员会(IPCC)在《国家温室气体清单指南》中规定的碳排放核算方法(简称IPCC碳排放核算方法), 将实测油耗量转换成碳排放量。计算方法如式(8)、式(9)所示。
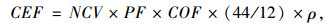
|
(8) |
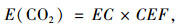
|
(9) |
式中, CEF为二氧化碳排放系数; NCV为燃料的平均低位发热量; PF为燃料潜在碳排放系数; COF为碳氧化率; E(CO2)为二氧化碳排放量; EC为燃料消耗量; ρ为燃料密度。
参考《综合能耗计算通则》(GB/T 2589—2008)和《中国能源统计年鉴2017》中的数据, 上述计算方法中各项参数的取值如表 7所示。计算得出柴油的二氧化碳排放系数为2.6, 即车辆每消耗1 L柴油, 就会产生2.6 kg二氧化碳。
| 能源类别 | 密度/(kg·L-1) | 平均低位发热量/(kJ·kg-1) | 潜在碳排放系数/(t-C·TJ-1) | 碳氧化率/% |
| 柴油 | 0.84 | 42 652 | 20.17 | 98 |
| 注:表中所列燃油密度为本研究对象车型所使用的燃料对应的密度。 | ||||
以陕西省省道107、省道108为主要试验道路, 选择半径小于等于550 m的圆曲线路段作为试验路段。研究表明, 小于等于2%的道路纵坡对车辆油耗及碳排放水平的影响较小[12]。因此, 要求试验路段的纵坡不超过2%, 且未设置竖曲线, 从而避免纵断面线形条件对试验结果产生干扰。根据对试验道路的车型分布情况调查结果, 综合考虑我国车型现状及未来发展趋势, 以一汽解放悍威某重型载货汽车作为试验车辆。采用由上海某汽车设计开发有限公司研发的测量精度为0.000 1L、测量误差小于0.5%的JDSZ-EP-1-1D型柴油油耗仪获取车辆累积油耗数据, 采用全站仪获取路段的线形参数。选择驾驶经验丰富、无不良驾驶习惯的驾驶员驾驶试验车辆行驶于试验路段。要求试验期间天气状况良好, 路段内无车祸、紧急停车等突发状况发生, 交通流呈自由流状态。
3.2 模型验证通过现场试验获取了20组圆曲线半径、圆曲线长度、初速度组合条件下的车辆油耗数据, 并按照式(8)、式(9)转换为碳排放量, 列于表 8中。对比对应条件下采用式(7)计算出的累积碳排放量预测值, 验证模型的预测精度。
| R/m | V0/(km·h-1) | L/m | 实测油耗/L | IPCC碳排量核算值/kg | 碳排量预测值/kg | 相对误差/% |
| 175.0 | 36.4 | 208.0 | 0.055 | 0.143 | 0.136 | 4.84 |
| 175.0 | 38.1 | 208.0 | 0.057 | 0.148 | 0.137 | 7.59 |
| 200.0 | 44.7 | 312.2 | 0.067 | 0.174 | 0.184 | 5.45 |
| 257.5 | 58.9 | 350.0 | 0.082 | 0.213 | 0.196 | 7.93 |
| 285.0 | 60.7 | 423.5 | 0.086 | 0.224 | 0.214 | 4.11 |
| 302.4 | 45.3 | 185.2 | 0.039 | 0.101 | 0.091 | 10.33 |
| 310.9 | 62.9 | 314.6 | 0.061 | 0.159 | 0.168 | 5.93 |
| 335.0 | 58.8 | 702.5 | 0.085 | 0.221 | 0.231 | 4.63 |
| 335.0 | 65.7 | 702.5 | 0.108 | 0.281 | 0.271 | 3.37 |
| 376.4 | 42.1 | 476.0 | 0.047 | 0.122 | 0.133 | 8.70 |
| 401.4 | 78.9 | 503.4 | 0.109 | 0.283 | 0.271 | 4.13 |
| 423.0 | 75.5 | 156.7 | 0.041 | 0.106 | 0.099 | 6.71 |
| 425.1 | 72.3 | 550.0 | 0.096 | 0.250 | 0.237 | 4.94 |
| 425.1 | 50.5 | 550.0 | 0.050 | 0.130 | 0.140 | 8.01 |
| 460.3 | 74.0 | 515.8 | 0.083 | 0.216 | 0.230 | 6.49 |
| 478.6 | 81.2 | 500.3 | 0.097 | 0.252 | 0.265 | 5.23 |
| 480.9 | 40.6 | 696.7 | 0.041 | 0.107 | 0.095 | 11.25 |
| 523.4 | 59.2 | 459.0 | 0.055 | 0.144 | 0.145 | 0.82 |
| 550.0 | 72.3 | 702.8 | 0.097 | 0.252 | 0.244 | 3.10 |
| 550.0 | 80.8 | 702.8 | 0.113 | 0.294 | 0.314 | 6.75 |
经计算, 预测值与实测值相对误差平均值为6.02%, 小于10%, 可以认为模型具有较高的预测精度。
4 结论(1) 本研究以地理、天气、车辆、燃油等信息调查与对比为基础, 对MOVES模型中的一部分参数进行了本地化修正及设置, 使之能够适用于我国的实际道路交通条件与车辆条件。
(2) 利用经过本地化设置的MOVES模型建立了载重柴油车在半径小于等于550 m的圆曲线路段的碳排量数据库, 在此基础上提出了以圆曲线半径、圆曲线长度、车辆驶入圆曲线路段的初速度这3个参数为自变量的多元非线性碳排量预测模型。
(3) 本研究的碳排放预测模型是针对车身长度大于等于6 000 mm且总质量大于12 000 kg的重型载重柴油车建立的, 是否适用于其他类型的载重汽车还有待于进一步验证。
| [1] |
李玲.中国交通各部门CO2排放差异和影响因素研究[D].长沙: 湖南大学, 2016. LI Ling. Study on CO2 Emission Differences among Chinese Transport Sectors and Their Influencing Factors[D]. Changsha: Hunan University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10532-1016237260.htm |
| [2] |
GREEN F, STERN N. China's Changing Economy:Implications for Its Carbon Dioxide Emissions[J]. Climate Policy, 2017, 17(4): 423-442. |
| [3] |
袁长伟, 张倩, 芮晓丽, 等. 中国交通运输碳排放时空演变及差异分析[J]. 环境科学学报, 2016, 36(12): 4555-4562. YUAN Chang-wei, ZHANG Qian, RUI Xiao-li, et al. Spatiotemporal Evolution and Difference of Transport Carbon Emissions in China[J]. Acta Scientiae Circumstantiae, 2016, 36(12): 4555-4562. |
| [4] |
李昊, 虞明远, 余艳春, 等. 基于车辆排放水平的差异化公路通行费率的分析[J]. 公路交通科技, 2018, 35(6): 137-144. LI Hao, YU Ming-yuan, YU Yan-chun, et al. Analysis on Differentiated Highway Toll Rate Based on Vehicle Emission Level[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 137-144. |
| [5] |
彭美春, 朱兵禄, 胡红斐, 等. 重型货运车辆碳排放特性研究[J]. 安全与环境学报, 2016, 16(1): 269-272. PENG Mei-chun, ZHU Bing-lu, HU Hong-fei, et al. Study on the Carbon Emission Characteristics of the Heavy Duty Freight Trucks[J]. Journal of Safety and Environment, 2016, 16(1): 269-272. |
| [6] |
FRANCO V, KOUSOULILDOU M, MUNTEAN M, et al. Road Vehicle Emission Factors Development:A Review[J]. Atmospheric Environment, 2013, 70(70): 84-97. |
| [7] |
张广昕, 孙晋伟, 张传桢, 等. 机动车污染物排放影响因素及控制措施研究[J]. 交通节能与环保, 2013, 9(2): 51-55. ZHANG Guang-xin, SUN Jin-wei, ZHANG Chuan-zhen, et al. Research on Motor Vehicle Emission Factors and Control Measures[J]. Energy Conservation & Environmental Protection in Transportation, 2013, 9(2): 51-55. |
| [8] |
贾洪飞, 隽志才, 张枭雄, 等. 高速公路后评价油耗指标的确定与对比[J]. 吉林大学学报:工学版, 2004, 34(2): 298-301. JIA Hong-fei, JUAN Zhi-cai, ZHANG Xiao-xiong, et al. Determination and Comparison of Fuel Consumption for Expressway Post-assessment[J]. Journal of Jilin University:Engineering and Technology Edition, 2004, 34(2): 298-301. |
| [9] |
章后忠, 潘玉利, 程珊珊, 等. 建立四类代表车型的理论油耗模型[J]. 华东公路, 2002(6): 63-66. ZHANG Hou-zhong, PAN Yu-li, CHENG Shan-shan, et al. Theoretical Fuel Consumption Models for Four Types of Vehicle[J]. East China Highway, 2002(6): 63-66. |
| [10] |
彭勃.高速公路汽车油耗模型研究[D].哈尔滨: 哈尔滨工业大学, 2014. PENG Bo. Research about Model of Vehicle's Fuel Consumption on Expressway[D]. Harbin: Harbin Institute of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014083534.htm |
| [11] |
刘真.道路线形指标对车辆尾气排放及燃油经济的影响研究[D].南京: 东南大学, 2017. LIU Zhen. Influence of Road Alignment Index on Vehicle Pollution and Fuel Consumption[D]. Nanjing: Southeast University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10286-1018003866.htm |
| [12] |
孙文圃, 许金良, 景立竹, 等. 基于MOVES的高速公路纵坡段载重柴油车辆碳排放预测模型的研究[J]. 公路交通科技, 2015, 32(12): 144-150. SUN Wen-pu, XU Jin-liang, JING Li-zhu, et al. Study on Carbon Emission Prediction Model of Heavy-duty Diesel Vehicle in Expressway Longitudinal Slope Sections Based on MOVES[J]. Journal of Highway and Transportation Research and Development, 2015, 32(12): 144-150. |
| [13] |
KO M, LORD D, ZIETSMAN J. Environmentally Conscious Highway Design for Vertical Grades[J]. Transportation Research Record, 2013, 2341: 53-65. |
| [14] |
JIAO S, HOU C, LI Y, et al. Establishing the CO2 Emission Model of Carbon Neutral Road Based on Gradient[C]//International Conference on Electrical and Control Engineering. Yichang: IEEE, 2011: 4494-4497.
|
| [15] |
ABOU-SENNA H, RADWAN E, WESTERLUND K, et al. Using a Traffic Simulation Model (VISSIM) with an Emissions Model (MOVES) to Predict Emissions from Vehicles on a Limited-access Highway[J]. Journal of the Air & Waste Management Association, 2013, 63(7): 819-831. |
| [16] |
HUISINGH D, ZHANG Z, MOORE J C, et al. Recent Advances in Carbon Emissions Reduction:Policies, Technologies, Monitoring, Assessment and Modeling[J]. Journal of Cleaner Production, 2015, 103: 1-12. |
| [17] |
LUQUE R, CASTRO M. Highway Geometric Design Consistency:Speed Models and Local or Global Assessment[J]. International Journal of Civil Engineering, 2016, 14(6): 1-9. |
| [18] |
NAVIN F. Some Factors in the Design of Rural Highway Curves[C]//94th Annual Meeting of the Transportation Research Board. Washington D.C.: Transportation Research Board, 2015: 1-14.
|
| [19] |
张志清, 李晨, 贺成林. 双车道公路小半径曲线段行车速度与行车轨迹关系研究[J]. 道路交通与安全, 2016, 16(5): 22-26. ZHANG Zhi-qing, LI Chen, HE Cheng-lin. Research on the Relationships Between Driving Speed and Driving Track Path on Small Radius Curves of Two-lane Highways[J]. Road Traffic and Safety, 2016, 16(5): 22-26. |
| [20] |
徐龙, 于雷, 虞明远, 等. 美国移动源排放测算机制与方法[J]. 公路交通科技, 2011, 28(8): 154-158. XU Long, YU Lei, YU Ming-yuan, et al. Estimation Mechanism and Methodology of Mobile Source Emission in America[J]. Journal of Highway and Transportation Research and Development, 2011, 28(8): 154-158. |
| [21] |
PARK S, AHN K, PAKHA H A, et al. Real-time Emissions Modeling with Environmental Protection Agency MOVES:Framework Development and Preliminary Investigation[J]. Transportation Research Record, 2015, 2503: 60-69. |
| [22] |
VALLAMSUNDAR S, LIN J. MOVES versus MOBILE:Comparison of Greenhouse Gas and Criterion Pollutant Emissions[J]. Transportation Research Record, 2011, 2233: 27-35. |
| [23] |
FITZPATRIK K, COLLINS J M. Speed-profile Model for Two-lane Rural Highways[J]. Transportation Research Record, 2000, 1737: 42-49. |
 2018, Vol. 35
2018, Vol. 35
