扩展功能
文章信息
- 应国刚, 张素磊, 周明, 陈立平
- YING Guo-gang, ZHANG Su-lei, ZHOU Ming, CHEN Li-ping
- 基于预留支护假设的小净距隧道中央岩墙应力简化计算方法
- A Simplified Method for Calculating Stresses in Middle Rock Wall of Small Interval Tunnels Based on Reserved Supporting Hypothesis
- 公路交通科技, 2018, 35(12): 95-103
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(12): 95-103
- 10.3969/j.issn.1002-0268.2018.12.014
-
文章历史
- 收稿日期: 2017-02-28
2. 青岛理工大学 土木工程学院, 山东 青岛 450001;
3. 慈溪市交通建设工程质量监督站, 浙江 慈溪 315300;
4. 宁波市交通建设工程试验检测中心有限公司, 浙江 宁波 315000
2. School of Civil Engineering, Qingdao University of Technology, Qingdao Shangdong 450001, China;
3. Cixi Traffic Construction Engineering Quality Supervision Station, Cixi Zhejiang 315300, China;
4. Ningbo Traffic Construction Project Testing and Inspection Center Co., Ltd., Ningbo Zhejiang 315124, China
小净距隧道是介于普通分离式隧道与连拱隧道之间的一种隧道结构型式,因其不受地形条件以及总体线路线型的限制,又较之连拱隧道施工工艺简单、易于防水处治、造价易于控制等诸多优点,这种隧道结构形式得以广泛应用[1-4]。
小净距隧道之间的岩墙厚度相对较小,且在施工过程中受到多次扰动,其力学行为特征对围岩稳定性和支护结构参数选取起着决定性的作用[5]。现行《公路隧道设计规范》明确指出:“小净距隧道设计与施工应遵循少扰动、快加固、勤测量、早封闭的原则,并将中间岩墙的稳定性与加固作为设计与施工的重点”。中央岩墙的稳定性判断的前提是得到岩墙较为准确的应力分布规律和计算方法。因此本文研究具有重要的理论和现实意义。
国内外学者针对小净距隧道研究的方法主要有复变函数法[6-8]、双极坐标法[9-10]、Schwarz交替法[11-12]等。此外数值计算与试验研究也是比较常用的研究手段[13-15]。张顶立等利用双击坐标法得到了小净距隧道中夹岩应力场分析过程和步骤,并结合塑性屈服准则给出了中央岩墙稳定性判别方法和程序[16]。Hoang和Abousleiman得到了无穷大平面中存在任意大小的两洞时的应力分布的闭合解[17]。卞晓林等采用Schwarz交替法推导了既有溶洞条件下开挖新隧道时的围岩应力和变形解析解[18]。
上述研究具有较为完善的理论基础和严密的逻辑推理,但难以直接应用于隧道工程的设计和施工过程中。本研究在隧道围岩内部“预留支护”的假设前提下,首先得到“预留支护”界面上荷载分布的表达式,并在此基础上得到中央岩墙所受平均正应力和附加弯矩,最后对小净距隧道中央岩墙受力特性及其影响因素进行了讨论,得到了中央岩墙在一定条件下的应力分布计算方法。
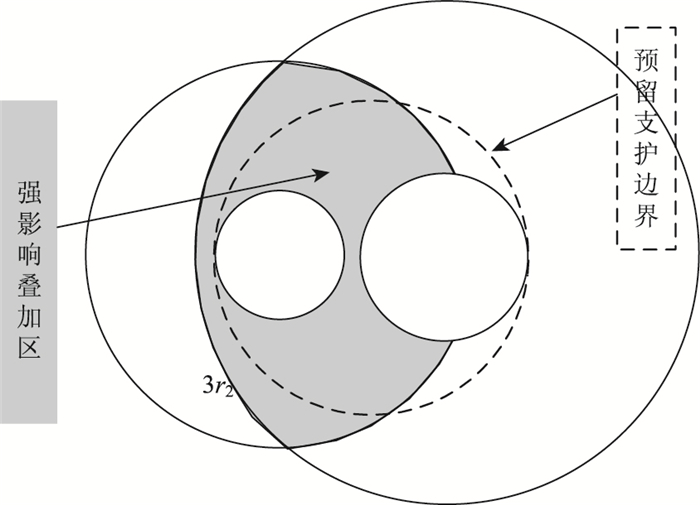
1 小净距隧道简化分析模型小净距隧道由于两隧道之间存在相互影响,在影响较强的范围内,围岩内某点的应力不能简单将两隧道的影响进行叠加,正因为这种强影响区域的叠加,使得中央岩柱受力特性难以计算,如图 1所示。但对于距离较远的位置(大于一倍洞径以上),叠加计算结果的误差很小[19]。
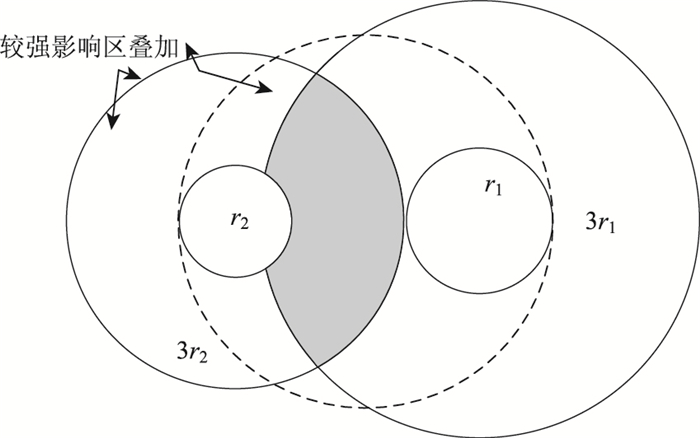
|
| 图 1 隧道强相互影响叠加区 Fig. 1 Strong interaction overlay zone of tunnels |
| |
为了对小净距隧道中央岩墙受力特性进行分析,本研究采取以下措施将小净距隧道问题分解为一个单洞隧道和一个“预留支护”结构的叠加问题,巧妙地将小净距隧道的多联域问题简化为单联域问题进行分析,如图 2所示。图 2中圆O1,O2为两小净距隧道,是实际开挖部分,虚线围成的大圆O表示“预留支护”的大圆边界,该边界为包含两隧道的最小圆,也即两隧道的最小外切圆。分析过程中将大圆O视为虚拟的隧道开挖的边界,其内部围岩视为虚拟的预留支护结构,最终将在半无限空间开挖两个小洞室的问题(图 2(a)),转为开挖一个大洞室(图 2(b))加上一个预留支护(图 2(c))的问题。
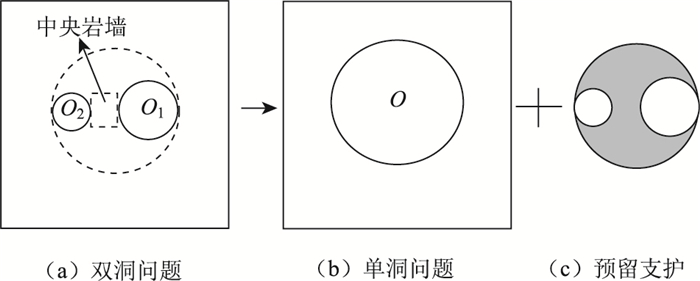
|
| 图 2 研究问题的分解模型 Fig. 2 Decomposition model of researched problem |
| |
当两隧道相距达到一定距离后,“预留支护”的大圆边界基本处于两隧道强影响区域叠加范围之外,这样就可以通过叠加原理计算“预留支护”大圆边界上的应力状态,然后据此进一步得到中央岩墙受力状态。
图 2所示计算模型的依据可用圣维南原理进行解释,通过避开两隧道相互影响较大的区域,选取预留支护这一独立结构进行分析,得到其界面应力分布规律,并以此为边界条件,结合该结构的受力特性进行进一步分析,最终得到处于强相互影响区的中央岩墙受力。
本研究只考虑初始围岩侧压系数为1的情况,此时分析模型中两洞室之间的上下关系将不再重要,可只研究洞室之间的相对距离以及洞室大小对中央岩墙应力的影响。此外,为叙述和图示方便,在不影响研究问题一般性的前提下,本研究规定半径较大的隧道始终位于右边,即认为图 2中隧道1半径不小于隧道2半径(r1≥r2)。
2 “预留支护”界面受力状态由于“预留支护”为一上下对称结构,当围岩荷载也对称时,可以取其上半部分进行分析,如图 3所示。图中r1,r2,R分别为两隧道半径和虚拟“预留支护”边界大圆半径,δ为中央岩墙厚度。分别以图 3中3个圆心为原点建立极坐标,则两小圆极坐标参数ρ1,ρ2,φ1,φ2与大圆极坐标参数R,φ之间存在如下关系:
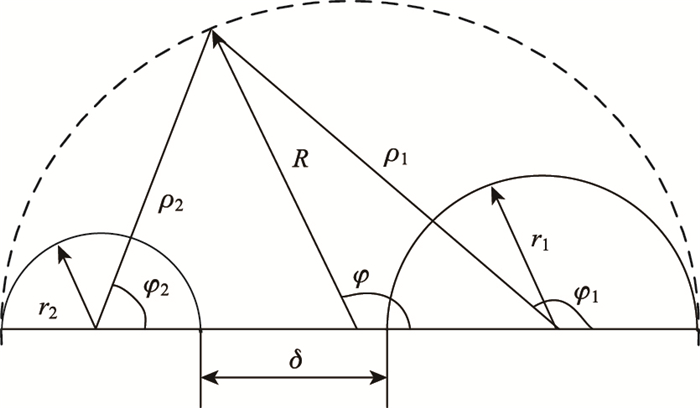
|
| 图 3 预留支护界面应力分析模型 Fig. 3 Stress analysis model of reserved support interface |
| |
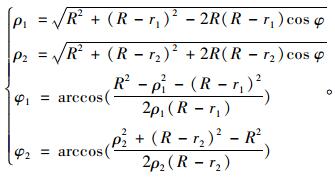
|
(1) |
根据前文分析结果,“预留支护”界面应力可按叠加原理进行近似计算。比如隧道1在“预留支护”大圆边界上的应力分别为:
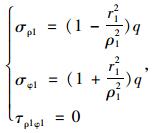
|
(2) |
式中,σρ1,σφ1,τρ1φ1分别为隧道1在预留支护结构界面上产生的径向应力、环向应力、剪应力;q为地层初始围岩压力。
将以上隧道1极坐标中的应力转为直角坐标系下的应力:
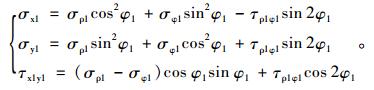
|
(3) |
再将以上直角坐标系中的应力转化为大圆极坐标下的应力:
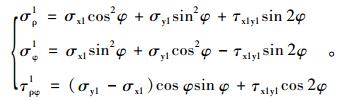
|
(4) |
通过式(1)~(4)即可得到隧道1在大圆界面上的正应力和剪应力。同样的方法可以得到隧道2在大圆界面上的正应力σρ2和剪应力τρφ2。最终得到叠加后的大圆界面正应力和剪应力分别为:
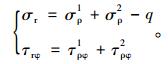
|
(5) |
通过以上分析,就可以对“预留支护”界面上的应力进行计算。选取以下算例对以上近似分析方法进行验证。
当r1=r2=δ=6 m,q=1 MPa,“预留支护”界面应力分布的计算结果和数值解如图 4所示。由图 4可知,在本研究所假设的“预留支护”界面上,叠加计算结果与数值分析结果基本一致,误差很小。由于图 4情况下两隧道半径相同,界面上正应力呈对称分布,剪应力呈反对称分布规律。
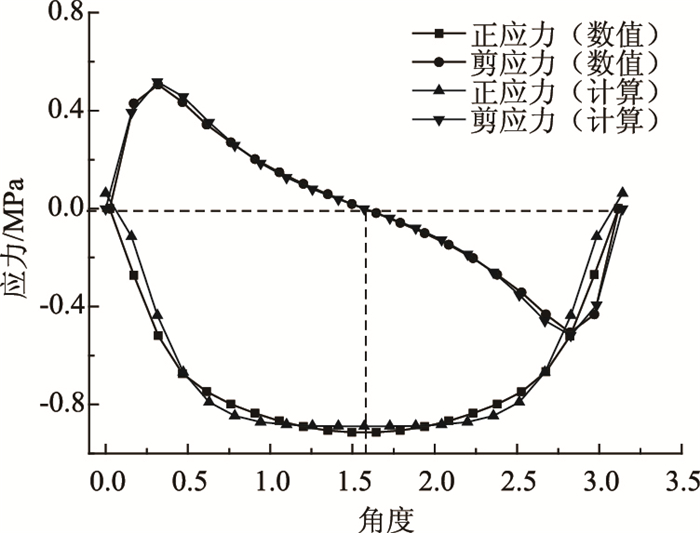
|
| 图 4 “预留支护”界面应力分布规律 Fig. 4 Stress distribution rule of"reserved support" interface |
| |
当r1=δ=6 m,q=1 MPa,r2分别等于2,3,4,5 m时,界面应力分布结果如图 5所示。
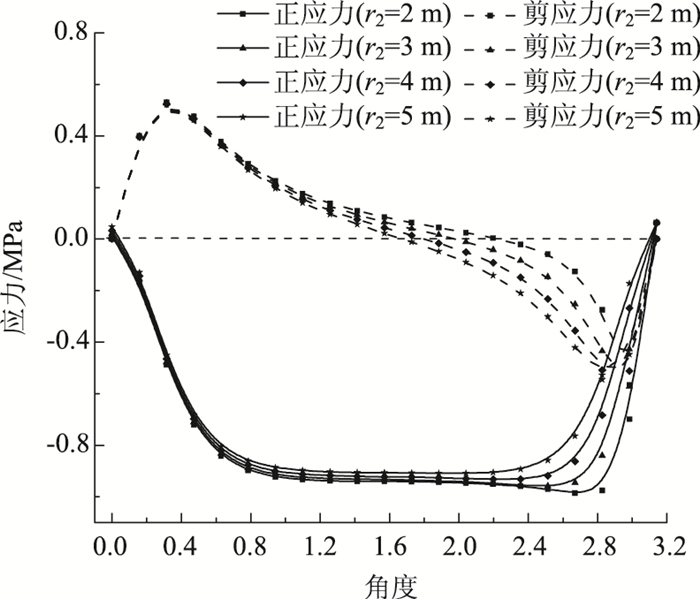
|
| 图 5 隧道2不同半径下的界面应力 Fig. 5 Interfacial stresses of tunnel 2 varying with radius |
| |
由图 5可知,当隧道2半径变化时,界面应力影响主要集中于其自身一侧,对隧道1一侧的应力分布影响有限,随着隧道2半径的逐渐减小,其自身一侧的正应力逐渐增大,剪应力逐渐减小,且剪应力中间0值点位置逐渐向隧道2靠近。
当r1=r2=6 m,q=1 MPa,δ分别等于3,6,9,12 m时,界面应力分布结果如图 6所示。
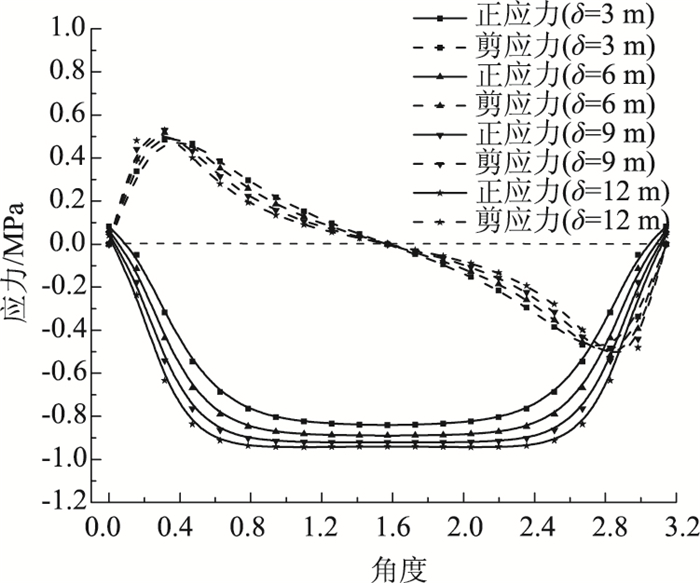
|
| 图 6 不同岩墙厚度下的界面应力 Fig. 6 Interfacial stresses varying with middle rock wall thickness |
| |
由图 6可知,随着中央岩墙厚度的逐渐增大,正应力整体都有所增大,剪应力在两个峰值中间区域逐渐减小,在两峰值之外区域逐渐增大。
预留支护界面的受力状态是通过一系列坐标转换得到的,“预留支护”假设的提出,根本目的是为计算中夹岩的受力,其理论依据类似于圣维南原理。中夹岩是受两隧道影响较大的区域(图 1),不宜进行简单叠加计算,而“预留支护”的边界受两隧道影响较小,该界面上的受力进行简单叠加计算误差较小(图 4)。在预留支护的基础上得到中夹岩受力会消除因没有考虑相互影响所带来的误差,使计算结果更加符合实际情况。
3 中央岩墙受力状态在第2节得到“预留支护”界面应力之后,可进一步得到岩墙的平均正应力与附加弯矩,选取岩墙中间最薄弱位置为分析对象。
3.1 平均应力与附加弯矩在“预留支护”界面上取一微段进行分析,该微段所对应的转角范围dφ,对应的弧长为Rdφ,如图 7所示。
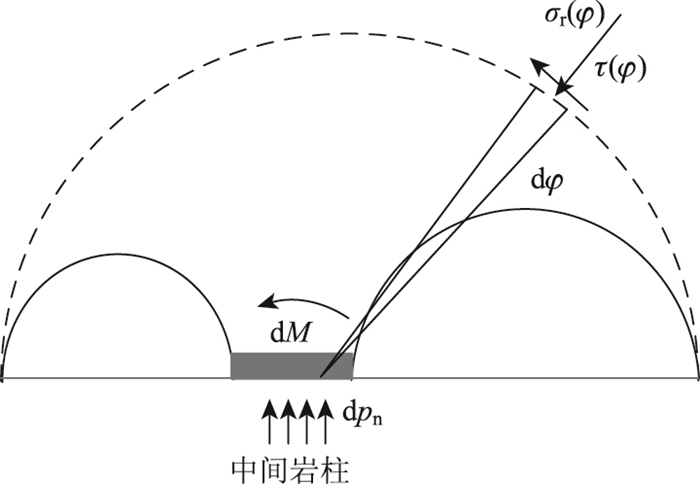
|
| 图 7 中央岩墙受力分析 Fig. 7 Analysis on stress of middle rock wall |
| |
则该微段内界面应力对中央岩墙产生的竖向应力分量和附加弯矩分量分别为:
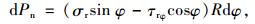
|
(6) |
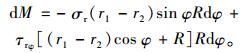
|
(7) |
将以上两式在区间0~π内进行积分,即得到界面应力在中央岩墙产生的合力与附加弯矩。
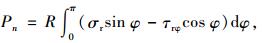
|
(8) |
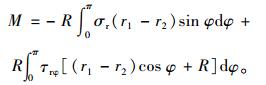
|
(9) |
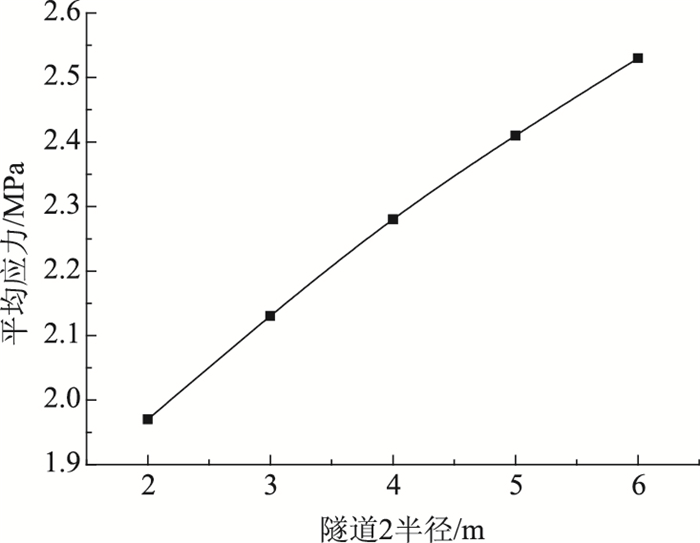
将所得合力除以岩墙厚度即可得到岩墙在厚度方向上的平均应力:
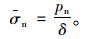
|
(10) |
根据以上计算方法,可以对中央岩墙平均应力和附加弯矩进行研究。图 8为隧道1半径等于6 m,隧道2半径分别为2,3,4,5,6 m时,岩墙平均应力随岩墙厚度的变化规律。
|
| 图 8 平均应力随中央岩墙厚度变化规律 Fig. 8 Mean stress varying with thickness of middle rock wall |
| |
由图 8可知,随着岩墙厚度增加,不同隧道半径情况下的岩柱平均应力都呈指数量级减小。以图 8中r2=6 m的曲线为例,岩墙厚度从3 m增大至6 m时,平均应力减小了1.37 MPa,而从9 m增加至12 m时,平均应力只减小了0.23 MPa。这说明在岩墙厚度较小时,适当增加岩墙厚度对减小其平均应力的效果很明显,而当岩墙厚度较大时,增加岩墙厚度对改善其受力的作用不大。
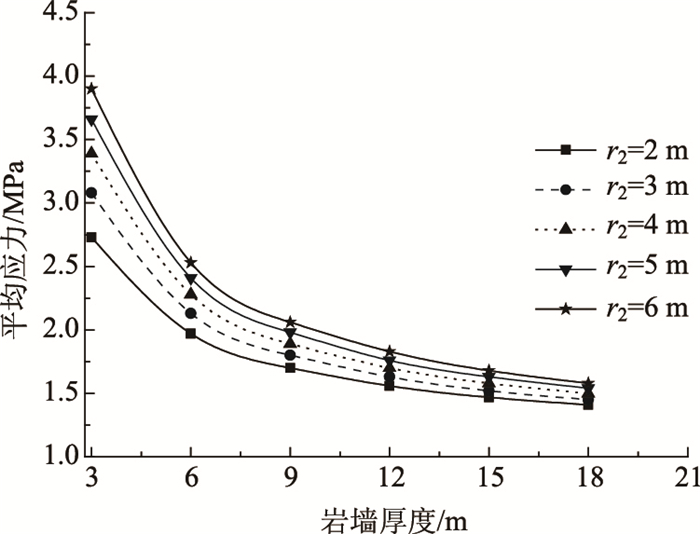
当中央岩墙厚度不变,隧道半径变化时,岩墙平均应力分布规律如图 9所示。图 9为隧道1半径和岩墙厚度均为6 m时,岩墙平均应力随隧道2半径的变化关系。
|
| 图 9 岩墙平均应力随隧道2半径的变化关系 Fig. 9 Mean stress of rock wall varying with radius of tunnel 2 |
| |
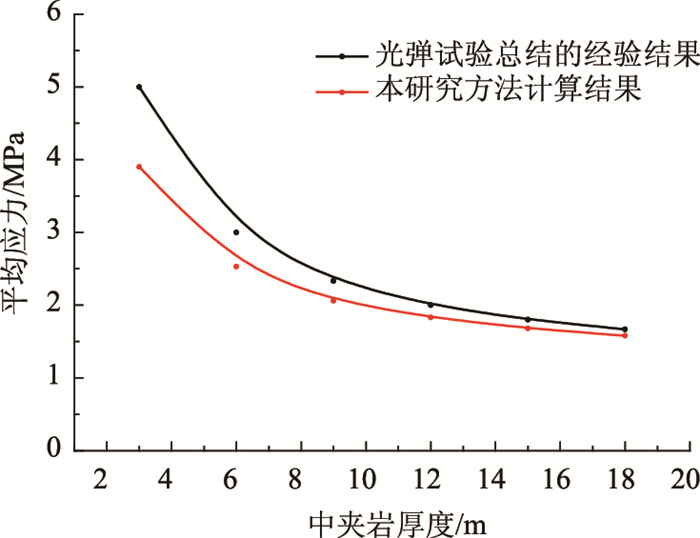
由图 9可知,在岩墙厚度一定时,随着隧道2半径逐渐增大,其所受平均应力近似线性增大。Obcrt和Duvall利用光弹试验对两等直径圆孔间的应力分布规律进行了研究,得到两洞室中间岩柱平均应力满足如下经验公式表达的关系[19]:
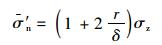
|
(11) |
式中σz为地层初始竖向荷载,式(11)仅适用于两隧道半径相同的情况,因此可与图 8中r2=6 m的结果进行对比,本研究方法所得平均应力与式(11)的对比结果如下:
由图 10可知,本研究计算结果与光弹实验结果整体符合较好,在岩墙厚度较小时有一定差别。其原因是当两隧道距离太近,预留支护边界将处于两隧道相互影响叠加区,导致边界上应力计算误差偏大,如图 11所示,红色虚线表示的预留支护边界很大一部分处于蓝色强影响叠加区域。这也是本研究方法适用范围为岩墙厚度至少应大于其中某一隧道的洞径的原因。
|
| 图 10 平均压力对比 Fig. 10 Comparison of mean stresses |
| |
|
| 图 11 预留支护边界与影响叠加区的位置关系 Fig. 11 Positional relationship between reserved support boundary and impacted overlay zone |
| |
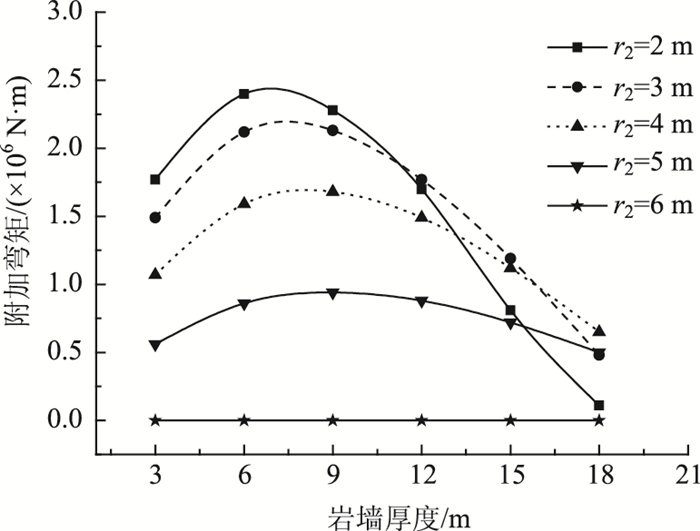
“预留支护”界面应力不仅在中央岩墙处产生平均应力,当两隧道半径不一样时,中央岩墙还会受到附加弯矩的影响,如图 12所示。图中5条曲线分别表示隧道2半径分别为2,3,4,5,6 m时中夹岩附加弯矩随岩墙厚度的变化关系。
|
| 图 12 附加弯矩随岩墙厚度的变化关系 Fig. 12 Additional bending moment varying with thickness of rock wall |
| |
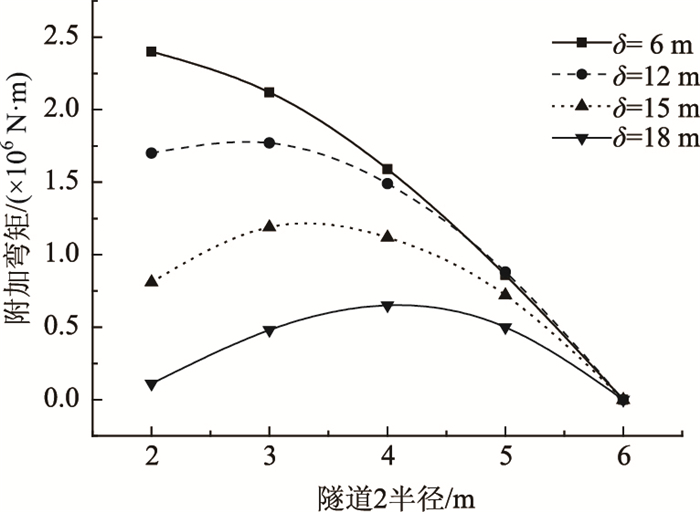
在中央岩墙厚度一定的情况下,随着隧道2半径逐渐增加到与隧道1半径相同,附加弯矩变化趋势如图 13所示。
|
| 图 13 附加弯矩随隧道2半径变化规律 Fig. 13 Additional bending moment varying with radius of tunnel 2 |
| |
由图 12和图 13可知,随着岩墙厚度逐渐增大,附加弯矩呈现先增大后减小的趋势,且随着隧道2半径逐渐增大,附加弯矩的峰值逐渐减小,直至两隧道半径相等时,附加弯矩减小为0。
3.2 中央岩墙应力分布规律中央岩墙的应力分布规律与隧道和地层空洞的尺寸、岩墙厚度以及初始围岩应力场有关。此外围岩力学特性不同,也会使岩墙的应力分布规律呈现不同的规律。在硬岩情况下,无论何种间距条件,中央岩墙墙腰水平线上垂直应力分布呈现明显的抛物线形式[19]。因此对于不考虑塑性状态的硬岩,可以用如下二次函数对岩墙应力分布进行表示:
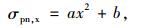
|
(12) |
式中a,b为待定参数,两参数只要得到其中一个,另一个可由前文所得岩墙的平均应力进行计算。b为岩墙中心处应力值,x为计算点到截面中心的距离。根据前文图 1所示两隧道相互影响范围的分析,当岩墙厚度超过较小隧道半径2倍时,可用叠加法对较大隧道边缘上的应力进行计算,也即如果满足δ>2r1,则可根据叠加法计算得到岩墙最右侧边缘处的竖向应力σn, x=δ/2,再根据以下两个方程得到参数a,b。
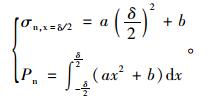
|
(13) |
由式(13)确定参数a,b后,就可以得到平均应力作用下,岩墙内部应力分布规律。进一步结合式(9)计算得到弯矩引起的应力分布:
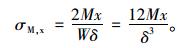
|
(14) |
式(14)中W为中夹岩单位长度上的弯曲截面系数,结合式(12),(14)即可得到岩墙应力分布规律的具体表达式。
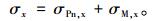
|
(15) |
根据本研究的分析方法,对2种不同初始参数下的岩墙应力分布进行计算,并结果进行具体说明。
当隧道1半径为r1=6 m,岩墙厚度为δ=12 m,隧道2半径r2分别等于3 m和6 m时,参数计算结果如表 1所示。
| r2/m | Pn/(×106 N) | M/(×106 N·m) | a/(×106 N·m-3) | b/MPa | σn, x=δ/2/MPa |
| 3 | 19.6 | 1.77 | 0.017 | 1.43 | 2.04 |
| 6 | 21.9 | 0.0 | 0.012 | 1.68 | 2.16 |
在表 1参数基础上,分别利用本研究方法和简单叠加法计算得到岩墙上应力分布规律,如图 14所示。
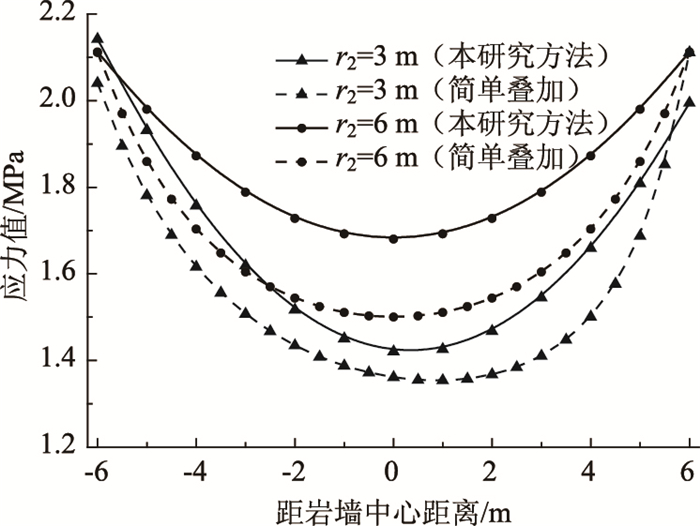
|
| 图 14 隧道2半径不同时中央岩墙竖向应力分布规律 Fig. 14 Vertical stress distribution rules of middle rock wall with radius of tunnel 2 |
| |
由图 14可知,在岩墙厚度一定的情况下,隧道2半径越大,岩墙总体应力也越大,在附加弯矩的影响下,岩墙左端应力稍大于右端应力,随着两洞室半径趋于相同,应力分布也呈现左右对称的趋势。通过本研究方法与简单叠加法的对比,可以发现简单叠加法所得结果整体偏小,且在岩墙厚度相同的情况下,隧道2半径越大,简单叠加法计算结果偏小越多。
当隧道1半径为r1=6 m,隧道2半径r2=3 m,岩墙厚度δ分别为9 m和12 m,参数计算结果如表 2所示。
| δ/m | Pn/(×106N) | M/(×106 N·m) | a/(×106 N·m-3) | b/MPa | σn, x=δ/2/MPa |
| 9 | 16.2 | 2.13 | 0.019 | 1.67 | 2.06 |
| 12 | 19.6 | 1.77 | 0.017 | 1.43 | 2.04 |
在表 2参数基础上,分别利用本研究方法和简单叠加法计算得到岩墙上应力分布规律,如图 15所示。
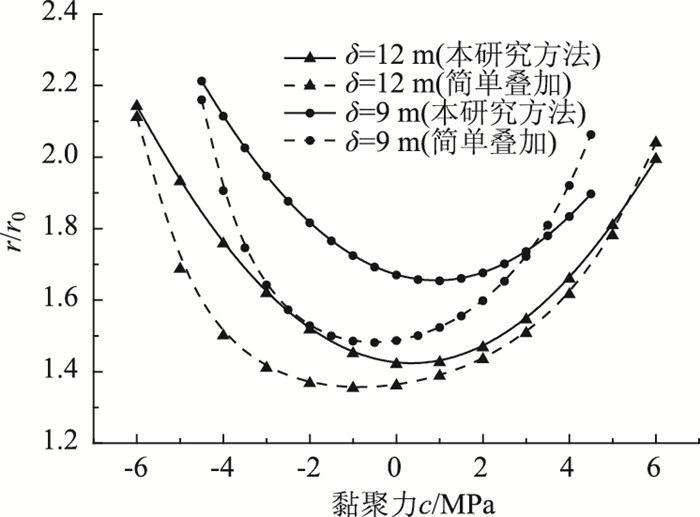
|
| 图 15 岩墙厚度不同时中央岩墙竖向应力分布规律 Fig. 15 Vertical stress distribution under different thickness of middle rock wall |
| |
由图 15可知,在两隧道半径不变时,随着岩墙厚度增加,应力分布整体减小,且逐渐变得均匀,应力集中程度逐渐降低。岩墙厚度越大,由于弯矩引起的两侧应力差别越小。简单叠加法计算结果整体上小于本研究计算结果,岩墙厚度越小,两种方法计算结果差别越大。
4 结论本研究针对小净距隧道中央岩墙受力特性及其影响因素进行了研究,得到了一种岩墙受力特性的简化计算方法,主要结论如下:
(1) 得到了一种小净距隧道中央岩墙应力分布规律的分析方法,该方法通过3个主要步骤完成:得到预留支护界面上的正应力和剪应力分布表达式;计算中央岩墙的平均应力和附加弯矩;得到岩墙应力分布规律。
(2) 作用在预留支护界面上应力对中央岩墙产生一个合力,并在两隧道半径不同时产生附加弯矩。附加弯矩产生的附加应力使岩墙内部左侧应力增大,右侧应力减小,最终导致岩墙两端应力呈现左高右低的现象。
(3) 在岩墙厚度较小时,适当增加岩墙厚度对减小其平均应力的效果很明显,而当岩墙厚度较大时,增加岩墙厚度对改善其受力的作用不显著。
(4) 在岩墙厚度一定的情况下,随着隧道2半径增大,岩墙总体应力增大,当两隧道半径趋于相同,应力分布也呈现左右对称的趋势;在两洞室半径一定的情况下,随着岩墙厚度增加,应力分布整体减小,且逐渐变得均匀,由弯矩引起的两侧应力差也随之越小。
| [1] |
周佳媚, 袁松, 高波. 小净距隧道地震动力响应下的围岩应力场[J]. 公路交通科技, 2012, 29(2): 92-97. ZHOU Jia-mei, YUAN Song, GAO Bo. Surrounding Rock Stress Field under Earthquake-induced Dynamic Response of Tunnels with Small Spacing[J]. Journal of Highway and Transportation Research and Development, 2012, 29(2): 92-97. |
| [2] |
彭从文, 朱向荣, 王金昌. 基于三维有限元模型的小净距隧道施工力学分析[J]. 公路交通科技, 2008, 25(12): 138-145. PENG Cong-wen, ZHU Xiang-rong, WANG Jin-chang. Mechanical Analysis of Small Interval Tunnel Based on Three-dimensional FEM Model[J]. Journal of Highway and Transportation Research and Development, 2008, 25(12): 138-145. |
| [3] |
陈秋南, 王勤荣, 谢小鱼, 等. 扁坦超大断面小净距隧道支护结构的力学性状[J]. 公路交通科技, 2012, 29(9): 89-94. CHEN Qiu-nan, WANG Qin-rong, XIE Xiao-yu, et al. Mechanical Characteristics of Supporting Structure for Flat Super-large Section Small Spacing Tunnels[J]. Journal of Highway and Transportation Research and Development, 2012, 29(9): 89-94. |
| [4] |
靳晓光, 刘伟, 郑学贵, 等. 小净距偏压公路隧道开挖顺序优化[J]. 公路交通科技, 2005, 22(8): 61-64. JIN Xiao-guang, LIU Wei, ZHENG Xue-gui, et al. Optimization of Excavating Sequence for Closely Spaced Bias Doubletube Tunnels[J]. Journal of Highway and Transportation Research and Development, 2005, 22(8): 61-64. |
| [5] |
赵秀绍, 庄锦彬, 徐长节, 等. 浅覆大跨度小净距隧道中岩墙及初支力学特性研究[J]. 公路交通科技, 2015, 32(12): 100-107. ZHAO Xiu-shao, ZHUANG Jin-bin, XU Chang-jie, et al. Study of Mechanical Properties of Middle Rock Wall and Preliminary Lining of Shallow Buried Large Span Tunnel with Small Clear Distance[J]. Journal of Highway and Transportation Research and Development, 2015, 32(12): 100-107. |
| [6] |
章慧健, 仇文革, 冯冀蒙. 小净距隧道夹岩力学特征分析[J]. 岩土工程学报, 2010, 32(3): 434-439. ZHANG Hui-jian, QIU Wen-ge, FENG Ji-meng. Mechanical Performance of Shared Rock of Neighborhood Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(3): 434-439. |
| [7] |
刘新宇, 侯学渊. 平行圆形隧道的应力分析[J]. 同济大学学报, 1985(3): 15-26. LIU Xin-yu, HOU Xue-yuan. Stress Analysis for Parallel Circular Tunnels[J]. Journal of Tongji University, 1985(3): 15-26. |
| [8] |
吕爱钟, 张路青. 地下隧洞力学分析的复变函数方法[M]. 北京: 科学出版社, 2007: 51-73. LÜ Ai-zhong, ZHANG Lu-qing. Mechanical Analysis of Underground Tunnel Using Function of Complex Variable[M]. Beijing: Science Press, 2007: 51-73. |
| [9] |
苏锋, 陈福全, 施有志. 深埋双隧洞开挖的解析延拓法求解[J]. 岩石力学与工程学报, 2012, 31(2): 365-374. SU Feng, CHEN Fu-quan, SHI You-zhi. Analytic Continuation Solution of Deep Twin-tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 365-374. |
| [10] |
KOOI C B, VEMIIJT A. Interaction of Circular Holes in an Infinite Elastic Medium[J]. Tunneling and Underground Space Technology, 2001, 16(1): 59-62. |
| [11] |
RADI E. Path-independent Integrals around Two Circular Holes in an Infinite Plate under Biaxial Loading Conditions[J]. International Journal of Engineering Science, 2011, 49(9): 893-914. |
| [12] |
潘龙, 王建国, 陈陆望. 连拱隧道浅埋偏压段的受力和变形机制研究[J]. 岩石力学与工程学报, 2011, 30(增2): 3557-3566. PAN Long, WANG Jian-guo, CHEN Lu-wang. Research on Stress and Deformation Mechanisms of Shallow Section with Unsymmetrical Loading of Multi-arch Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3557-3566. |
| [13] |
晏莉, 阳军生, 刘宝琛. 浅埋双孔平行隧道开挖围岩应力和位移分析[J]. 岩土工程学报, 2011, 33(3): 413-419. YAN Li, YANG Jun-sheng, LIU Bao-chen. Stress and Displacement of Surrounding Rock with Shallow Twin-parallel Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 413-419. |
| [14] |
王更峰, 熊晓晖, 张永兴, 等. 大跨小净距隧道合理开挖方法与支护参数对比研究[J]. 公路交通科技, 2011, 28(3): 27-33. WANG Geng-feng, XIONG Xiao-hui, ZHANG Yong-xing, et al. Comparative Study of Rational Excavation Method and Support Parameter for Large-span Small-spacing Tunnel[J]. Journal of Highway and Transportation Research and Development, 2011, 28(3): 27-33. |
| [15] |
胡元芳. 小线间距城市双线隧道围岩稳定性分析[J]. 岩石力学与工程学报, 2002(9): 1335-338. HU Yuan-fang. Stability Analysis of Surrounding Rocks of Double-hole Urban Tunnel with Small Interval[J]. Chinese Journal of Rock Mechanics and Engineering, 2002(9): 1335-1338. |
| [16] |
张顶立, 陈立平, 房倩, 等. 小净距隧道中央岩墙稳定性分析及应用[J]. 北京交通大学学报, 2016, 40(1): 1-11. ZHANG Ding-li, CHEN Li-ping, FANG Qian, et al. Research and Application on Central Rock Wall Dike Stability of Small Interval Tunnel[J]. Journal of Beijing Jiaotong University, 2016, 40(1): 1-11. |
| [17] |
HOANG S H, ABOUSLEIMAN Y N. Extended Green's Solution for the Stresses in an Infinite Plate with Two Equal or Unequal Circular Holes[J]. Journal of Applied Mechanics, 2008, 75(3): 031016.1-031016.13. |
| [18] |
卞晓林, 陈福全, 苏峰, 等. 岩溶区深埋隧道围岩力学特性分析[J]. 中国铁道科学, 2013, 34(1): 43-50. BIAN Xiao-lin, CHEN Fu-quan, SU Feng, et al. Mechanical Characteristics Analysis of Surrounding Rock in Deep Buried Tunnel in Karst Regions[J]. China Railway Science, 2013, 34(1): 43-50. |
| [19] |
晏莉.并行隧道施工相互影响分析及应用研究[D].长沙: 中南大学, 2008. YAN Li. Analysis of Interaetion between parallel Tunnel Excavations and Its Application[D]. Changsha: Central South University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1328212 |
 2018, Vol. 35
2018, Vol. 35
