扩展功能
文章信息
- 魏锋, 陈忠达, 张震, 朱耀庭, 吴福泉
- WEI Feng, CHEN Zhong-da, ZHANG Zhen, ZHU Yao-ting, WU Hu-quan
- 基于塑性铰线理论及强度折减法计算矩形钢筋混凝土板配筋率
- Calculation of Reinforcement Ratio of Rectangular RC Slabs Based on Plastic Hinge Line Theory and Strength Reduction Method
- 公路交通科技, 2018, 35(12): 19-27
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(12): 19-27
- 10.3969/j.issn.1002-0268.2018.12.004
-
文章历史
- 收稿日期: 2018-10-09
2. 陕西省公路局, 陕西 西安 710068;
3. 江西省交通科学研究院, 江西 南昌 330052;
4. 江西省高速公路投资集团有限责任公司, 江西 南昌 341000
2. Shaanxi Provincial Highway Bureau, Xi'an Shaanxi 710068, China;
3. Jiangxi Provincial Transport Science Institute, Nanchang Jiangxi 330052, China;
4. Jiangxi Provincial Expressway Investment Group Co., Ltd., Nanchang Jiangxi 341000, China
现行的钢筋混凝土结构设计方法以验算为主,需要根据经验拟定配筋率,经核算不满足截面抗弯和抗剪要求时,通常凭经验增加配筋再行复核,往往要经多次试算才能获得满意的结果。
为了寻求直接计算配筋率的方法,文献[1-7]以塑性铰线理论为基础,寻找配筋率的解析解,取得了较好的效果,缺点是需要假设塑性铰线,且在求解复杂问题时难以找到解答。数值解法[8-12]在求解复杂问题时具有优势,且已被广泛应用于钢筋混凝土结构分析,但大都侧重于分析应力分布和变形特点,而鲜有应用于配筋率的计算。
本研究根据塑性应变增量分布图,抽象出相应的破坏形式,并与经典塑性铰线假设进行对比,总结长宽比和支撑条件对塑性铰线的影响。分别使用塑性铰线理论和强度折减法计算矩形钢筋混凝土板配筋率,比较两者之间的类似点和不同点。
1 基于塑性铰线理论的解析解塑性铰线理论求解板的配筋率时,首先需假定一个几何可变的破坏机构图形,并给破坏机构以虚位移,然后分别计算内功和外功。按内功与外功相等的条件,就可确定在假定破坏机构下的极限弯矩及配筋率需求。
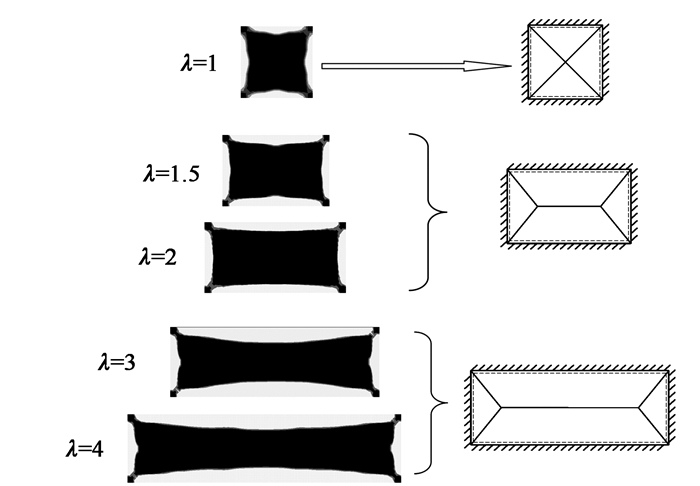
1.1 破坏形式及其影响因素塑性应变增量分布图[13-16]是一种用来描述破坏形式的常用手段。对于四周固支矩形钢筋混凝土板,取长宽比λ的变化范围为1~4,使用数值分析软件FLAC3D计算得到塑性应变增量分布图,并抽象出相应的破坏形式,结果如图 1所示。
|
| 图 1 四周固支矩形钢筋混凝土板在各长宽比条件下的破坏形式 Fig. 1 Failure modes of fix-supported rectangular RC slab with different aspect ratios |
| |
当λ=1(方形板)时,产生沿对角线的4条塑性铰线和沿固支边的4条负塑性铰线,分割成4个三角形刚性块体。
当1.5≤λ≤2(双向板)时,共产生5条塑性铰线和沿固支边的4条负塑性铰线,分割成沿短边的2个三角形刚性块体和沿长边的2个梯形刚性块体。
当3≤λ≤4(单向板)时,塑性铰线较之双向板更为狭长,短跨弯矩muy远大于长跨弯矩mux,受力方式更接近于梁。
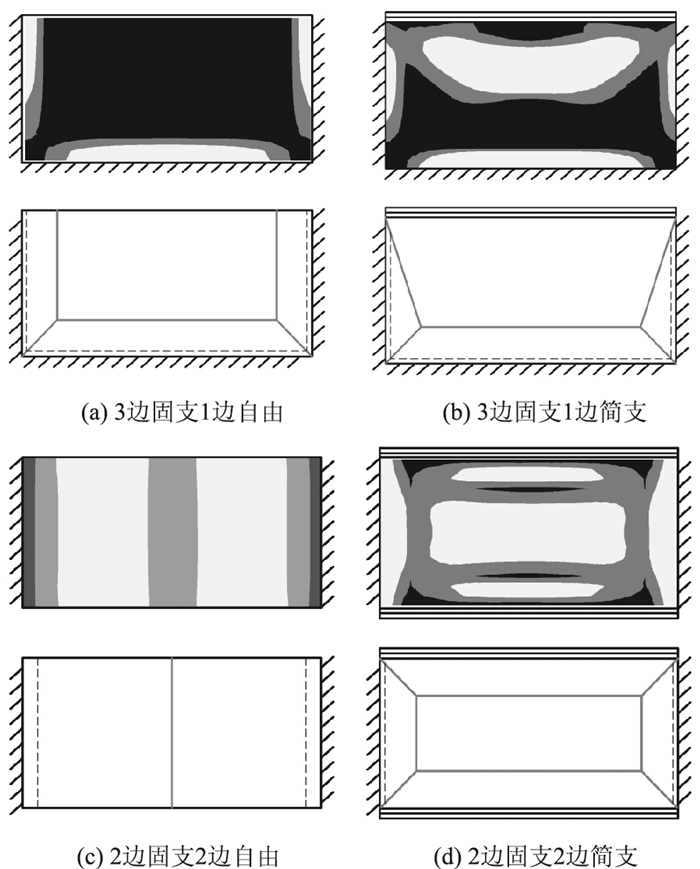
分别按固支边、简支边、自由边等类型的支撑条件计算,得到塑性应变增量分布图,并抽象出相应的破坏形式,结果如图 2所示。
|
| 图 2 矩形钢筋混凝土板在各支撑条件下的破坏形式 Fig. 2 Failure modes of rectangular RC slab with different support conditions |
| |
在3边固支1边自由和3边固支1边简支的情况下,共产生5条塑性铰线和沿固支边的3条负塑性铰线,分割成4个刚性块体。
在2边固支2边自由的情况下,共产生1条沿板中的塑性铰线和1条沿固支边的负塑性铰线,分割成2个矩形刚性块体。
在2边固支2边简支的情况下,破坏形式较为复杂,共产生8条塑性铰线和2条沿固支边的负塑性铰线,分割成5个刚性块体。
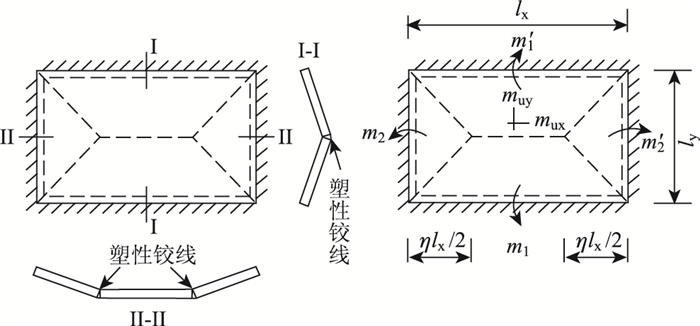
1.2 极限弯矩对于四周固支矩形钢筋混凝土板(λ > 1),在任意配筋条件下的破坏机构如图 3。图中:矩形板的长、短边跨度分别为lx,ly;mux,muy分别表示跨中塑性铰线上两个方向单位长度内的极限弯矩;ml,m′l,m2,m′2分别表示两个方向支座塑性铰线上单位长度内的极限弯矩;η为塑性铰线的位置参数。
|
| 图 3 四周固支矩形钢筋混凝土板的塑性铰线假设 Fig. 3 Plastic hinge line hypothesis of fix-supported rectangular RC slab |
| |
如果板上作用有均布荷载q,在板的微单元面积dxdy上引起的虚位移为δ,则总的外功为:
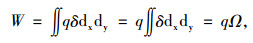
|
(1) |
式中,Ω为板下垂位置与原平面之间的体积。
设板中点的虚位移δ为1,则可计算得到Ω = (3λ-η)ly2/6,并将式(1)写为:
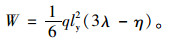
|
(2) |
板中塑性铰线所做的内功[6]为:
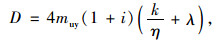
|
(3) |
式中,i=m1/muy;k=mux/muy。
利用虚功原理,令W=D,得:
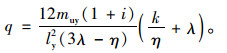
|
(4) |
令əq/əη=0,得到极值条件下的极限荷载:
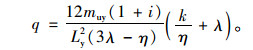
|
(5) |
以极限荷载q作为自变量,求解矩形钢筋混凝土板承受的极限弯矩muy:
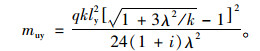
|
(6) |
板内沿x,y方向单位长度内的极限弯矩分别为mux,muy,所需的配筋面积Asx,Asy可由式(7)[7]计算:
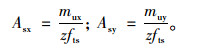
|
(7) |
式中,z为内力臂,即钢筋中心到受压区中心的距离,可以表示[17]为γsh0。γs为内力臂系数,范围一般为0.85~0.97,h0为截面有效高度。
板内钢筋总用量为:
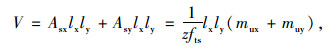
|
(8) |
将mux=kmuy,及式(6)代入式(8)中,可得:
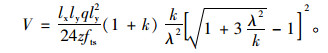
|
(9) |
令əV/ək=0可求得钢筋用量为最少时的k=1/(3λ2-2),代入式(9)中经化简后可得:
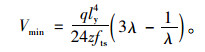
|
(10) |
钢筋总用量Vmin与矩形板总体积lxlyh之比即为配筋率:
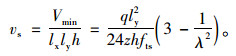
|
(11) |
在有限元程序中建立钢筋混凝土整体式模型,并引入强度折减法进行计算。整体式模型是有限元程序中用于模拟钢筋混凝土结构的一种主要模型类型。采用整体式模型,需要将钢筋弥散于整个单元中,视单元为连续均匀材料,并求解其等效材料参数。首先基于莫尔圆和应变协调原理,推导钢筋混凝土数值模型的等效抗剪强度、抗拉强度。最后引入强度折减法,并将其应用于配筋率的计算。
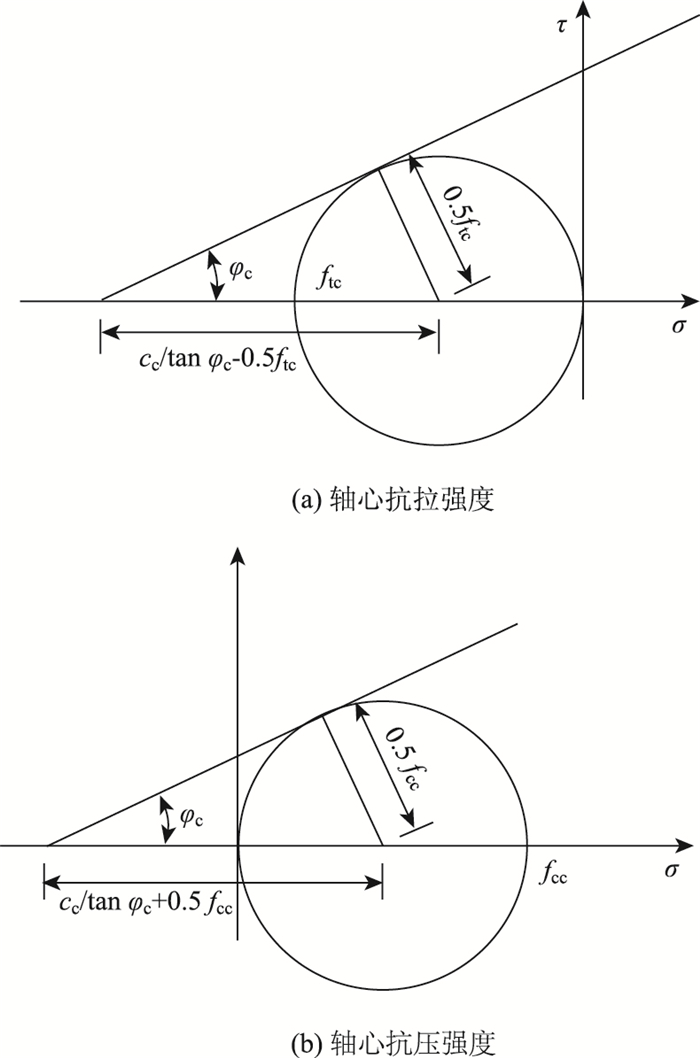
2.1 素混凝土的抗剪强度直接测试素混凝土的抗剪强度较为困难,但可以通过抗拉强度、抗压强度进行转换。采用莫尔圆表示轴心抗拉强度和轴心抗压强度试验结果(图 4),可以看出素混凝土的cc、φc值与抗拉强度ftc、抗压强度fcc存在如下关系:
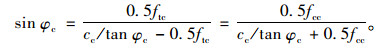
|
(12) |
|
| 图 4 素混凝土材料参数转换原理 Fig. 4 Parameter conversion principle of plain concrete |
| |
解之得素混凝土的抗剪强度:
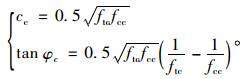
|
(13) |
按混凝土剪切破坏后钢筋混凝土失效计算,极限平衡状态下混凝土的剪应变γc为:
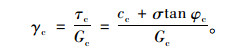
|
(14) |
式中,σ为剪切面上的正应力;τc为素混凝土的剪应力;Gc为素混凝土的剪切模量,根据GB 50010—2010《混凝土结构设计规范》,可按相应弹性模量Ec的40%采用。
假设钢筋与混凝土变形协调不产生相对滑移,钢筋的剪应变γs与混凝土的剪应变γc相等,则钢筋所承受的剪应力τs为:
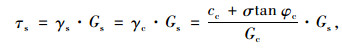
|
(15) |
式中Gs为钢筋的剪切模量。
钢筋混凝土承受的剪应力τ为:
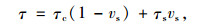
|
(16) |
式中vs为配筋率。
代入τ=c+σtan φ及式(14)、(15),得钢筋混凝土的等效抗剪强度[18]:
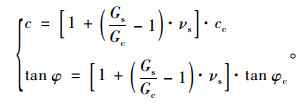
|
(17) |
按钢筋屈服后钢筋混凝土失效考虑,此时钢筋混凝土的拉应力全部由钢筋承担,则等效抗拉强度[18]为:
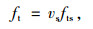
|
(18) |
式中fts为钢筋的抗拉强度。
2.4 配筋率计算流程强度折减法最早由Zienkiewicz提出[19],其原理是将材料强度不断折减直至达到极限状态,从而得到满足稳定性要求的最小材料强度以及相应的配筋率。本研究所计算的配筋率,是指结构在最不利作用效应组合下,为满足承载力要求所需的最小配筋百分率。当配筋率降低至该最小配筋百分率以下时,结构变成几何可变机构,变形将无限制地增长,从而丧失承载能力达到破坏,这种状态称为结构承载能力的极限状态。
在计算满足抗剪性能要求的配筋率时,需要将抗剪强度c,tan φ分别折减ws:
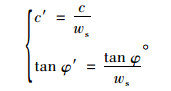
|
(19) |
使钢筋混凝土板达到抗剪极限平衡状态,此时抗剪强度c′,tan φ′对应的配筋率vs1即为满足抗剪性能要求的配筋率。将折减后的抗剪强度c′,tan φ′代入式(17)即可求得:
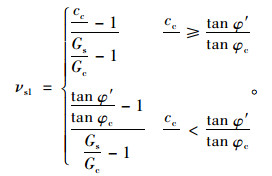
|
(20) |
由式(20)可知,配筋率vs1与c′,tan φ′正相关;由式(19)可知,c′,tan φ′与折减系数ws负相关。由此可见,抗剪强度折减就是不断提高折减系数ws,使抗剪强度c′,tan φ′和配筋率vs1减小,直至钢筋混凝土板达到抗剪极限平衡状态的过程。
在计算满足抗拉性能要求的配筋率时,需要将抗拉强度ft折减wt:
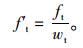
|
(21) |
使钢筋混凝土板达到抗拉极限平衡状态,此时抗拉强度f′t对应的配筋率vs2即为满足抗拉性能要求的配筋率。将折减后的抗剪强度f′t代入式(18)即可求得:
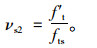
|
(22) |
由式(22)可知,配筋率vs2与f′t正相关;由式(21)可知,f′t与折减系数wt负相关。由此可见,抗剪强度折减就是不断提高折减系数wt,使抗拉强度f′t和配筋率vs2减小,直至钢筋混凝土板达到抗拉极限平衡状态的过程。
取配筋率vs1和配筋率vs2中较大的值,即为满足钢筋混凝土板稳定性的配筋率。
3 计算实例研究背景为江西省昌栗高速公路岩溶处治工程。岩溶区的地基塌陷通常是局部性的,且规模不大。如桂林市岩溶塌陷统计数据[20]显示:直径1~5 m的占总塌陷的85%。对于规模不大的塌陷,采用钢筋混凝土板是一种经济、有效的处理方法。
岩溶塌陷多为漏斗状,将钢筋混凝土板设置于路基底部较为有利。因此,需考虑路基自重(15 m高路基自重约300 kN/m2)、交通安全设施重量、施工过程中的压实机械荷载、使用过程中的车辆荷载等作用,最大合计约400 kN/m2,再考虑一定的安全系数,最终取为500 kN/m2。
拟定算例参数如下:四周固支矩形板长边跨度lx=6 m、短边跨度ly=3 m,板边长比λ=lx/ly=2;板厚h=0.5 m;保护层厚度hs=0.04 m;混凝土强度等级为C30,轴心抗压强度fcc=13.8 MPa,轴心抗拉强度ftc=1.39 MPa,弹性模量Ec=30 GPa,剪切模量Gc=12 GPa,密度ρc=2 600 kg/m3,泊松比μc=0.2;主拉钢筋等级为HRB335,抗拉强度fts=280 MPa,抗压强度fcs=280 MPa,直径为0.01 m,弹性模量Es=200 GPa,密度ρs=7 850 kg/m3,泊松比μs=0.3;板的均布荷载q=500 kN/m2,求该板满足稳定性要求的配筋率。
3.1 基于塑性铰线理论的配筋率计算本例中钢筋距离配筋板下缘0.04 m,而钢筋直径为0.01 m,因此截面有效高度h0=h-0.04-0.01/2=0.5-0.04-0.01/2=0.455 m。故0.387 m≤z=γsh0≤0.441 m。根据式(11)得到:
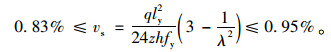
|
(23) |
再使用强度折减法进行计算。将模型剖分为负弯矩钢筋混凝土层、正弯矩钢筋混凝土层和素混凝土层等部分,如图 5所示。负弯矩钢筋混凝土层、正弯矩钢筋混凝土层的厚度均为0.09 m,中间素混凝土层的厚度为0.32 m。边界条件为四周固支,上下临空,并于顶部施加均布荷载。其中,负钢筋混凝土层和正弯矩钢筋混凝土层均采用整体式模型,将钢筋弥散于整个单元当中,视单元为连续均匀材料,且认为钢筋与混凝土之间无相对滑移。素混凝土的抗剪强度,钢筋混凝土的等效抗剪强度和抗拉强度分别按式(13)、(17)和(18)计算,并假设钢筋混凝土的等效泊松比、密度、弹性模量和抗压强度满足式(24),结果如表 1所示。
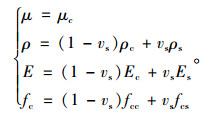
|
(24) |
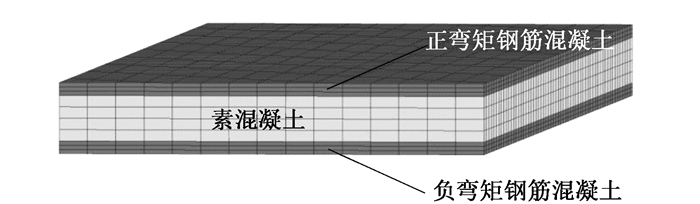
|
| 图 5 数值模型 Fig. 5 Numerical model |
| |
| 模型名称 | ρ/(kg·m-3) | E/GPa | G/GPa | μ | c/MPa | tan φ | fc/MPa | ft/MPa | vs/% |
| 正弯矩钢筋混凝土 | 2 892 | 39 | — | 0.2 | 2.85 | 1.84 | 28.59 | 15.56 | 1.00 |
| 负弯矩钢筋混凝土 | 6 538 | 44 | — | 0.2 | 3.18 | 2.06 | 35.98 | 23.33 | 1.50 |
| 素混凝土 | 2 600 | 30 | 12.0 | 0.2 | 2.19 | 1.42 | 13.80 | 1.39 | — |
| 钢筋 | 7 850 | 200 | 76.9 | 0.3 | — | — | 280.00 | 280.00 | — |
由式(19)和(21)可知,只需分别求得抗剪强度折减系数ws和抗拉强度折减系数wt即可求得极限平衡状态下的强度参数,进而根据式(20)和(21)找到配筋率的解答。此处详细介绍负弯矩钢筋混凝土抗拉性能的计算过程,并简要介绍抗剪性能的计算思路。
采用二分法求解折减系数,以缩短求解时间。根据表 1中钢筋混凝土强度参数和素混凝土强度参数之间的比例关系,分别将折减系数wt求解范围的下限值wt1定义为1(不进行折减),上限值wt2定义为17(负弯矩钢筋混凝土的抗拉强度水平降低至素混凝土的水平),将求解精度ks定义为0.1。根据二分法计算原理,定义初始折减系数wt0为求解范围的均值,即(1+17)/2=9。将wt0代入式(24),得到折减后的抗拉强度f′t,并按式(22)计算折减后的配筋率v′s。将v′s代入式(24),得到折减后的材料参数。
按此材料参数进行计算负弯矩钢筋混凝土的最大拉应力σt, max和素混凝土的最大拉应力σtc, max(遍历所有节点的σ3主应力即可得到)。若满足抗拉性能要求(σt, max < f′t且σtc, max < f′c),表明在当前折减系数wt的条件下,配筋板将处于平衡状态,故将求解范围的下限值wt1提高至9,并更新折减系数wt为(9+17)/2=13,从而加强对材料参数的折减;若不满足抗拉性能要求(σt, max ≥ f′t或σtc, max ≥ f′c),则将求解范围的上限值wt2缩小至10.5,并更新折减系数wt为(1+9)/2=5。若此反复计算,直至求解范围的下限值wt1和上限值wt2逼近一个稳定的数值,即(wt2-wt1) < ks。
在进行抗剪强度折减时,与上述步骤基本相同。但摩尔库伦剪切破坏准则与正应力挂钩,判别过程较复杂,故提出一种容易在数值模拟中实现的判别方法。如图 6所示,采用莫尔圆表示任一受力状态,其第一主应力为σ1,第三主应力为σ3。根据图中的几何关系,定义莫尔圆的半径为潜在破裂面的剪应力τr,定义圆心到抗剪强度包络线的距离为潜在破裂面的抗剪强度τl,并定义为RATIO=τl/τr为抗剪比例,若RATIO≤1则发生剪切破坏,反之则仍具备抗剪潜力:
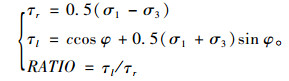
|
(25) |
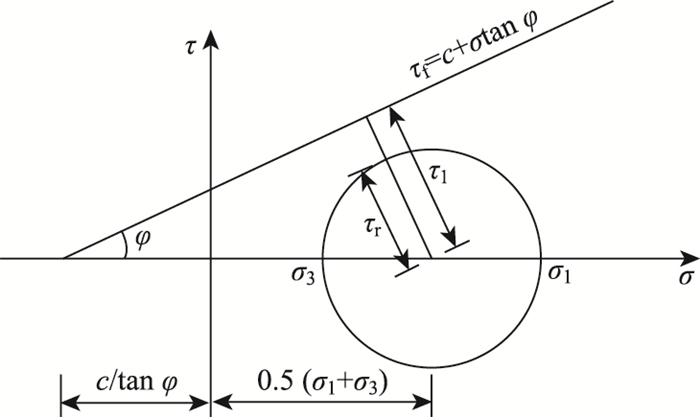
|
| 图 6 抗剪比例计算图示 Fig. 6 Illustration of shear ratio calculation |
| |
根据式(25),计算负弯矩钢筋混凝土的最大抗剪比例RATIOmax和素混凝土的最大抗剪比例RATIOc, max。若满足抗剪性能要求(RATIOmax>1且RATIOc, max>1),则应增大折减系数;若不满足抗剪性能要求(RATIOmax≤1或RATIOc, max≤1),则应减小折减系数,直至折减系数趋于稳定。
按上述方法,通过反复迭代最终求解得到极限平衡状态下正弯矩钢筋混凝土、负弯矩钢筋混凝土的折减系数及强度参数,并依据式(20)和式(22)计算其配筋率,计算结果如表 2所示。表 2中vs表示正弯矩钢筋混凝土、负弯矩钢筋混凝土的总配筋率(0.35%+0.43%=0.78%)。由表 2可知,满足钢筋混凝土抗剪稳定性和抗拉稳定性所需的配筋率有所不同,且满足抗拉稳定性所需的配筋率更大。
| 模型 | c′/MPa | tan φ′ | f′t/MPa | vs1/% | vs2/% | vs/% |
| 正弯矩钢筋混凝土 | 1.28 | 0.56 | 4.59 | 0.32 | 0.35 | |
| 负弯矩钢筋混凝土 | 1.32 | 0.57 | 5.68 | 0.39 | 0.43 | 0.78 |
由此可见,使用强度折减法计算得到的配筋率(0.78%)略小于使用塑性铰线理论的计算结果(0.83%~0.95%)。
3.3 两种计算方法的比较若定义塑性铰线函数ψ = ly2(3-1/λ2)/(24zhfy),则式(11)可简化为vs = qψ,即将配筋率vs表示为荷载q与塑性铰线函数ψ的乘积。其中,塑性铰线函数ψ主要与板的长宽、厚度、有效截面高度、钢筋强度等参数有关。
取均布荷载的变化范围为300~700 kN/m2,分别按强度折减法和塑性铰线理论进行计算,结果如图 7所示。两种方法的计算结果均表明,配筋率与荷载大小呈线性关系,故可将强度折减法的结果近似拟合为vs = qψ′。强度折减法的配筋率计算结果vs略小于按塑性铰线的极限平衡理论求得的上限解,同时回归得到的斜率ψ′略大于塑性铰线函数ψ,但总体差异不大,这表明强度折减法的计算结果较为合理。由于塑性铰线函数ψ是在塑性铰线假设的基础上经由虚功方程计算得到的,因此,二者的差异很可能与塑性铰线假设有关,如图 8所示。
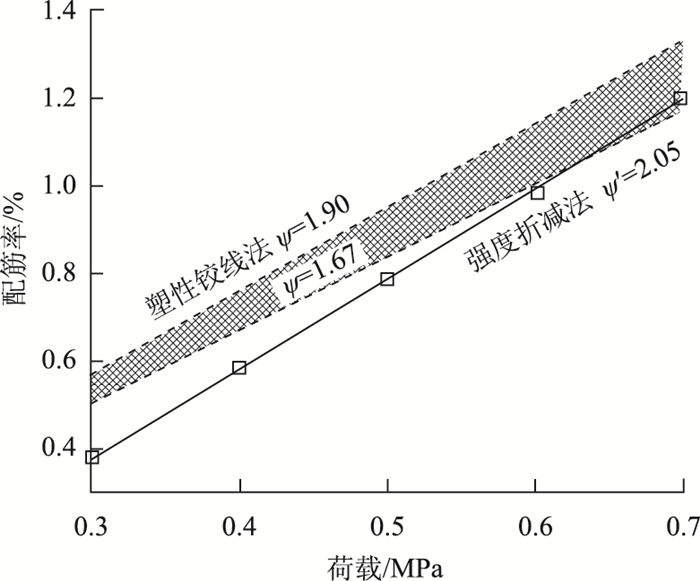
|
| 图 7 两种计算方法的比较 Fig. 7 Comparison of 2 calculation methods |
| |
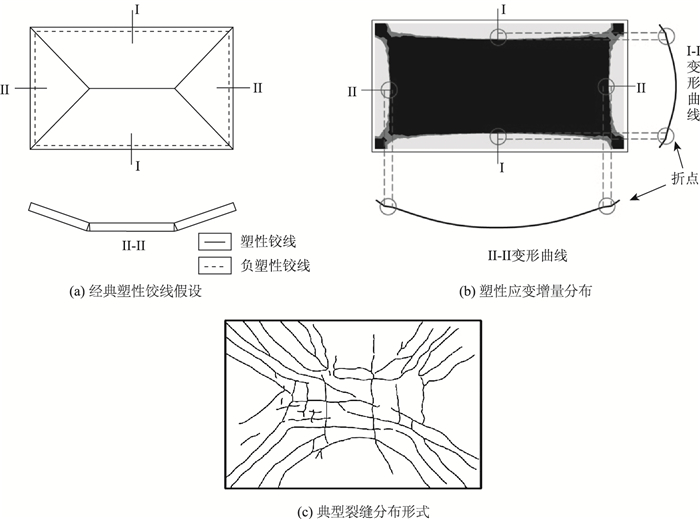
|
| 图 8 塑性应变增量分布图与塑性铰线假设的对比 Fig. 8 Comparison of plastic strain increment distribution diagram and plastic hinge line hypothesis |
| |
图 8表明,塑性应变增量分布图与典型裂缝分布形式[21]、塑性铰线的形状较为吻合。选取Ⅰ-Ⅰ截面和Ⅱ-Ⅱ截面绘制相应的变形曲线,发现变形曲线的折点与塑性应变增量的分布较为吻合。这进一步表明,使用塑性应变增量分布图可以有效描述塑性铰线的形状。由此可见,塑性铰线假设将较宽的破损带(图 8(b)中的塑性应变增量分布带和图 8(c)中的裂缝带)简化为直线(图 8(a)中的塑性铰线),可以简化钢筋混凝土板的分析。
4 结论(1) 方板和矩形板之间的塑性铰线存在明显差异;单向板的塑性铰线较之双向板更为狭长,短跨弯矩muy远大于长跨弯矩mux,受力方式更接近于梁;支撑条件对塑性铰线的影响较大,固支边、简支边、自由边的存在均会显著影响塑性铰线的形状。
(2) 根据塑性铰线理论,可将配筋率vs表示为荷载q与塑性铰线函数ψ的乘积;强度折减法的计算结果亦可近似拟合为荷载q与拟合斜率ψ′的乘积。强度折减法的计算结果略小于塑性铰线理论,同时ψ′虽略大于ψ,但总体差异不大。
(3) 使用强度折减法计算得到的配筋率(0.78%)略小于使用塑性铰线理论的计算结果(0.83%~0.95%)。二者的差异主要是因为塑性铰线理论所做出的塑性铰线假设将较宽的破损带简化为直线。
| [1] |
张大山, 董毓利, 房圆圆. 考虑受拉薄膜效应的板块平衡法修正及在混凝土双向板中的应用[J]. 工程力学, 2017, 34(3): 204-210, 240. ZHANG Da-shan, DONG Yu-li, FANG Yuan-yuan. Modification of Segment Equilibrium Method through Considering Tensile Membrane Effects and Its Application in Two-way Concrete Slabs[J]. Engineering Mechanics, 2017, 34(3): 204-210, 240. |
| [2] |
张大山, 董毓利, 吴亚平. 混凝土单向板的受拉薄膜效应计算[J]. 吉林大学学报:工学版, 2013, 43(5): 1253-1257. ZHANG Da-shan, DONG Yu-li, WU Ya-ping. Calculation of Tensile Membrane Effect of One-way Concrete Slabs[J]. Journal of Jilin University:Engineering and Technology Edition, 2013, 43(5): 1253-1257. |
| [3] |
王勇, 董毓利, 邹超英. 钢筋混凝土板极限承载力对比分析[J]. 哈尔滨工业大学学报, 2013, 45(8): 1-7. WANG Yong, DONG Yu-li, ZOU Chao-ying. Comparative Analysis of Limit Carrying Capacity of Reinforced Concrete Slabs[J]. Journal of Harbin Institute of Technology, 2013, 45(8): 1-7. |
| [4] |
蒋秀根, 剧锦三, 庄金钊. 矩形钢筋混凝土双向板板底塑性弯矩比设计取值研究[J]. 工程力学, 2007, 24(8): 77-80. JIANG Xiu-gen, JU Jin-san, ZHUANG Jin-zhao. Study on Design Value of Plastic Bending Moment Ratio at the Bottom of Rectangular Reinforced Concrete Slabs[J]. Engineering Mechanics, 2007, 24(8): 77-80. |
| [5] |
李贵乾, 唐光武, 郑罡. 圆形钢筋混凝土桥墩等效塑性铰长度[J]. 土木工程学报, 2016, 49(2): 87-97. LI Gui-qian, TANG Guang-wu, ZHENG Gang. Equivalent Plastic Hinge Length of Circular Reinforced Concrete Bridge Columns[J]. China Civil Engineering Journal, 2016, 49(2): 87-97. |
| [6] |
沈聚敏. 钢筋混凝土有限元与板壳极限分析[M]. 北京: 清华大学出版社, 1993. SHEN Ju-min. Finite Element Analysis of Reinforced Concrete and Limit Analysis of Plate and Shell[M]. Beijing: Tsinghua University Press, 1993. |
| [7] |
刘正保, 胡晓楠. 砼矩形板配筋的优化设计[J]. 中州建筑, 1996(3): 29-31. LIU Zheng-bao, HU Xiao-nan. Optimum Design of Reinforced Concrete Rectangular Plate Reinforcement[J]. Zhongzhou Architecture, 1996(3): 29-31. |
| [8] |
赵纪飞, 叶建龙, 王骁帆, 等. 连续配筋混凝土路面横向裂缝传荷作用的数值模拟和敏感性分析[J]. 公路交通科技, 2018, 35(6): 1-7. ZHAO Ji-fei, YE Jian-long, WANG Xiao-fan, et al. Numerical Simulation and Sensitivity Analysis on Load Transfer of Transverse Crack in Continuously Reinforced Concrete Pavement[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 1-7. |
| [9] |
王骁帆, 应正兵, 刘朝晖, 等. 温度场对连续配筋混凝土路面纵向配筋的影响[J]. 公路交通科技, 2017, 34(4): 16-24. WANG Xiao-fan, YING Zheng-bing, LIU Zhao-hui, et al. Effect of Temperature Field on Longitudinal Reinforcement of Continuously Reinforced Concrete Pavement[J]. Journal of Highway and Transportation Research and Development, 2017, 34(4): 16-24. |
| [10] |
SYROKA E, BOBIHSKI J, TEJCHMAN J. FE Analysis of Reinforced Concrete Corbels with Enhanced Continuum Models[J]. Finite Elements in Analysis & Design, 2011, 47(9): 1066-1078. |
| [11] |
STRAMANDINOLI R S B, ROVERE H L L. FE Model for Nonlinear Analysis of Reinforced Concrete Beams Considering Shear Deformation[J]. Engineering Structures, 2012, 35: 244-253. |
| [12] |
MOHAMED O A, KHATTAB R. Numerical Analysis of Reinforced Concrete Beam Strengthened with CFRP or GFRP Laminates[J]. Key Engineering Materials, 2016, 707: 51-59. |
| [13] |
郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381-3388. ZHENG Ying-ren, ZHAO Shang-yi. Application of Strength Reduction FEM in Soil and Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381-3388. |
| [14] |
赵尚毅, 郑颖人, 时卫民, 等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报, 2002, 24(3): 343-346. ZHAO Shang-yi, ZHENG Ying-ren, SHI Wei-min, et al. Analysis on Safety Factor of Slope by Strength Reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 343-346. |
| [15] |
路德春, 曹胜涛, 杜修力, 等. 平面应变条件下的土拱效应[J]. 岩土工程学报, 2011, 33(增1): 461-465. LU De-chun, CAO Sheng-tao, DU Xiu-li, et al. Soil Arching Effect under Plane Strain Condition[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S1): 461-465. |
| [16] |
汪洋, 曾雄辉, 尹健民, 等. 考虑卸荷效应的深埋隧洞围岩分区破坏数值模拟[J]. 岩土力学, 2012, 33(4): 1233-1239. WANG Yang, ZENG Xiong-hui, YIN Jian-min, et al. Numerical Simulation of Zonal Cracking of Deep Tunnel Surrounding Rock Considering Unloading Effect[J]. Rock and Soil Mechanics, 2012, 33(4): 1233-1239. |
| [17] |
付占明, 栗增欣. 混凝土楼板受弯承载力的简化计算[J]. 工程建设, 2012, 44(6): 14-16. FU Zhan-ming, LI Zeng-xin. Simplified Calculation on the Capacity of Concrete Bending Slabs[J]. Engineering Construction, 2012, 44(6): 14-16. |
| [18] |
李秀地, 郑颖人, 袁勇, 等. 沉管海底隧道强度折减法分析探讨[J]. 岩土工程学报, 2013, 35(10): 1876-1882. LI Xiu-di, ZHENG Ying-ren, YUAN Yong, et al. Strength Reduction Method for Submarine Immersed Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1876-1882. |
| [19] |
ZIENKIEWICZ O C, HUMPHESON C, LEWIS R W. Associated and Non-associated Visco-plasticity and Plasticity in Soil Mechanics[J]. Géotechnique, 1977, 25(4): 671-689. |
| [20] |
刘之葵. 桂林岩溶区岩土工程理论与实践[M]. 武汉: 地质出版社, 2009. LIU Zhi-kui. Theory and Practice of Geotechnical Engineering in Guilin Karst Area[M]. Wuhan: Geological Publishing House, 2009. |
| [21] |
戴自强, 赵彤, 谢剑. 钢筋混凝土房屋结构[M]. 天津: 天津大学出版社, 2002. DAI Zi-qiang, ZHAO Tong, XIE Jian. Reinforced Concrete Housing Structure[M]. Tianjin: Tianjin University Press, 2002. |
 2018, Vol. 35
2018, Vol. 35
