扩展功能
文章信息
- 唐羽, 吴国雄, 余苗, 杨大田
- TANG Yu, WU Guo-xiong, YU Miao, YANG Da-tian
- 沥青路面三点弯曲试验的离散元模拟
- Simulation of Three-point BENDING test of Asphalt Pavement
- 公路交通科技, 2018, 35(12): 14-18, 27
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(12): 14-18, 27
- 10.3969/j.issn.1002-0268.2018.12.003
-
文章历史
- 收稿日期: 2017-08-09
2. 重庆交通大学 交通土建工程材料国家地方联合工程实验室, 重庆 400074;
3. 重庆建筑工程职业学院, 重庆 400072
2. National and Local Joint Engineering Laboratory of Traffic Civil Engineering Materials, Chongqing Jiaotong University, Chongqing 400074, China;
3. Chongqing Jianzhu College, Chongqing 400072, China
路面按其力学特性可以分为刚性路面、柔性路面和半刚性路面。其中半刚性路面是指半刚性基层和铺筑在半刚性基层上面的沥青面层的统称。由于受到经济、沥青质量、施工技术等等因素制约,半刚性基层沥青路面具有高强度、稳定性和耐久性好等优点,目前在我国高等级公路中占据着主导地位。半刚性基层沥青路面是由半刚性基层和沥青混合料面层组成,其成分包括粗集料、细集料、水泥、沥青胶浆、矿料和空隙等,内在结构和力学性质非常复杂,并且对宏观的路用性能有着重要影响[1-4]。传统的路面设计理论和其数值分析方法往往将路面假设为连续均匀、各向同性、多层弹性体系,以连续介质力学研究方法来研究沥青路面。但是沥青路面的内在特性并不符合传统设计理论,用传统设计理论难以描述沥青混合料真实的物理形态和受力状态。另外由于集料的离散性和几何形态的不规则性,造成沥青混合料呈不连续和不均匀的特点,使得现行的路面设计理论与工程实际存在较大的差异。
近年来,离散元法被引入到沥青混合料的研究中。离散元法将整体结构离散化,每一个单元都是独立的,具有相应的尺寸,对其赋予质量和微观力学参数,采用牛顿第二定律来计算单元之间的接触力,得到合力和合力矩,可以解决不连续介质的数值模拟问题,允许结构断裂分开,从而较好地模拟沥青混合料的不连续性[5]。离散元法适合模拟材料的大变形和转动,并且具有能够对个别单元赋值的优点[6-7]。离散元法可以运用随机生成多面体或多边形技术重构其微观结构[8-10],建立微观力学模型,模拟沥青路面的实际受力状态和使用寿命,为沥青路面结构和材料研究提供了新方法[11]。陈俊[12]采用PFC2D程序建立了沥青混合料二维离散元模型,进行三点弯曲虚拟疲劳试验,结果表明虚拟试验结果与室内试验结果有良好的相关性,为沥青混合料的微观结构研究奠定了基础。然而对于半刚性基层沥青路面这一结构形态,目前还没有看到相关的离散元模型,因此本研究采用PFC2D程序对半刚性基层沥青路面三点弯曲试验进行离散元数值模拟,为研究沥青混合料开裂时的层底应力变化和裂纹发展规律提供了辅助手段。
1 离散元分析模型的建立离散元就是把宏观物体离散成多个细小颗粒单元,对这些单位赋予接触模型和边界条件,再进行数值模拟。选择单元尺寸至关重要,单位尺寸过大会影响计算结果的精度和准确度;单元尺寸过小会延长计算时间,降低计算效率。经过试算比较和参考已有的文献资料[13-14],选择直径为1 mm的单元作为最小单元。离散单元的排列方式采用矩形规则排列,模型是由二维颗粒随机生成,长度为24 cm,高为10 cm(分为两层,上层是沥青混合料,厚度为5 cm;下层是水泥稳定碎石,厚度为5 cm)。具体构建过程如下:根据级配组成(见表 1和表 2)可得知集料质量所占的百分比,进而可以转换成面积所占百分比。通过FISH语言设置颗粒的边界坐标,对颗粒进行聚粒识别,然后用“Cluster”进行聚粒操作,这样就能把球形颗粒组合在一起,形成不规则的多边形“Cluster”来模拟集料。当每一档级配的集料颗粒总面积达到该档级配要求,则这一档的集料颗粒就生成了,同理继续投递其他档级配的集料颗粒。最终没有形成“Cluster”的则用来模拟沥青砂浆或水泥胶浆。最终生成的二维离散元模型如图 1所示,由24 000个球形颗粒组成。孔隙率是采用FISH语言设置一个随机函数,随机删除一部分沥青砂浆单元颗粒,以实现孔隙率。
| 孔径/mm | 0.075 | 0.15 | 0.3 | 0.6 | 1.18 | 2.36 | 4.75 | 9.5 | 13.2 | 16 | 19 | 26.5 |
| 通过率/% | 7.0 | 8.1 | 9.0 | 11.7 | 16.3 | 20.7 | 34.5 | 57.7 | 75.1 | 84.2 | 92.4 | 100 |
| 孔径/mm | 0.075 | 0.6 | 2.36 | 4.75 | 9.5 | 19 | 26.5 | 31.5 |
| 通过率/% | 1.6 | 8.38 | 16.89 | 29.48 | 45.17 | 84.83 | 95 | 100 |

|
| 图 1 模型结构 Fig. 1 Model structure |
| |
2 接触模型及微观参数
沥青混合料层看作是集料和沥青砂浆组成,单元接触模型可以分为4种类型:集料内部的接触;集料与集料的接触;集料与沥青砂浆的接触;沥青砂浆内部的接触。其中集料与集料的接触可以看作是集料外面包裹了一层沥青砂浆之后的接触。水泥稳定碎石层看作是集料和水泥胶浆组成,单元接触模型同样分为4种类型:集料内部的接触;集料与集料的接触;集料与水泥胶浆的接触;水泥胶浆内部的接触。同样集料与集料的接触看作是集料外面包裹了一层水泥胶浆之后的接触。最后是两层之间的接触,即沥青砂浆与水泥胶浆的接触。
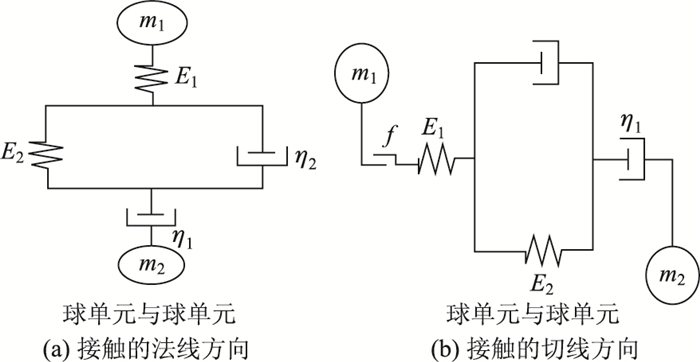
通过上述分析,对接触模型进行简化:沥青砂浆内部的接触采用Burgers黏弹性接触模型,集料与沥青砂浆的接触采用平行黏结模型和Burgers黏弹性接触模型,其余接触均采用平行黏结模型。其中Burgers黏弹性接触模型的设置如图 2所示。
|
| 图 2 Burgers黏弹性接触模型 Fig. 2 Burgers Viscoelastic contact model |
| |
模型的微观参数取值参考了已有的研究成果[15-18],见表 3~表 6。
| 微观 参数 | 密度/ (kg·m-3) | 法向刚度/ (N·m-1) | 切向刚度/ (N·m-1) | 摩擦系数 |
| 取值 | 2 500 | 5×108 | 2×108 | 0.5 |
| 微观 参数 | 平行黏结 | ||||
| 法向刚度/ (Pa·m-1) | 切向刚度/ (Pa·m-1) | 法向强度/ Pa | 切向强度/ Pa | 黏结半径/ mm | |
| 取值 | 2×109 | 2×109 | 2×106 | 1×107 | 0.5 |
| 微观参数 | Maxwell部分 | Kelvin部分 | |||||||
| 法向刚度/ (N·m-1) | 法向黏度/ (Pa·s) | 切向刚度/ (N·m-1) | 切向黏度/ (Pa·s) | 法向刚度/ (N·m-1) | 法向黏度/ (Pa·s) | 切向刚度/ (N·m-1) | 切向黏度/ (Pa·s) | ||
| 取值 | 2×109 | 10×109 | 1×109 | 1.5×109 | 2.3×109 | 11×109 | 1.2×109 | 1×109 | |
| 微观参数 | 平行黏结 | ||||
| 法向刚度/ (Pa·m-1) | 切向刚度/ (Pa·m-1) | 法向强 度/Pa | 切向强 度/Pa | 黏结半 径/mm | |
| 取值 | 3×1010 | 3×1010 | 2.3×106 | 1.7×107 | 0.5 |
3 加载模式
首先对模型进行伺服控制,模拟外界大气压强,使模型受力更加符合实际。然后用3个刚度较大的球形颗粒表征支座和加载装置,如图 3所示,表征支座的两个球形颗粒保持静止状态,对模型顶面表征加载装置的球形颗粒施加一个竖直向下的速度,加载速率为1 mm/s。

|
| 图 3 加载模式 Fig. 3 Loading mode |
| |
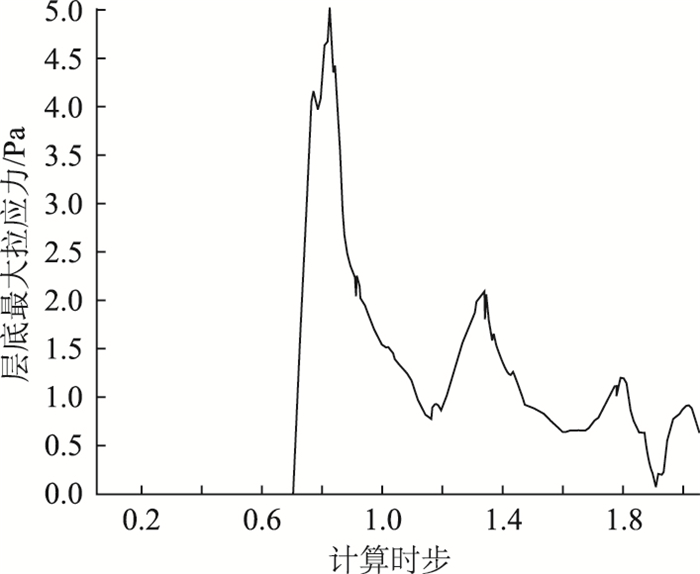
在模型中间的底部设置一个半径为1 cm的测量圆,对模型的应力进行监测,采集得到小梁跨中层底应力与计算时步关系曲线,如图 4所示。
|
| 图 4 应力与计算时步关系曲线 Fig. 4 Curve of stress vs. time step |
| |
从图 4可以看出:在计算时步达到0.7×106之前,应力都是0,这是因为加载装置还没有接触到试件顶面。当计算时步达到0.7×106时,应力快速地增大; 当计算时步达到0.84×106左右时,应力达到最大值5.0×105 Pa,然后应力大幅减小。因为加载速度是恒定的,随着计算时步的不断增加,应力又反复增大减小几次,这个过程中产生了更多的裂缝。
图 5是破坏后的模型,可以看出试件破坏后,有一条贯穿试件的主裂缝。裂缝发生的位置大部分是在沥青砂浆和水泥胶浆处,因为集料的刚度和强度高于沥青砂浆和水泥胶浆;也有部分裂纹发生在集料内部,这是因为使用Cluster理论进行聚粒操作,将代表集料的颗粒组合在一起,Cluster允许集料内部发生破坏,这更加符合室内试验规律。在沥青混合料与水泥稳定碎石中间的界面处,有一段水平裂纹,这是由于两层材料力学性质不相同,该层间界面成为一个薄弱环节,在水平剪力作用下,发生裂纹,这一现象在一定程度上符合实际路面的破坏状态,即层间脱空,界面处发生水平位移,严重的还会造成推挤、拥包等病害。

|
| 图 5 破坏后的模型 Fig. 5 Broken model |
| |
4 实验室对比试验
为了将数值模拟结果与实验室试验结果进行对比分析,在实验室进行了室内试验,半刚性基层选用水泥稳定碎石,沥青面层选用AC-20,透层采用阳离子乳化沥青并加铺ES-2型稀浆封层,沥青混合料和水泥稳定碎石的集料级配见表 1和表 2,由马歇尔试验确定该AC-20的最佳油石比为4.3%。由自制模具成型后,将试件切割成70 mm×100 mm×240 mm的小梁[19]。在与数值模拟相同的加载条件下进行三点弯曲试验,强度计算公式如下:
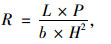
|
(1) |
式中,R为试件破坏时的三点弯曲强度;P为试件破坏时的最大荷载;b为试件的宽度;H为试件的高度;L为梁的跨度。
得到的试验结果如表 7所示。
| 试件编号 | 极限承载力/N | 应力强度/MPa | |||
| 单值 | 均值 | 单值 | 均值 | ||
| 1 | 1 934 | 1 936 | 0.55 | 0.55 | |
| 2 | 1 897 | 0.54 | |||
| 3 | 1 889 | 0.54 | |||
| 4 | 1 972 | 0.56 | |||
| 5 | 1 979 | 0.57 | |||
| 6 | 1 903 | 0.54 | |||
| 7 | 1 983 | 0.57 | |||
| 8 | 1 987 | 0.57 | |||
| 9 | 1 880 | 0.54 | |||
由表 7可以看到,用离散元数值模拟得到的试件破坏时的最大应力与实验室实测的应力相差不大,表明了用二维离散元方法可以很好地模拟沥青混合料三点弯曲试验,验证了本研究二维离散元模型虚拟试验的正确性。
5 结论基于二维离散元程序,对半刚性基层沥青路面结构建立了三点弯曲虚拟试验模型。
同步进行了室内试验,将虚拟试验结果与室内试验结果进行比较,验证了二维离散元模型虚拟试验的正确性。
离散元模型很好地监测了微裂纹的产生和扩展情况,弥补了实测试验肉眼观测的不足,为研究沥青混合料开裂时的层底应力变化和裂纹发展规律提供了辅助手段。
本研究采用的材料为AC-20和水泥稳定碎石,该二维离散元模型是否能用于其他沥青混合料或其他半刚性材料,还有待进一步研究。
| [1] |
万成, 张肖宁, 王邵怀. 基于X-CT技术的沥青混合料三维数值化试样重建[J]. 公路交通科技, 2010, 27(11): 33-37. WAN Cheng, ZHANG Xiao-ning, WANG Shao-huai. Reconstruction of 3D Digital Specimen of Asphalt Mixture Based on X-CT Technology[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11): 33-37. |
| [2] |
SHU X, HUANG B. Dynamic Modulus Prediction of HMA Mixtures Based on the Viscoelastic Micromechanical Model[J]. Journal of Materials in Civil Engineering, 2008, 20(8): 530-538. |
| [3] |
朱兴一, 黄志义, 陈伟球. 基于复合材料细观力学模型的沥青混凝土弹性模量预测[J]. 中国公路学报, 2010, 23(3): 30-34. ZHU Xing-yi, HUANG Zhi-yi, CHEN Wei-qiu. Elastic Modulus Prediction of Asphalt Concrete Based on Composite Material Micromechanics Model[J]. China Journal of Highway and Transport, 2010, 23(3): 30-34. |
| [4] |
李自林, 龚能飞, 栾小兵. 半刚性基层沥青路面温缩型反射裂缝的扩展机理分析[J]. 公路交通科技, 2008, 25(1): 43-46. LI Zi-lin, GONG Neng-fei, LUAN Xiao-bing. Elastic Modulus Prediction of Asphalt Concrete Based on Composite Material Micromechanics Model[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 43-46. |
| [5] |
肖昭然, 胡霞光, 刘玉. 沥青混合料细观结构离散元分析[J]. 公路, 2007(4): 145-148. XIAO Zhao-ran, HU Xia-guang, LIU Yu. Discrete Element Method Analysis for Micro Structure of Asphalt Mixtures[J]. Highway, 2007(4): 145-148. |
| [6] |
胡霞光. 沥青混合料微观力学分析综述[J]. 长安大学学报:自然科学版, 2005, 25(2): 6-9. HU Xia-guang. Review on Asphalt Mixture Micromechanics Analysis[J]. Journal of Chang'an University:Natural Science Edition, 2005, 25(2): 6-9. |
| [7] |
方韬, 龚顺风, 金伟良. 混凝土结构破坏过程的离散单元法模拟[J]. 浙江大学学报:工学版, 2004, 38(7): 921-925. FANG Tao, GONG Shun-feng, JIN Wei-liang. Failure Process Simulation of Concrete Structures by Discrete Element Method[J]. Journal of Zhejiang University:Engineering Science Edition, 2004, 38(7): 921-925. |
| [8] |
KIM H, WAGONER M P, BUTTLAR W. Simulation of Fracture Behavior in Asphalt Concrete Using a Heterogeneous Cohesive Zone Discrete Element Model[J]. Journal of Materials in Civil Engineering, 2008, 20(8): 552-563. |
| [9] |
MAHMOUD E, MASAD E, NAZARIAN S. Discrete Element Analysis of the Influences of Aggregate Properties and Internal Structure on Fracture in Asphalt Mixtures[J]. Journal of Materials in Civil Engineering, 2010, 22(1): 10-20. |
| [10] |
KUTAY M E, ADHIKARI S, YOU Z. Dynamic Modulus Simulation of the Asphalt Concrete Using the X-ray Computed Tomography Images[J]. Materials and Structures, 2009, 42(5): 617-630. |
| [11] |
陈俊, 黄晓明. 基于离散元方法的沥青混凝土断裂机理分析[J]. 北京工业大学学报, 2011, 37(2): 211-216. CHEN Jun, HUANG Xiao-ming. Analysis of Fracture Failure Mechanism of Asphalt Mixture Based on the Discrete Element Method[J]. Journal of Beijing University of Technology, 2011, 37(2): 211-216. |
| [12] |
陈俊, 黄晓明. 基于离散元法的沥青混合料虚拟疲劳试验方法[J]. 吉林大学学报:工学版, 2010, 40(2): 435-440. CHEN Jun, HUANG Xiao-ming. Virtual Fatigue Test of Asphalt Mixture Based on Discrete Element Method[J]. Journal of Jilin University:Engineering and Technology Edition, 2010, 40(2): 435-440. |
| [13] |
YOU Z P, ADHIKARI S, DAI Q L. Three-dimensional Discrete Element Models for Asphalt Mixtures[J]. Journal of Engineering Mechanics, 2008, 134(12): 1053-1062. |
| [14] |
裴建中. 沥青路面细观结构特性与衰变行为[M]. 北京: 科学出版社, 2010. PEI Jian-zhong. Mesostructure Characteristics and Decaying Behavior of Asphalt Pavement[M]. Beijing: Science Press, 2010. |
| [15] |
YOU Z P. Development of a Micromechanical Modeling Approach to Predict Asphalt Mixture Stiffness Using the Discrete Element Method[D]. Urbana-Champaign, US: University of Illinois at Urbana-Champaign, 2003. http://www.researchgate.net/publication/257292391_Development_of_a_micromechanical_modeling_approach_to_predict_asphalt_mixture_stiffness_using_discrete_element_method
|
| [16] |
ABBAS R A. Simulation of the Micromechanical Behavior of Asphalt Mixtures Using the Discrete Element Method[D].Pullman: Washington State University, 2004.
|
| [17] |
LIU Y, DAI Q L, YOU Z. Viscoelastic Model for Discrete Element Simulation of Asphalt Mixture[J]. Journal of Engineering Mechanics, 2009, 135(4): 324-333. |
| [18] |
冯师蓉, 胡霞光, 刘玉. 粘弹性材料的离散元数值分析[J]. 公路交通科技, 2008, 25(2): 12-15. FENG Shi-rong, HU Xia-guang, LIU Yu. Numerical Analysis of Viscoelastic Materials Based on Discrete Element Method[J]. Journal of Highway and Transportation Research and Development, 2008, 25(2): 12-15. |
| [19] |
TANG Y, ZHANG K. Analysis on the Fatigue Properties of Semi-rigid Base Asphalt Pavement Structures with Horizontal Interfacial Cracks[J]. Journal of Testing and Evaluation, 2017, 45(6): 2020-2028. |
 2018, Vol. 35
2018, Vol. 35
