扩展功能
文章信息
- 黄育凡, 吴庆雄, 袁辉辉, 陈宝春
- HUANG Yu-fan, WU Qing-xiong, YUAN Hui-hui, CHEN Bao-chun
- 地震作用下钢管混凝土组合桁梁-格构墩轻型桥梁行车安全性分析
- Analysis on Running Safety on Lightweight Bridge with CFST Composite Truss Girder and Lattice Piers under Earthquakes
- 公路交通科技, 2018, 35(11): 77-86
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(11): 77-86
- 10.3969/j.issn.1002-0268.2018.11.010
-
文章历史
- 收稿日期: 2017-11-16
2. 福建省土木工程多灾害防治重点实验室, 福建 福州 350116;
3. 工程结构福建省高校重点实验室, 福建 福州 350116
2. Fujian Provincial Key Laboratory on Multi-disasters Prevention and Mitigation in Civil Engineering, Fuzhou Fujian 350116, China;
3. Key Laboratory of Engineering Structure of Fujian Province University, Fuzhou Fujian 350116, China
中国西南部地区山高谷深、地形地貌多变,且处于地震带,地壳运动相对频繁,这些都对桥梁设计提出了更高要求。数据统计分析表明,该地区已建成或在建的高等级公路桥梁中,墩高超过40 m的高墩桥梁占比超过了40%[1]。我国桥梁设计者创新地将钢管混凝土高墩和钢管混凝土桁架梁通过合理、科学地组合,设计出一种钢管混凝土组合桁梁-格构墩轻型桥梁,国内第一座采用这一桥型是位于四川省雅泸高速公路上的干海子特大桥。
相关学者近年来开展了一系列关于干海子特大桥这一新型组合结构桥梁的课题研究,包括钢管混凝土组合桁梁抗弯性能试验研究[2-3],钢管混凝土格构柱和复合柱的静力性能研究[4-7],钢管混凝土格构柱拟静力试验研究[8-9],钢管混凝土组合桁梁-格构墩振动台三台阵试验研究和非线性地震响应分析[10-13]等。研究成果为这一桥型的计算理论和工程实践奠定了基础。
公路桥梁对地震作用下车桥耦合振动研究较少,主要是分别对桥梁抗震和车桥耦合振动进行研究,前者一般不考虑汽车荷载,或者将其作为移动荷载考虑;后者一般不考虑地震作用,仅采用路面不平整度作为激励。
高墩桥梁墩顶横桥向位移和转角在地震、风荷载等作用下较普通桥梁明显,因而行驶在其上的车辆易出现滑移、倾覆等。并且较大的墩顶相对位移容易导致主梁产生较大转角,影响行车舒适性。同时,高墩轻型桥梁的活载与恒载的比重比一般桥梁大得多,使得在进行桥梁动力性能分析时需要考虑桥上车辆质量的影响,这有别于一般桥梁地震反应分析中只考虑桥梁本身反应而不考虑桥上车辆的影响。在地震作用下,高墩轻型桥梁的振动和变形较普通钢筋混凝土梁桥可能更显著。
干海子特大桥采用柔性钢管混凝土高墩,最大墩高达107 m,主梁有可能在地震作用下出现过大的振动和位移,进而影响行车安全。新型结构有其可见的优势,但也可能存在尚未发现的问题,其在地震作用下的行车安全性分析目前未见相关报道。
本研究采用NL_Beam3D双重非线性有限元程序,模拟考虑地震作用下车桥耦合振动,对干海子特大桥第二联进行分析,得到该桥在地震作用下的车桥动力响应并进行行车安全性分析,研究成果可为今后地震作用下高墩轻型桥梁的行车安全性分析提供参考。
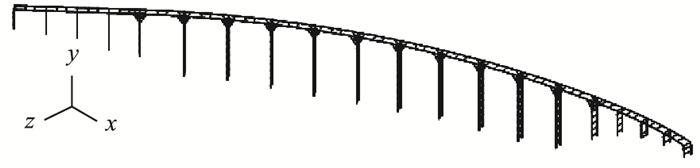
1 工程概况干海子特大桥是四川省雅安经石棉至泸沽高速公路上的一座多跨连续弯梁桥。桥梁总长1 811 m,共计36跨,分为3联,其中第2联的跨径布置为:45.1 m+3×44.5 m+11×62.5 m+3×44.5 m+45.1 m,见图 1。采用钢管混凝土组合桁梁、钢管混凝土格构式高墩的轻型组合结构。

|
| 图 1 干海子特大桥第二联总体布置图(单位:cm) Fig. 1 General layout of Ganhaizi Bridge(unit: cm) |
| |
主梁左右分幅,每幅的钢管混凝土组合桁梁由混凝土顶板,空钢管上弦管、腹杆,和钢管混凝土下弦管组成,在每跨支点和跨中位置加设钢管桁架横梁,以提高主梁截面抗扭性能,见图 2。
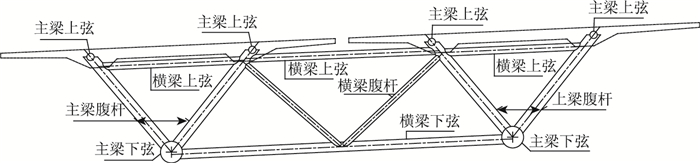
|
| 图 2 主梁横断面构造图 Fig. 2 Cross-section of main girder |
| |
根据不同墩高采用了2种桥墩形式。如图 3所示,钢管混凝土格构墩用于墩高在20~70 m范围,包括14# ~ 15#墩,26# ~ 30#墩;如图 4所示,钢管混凝土复合墩用于墩高在70 m以上范围,包括16#~25#墩。
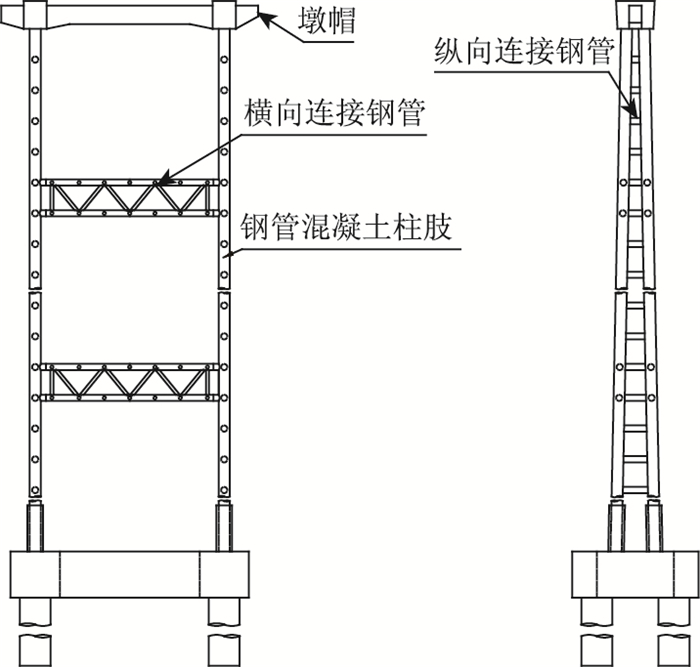
|
| 图 3 钢管混凝土格构墩 Fig. 3 CFST lattice pier |
| |
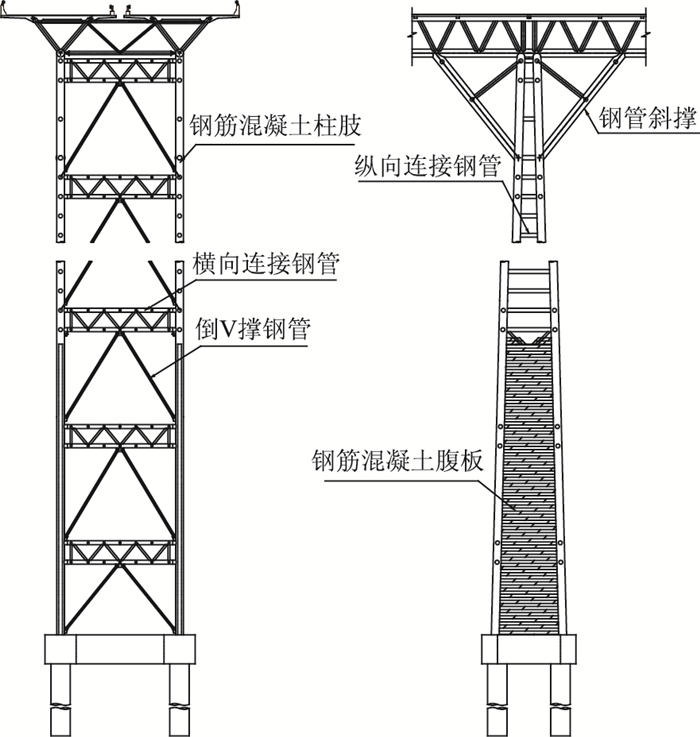
|
| 图 4 钢管混凝土复合墩 Fig. 4 CFST composite pier |
| |
2 地震作用下车桥耦合振动方程
地震作用下车桥耦合振动研究主要包含:(1)车桥系统振动,行车稳定性和安全性;(2)兼顾车桥耦合振动和地震作用的桥梁抗震问题。
考虑路面不平整度的车桥耦合作用计算模型,见文献[14]。考虑路面不平整度的车桥相互作用运动方程[15]为:
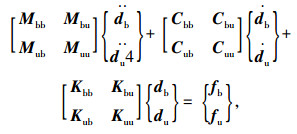
|
(1) |
式中,b为桥梁;u代表车辆;M,C,K分别为车桥系统的质量矩阵、阻尼矩阵和刚度矩阵;db,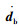
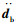
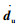
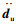
考虑地震作用时,车桥相互作用的运动方程需要在式(1)中添加地震作用力效应fe:
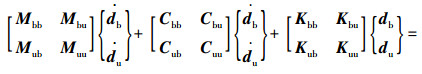
|
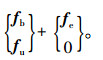
|
(2) |
基于时域分析法求解动力方程式(2),并结合Newmark-β法和Newton法直接积分得到结构动力响应。
有限元计算程序NL_BEAM3D[16-18]分为3个模块:前处理模块、分析计算模块和后处理模块。针对本研究内容,基于NL_BEAM3D现有功能,进行二次开发,使其能够计算考虑地震作用和车桥耦合作用,进而对地震作用下的桥梁行车舒适性进行较为准确的评价。
3 有限元分析 3.1 有限元模型干海子特大桥为多跨长联结构,主梁和桥墩构造复杂,节点众多,难以建立精细有限元模型进行分析。根据文献[12]简化模型的建模思路,将主梁和桥墩的桁式结构简化成单梁结构,从而大幅减少模型节点数量,节省计算时间。简化后的单梁杆系模型见图 5,有1 574个节点,1 873个单元。主梁和桥墩均采用Beam3D梁单元模拟。墩底节点固结,用弹簧单元模拟支座,刚臂单元连接主梁与桥墩;桁梁腹杆、横撑和二期荷载等,以节点质量形式施加于模型相应节点上。通过给主梁施加初始轴力来模拟预应力效应。
|
| 图 5 有限元计算模型 Fig. 5 FE model |
| |
3.2 计算参数 3.2.1 路面平整度
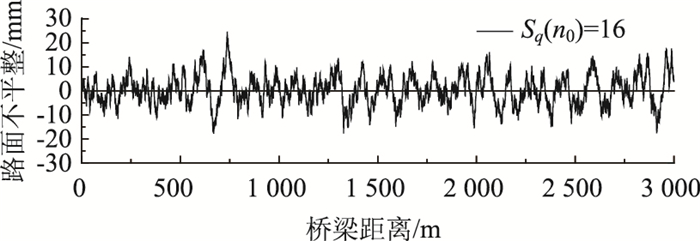
采用AR模型模拟路面平整度[19],路面不平整曲线见图 6,其中,路面总长和间隔分别为3 000 m和dx= 0.2 m,AR模型阶数取M= 2×(15 000)0.5=245,最小路面频率为1/(2dxM)=0.010 2,最大路面频率为1/(2dx)=2.5。路面平整度系数Sq(n0)=16 mm2/m[20]。
|
| 图 6 模拟路面不平整曲线 Fig. 6 Simulated road roughness curve |
| |
3.2.2 车辆模型
计算中平面车辆模型有单轴、双轴等。相对单轴模型,双轴模型更符合车辆的实际荷载分布情况,采用双轴车辆模型可不过高地评价桥梁在移动车辆荷载作用下动力特性[19],故本研究采用四自由度双轴接触的车辆模型,见图 7。在保证车辆总重量和第1阶频率相同的前提下,通过调整其刚度、阻尼,完成四自由度双轴车辆模型的参数设置,车辆参数见表 1。
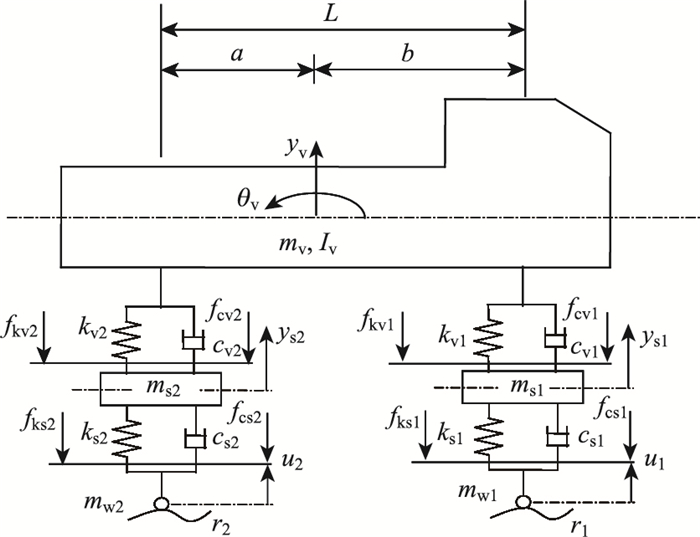
|
| 图 7 四自由度双轴车辆模型 Fig. 7 Bi-axle vehicle model with 4-DOF |
| |
| 参数 | 数值 |
| mv/kg | 18 000 |
| ms1/kg | 400 |
| ms2/kg | 1 600 |
| mw1/kg | 0 |
| mw2/kg | 0 |
| a/m | 2.5 |
| Iv/(kg·m2) | 60 990 |
| kv1/(kN·m) | 1 176 |
| kv2/(kN·m) | 4 704 |
| ks1/(kN·m) | 2 352 |
| ks2/(kN·m) | 9 408 |
| b/m | 1.5 |
| cv1/(kN·s·m-1) | 4.9 |
| cv2/(kN·s·m-1) | 19.6 |
| cs1/(kN·s·m-1) | 5.88 |
| cs2/(kN·s·m-1) | 23.52 |
3.2.3 地震波及输入方向
根据《公路桥梁抗震设计细则》[21]和干海子特大桥设计资料,该桥为B类桥梁,按照8度设防,桥位勘察区一般场地基准期50年超越概率10%的地震峰值加速度A = 0.362g,场地类别Ⅲ类,地震动反应谱特征周期Tg=0.45 s,对应地震基本烈度为Ⅷ度。通过三角级数模型合成[22-23]人工波,模拟地震动作用,如图 8所示,相应的反应谱见图 9。可以看出,E1设计地震动下,地面峰值加速度(PGA)为0.16g。
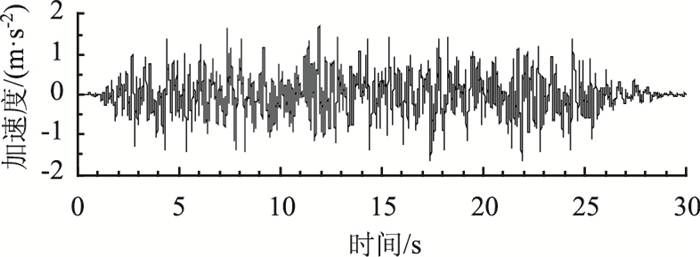
|
| 图 8 拟合E1人工地震波 Fig. 8 Fitting artificial E1 seismic wave |
| |
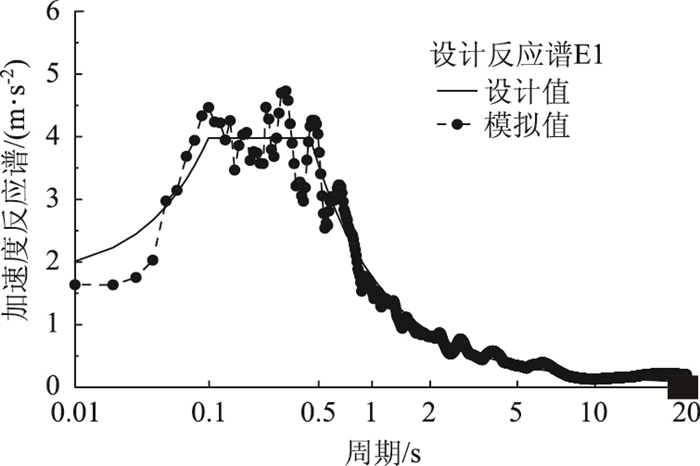
|
| 图 9 E1多遇地震动加速度反应谱 Fig. 9 Acceleration response spectrum of E1 ground motion |
| |
3.3 有限元模型验证 3.3.1 基本动力特性
表 2为有限元计算结果与实桥环境脉动测试得到的结构固有频率。有限元分析与实桥测试所得固有频率吻合良好,误差不超过5%,验证了有限元模型的准确性。
| 模态 | 计算频率/Hz | 实测频率/Hz | 实测值/计算值 |
| 横向一阶 | 0.273 | 0.28 | 1.03 |
| 竖向一阶 | 1.150 | 1.10 | 0.96 |
3.3.2 车辆作用下的动力响应
在不同车速下,有限元计算模型和实桥动载试验所得第20跨(最大跨径,最高墩)跨中最大动挠度对比结果见表 3。可以看出,随着车速的增大,主梁下弦杆动挠度也逐渐增加。计算结果与实测结果也吻合良好,因而进一步验证该有限元模型的准确性,同时证明了该有限元模型能够考虑车桥耦合作用的影响。
| 工况/(km·h-1) | 实测值/mm | 理论值/mm | 实测值/理论值 |
| 20 | 4.7 | 4.6 | 1.02 |
| 30 | 5.0 | 5.1 | 0.98 |
| 40 | 5.3 | 5.4 | 0.98 |
| 50 | 6.3 | 5.5 | 1.15 |
| 60 | 5.6 | 5.8 | 0.97 |
3.3.3 地震作用下动力响应
进行E1多遇地震下桥梁的动力响应研究,将数值模拟得到的20#墩墩顶纵、横桥向位移与缩尺模型振动台试验[10]相应结果进行对比,见图 10。图中上、下时间轴分别对应振动台试验模型和有限元模型的响应时间,地震动持时进行了1/8的缩尺,以满足缩尺模型振动台试验的相似比关系。可以看出,有限元计算得到的实桥在E1多遇地震作用下位移时程曲线与试验得到的数据吻合较好,两者位移满足动力学相似比关系,验证了计算模型和方法的有效性。
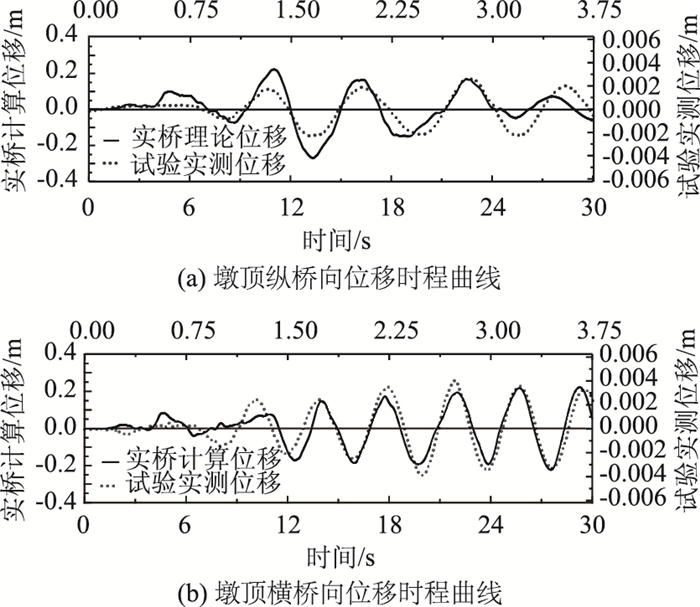
|
| 图 10 位移时程曲线结果对比 Fig. 10 Comparison of displacement time history curves |
| |
4 地震作用下轻型桥梁行车安全性 4.1 行车安全性评价指标
目前暂时没有关于汽车运行安全性评判标准的规范。汽车行驶安全比较冗杂,高墩桥梁墩顶在地震作用下可能出现较大位移,而车辆的走形性容易受相邻墩相对位移的影响,进而可能引起主梁发生较大转角和横向加速度,并导致桥上出现倾覆、滑移等。因此,鉴于高墩桥梁特性,车辆安全性进行评价需同时考虑车辆倾覆指标和桥梁横向变形的影响。
4.1.1 车辆倾覆指标假定车辆不发生变形,即不考虑车辆悬架及轮胎变形。刚性汽车在侧倾平面内的稳态转向模型见图 11。
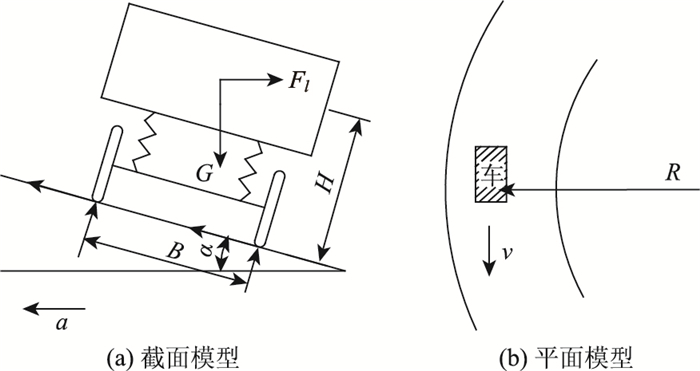
|
| 图 11 车辆受力分析图示 Fig. 11 Force analysis of vehicle |
| |
桥上行车在地震作用下,由于惯性力的作用点高于车轮着地点,当重力对车轮着地点的力矩小于外侧车轮着地点的倾覆力矩时,车辆将存在倾覆隐患。车辆的形状和质心决定了侧向倾覆力矩的大小,将质心高度和轮距分别记为H和B。此时,车辆所受力矩为:
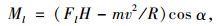
|
(3) |
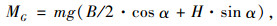
|
(4) |
式中,Ml为倾覆力矩;MG为重力产生的力矩;Fl=ma为惯性力;m为汽车质量;v为车速;R为桥面倾角;g为重力加速度。
汽车在行驶过程中,为了不发生侧倾现象,保持车辆平稳的条件是:
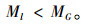
|
(5) |
当桥面倾角很小时,sinα≈α,cosα≈1。弯道半径很大时,1/R≈0,则上式可以简化为:
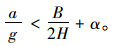
|
(6) |
将车辆由稳定状态过渡到侧倾状态时所受的侧向加速度ay定义成侧倾阈值,见式(7)。
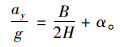
|
(7) |
不同类型汽车在几何尺寸、重心位置、轴距等有所差别,且上述各式也说明不同类型汽车的侧倾阈值不同。文献[24]列出未考虑路面倾角的几种类型汽车侧倾阈值,见表 4。
| 车辆类型 | 轮距/cm | 质心高度/cm | 侧倾阈值/(×g) |
| 重型货车 | 178~183 | 154~216 | 0.4~0.6 |
| 中型货车 | 165~178 | 114~140 | 0.6~0.8 |
| 客货两用车 | 165~178 | 76~102 | 0.8~1.1 |
| 轻型客货两用车 | 165~178 | 76~89 | 0.9~1.1 |
| 豪华轿车 | 154~165 | 51~61 | 1.2~1.6 |
| 微型跑车 | 127~154 | 51~58 | 1.1~1.5 |
| 跑车 | 127~154 | 46~51 | 1.2~1.7 |
4.1.2 桥梁横向变形
我国现有公路桥梁设计规范只限制了主梁竖向挠度,桥墩的变形控制横向变形。
《公路钢管混凝土桥梁设计与施工指南》[25]规定,墩顶水平位移在地震作用下不宜超过:
(1) 在E1多遇地震作用下(按弹性计算)H/300(H为墩高);
(2) 在E2罕遇地震作用下(按弹塑性计算)H/50。
根据上述规定,可得多遇地震下的干海子特大桥第2联墩高及墩顶水平位移限值,见表 5。
| 墩号 | 桥墩与主梁连接形式 | 墩高H/mm | 容许值H/300/mm |
| 14#墩 | 弹性连接 | 34 295 | 114 |
| 15#墩 | 固接 | 60 058 | 200 |
| 16#墩 | 固接 | 95 800 | 320 |
| 17#墩 | 固接 | 104 897 | 350 |
| 18#墩 | 固接 | 105 451 | 352 |
| 19#墩 | 固接 | 103 961 | 347 |
| 20#墩 | 固接 | 107 249 | 358 |
| 21#墩 | 固接 | 107 036 | 357 |
| 22#墩 | 固接 | 105 324 | 351 |
| 23#墩 | 固接 | 102 111 | 340 |
| 24#墩 | 固接 | 96 998 | 323 |
| 25#墩 | 固接 | 95 086 | 317 |
| 26#墩 | 固接 | 67 290 | 224 |
| 27#墩 | 弹性连接 | 54 771 | 183 |
| 28#墩 | 弹性连接 | 42 817 | 143 |
| 29#墩 | 弹性连接 | 32 446 | 108 |
| 30#墩 | 弹性连接 | 26 431 | 88.1 |
4.2 地震作用下轻型桥梁动力响应特性
文献[12]对比分析了桥梁在不同输入方向E1多遇地震动作用下的力学性能变化状况。最不利的地震动输入方向为垂直于连续梁两端点连线方向。
干海子特大桥为曲线梁桥,需要通过单元局部坐标转换得到各个位置的计算结果。具体结果见图 12。
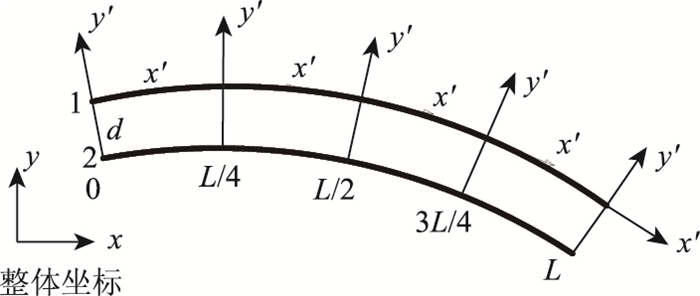
|
| 图 12 单跨桥面平面局部坐标示意图 Fig. 12 Schematic diagram of local coordinate of single span bridge deck 注:L为曲线梁单跨跨径 |
| |
如图 13所示,在进行桥面倾角计算时采用:
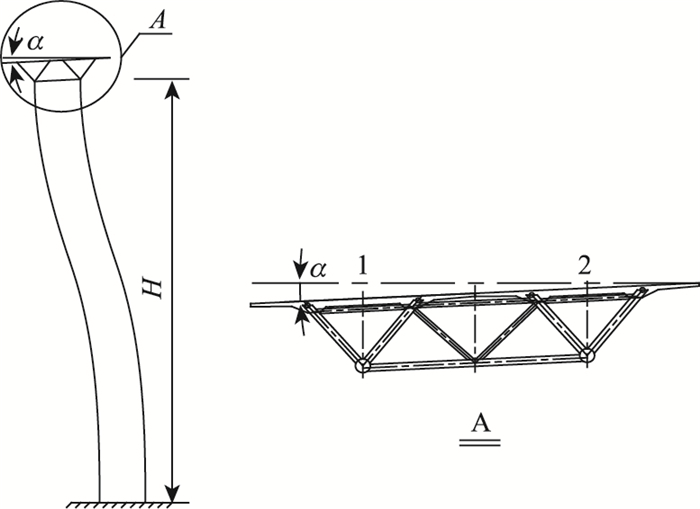
|
| 图 13 桥面倾角计算点示意图 Fig. 13 Schematic diagram of bridge deck inclination angle calculation points |
| |
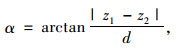
|
(8) |
式中,z1,z2是点1,2的竖向位移;d为点1,2之间的距离。
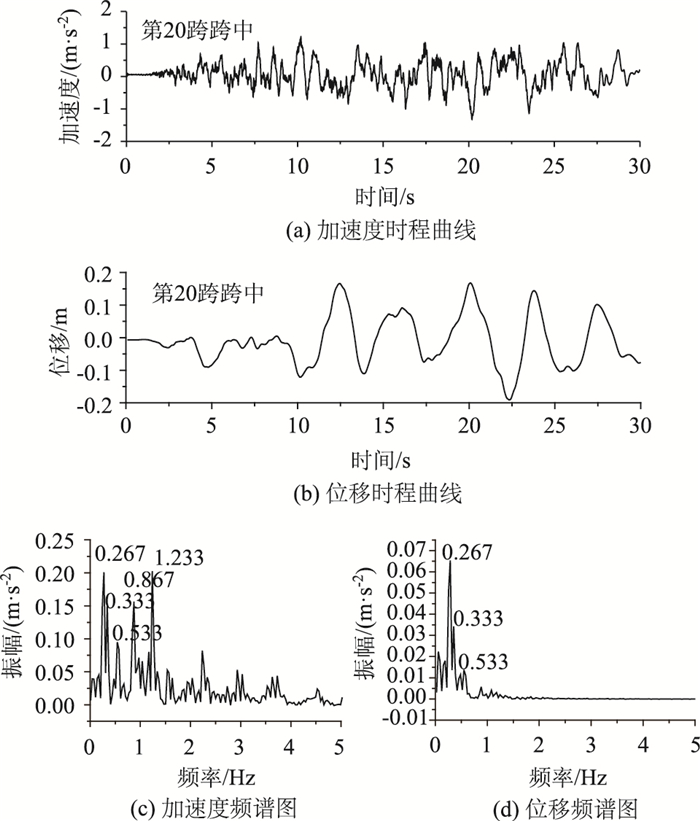
以第20跨跨中截面的结构响应为例,分析桥梁在E1多遇地震作用下的振动特性。
图 14给出了第20跨跨中截面的响应时程曲线及相应的频谱图。可以得到,主梁振动频率在E1多遇地震作用下,主要分布集中在0.267,0.333 Hz和0.533 Hz,分别与主梁的横向1,3,5阶对称频率相接近,即桥梁振动以对称振型为主。
|
| 图 14 第20跨跨中截面时程曲线与频谱图 Fig. 14 Time history curves and spectrogram of mid-span section at 20th span |
| |
各控制截面位置最大动力响应值见图 15。可以看出,E1多遇地震动作用下,各控制截面处桥面倾角均很小,这是由于主梁刚度相对于墩而言大得多,且高而柔的钢管混凝土格构墩能够通过桥墩变形耗散地震作用下的大部分能量。因此,在计算车辆倾覆指标和侧滑指标时可忽略桥面倾角的影响。

|
| 图 15 主梁支座和跨中截面动力响应最大值 Fig. 15 Maximum dynamic responses of main girder support and mid span cross-section |
| |
4.3 行车安全性分析 4.3.1 E1多遇地震作用下行车安全性
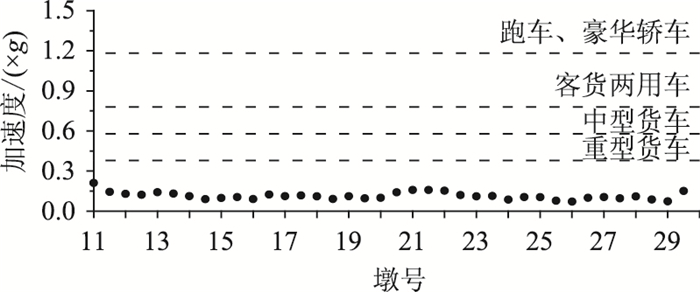
图 16为E1多遇地震动作用下桥面横向最大加速度响应与各种车型的侧倾阈值的比较。最不利的重型货车的倾覆指标阈值大于E1多遇地震时的桥面最大横向加速度,因而桥上行车不会发生侧倾。
|
| 图 16 E1多遇地震动下桥面横向响应与车辆侧倾阈值 Fig. 16 Comparison of transverse responses of bridge deck and vehicle rollover thresholds under E1 ground motion |
| |
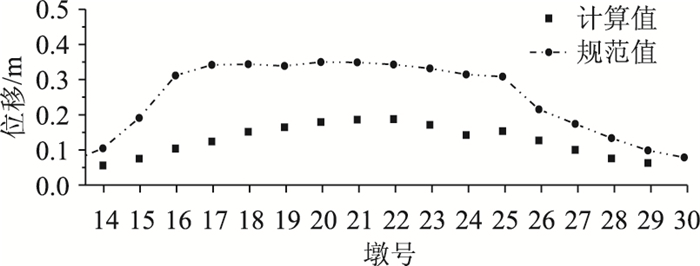
E1多遇地震作用下各墩墩顶最大位移见图 17,各墩墩顶位移均小于指南[25]的限值。因此,E1多遇地震作用下干海子特大桥的行车安全性能良好。
|
| 图 17 E1多遇地震动下墩顶最大横向位移 Fig. 17 Maximum transverse displacements on top of pier under E1 ground motion |
| |
4.3.2 不同地震动强度的行车安全性
强度指标取地面峰值加速度(PGA),按强度调整E1多遇地震波(PGA=0.16g),强度逐级增大,增大量级取0.02g,得到地震强度增大对行车安全的影响趋势。
不同地震动强度下桥面横向响应与车辆侧倾阈值的对比结果见图 18。当PGA=0.32g(2倍E1多遇地震动)时,最大桥面加速度大于侧倾阈值,即重型货车出现侧倾。
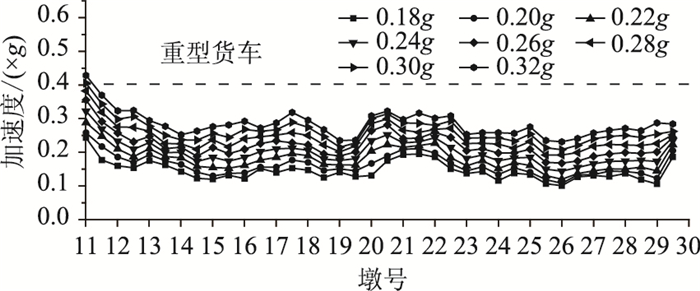
|
| 图 18 不同地震动下桥面横向响应与车辆侧倾阈值 Fig. 18 Transverse responses of bridge deck and vehicle rollover thresholds under different ground motions |
| |
墩顶横向位移响应与指南限值在不同地震强度下的对比分析结果见图 19。当PGA=0.26g(1.6倍E1多遇地震动)时,14#墩和26#~29#墩的墩顶横向位移已超出指南[25]限值。
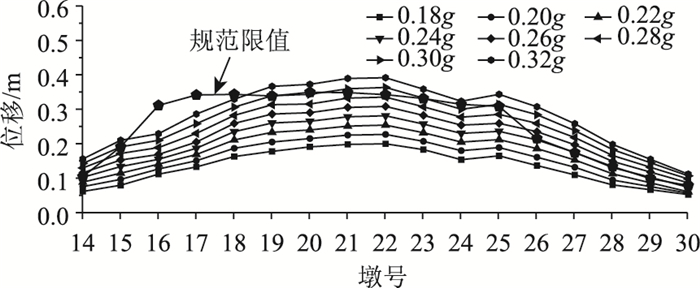
|
| 图 19 不同地震动下墩顶横向最大位移与规范限值比较 Fig. 19 Comparison of maximum transverse displacements on top of pier and limitation under different ground motions |
| |
PGA=0.32g时,墩顶横向位移与墩高比较见表 6。此时,最大墩顶横向位移与墩高间的比例系数达1/198,超过指南[25]限值1/300。因而现有规范对桥墩墩顶位移的限值相对比较保守。
| 墩号 | 墩高H/mm | 位移D/mm | 墩高/位移 |
| 14#墩 | 34 295 | 165 | 208 |
| 15#墩 | 60 058 | 219 | 274 |
| 16#墩 | 95 800 | 238 | 403 |
| 17#墩 | 104 897 | 295 | 356 |
| 18#墩 | 105 451 | 338 | 312 |
| 19#墩 | 103 961 | 375 | 277 |
| 20#墩 | 107 249 | 381 | 281 |
| 21#墩 | 107 036 | 398 | 269 |
| 22#墩 | 105 324 | 400 | 263 |
| 23#墩 | 102 111 | 367 | 278 |
| 24#墩 | 96 998 | 332 | 292 |
| 25#墩 | 95 086 | 352 | 270 |
| 26#墩 | 67 290 | 316 | 213 |
| 27#墩 | 54 771 | 267 | 205 |
| 28#墩 | 42 817 | 207 | 207 |
| 29#墩 | 32 446 | 164 | 198 |
| 30#墩 | 26 431 | 121 | 218 |
5 结论
(1) 建立考虑地震作用的车桥耦合振动方程,并将计算方法添加到已开发的自编程序NL_Beam3D中,实现了地震作用下车桥系统相互作用的耦合计算。
(2) 有限元计算得到的基频与实桥荷载试验得到的结果接近,误差在5%以内;有限元结果与实桥荷载试验的动挠度实测值较接近;与已有振动台试验结果相比,位移时程曲线形状吻合,位移幅值满足相似比关系,验证了计算模型和方法的有效性。
(3) 柔性高墩轻型桥梁对地震波有滤波效应,地震波传至桥面时强度明显减弱。E1多遇地震作用下,最不利的重型货车的倾覆指标阈值大于桥面最大横向加速度,即不存在车辆侧倾现象。墩顶位移满足设计要求。E1多遇地震作用下,干海子特大桥行车安全性能良好。
(4) 地面峰值加速度为0.26g时,14#墩、26#~29#墩的墩顶横向位移已大于《公路钢管混凝土桥梁设计与施工指南》给出的限值;地面峰值加速度为0.32g时,重型货车可能发生倾覆,此时最大墩顶横向位移与墩高之比为1/198,超过指南限值1/300,说明该指南对桥墩墩顶位移的限值规定相对比较保守。
| [1] |
李建中, 宋晓东, 范立础. 桥梁高墩位移延性能力的探讨[J]. 地震工程与工程振动, 2005, 25(1): 43-48. LI Jian-zhong, SONG Xiao-dong, FAN Li-chu. Investigation for Displacement Ductility Capacity of Tall Piers[J]. Earthquake Engineering and Engineering Vibration, 2005, 25(1): 43-48. |
| [2] |
周武.钢管混凝土弦杆-混凝土桥面板组合桁梁静力性能研究[D].福州: 福州大学, 2012. ZHOU Wu. Research on Static Behavior of Composite Truss Girder Structure with CFST Chord and Concrete Slab[D].Fuzhou: Fuzhou University, 2012. |
| [3] |
彭桂翰, 周武, 范碧琨, 等.钢管混凝土组合桁梁受弯性能有限元分析[C]//第二十届全国桥梁学术会议论文集(上册).北京: 人民交通出版社, 2012: 381-387. PENG Gui-han, ZHOU Wu, FAN Bi-kun, et al. Finite Element Analysis of CFST Composite Truss Girder Structure[C]//Proceedings of the 20th National Bridge Academic Conference. Beijing: China Communications Press, 2012: 381-387. |
| [4] |
晏巧玲, 陈宝春, 薛建阳. 钢管混凝土平缀管格构柱换算长细比计算方法[J]. 建筑科学与工程学报, 2016, 33(6): 98-105. YAN Qiao-ling, CHEN Bao-chun, XUE Jian-yang. Calculation Method on Equivalent Slenderness Ratio of Concrete-filled Steel Tube Battened Columns[J]. Journal of Architecture and Civil Engineering, 2016, 33(6): 98-105. |
| [5] |
陈宝春, 晏巧玲, 薛建阳. 钢管混凝土复合短柱轴压性能试验研究[J]. 建筑结构学报, 2016, 37(5): 82-91. CHEN Bao-chun, YAN Qiao-ling, XUE Jian-yang. Experimental Study on Compressive Property of Concrete-filled Steel Tubular Hybrid Stub Columns[J]. Journal of Building Structures, 2016, 37(5): 82-91. |
| [6] |
陈宝春, 晏巧玲, 薛建阳. 钢管混凝土复合柱静力试验与偏心率折减系数计算方法[J]. 建筑结构学报, 2016, 37(5): 92-102. CHEN Bao-chun, YAN Qiao-ling, XUE Jian-yang. Static Test and Calculation Method of Eccentricity Ratio Reduction Coefficient of Concrete-filled Steel Tubular Hybrid Columns[J]. Journal of Building Structures, 2016, 37(5): 92-102. |
| [7] |
晏巧玲, 陈宝春, 薛建阳. 钢管混凝土复合轴压短柱柱肢承载力折减系数[J]. 建筑结构学报, 2013, 34(增1): 294-300. YAN Qiao-ling, CHEN Bao-chun, XUE Jian-yang. Reduction Coefficient of Load Carrying Capacity of Longitudinal Members of Concrete-filled Steel Tubular Composite Strut Columns Subjected to Axial Loads[J]. Journal of Building Structures, 2013, 34(S1): 294-300. |
| [8] |
袁辉辉, 吴庆雄, 陈宝春, 等. 平缀管式等截面钢管混凝土格构柱抗震性能试验与有限元分析[J]. 工程力学, 2016, 33(10): 226-235. YUAN Hui-hui, WU Qing-xiong, CHEN Bao-chun, et al. Aseismic Performance Test and FEM Analysis of Uniform Sectional CFST Lattice Column with Flat Lacing Tubes[J]. Engineering Mechanics, 2016, 33(10): 226-235. |
| [9] |
袁辉辉, 吴庆雄, 陈宝春, 等. 平缀管式等截面钢管混凝土格构柱荷载-位移骨架曲线计算方法[J]. 工程力学, 2016, 33(12): 206-216. YUAN Hui-hui, WU Qing-xiong, CHEN Bao-chun, et al. Calculation Method of Load-displacement Skeleton Curve for Uniform Sectional CFST Lattice Column with Flat Lacing Tube[J]. Engineering Mechanics, 2016, 33(12): 206-216. |
| [10] |
吴庆雄, 黄育凡, 陈宝春. 钢管混凝土组合桁梁-格构墩轻型桥梁振动台阵试验研究[J]. 工程力学, 2014, 31(9): 89-97. WU Qing-xiong, HUANG Yu-fan, CHEN Bao-chun. Shaking Tables Testing Study of Lightweight Bridge with CFST Composite Truss Girder and Lattice Pier[J]. Engineering Mechanics, 2014, 31(9): 89-97. |
| [11] |
HUANG Y F, BRISEGHELLA B, ZORDAN T, et al. Shaking Table Tests for the Evaluation of the Seismic Performance of an Innovative Lightweight Bridge with CFST Composite Truss Girder and Lattice Pier[J]. Engineering Structures, 2014, 75(9): 73-86. |
| [12] |
吴庆雄, 黄育凡, 陈宝春. 钢管混凝土组合桁梁-格构墩轻型桥梁非线性地震响应分析[J]. 工程力学, 2015, 32(12): 90-98. WU Qing-xiong, HUANG Yu-fan, CHEN Bao-chun. Nonlinear Aseismic Performance of Lightweight Bridge with CFST Composite Truss Girder and Lattice Pier[J]. Engineering Mechanics, 2015, 32(12): 90-98. |
| [13] |
王海良, 王世广, 刘中宪, 等. 钢管混凝土空间组合桁架连续梁桥地震响应影响分析[J]. 世界地震工程, 2017, 33(2): 199-210. WANG Hai-liang, WANG Shi-guang, LIU Zhong-xian, et al. Seismic Response Analysis for the CFST and Space Composite Trussed Continuous Bridge[J]. World Earthquake Engineering, 2017, 33(2): 199-210. |
| [14] |
OKABAYASHI T. Mean Square Response Analysis of Highway Bridges under a Single Moving Vehicle[J]. Proceedings of the Japan Society of Civil Engineers, 2010, 1979(286): 15-27. |
| [15] |
吴庆雄, 黄宛昆, 陈宝春. 中、下承式钢管混凝土拱桥车振调查与动力分析[J]. 工程力学, 2013, 30(1): 147-155. WU Qing-xiong, HUANG Wan-kun, CHEN Bao-chun. Vehicle-induced Vibration Research and Dynamic Analysis for Concrete-filled Steel Tubular Arch Bridges[J]. Engineering Mechanics, 2013, 30(1): 147-155. |
| [16] |
吴庆雄, 陈宝春, 韦建刚. 三维杆系结构的几何非线性有限元分析[J]. 工程力学, 2007, 24(12): 19-24, 42. WU Qing-xiong, CHEN Bao-chun, WEI Jian-gang. A Geometric Nonlinear Finite Element Analysis for 3D Framed Structures[J]. Engineering Mechanics, 2007, 24(12): 19-24, 42. |
| [17] |
吴庆雄, 陈宝春, 韦建刚. 钢管混凝土结构材料非线性的一种有限元分析方法[J]. 工程力学, 2008, 25(6): 68-74. WU Qing-xiong, CHEN Bao-chun, WEI Jian-gang. A Finite Element Method for Analyzing Material Nonlinearity of Concrete-filled Steel Tubular Structures[J]. Engineering Mechanics, 2008, 25(6): 68-74. |
| [18] |
吴庆雄, 黄宛昆, 陈宝春. 中、下承式钢管混凝土拱桥面内振动模态分析[J]. 工程力学, 2012, 29(11): 221-227. WU Qing-xiong, HUANG Wan-kun, CHEN Bao-chun. Modal Analysis of In-plane Vibrations for Half-through and Through Concrete-filled Steel Tubular Arch Bridges[J]. Engineering Mechanics, 2012, 29(11): 221-227. |
| [19] |
吴庆雄, 陈宝春, 高桥和雄, 等. 新西海桥的振动特性及舒适性评价研究[J]. 公路交通科技, 2008, 25(5): 61-67. WU Qing-xiong, CHEN Bao-chun, TAKAHASHI K, et al. Vehicle-bridge Dynamic Analysis and Riding Comfort Evaluation of New Saikai Bridge[J]. Journal of Highway and Transportation Research and Development, 2008, 25(5): 61-67. |
| [20] |
GB7031-86, 车辆振动输入路面平度表示方法[S]. GB7031-86, Vehicle Vibration-Describing Method for Road Surface Irregularity[S]. |
| [21] |
JTG/T B02-01-2008, 公路桥梁抗震设计细则[S]. JTG/T B02-01-2008, Guidelines for Seismic Design of Highway Bridges[S]. |
| [22] |
陈永祁, 刘锡荟, 龚思礼. 拟合标准反应谱的人工地震波[J]. 建筑结构学报, 1981, 2(4): 34-43. CHEN Yong-qi, LIU Xi-hui, GONG Si-li. The Artificial Earthquake Ground Motions Compatible with Standard Response Spectra[J]. Journal of Building Structures, 1981, 2(4): 34-43. |
| [23] |
朱东生, 劳远昌, 沈大元, 等. 桥梁地震反应分析中输入地震波的确定[J]. 桥梁建设, 2000(3): 1-4. ZHU Dong-sheng, LAO Yuan-chang, SHEN Da-yuan, et al. Determination of Seismic Waves Introduced into Bridge Seismic Response Analysis[J]. Bridge Construction, 2000(3): 1-4. |
| [24] |
余志生. 汽车理论[M]. 5版. 北京: 机械工业出版社, 2009. YU Zhi-sheng. Automobile Theory[M]. 5th ed. Beijing: China Machine Press, 2009. |
| [25] |
四川省交通厅公路规划勘察设计研究院. 公路钢管混凝土桥梁设计与施工指南[M]. 北京: 人民交通出版社, 2008. Highway Planning Survey and Design Institute of Sichuan Provincial Communications Department. Guide to Design and Construction of Road Steel Tube Concrete Bridge[M]. Beijing: China Communications Press, 2008. |
 2018, Vol. 35
2018, Vol. 35
