扩展功能
文章信息
- 吴安杰, 杨万理, 赵雷
- WU An-jie, YANG Wan-li, ZHAO Lei
- 波流与地震共同作用下跨海斜拉桥动力反应研究
- Analysis on Dynamic Response of Sea-crossing Cable-stayed Bridge under Action of Wave Current and Earthquake
- 公路交通科技, 2018, 35(11): 69-76
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(11): 69-76
- 10.3969/j.issn.1002-0268.2018.11.009
-
文章历史
- 收稿日期: 2017-07-31
2. 西南交通大学 土木工程学院, 四川 成都 610031
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China
我国海域辽阔,海岸线蜿蜒绵长,近年来在沿海修建了许多跨海桥梁,因临近环太平洋地震带,这些桥址区常有地震活动。虽然目前还没有证据显示地震动水力会直接导致桥梁破坏,但已有大量研究表明动水力会对桥梁动力响应产生较大的影响,而这种影响往往不容忽视[1-6]。除了地震激励产生的动水力外,波浪、水流以动力荷载形式作用于桥墩,同样也会引起动水力。在各种动水力作用叠加及相互影响下,桥梁结构受力异常复杂[7]。
最初的莫里森(Morison)方程[8]只用来计算立于水中刚性桩柱的波浪力,后来,Penzien和Kaul[1]将Morison方程应用于计算水中结构地震动水压力。Yang和Li[9]将Morison方程进行扩展,用于计算圆形和矩形空心墩内域的附加动水压力。李悦和宋波[10]将Morison方程项中的非线性项线性化,提出了一种动水力简化计算方法,并以南京长江三桥为应用背景,表明动水对斜拉桥地震反应有显著的影响,且这种影响不容忽视。
由于开展大型水下振动台试验存在诸多困难,目前对于深水结构在多灾害荷载作用下的研究主要还是借助理论和数值分析手段。李忠献和黄信[11]采用绕射波浪理论考虑波浪作用,辐射波浪理论考虑地震动水压力,通过自编程序,分析了某桥墩在地震和波浪联合作用下动力响应,表明波浪和地震联合作用时桥墩的动力响应并不是两者单独作用下动力响应幅值的简单累加。袁卫国和刘沐宇[12]利用ANSYS建立了湛江东海岛大桥桥墩有限元模型,研究表明:与不考虑波浪荷载相比,波浪和地震同时作用下的桥梁桩顶水平力、桩顶弯矩增大。Lotfollahi等[13]借助Abaqus软件建立了丁坝模型,研究了地震和波浪对沿海防护结构的影响。Kawano等[14]通过随机理论研究了随机海浪和强震对海洋平台的作用,研究表明较小的随机海浪可以提高海洋结构的抗震性能。
我国开展深水桥梁研究工作较晚,新修建的跨海大桥以斜拉桥居多,服役时间短,其可靠性还未能在实际强震中得到直接检验。本研究开展大跨度跨海斜拉桥在波浪、水流、地震灾害荷载作用下的动力响应研究,对指导该类桥的设计是有意义的。
1 波流与地震作用下跨海斜拉桥动力分析方法及模型 1.1 水-结构体系动力平衡方程当桥梁结构处于海洋环境中,受到波浪、水流、地震作用时,可将结构瞬态动力学控制方程细化为:
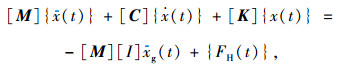
|
(1) |
式中,[M],[C],[K]分别为结构的质量矩阵、阻尼矩阵和刚度矩阵;
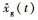
根据Morison修正公式[1, 15],动水力FH(t)的表达式为:

|
(2) |
其中,
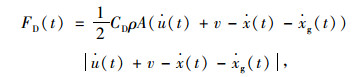
|
(3) |
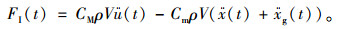
|
(4) |
式(2)右边两项分别为动水力的拖曳力项和惯性力项,
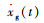
将式(2)~(4)代入式(1)中,即可得波流(行文中将波浪和水流简称为波流)和地震作用下水-结构体系动力平衡方程的具体形式,式中含有非线性项(拖曳力项),给方程求解带来了难度,需借助数值方法来求解,本研究采用ANSYS中的Newmark时间积分法。
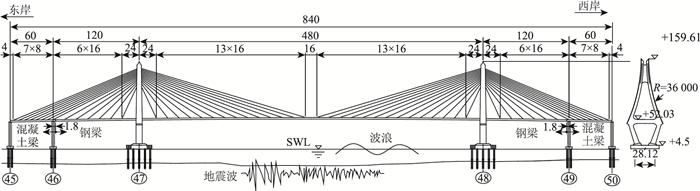
1.2 跨海大桥及有限元数值模型某跨海大桥主桥为(60+120+480+120+60)m双塔双索面钢-混凝土混合梁斜拉桥,如图 1所示。主桥两侧边跨为61.4 m长的预应力混凝土箱梁,单箱三室结构、结构外形与钢箱梁(鱼腹式流线型箱梁)保持一致,桥面宽28.5 m(不含风嘴),梁高3 m。全桥共有斜拉索112根,空间双索面扇形布置,两索面在桥面的横向间距为27.7 m,斜拉索在纵桥向钢梁上索距为16 m,在混凝土梁段上索距为8 m。主塔为大半径曲线火炬状钢筋混凝土结构,单箱单室截面,塔高自承台以上155.1 m。主塔承台平面尺寸47.7 m×29.6 m,尖端型,端部倒圆。主塔(47#、48#)群桩基础采用31根2.5 m钻孔摩擦桩。过渡墩(45#、50#)和辅助墩(46#、49#)采用分离式空心墩及分离式基础。单幅墩基础为4根1.8 m钻孔摩擦桩,承台平面尺寸8.6×8.6 m,四周倒圆角。
|
| 图 1 桥式立面图(单位:m) Fig. 1 Elevation of bridge (unit: m) |
| |
桥位处常水位水深25 m(承台部分淹没在水中),最大通航水位为+4.382 m,即此时水位深29.382 m。根据海况观察资料,波浪有效波高3 m,有效周期6 s,水流速度2 m/s。地震基本烈度7度,按8度设防。
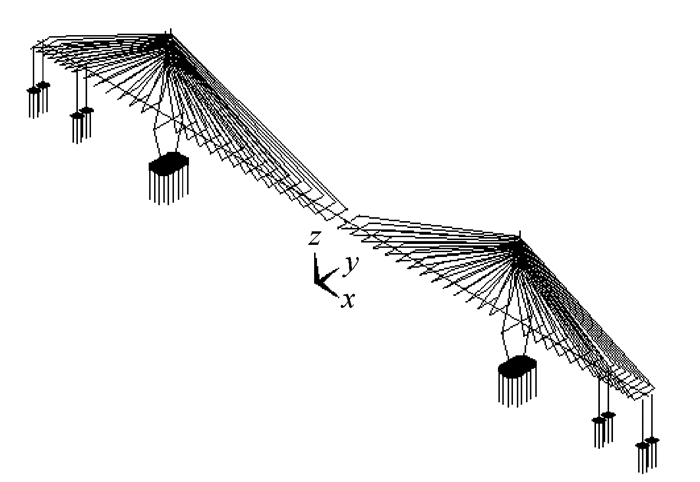
采用ANSYS软件对全桥结构进行有限元离散,单元数共计6 358个,跨海斜拉桥的三维有限元模型见图 2。其中,塔和主梁采用BEAM4单元离散,数值算例表明:BEAM188单元应力对结构划分的单元数量敏感性较大,同等条件下,优选BEAM4单元。主梁采用单梁鱼脊骨式模型,其与斜拉索的连接采用无质量的换算刚臂单元。斜拉索采用LINK10单元模拟,通过等效弹模的Ernst公式来间接修正索垂度非线性效应。引桥压重、桥面铺装和防撞隔离带重量采用质量单元MASS21等效。
|
| 图 2 三维空间有限元模型 Fig. 2 Three-dimensional finite element model |
| |
水中结构采用能够模拟海洋波浪和水流的PIPE59单元,该单元可选择4种波浪理论以及3种波流耦合作用方式,上述所有的流体载荷参数定义,除了在实常数里定义的水动力系数CD, CM等之外,需要在“WATER TABLE”参数表中定义波流要素来实现流体载荷的作用(流体单元详解可参考ANSYS帮助文档),本研究波浪运动描述采用非线性Stokes五阶波。在设计波流要素下,通过波浪弥散关系可求得波长为76.46 m,由于边墩和过渡墩的墩柱以及下面的承台和桩柱均满足D/L<0.2(D为结构迎水面宽度,L为波长),属于小尺度构件,按照我国船检局规范(1982),对于Stokes五阶波,圆形截面桩水动力系数CD, CM值分别取1和2;对于水中非圆形截面构件,将其等效为圆形截面,并考虑形状对水动力系数的影响,边墩和过渡墩处方形截面承台CD,CM值分别取2和2.51,矩形截面墩柱CD,CM值分别取2和2.58。由于主塔下矩形截面承台属于大尺度构件(D/L>0.2, D为承台短边尺寸,这里假定波流沿横桥方向作用),按照文献[16]需对惯性系数CM进行尺度修正,折减系数为0.4,未折减时为2.63,折减后为1.052,目的在于考虑大尺度构件对波浪场绕射影响。假定海流速度沿着水深呈线性变化(水面处最大,海底为0),海水密度取1 030 kg/m3,群桩效应(桩与桩之间的遮蔽和干扰效应)按文献[16]考虑;非水中桩(泥面下)采用PIPE20单元。根据文献[17]规定,本研究采用等效桩法,将土中的桩按6倍桩径取为刚性固定端来近似考虑土对桩的约束边界。计算模型的约束条件如表 1所示。
| 位置 | 线自由度 | 转动自由度 | |||||
| x | y | z | θx | θy | θz | ||
| 桥塔与主梁 | 1 | 1 | 1 | 1 | 0 | 0 | |
| 过渡墩与主梁 | 0 | 1 | 1 | 1 | 0 | 1 | |
| 辅助墩与主梁 | 0 | 0 | 1 | 1 | 0 | 1 | |
| 桩基础底部 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 注:x, y, z分别为顺桥向、横桥向及竖向;“0”代表自由,“1”代表互相约束或固结(桥塔和主梁x方向设置阻尼支座,采用阻尼弹簧约束单元COMBIN39)。 | |||||||
2 跨海斜拉桥动力响应分析
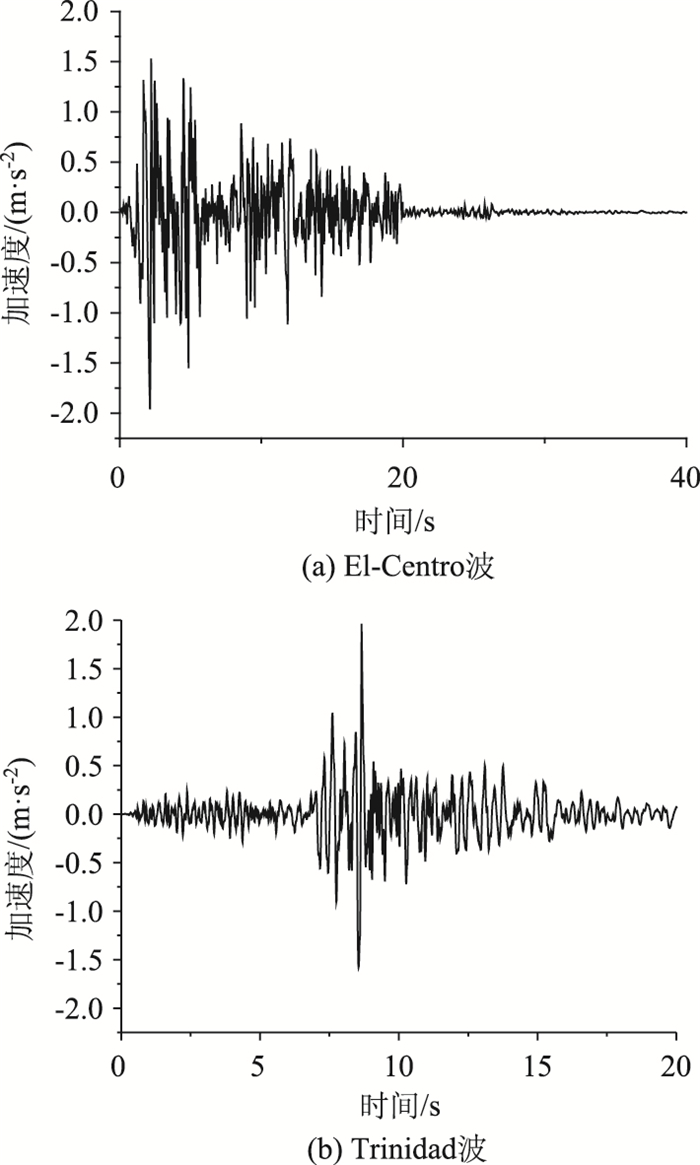
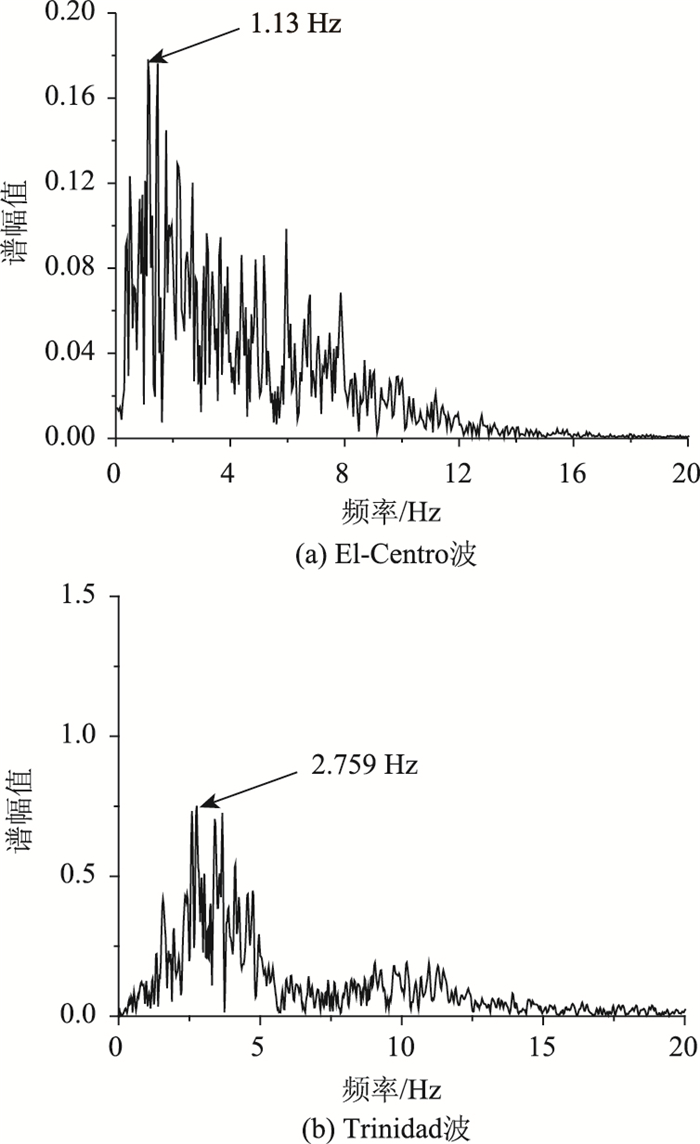
由于地震发生的随机性,按最不利海况,暂定将设计波流要素与地震设防时的加速度进行组合作为荷载分析基本工况,其中波浪、水流方向均沿横桥向,而地震作用与波流同向。选用两条与该桥位场地特性相似的具有一定频谱差异的典型地震波,统一将加速度幅值调整为桥址设计地震强度(地震峰值加速度0.2g)。经幅值和基线调整后的地震波加速度时程曲线如图 3所示,其相应的频谱曲线(傅氏谱)如图 4所示。由频谱图可知,El-Centro波主频小于Trinidad波,频率成分中以低频成分居多。
|
| 图 3 地震波加速度时程 Fig. 3 Seismic wave acceleration time-histories |
| |
|
| 图 4 地震波频谱曲线 Fig. 4 Seismic wave spectral curves |
| |
2.1 动水压力对跨海斜拉桥动力特性及地震响应的影响
通过模态分析,可得出结构的频率与振型,表 2列出了前8阶自振频率和振型。从频率大小来看,基本频率为0.092 835 Hz,频率较低,体现了跨海斜拉桥柔性特点;从振型出现的先后顺序来看,首先出现的振型特征为全桥纵飘,其次是主梁侧弯,最后是主梁竖弯,说明结构刚度在顺桥向较弱,横向刚度小于竖向刚度,这符合斜拉桥大跨度半飘浮体系的特征。定义水对结构频率影响变化率Rcf如下:

|
(5) |
| 频率阶次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 振型描述 | 全桥纵飘 | 主梁一阶对称侧弯 | 主梁一阶反对称侧弯 | 主梁一阶对称竖弯 | 主梁二阶对称侧弯 | 主梁一阶反对称竖弯 | 主梁二阶反对称侧弯 | 过渡墩相向弯曲 |
| 考虑水影响/Hz | 0.092 835 | 0.268 65 | 0.304 78 | 0.321 97 | 0.349 51 | 0.423 43 | 0.450 68 | 0.488 62 |
| 不考虑水影响/Hz | 0.092 836 | 0.269 22 | 0.305 93 | 0.321 97 | 0.350 72 | 0.423 53 | 0.454 38 | 0.496 16 |
| 频率变化率/% | -0.001 | -0.212 | -0.376 | 0.000 | -0.345 | -0.024 | -0.814 | -1.520 |
从水对结构动力特性影响的角度看:有水相比无水情况,前8阶结构振型出现的先后顺序没有变化,频率大小略有变化(减小),但不明显。在前100阶范围,常水位中自振频率最大降幅为13.4%,即使在最高通航水位下自振频率降幅不超过15%,说明水对跨海斜拉桥自振特性影响不显著,这主要是因为水对结构频率的影响主要体现在附加水质量上(假定附加水阻尼较小),然而下部结构水中附加质量相比整个跨海斜拉桥结构本身质量是一个小量,所以频率变化影响不明显。相对而言,水对该桥横向频率影响大于竖向和纵向频率,对高频影响大于低频,这与结构各向刚度大小以及水直接接触构件而产生的附加水质量在水-结构体系中各分配比例有关。
从表 3可知,相对无水情况,桥梁结构在有水环境中(静水中,没有考虑波流)地震反应有所增大,塔顶最大相对位移增幅25.0%,主梁跨中最大相对位移增幅17.1%,塔根最大弯矩增幅10.4%,主梁钢-混凝土结合处最大应力(轴向应力+弯曲应力)增幅27.6%。动水压力对地震响应影响程度大小因地震波类型不同而有所差异,地震激励频率较大时,动水压力的影响程度稍大。当地震激励频率变化时,则结构与水质点相对运动速度和加速度变化,从而影响结构总动水压力大小。
| 计算工况 | 动力响应 | ||||||||||
| 塔顶位移/cm | 主梁跨中位移/cm | 塔根弯矩/(MN·m) | 主梁钢-混凝土结合处应力/MPa | ||||||||
| El-Centro | Trinidad | El-Centro | Trinidad | El-Centro | Trinidad | El-Centro | Trinidad | ||||
| 无水 | 14.1 | 1.6 | 35.1 | 3.5 | 20.12 | 2.02 | 0.548 | 0.058 | |||
| 有水(常水位) | 15.7 | 2.0 | 38.9 | 4.1 | 22.09 | 2.23 | 0.661 | 0.074 | |||
| 响应变化率/% | 11.3 | 25.0 | 10.8 | 17.1 | 9.8 | 10.4 | 20.6 | 27.6 | |||
通过比较,我们可以了解到,水有降低跨海斜拉桥结构频率而增大其地震响应的作用,对地震响应的影响程度要大于对结构动力特性的影响。这一点与文献[18]中讨论的连续刚构桥结论一致。已有研究表明,水的深度对桥梁结构特性和地震响应有影响[2, 18],本研究对此不再做分析。
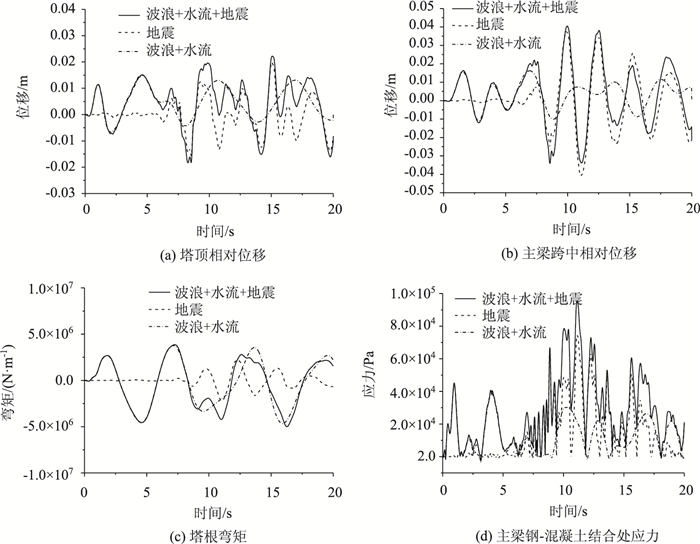
2.2 波流与地震作用下跨海斜拉桥荷载效应波流与地震作用下结构动力响应计算结果如表 4所示,表中响应量为地震持续时间内构件反应的最大幅值,图 5展示了相应的动力反应时程曲线(Trinidad波)。波流对地震响应影响增幅定义为:波流与地震共同作用的响应减去地震响应后与地震响应的百分比。不管是地震单独作用,还是地震与波流共同作用,结构响应峰值并不是出现在地震波加速度峰值对应的时刻(8.6 s),结构动力响应具有滞后现象。当跨海斜拉桥同时受到波流和地震作用时,在地震持续时间内,地震波强度较弱和消退阶段,共同响应主要趋向于波流响应;而在地震波较强和峰值附近,共同响应主要趋向于地震响应。波流与地震作用的总体效应中谁起主要作用,与地震波的幅值、主频、持时,波流参数的流速、波高、周期等都有关。一般而言,任意桥位处的地震加速度特征与波流参数之间没有必然的联系,由于波流荷载大小和地震作用大小之间没有必然的关系,地震、波流作用对结构动力响应贡献大小的比较,需要针对具体的跨海桥梁开展。而在本算例工况下,地震作用的贡献较大。
| 荷载工况 | 动力响应幅值 | ||||||||||
| 塔顶位移/cm | 主梁跨中位移/cm | 塔根弯矩/(MN·m) | 主梁钢-混凝土结合处应力/MPa | ||||||||
| El-Centro | Trinidad | El-Centro | Trinidad | El-Centro | Trinidad | El-Centro | Trinidad | ||||
| 地震 | 15.7 | 1.9 | 38.9 | 4.1 | 22.09 | 2.23 | 0.661 | 0.075 | |||
| 波浪+水流 | 1.5 | 1.5 | 1.6 | 1.6 | 4.67 | 4.67 | 0.044 | 0.044 | |||
| 地震+波浪+水流 | 15.5 | 2.2 | 39.8 | 4.1 | 21.10 | 5.00 | 0.685 | 0.096 | |||
| 波流对地震响应影响增幅/% | -1.3 | 15.8 | 2.3 | 0.0 | -4.5 | 124.2 | 3.6 | 28.0 | |||
| 注:“地震”工况指桥梁在静水中遭受地震作用; “波浪+水流”工况表示波浪和水流联合作用; “地震+波浪+水流”工况表示地震、波浪和水流联合作用。 | |||||||||||
|
| 图 5 波流与地震作用下跨海斜拉桥动力响应时程(Trinidad波) Fig. 5 Dynamic response time-histories of cable-stayed bridge under wave, current and earthquake loads(Trinidad wave) |
| |
从数据表 4可知,波流与地震共同作用时的响应并不是两者单独作用下的响应值的简单累加。共同响应的幅值要小于波流响应幅值和地震响应幅值的直接叠加值。一般当地震峰值力与波流作用同向时,可增大地震响应,反之则削减地震响应幅值,波流对地震响应影响可达124.2%,说明波流荷载对地震响应影响显著,因此,在跨海桥梁抗震分析时,进行波浪、水流与地震联合作用分析是有必要的。
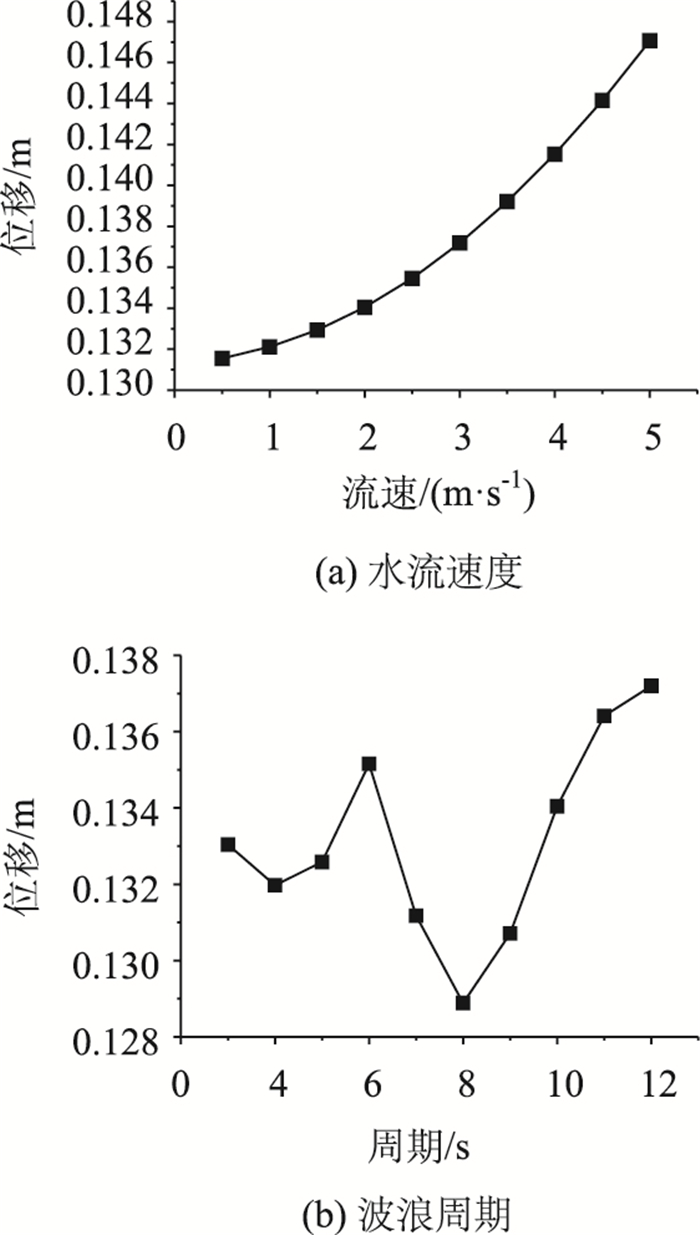
限于篇幅,图 6展示了塔顶位移随水流速度和波浪周期的变化曲线。由图 6(a)可知,波流与地震共同作用下塔顶位移随着水流速度的增大而增大,结构响应与水流速度之间存在明显的非线性关系。我们知道,在线性阶段内,结构响应与地震波加速度是线性关系,而速度与结构响应是平方关系(假设阻尼力系数不变)。波与流之间存在一定的耦合关系,改变流速,必将影响波浪参数,如可能让波长增大等。而波长、波速与波浪力之间又存在非线性关系(Stokes五阶波浪理论),所以这些影响叠加的结果是非线性关系。
|
| 图 6 波流与地震共同作用下塔顶位移随波流参数的变化(El-Centro波) Fig. 6 Pylon top displacement varying with wave-current parameters under action of wave, current and earthquake(El-Centro wave) |
| |
图 6(b)中保持水深不变,波浪振幅不变,那么改变周期,根据色散关系,波长、波数都会相应的改变。而波浪力是与波数、频率相关的。即使是波浪力峰值,也跟波数相关,而这种关系是一种非线性关系。同时改变波浪参数,将会影响水流速度,虽然有时候影响可能不大。那么这些因素叠加的结果是非线性的。另外,波浪周期变化之后,波浪力出现峰值的时刻将发生变化。也就是说,周期变化,波浪力的峰值本身发生变化,波浪力峰值出现的时刻t 也在变化,而不同t时刻对应的结构地震响应是不同的,两者叠加之后将产生毫无规律的峰值。换一个角度说,当波浪周期发生变化时,在结构地震响应峰值时刻对应的波浪力时程曲线上不同点,这些点有可能是峰值,有可能是任意点。并且在不同波浪周期下,波浪力的峰值将是不同的。叠加的结果将显示出强烈的无规律性。
由前面分析可知,结构的基本频率为0.093 Hz,地震主要成分频率为1.13 Hz,地震主频与结构基频相差较远。从图 6(b)可看到,当波浪周期为10.7 s,即频率约为0.093 Hz,与结构基频接近时,结构响应并不最显著,说明地震作用削弱了波浪与结构的共振效应,使单纯波流荷载偏离了结构周期,波流与地震共存场频率介于波流荷载和地震激励主频之间,从而进一步说明波浪、水流与地震三者作用之间存在相互影响。这种影响除了体现在地震激励引起的振荡流场对单纯波流场影响,从而改变波流力本身大小外,还与波流力和地震作用峰值的时间相位差有关。
3 结论(1) 大跨度跨海斜拉桥结构较柔(基本频率较低),水有降低该结构频率而增大其地震响应的作用,水对该跨海斜拉桥自振频率最大降幅为13.4%,最大响应增幅为27.6%,对结构动力特性的影响程度要弱于对地震响应的影响程度。
(2) 一般当地震峰值力与波流作用同向时,可增大地震响应,反之则削减地震响应幅值,地震作用可使单纯波流荷载偏离了结构周期,从而削弱波浪与结构的共振效应,波流与地震联合场频率介于波流荷载和地震激励主频之间。波流对地震响应影响可达124.2%,说明波流荷载对地震响应影响显著。因此,在跨海桥梁抗震分析时,进行波浪、水流与地震联合作用分析是有必要的。
| [1] |
PENZIEN J, KAUL M K. Response of Offshore Towers to Strong Motion Earthquakes[J]. International Journal of Earthquakes Engineering and Structural Dynamics, 1972, 1(1): 55-68. |
| [2] |
黄信, 李忠献. 动水压力作用对深水桥墩地震响应的影响[J]. 土木工程学报, 2011, 44(1): 65-73. HUANG Xin, LI Zhong-xian. Influence of Hydrodynamic Pressure on Seismic Response of Bridge Piers in Deep Water[J]. China Civil Engineering Journal, 2011, 44(1): 65-73. |
| [3] |
郑史雄. 深水桥墩考虑液固相互作用的地震反应分析[J]. 桥梁建设, 1998(1): 52-54. ZHENG Shi-xiong. The Effects of the Fluid-structure Interaction Seismic Response of Bridge Piers[J]. Bridge Construction, 1998(1): 52-54. |
| [4] |
吴安杰, 杨万理, 赵雷. 开孔圆形截面空心桥墩水动力研究[J]. 防灾减灾工程学报, 2017, 37(5): 725-731. WU An-jie, YANG Wan-li, ZHAO Lei. Study on Hydrodynamic Characteristics of Circular Hollow Pier with Holes[J]. Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(5): 725-731. |
| [5] |
杨维博, 巨能攀, 黄健, 等. 地震作用下深水矩形空心桥墩振动特性分析[J]. 安全与环境工程, 2014, 21(5): 33-38. YANG Wei-bo, JU Neng-pan, HUANG Jian, et al. Vibration Characteristic Analysis of Deep-water Rectangular Hollow Pier in Seismic Action[J]. Safety and Environment Engineering, 2014, 21(5): 33-38. |
| [6] |
李悦, 宋波, 黄帅. 地震时作用于深水桥墩上的动水力及对桥墩动力响应的影响[J]. 北京科技大学学报, 2011, 33(3): 388-394. LI Yue, SONG Bo, HUANG Shuai. Hydrodynamic Force and Its Effect on the Dynamic Response of Deep-water Bridge Piers in Earthquake[J]. Journal of University of Science and Technology Beijing, 2011, 33(3): 388-394. |
| [7] |
王志华, 席仁强, 陈国兴. 考虑流固耦合的桥梁桩基地震反应研究现状[J]. 南京工业大学学报:自然科学版, 2009, 31(1): 106-112. WANG Zhi-hua, XI Ren-qiang, CHEN Guo-xing. State of Arts on Response of Bridge of Pile Foundation under Earthquake Excitation[J]. Journal of Nanjing University of Technology:Natural Science Edition, 2009, 31(1): 106-112. |
| [8] |
MORISON J R, O'BRIEN M P, JOHNSON J W, et al. The Force Exerted by Surface Wave on Piles[J]. Journal of Petroleum Technology, 1950, 2(5): 149-154. |
| [9] |
YANG Wan-li, LI Qiao. The Expanded Morion Equation Considering Inner and Outer Water Hydrodynamic Pressure of Hollow Piers[J]. Ocean Engineering, 2013, 69(5): 79-87. |
| [10] |
李悦, 宋波. 动水对斜拉桥结构动力响应影响研究[J]. 土木工程学报, 2010, 43(12): 94-99. LI Yue, SONG Bo. Study of the Effect of Hydrodynamic Force on Cable-stayed Bridges under Earthquake[J]. China Civil Engineering Journal, 2010, 43(12): 94-99. |
| [11] |
李忠献, 黄信. 地震和波浪联合作用下深水桥梁的动力响应[J]. 土木工程学报, 2012, 45(11): 134-140. LI Zhong-xian, HUANG Xin. Dynamic Responses of Bridges in Deep Water under Combined Earthquake and Wave Actions[J]. China Civil Engineering Journal, 2012, 45(11): 134-140. |
| [12] |
袁卫国, 刘沐宇. 波浪和地震作用下的跨海大桥桥墩荷载效应分析[J]. 武汉理工大学学报, 2013, 35(12): 120-124. YUAN Wei-guo, LIU Mu-yu. Load Effect Analysis of Cross-sea Bridge's Pier on the Wave and Earthquake Effect[J]. Journal of Wuhan University of Technology, 2013, 35(12): 120-124. |
| [13] |
LOTFOLLAHI Y M A, AMINFAR M H, LASHTEH N M A, et al. Comparing the Behavior of Groins Constructed in the Estuary of Sefidrood River under the Wave and Earthquake Forces[J]. Water and Soil Science, 2011, 21(2): 1-14. |
| [14] |
KAWANO K, YAMADA Y, LEMURA H, et al. On the Reliability of Offshore Platforms Against Random Sea Waves and Earthquake Motion[J]. Structural Safety Reliability, 2015, 127-134. |
| [15] |
王树青, 梁丙臣. 海洋工程波浪力学[M]. 青岛: 中国海洋大学出版社, 2013. WANG Shu-qing, LIANG Bing-chen. Wave Mechanics for Ocean Engineering[M]. Qingdao: Ocean University of China Press, 2013. |
| [16] |
JTS145-2-2013, 海港水文规范[S]. JTS145-2-2013, Code of Hydrology for Sea Harbor[S]. |
| [17] |
CCS-1992, 海上固定平台入级与建造规范[S]. CCS-1992, Rules for the Classification and Construction of Fixed Offshore Platforms[S]. |
| [18] |
杨万理, 李乔. 动水压力对连续刚构桥梁地震响应的影响[J]. 西南交通大学学报, 2012, 47(3): 373-378. YANG Wan-li, LI Qiao. Effects of Hydrodynamic Pressure on Seismic Response of Continuous Rigid-Framed Bridge[J]. Journal of Southwest Jiaotong University, 2012, 47(3): 373-378. |
 2018, Vol. 35
2018, Vol. 35
