扩展功能
文章信息
- 汪峰, 彭章, 李浩然, 刘章军
- WANG Feng, PENG Zhang, LI Hao-ran, LIU Zhang-jun
- 考虑温度效应的斜拉桥塔-索-主梁耦合振动模型及影响分析
- Analysis on Pylon-cable-girder Coupled Vibration Model and Influence Considering Temperature Effect
- 公路交通科技, 2018, 35(11): 51-60
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(11): 51-60
- 10.3969/j.issn.1002-0268.2018.11.007
-
文章历史
- 收稿日期: 2017-04-27
现代斜拉桥是由斜拉索、桥面梁以及桥塔组合而成大跨度索梁结构。随着桥梁新技术和新材料的应用,现代斜拉桥跨度不断增大,桥塔越来越高耸,加劲梁越来越轻薄,温度变化的影响日益突出[1-3]。在车辆、强风、地震以及温度等复杂环境载荷作用下,大跨度索梁结构易发生大幅振动[4]。强烈振动会导致索梁锚固区出现疲劳裂纹,拉索防腐系统失效等工程病害,严重威胁桥梁使用和安全性能[5]。
针对温度效应对桥梁整体和局部结构振动特性的影响,国内外学者开展了广泛研究。文献[6]结合某斜拉桥实桥温度监测数据,研究了日照温度变化对索力的影响。文献[7]基于斜拉桥拉索有限元模型,分析了温度对拉索振动基频的影响,发现高温和低温均影响拉索的固有频率。文献[8]研究温度变化对拉索索力与频率的影响,通过理论推导得到了考虑温度变化下索力与频率的关系式,发现温度变化明显改变了索力和频率的大小。笔者[9]前期建立了温度场中单根拉索的非线性振动力学模型,研究了温度效应和桥面激励联合作用下拉索的振动响应。文献[10]建立了索梁组合结构的振动模型,研究了温度效应对索梁结构的振动影响,发现温度效应对索梁结构的振动特性影响较大。上述研究可知,温度效应作用下的大跨度索梁组合结构非线性振动特性十分复杂。温度变化不仅改变索力、频率以及振动过程中的分叉现象,引起边界条件变化,而且破坏振动控制的鲁棒性,甚至掩盖结构损伤识别参数以及状态评估[11-12]。
因此,为了进一步揭示斜拉桥在非均匀温度场中的动力行为机理,结合以往的研究成果,假定拉索初始线形为抛物线,考虑拉索几何非线性、阻尼、温度变化以及索梁的边界条件等因素,将桥塔和桥面简化为受轴力作用的Bernoulli-Euler梁,建立热力平衡状态下的桥塔-索-主梁连续耦合非线性振动精细化模型,研究大跨度柔索弹性梁组合结构在温度效应作用下的振动特征。分析结果为大跨度斜拉桥减振和隔震提供理论依据。
1 考虑温度效应的塔-索-主梁连续耦合振动模型考虑温度效应和塔、索和梁的协调振动,建立索梁组合结构耦合振动模型,如图 1所示。

|
| 图 1 热力平衡状态下的塔-索-梁耦合振动模型 Fig. 1 Coupled vibration model of pylon-cable-girder structure under thermodynamic equilibrium state |
| |
现代大跨度斜拉桥常采用半漂浮密索体系,其特点是塔墩固结,主梁在桥墩上设置竖向支撑,成为具有多点弹性支撑的连续梁。因此将桥塔视为一端固结,另一端与拉索铰接的Bernoulli-Euler梁。为了考虑其他拉索对桥塔的扶正作用,用刚度为kt的弹簧作为桥塔顶端的外力边界,并假定塔顶的横向位移W(t);桥梁受到地震、风荷载以及车辆荷载等作用时,主梁会将这些荷载传递至索塔,再通过索塔传至地基,主梁在斜拉索的各点支承作用下,像多跨弹性支承的连续梁,在外激励下易产生纵桥向位移,因此将主梁视为Bernoulli-Euler梁,一端固结边界,另一端受到拉索铰接,其竖向振动位移为vb。拉索与桥塔、主梁铰接,uc和vc分别为纵向和横向的动位移。索梁温差为ΔTcb,各构件参数定义如表 1所示。
| 参数 | 桥塔 | 拉索 | 主梁 |
| 质量 | mt | mc | mb |
| 长度 | lt | lc | lb |
| 阻尼 | ct | cc | cb |
| 弹模 | Et | Ec | Eb |
| 惯性矩 | It | — | Ib |
| 截面积 | — | Ac | Ab |
| 索力 | — | F | — |
| 倾角 | — | θ | — |
| 膨胀系数 | — | αc | αb |
| 初始温度 | — | Tc0 | Tb0 |
| 温度 | — | Tc | Tb |
1.1 基本假定
为了突出问题本质,作如下假设:(1)在弦向方向拉索只受沿索长均匀分布的自重荷载,忽略重力垂度以及热胀冷缩引起的拉索质量重分布;(2)拉索本构关系符合胡克定律,忽略拉索抗弯刚度、抗扭刚度和抗剪刚度的影响。
1.2 拉索热应力平衡状态为计入拉索重力弦向分力的影响,假定斜拉索静态线形为抛物线,其线形方程为:
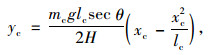
|
(1) |
式中,yc为拉索垂度;H为索力F的水平分力;g为重量加速度;xc为索弦向坐标值。
当环境温度发生改变时,拉索索力、构形也会随之发生改变,此时拉索处于热应力平衡状态,设温度变化引起的拉索索力增量为F′,则拉索热应力平衡方程为:
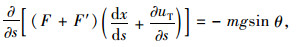
|
(2) |
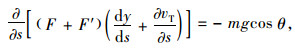
|
(3) |
式中, uT和vT分别为温度变化引起的拉索横向和纵向位移。
联立式(1)、式(2)和式(3)可得:
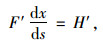
|
(4) |
边界条件为:
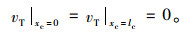
|
(5) |
联立式(3)、式(5)可得:

|
(6) |
由文献[8]可得H′与温度变化的关系:

|
(7) |
其中:
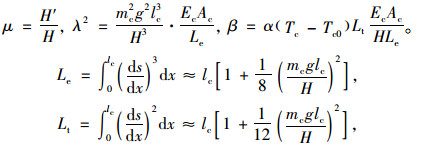
|
式中,μ为温度变化引起的拉索索力的水平增量H′与初始水平索力H的比值;λ为反映拉索几何垂度特性的Irvine参数;β为与温度变化相关的平方非线性项系数。
1.3 热力平衡状态下的拉索振动方程基于达朗贝尔原理,热力平衡状态下的拉索做横向振动时运动微分方程为[9]:
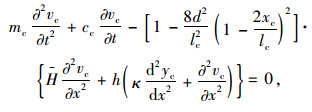
|
(8) |
式中,H为热力平衡状态下拉索水平静张力;h为动张力的水平分力;d为拉索跨中垂度;κ为初始水平索力H与H的比值。静张力和动张力表达式如下:
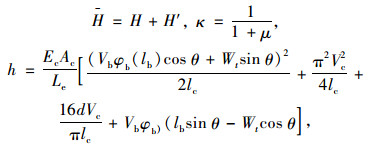
|
式中,φb(lb)为长度为lb的主梁振型。由式(8)可知,拉索运动会受温度变化的影响。研究表明,斜拉索振动时的一阶模态响应占总响应的比例较大[13]。因此,本研究仅考虑拉索的一阶振动模态,斜拉索yc方向振动位移为:
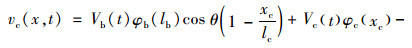
|
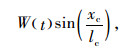
|
(9) |
式中,拉索振型φc(xc)为sin(πxc/lc),Vc为拉索跨中横向振幅。式(9)包含了桥塔和主梁振动引起的位移,因此可考虑桥塔和主梁动态振动引起的索梁组合结构动力学效应。
1.4 主梁振动方程主梁在温度作用下其变形方向上受到多余约束,会产生温度次内力。图 1索梁耦合模型中主梁受到悬臂端以及斜拉索的锚固,形成超静定结构,在温度激励下,主梁将在水平方向产生变形,而在索梁结合处,由于拉索为主梁提供了水平方向的多余约束,限制主梁变形,其受力形式与两端固定的悬臂梁类似,因此温度激励导致梁截面产生温度次应力,设主梁线膨胀系数为αb,则其温度应变为:
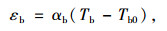
|
(10) |
其温度次内力为:
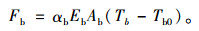
|
(11) |
由于主梁简化为Bernoulli-Euler悬臂梁,基于弯曲理论,其包含轴向力影响的运动方程为:
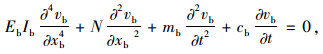
|
(12) |
式中,轴向力N=(H+h)cosθ+Fb,将其位移vb分离变量,且仅考虑它的一阶振动模态:
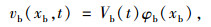
|
(13) |

|
式中,A1, A2, A3, A4为主梁振型函数系数。
将该振型方程代入边界条件可得:

|
βb满足:

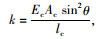
桥塔近似为刚体,抗变形能力强,而拉索和主梁为均轻柔结构,在风雨及车辆荷载作用下,拉索及主梁的振动幅值一般大于桥塔,该耦合结构的能量与整体温度变化无直接相关性,因此忽略温度变化对桥塔的作用效应,设桥塔横向位移为:vt(z, t)=
φt(z)·W(t),振型为: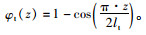
由课题组前期成果[17]可知桥塔动力方程:
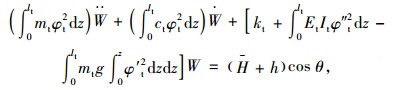
|
(14) |
令: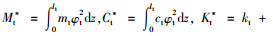
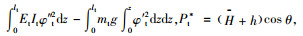
则式(19)可以化简为下面的形式:
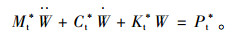
|
(15) |
式中,Mt*,Ct*,Kt*,Pt*分别为主塔的广义质量,广义阻尼,广义刚度和广义力。
1.6 系统耦合振动方程拉索、桥塔和主梁的振动方程分别如式(4)、(13)、(20)所示,可采用伽辽金方法进行方程模态截断,积分后可获得考虑温度效应的索梁组合结构振动方程组:
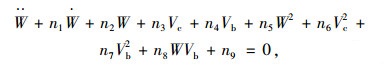
|
(16) |
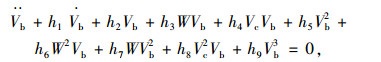
|
(17) |
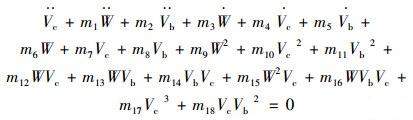
|
(18) |
式中,
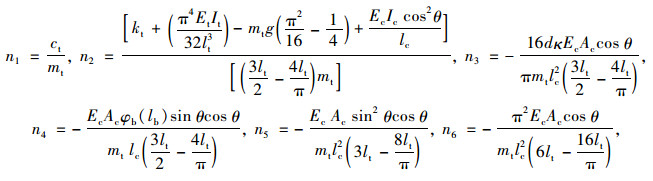
|
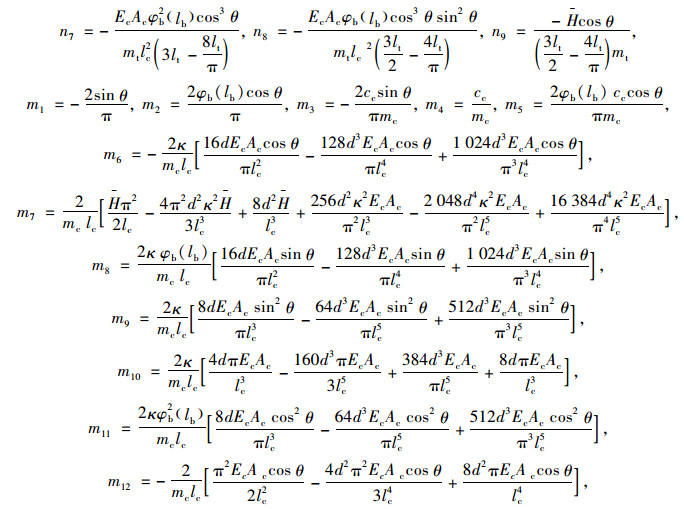
|

|
其中:
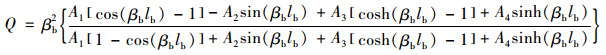
|
桥塔固有频率: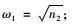
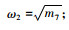
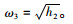
由上述方程组表达式可知,拉索、桥塔和主梁的振动相互耦合,温度影响着拉索和主梁的固有频率,且与温度变化呈非线性关系。
2 耦合振动数值分析上述式(16)、式(17)和式(18)是一组含有多次非线性项的复杂连续耦合振动方程组,其近似解析解可采用摄动法求解。当斜拉索振动频率与桥塔、主梁成一定比例时,端部较小的扰动会导致拉索强烈振动[18],此时解析解将无法掌握更多索梁组合结构的振动信息。因此本研究采用四阶Runge-Kutta法,编制MATLAB程序进行数值分析,研究系统温度变化对索、主梁固有频率的影响,重点分析索梁温差和端部激励联合作用下的超长拉索与主梁频率比为1:1的主共振、1:2的主参数共振的振动响应。
2.1 温度变化对索梁固有频率影响为了研究整体升降温对塔-索-主梁组合结构的频率影响,以武汉某长江大桥为实例进行计算分析。斜拉索阻尼小,柔度大,在外激力作用下,斜拉桥外侧的尾索易发生振动,因此取外侧最长一根拉索,计算参数如表 2所示。基于上述理论,可计算不考虑温度变化与阻尼的情况下,桥塔、拉索以及主梁固有频率分别为ω1=17.791 rad/s,ω2=8.864 rad/s,ω3=8.864 rad/s,塔-索-主梁耦合振动系统的频率比为2:1:1的主共振模式。选取斜拉索和主梁的初始温度为Tc0=Tb0=15 ℃,通过改变拉索温度Tb以及主温度Tc,研究3种不同索力时斜拉索和主梁固有频率随温度变化的规律,结果如图 2所示。
| 项目 | 拉索 | 桥塔 | 主梁 |
| 质量/(kg·m-1) | 80.72 | 3 010 | 878 |
| 长度/m | 292.57 | 165.0 | 242.5 |
| 弹模/Pa | 2.10×1011 | 3.45×1010 | 4×1010 |
| 截面积/m2 | 0.010 2 | — | 23.26 |
| 惯性矩/m4 | — | 5.0 | 26.1 |
| 阻尼 | 0 | 0 | 0 |
| 倾角/(°) | 30 | — | — |
| 张力H/N | 5.5×107 | — | — |
| 弹簧系数/(N·m-1) | — | 3.0×107 | — |
| 线膨胀系数 | 1.89×10-5 | — | 1×10-5 |
| 温度变化/℃ | 0 | — | 0 |
|
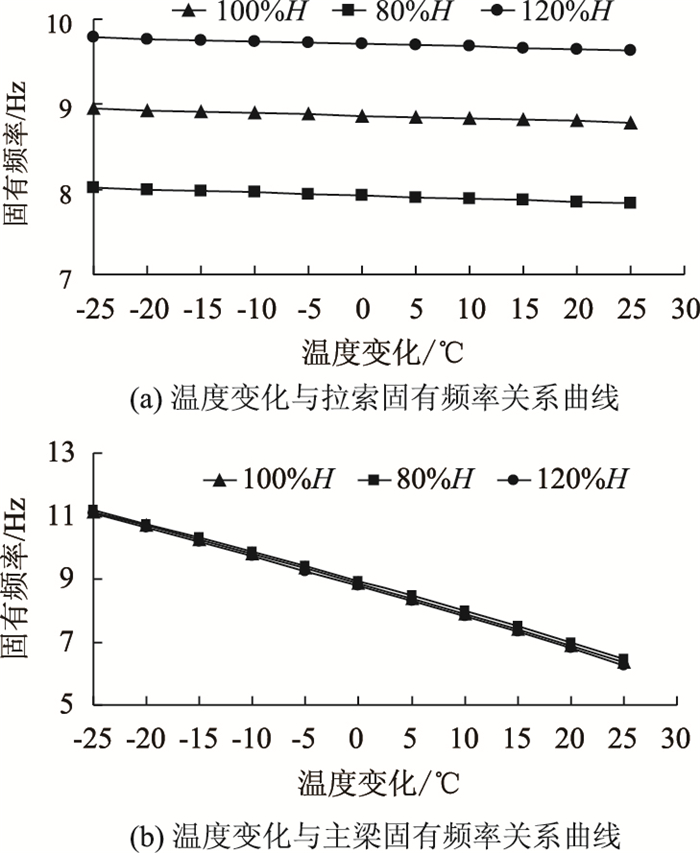
| 图 2 温度变化与结构频率影响关系图 Fig. 2 Natural frequency varying with temperature |
| |
由图 2(a)可知,在塔-索-主梁的频率比为2:1:1主共振模式下,随着温度变化量的增加,3种索力下的拉索固有频率都呈下降趋势,温度变化量每增加5 ℃时,斜拉索固有频率下降0.17%~0.2%;而且温度变化量相同时,3种不同索力下的拉索固有频率变化程度并不相同,由图 2(b)可知,随着温度变化量的增加,主梁固有频率下降较为明显,温度变化量每增加5 ℃,主梁固有频率下降4%~7%。由此可知,温度对拉索、主梁的固有频率影响程度不同,其原因是当温度作为一种激励施加到耦合系统时,主要通过影响拉索的索力和主梁的轴向力来改变其固有频率[19]。将表 2参数带入式(7),拉索、主梁的温度变化取20 ℃,可求得 μ=-0.014 7,即上升20 ℃引起的索力变化量仅占初始索力的1.47%;而主梁的温度次内力由式(11)可得:Fb=4.652×107 N,约占拉索对主梁轴向力的96%,相比而言,温度对拉索索力的影响较小,但对主梁温度次内力较大,故会出现上述现象;对于桥塔的固有频率,根据前面所求的系数n2的表达式,由于无温度项影响,认为桥塔的固有频率保持不变。
针对温度变化对索、梁固有频率的影响,湖南大学赵跃宇团队[6, 18]也展开深入又有趣的讨论。发现拉索一阶反对称模态与温度变化近似为线性关系,在相同温度变化下不同初始张力拉索的模态频率的变化量并不相同;随着温度的上升,梁各阶频率均下降,对于跤支-固支梁,在温度上升约为20 ℃时,梁的一阶频率变化幅度为13.0%。从定性及定量的角度,其结论与本研究分析结果较为吻合,也验证了本研究模型及分析方法的合理性。
2.2 索梁温差对索梁结构振动影响现代斜拉桥斜拉索多由钢缆制成,对温度的敏感性较高,但主梁截面积大,导热较慢,所以在日照不均匀温度作用下,主梁温度变化比拉索温度变化滞后,斜拉索和主梁两种构件间的索梁温差会影响索梁结构的振动响应[19]。
为了研究索梁温差效应对索梁组合结构振动特性的影响,取拉索、主梁以及桥塔的初始位移为0.01 m,三者初始速度为零,初始温度Tc0=Tb0=15 ℃。不考虑索梁温差时,取Tc=Tb=15 ℃,考虑索梁温差时,取Tc=35 ℃,Tb=25 ℃。图 3表示频率比为2:1:1时索、主梁的位移时程曲线。
|
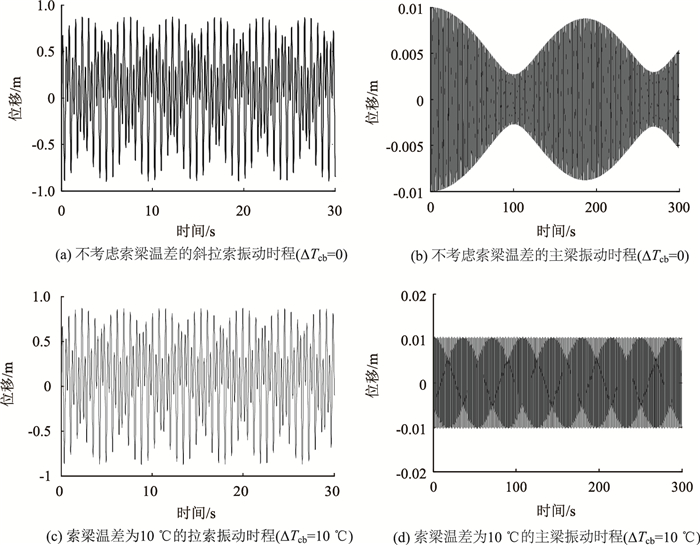
| 图 3 频率比为2:1:1时拉索和桥面位移时程 Fig. 3 Displacement-time curves of cable and deck with frequency ratio of 2:1:1 |
| |
当塔、拉索和桥面梁的频率比为2:1:2的主参数共振时,其余条件不变,可得到图 4所示的位移时程图。
|
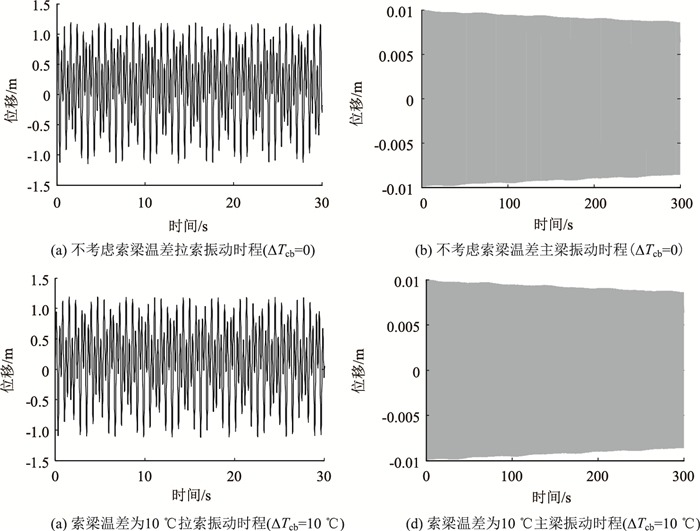
| 图 4 频率比为2:1:2时拉索和桥面的位移时程 Fig. 4 Displacement-time curves of cable and deck with frequency ratio of 2:1:2 |
| |
由图 3(a)、3(b)、图 4(a)及 4(b)可知,在2:1:1的主共振和2:1:2主参数共振模式下,不考虑索梁温差作用时,拉索均由初始位置开始振动,拉索振幅逐渐增大,在较短时间内达到第1个响应峰值分别为0.889 m,1.193 m;与主共振相比,主参数共振时拉索振幅较大,振动频率更快,且拉索振动有明显“拍”特征;桥面与拉索存在强烈的耦合现象,当拉索运动到最大振幅时,桥面则运动到初始位置,二者之间存在此消彼长的能量传递。
由图 3(c)、3(d)、图 4(c)及图 4(d)可知,在考虑索梁温差的主共振和参数共振模式下,拉索也在较短时间内达到第1个响应峰值,分别为0.871 m,1.191 m,拉索振动亦有明显“拍”特征,同样存在能量传递现象,然而主共振模式下主梁振动的“拍”现象并不明显,分析其原因由图 2可知,温度对主梁固有频率有很大影响,引入温度后对主梁的频率改变量较大,此时,拉索主梁的频率比不能满足1:1的比例关系,无法进一步与拉索产生耦合共振,故主梁一直处于平稳振动状态。
对比分析图 3和图 4可知,引入索梁温差后,30 s内拉索出现的波峰数增加,即拍频有所增大,索梁温差和端部激励联合作用下拉索振幅比单一端部激励作用时振幅略微降低,主要原因是拉索的固有频率随着温度的升高变化不大,其非线性没有明显变化。
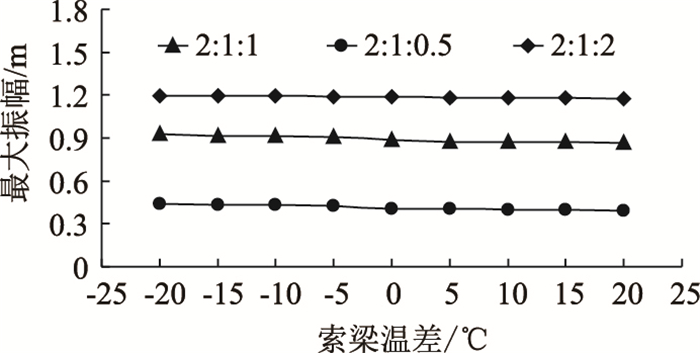
为了进一步说明索梁温差对耦合系统振动特性的影响,使塔、索和梁的频率比为2:1:0.5,拉索处于超谐波共振模式。因拉索导热系数较大,当大气温度变化时,拉索更容易与大气发生热传递,因此设Tc0=Tb0=15 ℃,在升温时,控制主梁温度Tb=20 ℃,降温时,控制主梁温度Tb=10 ℃,通过改变拉索的温度Tc得到不同索梁温差。图 5为不同索梁温对拉索最大振幅和固有频率的影响曲线。
|
| 图 5 不同索梁温差时拉索最大振幅 Fig. 5 Maximum amplitudes of cable with different temperature differences between cable and deck |
| |
由图 5可知,斜拉索在3种振动模式下,频率比为2:1:2时其振幅最大,2:1:1次之,2:1:0.5的振幅最小。随着气温上升,正索梁温差进一步扩大,拉索最大振幅呈现非线性减小趋势;当持续降温时,随着负索梁温差的扩大,拉索最大振幅均呈现非线性增大趋势;且2:1:2时拉索的振幅变化速率最小。
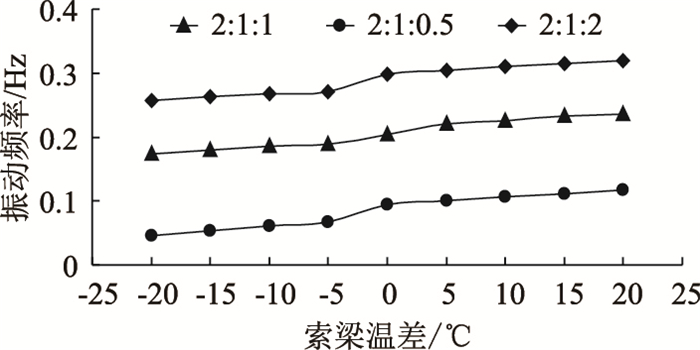
由图 6可知,斜拉索的振动频率随着正索梁温差的增大呈非线性增大趋势,随负索梁温差的增大呈非线性减小趋势,其中索梁温差从0到-5 ℃时,频率变化速率较快,分别达到7.4%,28.5%,9.2%,即在主梁低频激励的超谐波共振模式下,索梁温差对拉索的振动频率影响较大。因此,在大跨度斜拉桥斜拉索的抑振与控制设计中,建议考虑索梁温差影响。
|
| 图 6 不同索梁温差时拉索振动频率 Fig. 6 Vibration frequencies of cables with different temperature differences between cable and deck |
| |
3 结论
基于索梁热力平衡状态,建立了考虑温度效应的斜拉桥塔-索-主梁连续结构耦合振动模型,研究了温度效应对大跨度索梁组合结构振动的影响,得到如下结论:
(1) 温度效应对拉索和主梁的固有频率影响程度不同;在主共振模式下,温度对主梁固有频率的影响较大,平均每升高5 ℃,固有频率下降4%~7%;但对拉索固有频率影响较小,每升高5 ℃,其固有频率下降0.17%~0.2%;
(2) 相比于单一端部激励作用,索梁温差与端部激励联合作用下,拉索振动振幅降低,但拍频增大;考虑索梁温差的拉索主共振和参数共振具有明显“拍”特征,且索和主梁之间存在此起彼伏的能量传递;
(3) 随着正索梁温差逐渐增大,拉索最大响应振幅逐渐减小,振动频率增大;随着负索梁温差逐渐增大,拉索最大响应振幅逐渐增大,振动频率减小,其中索梁温差对参数共振的振幅、振动频率影响最小,对主梁低频激励的超谐波共振模式的影响最为显著。
| [1] |
王高新, 丁幼亮, 王晓晶, 等. 苏通大桥扁平钢箱梁温度场长期监测与统计分析[J]. 公路交通科技, 2014, 31(2): 69-73. WANG Gao-xin, DING You-liang, WANG Xiao-jing, et al. Long-term Monitoring and Statistical Analysis of Temperature Field of Flat Steel-box Girder of Sutong Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(2): 69-73. |
| [2] |
刘扬, 肖新辉. 寒流作用下钢管混凝土高墩温度场观测与效应分析[J]. 公路交通科技, 2011, 28(7): 61-66. LIU Yang, XIAO Xin-hui. Observation and Analysis of Temperature Effect of CFST High-rise Pier under Cold Current Effect[J]. Journal of Highway and Transportation Research and Development, 2011, 28(7): 61-66. |
| [3] |
DENG H Q, LI T J, XUE B J. Analysis of Thermally Induced Vibration of Cable-beam Structures[J]. Structural Engineering and Mechanics, 2015, 53(3): 443-453. |
| [4] |
MATSUMOTO M, SHIRAISHI N, SHIRATO H. Rain-wind Induced Vibration of Cables of Cable-stayed Bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(1): 2011-2022. |
| [5] |
HIKANI Y, SHIRAISHI N. Rain-wind Induced Vibrations of Cables Stayed Bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29(3): 409-418. |
| [6] |
侯俊明, 彭晓彬, 叶方才. 斜拉索索力的温度敏感性[J]. 长安大学学报:自然科学版, 2002, 22(4): 34-36. HOU Jun-ming, PENG Xiao-bin, YE Fang-cai. Temperature Effect on Cable's Forces Controlling of Cable-stayed Bridge[J]. Journal of Chang'an University:Natural Science Edition, 2002, 22(4): 34-36. |
| [7] |
吉伯海, 程苗, 傅中秋, 等. 环境因素对斜拉桥拉索振动基频的影响[J]. 工业建筑, 2013, 43(11): 121-125. JI Bo-hai, CHENG Miao, FU Zhong-qiu, et al. Influence of Environmental Factors upon Fundamental Vibration Frequency of Cables for Cable-stayed Bridge[J]. Industrial Construction, 2013, 43(11): 121-125. |
| [8] |
赵珧冰, 孙测世, 彭剑, 等. 温度变化对拉索频率与索力的影响[J]. 应用力学学报, 2013, 30(6): 905-908. ZHAO Yao-bing, SUN Ce-shi, PENG Jian, et al. Effects of Temperature Changes on the Frequencies and Tension Forces of Cables[J]. Chinese Journal of Applied Mechanics, 2013, 30(6): 905-908. |
| [9] |
汪峰, 陈福清, 文晓旭, 等. 考虑温度影响的斜拉索参数振动模型及响应分析[J]. 重庆交通大学学报:自然科学版, 2016, 35(2): 1-6. WANG Feng, CHEN Fu-qing, WEN Xiao-xu, et al. Analysis of Cable Parametric Vibration Model and Response with Consideration of Temperature Effect[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2016, 35(2): 1-6. |
| [10] |
赵珧冰.考虑温度效应的索梁结构建模及动力特性研究[D].长沙: 湖南大学, 2015. ZHAO Yao-bing. Temperature Effects on Modeling and Vibration Properties of Cable-beam Structures[D]. Changsha: Hunan University, 2015. |
| [11] |
闵志华, 孙利民, 仲政. 环境温度对斜拉桥动力特性的影响分析[J]. 同济大学学报:自然科学版, 2011, 39(4): 488-494. MIN Zhi-hua, SUN Li-min, ZHONG Zheng. Effect Analysis of Environmental Temperature on Dynamic Properties of Cable-stayed Bridge[J]. Journal of Tongji University:Natural Science Edition, 2011, 39(4): 488-494. |
| [12] |
李苗, 黄天立, 任伟新. 温度影响下基于主成分分析和模态柔度的结构异常检测[J]. 振动与冲击, 2011, 30(5): 83-87. LI Miao, HUANG Tian-li, REN Wei-xin. Structural Novelty Detection under Temperature Variation Based on PCA and Modal Flexibility[J]. Journal of Vibration and Shock, 2011, 30(5): 83-87. |
| [13] |
杨咏漪, 陈克坚. 大跨度铁路斜拉桥斜拉索参数振动分析[J]. 铁道工程学报, 2012, 169(10): 60-65. YANG Yong-yi, CHEN Ke-jian. Research on Parametric Oscillation of Cables for Long Span Railway Cable-stayed Bridge[J]. Journal of Railway Engineering Society, 2012, 169(10): 60-65. |
| [14] |
康厚军, 赵跃宇, 蒋丽忠. 参数振动和强迫振动激励下超长拉索的面内非线性振动[J]. 中南大学学报:自然科学版, 2011, 42(8): 2439-2445. KANG Hou-jun, ZHAO Yue-yu, JIANG Li-zhong. In-plane Nonlinear Vibration of Super Long Stay Cables under Parametric and Forced Excitations[J]. Journal of Central South University:Science and Technology Edition, 2011, 42(8): 2439-2445. |
| [15] |
WANG T M, NETTLETON R H, KEITA B. Natural Frequencies for Out-of-plane Vibrations of Continuous Curved Beams[J]. Journal of Sound and Vibration, 1980, 68(3): 427-436. |
| [16] |
GATTULLI V, MARTINELLI L, PEROTTI F, et al. Nonlinear Oscillations of Cables under Harmonic Loading Using Analytical and Finite Element Models[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(1/2): 69-85. |
| [17] |
汪峰, 文晓旭, 刘章军. 斜拉桥塔-索-桥面耦合参数振动模型及响应分析[J]. 固体力学学报, 2015, 36(5): 446-452. WANG Feng, WEN Xiao-xu, LIU Zhang-jun. Coupling Vibration Model for Tower-cable-deck of Long-span Cable-stayed Bridge and Its Response Analysis[J]. Chinese Journal of Solid Mechanics, 2015, 36(5): 446-452. |
| [18] |
孙测世, 王志搴, 赵珧冰, 等. 两端水平激励斜拉索面内非线性振动响应[J]. 地震工程与工程振动, 2014, 34(6): 122-126. SUN Ce-shi, WANG Zhi-qian, ZHAO Yao-bing, et al. In-plane Nonlinear Vibrations of Stayed Cables under Horizontal Excitations[J]. Earth Quake Engineering and Engineering Dynamics, 2014, 34(6): 122-126. |
| [19] |
姚昌荣, 李亚东. 大跨度桥梁健康监测过程中的温度影响研究[J]. 华东交通大学学报, 2008, 25(2): 26-28. YAO Chang-rong, LI Ya-dong. Research on Temperature Influences in Long-span Bridges Helath Monitoring[J]. Journal of East China Jiaotong University, 2008, 25(2): 26-28. |
| [20] |
赵珧冰, 赵跃宇, 孙测世, 等.温度变化对梁线性振动的影响分析[C]//第23届全国结构工程学术会议论文集.兰州: 兰州理工大学, 2014: 332-335. ZHAO Yao-bing, ZHAO Yue-yu, SUN Ce-shi, et al. Analysis of Temperature Affects on Linear Vibration of Beam[C]//Proceedings of Academic Conference of 23rd National Structural Engineering. Lanzhou: Lanzhou University of Technology, 2014: 332-335. |
| [21] |
孙君, 李爱群, 丁幼亮, 等. 润扬大桥悬索桥模态频率-温度的季节相关性研究及其应用[J]. 工程力学, 2009, 26(9): 50-55. SUN Jun, LI Ai-qun, DING You-liang, et al. Research on Correlation of Modal Frequency and Seasonal Temperature of Runyang Suspension Bridge[J]. Engineering Mechanics, 2009, 26(9): 50-55. |
 2018, Vol. 35
2018, Vol. 35
