扩展功能
文章信息
- 王智超, 周芊妤, 罗光财, 旷杜敏
- WANG Zhi-chao, ZHOU Qian-yu, LUO Guang-cai, KUANG Du-min
- 高填方压实土时效变形特征与长期沉降分析
- Analysis on Time-dependent Deformation Behavior and Long-term Settlement of Compacted Clay of High-filled Embankment
- 公路交通科技, 2018, 35(11): 1-10
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(11): 1-10
- 10.3969/j.issn.1002-0268.2018.11.001
-
文章历史
- 收稿日期: 2017-05-18
2. 中建五局土木工程有限公司, 湖南 长沙 410004
2. CCFEB Civil Engineering Co., Ltd., Changsha Hunan 410004, China
随着我国中西部地区新建高速公路及旧路改扩建的推进,高填方路堤大量涌现。它具有填筑高度大,工后沉降时间长,沉降量大,对地基承载力、压实效果要求高等特点。在高填方堤身低围压以及堤内高应力共同作用下的沉降变形会因压实土超固结、土体剪胀、应变软化等性质变得非常复杂,故有效地降低路堤沉降,消除路堤沉降所带来的危害已经成为公路建设领域一个重要的课题。高填方路堤在分层碾压填筑过程中形成了超固结的应力历史,不同的应力历史会对土体沉降产生不同的影响,如土体在高围压时候可能表现为应变硬化,但在低围压时表现为应变软化。其中,赵春风[1]提出了考虑法向应力历史的黏土界面模型,准确再现和预测不同法向应力历史条件下黏土接触界面的力学特性;Grammatikopoulou[2]分别研究了考虑和消除先前的应力历史对沉降影响的两种情形,并采用可模拟这两种情况的表面运动学硬化模型进行有限元分析;冷艺[3]进行了复杂条件下应力路径变化的应力控制式排水剪切试验,着重探讨应力历史对饱和砂土剪切强度和应力-应变关系的影响;王志亮[4]介绍在无高压固结试验时将av法、e-p法中计入土体应力历史影响,分析沉降修正系数对于不同状态土体的大致取值范围。王智超[5]对路基回填土分别开展室内击实和一维固结试验,研究了含水率、击实功等因素对于路基回填土的超固结应力历史的影响,为考虑超固结应力历史的土体本构模型开发提供了试验基础。张好[6]在考虑土体应力历史的基础上,通过p-y方法分析了桩基的冲刷影响行为,并采用现场试验作参考案例,考察了应力历史、冲刷深度等对软土中横向受力桩响应的影响。时间效应是高填路堤工后长期沉降的又一关键因素。其中,周爱兆[7]分析了时间依赖性沉降过程曲线并提出Weibull模型来描述路基的时间依赖性沉降过程;Shukla[8]采用力学模型研究饱和土的时间依赖性沉降特征,并揭示了各种参数对土固结不同阶段模型的沉降影响;黄广龙[9]建立了考虑时间效应的地基柔度矩阵,并编制相应程序,计算得出其内力、变形等随时间发展的规律;胡亚元[10]研究了超固结土次固结系数的时间效应,提出了相应的次固结系数随时间增长的双曲线理论模型,供工程界评估工后次固结沉降之用。目前,国内外虽有众多压实土应力历史或时间效应的研究,但鲜有将应力历史和时间相依的关系相结合来研究高填方路堤的沉降问题。近似的研究如:李西斌[11]综合考虑软土的应力历史及流变性,并利用GDS先进固结试验系统对软土进行一系列一维固结和渗透试验,结果表明:超固结土孔压消散速度比正常固结土快,应力历史和超固结比对次固结系数有显著的影响;殷建华[12]在正常固结土弹黏塑性本构模型(EVP)基础上,通过新引入临界状态线上的屈服面来表征重超固结土的变形特征,模型中的n无实际物理意义,需要通过拟合试验数据确定;姚仰平[13]在UH模型屈服面方程中引入折算时间,建立了考虑土体超固结的弹黏塑本构模型,以此表征超固结土的力学特性,但该模型的时间不是真实时间,用于复杂时效问题数值计算存在困难。
基于以上研究现状,本研究将结合高填方路堤压实土的应力历史和沉降时间效应,以Hashiguchi提出的下负荷面作为参考面的弹黏塑性本构模型来分析高填方路堤的施工和工后沉降,并对压实土的弹黏塑性本构模型进行研究和验证。通过UMAT子程序将提出的新模型嵌入ABAQUS软件用于模拟高填方路堤的工程性状,着重研究在复杂的三维边界条件下高填方路堤的流变沉降特征,并考虑了回填过程和回填土的超固结应力历史以及时间效应等因素对高填方路堤流变沉降的影响,最后将新建模型的沉降预测结果与现场沉降观测的数据进行对比分析,表明新模型适用于分析高填方路堤的施工和工后长期沉降。
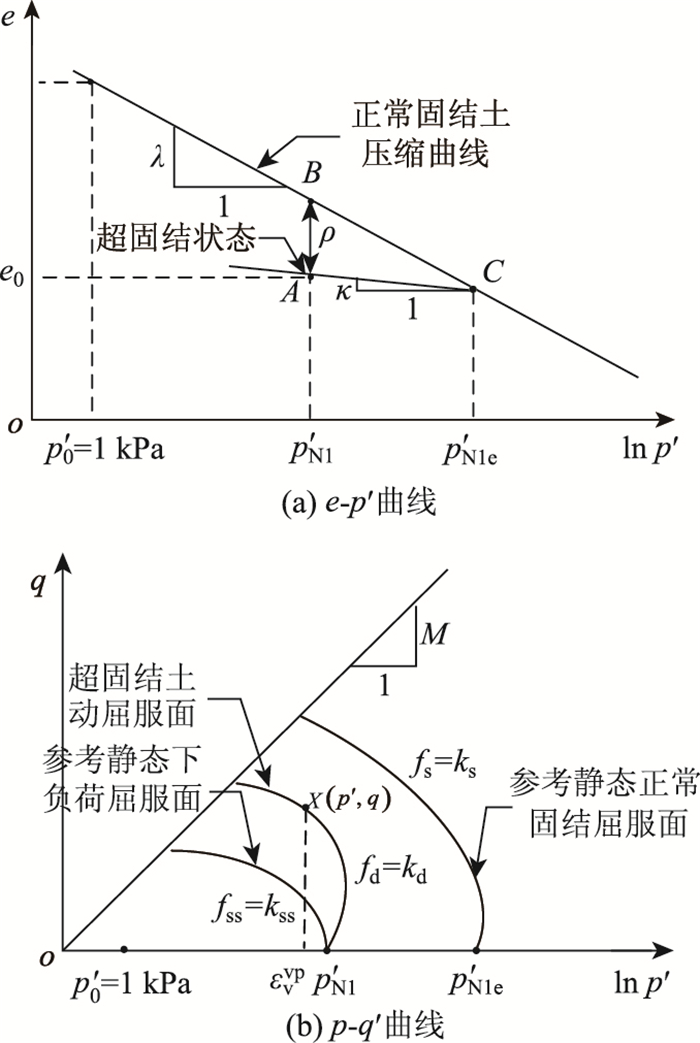
1 压实土的应力历史与流变特性 1.1 应力历史的基本概念土在历史上曾经受过的最大有效竖向压力称为先期固结应力。高填方路堤在填筑过程中采用分层碾压,而在碾压过程中会形成先期固结压力,或把它称为压实土的应力历史,在一定的荷载作用下可能发生剪胀和软化。如图 1(a)所示,C1点为碾压过程中形成的先期固结压力,应力大小为pN1e,而碾压过后,发生卸载而形成超固结。高填路堤填筑时无侧限,容易形成堤身低围压以及堤内高应力共同作用。为了验证这种现象,我们曾在室内开展不同压实度土在围压50 kPa下的三轴剪切试验,如图 1(b)所示,可以看出压实土有明显的应变软化现象。

|
| 图 1 超固结压实土的应力历史及变形特征 Fig. 1 Stress history and deformation characteristics of over-consolidated compacted clay |
| |
1.2 应力历史试验
为了研究击实功、击实冲量、含水率和压实度对其应力历史的影响,王智超等[14]采用击实钻芯取样对压实土的应力历史开展了试验研究,试验结果如表 1所示。
| 影响因素 | 含水率/ % |
压实度/ % |
单位体积击实功/ (kJ·m-3) |
单位面积击实冲量/ (N·s·cm-2) |
先期固结应力/ kPa |
| 含水率 | 23.7 | 91 | 2 687 | 68.1×10-2 | 530 |
| 19.7 | 101 | 2 687 | 68.1×10-2 | 605 | |
| 15.7 | 93 | 2 687 | 68.1×10-2 | 485 | |
| 压实度 | 19.7 | 98 | 2 687 | 68.1×10-2 | 585 |
| 19.7 | 101 | 2 687 | 68.1×10-2 | 605 | |
| 19.7 | 104 | 2 687 | 68.1×10-2 | 615 | |
| 击实功、击实冲量 | 23.7 | 93 | 683 | 5.8×10-2 | 410 |
| 2 687 | 68.1×10-2 | 550 | |||
| 504 | 18.6×10-2 | 450 |
表 1表明:压实土在形成过程中受到的单位面积击实冲量起决定性作用,击实冲量越大,应力历史就越大。试样在最佳含水率ω=19.7%时应力历史最大,ω=23.7%时次之,ω=15.7%时应力历史最小,含水率相对最佳含水率上下浮动;试样在相同条件下应力历史呈现出随压实度的增大而增大的现象,故密实程度越高,土体强度和稳定性越高。可见,击实冲量、含水率和压实度均是决定应力历史的主要因素。因此,在分析压实土变形的本构模型中应力历史的影响不可忽略。
1.3 压实土的率敏性试验压实土除了有应力历史外,还有很明显的时间相依性,如率敏性。为了揭示率敏性对超固结土应力-应变演化规律的影响,本研究分别对饱和超固结土以及非饱和压实土开展了率敏性三轴试验。
1.3.1 非饱和压实土的率敏性影响由于高填方压实土位于地下水位以上,因此都处于非饱和状态,本研究按总应力法(暂不考虑基质吸力的影响),对非饱和压实土按不同的加载速率开展了三轴剪切试验,试验结果如图 2所示。其中,非饱和压实土的体变测量借助GDS饱和土静态三轴仪的围压控制器来间接测定。
|
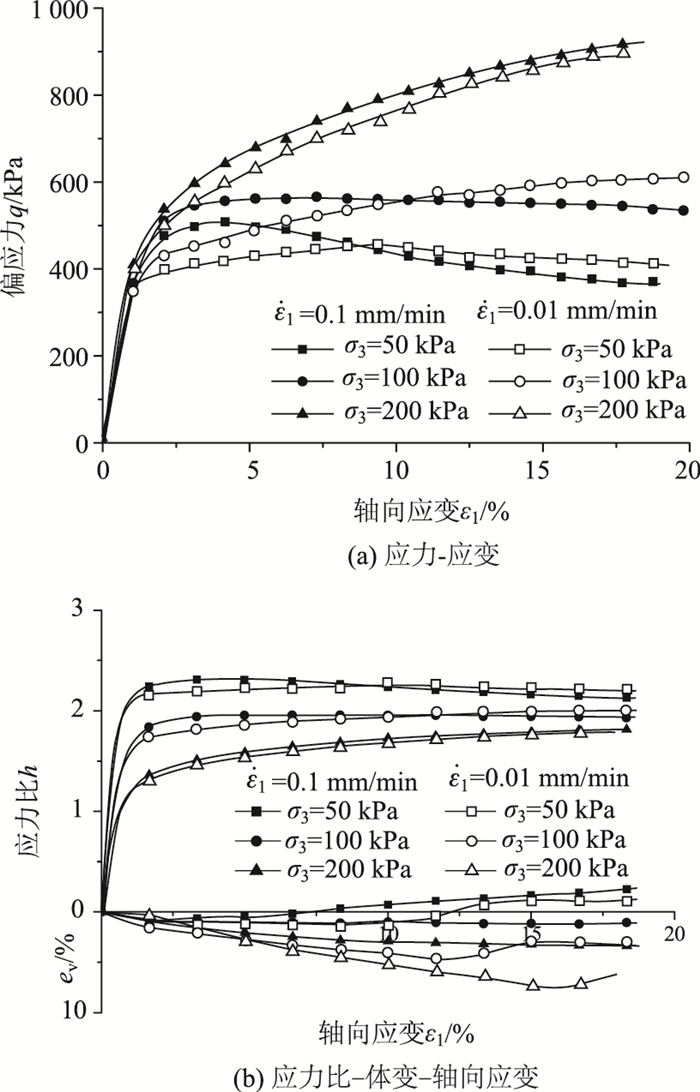
| 图 2 压实土的率敏性关系曲线 Fig. 2 Rate-sensitivity relation curves of compacted soil |
| |
从图 2反映的压实土率敏性特征关系曲线中可看出:低围压下,压实土的应力-应变曲线呈软化型,随着加载速率的减小,应力-应变曲线逐渐过渡为硬化型;高围压下,压实土呈剪缩变形,且加载速率越小,体缩变形越明显。图 2(b)曲线的整体趋势能合理反映慢速率时压实土的体积变化,且加载速率越大,压实土的强度和应力比越大。由此可见,加载速率对压实土的强度特征有明显影响,非饱和压实土的变形特征具有明显的时间相依性。
1.3.2 饱和超固结土的率敏性影响由于非饱和压实土的强度变形特性受含水率、压实度和基质吸力等因素影响,其应力变形特性复杂,在建立弹黏塑性本构时忽略这些因素会造成一定的不确定性,故本研究也对按一定超固结比形成的饱和超固结土的率敏性开展了研究,如图 3所示。
|
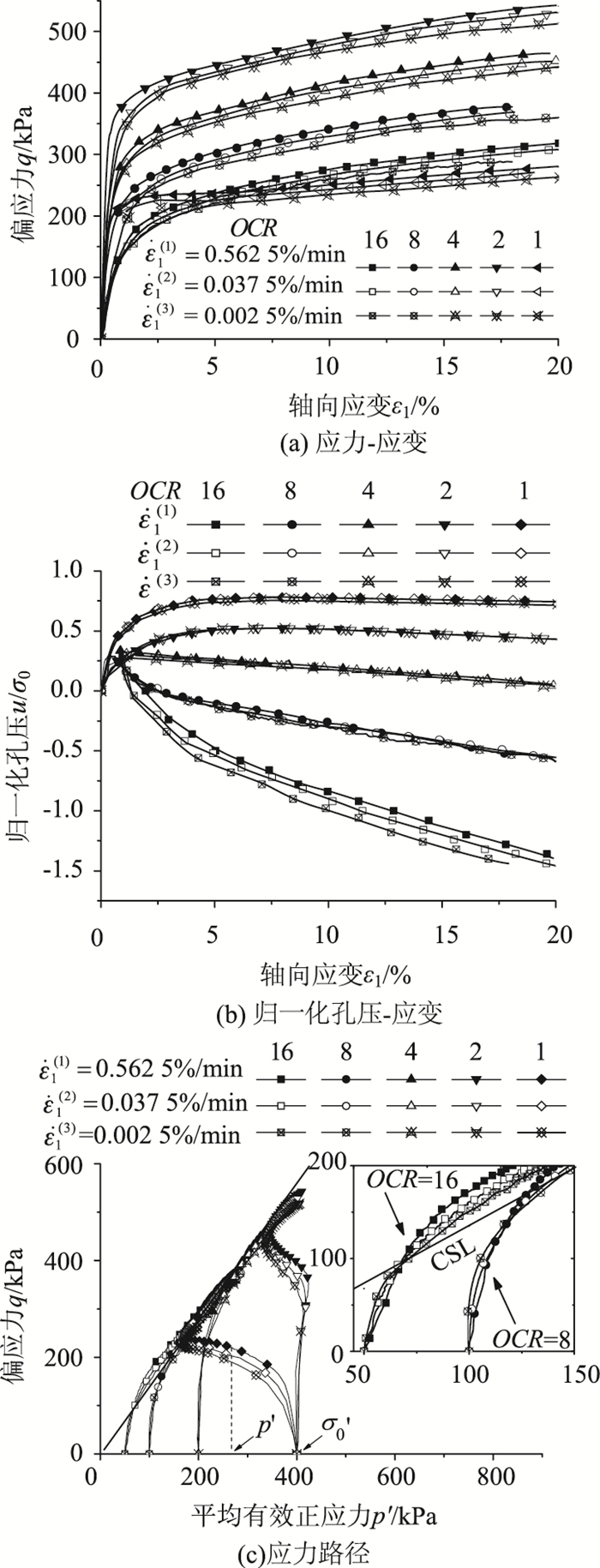
| 图 3 超固结土率敏性试验结果 Fig. 3 Test result of rate-sensitivity of over-consolidated clay |
| |
在图 3反映的饱和超固结重塑土率敏性试验结果中,应力应变曲线显示:不同超固结状态下,不排水抗剪强度均随加载速率的升高而不同程度增大。图 3(b)可以看出,3种速率下的孔隙水压力差异较小,说明孔压受应变速率影响不大,尤其对于弱超固结和正常固结土。图 3(c)中,率敏性对应力路径具有一定的影响,即无论重超固结土还是轻超固结土,不排水应力路径相交前均是低速率在上高速率在下,相交后均是高速率的路径在上方。为了更好地描述其率敏性,采用Sheahan等[15]提出的应变率参数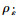
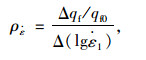
|
(1) |
式中,qf0为参考不排水抗剪强度,即在参考应变速率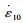
| OCR | 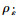 |
||
| ε1=5% | ε1=10% | ε1=15% | |
| 16 | 13.945 | 16.155 | 18.706 |
| 8 | 8.545 | 9.948 | 10.458 |
| 4 | 4.251 | 4.847 | 5.016 6 |
| 2 | 2.041 | 2.274 | 2.508 |
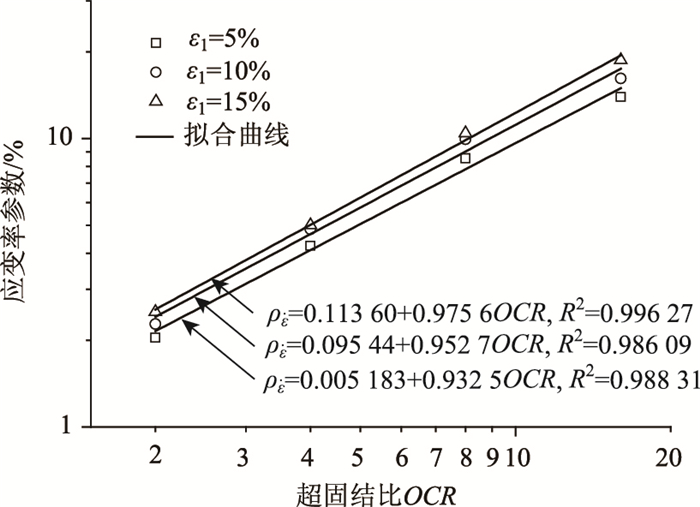
如图 4所示应变率参数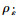
|
| 图 4 应变率参数与超固结比关系曲线 Fig. 4 Relationship between strain rate parameters and over-consolidation ratio |
| |
1.4 超固结土的压缩蠕变试验
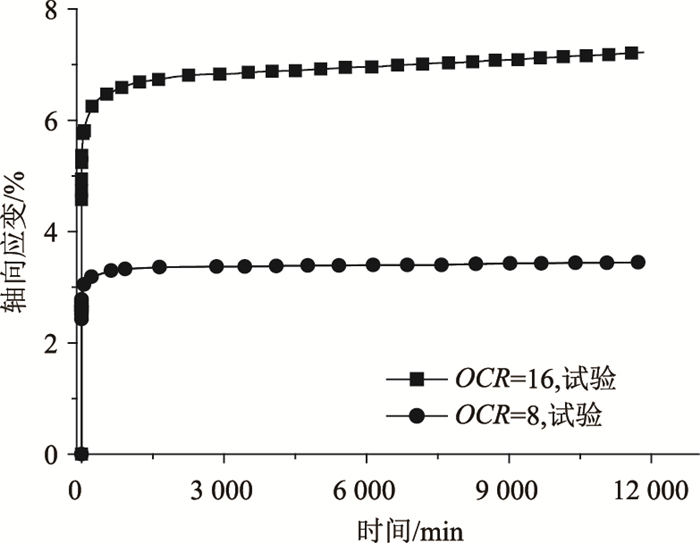
本研究采用饱和土率敏性试验的方法获取两组饱和超固结土(OCR=16和OCR=8),开展了超固结土三轴剪切蠕变试验,其应力水平分别为250 kPa和300 kPa。从图 5中可以看出开始时轴向应变急剧增大,随着偏应力的减小,最终的轴向应变趋于稳定。
|
| 图 5 超固结土蠕变试验结果 Fig. 5 Creep test result of over-consolidated clay |
| |
2 压实土的弹黏塑性本构模型
王智超等[16]基于下负荷面理论提出一类可考虑饱和超固结土以及非饱压实土(暂不考虑基质吸力的影响)的应变软化型弹黏塑性本构模型,本研究采用该模型对非饱和压实以及饱和超固结土的率敏性进行了模拟,给出了相应模型参数,并利用蠕变试验结果对模型的适用性进行了验证,其基本原理如图 6所示。
|
| 图 6 超固结重塑土弹黏塑本构模型示意 Fig. 6 Schematic diagram of elasto-viscoplastic constitutive model of over-consolidated reconstituted clay |
| |
2.1 基本理论
该模型中,黏塑性应变分量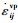
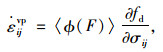
|
(2) |
式中,fd为动屈服面; σij为应力分量,相对过应力函数〈ϕ(F)〉定义为:
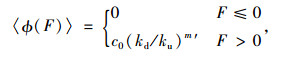
|
(3) |
式中,c0为黏性系数; m′为过应力系数; c0和m′均可通过不同应变速率三轴压缩试验测定; kd为体积硬化以及应变速率共同影响的硬化参数; ku为体积硬化参数,动态屈服函数fd定义为:
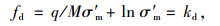
|
(4) |
式中,M为临界状态时有效应力比; σ′m和q分别为当前有效平均应力和偏应力。参考图 6(b)所示的新屈服函数fu,下负荷面硬化参数ku为:
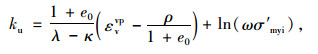
|
(5) |
式中,λ为压缩系数;k为膨胀系数;e0为初始孔隙比;εvvp为累积黏塑性体积应变;σ′myi为初始围压;ω为超固结比。如图 6(a)所示,ρ为超固结演化函数,其定义为:
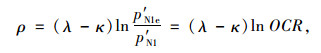
|
(6) |
式中,OCR=p′N1e/p′N1为初始应力状态的超固结比(下文中用ω代替);p′N1e和p′N1分别是正常固结屈服轨迹平均有效应力p′轴的截距和下负荷面超固结屈服轨迹平均有效应力p′轴的截距。
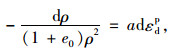
|
(7) |
式中,dεdp为黏塑性偏应变增量;a为一材料参数,决定超固结比的变化速率,a越大超固结重塑土的峰值强度越低,当a=0时,超固结土将成为正常固结土。超固结土的动态平衡方程g(σij, εvvp, 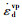
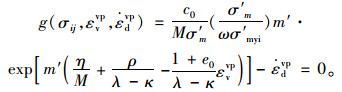
|
(8) |
饱和超固结土以及非饱压实土这两种应变软化型土本构模型的输入参数如表 3所示,表中K为压实度;μ为泊松比,其他参数含义同上文。需要指出的是,超固结比ω由不同压实度土的先期固结应力(见表 3)与围压比值确定;应变增量每0.2‰所对应的时间步长ΔT由加载速率确定,当加载速率为0.01 mm/min时,ΔT=96 s。
| 土类 | K/% | e0 | a | μ | M | λ | κ | c0/s-1 | m′ |
| 非饱和 | 90 | 0.72 | 1 100 | 0.3 | 1.9 | 0.324 | 0.025 | 5.6×10-13 | 20 |
| 93 | 0.66 | 1 000 | |||||||
| 96 | 0.61 | 900 | |||||||
| 饱和 | — | 0.694 | 505 | 0.3 | 1.325 | 0.109 | 0.051 | 1.2×10-9 | 39.5 |
2.3 模型验证
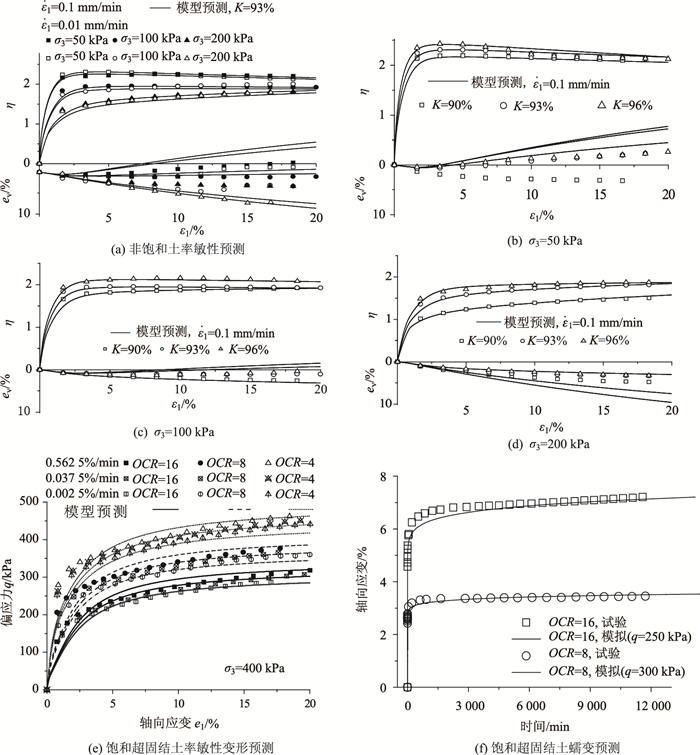
为了验证模型的适用性,采用表 3的模型参数分别预测了非饱和压实土以及饱和超固结土的率相关变形,如图 7所示。从图 7(a)~(d)中可以看出,新模型能够正确地预测非饱和压实土以及饱和超固结土的率敏性、剪胀和应变软化等特性,其中抗剪强度数据吻合良好,体变曲线的变化趋势基本一致,能够合理反映试验规律。需要特别指出图 7(e)和(f)中的预测结果使用了同一套材料参数,即新模型能利用土体率敏性试验确定的材料正确预测出其蠕变变形。
|
| 图 7 应变软化型土体试验数据与预测结果比较 Fig. 7 Comparison between predict result and test data of strain softened clay |
| |
3 工程案例
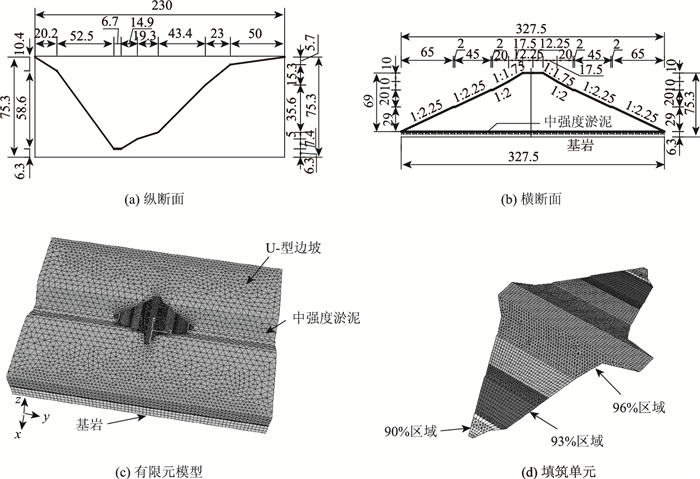
本节以某高速公路坝式路堤工程实例[17-18]为基础,采用提出的本构模型,并通过三维非线性有限元软件ABAQUS,对三维复杂边界条件下高填方路堤的施工和工后沉降进行了分析和预测。该坝式路堤的三维几何模型及尺寸如图 8所示,路堤填料根据回填土压实度从下往上依次分为3个区:90%, 93%和96%,其中图 8(a)和8(b)分别给出了纵断面和横断面轮廓尺寸。此外,边界条件应用于几何模型最外侧的面上,以限制垂直于面方向上的位移,底面各方向位移均受限。
|
| 图 8 某公路坝式路堤三维模型[18](单位:m) Fig. 8 Three-dimensional model of dam-embankment (unit: m) |
| |
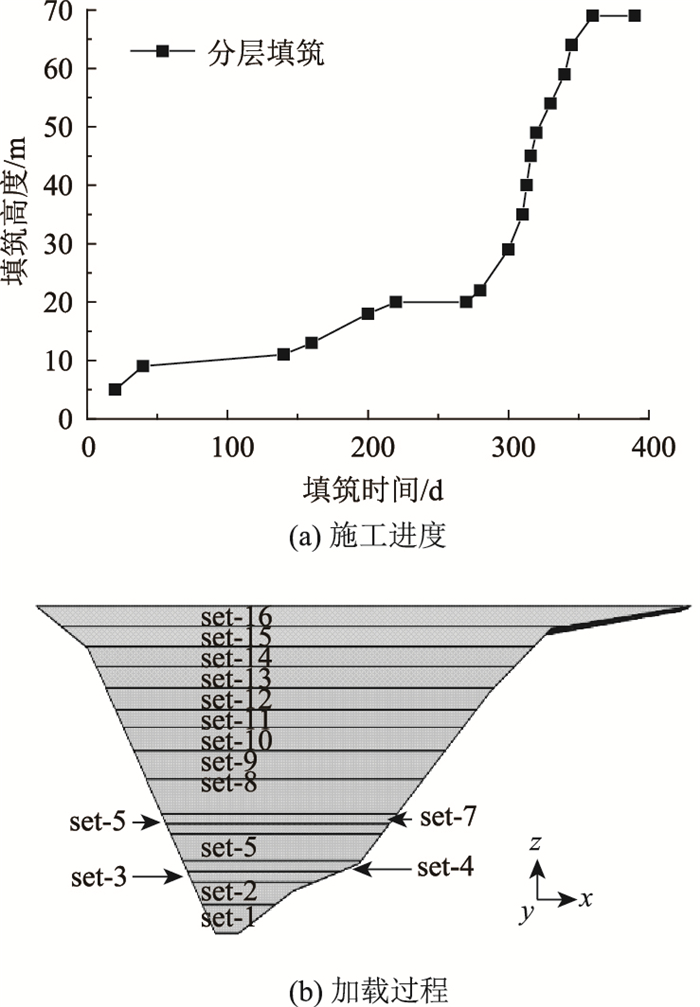
如图 9和表 4将路堤分成16个层,结合单元生死技术让其逐次“重生”,来模拟分层填筑过程。
|
| 图 9 高速公路填筑过程 Fig. 9 Construction progress of an expressway |
| |
| 路堤高度/m | 压实度/ % |
分层填筑/m | 监测点 | 加载顺序 | 加载时间/d | 时间步长/d |
| 5 | 90 | 5 | 底层 | set-1 | 20 | 20 |
| 9 | 4 | — | set-2 | 40 | 20 | |
| 11 | 2 | — | set-3 | 140 | 100 | |
| 13 | 93 | 2 | 2层 | set-4 | 160 | 20 |
| 18 | 5 | — | set-5 | 200 | 40 | |
| 20 | 2 | — | set-6 | 220 | 20 | |
| 20 | 0 | — | — | 270 | 50 | |
| 22 | 2 | — | set-7 | 280 | 10 | |
| 29 | 7 | — | set-8 | 300 | 20 | |
| 35 | 6 | — | set-9 | 310 | 10 | |
| 40 | 96 | 5 | 4层 | set-10 | 313 | 3 |
| 45 | 5 | — | set-11 | 316 | 3 | |
| 49 | 4 | — | set-12 | 320 | 4 | |
| 54 | 5 | — | set-13 | 330 | 10 | |
| 59 | 5 | — | set-14 | 340 | 10 | |
| 64 | 5 | — | set-15 | 345 | 15 | |
| 69 | 5 | — | set-16 | 360 | 15 | |
| 工后(10年) | 3 630 | 3 240 | ||||
3.1 有限元模型参数
前文中介绍了对非饱和路基压实土开展的一维固结试验以及三轴剪切压缩试验。通过一维固结试验,得到了不同压实度(90%,93%,96%)压实土的先期固结压力、初始孔隙比、压缩指数、回弹指数;通过压实土在不同加载速率和围压条件下的固结排水三轴试验,得到了黏聚力c以及时间相依参数c0, m′。由于室内试验得到的压实土的先期固结压力往往低于实际填筑路堤压实土,现场参数(先期固结压力和黏聚力)通过实际观测沉降反演得到,该有限元本构模型具体参数,如表 5所示。
| K/% | e0 | μ | M | λ | κ | c0/s-1 | m′ | a | pc/kPa | c/kPa | |||
| 室内 | 现场 | 室内 | 现场 | ||||||||||
| 96 | 0.646 | 0.3 | 1.42 | 0.125 | 0.051 | 1.2E-8 | 25.5 | 490 | 510 | 550 | 155.0 | 214.6 | |
| 93 | 0.703 | 0.3 | 1.42 | 0.125 | 0.051 | 1.2E-8 | 25.5 | 490 | 390 | 430 | 107.8 | 150.6 | |
| 90 | 0.767 | 0.3 | 1.42 | 0.125 | 0.051 | 1.2E-9 | 25.5 | 490 | 310 | 350 | 68.3 | 86.6 | |
3.2 数值模拟结果及分析
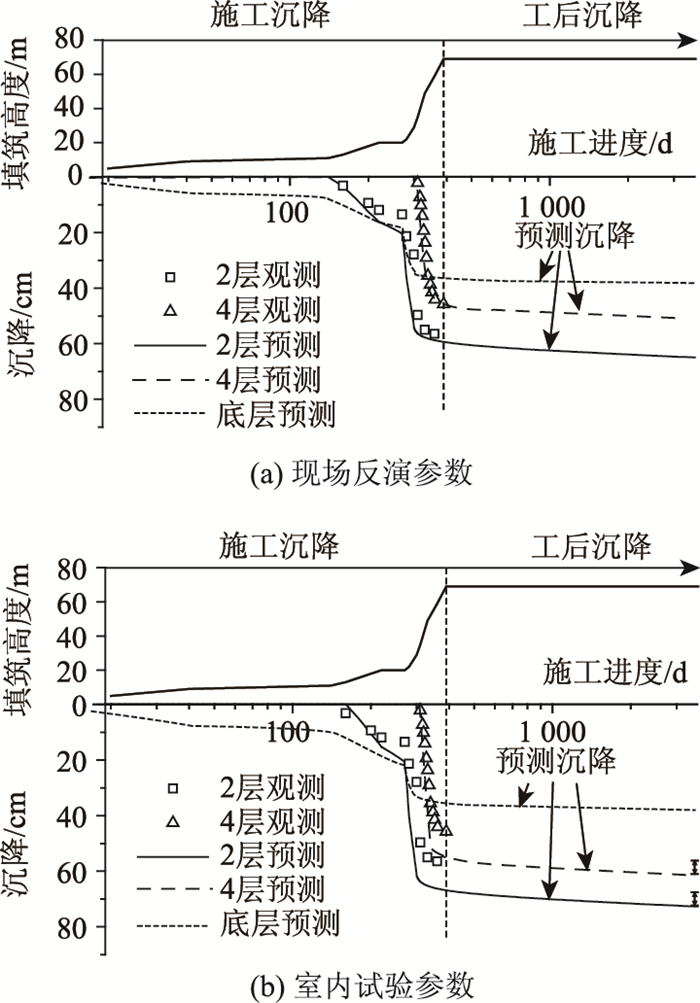
分层填筑16层的高填方路堤沉降计算结果如图 10所示,其中,模型参数中的先期固结压力和黏聚力采用室内试验数据或现场反演确定。
|
| 图 10 路堤预测沉降与观测沉降对比 Fig. 10 Comparison of predicting and monitoring settlements of embankment |
| |
从图 10可以看出:通过参数反演得到的先期固结压力pc和黏聚力c大于室内试验结果;直接采用室内试验得到的pc和c,计算的沉降结果将大于观测值。总之,提出的基于下负荷面的弹黏塑性本构模型能够合理预测高填方路堤的长期沉降,计算结果能与沉降观测吻合良好。
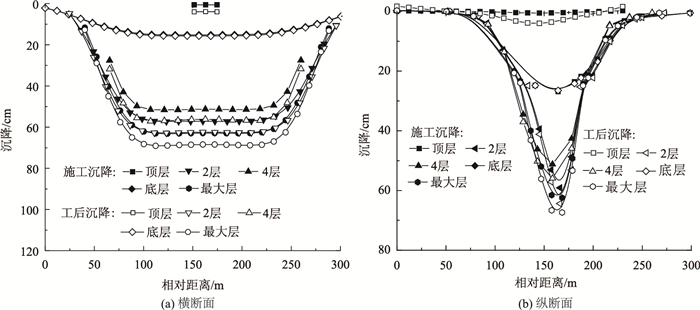
图 11为不同回填层的横、纵切面的沉降曲线计算结果,从图中可以看出,16层填筑的沉降位移最大处为位移第5层(set-5),说明路堤沉降最大层不发生在一般认为的顶端或底端,而在路堤中间层,应在施工中引起重视。
|
| 图 11 不同回填层沉降预测曲线 Fig. 11 Predicted settlement curves of various back filling layer |
| |
4 结论
本研究结合试验分析了路基压实土的超固结、剪胀以及率敏性、蠕变等力学特性,并对提出的基于下负荷面的弹黏塑性本构模型进行了验证和应用,得到的主要结论有:
(1) 压实土在碾压过程中会形成一定的应力历史,不同的应力历史下,压实土发生剪缩或剪胀变形。其中,击实冲量、含水率和压实度是决定应力历史的主要因素。
(2) 超固结土有明显的蠕变、率敏性等时间相依特征。其不排水抗剪强度均随加载速率的升高而不同程度增大,孔压受应变速率影响不大,这表明土的孔压不是造成土体时间相依性特征的主因。
(3) 与传统的有限元弹塑性分析方法相比,提出的基于下负荷面的超固结土弹黏塑性本构模型不仅考虑了时间相依性、率敏性、蠕变特性,还考虑了剪胀和应变软化等特性,可以成功预测高填方路堤的施工及工后沉降。
| [1] |
赵春风, 龚辉, 赵程, 等. 考虑法向应力历史的黏土-混凝土界面弹塑性分析[J]. 岩石力学与工程学报, 2012, 31(4): 848-855. ZHAO Chun-feng, GONG Hui, ZHAO Chen, et al. Elastoplastic Analysis of Interface between Clay and Concrete Considering Effect of Normal Stress History[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(4): 848-855. |
| [2] |
GRAMMATIKOPOULOU A, ZDRAVKOVIC L, POTTS D M. The Influence of Previous Stress History and Stress Path Direction on the Surface Settlement Trough Induced by Tunnelling[J]. Géotechnique, 2008, 58(4): 269-281. |
| [3] |
冷艺, 栾茂田, 许成顺, 等. 应力历史对饱和砂土力学性状影响的试验研究[J]. 岩土力学, 2009, 30(5): 1257-1263. LENG Yi, LUAN Mao-tian, XU Cheng-shun, et al. Experimental Study of Effect of Stress History on Mechanical Properties of Saturated Sand under Complex Stress Conditions[J]. Rock and Soil Mechanics, 2009, 30(5): 1257-1263. |
| [4] |
王志亮, 孙锡杰. 考虑土体应力历史影响的沉降修正初探[J]. 岩土力学, 2006, 27(10): 1723-1726. WANG Zhi-liang, SUN Xi-jie. Discussion of Settlement Modification Considering Stress History of Soil Mass[J]. Rock and Soil Mechanics, 2006, 27(10): 1723-1726. |
| [5] |
王智超, 金刚, 邓旭华, 等. 路基压实土的超固结应力历史试验研究[J]. 公路交通科技, 2015, 32(7): 41-46. WANG Zhi-chao, JIN Gang, DENG Xu-hua, et al. Experimental Study on Over-consolidation Stress History of Subgrade Compacted Clay[J]. Journal of Highway and Transportation Research and Development, 2015, 32(7): 41-46. |
| [6] |
ZHANG Hao, CHEN Sheng-li, LIANG Fa-yun. Effects of Scour-hole Dimensions and Soil Stress History on the Behavior of Laterally Loaded Piles in Soft Clay under Scour Conditions[J]. Computers and Geotechnics, 2017, 84: 198-209. |
| [7] |
ZHOU Ai-zhao, GU Wei-wei, WANG Wei. Study on Prediction Models for Time-dependent Settlement of Soft Road Foundation[J]. Applied Mechanics & Materials, 2012, 204-208: 1880-1885. |
| [8] |
SHUKLA S, CHANDRA S. Time-dependent Settlement Response of Granular Fill on Soft Soil[J]. Journal of the Japanese Geotechnical Society Soils & Foundation, 1995, 35(4): 105-108. |
| [9] |
黄广龙, 梅国雄, 宰金珉, 等. 考虑时间效应的刚性基础沉降分析[J]. 岩土力学, 2006, 27(11): 1983-1986. HUANG Guang-long, MEI Guo-xiong, ZAI Jin-min, et al. Settlement Analysis of Rigid Foundation Considering Time Effect[J]. Rock and Soil Mechanics, 2006, 27(11): 1983-1986. |
| [10] |
胡亚元, 杨平, 余启致. 超固结土次固结系数的时间效应[J]. 中国公路学报, 2016, 29(9): 29-37. HU Ya-yuan, YANG Ping, YU Qi-zhi. Time Time Effect of Secondary Consolidation Coefficient of Over-consolidated Soil[J]. China Journal of Highway and Transport, 2016, 29(9): 29-37. |
| [11] |
李西斌, 谢康和, 陈福全. 考虑软土流变特性和应力历史的一维固结与渗透试验[J]. 水利学报, 2013, 44(1): 18-25. LI Xi-bin, XIE Kang-he, CHEN Fu-quan. One Dimensional Consolidation and Permeability Tests Considering Stress History and Rheological Characteristic of Soft Soils[J]. Journal of Hydraulic Engineering, 2013, 44(1): 18-25. |
| [12] |
YIN Jian-hua, ZHU Jun-gao, GRAHAM J. A New Elastic Viscoplastic Model for Time-dependent Behaviour of Normally and Over Consolidated Clays:Theory and Verification[J]. Canadian Geotechnical Journal, 2002, 39(1): 157-173. |
| [13] |
姚仰平, 孔令明, 胡晶. 考虑时间效应的UH模型[J]. 中国科学:技术科学, 2013, 43(3): 298-314. YAO Yang-ping, KONG Ling-ming, HU Jin. UH Model Considering Time Effect[J]. Scientia Sinica Technologica, 2013, 43(3): 298-314. |
| [14] |
WANG Zhi-chao, JIN Gang, DENG Xu-hua, et al. Experimental Study on the Over-consolidation Stress History of Subgrade Compacted Clay[J]. Journal of Highway and Transportation Research and Development:English Edition, 2016, 10(1): 26-32. |
| [15] |
SHEAHAN T C. Interpretation of undrained Creep Tests in Terms of Effective Stresses[J]. Canadian Geotechnical Journal, 1995, 32(32): 373-379. |
| [16] |
王智超, 金刚, 吴晓峰, 等. 非饱和压实土率相关变形特征与时效模型[J]. 岩土力学, 2016, 37(3): 719-727. WANG Zhi-chao, JIN Gang, WU Xiao-feng, et al. Rate-dependent Deformation Characteristics and Time-dependent Constitutive Model of Unsaturated Compacted Clay[J]. Rock and Soil Mechanics, 2016, 37(3): 719-727. |
| [17] |
景宏君. 土质路基三维固结变形理论及其应用[M]. 北京: 科学出版社, 2008. JING Hong-jun. Theory and Application of 3D Consolidation Deformation of Soil Roadbed[M]. Beijing: Science Press, 2008. |
| [18] |
WANG Zhi-chao, KUANG Du-min, ZHAO Tao. Research on a Calculation Method and Three-dimensional Simulation of a High-filled Embankment Rheological Settlement[C]//Fourth Geo-China International Conference. Jinan: ASCE, 2016: 201-209. http://or.nsfc.gov.cn/handle/00001903-5/144569
|
 2018, Vol. 35
2018, Vol. 35
