扩展功能
文章信息
- 孙静怡, 牟若瑾, 刘拥华
- SUN Jing-yi, MOU Ruo-jin, LIU Yong-hua
- 考虑大型车因素的支持向量机短时交通状态预测模型研究
- Study on Short-term Traffic State Forecasting Model of SVM Considering Proportion of Large Vehicles
- 公路交通科技, 2018, 35(10): 126-132
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(10): 126-132
- 10.3969/j.issn.1002-0268.2018.10.017
-
文章历史
- 收稿日期: 2017-07-20
随着小汽车拥有率的快速增长,道路交通的供需矛盾日益突出,特别是承担着城市间及城市各功能区之间的快速通道频繁出现常发性及偶发性拥堵。如何提高高速公路及城市快速路的通行能力,减少交通拥堵造成的损失成为道路交通管理部门的重要任务。根据交通流特性,保持良好的交通运行状态才能维持较高的整体通行能力水平。因此,及时发现交通状态异常并采取相应的管制措施有助于及时控制交通瓶颈效应,保持高速公路的通行能力。交通状态的短时预测技术能够在实时交通状态数据基础上对交通状态发展趋势进行预测,为高速公路的控制策略,特别是匝道控制的决策提供支撑。因此快速、准确的短时交通流状态预测技术的研究和应用具有重要的现实意义[1]。
交通状态短时预测模型的核心技术是依据实时交通状态数据对后续短时交通状态数据进行快速、准确地预测与提供。近年来,国内外短时交通流状态预测的方法包括神经网络预测模型及其改进形式[2-4]、支持向量机模型及其改进形式[5-7]、卡尔曼滤波方法[8-9]、组合算法等智能算法。这些智能算法对大数据的处理能力强,预测准确性高。各种算法在实际运用中各有特点:组合算法的预测,虽然可以得到较好的结果,但对数据的处理存在冗杂的问题。而神经网络模型所需要的训练样本较大,对参数调整时间过长,泛化能力低,容易陷入局部最优。卡尔曼滤波算法则随着递推的滤波步数的增加,容易出现发散现象,从而影响预测的精准度等。与这些算法相比较,支持向量机(SVM)模型针对小样本问题,可以在有限样本的情况下获得最优解。与传统的神经网络模型相比避免了神经网络模型需要大量数据反复试凑来确定网络结构的问题。与卡尔曼滤波方法相比,克服了维数灾难,且解为全局最优,有很好的泛化能力。
短时交通流状态参数的预测时间间隔不超过15 min, 包括交通流量、速度或密度等参数。随着时间间隔的缩短,交通流的非线性、不确定性越强,预测难度越大。当前预测模型的建立主要从时间和空间两方面考虑。从时间角度研究,如邱敦国等[10],充分考虑城市道路工作日与非工作日交通流特点,采用当前时刻前N1天与前N2天同一时段的交通流同时进行预测,根据2种预测结果与实际值的误差来确定权值,得到推荐结果。邵春福等[11]对路网中多个断面交通流量数据进行主成分分析,并应用支持向量机将主成分作为输入,对流量进行预测,是从空间的研究角度进行。李林超等[12]结合了空间因素与时间因素,应用支持向量机模型进行预测,具有较好的预测效果。
本研究以高速公路车流平均车速作为交通状态评价参数。针对山区高速公路纵断面线型受到地形条件的制约,往往是上下坡的坡度大,且坡长长,这样的线型条件对大型车的运行速度影响很大。如果大型车数量多,占比大,那么对整体车流运行速度的影响就大。本研究首先分析了大型车的比例与平均速度的关联度,进而提出了考虑大型车因素与时间因素相结合的支持向量机交通流速度预测模型。根据昆玉高速公路晚高峰交通运行数据,运用模型进行了预测数据与实际数据的对比分析,验证了预测模型的精度。
1 大型车比例与运行速度的灰色关联度分析高速公路的车辆运行特征受到道路特性、驾驶员特性、环境特性等多因素影响,呈现出随机性、不确定性的特点,高速公路基本路段的交通流速度变化模型可以视为灰色系统。研究表明,大型车在交通组成中的比例对车流运行速度有着显著的影响。本研究运用灰色关联度理论[13]分析交通流车辆构成对速度的影响情况。
1.1 灰色关联度理论灰色关联度建模步骤[14]:
Step 1:建立各相关的原始数据矩阵Xi。

|
(1) |
式中xi(k)为i因素在第k阶段的原始数据。
Step 2:求初值化变换矩阵X′i。
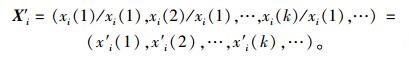
|
(2) |
Step 3:求差序列Δ0i(k)。
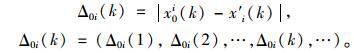
|
(3) |
Step 4:对关联系数ξ0i(k)进行计算并且对灰色关联度Δ0i(k)进行计算。
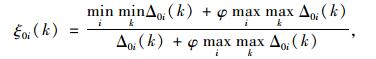
|
(4) |
式中φ为分辨系数,可以提升关联系数间所存在的显著性差别,φ∈(0, 1),一般取φ∈0.5。
则可得到灰色关联度的表达式为:
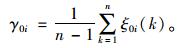
|
(5) |
灰色关联度的范围在[0, 1]之间,越接近1,表明其关联程度越大,本研究将关联度的相关性强度分为4个强度关系,如表 1所示。
1.2 基于灰色关联度理论的速度影响模型 1.2.1 大型车速度分布情况
昆玉高速是连接昆明与玉溪的重要高速公路,双向6车道,车型构成分为小型客车、小型货车和大型车3类。研究数据是昆玉高速某单向路段6天的晚高峰数据,该路段部分纵坡达到4%。采样时间间隔为1 min。
对大型车速度发布区间进行统计,得到昆玉高速晚高峰大型车速度分布区间图,如图 1所示。
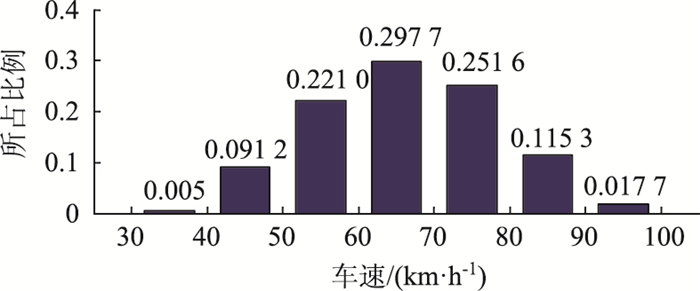
|
| 图 1 大型车车速分布区间图 Fig. 1 Speed distribution range of large vehicles |
| |
数据显示,31.72%的大型车速度低于60 km/h,只有1.77%的大型车速度高于90 km/h。
1.2.2 不同流量状态下、不同大型车比例对平均速度的影响分析通过VISSIM仿真软件,建立了三车道高速公路基本路段模型,取车道宽为3.5 m。根据高速公路服务水平分级,选取设计速度为120 km/h的一、二、三级服务水平对应的流量进行输入。大型车期望速度为30~80 km/h,大型车率分别取10%,20%,30%,小型车期望速度为75~110 km/h。仿真结果如表 2所示。
| 交通流量/[pcu·(h·ln)-1] | 大型车率 | ||
| 10% | 20% | 30% | |
| 750 | 82.2 | 78.6 | 72.3 |
| 1 600 | 72.1 | 63.6 | 55.4 |
| 1 950 | 63.9 | 54.4 | 45.6 |
对相同流量下的不同大型车率的速度减少幅度进行比较,速度差值如表 3所示。
| 交通流量/[pcu·(h·ln)-1] | 大型车率 | |
| 10%~20% | 20%~30% | |
| 750 | 3.6 | 6.3 |
| 1 600 | 8.5 | 8.2 |
| 1 950 | 9.5 | 8.8 |
由仿真分析可得:
(1) 在流量相同的情况下,随着大型车率的增加,车辆平均速度减小。
(2) 对于不同的流量来说,流量较小的情况下,大型车率的增加对速度影响较小。随着流量的增加,大型车率对速度影响越大。
因此大型车比例的增加对平均速度降低的影响显著,特别是大型车比例超过10%以上。
1.2.3 灰色关联度分析的速度模型根据交通波理论,后车状态跟随前车的变化而变化,且由近及远地传播,则第N阶段的车流速度受到N-1阶段的车流速度影响,且以一定的速度向N-2,…, N-i(i=2, 3, 4, …, n)阶段传播。本研究从时间序列角度考虑关联时间单元中大型车比例、速度、密度等特征值与当前速度的关联特性。
应用灰色关联度理论,从时间序列角度,采用了连续6天的数据进行处理,分析了第N-1,N-2, …, N-17个采样阶段的速度、密度、大型车率对第N阶段高速公路交通流速度的关联度,分辨率φ=0.5, 结果如图 2所示。
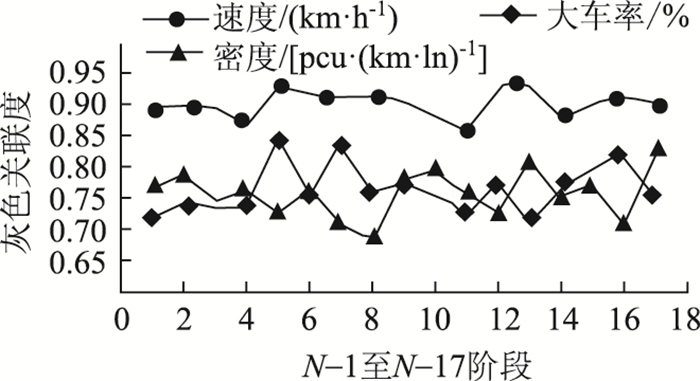
|
| 图 2 速度关联度分析 Fig. 2 Velocity correlation analysis |
| |
结果表明,N-1,N-2, …, N-17个阶段的速度、密度、大型车率,均对N阶段的车流速度产生较大影响。与密度、大型车率相比,N-1,N-2, …, N-17的速度对N阶段速度的关联度最高,即为关键影响因素,密度与大型车率均对速度有较高的影响。
2 基于支持向量机的短时交通流状态预测模型支持向量机[15](Support Vector Machine, SVM)是新一代的基于统计理论的学习系统。SVM作为一种有监督(有导师)的学习方式,可用于分类分析,亦可用于回归拟合。用于分类分析时,即训练点的类别已知,对类别与训练点之间求解对应关系,可以使训练集得以按照类别分类。用于拟合时,其目标是寻找一个平面,使得所有的样本离该平面误差最小。本研究应用回归型支持向量机[16](support vector machine for regression, SVR)方法建立预测模型,其基本思想是在高维空间建立线性的回归函数,用核函数代替线性方程中的线性项,这就可以使之前的线性算法“非线性化”,可以对非线性系统进行回归分析。高速公路系统是非线性系统,其交通流状态可用回归型支持向量机来预测。
2.1 回归模型设训练样本有l个,则训练集样本为{(xi, yi), i=1, 2, …, l}, xi(xi∈Rd)是第i个样本的输入列向量,文中包括速度、密度、大型车率。yi∈R为与xi对应的输出量,即交通流速度。
在高维空间中建立函数:
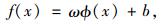
|
(6) |
式中ϕ(x)为将数据映射到高维空间的非线性映射函数。
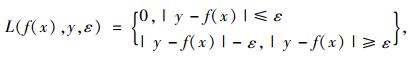
|
(7) |
式中,ε为线性不敏感损失函数,其值越小,表明回归函数的误差越小。f(x)为预测值,而y为真实值,与之对应。
寻找ω, b,并引入松弛变量ξi, ξi*, 其数学语言见式(8):
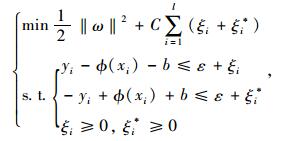
|
(8) |
式中C为惩罚因子,值越大对超过误差ε的惩罚越大。
引入拉格朗日函数,将问题转化为本问题的对偶形式:
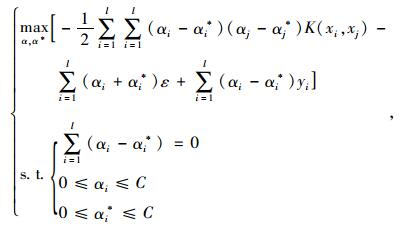
|
(9) |
式中K(xi, xj)=ϕ(xi)ϕ(xj)是核函数,设式(9)的最优解为:α=[α1, α2, …, αl], α*=[α1*, α2*, …, αl*], 则可以得到最优解w*,b*:
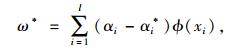
|
(10) |
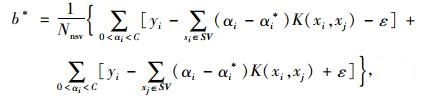
|
(11) |
式中,Nnsv为支持向量的数量;SV为支持向量。
则可以得到,回归函数的形式为:
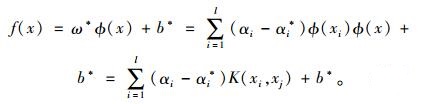
|
(12) |
核函数K(xi, xj)代替了高维空间中两点之间的内积形式,解决了内积计算量大的问题,可以对非线性系统进行分析。常用的核函数主要有以下3种[17]:
(1) 径向基(RBP)核函数:
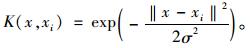
|
(13) |
(2) d阶多项式核函数:
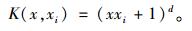
|
(14) |
(3) 具有参数k和θ的Sigmoid核函数:
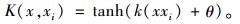
|
(15) |
本研究选取径向基(RBP)核函数,已有研究表明[18],该核函数的泛化能力好,有较高的准确率。
2.3 评价指标为进行预测结果与实际情况的比较,引入2个评价指标[16]:
(1) 均方误差MSE(Mean Squared Error)
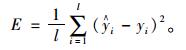
|
(16) |
(2) 决定系数R2(Coefficient of Determination)
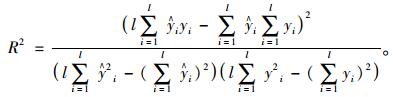
|
(17) |
均方误差越小,表明效果越好。决定系数的范围为[0, 1]之间, 越靠近1表明建立模型性能越好;反之趋近0,表明模型性能差。
应用MATLAB对数据进行仿真预测,在预测方面,支持向量机预测采用增量学习算法,并与BP神经网络模型进行对比。由灰色关联度分析可知前N-17个阶段的大型车率对第N阶段的速度有较大的影响,存在较大相关性,关联度范围为0.708 4-0.850 6。预测时,为了研究大型车比例的相关性,以速度、密度、添加大型车率或未添加大型车率的不同模型进行对比分析。
根据对预测过程的数据分析,输入的关联时间点数据过多或过少,都会对预测结果产生影响。为寻找最佳预测时间序列个数,分别应用N阶段前1~10个时间点对速度进行预测。以速度、密度、大型车率为输入,速度为输出,仿真预测结果的均方误差与决定系数参见表 4、表 5。
| MSE | R2 | |
| 1 | 0.105 83 | 0.38 |
| 2 | 0.069 56 | 0.40 |
| 3 | 0.067 09 | 0.14 |
| 4 | 0.053 53 | 0.19 |
| 5 | 0.047 94 | 0.28 |
| 6 | 0.038 686 | 0.61 |
| 7 | 0.024 19 | 0.58 |
| 8 | 0.028 628 | 0.55 |
| 9 | 0.545 68 | 0.47 |
| 10 | 0.057 848 | 0.19 |
| MSE | R2 | |
| 1 | 0.125 92 | 0.27 |
| 2 | 0.071 07 | 0.38 |
| 3 | 0.060 43 | 0.22 |
| 4 | 0.061 70 | 0.19 |
| 5 | 0.054 63 | 0.19 |
| 6 | 0.059 87 | 0.40 |
| 7 | 0.046 11 | 0.31 |
| 8 | 0.070 36 | 0.52 |
| 9 | 0.057 16 | 0.43 |
| 10 | 0.071 19 | 0.10 |
随着输入时间点的增多,预测精确度得到提高,前6,7个时间点作为输入的预测效果较为准确,达到最优,当输入点继续增加预测效果反而不好,说明时间点选取得过多,将对模型产生干扰作用。与BP神经网络模型相比,支持向量机回归模型效果更好,以前7个时间序列作为输入的预测结果如图 3、图 4所示。
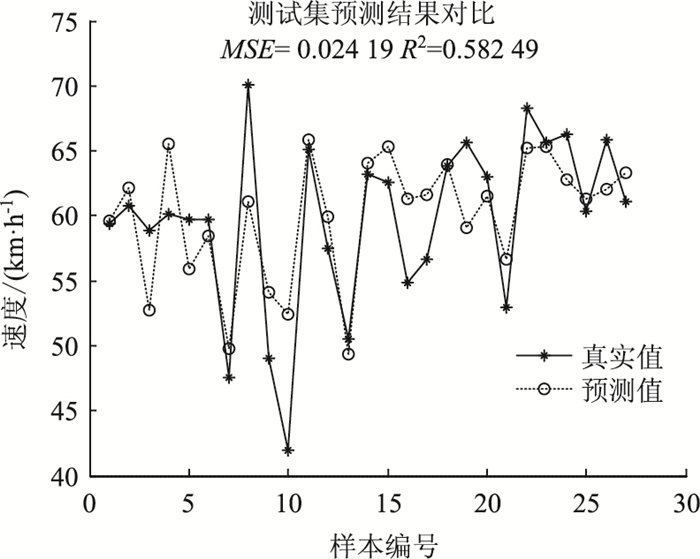
|
| 图 3 支持向量机回归模型预测 Fig. 3 SVM regression model prediction |
| |
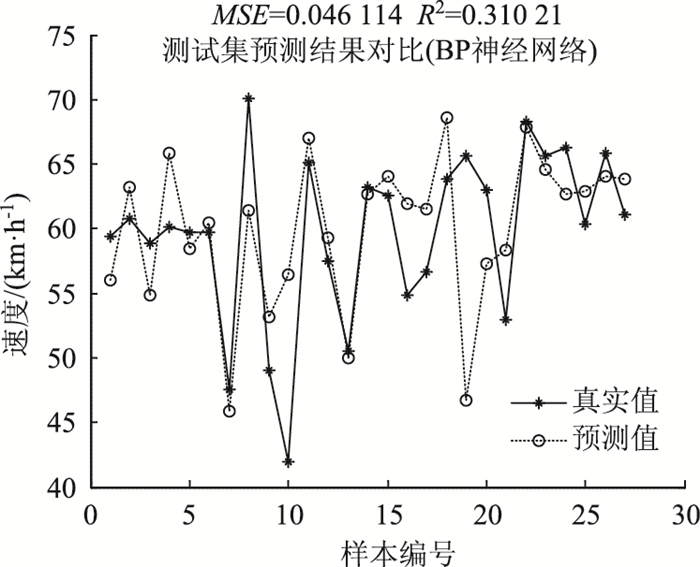
|
| 图 4 BP神经网络预测 Fig. 4 BP neural network prediction |
| |
以前7个时间点作为输入,未加入大型车率的支持向量机模型与BP神经网络模型预测结果如图 5、图 6所示。
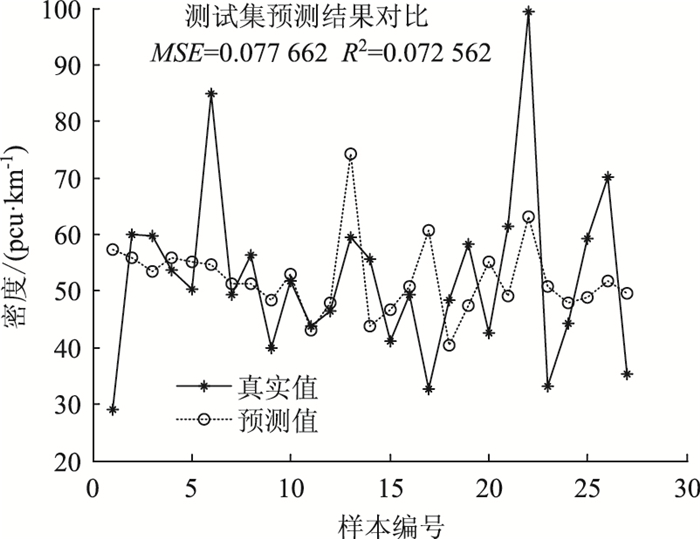
|
| 图 5 未添加大型车率的支持向量机回归模型预测 Fig. 5 SVM regression model prediction without proportions of large vehicles |
| |
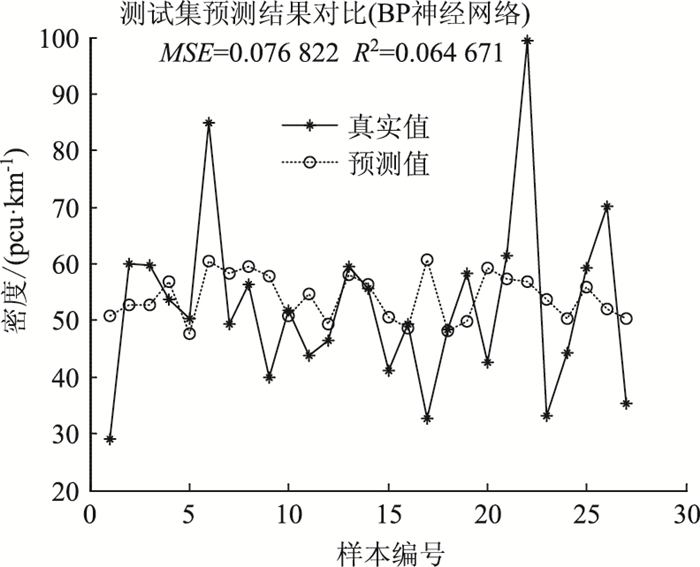
|
| 图 6 未添加大型车率的BP神经网络预测 Fig. 6 BP neural network prediction without proportions of large vehicles |
| |
检验结果表明:
(1) 加入大型车因素的支持向量机回归模型可更准确预测出短时的交通流量变化情况,效果较好。未加入大型车因素的平均均方误差为0.076 62,而加入大型车因素的平均均方误差为0.024 19。
(2) 与BP神经网络模型相比,支持向量机预测模型的均方误差小,决定系数大,具有较好的预测效果,更加接近交通状态的真实情况。
综上所述,大型车比例因素对交通流状态有很大影响,考虑此因素的支持向量机预测模型优于未添加该因素的效果,且支持向量机状态预测优于BP神经网络模型预测。
3 结论本研究提出了基于时间序列的考虑大型车比例影响因素的支持向量机交通流短时状态预测模型。通过仿真技术,明确了大型车比例这一因素对交通流状态的影响,运用灰色关联度理论,定量研究了不同大型车比例(10%~30%之间),不同交通流量状态下该因素对车流平均车速的影响。通过预测数据与实测数据的对比分析,验证了考虑大型车因素可以提高预测结果的准确性。
与传统的BP神经网络模型相比,支持向量机短时交通状态预测模型准确性更好。研究表明,通过前6~7个时间序列样本预测能取得较好的预测效果,样本过多或过少都会降低预测准确性。因此该预测模型对于短时交通状态预测具有数据样本需求少、预测效率高的优点,为高速公路,特别是山区高速公路的主线及匝道运行的管理与控制提供了决策依据。
| [1] |
VLAHOGIANNI E I, GOLIAS J C, KARLAFTIS M G. Short-term Traffic Forecasting:Overview of Objectives and Methods[J]. Transport Reviews, 2004, 24(5): 533-557. |
| [2] |
杨春霞, 符义琴, 鲍铁男. 基于相似性的短时交通流预测[J]. 公路交通科技, 2015, 32(10): 124-128. YANG Chun-xia, FU Yi-qin, BAO Tie-nan. Short-term Traffic Flow Prediction Based on Similarity[J]. Journal of Highway and Transportation Research and Development, 2015, 32(10): 124-128. |
| [3] |
许榕, 周东, 蒋士正, 等. 自适应粒子群神经网络交通流预测模型[J]. 西安交通大学学报, 2015, 49(10): 103-108. XU Rong, ZHOU Dong, JIANG Shi-zheng, et al. A Traffic Forecasting Model Using Adaptive Particle Swarm Optimization Trained Neural Network[J]. Journal of Xi'an Jiaotong University, 2015, 49(10): 103-108. |
| [4] |
LI X. RBF Neural Network Optimized by Particle Swarm Optimization for Forecasting Urban Traffic Flow[C]//2009 Third International Symposium on Intelligent Information Technology Application. Shanghai: IEEE, 2009: 124-127.
|
| [5] |
WU J, ZOU J H. Combination Prediction Based on RBF-SVM Model for Short-term Traffic Flow[J]. Applied Mechanics & Materials, 2014, 475-476: 729-732. |
| [6] |
胡志刚, 杨广全, 乔现玲. 基于小波支持向量机的电梯交通流预测模型[J]. 系统仿真学报, 2009, 21(19): 6321-6324. HU Zhi-gang, YANG Guang-quan, QIAO Xian-ling. WSVMs-based Prediction Model of Elevator Traffic Flow[J]. Journal of System Simulation, 2009, 21(19): 6321-6324. |
| [7] |
韩志聪, 樊彦国, 吴会胜, 等. 基于GA-SVR模型的短期交通流量预测方法研究[J]. 公路交通科技, 2017, 34(1): 130-136. HAN Zhi-cong, FAN Yan-guo, WU Hui-sheng, et al. Study on Methods of Short-time Traffic Volume Forecasting Based on GA-SVR Model[J]. Journal of Highway and Transportation Research and Development, 2017, 34(1): 130-136. |
| [8] |
王祺, 胡坚明, 慕春棣. 基于自适应Kalman滤波的交通流量监测算法[J]. 公路交通科技, 2009, 26(7): 121-126. WANG Qi, HU Jian-ming, MU Chun-di. Algorithm of Traffic Flow Monitoring Based on Adaptive Kalman Filtering[J]. Journal of Highway and Transportation Research and Development, 2009, 26(7): 121-126. |
| [9] |
GAO J, LENG Z, LI X. Traffic Flow Forecasting Based on Adaptive Kalman Filter[J]. ICIC Express Letters. Part B, Applications:An International Journal of Research & Surveys, 2013, 4: 1435-1441. |
| [10] |
邱敦国, 杨红雨. 一种基于双周期时间序列的短时交通流预测算法[J]. 四川大学学报:工程科学版, 2013, 45(5): 68-72. QIU Dun-guo, YANG Hong-yu. A Short-term Traffic Flow Forecast Algorithm Based on Double Seasonal Time Series[J]. Journal of Sichuan University:Engineering Science Edition, 2013, 45(5): 68-72. |
| [11] |
姚智胜, 邵春福, 熊志华, 等. 基于主成分分析和支持向量机的道路网短时交通流量预测[J]. 吉林大学学报:工学版, 2008, 38(1): 48-52. YAO Zhi-sheng, SHAO Chun-fu, XIONG Zhi-hua, et al. Short-term Traffic Volumes Forecasting of Road Network Based on Principal Component Analysis and Support Vector Machine[J]. Journal of Jilin University:Engineering and Technology Edition, 2008, 38(1): 48-52. |
| [12] |
李林超, 何赏璐, 张健. 时空因素影响下在线短时交通量预测[J]. 交通运输系统工程与信息, 2016, 16(5): 165-171. LI Lin-chao, HE Shang-lu, ZHANG Jian. Online Short-term Traffic Flow Prediction Considering the Impact of Temporal-spatial Features[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(5): 165-171. |
| [13] |
张利萍.灰色理论在智能控制中的应用[D].北京: 北京化工大学, 2005. ZHANG Li-ping. Application of Grey Theory in Intelligent Control[D]. Beijing: Beijing University of Chemical Technology, 2005. http://cdmd.cnki.com.cn/article/cdmd-10010-2005123263.htm |
| [14] |
卓金武. MATLAB在数学建模中的应用[M]. 北京: 北京航空航天大学出版社, 2014. ZHUO Jin-wu. Application of MATLAB in Mathematical Modeling[M]. Beijing: Beihang University Press, 2014. |
| [15] |
王小川. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013. WANG Xiao-chuan. Analysis on 43 Cases of MATLAB Neural Network[M]. Beijing: Beihang University Press, 2013. |
| [16] |
史峰, 王辉, 郁磊, 等. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011. SHI Feng, WANG Hui, YU Lei, et al. Analysis on 30 Cases of MATLAB Intelligent Algorithm[M]. Beijing: Beihang University Press, 2011. |
| [17] |
张学工. 关于统计学习理论与支持向量机[J]. 自动化学报, 2000, 26(1): 32-42. ZHANG Xue-gong. Introduction to Statistical Learning Theory and Support Vector Machines[J]. Acta Automatica Sinica, 2000, 26(1): 32-42. |
| [18] |
傅贵, 韩国强, 逯峰, 等. 基于支持向量机回归的短时交通流预测模型[J]. 华南理工大学学报:自然科学版, 2013, 41(9): 71-76. FU Gui, HAN Guo-qiang, LU Feng, et al. Short-term Traffic Flow Forecasting Model Based on Support Vector Machine Regression[J]. Journal of South China University of Technology:Natural Science Edition, 2013, 41(9): 71-76. |
 2018, Vol. 35
2018, Vol. 35
