扩展功能
文章信息
- 席利贺, 张欣, 吴建政, 宋雯
- XI Li-he, ZHANG Xin, WU Jian-zheng, SONG Wen
- 基于动态规划与神经网络的增程式电动汽车能量管理策略研究
- Study on Energy Management Strategy for Extended-range Electric Vehicle Based on Dynamic Programming and Neural Network
- 公路交通科技, 2018, 35(9): 128-136
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(9): 128-136
- 10.3969/j.issn.1002-0268.2018.09.019
-
文章历史
- 收稿日期: 2017-03-22
燃油机动车尾气排放是城市交通污染的主要因素之一。全球59%的CO排放以及43%的NOx排放来自交通运输业[1]。为实现节能减排、绿色低碳城市的发展,纯燃油汽车向新能源汽车转型是一项重要举措,其中电动汽车因其“零污染,零排放”的优势将发挥重要作用[2]。但电动汽车由于动力电池等技术因素的制约,导致其具有续驶里程短、充电时间长等问题,极大地影响电动汽车的推广[3]。增程式电动汽车是在电动汽车基础上添加一个增程器,不但具有低排放、低污染的特点,又可以延长电动汽车的续驶里程,成为新的研究热点[4]。
能量管理策略是整车控制系统的核心内容[5]。现今,国内外对增程式电动汽车能量管理策略的分类主要有:电能消耗-电能维持型(Charging Deplete-Charging Sustain, CD-CS)控制策略和混合型(Blended)控制策略[6-11]。其中CD-CS策略的基本思路为:在行程的初始阶段,车辆以纯电动行驶,即电能消耗阶段。当动力电池SOC降低到最低值时增程器开启,承担汽车行驶的平均需求功率,维持动力电池SOC在最低值附近变化,即为电能维持阶段。CD-CS控制策略具有控制算法简单、实时性好的特点。Blended控制策略的基本思想是通过合理开启增程器,与动力电池协同为驱动电机提供电能,使动力电池SOC缓慢下降。Blended控制策略可根据车辆当前行驶状态,合理开启增程器,并使之工作在最优效率区域内。而CD-CS控制策略在电能维持阶段,增程器作为主要动力源,工作在高负荷状态,相比Blended控制策略,CD-CS控制策略的燃油经济性差[12],这是因为Blended控制策略可根据车辆当前行驶状态,合理开启增程器,并使之工作在高效率区域内;而CD-CS控制策略在电能维持阶段,增程器作为主要动力源,需满足车辆不同工况的需求功率,增程器有时会工作在非高效率区域内。然而在以往设计Blended控制策略过程中,控制参数是通过工程经验得到的,需要花费研究人员大量的时间进行标定才能获得较好的控制效果。
随着计算机技术的发展,一些优化算法可用来设计能量管理策略,例如神经网络、动态规划、粒子蚁群算法、模型预测控制算法等[13-15]。其中动态规划(Dynamic Programming,DP)算法能对固定工况下的能量管理问题进行求解,获得全局最优结果。由于需要大量的迭代计算,很难应用于实时控制[16]。但其优化结果可为其他控制策略提供参考,作为理论最优的基准[17]。文献[18]运用动态规划算法求解增程式电动汽车在不同行驶工况下的能量管理问题,通过总结优化结果中增程器开启工作点与动力电池SOC及需求功率之间的分布规律,提取出增程器开启及增程器输出功率的控制规则,用于设计基于规则的控制策略。文献[19]采用理论分析和工程经验相结合的方式对车辆系统部件的工作区域进行划分,针对不同动力系统部件的工作特点,以需求功率为单一控制参数限定各部件的输出功率,得到基于规则的控制策略。由于增程式电动汽车动力系统具有多输入多输出、非线性耦合等特性[20],不同车辆的结构参数与性能参数差异性较大,使得增程器开启与其输出功率的变化规律并非按照某单一参数变化,因此该方法并不适用于所有增程式电动汽车的能量管理问题。
BP神经网络具有较强的非线性问题处理能力,适合于复杂信息、知识背景不清楚及推理规则不明确等问题的建模,能够有效获得不同数据间的非线性映射关系,且所训练的模型可用于实时控制[21]。因此,本研究首先采用动态规划算法对增程式电动汽车在NEDC工况下的能量管理问题进行求解,获得增程器输出功率分布的最优结果。再采用BP神经网络算法对优化结果进行训练,得到具有实时控制效果的神经网络控制模型,并建立基于神经网络控制模型的混合型控制策略。最后,通过增程式电动汽车前向仿真模型,对该控制器模型进行硬件在环仿真验证。
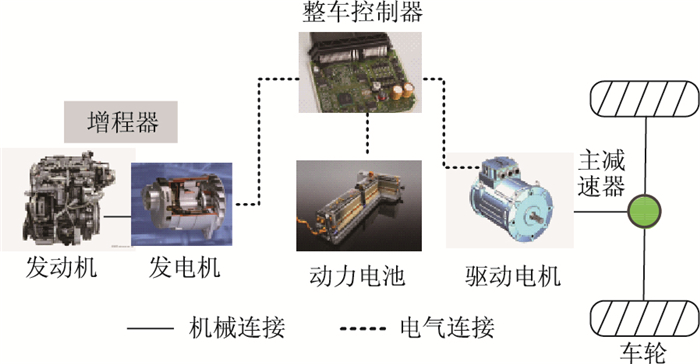
1 EREV动力系统模型 1.1 EREV动力系统结构与主要参数EREV的结构形式如图 1所示。有两个动力源为驱动电机提供电能,即增程器与动力电池。发动机通过连接轴与发电机的转子相连接,组成增程器。增程式电动汽车的动力电池具有较大的电池容量,其工作特性偏向功率型电池,可以单独为驱动电机提供电能。整车控制器能够根据当前车辆行驶状态,综合考虑动力性与燃油经济性等因素,协调驱动电机需求功率在增程器与动力电池之间的分配比例。EREV主要动力系统部件参数见表 1。
|
| 图 1 EREV动力系统结构 Fig. 1 EREV power system configuration |
| |
| 部件 | 参数 | 数值 |
| 排量/L | 0.9 | |
| 发动机 | 最大功/kW | 52 |
| 最大扭矩/(N·m) | 90 | |
| 发电机 | 最大功率/kW | 53 |
| 最大扭矩/(N·m) | 155 | |
| 驱动电机 | 最大功率/kW | 130 |
| 最大扭矩/(N·m) | 480 | |
| 动力电池 | 电容量/(A·h) | 37 |
| 电压/V | 360 | |
| 主减速器传动比 | 7.793 | |
| 整备质量/kg | 1 400 | |
| 其他 | 迎风面积/m2 | 2.9 |
| 轮胎滚动半径/m | 0.298 | |
| 传动系统效率/% | 92 |
在应用动态规划算法求解增程式电动汽车能量管理问题之前,首先建立EREV动力系统模型。考虑到动态规划算法对系统状态方程依赖很大,若系统数学模型的阶数较多,计算量会很大。因此采用建立对象简化模型的方式构建增程式电动汽车动力系统模型[22-23]。
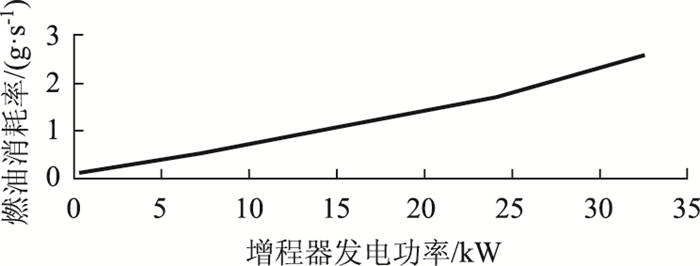
1.2 增程器模型增程器是增程式电动汽车的独立动力单元之一,是将发动机内燃料的化学能转化为电能的装置。由于增程器与驱动电机不存在机械连接,使得增程器中发动机可以自由调节工作点在燃油消耗图上的分布。为了使发动机具有较高的燃油经济性,在增程器工作时控制发动机沿着最优燃油效率曲线工作。该最优效率曲线通过发动机燃油消耗数据与发电机发电效率数据插值计算获得,如图 2所示。
|
| 图 2 增程器发电功率与燃油消耗率关系曲线 Fig. 2 Relationship between extender generating power and its fuel consumption rate |
| |
增程器输出功率所对应的燃油消耗表达式为:
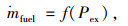
|
(1) |
式中,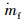
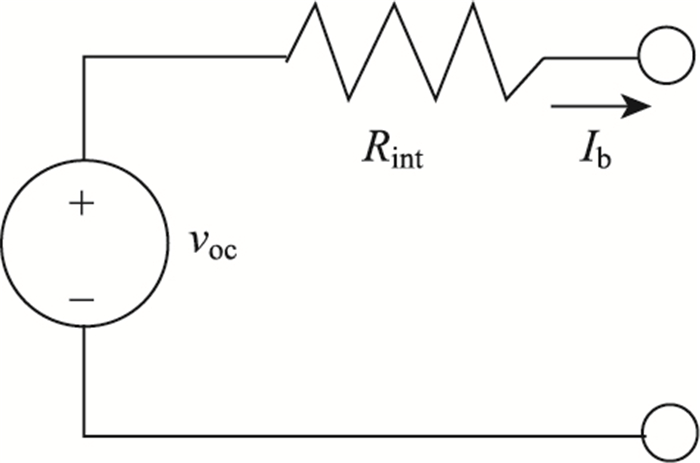
动力电池是将电化学能直接转化为电能的转置。动力电池建模类型主要有RC等效模型与内阻模型。虽然RC等效模型可以较为准确地估计动力电池SOC等参数,但是建模方法复杂,不适用于动态规划[24]。因此本研究采用动力电池内阻模型,如图 3所示,即将动力电池看成由一个开路电源和一个等效内阻组成的装置,忽略温度对动力电池充放电特性的影响。
|
| 图 3 动力电池内阻模型 Fig. 3 Battery internal resistance model |
| |
在图 3中,voc是动力电池的开路电压,是等效内阻Rint的查表函数;Ib为输出电流。
动力电池SOC的变化率计算式为:
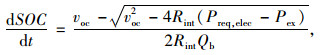
|
(2) |
式中,Preq, elec为驱动电机需求电功率; Pex为增程器发电功率; Qb为动力电池容量。
1.4 整车与传动系统模型利用汽车动力学理论,将车辆在纵向看为质点。整车需求功率PM, mech为[25-27]:
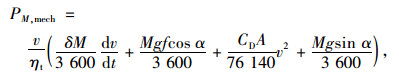
|
(3) |
式中,M为车辆总重量;δ为旋转质量换算系数;g为重力加速度;ηt为传动系统效率;v为车辆纵向行驶速度;f为滚动阻力系数;α为道路坡度;A为迎风面积;CD为空气阻力系数。
2 动态规划算法动态规划算法可求解增程式电动汽车能量管理优化问题,为设计混合型控制策略提供需求功率分配数据基础。在动态规划算法求解过程中,将行驶循环划分为N个阶段,每个阶段步长为1 s。在求解过程中,将以下代价函数作为优化目标[28]:
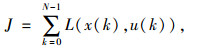
|
(4) |
式中,J为代价函数;L为一步转移代价;N为所划分阶段总数;k为迭代步数。
系统状态方程一般形式为:
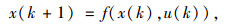
|
(5) |
式中,x为系统状态变量;u为控制变量。
依据总功率不变原则,在工况已知的条件下,可以通过增程器输出功率确定动力电池输出功率,所以选择增程器输出功率Pex为控制量。由于动力电池SOC变化与增程器输出功率存在式(2)的关系,选定动力电池SOC为状态量。
本研究采用的目标函数包含两部分:增程器燃油消耗量、当前动力电池SOC与目标值之间的差值。所建立的目标函数表达式为:
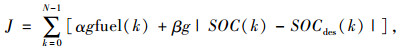
|
(6) |
式中,fuel(k)为每迭代步的燃油消耗量;α和β均为非负加权因子;SOC(k)为当前SOC值,SOCdes(k)为目标SOC值。混合型控制策略的控制目标是车辆在运行过程中动力电池SOC缓慢下降,当车辆结束行程时动力电池SOC刚好降到最低值。因此采用代价函数中的第2项来限制动力电池SOC的变化。其中目标SOC值SOCdes(k)为:
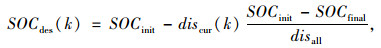
|
(7) |
式中,SOCinit为动力电池SOC初始值;discur(k)为当前累计行驶里程;SOCfinal为行驶里程结束时动力电池SOC目标值;disall为整个行程行驶距离。
为了使动力系统部件在优化求解过程中工作在合理状态下,加入相关物理条件进行约束,如式(8)所示:
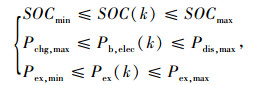
|
(8) |
式中,P代表功率;下角标中ex代表增程器;chg代表充电状态;dis代表放电;min代表下限值;max代表上限值;b代表电池;elec代表电能。
动态规划算法是基于Bellman最优原理的一种全局优化算法[29],它将整体优化过程分解为可递归求解的最小化问题序列。
第N阶段:
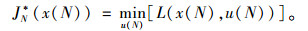
|
(9) |
第k阶段:

|
(10) |
式中, J*(x(k))为在第k阶段,系统由状态x(k)按最优控制序列运行到结束时获得的代价函数;L(x(k), u(k))为状态x(k)在控制量u(k)作用下的一步转移代价。
动态规划算法首先对状态量和控制量进行离散化,在时间轴上形成离散网格空间,仅在网格点间进行计算。在逆向求解时,每阶段状态点所对应的代价函数和最优控制量一般不会落在网格点上,采用如图 4所示[30]的插值方法获得。

|
| 图 4 动态规划算法求解示意图 Fig. 4 Schematic diagram of DP algorithm solving process |
| |
3 BP神经网络
虽然应用动态规划算法可以获得全局优化结果,但由于其在优化过程中需要大量的数值计算,且需要详细的工况信息,例如行驶里程、时间、车速等信息,使得动态规划算法仅作为其他算法的优化基准。BP神经网络具有较强的非线性问题处理能力,能够在信息复杂、推理规则不明确的条件下有效获得不同数据间的非线性映射关系,并可得到具有实时控制能力的训练模型[31]。因此,为了寻找增程器开启时刻及输出功率与车辆运行状态参数之间的非映射关系,本研究构建的神经网络训练结构如图 5所示。

|
| 图 5 BP神经网络结构 Fig. 5 Framework of BP Neural Network |
| |
如图 5所示,神经网络分为输入层、隐含层和输出层。其中输入层共有5个节点,分别为需求功率、小计里程、当前SOC、目标SOC、行驶状态,其中行驶状态分为驻车、加速、制动。输出层为增程器输出功率。
神经网络训练指标为均方差(MSE)为:
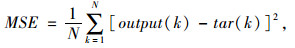
|
(11) |
式中,output(k)为神经网络训练输出;tar(k)为目标值。
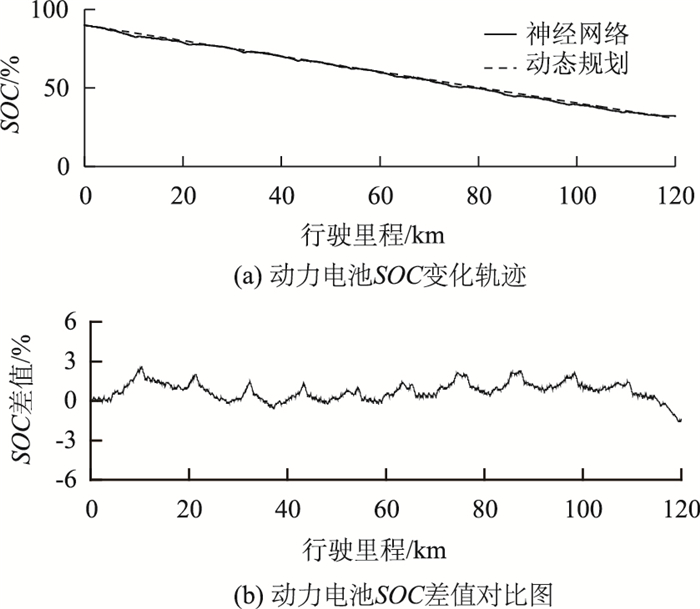
对行驶里程为120 km的NEDC工况采用上述训练方法得到神经网络控制模型。图 6为神经网络控制模型仿真结果与动态规划最优结果对比。其中图 6(a)实线为采用神经网络训练模型得到的动力电池SOC变化曲线,虚线为采用动态规划算法得到的动力电池SOC的最优变化曲线。图 6(b)为两种方式下动力电池SOC的差值。可以看出,神经网络训练模型能够控制动力电池SOC在目标值的3%误差带内,表明训练得到的控制模型具有较好的学习优度。
|
| 图 6 在120 km的NEDC工况下,动态规划与神经网络模型仿真结果 Fig. 6 Simulation result of DP and Neural Network model under 120 km NEDC condition |
| |
另外,采用MAHATTAN标准工况建立了1组行驶里程为120 km的仿真工况,并训练得到该仿真工况下的神经网络控制模型。仿真结果显示,动力电池SOC在仿真结束时能够降到最低值,且与动态规划最优值误差保持在3.5%以内,满足整车控制要求。
4 硬件在环试验与分析 4.1 仿真模型为了验证控制策略在控制器硬件中具有实时控制能力,开展了控制器硬件在环仿真试验。根据动力系统各个部件的数学模型,在Matlab/Simulink环境下建立增程式电动汽车前向仿真模型,如图 7所示。前向模型包括组合仿真工况模型、驾驶员模型、增程器模型、动力电池模型、驱动电机模型、整车动力学模型及整车控制器。其中驾驶员模型是一种车速控制器,内部采用PID控制器将输入的目标车速与当前转速误差转化为加速踏板指令或制动踏板指令。

|
| 图 7 增程式电动汽车前向仿真模型 Fig. 7 EREV forward simulation model |
| |
4.2 仿真工况
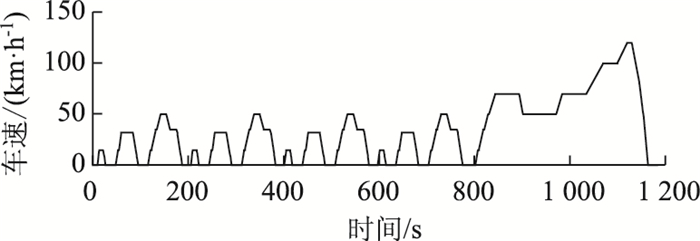
采用NEDC循环工况作为基础工况,其车速曲线如图 8所示。将该基础工况重复10次构建仿真验证工况,所构建的仿真工况数据见表 2。
|
| 图 8 NEDC工况 Fig. 8 NEDC condition |
| |
采用动态规划算法对组合仿真工况进行计算求解,得到理论最优的Blended控制策略,求解过程中SOC初始值为90%,仿真结束时目标SOC为30%。将所产生的优化结果采用第3节构建的BP神经网络进行训练,形成基于BP神经网络的Blended控制策略模型。将所训练的神经网络控制器应用到前面所建立的整车模型当中,形成基于神经网络控制器的前向仿真模型,为验证控制器有效性开展硬件在环仿真。
4.3 试验系统如图 9所示,硬件在环试验系统主要由4个子系统组成:

|
| 图 9 硬件在环试验平台 Fig. 9 Hardware-in-loop test platform |
| |
(1) AutoBox dSPACE系统。内部下载整车前向仿真模型,包括NEDC工况数据。
(2) 控制器开发板。采用英飞凌TC1782开发板作为整车控制器,将基于神经网络的控制策略下载至开发板中。
(3) 监控界面。采用Control Desk自带的监控资源进行监控资源的建立。
(4) 控制器开发板。通过CAN通讯与dSPACE进行各个控制参数的通讯。
在硬件在环试验过程中,为了验证控制器在实际控制中的有效性,结合实车控制器各项参数的精度,对开发板中整车控制器的输入与输出参数进行了调整,如表 3所示。
| 参数类型 | 参数 | 精度 |
| 输入参数 | 需求功率/kW | 0.1 |
| 里程小计/km | 0.1 | |
| 当前SOC/% | 0.1 | |
| 目标SOC/% | 0.1 | |
| 行驶模式 | 1 | |
| 输出参数 | 增程器输出功率/kW | 0.1 |

|
| 图 10 车速误差分布直方图 Fig. 10 Velocity error histogram |
| |

|
| 图 11 动力电池SOC对比 Fig. 11 Comparison of battery SOCs |
| |
|
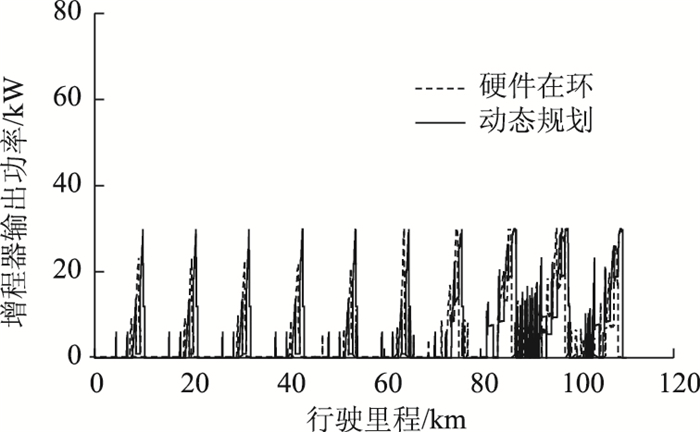
| 图 12 增程器输出功率对比 Fig. 12 Comparison of range extender output powers |
| |
图 10为组合NEDC工况中目标车速与硬件在环仿真车速之间的误差分布直方图。可以看出,控制器模型能够很好地跟随目标车速,满足整车动力性需求。
图 11为硬件在环仿真结果与动态规划优化结果的SOC对比。控制模型能够保持动力电池SOC沿着理论最优的轨迹变化,在行程结束时动力电池SOC刚好降至最低值。
图 12为硬件在环仿真结果与动态规划优化结果中增程器输出功率的对比,表明训练控制具有类似动态规划的控制效果。而且增程器输出功率变化波动较小,可以提高增程器的使用寿命。
对硬件在环试验结果、动态规划优化结果及实车采用的电能消耗-电能维持仿真结果的燃油经济性进行了对比,如表 4所示。可以看出,相比于CD-CS控制策略,混合型控制策略使整车燃油经济性提高了9.5%。
| 项目 | 百公里油耗/L | 节省燃油百分比/% |
| 电能消耗-电能维持控制策略 | 4.12 | — |
| 动态规划优化(理论最优) | 3.64 | 11.7 |
| 硬件在环试验(混合型控制策略) | 3.73 | 9.5 |
5 结论
设计了一种基于动态规划算法与BP神经网络的增程式电动汽车混合型能量管理策略。运用动态规划算法求解增程式电动汽车的能量管理问题,获得了理论最优的优化结果。采用BP神经网络算法对增程器输出功率分布结果进行训练,得到了能量管理控制模型。通过仿真试验可知,训练得到的控制模型能够很好地学习动态规划的优化结果。进行了硬件在环仿真试验,采用组合NEDC工况的试验结果表明,训练得到的神经网络控制模型具有实时控制能力,并且与电能消耗-电能维持型(CD-CS)控制策略相比,本研究建立的混合型控制策略能够提高燃油经济性9.5%。
| [1] |
施晓清, 孙赵鑫, 李笑诺, 等. 北京电动出租车与燃油出租车生命周期环境影响比较研究[J]. 环境科学, 2015, 36(3): 1105-1116. SHI Xiao-qing, SUN Zhao-xin, LI Xiao-nuo, et al. Comparative Life Cycle Environmental Assessment between Electric Taxi and Gasoline Taxi in Beijing[J]. Environmental Science, 2015, 36(3): 1105-1116. |
| [2] |
施晓清, 李笑诺, 杨建新. 低碳交通电动汽车碳减排潜力及其影响因素分析[J]. 环境科学, 2013, 34(1): 385-394. SHI Xiao-qing, LI Xiao-nuo, YANG Jian-xin. Research on Carbon Reduction Potential of Electric Vehicles for Low-carbon Transportation and Its Influencing Factors[J]. Environmental Science, 2013, 34(1): 385-394. |
| [3] |
林歆悠, 林海波, 翟柳清, 等. 基于PSO-fuzzy的PHEV电量保持模式多目标控制策略[J]. 中国公路学报, 2016, 29(10): 132-139. LIN Xin-you, LIN Hai-bo, ZHAI Liu-qing, et al. PSO-fuzzy Multi-objective Control Strategy Based on PHEV Charge-sustaining Mode[J]. China Journal of Highway and Transport, 2016, 29(10): 132-139. |
| [4] |
王耀南, 孟步敏, 申永鹏, 等. 燃油增程式电动汽车动力系统关键技术综述[J]. 中国电机工程学报, 2014, 34(27): 4629-4639. WANG Yao-nan, MENG Bu-min, SHEN Yong-peng, et al. Researches on Power Systems of Extended Range Electric Vehicles[J]. Proceedings of the Chinese Society for Electrical Engineering, 2014, 34(27): 4629-4639. |
| [5] |
陈汉玉, 左承基, 袁银男, 等. 轻度混合动力汽车运行模式控制[J]. 农业工程学报, 2011, 27(10): 61-67. CHEN Han-yu, ZUO Cheng-ji, YUAN Yin-nan, et al. Operating Mode Control Research of Mild Hybrid Electric Vehicle[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(10): 61-67. |
| [6] |
ŠKUGOR B, CIPEK M, DEUR J. Control Variables Optimization and Feedback Control Strategy Design for the Blended Operating Regime of An Extended Range Electric Vehicle[J]. SAE International Journal of Alternative Powertrains, 2014, 3(1): 152-162. |
| [7] |
秦大同, 赵新庆, 苏岭, 等. 插电式混合动力汽车变参数能量管理策略[J]. 中国公路学报, 2015, 28(2): 112-118. QIN Da-tong, ZHAO Xin-qing, SU Ling, et al. Variable Parameter Energy Management Strategy for Plug-in Hybrid Electric Vehicle[J]. China Journal of Highway & Transport, 2015, 28(2): 112-118. |
| [8] |
陈汉玉, 左承基, 滕勤, 等. 增程型电动轿车动力系统的参数匹配及试验研究[J]. 农业工程学报, 2011, 27(12): 69-73. CHEN Han-yu, ZUO Cheng-ji, TENG Qin, et al. Parameter Matching and Experimental Study of Powertrain for Extended-range Electric Car[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(12): 69-73. |
| [9] |
顾强, 程秀生. 基于粒子群算法的电动汽车DCT升档动力协调控制[J]. 农业工程学报, 2012, 28(8): 84-91. GU Qiang, CHENG Xiu-sheng. Coordinated Control of Upshift Power of Double Clutch Transmission for Electric Vehicle Based on Particle Swarm Optimization[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(8): 84-91. |
| [10] |
胡明寅. 增程式电动车动力系统设计及能效优化研究[D]. 北京: 清华大学, 2012. HU Ming-yin. Research on Development of Powertrain System for Extended-range Electric Vehicle and Energy Optimization[D]. Beijing: Tsinghua University, 2012. |
| [11] |
WALSH P, NELSON D. Impact of Supervisory Control on Criteria Tailpipe Emissions for an Extended-range Electric Vehicle[C]//SAE 2012 World Congress & Exhibition. Detroit: SAE, 2012.
|
| [12] |
SHARER P B, ROUSSEAU A, KARBOWSKI D, et al. Plug-in Hybrid Electric Vehicle Control Strategy: Comparison between EV and Charge-depleting Options[C]//SAE 2008 World Congress & Exhibition. Detroit: SAE, 2008.
|
| [13] |
钱立军, 邱利宏, 辛付龙, 等. 插电式四驱混合动力汽车能量管理控制策略及其优化[J]. 农业工程学报, 2015, 31(13): 68-76. QIAN Li-jun, QIU Li-hong, XIN Fu-long, et al. Energy Management Control Strategy and Optimization for Plug-in 4WD Hybrid Electric Vehicle[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(13): 68-76. |
| [14] |
IVERSEN E B, MORALES J M, MADSEN H. Optimal Charging of an Electric Vehicle Using a Markov Decision Process[J]. Applied Energy, 2014, 123: 1-12. |
| [15] |
CHEN S Y, HUNG Y H, WU C H, et al. Optimal Energy Management of a Hybrid Electric Powertrain System Using Improved Particle Swarm Optimization[J]. Applied Energy, 2015, 160: 132-145. |
| [16] |
李卫民. 混合动力汽车控制系统与能量管理策略研究[D]. 上海: 上海交通大学, 2008. LI Wei-min. Research on Control System and Energy Management Strategy of Hybrid Electric Vehicle[D]. Shanghai: Shanghai Jiaotong University, 2008. |
| [17] |
敖国强. ISG混合动力城市客车动力系统集成与优化控制研究[D]. 上海: 上海交通大学, 2009. AO Guo-qiang. The Research on Powertrain Integration and Optimization Control of ISG Hybrid Electric Bus[D]. Shanghai: Shanghai Jiaotong University, 2009. |
| [18] |
CHEN B C, WU Y Y, TSAI H C. Design and Analysis of Power Management Strategy for Range Extended Electric Vehicle using Dynamic Programming[J]. Applied Energy, 2014, 113: 1764-1774. |
| [19] |
杜玖玉, 王贺武, 黄海燕. 基于规则的混联式混合动力系统控制策略[J]. 农业工程学报, 2012, 28(增1): 152-157. DU Jiu-yu, WANG He-wu, HUANG Hai-yan. Rule-based Control Strategy Application on Power-split Hybrid Powertrain[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(S1): 152-157. |
| [20] |
HE B, OUYANG M, LI J. Reduced Order Robust Gain-Scheduling Control of the Diesel APU for Series Hybrid Vehicles[J]. Asian Journal of Control, 2006, 8(3): 227-236. |
| [21] |
吴剑, 张承慧, 崔纳新. 并联式混合动力汽车的BP网络实时能量管理[J]. 电机与控制学报, 2008, 12(5): 610-614. WU Jian, ZHANG Cheng-hui, CUI Na-xin. Real-time Energy Management of Parallel Hybrid Electric Vehicle Based on BP Neural Network[J]. Electric Machines and Control, 2008, 12(5): 610-614. |
| [22] |
ZHANG S, XIONG R. Adaptive Energy Management of a Plug-in Hybrid Electric Vehicle Based on Driving Pattern Recognition and Dynamic Programming[J]. Applied Energy, 2015, 155: 68-78. |
| [23] |
PATIL R M, FILIPI Z, FATHY H K. Comparison of Supervisory Control Strategies for Series Plug-in Hybrid Electric Vehicle Powertrains through Dynamic Programming[J]. IEEE Transactions on Control Systems Technology, 2014, 22(2): 502-509. |
| [24] |
邹渊, 侯仕杰, 韩尔樑, 等. 基于动态规划的混合动力商用车能量管理策略优化[J]. 汽车工程, 2012, 34(8): 663-668. ZOU Yuan, HOU Shi-jie, HAN Er-liang, et al. Dynamic Programming-based Energy Management Strategy Optimization for Hybrid Electric Commercial Vehicle[J]. Automotive Engineering, 2012, 34(8): 663-668. |
| [25] |
余志生. 汽车理论[M]. 北京: 机械工业出版社, 2009. YU Zhi-sheng. Automobile Theory[M]. Beijing: China Machine Press, 2009. |
| [26] |
舒红, 潘文军, 袁景敏, 等. 混合动力汽车匀速下坡再生制动模型预测控制[J]. 公路交通科技, 2011, 28(2): 137-143. SHU Hong, PAN Wen-jun, YUAN Jing-min, et al. Model Predictive Control of Regenerative Braking for a Hybrid Electric Vehicle Cruising Downhill[J]. Journal of Highway & Transportation Research & Development, 2011, 28(2): 137-143. |
| [27] |
秦大同, 周孟喜, 胡明辉, 等. 电动汽车的加速转矩补偿控制策略[J]. 公路交通科技, 2012, 29(5): 146-151. QIN Da-tong, ZHOU Meng-xi, HU Ming-hui, et al. Strategy of Acceleration Torque Compensation Control for Electric Vehicle[J]. Journal of Highway and Transportation Research and Development, 2012, 29(5): 146-151. |
| [28] |
YI L M, PARK J, CHEN Z, et al. Intelligent Hybrid Vehicle Power Control-Part Ⅰ:Machine Learning of Optimal Vehicle Power[J]. IEEE Transactions on Vehicular Technology, 2012, 61(8): 3519-3530. |
| [29] |
BELLMAN R E, DREYFUS S E. Applied Dynamic Programming[M]. Princeton: Princeton University Press, 1962.
|
| [30] |
浦金欢, 殷承良, 张建武. 并联型混合动力汽车燃油经济性最优控制[J]. 上海交通大学学报, 2006, 40(6): 947-951. PU Jin-huan, YIN Cheng-liang, ZHANG Jian-wu. Fuel Optimal Control of Parallel Hybrid Electric Vehicle[J]. Journal of Shanghai Jiaotong University, 2006, 40(6): 947-951. |
| [31] |
孟祥海, 覃薇, 邓晓庆. 基于神经网络的山岭重丘区高速公路事故预测模型[J]. 公路交通科技, 2016, 33(3): 102-108. MENG Xiang-hai, QIN Wei, DENG Xiao-qing. An Accident Prediction Model for Expressways in Mountainous and Rolling Areas Based on Neural Network[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3): 102-108. |
 2018, Vol. 35
2018, Vol. 35
