扩展功能
文章信息
- 赵朋, 王建伟, 孙茂棚, 周雅欣
- ZHAO Peng, WANG Jian-wei, SUN Mao-peng, ZHOU Ya-xin
- 基于贝叶斯网络的高速公路突发事件态势评估研究
- Study on Expressway Emergency Situation Assessment Based on Bayesian Network
- 公路交通科技, 2018, 35(9): 115-121
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(9): 115-121
- 10.3969/j.issn.1002-0268.2018.09.017
-
文章历史
- 收稿日期: 2018-04-15
随着我国社会经济的发展,交通基础设施的逐渐完善,安全出行成为人们关注的重点问题,高速公路突发事件预警、处置和态势评估已越来越受到管理者的重视和研究者的关注。如何在多源异构交通安全数据的基础上,通过数据融合和数据挖掘提取现有的事故状态因素,综合各类因素分析和确定各要素之间的深层联系,全面识别已发生的交通突发事件,推断突发事件后续发展方向以及可能造成的危害,构建处理不确定性信息的态势评估系统,并制定合理、可靠的交通管理和控制策略,降低交通事故人员伤亡率和经济损失,获得最佳的交通运输效益,已成为高速公路交通安全研究中迫切需要解决的实践难题和理论研究的前沿性课题。
自20世纪70年代以来,国内外许多国家对态势评估从理论体系和系统实现方法等方面进行了研究,并取得了很大进展,主要的实现技术包括:基于知识的系统、模板技术、品质因数方法、贝叶斯网络、模糊逻辑技术、遗传算法等。其中贝叶斯网络基于其严密的推理过程、清晰的语义表达和灵活的学习机制等特点,成为了目前人工智能领域一种很重要的推理技术,被广泛应用于各个领域。Robin Schubert和Gerd Wanielik提出了一种将低层融合数据和高层态势估计通过贝叶斯网络进行链接的方法[1]。L Zhao和X Wang应用贝叶斯网络对影响危险品运输事故的因素进行了排序,使用了Dempster-Shafer证据理论并对结构进行修改,为危险品运输公司减少事故风险提供了理论基础[2]。Ivanescu C和Skaltsa K等探讨了不同方法在贝叶斯NMA稀疏网络中处理效果[3]。MR Martins和MC Maturana提出了基于BBN的分析人的可靠性的方法,并将其应用在油轮的运行中[4]。F Goerlandt和J Montewka将贝叶斯网络(BN)建模应用于概率风险量化,提出了海上运输系统风险分析的框架,并将其应用在油轮碰撞溢油事故的案例研究[5]。Almond R G和Mislevy R J等将贝叶斯网络应用在教育评估中[6]。Zhao J和Deng W用贝叶斯网络研究中国城市交叉口碰撞事故[7]。陈为,朱标和张宏鑫等基于贝叶斯网络针对地理空间数据提出了一种新颖的可视分析方法[8]。Mumtaz W和Xia L等基于朴素贝叶斯对提出的传统ML方案进行改进[9]。E Zarei和A Azadeh等利用bowtie图和Bayesian网络对最坏的事故场景进行建模并评估风险,有效降低了事故发生的可能性[10]。姚宏亮和张一鸣等对动态贝叶斯网络的灵敏性进行分析研究[11]。孙剑和孙杰应用贝叶斯网络(BN)模型对快速路实时交通流参数与事故风险进行建模分析,并利用高斯混合模型和最大期望算法评估安全运行风险,对事故状态提前做出预警[12]。杨超和汪超结合贝叶斯网络和非参数回归方法,提出了一种新的快速路交通事件持续时间预测模型[13]。张敬磊和王晓原提出了基于动态贝叶斯网络的交通流状态辨识方法,并利用英国南安普敦市的实际数据对上述方法进行了仿真验证[14]。杨能普,杨月芳和冯伟基于模糊贝叶斯网络对铁路危险货物运输过程进行风险评估[15]。姚成玉,陈东宁和王斌提出了基于T-S故障树和贝叶斯网络的模糊可靠性评估方法[16]。严利鑫和黄珍采用马尔科夫毯特征抽取算法提取出速度、纵向加速度、前轮转角变化率、车道偏离量以及车辆位置作为构建驾驶行为险态辨识的特征集,基于朴素贝叶斯(HNB)构建驾驶行为险态辨识模型[17]。吴静娴和杨敏构建基于贝叶斯网络的迁居人群通勤方式转移模型,模拟并分析个人家庭信息、迁居属性,以及小区建成环境感知变化对原非机动(步行、自行车或电动车)通勤人群出行方式转移的影响[18]。
本研究将贝叶斯网络应用于高速公路突发事件应急处置的态势评估,建立了基于贝叶斯网络的高速公路交通突发事件应急处置态势评估模型,研究贝叶斯网络在高速公路突发事件应急处置方面的应用。
1 高速公路交通突发事件贝叶斯网络态势评估模型 1.1 贝叶斯网络总体工作流程本研究贝叶斯网络构造主要包括以下4个步骤,值得指出的是这4个步骤有时要根据实际情况相互交叉进行。
步骤1:确定网络节点要素。选择事件及解决事件实际问题的相关要素,表达为节点变量。
步骤2:建立表示节点之间相互关系的有向无环图。根据节点之间的相互关系用有向边将各个节点连接起来,描述突发事件各节点间的相互影响作用。
步骤3:进行条件概率估计。网络中的节点必须赋予相应的条件概率,以描述节点与其父节点之间的关联程度,条件概率的生成需要对历史数据进行学习。
步骤4:实现贝叶斯网络推理。利用网络结构及条件概率表进行推理,得到最终结果。其总体工作流程如图 1所示。

|
| 图 1 贝叶斯网络工作流程 Fig. 1 Working process of Bayesian network |
| |
1.2 交通突发事件贝叶斯网络节点
交通突发事件具有一定的演化机理,根据交通突发事件演化特点,将其相关的要素划分为基本要素、状态要素与结果要素3类,这些要素构成交通突发事件贝叶斯网络节点。
(1) 基本要素(B):依据现场获取信息,针对某一特定交通突发事件,明确事故基本特征,对影响事故发生发展的主要危险因素进行标定并离散化表示,以此作为构建贝叶斯网络的上层节点。
(2) 状态要素(S):事故状态要素包括两方面:一是表征事故行为特点的特征变量,按照变量的临界取值范围将事故状态变量进行离散化表示;二是描述事故危险因素对各类承灾体的影响程度。将状态要素作为构建贝叶斯网络的中层节点。
(3) 结果要素(O):交通事故到达终止状态时所造成的最终损失,根据损失程度对变量进行离散化表示,以此作为贝叶斯网络的下层节点。
依据历史高速公路交通突发事件产生的情况,并结合相关领域专家知识确定事故基本要素、状态要素及结果要素,这些要素共同构成了交通突发事件贝叶斯网络中的节点。据此,得到表 1所示的网络节点。
| 基本要素 | 救援车辆到达时间(B1) | 小于等于30 min\大于30 min |
| 得到事故信息的时间 (B2) |
小于等于15 min\大于15 min | |
| 事故车辆类型(B3) | 小汽车\小客车\大客车\货车 | |
| 事发时天气(B4) | 恶劣\良好 | |
| 事发时段(B5) | [0:00—4:00)\[4:00—8:00)\[8:00—12:00)\[12:00—16:00)\[16:00—20:00)\[20:00—24:00) | |
| 道路拥堵状况(B6) | 畅通\一般拥堵\十分拥堵 | |
| 事故车辆数(B7) | 1辆\2辆\2辆以上 | |
| 状态要素 | 失火(S1) | 无\小火\大火 |
| 有毒物质泄漏速度(S2) | 无泄漏\慢速泄漏\快速泄漏 | |
| 事故碰撞规模(S3) | 轻微碰撞\严重碰撞 | |
| 伤亡人数(S4) | 无; 轻伤1~2人\重伤1~2人,或者轻伤3人以上; 死亡1~2人,或者重伤3人以上10人以下; 死亡3人以上,或者重伤11人以上; 或者死亡1人,同时重伤8人以上; 或者死亡2人,同时重伤5人以上 |
|
| 结果要素 | 受污染面积(O1) | 无\小规模污染\大规模污染 |
| 拥堵时间(O2) | 30 min~1 h\1 h~2 h\2 h以上 | |
| 伤亡人数(O3) | 无; 轻伤1~2人\重伤1~2人,或者轻伤3人以上; 死亡1~2人,或者重伤3人以上10人以下; 死亡3人以上,或者重伤11人以上; 或者死亡1人,同时重伤8人以上; 或者死亡2人,同时重伤5人以上 |
1.3 交通突发事件贝叶斯网络结构
根据交通突发事件的发生、发展、演化过程,基本要素是状态要素发生变化的原因,结果要素是状态要素演化到最后的表征,因此交通生产事故贝叶斯网络中的各节点形成上层(基本要素)-中层(状态要素)-下层(结果要素)的3层拓扑结构,详细描述如下:
(1) 基本要素-基本要素子网络:引发事故发生发展的基本要素间会有其内在联系,因此设立基本要素间子网络。
(2) 基本要素-状态要素子网络:该网络主要指基本要素与状态要素之间的因果关系,其描述为基本要素对事件状态的影响程度及对事故状态与承灾体状态的影响程度。
(3) 状态要素-状态要素子网络:该网络主要用于描述状态变量之间的因果关系,可以描述为事件状态变量之间的影响程度,事故状态变量对承灾体状态变量的影响程度以及在不同的事件状态和承灾体状态下该突发事件是否处于发生状态。
(4) 状态要素-结果要素子网络:该网络包括了状态要素与结果要素之间的因果关系,表示当事件或承灾体处于特定状态时,交通突发事件对外部环境的影响或造成特定损失的概率。
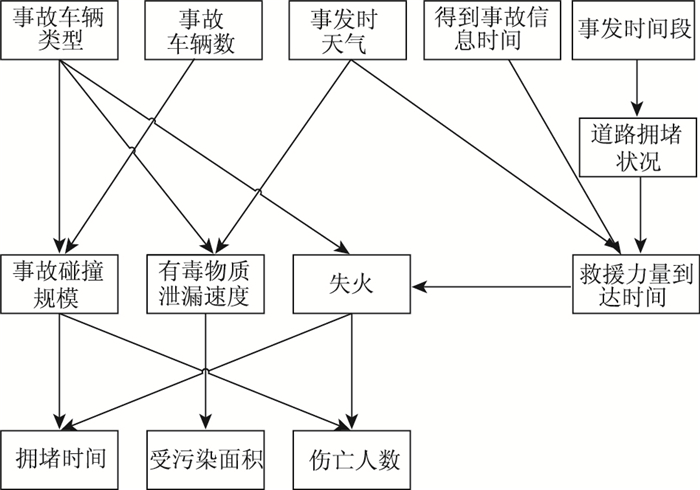
根据上述描述,针对目标交通突发事件,建立的贝叶斯网络如图 2所示。
|
| 图 2 交通突发事件贝叶斯网络结构 Fig. 2 Bayesian network structure of traffic emergencies |
| |
1.4 交通突发事件贝叶斯网络条件概率估计
网络结构确定后,需要对网络中每个节点进行条件概率赋值。网络结构可由多个领域专家合成,但网络节点先验概率与条件概率等定量信息,由专家赋值往往是不准确的。因此,需要收集样本数据,学习各节点的条件概率表。
假设数据样本中包含有事故各个要素及其取值,这时只需要计算突发事件贝叶斯网络中每个节点及其双亲节点的采样统计信息即可。假设节点Vi的直接双亲节点为P(Vi),共有Ki个,用vi表示Vi的取值,Pi表示直接双亲节点变量组成的向量,向量值pi表示向量Pi的取值,那么节点的条件概率表可以根据下式进行采样统计获得。
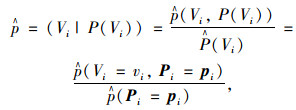
|
(1) |
即由样本数据中Vi=vi,Pi=pi除以Pi=pi的采样数得到。
例如:如图 2所示交通突发事件贝叶斯网络,假设事发时天气(B4)按天气状况取值“良好/恶劣”,救援车辆到达时间(B1)取值“小于等于30 min/大于30 min”,取10组交通运输事故,采样如表 2所示。
| 天气状况(B4) | 救援车辆到达时间(B1) | 采样数量 |
| 良好 | 30 min内 | 5 |
| 良好 | 30 min外 | 1 |
| 恶劣 | 30 min内 | 2 |
| 恶劣 | 30 min外 | 2 |
根据式(1)可知,B1与B4的条件概率估计如下:

|
同理可得:

|

|
则天气状况(B4)与救援车辆到达时间(B1)的条件概率,如表 3所示。
| 天气状况(B4) | (B1)30 min内 | (B1)30 min外 |
| 良好 | 0.83 | 0.17 |
| 恶劣 | 0.5 | 0.5 |
依照此方法得到各节点间的条件概率表。
1.5 交通突发事件贝叶斯网络推理节点条件概率的取得不是最终目的,要在条件概率的基础上进行更进一步的推理,态势评估模型才能得以进一步地建立起来。
贝叶斯网络的精确推理实质上是通过联合概率分布公式,在给定的结构和己知证据下,计算某一事件发生的后验概率P(X|E),E为证据信息。图 2的联合概率可表示为:
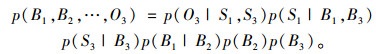
|
(2) |
理论上,在已知网络结构和概率分布表的前提下,任何精确推理都可以通过反复应用贝叶斯公式得到,但是随着网络节点的增加,其计算将花费大量时间,这时可以采用联合树推理算法进行求解。
联合树推理算法的主要思想是将贝叶斯网络转化为联合树,然后通过定义在联合树上的消息传递过程,进行概率计算。联合树算法的步骤如下。
步骤1:构造Moral图,将原贝叶斯网络中同一节点的父节点两两相连,即Marrying Parents,同时去掉每一条连接边的箭头。
步骤2:三角化图(Triangulating),对包含4个及以上节点数的环,增加一条无向边将环中两个非相邻节点连接起来,完成对Moral图的三角化。
步骤3:区分团节点(Identifying Cliques),在三角化图中,确定团节点,每个团节点都是无向图的子图。
步骤4:建立联合树,建立的联合树必须包含所有团节点,交集作为连接两个团节点的分隔节点。
构建联合树的目的是实现在联合树上进行消息传递,求出各随机变量的条件概率。其推理过程见图 3。

|
| 图 3 联合树推理过程 Fig. 3 Reasoning process of joint tree |
| |
联合树形成后,要将贝叶斯网络中的条件概率表转化到联合树中,为所有节点指定参数,利用公式ϕc=φc×P(V|Pa(V))对各团节点初始化,通过消息传递得到满足全局一致性的联合树,即可以求出原贝叶斯网络中任意随机变量的概率分布,选取包含该随机变量的任意团节点,通过边缘化可求出概率分布。
2 实证与讨论随机抽取某省50次高速公路交通突发事件数据,按照上一节方法进行条件概率估计后,通过软件GeNie2.2,以事故车辆类型、事故车辆数量、得到事故信息的时间、事发时天气及事发时段为证据信息,得到事故伤亡情况、道路拥堵情况及受污染面积后验概率。结果如表 4所示,可以看到,当两辆小型客车相撞,救援及时的情况下,造成拥堵时间小于1 h的概率为0.64,不造成人员伤亡的概率为0.56,这与一般高速公路交通事故情况基本一致,预测结果与实际情况较为相符。
| 节点名称 | 取值范围 | 先验概率 | 后验概率 |
| 救援车辆到达时间(B1) | 小于等于30 min\大于30 min | 0.68\0.32 | 0.71\0.29 |
| 得到事故信息的时间(B2) | 小于等于15 min\大于15 min | 0.94\0.06 | 1\0 |
| 事故车辆类型(B3) | 小汽车\小客车\大客车\货车 | 0.16\0.28\0.32\0.24 | 0\1\0\0 |
| 事发时天气(B4) | 恶劣\良好 | 0.34\0.66 | 0\1 |
| 事发时段(B5) | [0:00—4:00)\[4:00—8:00)\[8:00—12:00)\ | 0.12\0.12\0.16 | 0\0\0 |
| [12:00—16:00)\[16:00—20:00)\[20:00—24:00) | 0.32\0.14\0.14 | 1\0\0 | |
| 道路拥堵状况(B6) | 畅通\一般拥堵\十分拥堵 | 0.59\0.29\0.12 | 0.51\0.32\0.17 |
| 事故车辆数(B7) | 1辆\2辆\2辆以上 | 0.2\0.5\0.3 | 0\1\0 |
| 失火(S1) | 无\小火\大火 | 0.77\0.15\0.08 | 0.87\0.09\0.04 |
| 有毒物质泄漏速度(S2) | 无泄漏\慢速泄漏\快速泄漏 | 0.9\0.06\0.04 | 1\0\0 |
| 事故碰撞规模(S3) | 轻微碰撞\严重碰撞 | 0.59\0.41 | 0.6\0.4 |
| 伤亡人数(S4) | 无 | 0.52 | 0.56 |
| 轻伤1~2人\重伤1~2人,或者轻伤3人以上\ | 0.2\0.09 | 0.2\0.07 | |
| 死亡1~2人,或者重伤3人以上10人以下\ | 0.12 | 0.11 | |
| 死亡3人以上,或者重伤11人以上; | |||
| 或者死亡1人,同时重伤8人以上; | 0.07 | 0.06 | |
| 或者死亡2人,同时重伤5人以上 | |||
| 受污染面积(O1) | 无\小规模污染\大规模污染 | 0.9\0.06\0.04 | 1\0\0 |
| 拥堵时间(O2) | 0.5~1 h\1~2 h\2 h以上 | 0.61\0.28\0.11 | 0.64\0.27\0.09 |
| 伤亡人数(O3) | 无 | 0.52 | 0.56 |
| 轻伤1~2人\重伤1~2人,或者轻伤3人以上\ | 0.2\0.09 | 0.2\0.07 | |
| 死亡1~2人,或者重伤3人以上10人以下\ | 0.12 | 0.11 | |
| 死亡3人以上,或者重伤11人以上; | |||
| 或者死亡1人,同时重伤8人以上; | 0.07 | 0.06 | |
| 或者死亡2人,同时重伤5人以上 |
3 结论
(1) 本研究从高速公路交通突发事件演化机理着手,确定贝叶斯网络节点,通过专家和历史数据确定贝叶斯网络结构及条件概率,逐步构建交通突发事件贝叶斯网络,并运用联合树算法进行贝叶斯网络推理,得到事故发生后产生各种危害的概率。
(2) 突发事件的发生是人-车-路-环境相互作用的结果,各变量间表现出明显的影响和被影响的层次性关系。贝叶斯网络的有向无环图以形象直观的表达形式,充分体现了高速公路交通突发事件变量间的层次性关系,能够对高速公路突发事件的特点进行很好的预测分析。
(3) 本研究所建的高速公路突发事件态势评估的贝叶斯网络,推理学习了不同情况下的交通事故概率。所建的模型对于基于贝叶斯网络的高速公路突发事件态势评估的深入和优化高速公路交通管理措施以降低事故损失有一定借鉴意义。
(4) 运用贝叶斯网络进行的交通突发事件态势评估,有很强的理论基础,比起目前依赖决策者经验进行的人工决策有很大优势,辅助决策者在极短时间内做出有效决策,最大程度减少事后伤亡和损失。
| [1] |
SCHUBERT R, WANIELIK G. A Unified Bayesian Approach for Tracking and Situation Assessment[C]//Intelligent Vehicles Symposium. IEEE: San Diego, 2010: 738-745.
|
| [2] |
ZHAO L, WANG X, QIAN Y. Analysis of Factors that Influence Hazardous Material Transportation Accidents Based on Bayesian Networks:A Case Study in China[J]. Safety Science, 2012, 50(4): 1049-1055. |
| [3] |
IVANESCU C, SKALTSA K, HEEMSTRA L, et al. PRM219-Dealing with Zero Cells in Sparse Networks in Bayesian Network Meta-analysis[J]. Value in Health, 2013, 16(7): A614-A614. |
| [4] |
MARTINS M R, MATURANA M C. Application of Bayesian Belief Networks to the Human Reliability Analysis of an Oil Tanker Operation Focusing on Collision Accidents[J]. Reliability Engineering & System Safety, 2013, 110(2): 89-109. |
| [5] |
GOERLANDT F, MONTEWKA J. A Framework for Risk Analysis of Maritime Transportation Systems:A Case Study for Oil Spill from Tankers in a Ship-ship Collision[J]. Safety Science, 2015, 76: 42-66. |
| [6] |
ALMOND R G, MISLEVY R J, STEINBERG L, et al. Bayesian Networks in Educational Assessment[M]. New York: Springer, 2015.
|
| [7] |
ZHAO J, DENG W. The Use of Bayesian Network in Analysis of Urban Intersection Crashes in China[J]. Transport, 2015, 30(4): 411-420. |
| [8] |
陈为, 朱标, 张宏鑫. BN-Mapping:基于贝叶斯网络的地理空间数据可视分析[J]. 计算机学报, 2016, 39(7): 1281-1293. CHEN Wei, ZHU Biao, ZHANG Hong-xin. BN-Mapping:Visual Analysis of Geospatial Data with Bayesian Network[J]. Chinese Journal of Computers, 2016, 39(7): 1281-1293. |
| [9] |
MUMTAZ W, XIA L, ALI S S A, et al. Electroe ncephalogram (EEG)-based computer-aided Technique to Diagnose Major Depressive Disorder (MDD)[J]. Biomedical Signal Processing & Control, 2017, 31: 108-115. |
| [10] |
ZAREI E, AZADEH A, KHAKZAD N, et al. Dynamic Safety Assessment of Natural Gas Stations Using Bayesian Network[J]. Journal of Hazardous Materials, 2016, 321: 830-840. |
| [11] |
姚宏亮, 张一鸣, 李俊照, 等. 动态贝叶斯网络的灵敏性分析研究[J]. 计算机研究与发展, 2014, 51(3): 536-547. YAO Hong-liang, ZHANG Yi-ming, LI Jun-zhao, et al. Research on Sensitivity Analysis for Dynamic Bayesian Networks[J]. Journal of Computer Research and Development, 2014, 51(3): 536-547. |
| [12] |
孙剑, 孙杰. 城市快速路实时交通流运行安全主动风险评估[J]. 同济大学学报:自然科学版, 2014, 42(6): 873-879. SUN Jian, SUN Jie. Proactive Assessment of Real-time Traffic Flow Accident Risk on Urban Expressway[J]. Journal of Tongji University:Natural Science Edition, 2014, 42(6): 873-879. |
| [13] |
杨超, 汪超. 快速路交通事件持续时间预测模型[J]. 同济大学学报:自然科学版, 2013, 41(7): 1015-1019. YANG Chao, WANG Chao. Traffic Incident Duration Forecast Model of Expressway[J]. Journal of Tongji University:Natural Science Edition, 2013, 41(7): 1015-1019. |
| [14] |
张敬磊, 王晓原, 马立云, 等. 基于动态贝叶斯网络的交通流状态辨识方法[J]. 北京理工大学学报, 2014, 34(1): 45-49. ZHANG Jing-lei, WANG Xiao-yuan, MA Li-yun, et al. Research on Traffic Flow States Identification Method Based on Dynamic Bayesian Networks[J]. Transactions of Beijing Institute of Technology, 2014, 34(1): 45-49. |
| [15] |
杨能普, 杨月芳, 冯伟. 基于模糊贝叶斯网络的铁路危险货物运输过程风险评估[J]. 铁道学报, 2014, 36(7): 8-15. YANG Neng-pu, YANG Yue-fang, FENG Wei. Risk Assessment of Railway Dangerous Goods Transport Process Based on Fuzzy Bayesian Network[J]. Journal of the China Railway Society, 2014, 36(7): 8-15. |
| [16] |
姚成玉, 陈东宁, 王斌. 基于T-S故障树和贝叶斯网络的模糊可靠性评估方法[J]. 机械工程学报, 2014, 50(2): 193-201. YAO Cheng-yu, CHEN Dong-ning, WANG Bin. Fuzzy Reliability Assessment Method Based on T-S Fault Tree and Bayesian Network[J]. Journal of Mechanical Engineering, 2014, 50(2): 193-201. |
| [17] |
严利鑫, 黄珍, 朱敦尧, 等. 基于马尔科夫毯和隐朴素贝叶斯的驾驶行为险态辨识[J]. 吉林大学学报:工学版, 2016, 46(6): 1851-1857. YAN Li-xin, HUANG Zhen, ZHU Dun-yao, et al. Driving Risk Status Identification Based on Markov Blanket Hidden Naive Bayes[J]. Journal of Jilin University:Engineering and Technology Edition, 2016, 46(6): 1851-1857. |
| [18] |
吴静娴, 杨敏. 基于贝叶斯网的城市迁居者通勤方式变迁模型[J]. 交通运输系统工程与信息, 2017, 17(6): 94-100. WU Jing-xian, YANG Min. Commuting Modal Shift of Relocated Residents in City Based on Bayesian Networks[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 94-100. |
 2018, Vol. 35
2018, Vol. 35
