扩展功能
文章信息
- 闫欣欣, 袁振洲, 毛思捷, 吴玥琳
- YAN Xin-xin, YUAN Zhen-zhou, MAO Si-jie, WU Yue-lin
- 基于熵权-TOPSIS模型的慢行交通与城市设计协调评价方法
- Coordination Evaluation of Non-motorized Traffic and Urban Design Based on Entropy Weight-TOPSIS Model
- 公路交通科技, 2018, 35(9): 107-114
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(9): 107-114
- 10.3969/j.issn.1002-0268.2018.09.016
-
文章历史
- 收稿日期: 2018-03-25
近年来,慢行交通与城市设计的协调发展越来越受到管理重视,如何在管理过程中进行量化分析是实践中急需解决的问题。控制性详细规划是城市规划管理中既具法律效力又具控制能力的技术管理手段,指标调控操作性在规划管理层级中最强。在该层面以城市设计和慢行交通二者的紧密联系为切入点,建立评价模型,对协调程度做出定量评价和改进措施,能够帮助管理部门高效、有针对性地实现动态管理。因此,控规层面的慢行交通与城市设计协调关系研究具有重要的理论和实践意义。
目前国内外关于控规层面慢行交通与城市设计协调性评价的研究实践较少,且两者协调关系的研究多偏于定性方面。具体而言,两者协调研究主要体现在5个方面:一是城市设计运用于交通枢纽,对整体空间环境、用地功能、交通系统和景观综合提升,如段进等以南京青奥轴线交通枢纽系统为例,提出以城市设计代替交通导向的新思路,以横向多点的地段交通网络代替集中单点式交通枢纽的系统疏散方法,解决复杂交通问题[1]。二是在城市道路规划中运用城市设计,对景观绿化,街道家具、临街建筑色彩的整体控制,如2011年建成的新西兰艾略特街,通过城市设计为慢行使用者提供安全区,为行人提供街道家具,指定临时零售活动空间以增加场所性,并在进出口处设置明显标志,显示出活跃的临街建筑、行人数量与鼓励道路空间中行人与机动车互动中进行城市设计的重要性。三是增强慢行交通的吸引力需要考虑城市设计因素,如里德·尤因和苏珊·汉迪采用专家小组评级法用意象、围合空间、人的尺度、透明度和复杂性来衡量城市设计,为研究者测试步行行为与街道环境间的联系提供指导[2]。Cervero R等采用统计方法对波哥大地区的慢行系统进行了研究,指出影响慢行活动的关键是道路设施的设计(如街道密度、连接度等),说明城市设计对慢行系统的重要性[3]。四是城市设计运用于TOD实践,如吴放以公共交通与慢行交通的高可达性为核心原则,构建起基于“空间结构”、“网路连接”、“功能关联”、“活动层级”的TOD城市空间设计策略框架体系[4]。五是“小街区、密路网”的道路规划趋势凸显城市设计的影响,如Kevin Lynch曾通过视觉层次分析了美国3个城市的形态与公共形象,提出城市形象的骨架是街道和小径[5];卞洪滨将“4 hm用地规模、1 500~2 000人口规模”作为住区中居住街坊的基本尺度,通过控制性详细规划的操作管理方法运用到天津实践中[6]。
TOPSIS方法在交通领域的应用已有很多研究。辛督强基于熵权-TOPSIS方法对陕西省10个地级市的道路交通安全水平进行了综合评价[7];吴瑶等采用基于AHP的TOPSIS模型对3个城市常规公共交通适应性进行分析[8]。在协调性评价方面,罗文斌等利用TOPSIS方法对杭州城市旅游与城市发展协调性进行了评价研究[9];王迎等运用TOPSIS模型结合AHP法与熵权法对西安4个轨道交通线网预选方案进行评价,推选最优方案[10]。本研究在构建了单元控规层面慢行交通与城市设计的协调评价指标体系的基础上,利用熵权-TOPSIS模型建立了慢行交通与城市设计协调性评价模型,并通过对邯郸市南湖单元12个街区进行实例分析,研究了熵权-TOPSIS模型在协调性评价上的合理性和适用性。
1 面向城市控规的慢行交通与城市设计协调评价指标体系的构建指标体系作为规划管理的手段广为应用,英国在2004年曾对规划体系进行了全面改革,从“土地利用”时代迈入“空间”时代,通过量化指标监测规划实施情况;国内指标体系的研究以现版使用的国家控规指标体系为基础,结合相关国家标准和学术研究综合进行归纳。国内外的评价指标体系都体现了多学科融合的趋势,Daniel A. Rodrlguez研究慢行设施环境,包括地形、住宅密度、慢行交通专用道可用性等要素对于慢行出行的影响[11];Meghan Winters等构建了包含自行车设施密度、与机动车交通分离度、自行车友好街道连通性、坡度、目的位置密度的指标体系[12];李清波利用AHP层次分析法,结合隶属度函数,评价慢行交通系统合理度[13];周建琴构建了慢行交通友好程度的评价指标体系,利用模糊综合评价的方法结合数据包络模型建立评价模型并实际应用[14];Serge Salat通过对126个城市实证研究梳理出城市设计的160项指标,涵盖了多种计量指标和计算方法[15];翟宇佳等对城市设计品质量化模型进行综述,剖析这些模型涵盖的维度和指标项,并对数据来源进行细化分类[16]。
在评价指标的选取上,本研究以慢行交通与城市设计协调性评价为出发点,对各自评价指标按照可量化原则进行对比筛选,从控规中的土地利用指标与城市设计指标、城市设计角度的控规开发强度控制指标等多方面切入进行分析,同时借鉴国内外相关评价指标体系,最终构建面向城市控规的慢行交通与城市设计协调评价指标体系如表 1所示,各项指标的计算方法见表 2和表 3。
| 控规层面慢行交通与城市设计协调评价指标体系 | ||||
| 慢行交通指标 | 城市设计指标 | |||
| 区域内有慢行设施道路平均限速值 | 过街设施平均间距 | 公交站点慢行交通可达性 | 用地混合度 | |
| 人非隔离路段比例 | 慢行路网密度 | 步行路网面积比例 | 街区尺度 | |
| 机非隔离路段比例 | 慢行道路平均间距 | 自行车路网面积比例 | 人性化尺度(高宽比) | |
| 交叉口平均过街距离 | 慢行交通节点连通率 | — | 建筑界面贴线率 | |
| 安全岛设置比例 | 公共设施慢行交通可达性 | — | 绿容比 | |
| 指标名称 | 指标类别 | 计算公式 | 指代含义 |
| 交叉口平均过街 距离 |
慢行交通指标 | 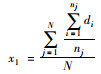 |
nj为区域路网中第j条道路的平面交叉口数量 di为区域路网中第j条道路的第i个交叉口的进口宽度;N为区域路网中的道路数量 |
| 过街设施平均间距 | 慢行交通指标 | 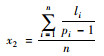 |
li为非一块板道路的路段长度;pi为非一块板道路中过街设施的数量,其中pi≥2; n为非一块板道路的路段数量,路段两端为过街设施 |
| 街区尺度 | 城市设计指标 | 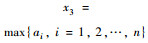 |
ai为街区周边道路相邻交叉口中心间的路段长度;n为街区周边道路相邻交叉口中心间的路段数量 |
| 人性化尺度(高宽比) | 城市设计指标 | x4=D/H | D为道路宽度;H为沿路两侧建筑物高度 |
| 慢行道路平均间距 | 慢行交通指标 | 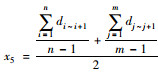 |
n为区域路网中横向慢行道路数;di~i+1为区域路网中第i条横向慢行道路与第i+1条横向慢行道路间的距离;m为区域路网中纵向慢行道路数;dj~j+1为区域路网中第j条纵向慢行道路与第j条间的距离 |
| 区域内有慢行设施道路平均限速值 | 慢行交通指标 | 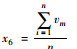 |
n为区域路网内规划慢行设施的道路数量;vm为区域路网内各条规划慢行设施道路的限速值 |
| 指标名称 | 类别 | 计算公式 | 指代含义 |
| 人非隔离路段比例 | 慢行交通指标 | 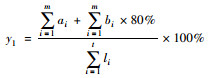 |
ai为人非物理分隔道路中非机动车道长度; bi为人非标线分隔道路中非机动车道长度 |
| 机非隔离路段比例 | 慢行交通指标 | 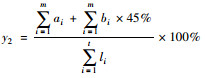 |
ai为机非物理分隔道路中非机动车道长度; bi为机非标线分隔道路中非机动车道长度; li为区域路网各道路长度 |
| 安全岛设置比例 | 慢行交通指标 | 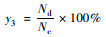 |
Nd为区域路网双向机动车道宽度超过16 m的城市道路中,设置有安全岛的路口、路段过街数量;Nc为区域路网双向机动车道宽度超过16 m的城市道路的路口、路段过街总数 |
| 慢行路网密度 | 慢行交通指标 | 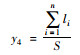 |
li为区域路网内各条步行道的长度; S为区域面积 |
| 步行道路面积比例 | 慢行交通指标 | 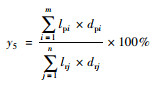 |
lpi为第i条步行道路长度; dpi为第i条步行道路的宽度; lrj为第j条道路长度; drj为第j条道路红线宽度 |
| 自行车道路面积比例 | 慢行交通指标 | 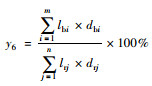 |
lbi为第i条自行车道长度; dbi为第i条自行车道的宽度; lrj为第j条道路长度; drj为第j条道路红线宽度 |
| 慢行交通节点连通率 | 慢行交通指标 | 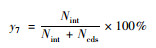 |
Nint为路网中的交叉口数; Ncds为路网中的尽端路口数 |
| 用地混合度 | 城市设计指标 | 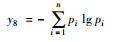 |
n为土地利用类型的划分数目; pi为第i类土地面积所占比例 |
| 公共设施慢行交通 可达性 |
慢行交通指标 | 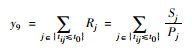 |
Rj为设施j的服务能力和设施j服务范围内总人口数的比值;Sj为设施j的服务能力,根据设施对象确定;Pj为设施j服务范围内的人口数量;tij为研究单元i中心和设施j之间的出行时间或出行距离;t0为出行极限时间或距离 |
| 公交站点慢行交通 可达性 |
慢行交通指标 | 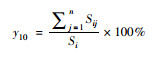 |
n为研究片区内的公交站点数; Sij为公交站点j的服务范围在研究单元i内的面积; Si为研究单元i的总面积 |
| 建筑贴线率 | 城市设计指标 | 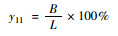 |
B为街墙立面线长度; l为建筑控制线长度 |
| 绿容比 | 城市设计指标 | 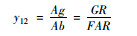 |
Ag为区域绿地总面积;Ab为区域土地开发总建筑面积;GR为区域绿地率;FAR为区域容积率 |
2 熵权-TOPSIS模型建立 2.1 TOPSIS方法基础理论
TOPSIS方法的基本原理:假设有m个备选方案(评价对象)及n个属性(评价指标),将该多属性决策问题视为n维空间中的m个点构成的几何系统,构造正、负理想点,即最优、最劣方案,分别计算各个备选方案与正、负理想点之间的欧式距离,从而得到接近正理想点和远离负理想点的相对贴近度,以此作为评价优劣的依据[17]。
2.2 慢行交通与城市设计协调评价的熵权-TOPSIS模型建立 2.2.1 确定正、负理想解TOPSIS方法的核心是正、负理想解的确定。通常采用在归一化的原始矩阵中,找出有限方案的最优和最劣方案,作为正、负理想解。
在协调评价指标体系中,其值越小越好的指标称之为成本型指标,越大越好的指标称之为效益型指标。以最优方案(正理想解)为例,方案中包含了所有指标,其中成本型指标取所有评价方案中的最小值,产出指标则取所有评价方案中的最大值,以此构造最优方案;相反则可构造最劣方案(负理想解)。
本研究构建的慢行交通与城市设计协调评价指标体系中,成本型和效益型指标的分类如表 2和表 3所示。
2.2.2 熵权-TOPSIS模型建立过程根据TOPSIS方法的基本原理,基于已构建的指标体系,建立如下慢行交通与城市设计协调评价的TOPSIS模型[18]:
(1) 假设评价对象有n个街区,协调评价指标体系包含18个指标,原始数据矩阵如下:
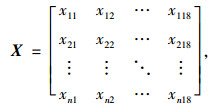
|
(1) |
式中,xij为第i个街区的第j个指标值,i=1, 2, …, n, j=1, 2, …, 18。
(2) 对原始数据规范化处理,得到规范化矩阵如下:
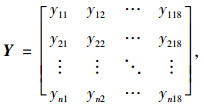
|
(2) |
式中,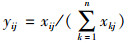
(3) 考虑各个指标的权重,得到加权的规范化矩阵如下:

|
(3) |
式中,zij=yij×ωj, i=1,2,…, n, j=1, 2, …, 18;ωj为第j个指标的权重。本研究采用熵权法计算指标的权重,其计算步骤如下:
① 构建判断矩阵
对n个街区进行评价,包含18个评价指标,相应的指标值为xij(i=1, 2, …, n; j=1, 2, …,18),从而构建判断矩阵R=(xij)n×18。
② 标准化处理
将评价指标的判断矩阵进行标准化处理,得到标准化判断矩阵B=(bij)n×18(i=1, 2, …, n; j=1, 2, …, 18)。
对于越大越好的指标(效益型指标):
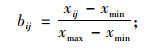
|
(4) |
对于越小越好的指标(成本型指标):
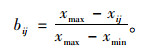
|
(5) |
式中,xij为第i个街区的第j个指标值;xmin为第i个街区的第j个指标的最小值;xmax为第i个街区的第j个指标的最大值。
③ 确定指标的熵
根据熵的定义,可以确定第j个指标的熵值为:
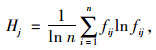
|
(6) |
式中,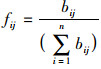
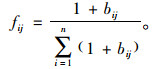
|
(7) |
④ 计算指标的熵权
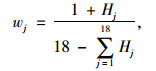
|
(8) |
各个指标的权重满足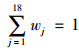
(4) 正、负理想解的计算方法为
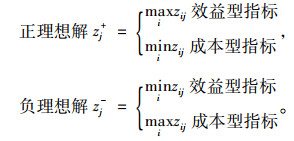
|
从而构成最优方案Z+=(z1+, z2+, …, z18+), 和最劣方案Z-=(z1-, z2-, …, z18-)。
(5) 计算各个街区分别与最优方案和最劣方案的距离:
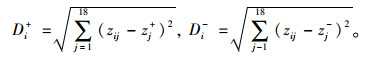
|
(9) |
(6) 计算各街区与最优方案的相对贴近度:
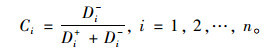
|
(10) |
Ci越大,表明第i个街区越接近最优水平,即慢行交通与城市设计协调程度越高。为确定街区的慢行交通与城市设计是否协调,需对相对贴近度的取值范围(0-1)进行协调状态等级划分,划分标准参见表 4。
达到三级及以上的评价结果,认为该街区的慢行交通与城市设计协调。
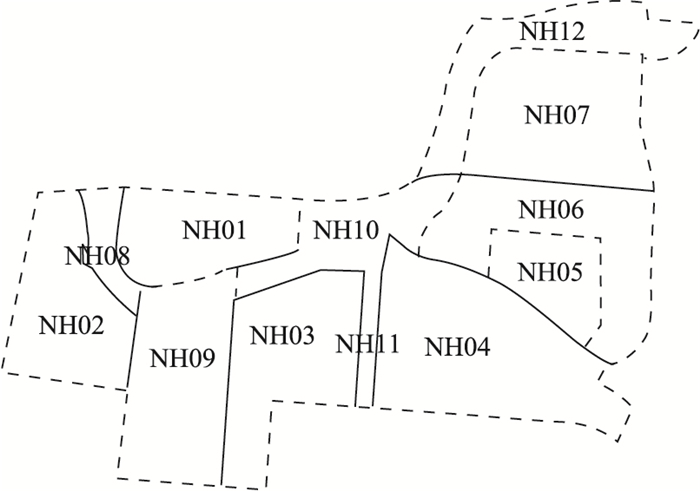
3 实例分析选取河北省邯郸市控制性详细规划中南湖区(编制单元)的12个街区(管理单元)作为应用案例。南湖区的街区划分(NH01-NH12)如图 1所示。
|
| 图 1 南湖单元12个街区划分示意图 Fig. 1 Dividing of 12 blocks of Nanhu unit |
| |
3.1 数据获取
根据调研所得的相关控规文件,结合指标的计算公式,从中获取所需数据,并分别计算12个街区的18个评价指标的规划值。计算结果汇总如表 5、表 6所示。
| 街区 编号 |
成本型指标 | |||||
| 交叉口 平均过街 距离/m |
过街设施 平均 间距/m |
街区 尺度/m |
高宽比 | 慢行道路 平均间 距/m |
有慢行 设施道路 平均限速/ (km·h-1) |
|
| NH01 | 32 | 294 | 1 994.9 | 1.31 | 339 | 40 |
| NH02 | 33 | 297 | 2 000.3 | 1.96 | 283 | 41 |
| NH03 | 35 | 306 | 2 114.5 | 2.09 | 316 | 46 |
| NH04 | 36 | 297 | 2 792.1 | 2.37 | 267 | 44 |
| NH05 | 34 | 335 | 1 223.1 | 2.26 | 282 | 40 |
| NH06 | 36 | 343 | 2 457.2 | 2.27 | 320 | 41 |
| NH07 | 33 | 285 | 2 110.8 | 2.05 | 239 | 41 |
| NH08 | 36 | 365 | 1 412.4 | 1.45 | 455 | 44 |
| NH09 | 30 | 309 | 2 421.4 | 1.7 | 423 | 40 |
| NH10 | 43 | 313 | 2 731.8 | 2.02 | 605 | 48 |
| NH11 | 42 | 239 | 1 491.7 | 2.8 | 465 | 52 |
| NH12 | 47 | 484 | 2 741.4 | 2.6 | 636 | 51 |
| 街区编号 | 效益型指标 | |||||||||||
| 人非隔离 比例/% |
机非隔离 比例/% |
安全岛设 置比例/% |
慢行路网 密度/ (km·km-2) |
步行道路 面积 比例/% |
自行车 道路面积 比例/% |
慢行交通 节点连通 率/% |
用地混 合度 |
公共设施 可达性 |
公交站点 可达性/% |
建筑贴 线率/% |
绿容比 | |
| NH01 | 75.2 | 70.9 | 20 | 7.04 | 21.3 | 22.5 | 75 | 0.637 | 4.53 | 67.3 | 70 | 0.086 |
| NH02 | 62.5 | 87.5 | 30 | 7.29 | 16.8 | 19.6 | 97.1 | 0.826 | 18.6 | 31.8 | 69 | 0.161 |
| NH03 | 60.1 | 86.7 | 11 | 7.95 | 15.8 | 18.8 | 100 | 0.685 | 177 | 27.5 | 69 | 0.115 |
| NH04 | 60.9 | 91.4 | 33.3 | 7.61 | 14.6 | 18.8 | 94.7 | 0.753 | 33.1 | 30.6 | 68 | 0.138 |
| NH05 | 73.3 | 89.7 | 20 | 8.24 | 14.8 | 19.5 | 100 | 0.626 | 120 | 53 | 70 | 0.692 |
| NH06 | 47 | 95.2 | 30 | 7.7 | 17.6 | 21.9 | 73 | 0.55 | 4.02 | 46.7 | 68 | 0.133 |
| NH07 | 38.9 | 90.1 | 20 | 8.26 | 20.5 | 22.1 | 80.4 | 0.64 | 15.7 | 39.2 | 68 | 0.177 |
| NH08 | 86.3 | 75.3 | 33.3 | 7.04 | 25.2 | 25.2 | 83.3 | 0.383 | 25.4 | 30.8 | 66 | 0.74 |
| NH09 | 97.9 | 97.9 | 50 | 5.79 | 16.1 | 20.8 | 100 | 0.743 | 229.3 | 35 | 71 | 0.348 |
| NH10 | 46 | 90.9 | 60 | 6.78 | 24 | 26.6 | 63.6 | 0.608 | 58.8 | 25.5 | 64 | 0.34 |
| NH11 | 52.5 | 100 | 20 | 13.44 | 22.3 | 22.3 | 100 | 0.378 | 13.3 | 0 | 66 | 0.638 |
| NH12 | 55.2 | 100 | 37.5 | 6.82 | 21.4 | 23.3 | 60 | 0.546 | 124 | 82.2 | 62 | 0.499 |
3.2 评价结果及分析
TOPSIS方法对评价街区和评价指标的数目没有特殊要求,因此可将指标值直接代入模型计算。应用TOPSIS方法之前,通过熵权法计算各个指标的权重,其结果见表 7和表 8。
| 成本型 指标 |
交叉口 平均过街 距离 |
过街设施 平均 间距 |
街区尺度 | 人性化 尺度 (高宽比) |
慢行道路 平均 间距 |
区域内有 慢行设施道路 平均限速 |
| 指标权重 | 0.055 6 | 0.055 7 | 0.055 5 | 0.055 6 | 0.055 6 | 0.055 5 |
| 效益型 指标 |
人非隔离 路段比例 |
机非隔离 路段比例 |
安全岛 设置比例 |
慢行路网 密度 |
步行道路 面积比例 |
自行车 道路面 积比例 |
慢行交通 节点连通 率 |
用地 混合度 |
公共设施 慢行交通 可达性 |
公交站点 慢行交通 可达性 |
建筑界面 贴线率 |
绿容比 |
| 指标权重 | 0.055 6 | 0.055 6 | 0.055 6 | 0.055 6 | 0.055 5 | 0.055 5 | 0.055 5 | 0.055 6 | 0.055 5 | 0.055 6 | 0.055 6 | 0.055 4 |
将表 7、表 8中各指标的权重值以及原始指标数据代入TOPSIS模型,利用MATLAB软件计算,得到南湖单元12个街区的相对贴近度,见表 9。
| 街区 | NH01 | NH02 | NH03 | NH04 | NH05 | NH06 | NH07 | NH08 | NH09 | NH10 | NH11 | NH12 |
| 相对贴近 度Ci |
0.360 7 | 0.324 2 | 0.482 1 | 0.319 8 | 0.565 8 | 0.297 2 | 0.313 3 | 0.427 6 | 0.650 2 | 0.387 7 | 0.352 7 | 0.531 2 |
(1) 协调性评价结果分析
依据协调状态等级划分标准,12个街区的协调状态判定如表 10所示。
| 街区 | NH01 | NH02 | NH03 | NH04 | NH05 | NH06 | NH07 | NH08 | NH09 | NH10 | NH11 | NH12 |
| 级别 | 二级 | 二级 | 三级 | 二级 | 三级 | 二级 | 二级 | 三级 | 四级 | 二级 | 二级 | 三级 |
| 协调状态 | 较不协调 | 较不协调 | 一般 | 较不协调 | 一般 | 较不协调 | 较不协调 | 一般 | 较协调 | 较不协调 | 较不协调 | 一般 |
因此,只有NH03街区、NH05街区、NH08街区、NH09街区、NH12街区的慢行交通规划与城市设计方案是协调的。但从整体来看,只有NH09街区达到了四级,其余协调的街区均为三级,说明南湖单元的慢行交通与城市设计整体协调程度较差。
(2) 评价模型适用性分析
NH08、NH10等街区评价结果相对较差,分析认为这是因为街区几乎只有绿地和水域,而同样是绿地功能街区的NH09街区还涵盖了其他建设用地及交通用地,用地布局相对合理,更适宜发展慢行交通。
此外,NH06街区中居住用地占了很大面积,而其他功能用地比例很小,导致了该街区的用地混合度相对较小。同时,NH06街区的北边界和东边界均为快速路,导致了慢行路网的阻断,大大降低了路网连通性。所以,NH06街区得到较差的评价结果比较符合实际情况。
由此,评价结果相对于实际情况具有合理性,表明基于熵权的TOPSIS协调性评价方法在城市控规层面的慢行交通与城市设计协调性评价上较为适用,指标的选取有效。
4 结论本研究构建了单元控规层面的慢行交通与城市设计协调评价指标体系,采用熵权-TOPSIS模型对慢行交通与城市设计的协调性进行评价。实例计算结果证明选取指标及模型在协调性评价方法上是合理可行的。在今后的应用中,可以针对模型的使用情况进一步改进,具体从以下几点进一步完善和深化:
(1) 改进距离公式:由于基本TOPSIS模型所采用的欧式距离计算自身的局限性,可对其公式加以改进,如采用广义马氏距离[19],尽量消除量纲的影响;
(2) 消除逆序现象:TOPSIS方法计算得到的相对贴近度会随着正、负理想解的改变而发生变化,为消除理想解改变引起的逆序现象,可采用绝对理想解,即取评价对象各指标理论上所能出现的最优状态和最劣状态的极限值。
| [1] |
段进, 陈晓东, 钱艳. 城市设计引导下的空间使用与交通一体化设计:南京青奥轴线交通枢纽系统疏散的设计方法与创新[J]. 城市规划, 2014, 38(7): 91-96. DUAN Jin, CHEN Xiao-dong, QIAN Yan. Space Utilization and Transport Integrated Design under the Guidance of Urban Design:Methods and Innovations on Systematic Dispersion of Transport Hubs along Youth Olympics Axis in Nanjing[J]. City Planning Review, 2014, 38(7): 91-96. |
| [2] |
EWING R, HANDY S. Measuring the Unmeasurable:Urban Design Qualities Related to Walkability[J]. Journal of Urban Design, 2009, 14(1): 65-84. |
| [3] |
CERVEROR, LSARMIENTOO, JACOBYE, 等. 建成环境对步行和自行车出行的影响:以波哥大为例[J]. 城市交通, 2016, 14(5): 83-96. CERVERO R, LSARMIENTO O, JACOBY E, et al. Influences of Built Environments on Walking and Cycling:Lessons from Bogotá[J]. Urban Transport of China, 2016, 14(5): 83-96. |
| [4] |
吴放. 基于可持续宜居城市发展的TOD城市空间设计策略研究[D]. 杭州: 浙江大学, 2014. WU Fang. Research on TOD Urban Space Design Strategy on the Basis of Sustainable and Livable Urban Development[D]. Hangzhou: Zhenjiang University, 2014. |
| [5] |
LYNCH K. The Image of the City[M]//The Image of the City. Caonbridge: MIT. Press, 1960: 46-68.
|
| [6] |
卞洪滨. 小街区密路网住区模式研究: 以天津为例[D]. 天津: 天津大学, 2010. BIAN Hong-bin. The Study on Pattern of Small Block Residential Space: Taking Tianjin as an Example[D]. Tianjin: Tianjin University, 2010. |
| [7] |
辛督强. 基于熵权-TOPSIS的陕西省各市区道路交通安全评价[J]. 中国安全生产科学技术, 2015, 11(10): 116-120. XIN Du-qiang. Evaluation on Road Traffic Safety of the Cities in Shanxi Province Based on Entropy-TOPSIS Method[J]. Journal of Safety Science and Technology, 2015, 11(10): 116-120. |
| [8] |
吴瑶, 陆建, 邱红桐, 等. 基于TOPSIS模型城市常规公共交通适应性评价[J]. 交通信息与安全, 2014, 32(6): 153-158, 165. WU Yao, LU Jian, QIU Hong-tong, et al. Evaluation of Adaptability of Urban Public Transit Based on TOPSIS Model[J]. Journal of Transport Information and Safety, 2014, 32(6): 153-158, 165. |
| [9] |
罗文斌, 汪友结, 吴一洲, 等. 基于TOPSIS法的城市旅游与城市发展协调性评价研究:以杭州市为例[J]. 旅游学刊, 2008, 23(12): 13-17. LUO Wen-bin, WANG You-jie, WU Yi-zhou, et al. A Study on the Evaluation of Coordination between Urban Tourism and Urban Development Based on the Method of TOPSIS:A Case Study of Hangzhou[J]. Tourism Tribune, 2008, 23(12): 13-17. |
| [10] |
王迎, 陈宽民, 周燕. 基于TOPSIS模型的轨道交通线网评价[J]. 公路交通科技, 2015, 32(6): 130-134. WANG Ying, CHEN Kuan-min, ZHOU Yan. Assessment of Rail Transit Network Based on TOPSIS Model[J]. Journal of Highway and Transportation Research and Development, 2015, 32(6): 130-134. |
| [11] |
RodríGuez D A, JOO J. The Relationship between Non-motorized Mode Choice and the Local Physical Environment[J]. Transportation Research Part D Transport & Environment, 2004, 9(2): 151-173. |
| [12] |
WINTERS M, BRAUER M, SETTON E M, et al. Mapping Bikeability:A Spatial Tool to Support Sustainable Travel[J]. Environment & Planning B Planning & Design, 2013, 40(5): 865-883. |
| [13] |
李清波, 罗进锋, 宋鸿. 基于层次分析法的慢行交通系统评价研究[J]. 现代交通技术, 2014, 11(1): 58-60, 69. LI Qing-bo, LUO Jin-feng, SONG Hong. Research on Slow Traffic System Evaluation Based on Analytic Hierarchy Process[J]. Modern Transportation Technology, 2014, 11(1): 58-60, 69. |
| [14] |
周建琴. 城市慢行交通友好性综合评价研究[D]. 北京: 北京交通大学, 2011. ZHOU Jian-qin. Study on the Comprehensive Evaluation of Urban Slow Traffic Friendliness[D]. Beijing: Beijing Jiaotomg University, 2011. |
| [15] |
SALATS. 城市与形态:关于可持续城市化的研究[M]. 北京: 中国建筑工业出版社, 2012. SALAT S. Cities and Forms:On Sustainable Urbanism[M]. Beijing: China Architecture & Building Press, 2012. |
| [16] |
翟宇佳, 徐磊青. 城市设计品质量化模型综述[J]. 时代建筑, 2016(2): 133-139. ZHAI Yu-jia, XU Lei-qing. Review of Measurement Tools of Urban Design Quality[J]. Time Architecture, 2016(2): 133-139. |
| [17] |
周亚. 多属性决策中的TOPSIS法研究[D]. 武汉: 武汉理工大学, 2009. ZHOU Ya. The Research on the Methods of TOPSIS in the Multiple Attribute Decision Making[D]. Wuhan: Wuhan University of Technology, 2009. |
| [18] |
邓朝晖, 薛惠锋. 熵权灰色关联分析法的区域E-E-S协调评价[J]. 西安工业大学学报, 2011, 31(6): 566-569. DENG Zhao-hui, XUE Hui-feng. Evaluation of Coordination Degree of Economy Environment Society Structure Based on Entropy Weighted Gray Correlation Analysis[J]. Journal of Xi'an Technological University, 2011, 31(6): 566-569. |
| [19] |
关宏艳, 李宗坤, 葛巍, 等. 基于加权广义马氏距离的TOPSIS方法在水库防洪调度决策中的应用[J]. 天津大学学报:自然科学与工程技术版, 2016, 49(12): 1276-1281. GUAN Hong-yan, LI Zong-kun, GE Wei, et al. TOPSIS Method Based on Weighted Generalized Mahalanobis Distance:An Application to Eservoir Flood Control Operation[J]. Journal of Tianjin University, 2016, 49(12): 1276-1281. |
 2018, Vol. 35
2018, Vol. 35
