扩展功能
文章信息
- 刘澜, 李新
- LIU Lan, LI Xin
- 基于MFD的路网可扩展边界控制策略
- Scalable Perimeter Control Strategy of Road Network Based on MFD
- 公路交通科技, 2018, 35(9): 85-91
- Journal of Highway and Transportation Research and Denelopment, 2018, 35(9): 85-91
- 10.3969/j.issn.1002-0268.2018.09.013
-
文章历史
- 收稿日期: 2017-05-18
2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室, 四川 成都 610031
2. Comprehensive Transportation Intelligent National Local United Engineering Laboratory, Southwest Jiaotong University, Chengdu Sichuan 610031, China
随着城市机动化进程的不断加快,拥堵已成为城市的常态化问题。无论是从发生时间的频度、强度,还是从影响范围,中心区域大面积的交通拥堵对城市发展的总体影响日益明显。国内外学者在大量研究后对交通拥堵的成因形成基本共识,交通拥堵与区域的交通需求有关,当路网通行能力达到上限时就会出现拥堵。因此合理控制路网的输入流量是解决交通拥堵的关键点,尤其是对于进入中心城区交通总流量的调控。
目前我们通常采用的区域交通总量控制的手段有尾号限行、拥挤收费、错峰出行等。然而这些都是通过政策法规来对控制区域的交通总量进行宏观调控,涉及多元利益权衡,易引起争议,而且没有考虑到微观交通流供需平衡关系,难以对应到具体的交通拥挤问题上,没有有效利用当下流行的智能交通技术。因此,为了更为有效地控制路网交通拥挤,管理者们从技术角度考虑来调控区域交通总量。
在智能交通条件下,对路网交通状态的刻画出现了一个新的量化工具MFD,基于MFD对过饱和路网的控制问题,相关学者已经取得了许多代表性的研究成果。张勇等[1]提出了一种超饱和路网边界控制策略, 即Bang-Bang控制,将拥堵区路网上的累积车辆数作为状态变量,建立了拥堵区路网宏观交通流状态方程,并根据庞特里亚金极小值原理求解状态方程,确定Bang-Bang控制为最优边界控制策略。李轶舜等[2-3]通过探索MFD的基本特征,对拥堵网络提出了一种定时信号配时的边界控制方法。Haddad等[4-5]以两个交通小区为研究对象提出了一种最优边界控制方法, 即模型预测控制法(MPC),构建一个预测控制模型,最后以城市不同拥挤程度下MFD的稳定性作为分析指标。赵靖等[6]提出基于宏观基本图的相邻两个子区协调控制方法,建立控制子区间驶入驶出交通量的协调控制模型,通过博弈论分析了相邻子区之间的协调关系,提出了一种以两个子区整体运行效益最大化为目标的博弈控制逻辑及其求解流程。杜怡曼等[7]提出一种以基于宏观基本图的针对堵塞区域的边界交通反馈控制方法,用于改善饱和状态下的区域交通,对区域总量进行动态调控。丁恒等[8]提出了宏观交通网络拥堵区边界最优控制方法,提出了子区边界交叉口流量分配及信号配时参数优化方法。张逊逊等[9]提出了基于MFD的多子区协调控制策略,建立了基于MFD的多子区交通流模型,以提升路网的整体运行效益。
然而上述所有的控制策略,总体上都是在受控路网的边界交叉口进行流量控制,是一种确定性的边界控制方法。如果边界交叉口上游路段没有足够储存空间,可能会造成边界路口的上游路段排队溢出,这会扩大被控堵塞区的影响范围,降低边界外的路网运行效率。由于路网流量的变化,不同交叉口间距的差异,对交通流调控空间这方面的研究有所缺失。基于此,本研究将考虑边界控制的约束条件,以MFD为研究路网交通状态的工具,通过实时动态调整堵塞区域的控制边界,形成一种新的扩展边界,在扩展边界路口设置反馈“闸门”动态截流,限制车流进入堵塞区路网,提出一种可扩展的边界反馈控制策略,对拥堵区的边界控制可有效降低高峰期间堵塞区的拥堵程度,提高整个路网的疏散能力。
1 MFD对路网交通状态的辨识在智能交通条件下,对路网交通状态的刻画出现了一个新的量化工具MFD(Macroscopic Fundamental Diagram),即宏观基本图。它是客观存在的普遍规律,是路网的固有属性,可以从宏观层面监测路网运行状态[10-11]。根据MFD的相关理论[12],其有关参数的计算公式为:
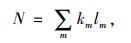
|
(1) |
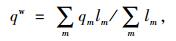
|
(2) |
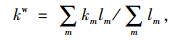
|
(3) |
式(1)~式(3)中,N为路网车辆数;qw,kw分别为加权流量、加权密度;m,lm分别为路段m和该路段长度;qm和km分别为路段m的流量和密度。
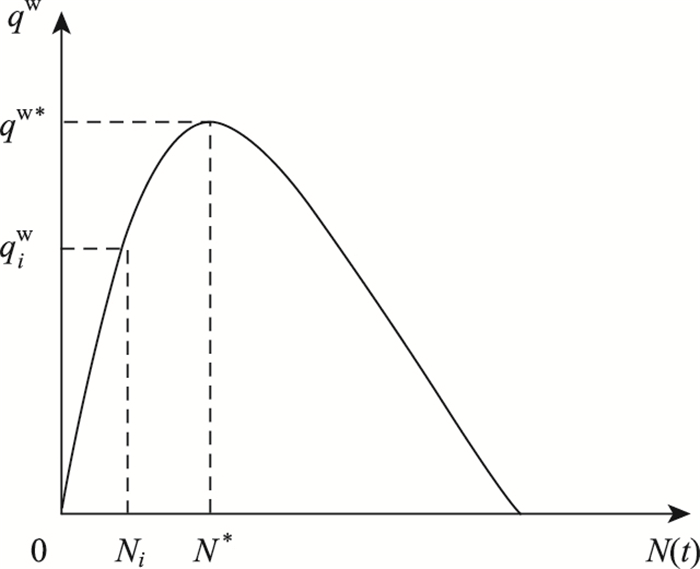
依据上述MFD计算公式,可以建立城市路网中加权流量(qw)与路网车辆数(N)之间的关系,如图 1所示。
|
| 图 1 路网宏观基本图 Fig. 1 MFD of road network |
| |
当N < N*(临界车辆数)时,路网处于非拥堵状态,随着N的增加,qw逐步增加,直到增至qw*最大加权流量)时,路网处于饱和状态;当N>N*(临界车辆数)时,路网处于过饱和状态,此时qw随着N的增加而减少。
根据MFD的曲线形状,为保证被控堵塞路网运行畅通,在实施边界控制时,路网累积车辆数N(t)应尽量保持在临界交通量N*以下,这样可以使得路网运行效益最大。
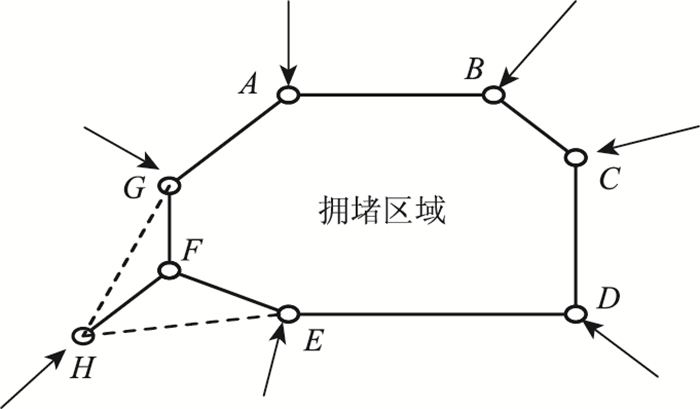
2 过饱和路网可扩展边界控制方法 2.1 可扩展边界控制的基本思路可扩展边界控制的思路是,根据智能交通检测系统确定路网发生拥堵状态,以拥挤交叉口或路段的相邻交叉口为节点,由这些节点虚拟连接围绕拥挤交叉口及其进出路段形成一个相对闭合的拥堵控制范围,各节点虚拟连线即为初始控制边界,如图 2所示,由此即决定边界控制规模的大小。依据MFD相关控制理论,为维持拥挤区路网内累积车辆数在一个最佳范围内,在边界节点路口设置反馈“闸门”动态截流,限制车流进入拥挤区路网[13-15],同时判断在控制边界节点路口受限车辆的排队情况,如果边界路口上游路段长度过短,没有足够的储存空间,此时若在该边界路口上设“闸门”截流,就容易引起此路口上游路段排队溢出,扩大被控堵塞区的影响范围,降低边界外路网运行效率,于是就将该处堵塞区边界外推至上游该路口,动态调整堵塞区的边界,形成一种新的扩展边界,在新的扩展边界路口设“闸门”截流。如图 2所示,由于边界路口F的上游路段FH过短,就将F控制路口外推至H,从而形成新的扩展边界A-B-C-D-E-H-G。这样,考虑边界路口上游路段的储存车队能力,建立边界控制的约束条件以及区域反馈控制模型,可实时动态调整堵塞区域的控制边界,避免边界路口上游路段出现排队溢出现象,有效降低高峰期间堵塞区的拥堵程度,提高整个路网的疏散能力。具体的可扩展边界控制流程如图 3所示。
|
| 图 2 受控区域可扩展边界示意图 Fig. 2 Schematic diagram of scalable boundary of controlled area |
| |
|
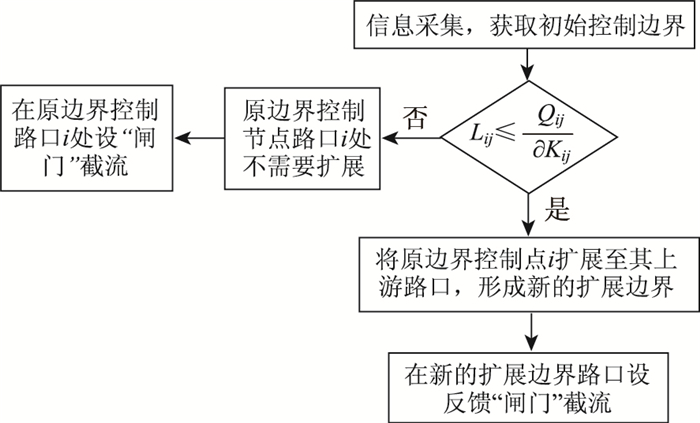
| 图 3 过饱和路网可扩展边界控制的流程图 Fig. 3 Flowchart of scalable perimeter control of oversaturated road network |
| |
2.2 建立边界控制约束条件,确定反馈“闸门”的控制位置
以上述图 2拥堵区域作为被控区域,A,B,C,D,E,F,G分别是被控区域的边界交叉口,AB,BC,CD,DE,EF,FG分别为被控区域的边界路段,图中箭头表示设置反馈“闸门”的位置。作为边界控制交叉口的上游路段必须要有足够能力存储车辆排队,保证不会发生排队溢出现象。
设边界交叉口i的周期时长为Ci,绿灯损失时间为Li,主要相关相位饱和流率为Si,相位车辆的到达率为qi,相位流量比与交叉口总流量之比为:wi=yi/Yi。
则在未启用反馈“闸门”控制的状态下,该主要相关相位每周期绿灯结束后剩余的车辆数为Qia:

|
(4) |
在n′周期内剩余的车辆数Qib:
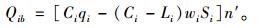
|
(5) |
在开启反馈“闸门”控制状态下,从第n+1到第n′周期内,每周期压缩绿灯时间为Δti,则每周期该相位增加排队车辆数为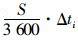
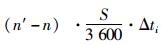
因此在实行反馈“闸门”控制后的第n′周期末,边界路口i的上游路段j的主要相关相位剩余的排队车辆数为:
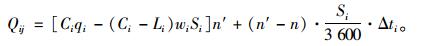
|
(6) |
由式(7)可以判断某边界交叉口i的上游路段j主要相关相位是否有足够能力存储排队车辆,满足式(7)的上游路段即有足够存储能力,便可以选择在此边界交叉口作为边界控制点,设反馈“闸门”截流。否则就将此边界路口外推至上游路口,从而形成新的扩展边界,在此扩展边界路口设反馈“闸门”动态截流。
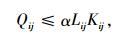
|
(7) |
式中,α为可靠性因子,α=(0, 1);Lij为边界交叉口i的上游路段j的长度;Kij为边界交叉口i的上游路段j的阻塞密度。可靠性因子α是为了边界交叉口上游路段主要相关相位存储车队能力有一定的安全余量而设置的,一般取0.8。
3 建立控制模型可扩展边界反馈“闸门”控制是根据路网宏观基本图MFD,对堵塞区路网交通运行状态进行监控,利用检测器返回的数据对进入被控区域车流量qin、区域内部车辆总数N、流出区域车流量qout进行监控,通过堵塞区扩展边界的流量控制,限制进入被控区域的车辆数,将区域内部车辆总数N维持在一个合理可行范围内,使得被控区域运行效益最高。控制模型结构如图 4所示。

|
| 图 4 区域控制逻辑结构图 Fig. 4 Structure diagram of regional control logic |
| |
(1) 输入ΔN(t)经过累积和时间延误得到:qin=qg(t-τ);其中, qg为通过闸门控制后的流量; t为时间参数; τ为时间延误(边界上游交叉口到达受控区域边界所需的延误时间)。
(2) 受控堵塞区域内车辆数的微小变化为:ΔN(t)=qin(t)-qout(t)。
(3) 根据路网宏观基本图,可以推导出关系式:qw(t)=F[N(t)]+ε(t),其中F为被控区域MFD的一个非线性的拟合函数,ε为MFD的一个拟合误差。
(4) 在区域控制模型中,假定流出被控区域车流量qout与区域加权流量qw成正相关: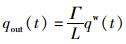
(5) 由于反馈“闸门”一般设置在被控区域的边界,只有当边界交叉口的上游路段过短易引起车辆排队溢出时,才设在靠近边界的上游交叉口,因此在模型求解中不考虑时间延误τ。于是将步骤(1),(3),(4)中的关系式代入步骤(2)中关系式,可以得到一个非线性的一阶函数:
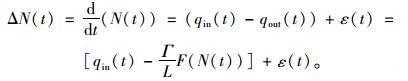
|
(8) |
令被控区域内车辆数微小变动ΔN(t)=0,将此方程在最优值:qin*=qout*和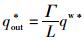
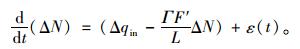
|
(9) |
由于在实际系统中是根据时间间隔计算的,于是将上述连续时间状态方程转换成离散形式如下:

|
(10) |
本研究采用Sioux Falls测试路网来验证上述可扩展边界控制方法的有效性,该网络有24个节点,76条边,网络基本参数以及待分配OD参见文献[16]。在该路网周边选取8个路口作为反馈“闸门”控制路口,通过式(7)考虑边界控制的约束条件,判断某边界交叉口i的上游路段j主要相关相位是否有足够能力存储排队车辆,从而确定该边界控制路口是否需外推至上游路口[17]。通过对这8个反馈门进行信号控制,维持路网内车辆数在一个最佳范围内,从而提高路网运行效率,如图 5所示。

|
| 图 5 研究区域反馈“闸门”示意图 Fig. 5 Schematic diagram of feedback "gate" of study area |
| |
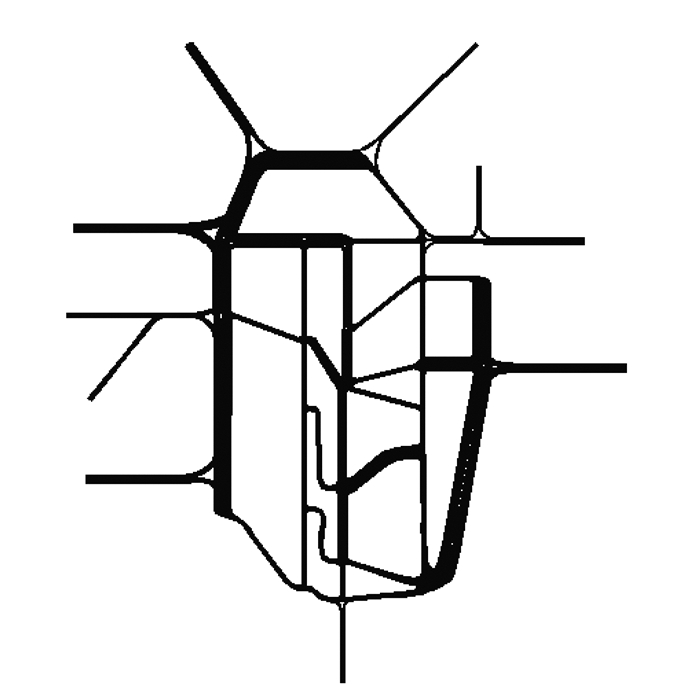
本研究通过德国PTV公式开发的Vissim交通仿真软件对Sioux Falls网络实施可扩展边界控制策略进行微观仿真。首先在仿真软件中建立Sioux Falls仿真路网,并按照图 5在路网的边界路口设置交通量出入口,如图 6所示。将路网OD需求,信号控制方案在路网仿真模型中设置。路网仿真模型中,每次仿真时间长度设为1 h,每隔10 s统计一次数据,统计数据包括各入口进入路网车流量、各出口流出路网车流量、各路段的流量、路网平均延误时间、路网平均速度、路网总延误时间。
|
| 图 6 测试路网边界路口进出流量控制示意图 Fig. 6 Schematic diagram of traffic flow control of boundary junction of test network |
| |
4.2 获得仿真路网的MFD,设定反馈“闸门”启动阈值
在进出路网的路段布设数据采集点,通过进口车道收集的数据减去出口车道的数据,就可以得到仿真时间间隔路网内部的车辆数,然后将Vissim的仿真输出结果导入Excel中进行初步处理,对仿真路网进行了多次仿真,得到路网加权流量与路网累积车辆数的关系如图 7所示。

|
| 图 7 仿真路网MFD散点拟合图 Fig. 7 MFD scatter fitting diagram of simulation network |
| |
图 7为此试验仿真网络数据叠加的MFD散点拟合图,通过Matlab对散点图进行函数拟合,发现该系列数值点符合二次函数曲线形式。拟合函数如式(11)所示,准确度到达0.85以上。
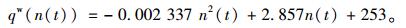
|
(11) |
从仿真路网的MFD散点拟合图中,可以看出横轴表示测试路网的累积车辆数,即每隔一段时间内在路网中出现过的总交通量,纵轴表示测试路网的加权车流量,即对每一段时间内通过部分路段的净车公里数与路段总长度的比值。从图中可以看出,在仿真初始阶段,由于路段上车辆较少,路网加权流量随网络中累积车辆数的增加而逐渐增加;当路网累积交通量达到N*时,路网加权流量达到最大值qw*,此时区域路网达到饱和状态,之后如果路网中的累积车辆数持续增加时,路网加权流量反而呈现下降的趋势,这表明网络已经开始出现拥堵,处于过饱和的状态[18]。从图 7可以看出,当仿真区域内的机动车流量达到600辆左右时,区域路网的加权流量最大,因此该区域的控制阈值就被确定下来。
本研究的可扩展边界控制策略就是在路网将要达到饱和状态时,考虑边界控制的约束条件,确定反馈“闸门”设置位置,实时动态调整堵塞区控制边界,形成新的扩展边界,通过在路网扩展边界交叉口设置反馈“闸门”截流,限制进入路网的车辆流入率,使路网在接近饱和状态下运行较长一段时间,这样就可以缓解网络交通拥堵,提高路网疏散能力。
4.3 可扩展边界控制策略仿真及结果分析本研究通过对测试路网进行多次仿真,得到其MFD,从MFD中可以得到该测试路网的控制阈值为600辆,即当路网内车辆数为600辆左右时,网络的通行效率最高,疏散能力最大。如图 5所示,在仿真过程中,不实施边界调整的路网原边界由A-B-C-D-E-F-G-H构成,考虑路网边界路口上游路段的储存能力,由式(6)和式(7)可得,边界控制点G处的上游路段p长度LGp=200 m,调控的前5个周期内,其主要相关相位剩余排队车辆数为:QGp=30 pcu,取∂=0.8,KGp=KCq=160 pcu/km,同理边界控制点C处的上游路段q的长度LCq=215 m,调控的前5个周期内,其主要相关相位剩余排队车辆数为:QCq=36 pcu,由此算得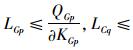
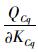
| 路网平均延误时间/s | 路网平均速度/(km·h-1) | 路网平均出行时间/s | 路网平均停车次数/s | 离开路网车辆数/辆 | |
| 无边界控制 | 242.67 | 23.24 | 435.38 | 6.85 | 2 560 |
| 确定性边界控制 | 179.34 | 28.375 | 392.78 | 5.41 | 2 761 |
| 扩展边界控制 | 158.57 | 30.22 | 372.05 | 4.79 | 2 891 |
| 改善程度/% | 34.66 | 30.03 | 14.55 | 30.07 | 12.93 |
从表 1可以看出,对路网不实施控制时,路网的平均延误时间为242.67 s,路网平均速度为23.24 km/h,路网平均出行时间为435.38 s,路网平均停车次数为6.85次,离开路网的车辆数为2 560辆,在实施确定性边界控制时,各项指标均有小幅改善,但是由于边界路口C和G的上游路段过短,造成排队溢出,引起边界外效率降低。在实施可扩展边界控制策略后,路网平均延误时间降低了34.66%,路网平均速度提高了30.03%,路网平均出行时间减少了14.55%,平均停车次数也减少了30.07%,离开路网的车辆数增加了12.93%。仿真结果表明,当路网趋于饱和时,在路网边界实施可扩展边界控制策略后,路网的各项交通信号控制指标均有明显改善,并且不影响边界外的路网运行效率。
5 结论(1) 建立了边界控制的约束条件,考虑边界路口上游路段的储存车队能力,实时动态调整堵塞区域的控制边界,形成一种新的扩展边界。
(2) 建立了区域反馈控制模型,通过在路网的扩展边界路口设置反馈“闸门”控制网络流入量,限制车流进入堵塞区路网,将网络车辆总数维持在其合理可行范围内,以提高路网运行效率。
(3) 仿真结果表明,基于MFD的路网可扩展边界控制方法,能有效缓解路网内部交通拥堵,路网的各项交通信号控制指标均有明显改善,提升路网的整体运行效益。
| [1] |
张勇, 白玉, 杨晓光. 城市道路交通网络死锁控制策略[J]. 中国公路学报, 2010, 23(6): 96-102. ZHANG Yong, BAI Yu, YANG Xiao-guang. Strategy of Traffic Gridlock Control for Urban Road Network[J]. China Journal of Highway and Transport, 2010, 23(6): 96-102. |
| [2] |
LI Yi-shun, XU Jian-min, SHEN Lü-ou. A Perimeter Control Strategy for Oversaturated Network Preventing Queue Spillback[J]. Procedia-social and Behavioral Sciences, 2012, 43: 418-427. |
| [3] |
李轶舜, 徐建闽, 王琳虹. 过饱和交通网络的多层边界主动控制方法[J]. 华南理工大学学报:自然科学版, 2012, 40(7): 27-32. LI Yi-shun, XU Jian-min, WANG Lin-hong. Active Multi-layer Perimeter Control Strategy of Oversaturated Traffic Networks[J]. Journal of South China University of Technology:Natural Science Edition, 2012, 40(7): 27-32. |
| [4] |
HADDAD J, RAMEZANI M, GEROLIMINIS N.Model Predictive Perimeter Control for Urban Areas with Macroscopic Fundamental Diagram[C]//American Control Conference, 2012. Montreal, Canada: IEEE, 2012.
|
| [5] |
GEROLIMINIS N, HADDAD J, RAMEZANI M. Optimal Perimeter for Two Urban Regions with Macroscopic Fundamental Diagram:A Model Predictive Approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(1): 348-359. |
| [6] |
赵靖, 马万经, 汪涛, 等. 基于宏观基本图的相邻子区协调控制方法[J]. 交通运输系统工程与信息, 2016, 16(1): 78-84. ZHAO Jing, MA Wan-jing, WANG Tao, et al. Coordinated Perimeter Flow Control for Two Subareas with Macroscopic Fundamental Diagrams[J]. Transportation System Engineering and Information Technology, 2016, 16(1): 78-84. |
| [7] |
杜怡曼, 吴建平, 贾宇涵. 基于宏观基本图的区域交通总量动态调控技术[J]. 交通运输系统工程与信息, 2014, 14(3): 162-167. DU Yi-man, WU Jian-ping, JIA Yu-han. MFD-Based Regional Traffic Volume Dynamic Control[J]. Transportation System Engineering and Information Technology, 2014, 14(3): 162-167. |
| [8] |
丁恒, 郑小燕, 张宇, 等. 宏观交通网络拥堵区边界最优控制[J]. 中国公路学报, 2017, 30(1): 111-120. DING Heng, ZHENG Xiao-yan, ZHANG Yu, et al. Optimal Control for Traffic Congested Area Boundary in Macroscopic Traffic Network[J]. China Journal of Highway and Transport, 2017, 30(1): 111-120. |
| [9] |
张逊逊, 许宏科, 闫茂德. 基于MFD的城市区域路网多子区协调控制策略[J]. 交通运输系统工程与信息, 2017, 17(1): 98-105. ZHANG Xun-xun, XU Hong-ke, YAN Mao-de. Coordinated Control Strategy for Multi-subarea Based on MFD in Urban Zonal Road Networks[J]. Transportation System Engineering and Information Technology, 2017, 17(1): 98-105. |
| [10] |
GEROLIMINIS N, DAGANZO C F. Existence of Urban-scale Macroscopic Fundamental Diagrams:Some Experimental Findings[J]. Transportation Research Part B:Methodological, 2008, 42(9): 759-770. |
| [11] |
DAGANZO C F. Urban Gridlock:Macroscopic Modeling and Mitigation Approaches[J]. Transportation Research Part B:Methodological, 2007, 41(1): 49-62. |
| [12] |
GEROLIMINIS N, DAGANZO C F.Macroscopic Modeling of Traffic in Cities[C]//Transportation Research Board 86th Annual Meeting.Washington, D. C.: Transportation Research Board, 2007: 413.
|
| [13] |
LEBLANC L J. An Algorithm for the Discrete Network Design Problem[J]. Transportation Science, 1975, 9(3): 183-199. |
| [14] |
KEYVAN-EKBATANI M, KOUVELAS A, PAPAMICHAIL I, et al. Exploiting the Fundamental Diagram of Urban Networks for Feedback-based Gating[J]. Transportation Research Part B:Methodological, 2012, 46(10): 1393-1403. |
| [15] |
KEYVAN-EKBATANI M, PAPAGEORGIOU M, PAPAMICHAIL I. Urban Congestion Gating Control Based on Reduced Operational Network Fundamental Diagrams[J]. Transportation Research Part C:Emerging Technologies, 2013, 33(4): 74-87. |
| [16] |
ABOUDOLAS K, GEROLIMINIS N. Perimeter and Boundary Flow Control in Multi-reservoir Heterogeneous Networks[J]. Transportation Research Part B:Methodological, 2013, 55(9): 265-281. |
| [17] |
刘澜, 马亚峰. 基于出入流率的交通拥挤量化研究[J]. 公路交通科技, 2013, 30(3): 111-118. LIU Lan, MA Ya-feng. Traffic Congestion Measurement Based on Inflow and Outflow Rates[J]. Journal of Highway and Transportation Research and Development, 2013, 30(3): 111-118. |
| [18] |
JI Y, GEROLIMINIS N.Spatial and Temporal Analysis of Congestion in Urban Transportation Networks[C]//Transportation Research Board 90th Annual Meeting. Washington, D.C.: Transportation Research Board, 2011: 1791-1808.
|
 2018, Vol. 35
2018, Vol. 35
